3555. 二叉树（北京邮电大学考研机试题）

3555. 二叉树

⭐️难度：简单（其实困难）

⭐️类型：树

📖题目：题目链接

输入样例：

1

8 4

2 3

4 5

6 -1

-1 -1

-1 7

-1 -1

8 -1

-1 -1

1 6

4 6

4 5

8 1

输出样例：

2

4

2

4

🌟思路：

先试着把样例中的树画出来：

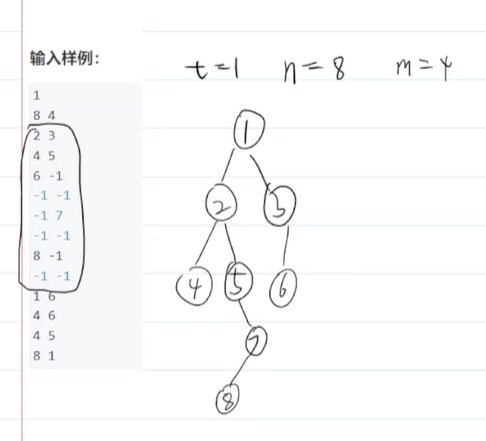
再思考怎么找两个结点的最小距离。

第一种情况：2和8的距离，2已经在8的路径上了，很容易算得2到8的距离；

第二种情况：4和8的距离，4和8不在同一条路径上，此时需要找4和8路径共同的交点 ，也就是2，再计算4到2的距离+8到2的距离。

步骤：

1️⃣先构造树

2️⃣找到结点到根的路径

3️⃣找交点

4️⃣总结规律

笔记：

📚题解：

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<vector>  // vector不需要.h
#include<list>
#include<set>  // // 可以用 set 和 multiset
#include<unordered_set> // 可以用 unordered_set 和 unordered_multiset
#include<map>  // 可以用 map 和 multimap
#include<unordered_map> // 可以用 unordered_map 和 unordered_multimap
#include<algorithm>
#include<string>
#include<iostream>
#include<queue>
#include<stack>

using namespace std;


struct TreeNode {
    int num;
    TreeNode* left; 
    TreeNode* right;
    TreeNode* parent;  // 因为要沿上找路径，定义parent会更方便
};

int main() {
 
    int t;
    scanf("%d", &t);
    for (int i = 0;i < t;i++) {
        int n, m;
        scanf("%d%d", &n, &m);

        vector<TreeNode*> nodearr(n + 1);  // 定义n+1空间，方便与结点编号对应
        for (int j = 1;j <= n;j++) {
            nodearr[j] = new TreeNode;
            nodearr[j]->num = j;
        }

        nodearr[1]->parent = NULL;

        // 构建树
        for (int j = 1;j <= n;j++) {  // 输入n组数据
            int left,right;
            scanf("%d%d", &left, &right);
            if (left != -1) {
                nodearr[j]->left = nodearr[left];   // 第i行输入表示第i个结点左右孩子的情况
                nodearr[left]->parent = nodearr[j];
            }
            else {
                nodearr[j]->left = NULL;
            }
            if (right != -1) {
                nodearr[j]->right = nodearr[right];
                nodearr[right]->parent = nodearr[j];
            }
            else {
                nodearr[j]->right = NULL;
            }
        }

        int lhs, rhs;
        for (int j = 0;j < m;j++) {  // 输入m组待测数据
            scanf("%d%d", &lhs, &rhs);
            vector<int> lvec;  // 存所给第一个结点的路径
            TreeNode* p = nodearr[lhs];
            while (p != NULL) {
                lvec.push_back(p->num);
                p = p->parent;
            }
            vector<int> rvec;  // 存所给第二个结点的路径
            p = nodearr[rhs];
            while (p != NULL) {
                rvec.push_back(p->num);
                p = p->parent;
            }

            // 找交点
            int l = lvec.size() - 1;
            int r = rvec.size() - 1;
            while (true) {
                if (l < 0 || r < 0|| (lvec[l] != rvec[r])) {  // 没有找到公共点 或 左结点和右节点到公共交点前一个结点
                    break;
                }
                l--;
                r--;
            }
            printf("%d\n", l + r + 2);
        }

    }

    

    return 0;
}