2026年寒假牛客训练赛补题（二）

写在前面

笔者是大二ACM选手，正在打牛客寒假训练赛，每一场都会写一个能力范围的补题博客

今天要补的是2月5号场，非常幸运的是这一场题面还有PDF

（笔者写这篇的时间是第四场，第三第四场题面都没有PDF了）

今天要补的题是异或和贪心、思维+推式子、构造

注：本篇博客题面来自于牛客训练赛，题解参考牛客竞赛

比赛链接：https://ac.nowcoder.com/acm/contest/120562

F

题面

注：题面来自牛客竞赛，仅个人补题使用

解释一下题意，就是说指定一个整数，然后要找到两个数，保证这两个数的最大公约数是指定的数，并且要使这两个数按位异或的结果最小

按位异或是二进制运算，就是二进制下，同一位相同为0，不同为1

解题思路：

规定x!=y，所以x和y应该是n的不同倍数，明确按位异或有一个性质：|x-y|<=x^y

现在证明一下，规定x>y，将x和y化为二进制，针对每一位讨论

规定xi,yi为每一位的数字，若当前位xi=1,yi=0，则异或和相减结果一致

若当前位xi=0,yi=0或xi=1,yi=1，异或和相减结果也一致

若当前位xi=0,yi=1，这一位结果仍一致，但是后边至少有一位会因为借位导致相减结果小于异或

因此相减结果小于等于异或

有了这个结论这道题就简单了，已知x和y是n的不同倍数，则他们最小相差n，题目要求找到x^y的最小值，则有n<=|x-y|<=x^y，所以x^y最小为n

x^y为n且都是n的倍数很好构造：n000000和nn这种二进制格式即可

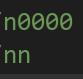明显异或结果为n，且都是n的倍数，注意这里的n是n的二进制形式

代码：

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

void solve() 
{
	/*
	n00000
	nn
	异或得n
	*/
	ll n;
	cin>>n;
	ll temp=n;
	ll num=0;
	while(temp!=0)
	{
		temp/=2;
		num++;
	}
	cout<<(n<<num)<<" "<<((n<<num)+n)<<endl;
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll t = 1;
	cin >> t;
	while (t--) 
	{
		solve();
	}
	return 0;
}

H

题面

解释一下题意：

输入一个数组，然后通过题面中的方法来计算所有子数组的权值之和

计算一个区间权值的规则为：遍历整个区间，每遍历到一个元素，都要加上从区间左端点到这个元素的出现的不同元素的个数

思路：

想要计算所有子数组的权值之和，可以考虑单个元素能对权值产生的贡献和

针对某一个位置的元素，它能够产生的贡献取决于前边有没有出现过这个元素，若没出现过，那么这个元素可以对整个数组所有包含它的子数组都产生一个贡献，若前边出现过相同元素，那么这个元素可以对左端点从相同元素开始的所有包含它的子数组产生一个贡献，以此类推，就可以算出贡献和

子数组的左右端点都是可以移动的，明显的，左端点的移动并不影响这个元素产生的贡献，只影响结果的种数，而右端点每往右移一个长度，元素就多产生一个贡献，同时影响结果的种数

规定该元素的位置为i，上一个相同元素出现的位置是j

可以计算单个元素产生的贡献：

若右端点一个一个移动的话，可以发现产生的贡献是等差数列，即1，2，3，......n-i+1

右端点移动得种数是（n-i+1）种，所以结果就是种数*等差数列之和，即(n-i+1)*(1+n-i+1)/2

再乘上左端点的种数，就是单个元素产生的贡献

单个元素产生的贡献即为：(i-j)*(n-i+1)*(1+n-i+1)/2

遍历所有元素累加就能得到答案

代码：

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=1e9+7;

void solve() 
{
	ll n;
	cin>>n;
	vector<ll>a(n+1);
	map<ll,vector<ll>>p;
	for(int i=1;i<=n;i++) 
	{
		cin>>a[i];
		p[a[i]].push_back(i);
	}
	ll sum=0;
	for(auto &[i,j]:p)
	{
		j.insert(j.begin(),0);
		for(int k=1;k<j.size();k++)
		{
			sum+=(j[k]-j[k-1])*(n-j[k]+1)*(1+n-j[k]+1)/2;
		}
	}
	cout<<sum<<endl;
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll t=1;
	cin>>t;
	while(t--) 
	{
		solve();
	}
	return 0;
}

E

题面

题意解释

若一个矩阵由01构成，且所有行的单行数字和由0~n-1的排列组成，所有列的单列数字和由0~n-1的排列组成，且0的连通块个数和1的连通块个数总和恰好为n个，这个矩阵就叫好矩阵

现在指定矩阵边长，要求输出一个好矩阵、

思路：

这道题其实只是看着麻烦，实际上很好构造，很多人都是看到题觉得太麻烦就不做了，包括我在内

赛后看了官方题解，方法是很多的

这里解释官方的两种方法：

方法一

先保证行和列的要求：

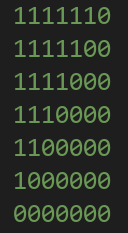这种阶梯型，明显符合行和列的要求，但是连通块还没有构造

我们可以把0全部联通，然后把1拆成n-1个连通块，由图可知，1一共有6行，刚好能拆成6个连通块

具体构造可以这样：横着隔开，把偶数行取出来然后纵着放，纵着也隔一行

这样构造是符合连通块的条件的

可能有人疑惑为什么行和列的要求没有被破坏，我们来证明一下：

将第二行抠出来的话，第二行和为0，放在倒数第二列，这样倒数第一列和仍是0，同时因为从上向下扣，没扣一行这行基础和为0，但是因为列的放置，从下向上，和依次变成3、2、1，奇数行在加上2和1之后凑出了4和5，列也同理保持了0~6的排列

方法二

参考样例给的对称型构造：

这种构造核心在于以对角线为轴的轴对称

例如：

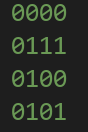
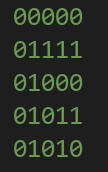
这样明显可以保证行和列的和这一限制

连通块的限制也很明显，一层一层作为不同的连通块，所以这样构造也可

代码：

这里仅附方法二的代码：

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=1e9+7;

void solve() 
{
	/*
	00000000
	01111111
	01000000
	01011111
	01010000
	01010111
	01010100
	01010101
	*/
	ll n;
	cin>>n;
	vector<vector<ll>>vec(n+1,vector<ll>(n+1));
	ll temp=n;
	while(n!=0)
	{
		for(int i=temp-n;i<temp;i++)
		{
			if((temp-n)%2==0) vec[temp-n][i]=0;
			else vec[temp-n][i]=1;
		}
		for(int i=temp-n;i<temp;i++)
		{
			if((temp-n)%2==0) vec[i][temp-n]=0;
			else vec[i][temp-n]=1;
		}
		n--;
	}
	for(int i=0;i<temp;i++)
	{
		for(int j=0;j<temp;j++)
		{
			cout<<vec[i][j];
		}
		cout<<endl;
	}
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll t=1;
	//cin>>t;
	while(t--) 
	{
		solve();
	}
	return 0;
}

篇末总结

这场比赛对我来说难度还是有点高，补完这三道我也就是六题水平，E赛时多想想其实有机会开出来的，平时也做过比这个更难的构造，H这种正难则反的思想还是太完美了，这道题给我的启发也很大，至于F题，则是那个结论的证明算一个难点