【C++】树的基础

1.引言

不好意思这段时间没更编程，现在开始更了！

我们从今天开始，C++要进入数据结构的环节了，数组啥的都学过了，那我必须拿树来打头阵。这是一个十分著名的数据结构，我们平时生活中也经常用到树形图来统计一些数据，那么我们来讲一下编程里面的树是什么样子的！

2.树的概念

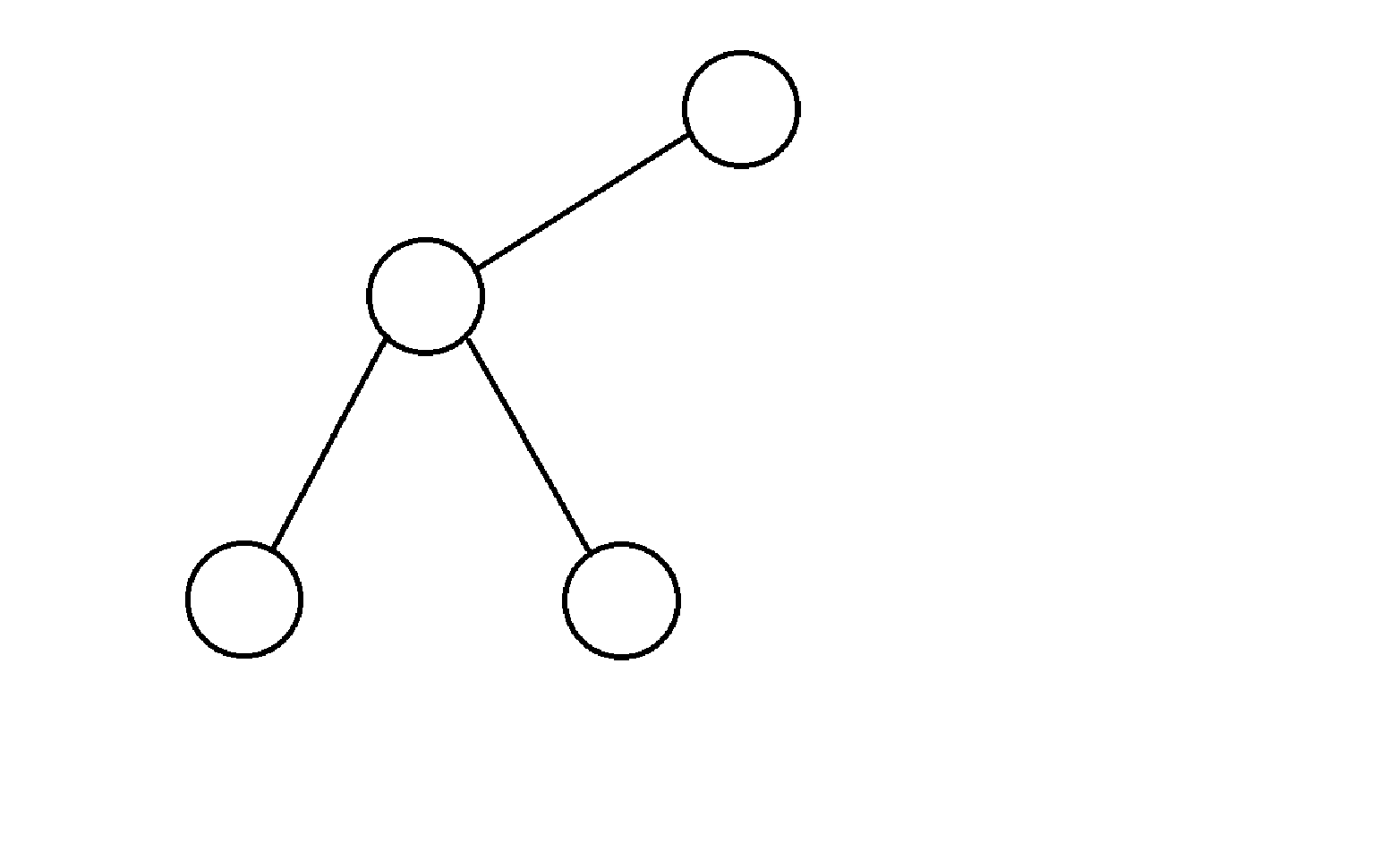
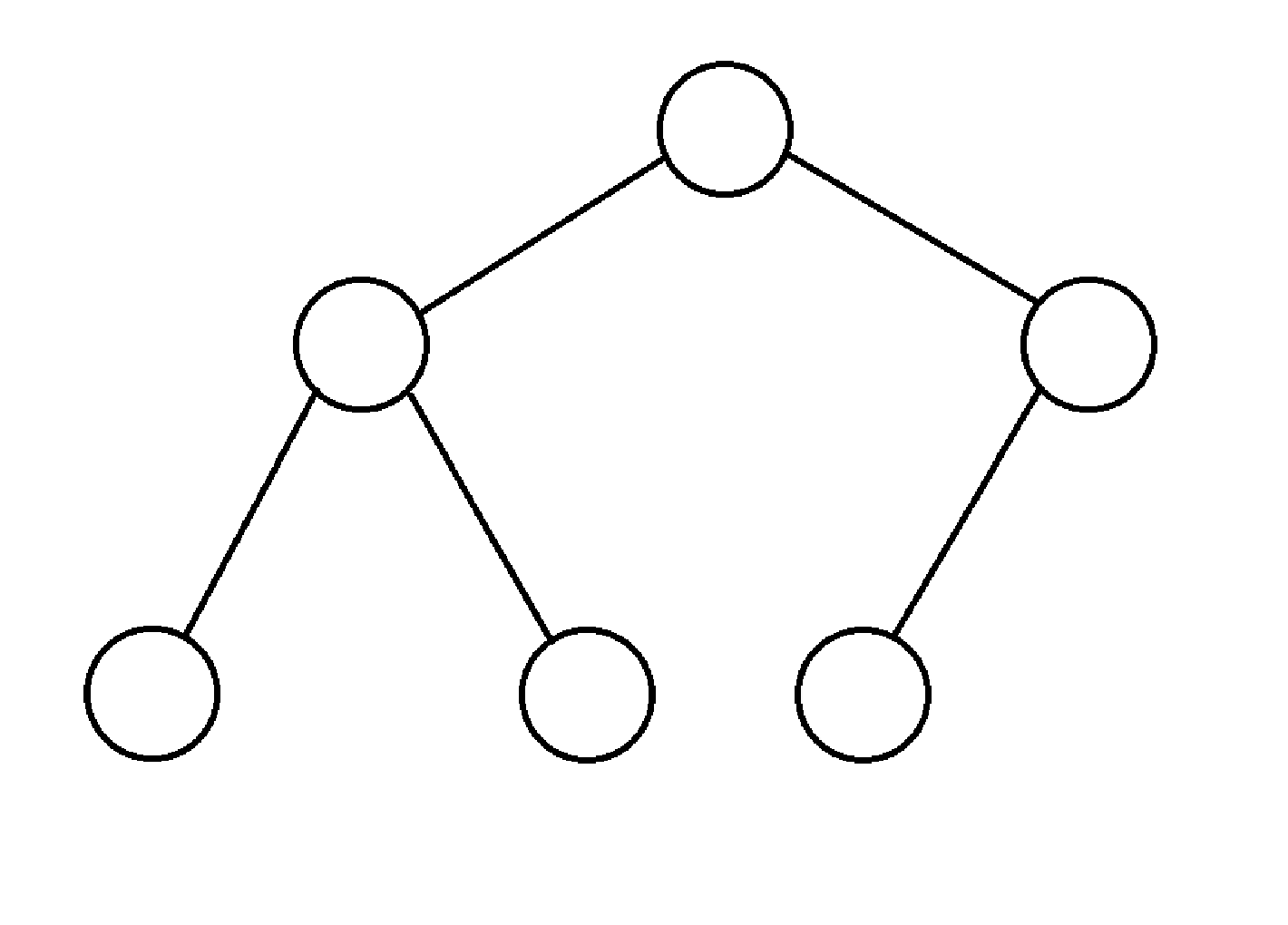
首先，树是由一些节点构成的，例如（纯手绘，略有粗糙，请见谅）：

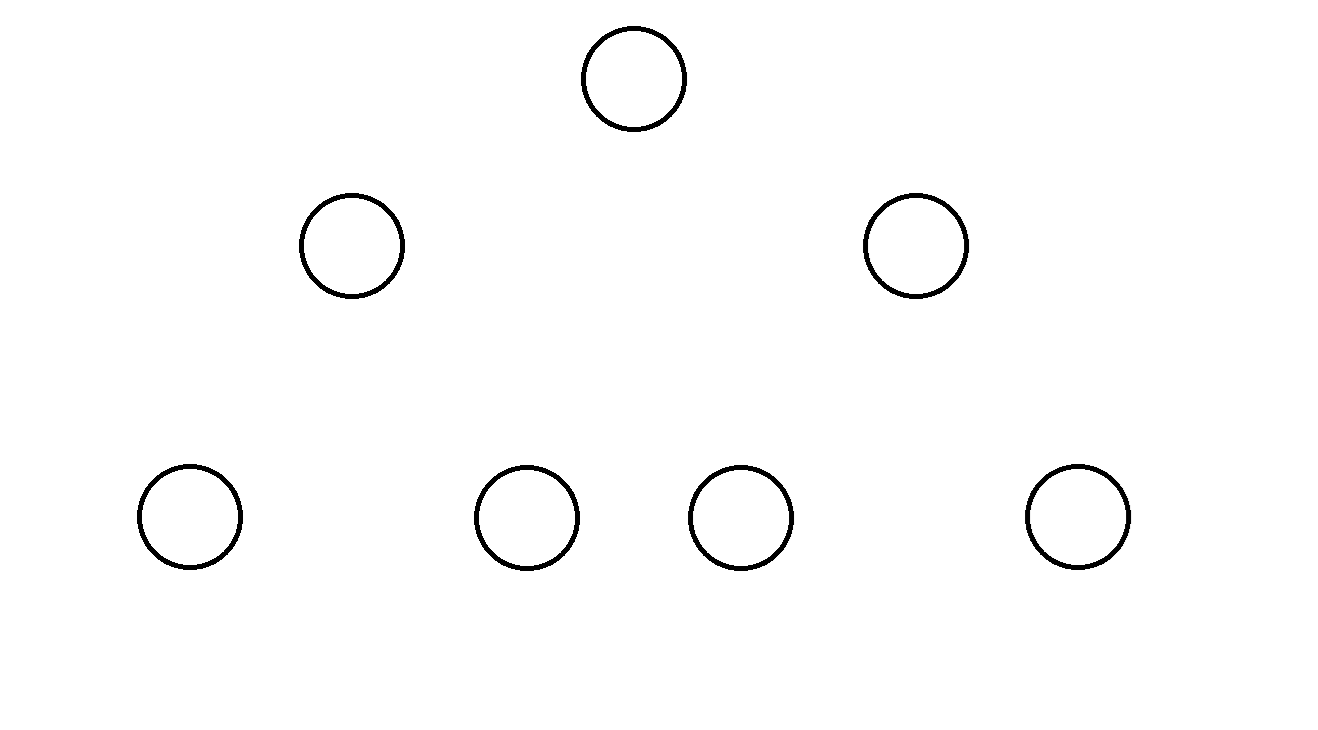
但是，这样的话这些节点就会显得十分零散，所以我们得用一些线把它们给串起来：

这样，我们就得到了一棵树，我们先来说一下树的一些基本概念。

最上面的一个节点叫做根节点。

一棵树的层数叫做树的深度。

每个节点下一层能够直接通往的节点叫做这个节点的孩子节点。

一个节点的孩子数量称为这个节点的度。

一棵树的若干个节点里面，度最大的节点，这个节点的度就是这棵树的度。

一棵树上面能通过一条连接线直接到达的节点叫做这个节点的父节点或双亲节点。

一个节点上面能到达的所有节点叫做这个节点的祖先节点。

一个节点下面能到达的所有节点叫做这个节点的孙子节点。

一个节点和它同一层的所有节点叫做这个节点的兄弟节点。

一个没有孩子的节点叫做叶子节点。

例如上面的这棵树的深度就是3，度就是2。

然后，从树的根节点到下面任意一个节点都只有一条路径，如果由多条路径就不叫树了，叫图，例如：

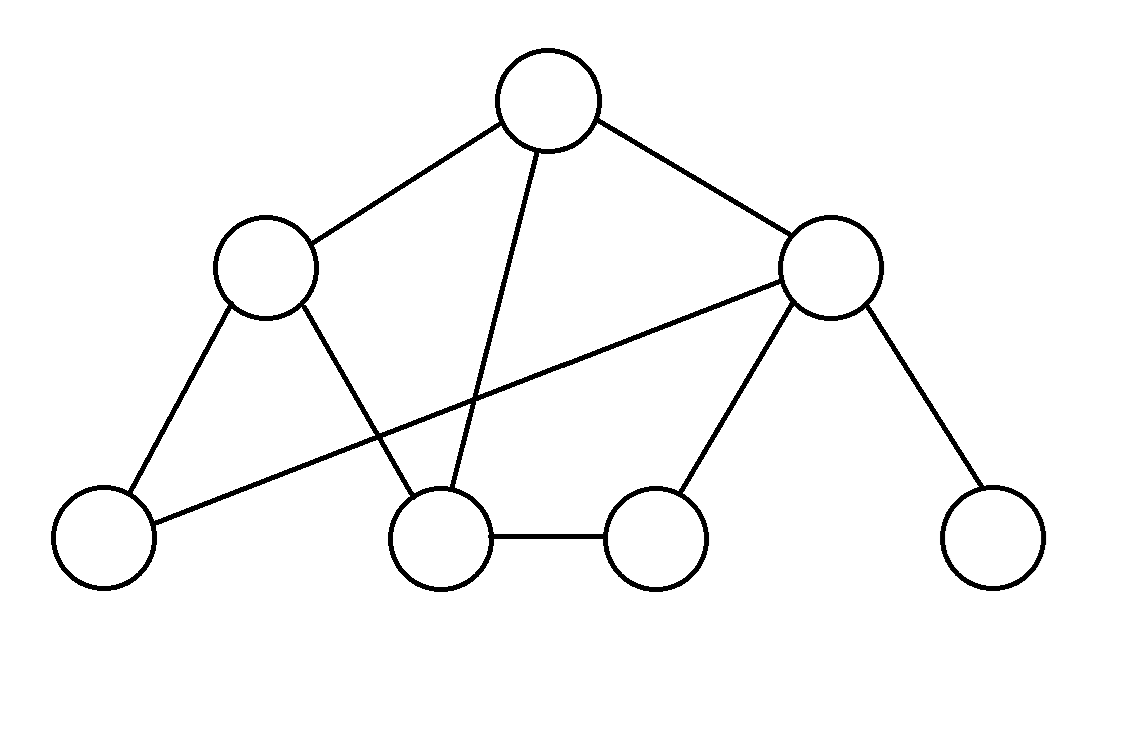
这就是一个图，因为它的节点到另一个节点的路径≥1。

我们就不在这种树上面浪费时间了，这种普通的树不重要，以后再讲，我们先讲一种重要的树。

3.二叉树

3.1 二叉树的概念

二叉树就是一种度≤2的树，例如上面的那一棵树就是二叉树。下面是二叉树独有的一些概念：

二叉树一个节点最多只有两个孩子，左边的叫左孩子，右边的叫右孩子。

二叉树的两个孩子只能在节点的左右两边，不能在中间。

二叉树里面度为2的节点刚好比叶子节点多1个，写成公式就是。

二叉树里面最多有（k是树的深度）个节点。

二叉树里面最多有（k是树的深度）个叶子节点。

相比大家对于二叉树的概念已经很了解了，那么我们再来认识两种特殊的二叉树：

满二叉树 和完全二叉树。

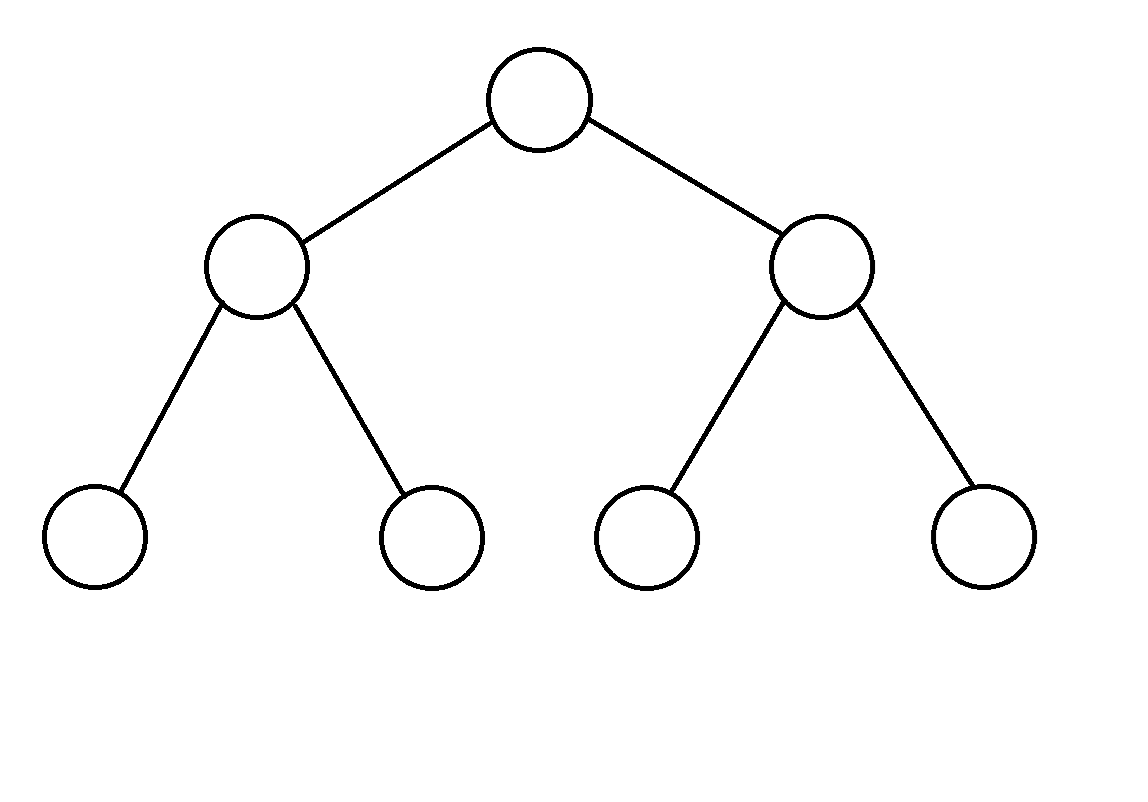
满二叉树是指一共有个节点的二叉树。用大白话讲，就是这个二叉树能插进去节点的空位都插进去了节点，里面每个空位都有节点。

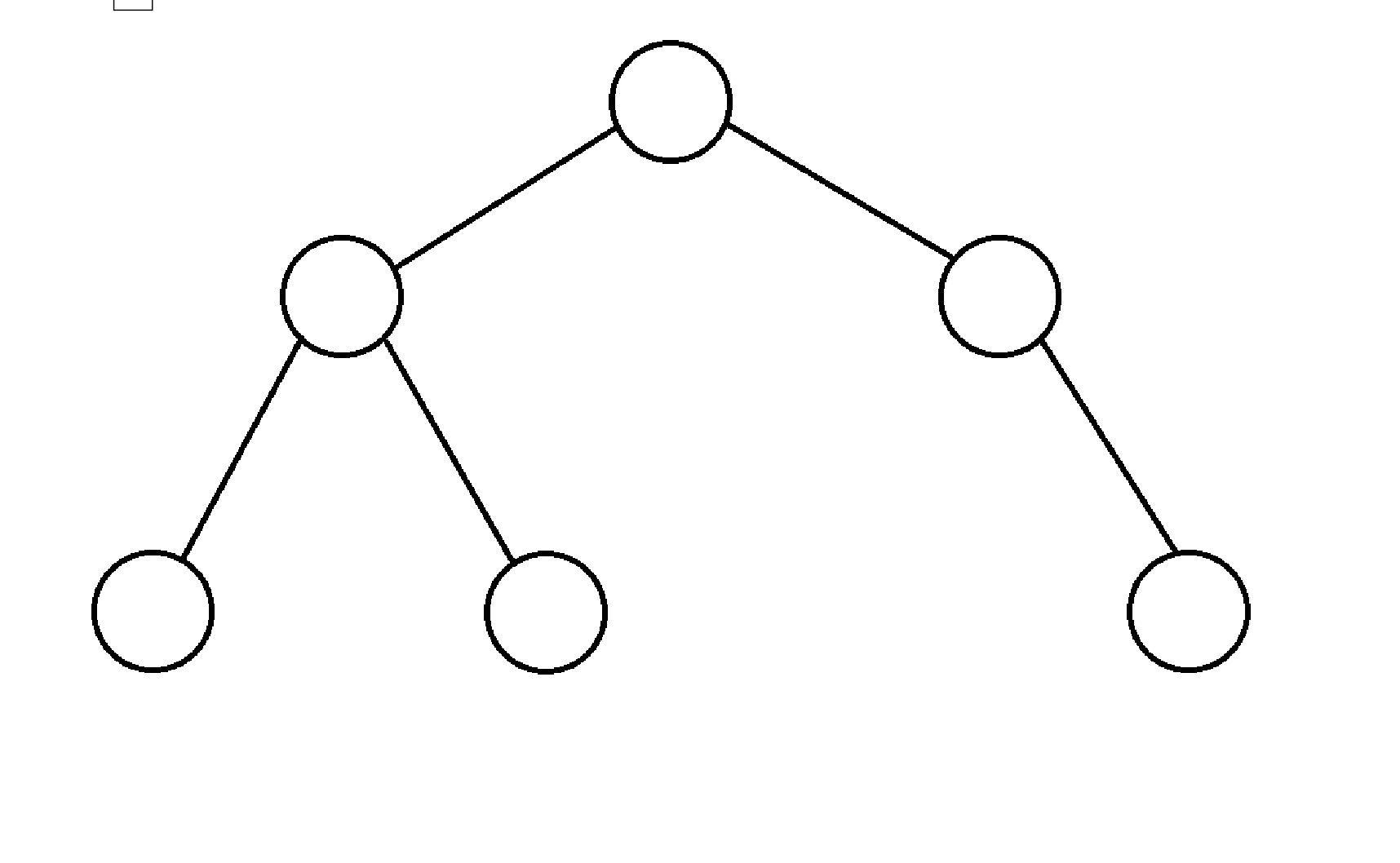
完全二叉树是再满二叉树的基础上，再下面再增加一些连续的节点的二叉树。这个描述有亿点儿抽象哈，所以我们来一张图来描述一下：

这就是一棵完全二叉树，而：

这两个就不是完全二叉树，因为第一个最后一行不是连续的，第二个虽然最后一行是连续的，但是上面不是一棵满二叉树，这样就很直观，应该都能看懂吧！看不懂评论区聊聊，我七日之内必回！

3.2 二叉树的构建

3.2.1 数组实现

那么我们知道了二叉树是一个什么东西，那么我们就要学习二叉树如何去用代码实现了。毕竟我这篇文章不是专门讲数据结构的，是讲C++的。

我们首先讲如何去用数组实现哈！

我们要用数组去实现二叉树，那么我们就必须知道一个事情，那就是数组是一种线性的数据结构，是一片连续的空间，里面的所有数据都是通过下标来实现的，那么我们要构建二叉树，就要通过节点与节点之间的父子关系，这种表示方式叫做父亲孩子表示法。

首先，一个节点的左孩子 的下标是（i是当前节点的下标），右孩子 是。如果是叶子节点的话，那么这两个节点就会越界，但是这样表示就会有一个弊端：

问题是三号节点（即根节点的右孩子）的左孩子该如何表示呢？毕竟这不是一棵树的最后一个节点，而是倒数第二个节点，所以我们不能直接结束，所以这个时候我们通常用0或者-1来表示，但是这样就白白浪费了一个空间，所以这种方式我并不提倡，而且代码毫无技术含量，我就不写了，如果想要就私信我，我看到了七日之内必把代码给你！

3.2.2 结构体指针实现

这是我比较提倡的一种方式，虽然代码可能会略有一些复杂，但是它是如果一个节点有孩子，就创建一个树的节点，如果没有孩子，那么就设为nullptr，防止野指针的出现。

但是毕竟一个节点的孩子也是可能有孩子的，所以我们就要进行一个嵌套：

cpp 复制代码

struct TreeNode {
    int val;  // 节点的值
    TreeNode left, right;  // 左孩子和右孩子
};

为什么左孩子和右孩子也要用TreeNode类型呢，左孩子和右孩子也是有val、left和right的。

但是，如果你就这么写的话，那么，恭喜你，喜提一个CE或RE（编译错误或运行时错误）！

因为C++的底层代码逻辑是不允许结构体内调用自己的，这种结构体内的"递归"会导致它永远都没有一个头，会超时或者栈溢出，所以我们不能直接这样，要用指针的形式：

cpp 复制代码

struct TreeNode {
    int val;  // 节点的值
    TreeNode* left;  // 左孩子，用结构体指针的形式定义
    TreeNode* right;  // 右孩子，用结构体指针的形式定义
};

这样就不会出现无限调用的问题了。具体原因到后面的时候再讲，这里讲就太深奥了。

但是我们这样还是不行，因为如果定义的时候直接这样：

cpp 复制代码

TreeNode* root;

那么在使用的时候就会被判定为野指针，然后就报错了！

所以我们必须得给他初始化，我们要用到一个叫new的东西，首先，我们要在结构体里面加一个这样的东西：

cpp 复制代码

struct TreeNode {
    int val;  // 节点的值
    TreeNode* left;  // 左孩子，用结构体指针的形式定义
    TreeNode* right;  // 右孩子，用结构体指针的形式定义
    TreeNode(int n) : val(n), left(nullptr), right(nullptr) {}  // 初始化函数
};

然后我们这样：

cpp 复制代码

TreeNode* root = new TreeNode(n);  // n是一个变量，这样root->val就是n了

这样做等同于：

cpp 复制代码

TreeNode* root;
root->val = n;
root->left = nullptr;
root->right = nullptr;

但是这样更加简单。

3.3 二叉树的遍历

3.3.1 二叉树遍历分类

我们讲完了如何构建一棵二叉树，那么我们就要来遍历它，要不然构建了遍历不了，那还不如不构建。

二叉树的遍历分为四种：前序遍历 、中序遍历 、后序遍历 和层序遍历。

我们主要学习前三种，因为层序遍历就是数组构建二叉树顺序输出的结果。

3.3.2 前序遍历

前序遍历的主要遍历方法为根左右，它遍历一棵二叉树的顺序如下：

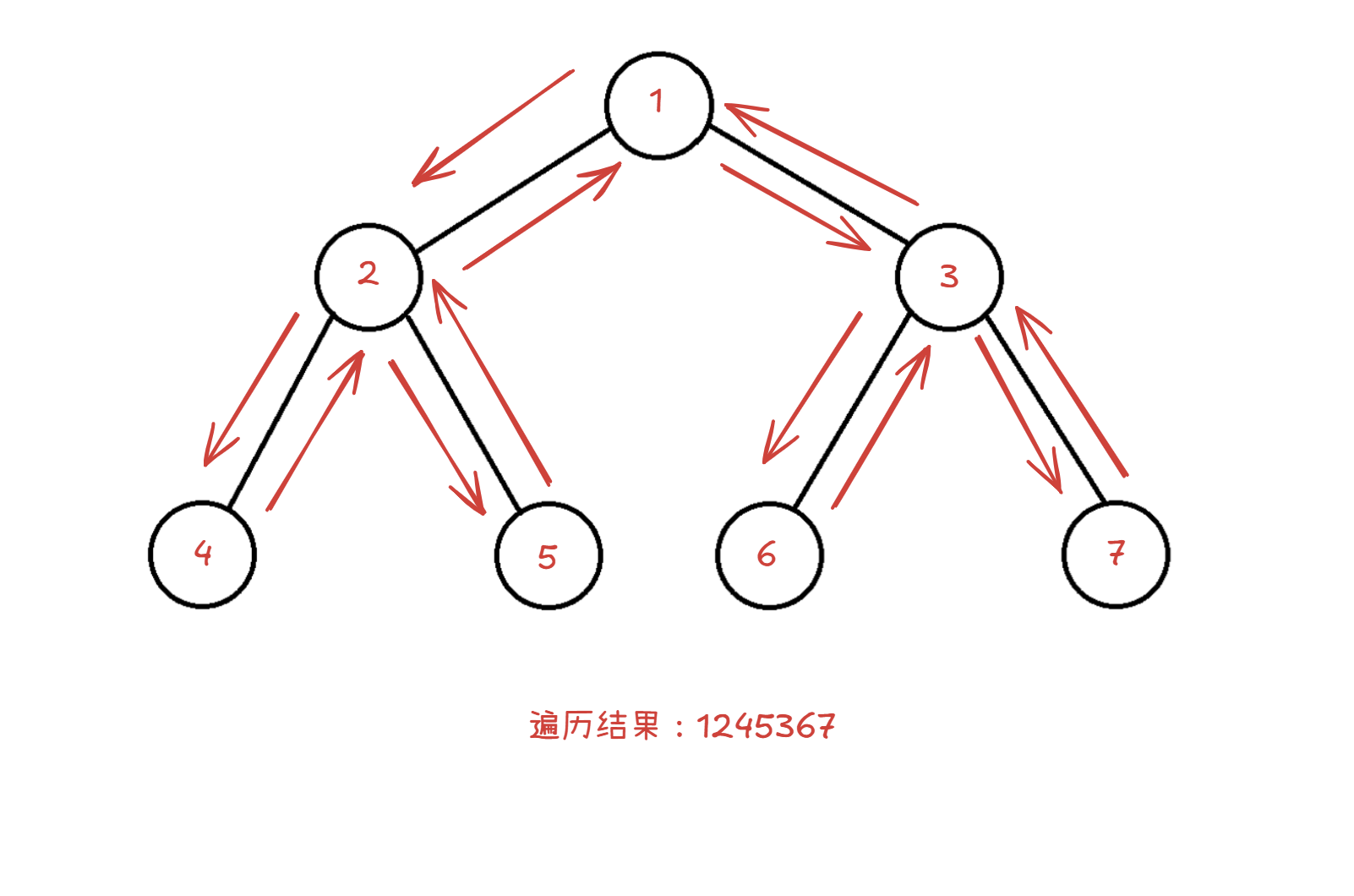
箭头从根节点出发，向子节点进发。

我们通过箭头的回溯过程就可以发现这个过程是要通过递归来实现的，事实是三种遍历都要通过遍历来实现哈！

这个根左右就是代表，先遍历根节点，再遍历左子树，最后遍历右子树。但是要注意了，这里的是左子树和右子树，不是左子节点和右子节点，所以这个后面的两个过程也要通过根左右这个规则来，这个规则在前序遍历还不是很明显，但是在后面两种遍历里会变得非常明显。

先放代码，再讲过程：

cpp 复制代码

void PreOrderTraversal(TreeNode* root) {
    cout << root->val << " ";
    if(root->left)
        PreOrderTraversal(root->left);
    if(root->right)
        PreOrderTraversal(root->right);
}

我们先输出根节点，然后再判断有没有左右子树，如果有左子树就继续遍历左子树（用递归），如果有右子树就继续遍历右子树，这个道理很简单，我就不解答了！

3.3.3 中序遍历

中序遍历是左根右，过程如下：

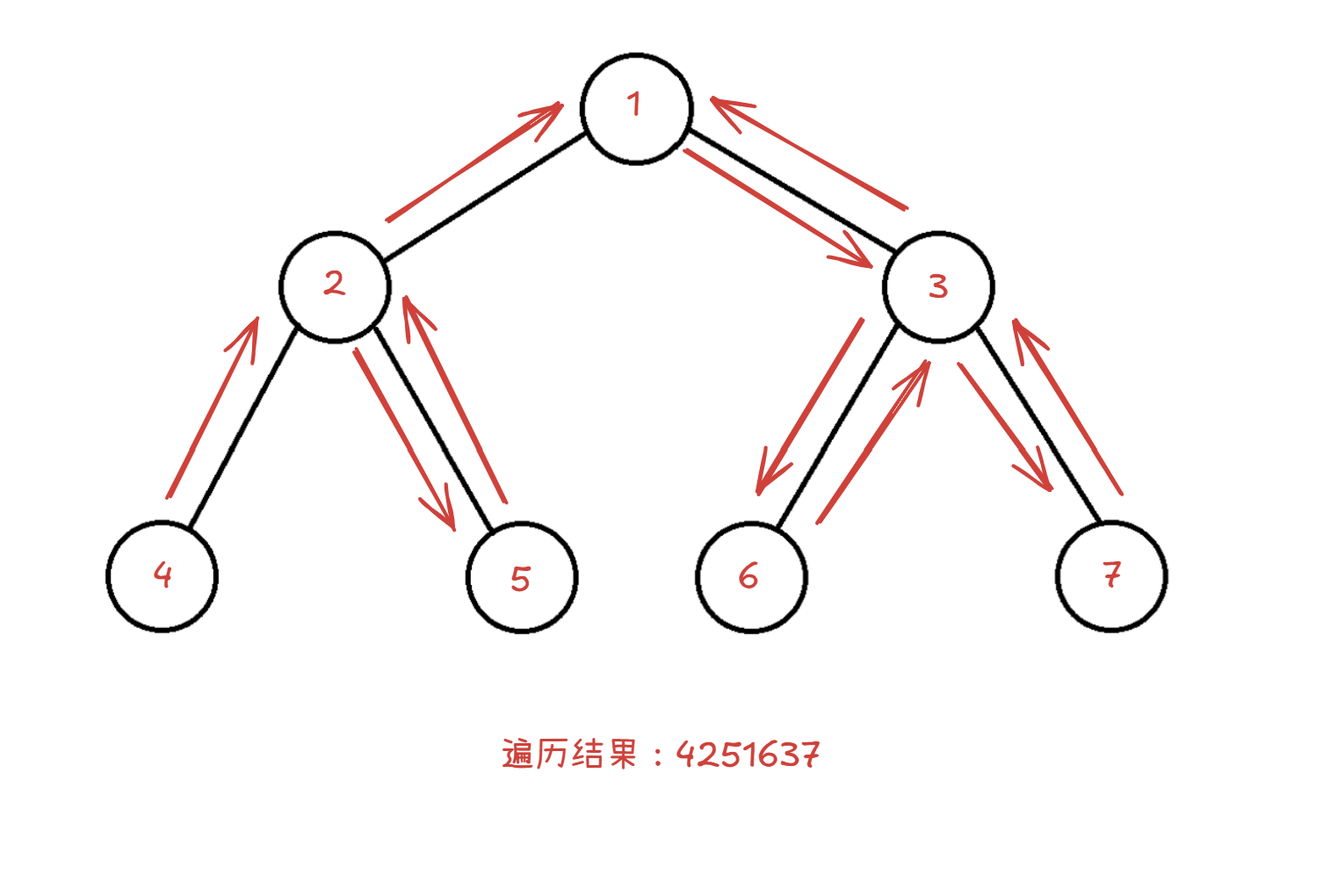
这个既然是左根右，那么就得先遍历左子树，但是左子树还有左子树，所以还得往下找，发现没有左子树了，那么就可以遍历了，然后再遍历根节点，最后右子树是同样的道理，代码：

cpp 复制代码

void InOrderTraversal(TreeNode* root) {
    if(root->left)
        InOrderTraversal(root->left);
    cout << root->val << " ";
    if(root->right)
        InOrderTraversal(root->right);
}

代码就是把根和左子树换了个位置，改个函数名，其他就直接Ctrl+c Ctrl+v（或Commend）。

3.3.4 后序遍历

后序遍历是左右根，过程如下：

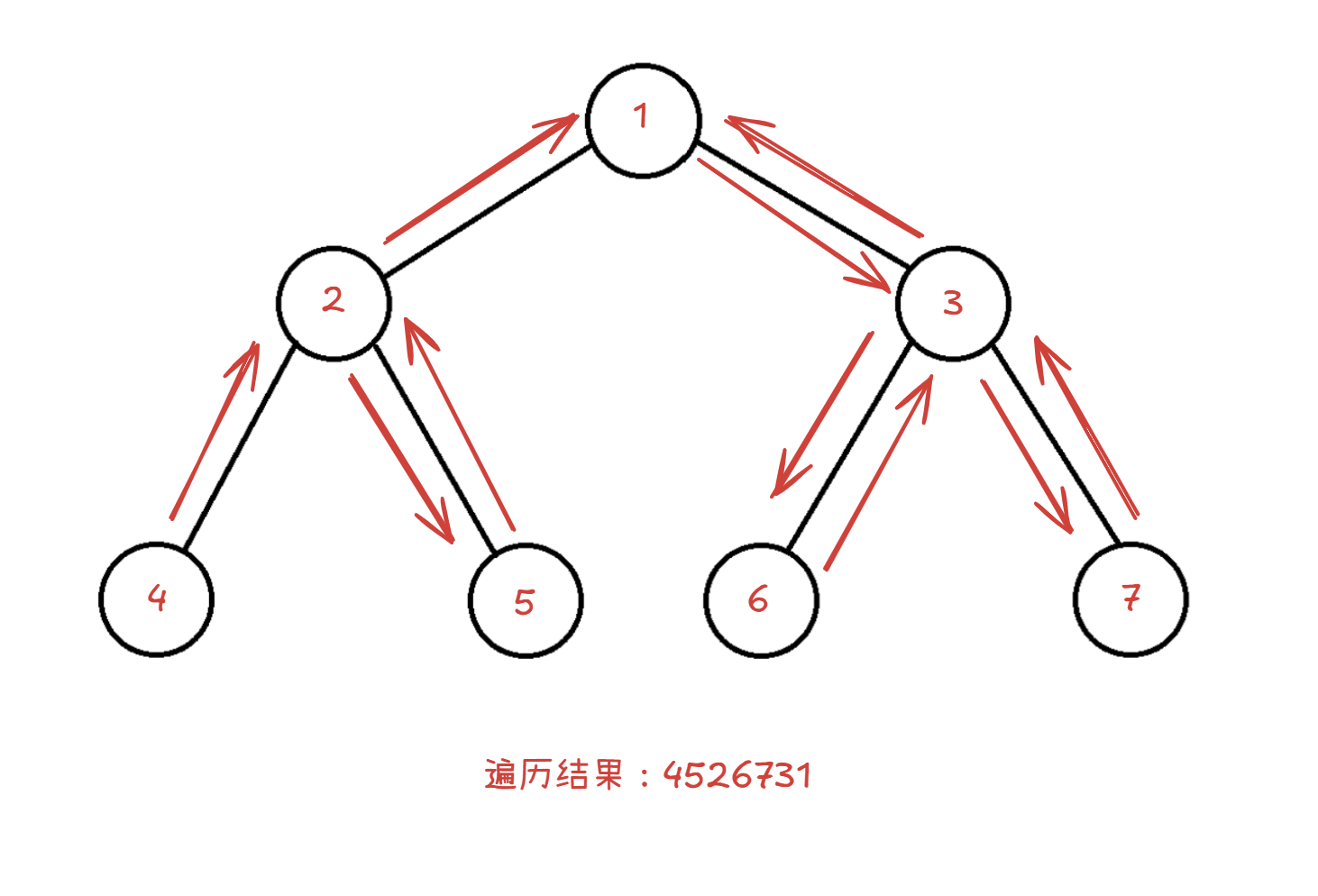
这个也很简单，就是再中序遍历的基础下把根和右再换一个位置就可以了，我也懒得讲了，还是老规矩，不会评论区或私信，七天内必回！代码：

cpp 复制代码

void PostOrderTraversal(TreeNode* root) {
    if(root->left)
        PostOrderTraversal(root->left);
    if(root->right)
        PostOrderTraversal(root->right);
    cout << root->val << " ";
}

代码也只是把右和根换一个位置就行！

4.总结

今天我们先简单的过了一遍树的基本知识，进阶知识我们后面再说！一定要消化的主要知识点：

树的基本概念

二叉树的基本概念

二叉树的结构体指针构建

二叉树的遍历

二叉树的遍历的代码实现

以后我还会更其他语言的版本，但其他语言就知识讲一下构建、遍历和代码了，概念直接套，所以就算你学的是其他语言，你也要掌握树和二叉树的基本概念那一块！

再见！