108. 将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

简单

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

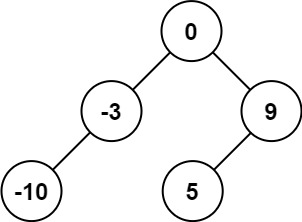
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

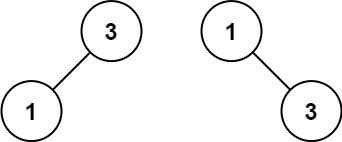
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

📝 核心笔记：有序数组转 BST (Convert Sorted Array to BST)

1. 核心思想 (一句话总结)

"二分查找的逆向工程：数组的中点就是树的根。"

• 平衡性 ：为了保证生成的是 高度平衡 的 BST，我们必须每次都选数组中间的元素作为根节点，这样左右子树的节点数量差不会超过 1。
• 结构映射：

• • 数组中间元素 -> 根 (Root)
  • 数组左半边 -> 左子树 (Left Subtree)
  • 数组右半边 -> 右子树 (Right Subtree)

2. 算法流程 (分治三部曲)

1. 找中点 (Find Mid) ：计算当前范围 [left, right) 的中间位置 m。
2. 造节点 (Build Node) ：new TreeNode(nums[m])。
3. 递归连线 (Connect)：

• • 左孩子 = 递归处理 [left, m)。
  • 右孩子 = 递归处理 [m + 1, right)。

🔍 代码回忆清单

// 题目：LC 108. Convert Sorted Array to Binary Search Tree
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        // 初始范围：[0, length)，左闭右开
        return dfs(nums, 0, nums.length);
    }

    // 辅助函数：在 nums[left...right-1] 范围内构建树
    private TreeNode dfs(int[] nums, int left, int right) {
        // 1. Base Case: 
        // 因为是右开区间 [ )，所以当 left == right 时区间为空，返回 null
        if (left == right) {
            return null;
        }

        // 2. 计算中点 (防止溢出写法)
        // 比如 left=0, right=5 (5个数), m=2 (第3个数)
        int m = (left + right) >>> 1;
        
        // 3. 构建当前节点，并直接在构造函数中递归连接左右子树
        // 左区间：[left, m) -> 不包含 m
        // 右区间：[m + 1, right) -> 不包含 m
        return new TreeNode(
            nums[m], 
            dfs(nums, left, m), 
            dfs(nums, m + 1, right)
        );
    }
}

⚡ 快速复习 CheckList (易错点 & 区间对比)

• \] **左闭右开** **[ )****vs 左闭右闭** **[ ]****？**

• • 您的写法 (左闭右开)：

• • • 入口：dfs(0, len)
    • 终止：left == right
    • 递归：dfs(left, m) 和 dfs(m+1, right)

• • 传统写法 (左闭右闭)：

• • • 入口：dfs(0, len - 1)
    • 终止：left > right
    • 递归：dfs(left, m-1) 和 dfs(m+1, right)

• • 评价：您的写法在处理数组索引时通常更不容易出错。

• \] **为什么要平衡？**

• • 如果不选中间，而是选第一个元素做根，有序数组会退化成一个 链表，查找效率从 O(\\log N) 降为 。

• \] **偶数个元素选哪个？**

• • [1, 2, 3, 4]。
  • >>> 1 会选偏右的那个（或偏左，取决于具体计算），这不影响平衡性，只要逻辑一致即可。

🖼️ 数字演练

数组：[-10, -3, 0, 5, 9] (Length = 5)

1. dfs(0, 5):

• • m = 2. Val = 0.
  • Root is 0.
  • Left: dfs(0, 2) ([-10, -3]). Right: dfs(3, 5) ([5, 9]).

1. dfs(0, 2) (Left side):

• • m = 1. Val = -3.
  • Node -3.
  • Left: dfs(0, 1). Right: dfs(2, 2) -> null.

1. dfs(0, 1):

• • m = 0. Val = -10.
  • Node -10. Left/Right null.

结果结构：

      0
     / \
   -3   9
   /   /
 -10  5

(注：根据算中点的细节，9 和 5 的位置可能互换，或者是 5 做父节点 9 做子节点，都是合法的平衡 BST)