小蓝在 LQ 集市上发现一个套手镯的游戏,在一个大小为 1e8 × 1e8 矩形平面上摆放着 N 个圆形的手镯。玩家可以将一个大小为 w × h 的矩形方框放置在这个平面上(玩家只可以沿着水平/垂直方向放置方框,即可以将方框旋转 90度,但不可以旋转至其他角度),位于这个矩形方框内部的手镯就是玩家获得的奖励。
可以将这个矩形平面看作是一个二维坐标系,左下角的坐标为 (0, 0)。手镯和方框的厚度可以忽略不计, 允许多个手镯重叠放置。
小蓝想要尝试一次,请问他最多可以获得多少手镯?
输入格式
第一行输入三个整数 N、w、h。
接下来输入 N 行,每行三个整数 x, y,r,表示第 i 个手镯的圆心坐标和半径。
输出格式
输出一个整数表示答案。
样例输入
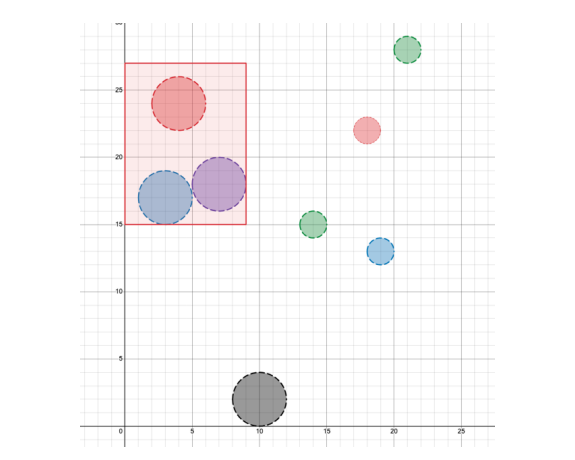
8 12 9
18 22 1
3 17 2
21 28 1
7 18 2
10 2 2
4 24 2
19 13 1
14 15 1样例输出
3提示
【评测用例规模与约定】
对于 50% 的评测用例:1 ≤ N ≤ 100,1 ≤ w, h, x, y,r ≤ 200。
对于 100% 的评测用例:1 ≤ N ≤ 1000,1 ≤ w, h, x, y,r ≤ 1e8,1 ≤min{w, h} ≤ 200。保证所有手镯都位于平面内部。
//这道题显然对于某些点能否共同待在一个矩形内是好判断的,但是难点就在于自己并不知道该选哪一堆点,根据数据规模暴搜的话绝对从超时,那咋办?我们首先对于每个点进行处理,显然每个圆都有上下左右四个边界,我们收集起来然后按照右边界升序排序。然后不妨转换下思路,我们可以把研究方向从点上转移到矩形位置上,我们大可以枚举矩形的位置不是吗?但是也不是暴力枚举,我们只枚举那些有必要的位置,那什么是有必要的位置,就是与某个圆相切绝对是最好情况。我们不妨外部循环枚举矩形的下边界,也就是每一个圆的下边界(因为正好相切),这样上边界其实也就确定了,那么内部循环枚举的就是每一个点,判断其是否在矩形的上下范围之内,如果在就加入一个堆中,该堆按照圆的左边界升序排列。当然上下范围符合那还要判断左右范围是否符合,那这就体现了刚才为啥要引入堆,堆顶的左边界显然最小,如果堆顶左边界与当前遍历到的节点(不用管当前节点是否在堆中,因为我们的每个圆是按照右边界升序排序的,如果当前点都不能满足,后续一定不会满足)的右边界差的绝对值超过规定,那就不断弹出堆。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10; // 定义数组大小的上限
const int MOD = 1e9 + 7; // 常用的大质数MOD
ll n, w, h; // n是手镯数量,w和h是矩形的宽度和高度
// 定义结构体Node表示一个手镯的四个边界
struct Node {
int l, r, b, t; // 左、右、下、上边界
// 重载小于运算符,按照左边界从大到小排序,优先队列中会保持左边界从小到大排列
bool operator< (const Node &u) const {
return l > u.l;
}
} a[N];
// solve函数:计算矩形区域内可以容纳最多的手镯数
int solve(int tw, int th) {
int res = 0; // 记录结果(最大手镯数)
// 外层循环:固定矩形的下边界line
for (int i = 0; i < n; i++) {
int bottom = a[i].b; // 当前手镯的下边界
int top = bottom + th; // 计算矩形的上边界
priority_queue<Node> q; // 优先队列,用来存储在当前上下边界之内的手镯
// 内层循环:检查所有手镯是否在当前的上下边界范围内
for (int j = 0; j < n; j++) {
// 如果手镯的上下边界在当前矩形范围内
if (a[j].b >= bottom && a[j].t <= top) {
q.push(a[j]); // 将符合条件的手镯加入优先队列
}
// 移除不再符合当前左右边界范围的手镯
while (!q.empty() && q.top().l < a[j].r - tw) {
q.pop(); // 移除左边界小于当前手镯右边界-矩形宽度的手镯
}
// 更新最大值,计算当前矩形内的手镯数量
res = max(res, (int)q.size());
}
}
return res; // 返回最大手镯数
}
// cmp函数:按照手镯右边界从小到大排序
bool cmp(Node a, Node b) {
return a.r < b.r;
}
int main() {
cin >> n >> w >> h; // 输入手镯数量n和矩形的宽度w和高度h
// 输入每个手镯的坐标和半径,并计算出每个手镯的四个边界
for (int i = 0; i < n; i++) {
int x, y, r;
cin >> x >> y >> r; // 输入手镯的中心坐标(x, y)和半径r
a[i].l = x - r; // 计算左边界
a[i].r = x + r; // 计算右边界
a[i].b = y - r; // 计算下边界
a[i].t = y + r; // 计算上边界
}
sort(a, a + n, cmp); // 根据右边界升序排序所有手镯
// 分别尝试两种矩形方向,w x h 和 h x w
int res1 = solve(w, h);
int res2 = solve(h, w);
// 输出两种方向中的最大手镯数
cout << max(res1, res2) << endl;
return 0;
}