E=[T]×R 的证明

Σίσυφος19002026-02-13 8:49

一、简介

最清晰、最短、最本质 的推导，解释为什么：

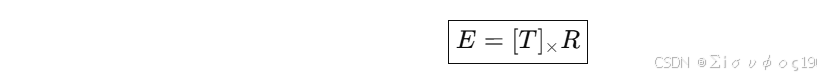
二、为什么 E = [T]× R？（严格数学推导）

给定两个相机：

第一相机坐标系：C₁
第二相机坐标系：C₂
第二相机相对第一相机的姿态：
- 旋转：R
- 平移：T

3D 点 X在两个相机的成像点满足：

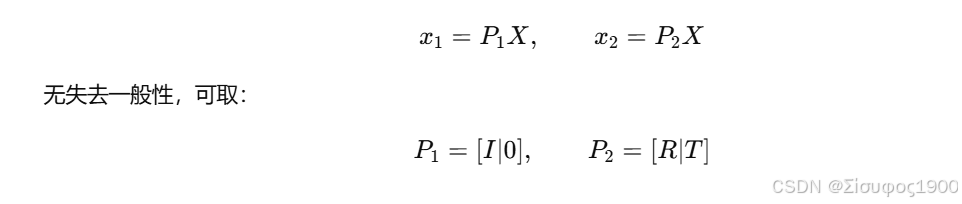
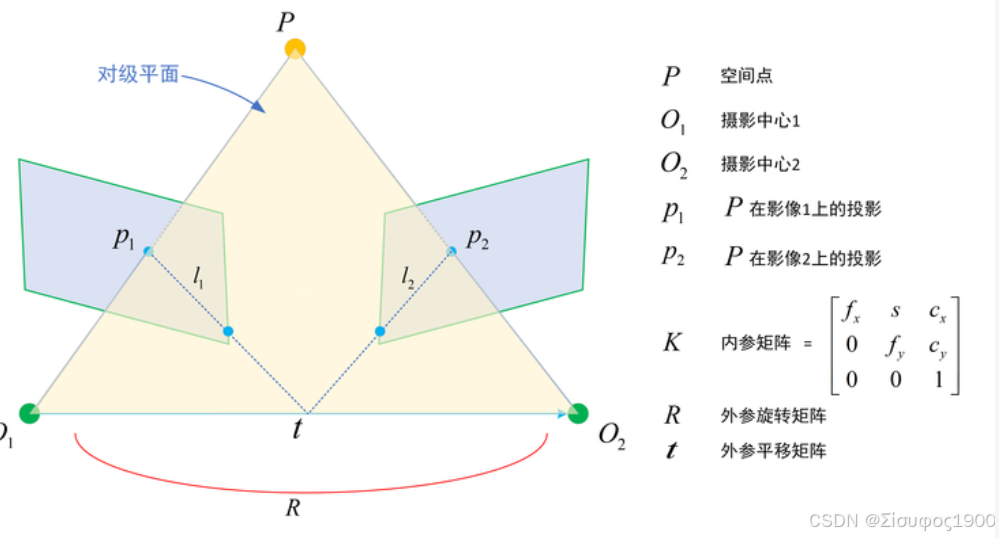
几何约束：点、极线、极平面

三、Matlab 测试

计算本质矩阵E

cpp 复制代码

%% 随机生成一个旋转矩阵 R
[U,~,V] = svd(randn(3,3));
R = U*V';

% 确保 det(R)=1
if det(R)<0
    U(:,3) = -U(:,3);
    R = U*V';
end

%% 随机平移 T（非零）
T = randn(3,1);
T = T / norm(T);

%% 构造叉乘矩阵 [T]×
Tx = [  0   -T(3)   T(2);
       T(3)   0    -T(1);
      -T(2)  T(1)    0 ];

%% 按理论构造本质矩阵 E
E = Tx * R;

disp('E = [T]x R =');
disp(E)

cpp 复制代码

%% ====== 数值验证：x2^T E x1 = 0 ======
% 随机生成空间 3D 点
X = randn(3,20);

% 第一相机投影
x1 = X ./ X(3,:);

% 第二相机投影：x2 = R*X + T
X2 = R * X + T;
x2 = X2 ./ X2(3,:);

% 验证 epipolar constraint
err = zeros(1,size(X,2));
for i = 1:size(X,2)
    err(i) = x2(:,i)' * E * x1(:,i);
end

disp('数值误差（应接近 0）：');
disp(err);

fprintf('\n最大误差: %.3e\n', max(abs(err)));
E = [T]x R =
   -0.7750    0.5902   -0.1374
   -0.5141   -0.7866   -0.3197
    0.2064   -0.0104    0.0651

数值误差（应接近 0）：
   1.0e-14 *

  列 1 至 11

   -0.0056   -0.0652         0   -0.3553    0.0333   -0.0444   -0.0111         0         0    0.0888   -0.0042

  列 12 至 20

   -0.0222   -0.0444    0.0444    0.0139   -0.1332         0   -0.0087         0   -0.1332


最大误差: 3.553e-15