接上集:
本文参考Kian Sen Ang and I. D. Robertson, "Analysis and design of impedance-transforming planar Marchand baluns ," in IEEE Transactions on Microwave Theory and Techniques, vol. 49, no. 2, pp. 402-406, Feb. 2001, doi: 10.1109/22.903108.
keywords: {Impedance matching;Couplers;Coupling circuits;Diodes;Microstrip;Frequency;Microwave integrated circuits;MMICs;Monolithic integrated circuits;Wideband},详细推导一下下公式,仅供学习使用
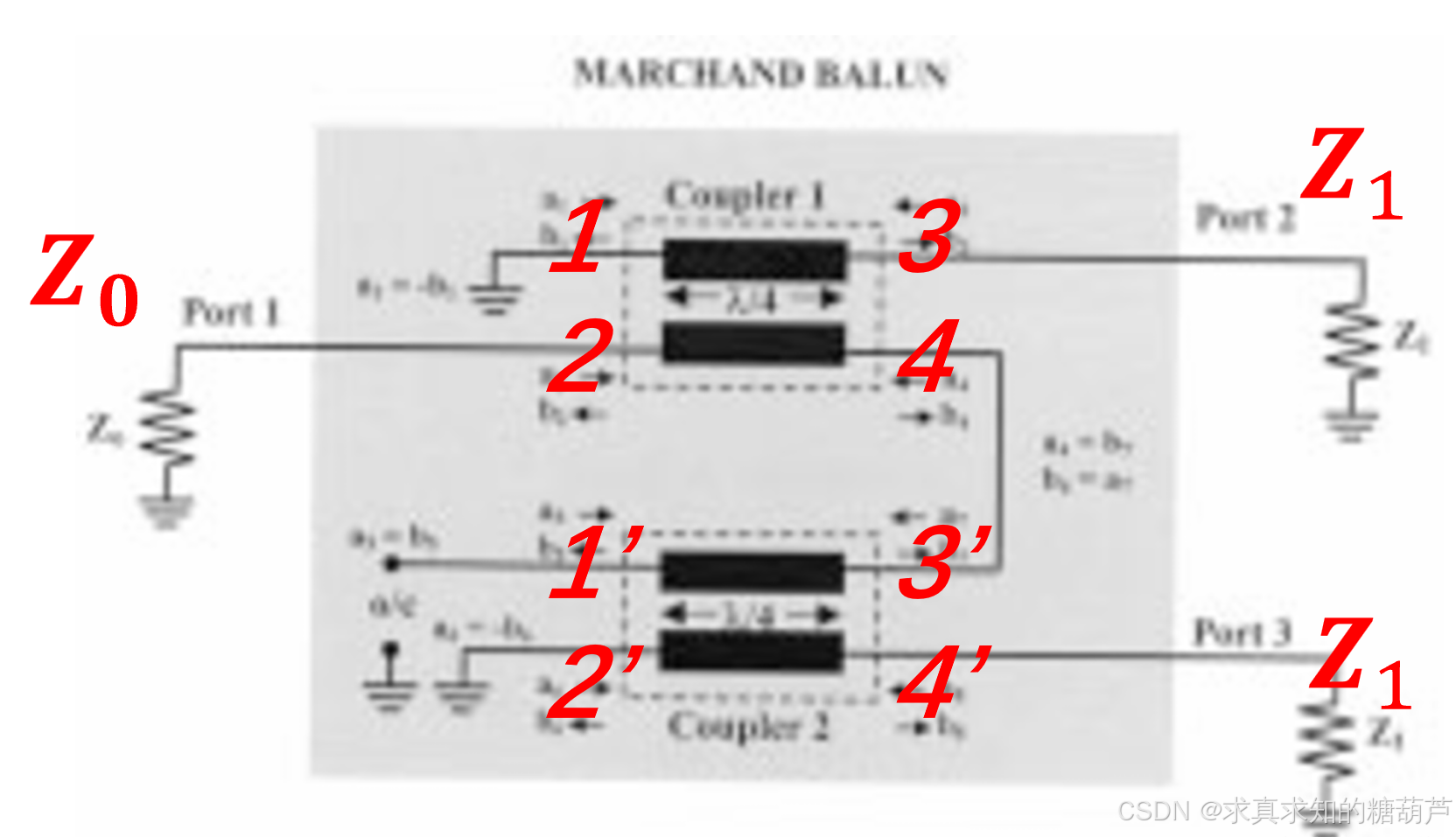
图 1. 作为两个相同耦合器的对称Marchand巴伦框图。
有趣的是,当所有端口都端接相同阻抗(例如50Ω),即阻抗变换比为1时,所需的耦合系数是-4.8 dB,而不是-3 dB。根据(5)式,使用通常假设的-3 dB耦合器[6]将导致中心频率处的插入损耗和输出隔离为-3.5 dB,输入和输出回波损耗为-9.5 dB。当满足(7)式时,(5)式给出的巴伦S矩阵简化为:
S\]balun=\[0j2−j2j21212−j21212\].(8) \[S\]_{\\text{balun}}=\\begin{bmatrix}0\&\\frac{j}{\\sqrt{2}}\&-\\frac{j}{\\sqrt{2}}\\\\\\frac{j}{\\sqrt{2}}\&\\frac{1}{2}\&\\frac{1}{2}\\\\-\\frac{j}{\\sqrt{2}}\&\\frac{1}{2}\&\\frac{1}{2}\\end{bmatrix}.\\quad{(8)} \[S\]balun= 02 j−2 j2 j2121−2 j2121 .(8) 这是一个无耗使用图1所示结构巴伦可达到的最佳S矩阵。它在输入端匹配,传输系数为-3 dB且相位相反。 ## 一、理想巴伦的S矩阵 为了实现完美的输出端口匹配和隔离,需要在输出端口之间添加某种形式的电阻网络,就像威尔金森功分器那样。将使用Y参数来推导所需的电阻网络。具有完美输出匹配和隔离的巴伦的S矩阵形式为: \[S\]balun,ideal=\[0j/2−j/2j/200−j/200\].(9)\[S\]_{\\text{balun,ideal}} = \\begin{bmatrix} 0 \& j/\\sqrt{2} \& -j/\\sqrt{2} \\\\ j/\\sqrt{2} \& 0 \& 0 \\\\ -j/\\sqrt{2} \& 0 \& 0 \\end{bmatrix}.\\quad(9)\[S\]balun,ideal= 0j/2 −j/2 j/2 00−j/2 00 .(9) > 该矩阵满足以下特性: > **\>- 输入端口匹配(S11=0S_{11}=0S11=0); > \>- 输出端口匹配(S22=S33=0S_{22}=S_{33}=0S22=S33=0); > \>- 输出端口间隔离(S23=S32=0S_{23}=S_{32}=0S23=S32=0); > \>- 传输系数幅值为1/21/\\sqrt{2}1/2 (-3dB),且相位相反(S21=j/2S_{21}=j/\\sqrt{2}S21=j/2 ,S31=−j/2S_{31}=-j/\\sqrt{2}S31=−j/2 )** ## 二、从理想S矩阵到Y矩阵的转换 已知端口参考阻抗矩阵为: ZR=diag(Z0,Z1,Z1).Z_R= \\operatorname{diag}(Z_0, Z_1, Z_1).ZR=diag(Z0,Z1,Z1). 散射矩阵SSS与导纳矩阵YYY的转换关系为: ### 2.1散射矩阵SSS与导纳矩阵YYY的转换关系推导 #### 2.1.1归一化波的定义 对于一个NNN端口网络,每个端口iii有一个**实数**参考阻抗ZRiZ_{Ri}ZRi。定义归一化入射波aia_iai和反射波bib_ibi: ai=Vi+ZRiIi2ZRi,bi=Vi−ZRiIi2ZRia_i=\\frac{V_i+Z_{Ri}I_i}{2\\sqrt{Z_{Ri}}},\\quad b_i=\\frac{V_i-Z_{Ri}I_i}{2\\sqrt{Z_{Ri}}}ai=2ZRi Vi+ZRiIi,bi=2ZRi Vi−ZRiIi 其中ViV_iVi是端口电压,IiI_iIi是流入端口的电流(电流方向为流入网络)。写成矩阵形式: a=12ZR−1/2(V+ZRI),b=12ZR−1/2(V−ZRI)\\mathbf{a}=\\frac{1}{2}Z_R\^{-1/2}(\\mathbf{V}+Z_R\\mathbf{I}),\\quad\\mathbf{b}=\\frac{1}{2}Z_R\^{-1/2}(\\mathbf{V}-Z_R\\mathbf{I})a=21ZR−1/2(V+ZRI),b=21ZR−1/2(V−ZRI) 这里ZR=diag(ZR1,ZR2,...,ZRN)Z_R=\\operatorname{diag}(Z_{R1},Z_{R2},\\dots,Z_{RN})ZR=diag(ZR1,ZR2,...,ZRN)是对角参考阻抗矩阵, ZR−1/2=diag(1/ZR1,1/ZR2,...,1/ZRN)Z_R\^{-1/2}=\\operatorname{diag}(1/\\sqrt{Z_{R1}},1/\\sqrt{Z_{R2}},\\dots,1/\\sqrt{Z_{RN}})ZR−1/2=diag(1/ZR1 ,1/ZR2 ,...,1/ZRN )。 #### 2.1.2散射矩阵SSS的定义 散射矩阵SSS定义为: b=Sa\\mathbf{b}=S\\mathbf{a}b=Sa #### 2.1.3电压和电流与波的关系 从波的定义反解电压和电流: V=ZR1/2(a+b),I=ZR−1/2(a−b)\\mathbf{V}=Z_R\^{1/2}(\\mathbf{a}+\\mathbf{b}),\\quad\\mathbf{I}=Z_R\^{-1/2}(\\mathbf{a}-\\mathbf{b})V=ZR1/2(a+b),I=ZR−1/2(a−b) 其中ZR1/2=diag(ZR1,ZR2,...,ZRN)Z_R\^{1/2}=\\operatorname{diag}(\\sqrt{Z_{R1}},\\sqrt{Z_{R2}},\\dots,\\sqrt{Z_{RN}})ZR1/2=diag(ZR1 ,ZR2 ,...,ZRN )。 导纳矩阵YYY定义为: I=YV\\mathbf{I}=Y\\mathbf{V}I=YV 将b=Sa\\mathbf{b}=S\\mathbf{a}b=Sa代入电压和电流表达式: V=ZR1/2(I+S)a\\mathbf{V}=Z_R\^{1/2}(I+S)\\mathbf{a}V=ZR1/2(I+S)a I=ZR−1/2(I−S)a\\mathbf{I}=Z_R\^{-1/2}(I-S)\\mathbf{a}I=ZR−1/2(I−S)a 从电压表达式解出a\\mathbf{a}a(假设I+SI+SI+S可逆): a=(I+S)−1ZR−1/2V\\mathbf{a}=(I+S)\^{-1}Z_R\^{-1/2}\\mathbf{V}a=(I+S)−1ZR−1/2V 代入电流表达式: I=ZR−1/2(I−S)(I+S)−1ZR−1/2V\\mathbf{I}=Z_R\^{-1/2}(I-S)(I+S)\^{-1}Z_R\^{-1/2}\\mathbf{V}I=ZR−1/2(I−S)(I+S)−1ZR−1/2V 因此: Y=ZR−1/2(I−S)(I+S)−1ZR−1/2Y=Z_R\^{-1/2}(I-S)(I+S)\^{-1}Z_R\^{-1/2}Y=ZR−1/2(I−S)(I+S)−1ZR−1/2 在讨论的Marchand巴伦中,端口1的参考阻抗为Z0Z_0Z0,端口2和3的参考阻抗为Z1Z_1Z1,所以: ZR=diag(Z0,Z1,Z1),ZR−1/2=diag(1/Z0,1/Z1,1/Z1)Z_R=\\operatorname{diag}(Z_0,Z_1,Z_1),\\quad Z_R\^{-1/2}=\\operatorname{diag}(1/\\sqrt{Z_0},1/\\sqrt{Z_1},1/\\sqrt{Z_1})ZR=diag(Z0,Z1,Z1),ZR−1/2=diag(1/Z0 ,1/Z1 ,1/Z1 ) ### 2.2计算 #### 2.2.1计算I±SI \\pm SI±S: I−S=\[1−j/2j/2−j/210j/201\],I+S=\[1j/2−j/2j/210−j/201\].I - S = \\begin{bmatrix} 1 \& -j/\\sqrt{2} \& j/\\sqrt{2} \\\\ -j/\\sqrt{2} \& 1 \& 0 \\\\ j/\\sqrt{2} \& 0 \& 1 \\end{bmatrix}, \\quad I + S = \\begin{bmatrix} 1 \& j/\\sqrt{2} \& -j/\\sqrt{2} \\\\ j/\\sqrt{2} \& 1 \& 0 \\\\ -j/\\sqrt{2} \& 0 \& 1 \\end{bmatrix}.I−S= 1−j/2 j/2 −j/2 10j/2 01 ,I+S= 1j/2 −j/2 j/2 10−j/2 01 . #### 2.2.2 求(I+S)−1(I+S)\^{-1}(I+S)−1: 通过伴随矩阵法或分块求逆,得到: (I+S)−1=\[1/2−j/(22)j/(22)−j/(22)3/41/4j/(22)1/43/4\].(I+S)\^{-1} = \\begin{bmatrix} 1/2 \& -j/(2\\sqrt{2}) \& j/(2\\sqrt{2}) \\\\ -j/(2\\sqrt{2}) \& 3/4 \& 1/4 \\\\ j/(2\\sqrt{2}) \& 1/4 \& 3/4 \\end{bmatrix}.(I+S)−1= 1/2−j/(22 )j/(22 )−j/(22 )3/41/4j/(22 )1/43/4 . #### 2.2.3 计算(I−S)(I+S)−1(I-S)(I+S)\^{-1}(I−S)(I+S)−1: (I−S)(I+S)−1=\[0−j/2j/2−j/21/21/2j/21/21/2\].(I-S)(I+S)\^{-1} = \\begin{bmatrix} 0 \& -j/\\sqrt{2} \& j/\\sqrt{2} \\\\ -j/\\sqrt{2} \& 1/2 \& 1/2 \\\\ j/\\sqrt{2} \& 1/2 \& 1/2 \\end{bmatrix}.(I−S)(I+S)−1= 0−j/2 j/2 −j/2 1/21/2j/2 1/21/2 . #### 2.2.4左乘和右乘ZR−1/2Z_R\^{-1/2}ZR−1/2: Yij=1Zi\[(I−S)(I+S)−1\]ij1Zj,Y_{ij} = \\frac{1}{\\sqrt{Z_i}} \\left\[(I-S)(I+S)\^{-1}\\right\]_{ij} \\frac{1}{\\sqrt{Z_j}},Yij=Zi 1\[(I−S)(I+S)−1\]ijZj 1, 代入后得到公式(10): \[Y\]balun=\[0−j/2Z0Z1j/2Z0Z1−j/2Z0Z11/(2Z1)1/(2Z1)j/2Z0Z11/(2Z1)1/(2Z1)\].\[Y\]_{\\text{balun}} = \\begin{bmatrix} 0 \& -j/\\sqrt{2Z_0 Z_1} \& j/\\sqrt{2Z_0 Z_1} \\\\ -j/\\sqrt{2Z_0 Z_1} \& 1/(2Z_1) \& 1/(2Z_1) \\\\ j/\\sqrt{2Z_0 Z_1} \& 1/(2Z_1) \& 1/(2Z_1) \\end{bmatrix}.\[Y\]balun= 0−j/2Z0Z1 j/2Z0Z1 −j/2Z0Z1 1/(2Z1)1/(2Z1)j/2Z0Z1 1/(2Z1)1/(2Z1) . *** ** * ** *** ## 三、Marchand巴伦S矩阵到Y矩阵的转换 公式(8)给出了最佳耦合系数下Marchand巴伦的S矩阵: \[S\]balun=\[0j/2−j/2j/21/21/2−j/21/21/2\].\[S\]_{\\text{balun}} = \\begin{bmatrix} 0 \& j/\\sqrt{2} \& -j/\\sqrt{2} \\\\ j/\\sqrt{2} \& 1/2 \& 1/2 \\\\ -j/\\sqrt{2} \& 1/2 \& 1/2 \\end{bmatrix}.\[S\]balun= 0j/2 −j/2 j/2 1/21/2−j/2 1/21/2 . 类似2.2的过程使用相同的转换公式: ### 3.1 计算I±SI \\pm SI±S: I−S=\[1−j/2j/2−j/21/2−1/2j/2−1/21/2\],I+S=\[1j/2−j/2j/23/21/2−j/21/23/2\].I - S = \\begin{bmatrix} 1 \& -j/\\sqrt{2} \& j/\\sqrt{2} \\\\ -j/\\sqrt{2} \& 1/2 \& -1/2 \\\\ j/\\sqrt{2} \& -1/2 \& 1/2 \\end{bmatrix}, \\quad I + S = \\begin{bmatrix} 1 \& j/\\sqrt{2} \& -j/\\sqrt{2} \\\\ j/\\sqrt{2} \& 3/2 \& 1/2 \\\\ -j/\\sqrt{2} \& 1/2 \& 3/2 \\end{bmatrix}.I−S= 1−j/2 j/2 −j/2 1/2−1/2j/2 −1/21/2 ,I+S= 1j/2 −j/2 j/2 3/21/2−j/2 1/23/2 . ### 3.2 求(I+S)−1(I+S)\^{-1}(I+S)−1: (I+S)−1=\[1/2−j/(22)j/(22)−j/(22)1/20j/(22)01/2\].(I+S)\^{-1} = \\begin{bmatrix} 1/2 \& -j/(2\\sqrt{2}) \& j/(2\\sqrt{2}) \\\\ -j/(2\\sqrt{2}) \& 1/2 \& 0 \\\\ j/(2\\sqrt{2}) \& 0 \& 1/2 \\end{bmatrix}.(I+S)−1= 1/2−j/(22 )j/(22 )−j/(22 )1/20j/(22 )01/2 . ### 3.3 计算(I−S)(I+S)−1(I-S)(I+S)\^{-1}(I−S)(I+S)−1: (I−S)(I+S)−1=\[0−j/2j/2−j/200j/200\].(I-S)(I+S)\^{-1} = \\begin{bmatrix} 0 \& -j/\\sqrt{2} \& j/\\sqrt{2} \\\\ -j/\\sqrt{2} \& 0 \& 0 \\\\ j/\\sqrt{2} \& 0 \& 0 \\end{bmatrix}.(I−S)(I+S)−1= 0−j/2 j/2 −j/2 00j/2 00 . ### 3.4 左乘和右乘ZR−1/2Z_R\^{-1/2}ZR−1/2,得到公式(11): \[Y\]balun=\[0−j/2Z0Z1j/2Z0Z1−j/2Z0Z100j/2Z0Z100\].(11)\[Y\]_{\\text{balun}} = \\begin{bmatrix} 0 \& -j/\\sqrt{2Z_0 Z_1} \& j/\\sqrt{2Z_0 Z_1} \\\\ -j/\\sqrt{2Z_0 Z_1} \& 0 \& 0 \\\\ j/\\sqrt{2Z_0 Z_1} \& 0 \& 0 \\end{bmatrix}.\\quad(11)\[Y\]balun= 0−j/2Z0Z1 j/2Z0Z1 −j/2Z0Z1 00j/2Z0Z1 00 .(11) *** ** * ** *** 公式(9)是理想巴伦的S参数描述;公式(10)和(11)分别对应理想巴伦和实际Marchand巴伦的导纳矩阵。通过比较两者,**发现Marchand巴伦在输出端口缺少对地导纳和互导纳,因此需并联一个电阻网络(公式(12))以实现完美匹配和隔离。**比较(10)式和(11)式,可以推断出电阻网络的Y矩阵形式为: \[Y\]R=12Z1\[1111\].(12) \[Y\]_{R}=\\frac{1}{2Z_{1}}\\left\[\\begin{array}{ll}1 \& 1\\\\ 1 \& 1\\end{array}\\right\].\\qquad(12) \[Y\]R=2Z11\[1111\].(12) 该网络可以通过一个相位反转器和一个阻值为2Z12Z_{1}2Z1的电阻串联来实现。这个电阻网络也可以直观地推导出来。两个输出之间的信号路径是通过两个耦合器的耦合端口,如(8)式所示,其衰减为-6 dB且相移为零。因此,通过添加另一条具有-6 dB衰减和180°相移的信号路径,可以实现输出之间信号路径的完美抵消。 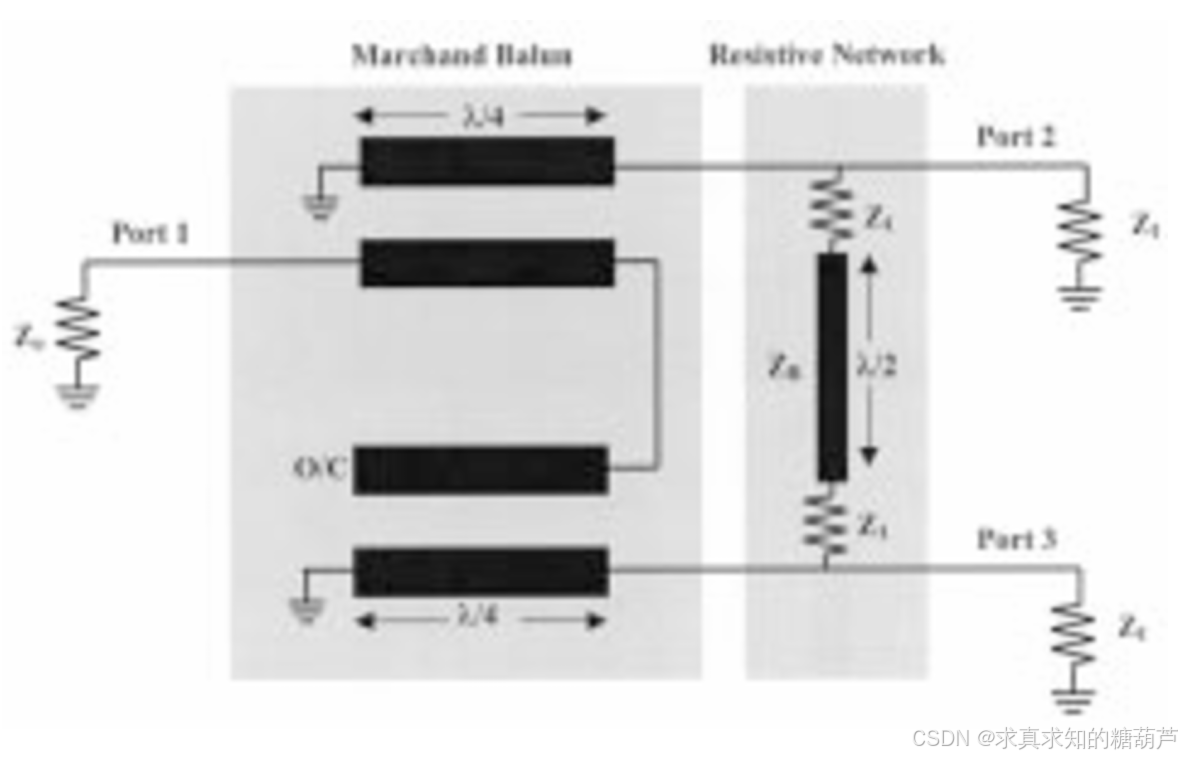 **图2. 通过在Marchand巴伦上添加电阻网络来实现具有隔离输出的完美匹配巴伦。** 图2显示了带有电阻网络的完美匹配巴伦的示意图。相位反转器通过简单的半波长传输线实现。为了保持输出端口之间的对称性,电阻被分成两个阻值为Z1Z_{1}Z1的电阻,分别位于传输线的两端。电阻网络的性能在中心频率处与传输线特性阻抗ZRZ_{R}ZR无关。但是,ZRZ_{R}ZR应尽可能设置得高,以确保原始巴伦的工作带宽不会显著减小。还应注意,所提出的电阻网络也可以应用于其他无耗巴伦结构,以实现输出匹配和隔离。此外,电阻网络中的相位反转器也可以使用其他宽带结构实现\[13\]。