数据结构---链表的奇特（下）双向链表的多样魅力

个人主页：
wengqidaifeng

✨ 永远在路上，永远向前走

个人专栏：
数据结构
C语言
嵌入式小白启动！

文章目录

• 前言：从单向到双向的数据演化之旅
• • 双向链表的起源与意义
  • • 历史背景：从限制中诞生
    • 设计哲学：空间的代价换取时间的自由
    • 在现代编程中的实际价值
  • 数据结构的艺术
• 一.双向链表的意义
• • [1. 双向链表的概念和结构](#1. 双向链表的概念和结构)
  • • [1.1 双向链表的结构](#1.1 双向链表的结构)
    • [1.2 双向链表中的头节点：导航员的角色](#1.2 双向链表中的头节点：导航员的角色)
    • • [1.2.1 什么是头节点？](#1.2.1 什么是头节点？)
      • [1.2.2 头节点的双重角色](#1.2.2 头节点的双重角色)
      • • [**入口点** - 链表的"大门"](#入口点 - 链表的“大门”)
        • [**边界哨兵** - 简化操作](#边界哨兵 - 简化操作)
      • [1.2.3 有无头节点的区别](#1.2.3 有无头节点的区别)
      • • 没有头节点的问题
        • 有头节点的优势
      • [1.2.4 头节点的关键特性](#1.2.4 头节点的关键特性)
  • 2.双向链表的主要类型及其应用
  • • [2.1 基础双向链表](#2.1 基础双向链表)
    • [2.2 带哨兵节点的双向链表](#2.2 带哨兵节点的双向链表)
    • [2.3 双向循环链表](#2.3 双向循环链表)
    • [2.4 有序双向链表](#2.4 有序双向链表)
    • [2.5 内存高效型双向链表（XOR链表）](#2.5 内存高效型双向链表（XOR链表）)
• [二. 双向链表的实现](#二. 双向链表的实现)
• • [1. 头文件函数声明及链表结构体](#1. 头文件函数声明及链表结构体)
  • [2. 各功能函数实现](#2. 各功能函数实现)
  • • [2.1 双向链表初始化](#2.1 双向链表初始化)
    • • [2.1.1 方式1：二级指针传参](#2.1.1 方式1：二级指针传参)
      • [2.1.2 方式2：返回值](#2.1.2 方式2：返回值)
      • [2.1.3 那么哪种方式更好呢？下面直接给出结论和理由。](#2.1.3 那么哪种方式更好呢？下面直接给出结论和理由。)
    • [**2.2 双向链表的打印 `LTPrint`**](#2.2 双向链表的打印 LTPrint)
    • [**2.3 申请节点 `LTBuyNode`**](#2.3 申请节点 LTBuyNode)
    • [**2.4 尾插 `LTPushBack`**](#2.4 尾插 LTPushBack)
    • [**2.5 头插 `LTPushFront`**](#2.5 头插 LTPushFront)
    • [**2.6 尾删 `LTPopBack`**](#2.6 尾删 LTPopBack)
    • [**2.7 头删 `LTPopFront`**](#2.7 头删 LTPopFront)
    • [**2.8 查找 `LTFind`**](#2.8 查找 LTFind)
    • [**2.9 特定位置插入 `LTInsert`**](#2.9 特定位置插入 LTInsert)
    • [**2.10 删除特定位置 `LTErase`**](#2.10 删除特定位置 LTErase)
    • [**2.11 双向链表的销毁 `LTDesTroy`**](#2.11 双向链表的销毁 LTDesTroy)
• 总结：双向链表的完整图景
• • 一、核心思想回顾
  • 二、函数设计的黄金法则
  • • 法则1：先连接新节点，再断开旧节点
    • 法则2：删除节点前必须先保存后继
    • 法则3：哨兵位永不删除、永不移动
    • 法则4：函数接口的设计要自洽
  • 三、常见陷阱与避坑指南
  • 四、下一步：你能做什么？

---

前言：从单向到双向的数据演化之旅

在计算机科学的浩瀚宇宙中，数据结构如同支撑起整个数字世界的基石。而链表，作为其中最灵活、最基础的数据结构之一，已经陪伴程序员走过了数十年的编程历程。今天，让我们聚焦于链表家族中一个特别的存在------双向链表，它不仅仅是单向链表的简单扩展，更是数据结构设计思想的一次精彩飞跃。

双向链表的起源与意义

历史背景：从限制中诞生

双向链表的概念最早出现在20世纪60年代，当时计算机科学家们正在探索更高效的数据组织方式。单向链表虽然解决了数组固定大小的限制，但存在一个明显的缺陷：只能单向遍历。这种局限性在某些应用场景下变得尤为突出，比如需要频繁反向查找或同时维护前后关系的数据处理任务。

想象一下，你正在阅读一本纸质书，却发现自己没有书签，也没有快速翻回前一页的方法------这就是单向链表的困境。而双向链表就像一本带有智能书签和双向导航功能的电子书，让你可以在数据的世界里自由穿梭。

设计哲学：空间的代价换取时间的自由

双向链表的核心设计理念是"以空间换时间"。它在每个节点中增加了一个指向前驱节点的指针，从而：

• 使逆向遍历成为可能
• 简化了某些删除和插入操作
• 提高了特定场景下的算法效率

这种权衡体现了计算机科学中一个永恒的主题：没有完美的解决方案，只有最适合特定场景的选择。

在现代编程中的实际价值

1. 框架与库的基石：许多现代编程框架（如Linux内核的list.h、C++ STL的list）内部都使用双向链表作为基础数据结构。

2. 复杂系统的构建模块：数据库管理系统、文件系统、GUI框架中的撤销/重做功能等都依赖双向链表。

3. 算法优化的关键：LRU缓存淘汰算法、高级调度算法等都需要双向链表的支持。

数据结构的艺术

双向链表的演化史，是计算机科学家们不断追求更优雅解决方案的缩影。从最初为解决单向链表的限制而诞生，到如今衍生出多种适应不同场景的变体，双向链表教会我们一个重要的编程哲学：

优秀的数据结构设计，总是在约束与自由之间、在简单与强大之间、在现在与未来之间寻找那个恰到好处的平衡点。

让我们一同探索这个看似简单却内涵丰富的数据结构，发现其中蕴含的计算机科学之美。

---

一.双向链表的意义

1. 双向链表的概念和结构

1.1 双向链表的结构

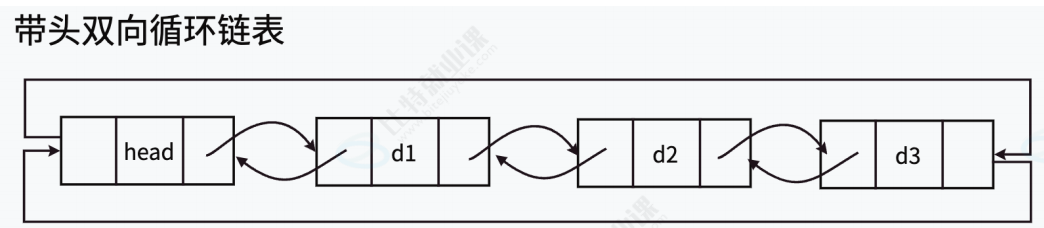
注意：这⾥的"带头"跟前⾯我们说的"头节点"是两个概念，实际前⾯的在单链表阶段称呼不严

谨，但是为了同学们更好的理解就直接称为单链表的头节点。

带头链表⾥的头节点，实际为"哨兵位"，哨兵位节点不存储任何有效元素，只是站在这⾥"放哨的"

"哨兵位"存在的意义：

遍历循环链表避免死循环。

1.2 双向链表中的头节点：导航员的角色

1.2.1 什么是头节点？

在双向链表中，头节点是一个特殊的引用节点，它不存储实际数据，而是作为整个链表的"入口"和"导航起点"。它指向链表中的第一个实际数据节点（如果链表不为空）。

1.2.2 头节点的双重角色

入口点 - 链表的"大门"

// 头节点通常是这样的一个指针变量
Node* head = NULL;  // 初始为空链表

// 当链表有数据时
head = &first_node;  // 指向第一个实际节点

边界哨兵 - 简化操作

头节点作为固定的起点，使得：

• 插入第一个节点时不需要特殊处理
• 判断链表是否为空 只需检查 head == NULL
• 遍历起点始终明确

1.2.3 有无头节点的区别

没有头节点的问题

如果没有头节点，我们需要：

// 直接操作第一个节点
Node* first = NULL;

// 插入第一个节点时要特殊处理
if (first == NULL) {
    first = new_node;  // 特殊情况
} else {
    // 正常插入逻辑
}

有头节点的优势

// 统一的操作逻辑
new_node->next = head->next;
if (head->next != NULL) {
    head->next->prev = new_node;
}
head->next = new_node;
new_node->prev = head;
// 无论链表是否为空，插入逻辑都一致

1.2.4 头节点的关键特性

1. 永远存在：即使链表为空，头节点（或头指针）也始终存在
2. 不存储数据：只负责指向和管理
3. 固定位置：始终在链表的最前端
4. prev为NULL：头节点的前驱指针总是NULL（因为它是最前面的）

可以把头节点想象成：

• 书的封面：不是书的内容，但告诉你从哪里开始读
• 酒店的接待台：不是客房，但指引你找到房间
• 地铁的起点站：不是你要去的地方，但必须从这里出发

头节点是双向链表的逻辑起点 和管理中枢，它虽然不存储实际数据，但极大地简化了链表操作的边界条件处理，使得插入、删除、遍历等操作更加统一和健壮。理解头节点的概念是掌握双向链表操作的关键第一步。

记住：头节点是你的导航仪，有了它，你永远不会在数据结构的海洋中迷失方向。

2.双向链表的主要类型及其应用

2.1 基础双向链表

这是最标准的双向链表形式，每个节点包含数据域、前驱指针和后继指针。

typedef struct Node {
    int data;
    struct Node* prev;
    struct Node* next;
} DNode;

应用场景：需要在两个方向上频繁遍历的数据集合，如浏览器历史记录、音乐播放列表等。

2.2 带哨兵节点的双向链表

哨兵节点（dummy node）是一个不存储实际数据的特殊节点，它的存在简化了边界条件的处理。

typedef struct {
    DNode* head;  // 哨兵头节点
    DNode* tail;  // 哨兵尾节点
    int size;
} DoublyLinkedList;

设计优势：永远不需要检查空链表的情况，代码更加简洁、健壮。

2.3 双向循环链表

这是双向链表与循环链表的结合体，尾节点的next指向头节点，头节点的prev指向尾节点，形成一个闭环。

独特价值：在需要周期性访问数据的应用中表现卓越，如轮转调度算法、环形缓冲区等。

2.4 有序双向链表

在插入时自动保持数据有序排列的双向链表，结合了双向遍历的优势和有序结构的检索效率。

实现要点：需要精心设计插入算法，确保在正确位置插入新元素。

2.5 内存高效型双向链表（XOR链表）

一种利用异或运算存储相邻节点地址的巧妙实现，只需要一个指针字段的空间：

typedef struct XNode {
    int data;
    struct XNode* npx;  // prev XOR next
} XNode;

创新之处：用计算复杂度换取内存空间，适合内存受限的嵌入式系统。

二. 双向链表的实现

我们在这里实现一个最基础的双向链表。

1. 头文件函数声明及链表结构体

typedef int LTDataType;
typedef struct ListNode
 {
 struct ListNode* next; //指针保存下⼀个节点的地址
 struct ListNode* prev; //指针保存前⼀个节点的地址
 LTDataType data;
}LTNode;
//void LTInit(LTNode** pphead);
LTNode* LTInit();
void LTDestroy(LTNode* phead);
void LTPrint(LTNode* phead);
bool LTEmpty(LTNode* phead);
void LTPushBack(LTNode* phead, LTDataType x);
void LTPopBack(LTNode* phead);
void LTPushFront(LTNode* phead, LTDataType x);
void LTPopFront(LTNode* phead);
//在pos位置之后插⼊数据
void LTInsert(LTNode* pos, LTDataType x);
void LTErase(LTNode* pos);
LTNode *LTFind(LTNode* phead,LTDataType x);

2. 各功能函数实现

2.1 双向链表初始化

有两种初始化方式，如下：

2.1.1 方式1：二级指针传参

void LTInit(LTNode** pphead)
{
    *pphead = LTBuyNode(-1);
}

• 调用方式 ：LTInit(&phead);
• 内存位置：直接在传入的指针变量中存储新节点地址
• 特点：无需返回值，通过参数"带回"结果

2.1.2 方式2：返回值

LN* LTInit()
{
    LTNode* phead = LTBuyNode(-1);
    return phead;
}

• 调用方式 ：LN* phead = LTInit();
• 内存位置：函数内部创建指针，通过返回值传递
• 特点：简洁直观，直接获取结果

2.1.3 那么哪种方式更好呢？下面直接给出结论和理由。

结论：方式2（返回值）更好，是现代C语言推荐写法

理由：

1. 代码简洁性

   • 无需二级指针，逻辑更清晰
   • 符合"函数最好有返回值"的设计理念

2. 可读性

   • LN* phead = LTInit(); 一目了然
   • 二级指针容易让初学者困惑

3. 安全性

   • 避免了对传入指针为NULL的检查
   • 不会因为误操作修改传入指针外的内容

4. 一致性

   • 与LTBuyNode的设计一致（都是返回值）
   • 标准库也常用这种模式：fopen、malloc等

二级指针仍有其价值，主要在以下场景：

// 1. 需要修改多个指针时
void LTInit(LTNode** pphead, LTNode** ptail)

// 2. 函数需要返回其他状态时
int LTInit(LTNode** pphead)  // 返回0成功，-1失败

// 3. 已存在的初始化函数需要统一接口

但在该双向链表初始化场景中，返回值方式更优。

2.2 双向链表的打印 LTPrint

void LTPrint(LTNode* phead)
{
	LTNode* pcur = phead->next;  // 跳过哨兵位，从第一个有效节点开始
	while (pcur != phead)        // 循环回到哨兵位时结束
	{
		printf("%d->", pcur->data);
		pcur = pcur->next;       // 指针后移
	}
	printf("\n");
}

实现原理：

• 双向链表带头结点（哨兵位），第一个有效节点是phead->next
• 遍历结束条件：pcur != phead，因为哨兵位是环的入口
• 不打印哨兵位的-1数据，只打印有效节点

为何如此设计：

• 带头结点的好处：空链表时phead->next == phead，不会进入循环，安全
• 环形结构特性：遍历一圈回到起点即结束

---

2.3 申请节点 LTBuyNode

LTNode* LTBuyNode(LTDataType x)
{
	LTNode* node = (LTNode*)malloc(sizeof(LTNode));
	if (node == NULL)           // 内存分配失败处理
	{
		perror("malloc fail!");
		exit(1);
	}
	node->data = x;
	node->next = node->prev = node;  // 新节点自己指向自己（环形）
	return node;
}

实现原理：

• 动态内存分配，返回新节点指针
• 关键操作 ：将新节点的next和prev都指向自己

为何如此设计：

• 单个节点自成环形，符合双向循环链表的特性
• 后续插入时无需特殊处理prev/next的初始值
• 封装成独立函数，避免重复写内存分配代码

---

2.4 尾插 LTPushBack

void LTPushBack(LTNode* phead, LTDataType x)
{
	assert(phead);                     // 哨兵位必须存在
	LTNode* newnode = LTBuyNode(x);
	
	// 新节点连接前后节点
	newnode->prev = phead->prev;       // 新节点的prev指向原尾节点
	newnode->next = phead;            // 新节点的next指向哨兵位
	
	// 前后节点连接新节点
	phead->prev->next = newnode;      // 原尾节点的next指向新节点
	phead->prev = newnode;            // 哨兵位的prev指向新节点（新尾）
}

实现原理：

• 在哨兵位phead的前一个节点 之后插入（因为循环链表，尾节点是phead->prev）
• 4步指针操作：新节点连接前后 + 前后节点连接新节点

为何如此设计：

• 双向链表尾插时间复杂度O(1)，不需要遍历
• 顺序很重要：先处理新节点 （它还没在链表中），再处理旧节点（避免丢失节点）
• 无需特殊处理空链表，因为哨兵位prev指向自己

---

2.5 头插 LTPushFront

void LTPushFront(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* newnode = LTBuyNode(x);
	
	// 新节点连接前后
	newnode->next = phead->next;       // 新节点的next指向原第一个节点
	newnode->prev = phead;            // 新节点的prev指向哨兵位
	
	// 前后节点连接新节点
	phead->next->prev = newnode;      // 原第一个节点的prev指向新节点
	phead->next = newnode;           // 哨兵位的next指向新节点（新第一个）
}

实现原理：

• 在哨兵位phead的下一个节点之前插入
• 4步指针操作，与尾插对称

为何如此设计：

• 头插O(1)时间复杂度
• 注意：必须先改phead->next->prev，不能先改phead->next
• 如果先改phead->next，会丢失原第一个节点的地址

---

2.6 尾删 LTPopBack

void LTPopBack(LTNode* phead)
{
	// 链表必须有效且不能为空（只有哨兵位）
	assert(phead && phead->next != phead);
	
	LTNode* del = phead->prev;        // 待删除的尾节点
	
	// 跳过del节点，连接前后
	del->prev->next = phead;         // 尾节点的前一个节点的next指向哨兵位
	phead->prev = del->prev;        // 哨兵位的prev指向尾节点的前一个节点
	
	// 删除del节点
	free(del);
	del = NULL;
}

实现原理：

• 删除哨兵位的前一个节点（尾节点）
• 先让链表绕过del节点，再释放内存

为何如此设计：

• 必须断言链表不为空 ：phead->next != phead
• 先修改链表结构，再释放节点
• 释放后置NULL是好习惯，防止野指针

---

2.7 头删 LTPopFront

void LTPopFront(LTNode* phead)
{
	assert(phead && phead->next != phead);
	
	LTNode* del = phead->next;        // 待删除的第一个有效节点
	
	// 跳过del节点
	phead->next = del->next;         // 哨兵位的next指向第二个节点
	del->next->prev = phead;        // 第二个节点的prev指向哨兵位
	
	// 删除del节点
	free(del);
	del = NULL;
}

实现原理：

• 删除哨兵位的下一个节点（第一个有效节点）
• 让哨兵位直接指向第二个节点

为何如此设计：

• 对称于尾删
• 注意：如果只有一个有效节点，删除后phead->next == phead（空链表状态）

---

2.8 查找 LTFind

LTNode* LTFind(LTNode* phead, LTDataType x)
{
	LTNode* pcur = phead->next;
	while (pcur != phead)           // 遍历有效节点
	{
		if (pcur->data == x)
		{
			return pcur;           // 找到立即返回节点指针
		}
		pcur = pcur->next;
	}
	return NULL;                  // 遍历完没找到
}

实现原理：

• 遍历有效节点，比较数据值
• 返回节点指针，而非位置索引

为何如此设计：

• 返回指针便于后续的插入（LTInsert）和删除（LTErase）操作
• 时间复杂度O(n)
• 找不到返回NULL，调用方需判断

---

2.9 特定位置插入 LTInsert

// 在pos位置之后插入数据
void LTInsert(LTNode* pos, LTDataType x)
{
	assert(pos);
	
	LTNode* newnode = LTBuyNode(x);
	
	// 新节点连接前后
	newnode->next = pos->next;
	newnode->prev = pos;
	
	// 前后节点连接新节点
	pos->next->prev = newnode;
	pos->next = newnode;
}

实现原理：

• 在pos之后插入，不是之前
• 4步指针操作，与头插/尾插本质相同

为何如此设计：

• 为什么不实现在pos之前插入？
  • 因为双向链表对称，之后插入已经够用
  • 想插之前，调用LTInsert(pos->prev, x)即可
• pos不能是NULL，需要断言
• 这个函数可以替代头插和尾插 ：
  • 头插：LTInsert(phead, x)
  • 尾插：LTInsert(phead->prev, x)

---

2.10 删除特定位置 LTErase

void LTErase(LTNode* pos)
{
	// pos理论上来说不能为phead，但没有参数phead，无法校验
	assert(pos);
	
	// 跳过pos节点
	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;
	
	free(pos);
	pos = NULL;
}

实现原理：

• 删除指定的节点pos
• 让pos的前后节点直接相连

为何如此设计：

• 缺陷：无法校验pos是否为哨兵位，因为没有phead参数
• 解决方案1：增加phead参数
• 解决方案2：调用方自己保证不传哨兵位
• 这个函数可以替代头删和尾删 ：
  • 头删：LTErase(phead->next)
  • 尾删：LTErase(phead->prev)

---

2.11 双向链表的销毁 LTDesTroy

void LTDesTroy(LTNode* phead)
{
	assert(phead);
	
	LTNode* pcur = phead->next;
	while (pcur != phead)           // 遍历有效节点
	{
		LTNode* next = pcur->next;  // 先保存下一个节点
		free(pcur);                // 释放当前节点
		pcur = next;              // 指向下一个节点
	}
	// 此时pcur指向phead，释放哨兵位
	free(phead);
	phead = NULL;
}

实现原理：

• 分两步：先释放所有有效节点 ，再释放哨兵位
• 遍历时需要先保存下一个节点指针，再释放当前节点

为何如此设计：

• 为什么要先保存next？
  • 因为free(pcur)后，pcur->next是野指针，无法访问
• 为什么有效节点和哨兵位分开释放？
  • 环形结构，不能一次性释放全部
  • 先断开环，逐个释放有效节点，最后释放哨兵位
• 注意 ：函数内部的phead = NULL对外部无效
  • 外部需要手动置空：phead = NULL;
  • 或使用二级指针解决

---

总结：双向链表的完整图景

一、核心思想回顾

双向链表 不仅仅是一种数据结构，更是一种空间与时间的权衡艺术。通过在每个节点中增加一个前驱指针，我们获得了：

收获	代价
✅ 双向遍历能力	⚠️ 每个节点多8字节（64位系统）
✅ O(1)尾插尾删	⚠️ 指针维护更复杂
✅ 任意位置高效删除	⚠️ 内存占用增加
✅ 代码逻辑统一	⚠️ 初学者理解门槛提高

但在这个实现中，我们做了一个更聪明的选择------带头节点的双向循环链表，它让所有边界条件都消失了：空链表、第一个节点、最后一个节点...全部统一处理。

---

二、函数设计的黄金法则

链表操作的四大法则：

法则1：先连接新节点，再断开旧节点

// 插入时：新节点先"伸手"握住前后
newnode->prev = pos;
newnode->next = pos->next;
// 然后再让前后节点"回握"新节点
pos->next->prev = newnode;
pos->next = newnode;

法则2：删除节点前必须先保存后继

// 销毁时：先保存next，再free当前
LTNode* next = pcur->next;  // ✨ 救生索
free(pcur);
pcur = next;

法则3：哨兵位永不删除、永不移动

• 哨兵位是链表的"定海神针"
• 所有操作都围绕它展开，但绝不释放它（直到最终销毁）

法则4：函数接口的设计要自洽

• 初始化：返回值 （优于二级指针）
• 插入/删除：传哨兵位或pos指针
• 查找：返回节点指针，便于直接操作

---

三、常见陷阱与避坑指南

陷阱	后果	解决方案
忘记断言phead	对NULL指针操作	所有函数第一行assert
释放后不置NULL	野指针	free后手动置NULL
销毁后外部仍使用	内存错误	外部需手动phead=NULL
误删哨兵位	链表结构破坏	LTErase需调用方保证
遍历时直接free	丢失next指针	先保存，再释放

---

四、下一步：你能做什么？

掌握了基础双向链表，你可以：

🔹 实现更高级的数据结构 ：双向队列、循环双链表、跳表

🔹 阅读源码 ：Linux内核链表、STL list实现

🔹 解决实际问题 ：约瑟夫环、文本编辑器的撤销重做

🔹 优化改进：加入尾指针、实现迭代器接口、泛型化

---

数据结构的学习从来不是终点，而是起点。 双向链表教会我们的不仅是几个函数如何写，更是如何在约束中寻找优雅，在复杂中提炼简单。

当你下次面对一个看似棘手的数据组织问题时，不妨问问自己："我能用哨兵位简化边界吗？我能用对称性统一逻辑吗？"

感谢各位大佬的观看！