[深度学习网络从入门到入土] 拓展 - 激活函数

深度学习网络从入门到入土 拓展 - 激活函数

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

• [深度学习网络从入门到入土 拓展 - 激活函数](#[深度学习网络从入门到入土] 拓展 - 激活函数)
• 个人导航
• Sigmoid
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• Tanh
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• [Tanh - LeNet5](#Tanh - LeNet5)
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• ReLU
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• Leaky_ReLU
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• PReLU
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)
• GeLU
• • • • [1. 好处](#1. 好处)
      • [2. 坏处](#2. 坏处)
      • [3. 结论](#3. 结论)

Sigmoid

Sigmoid 是最早被广泛用于神经网络的激活函数之一，源于生物神经元发放率模型
f ( x ) = 1 1 + e − x f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f(x)=\frac{1}{1+e^{-x}} \\ f'(x)=f(x)(1-f(x)) f(x)=1+e−x1f′(x)=f(x)(1−f(x))

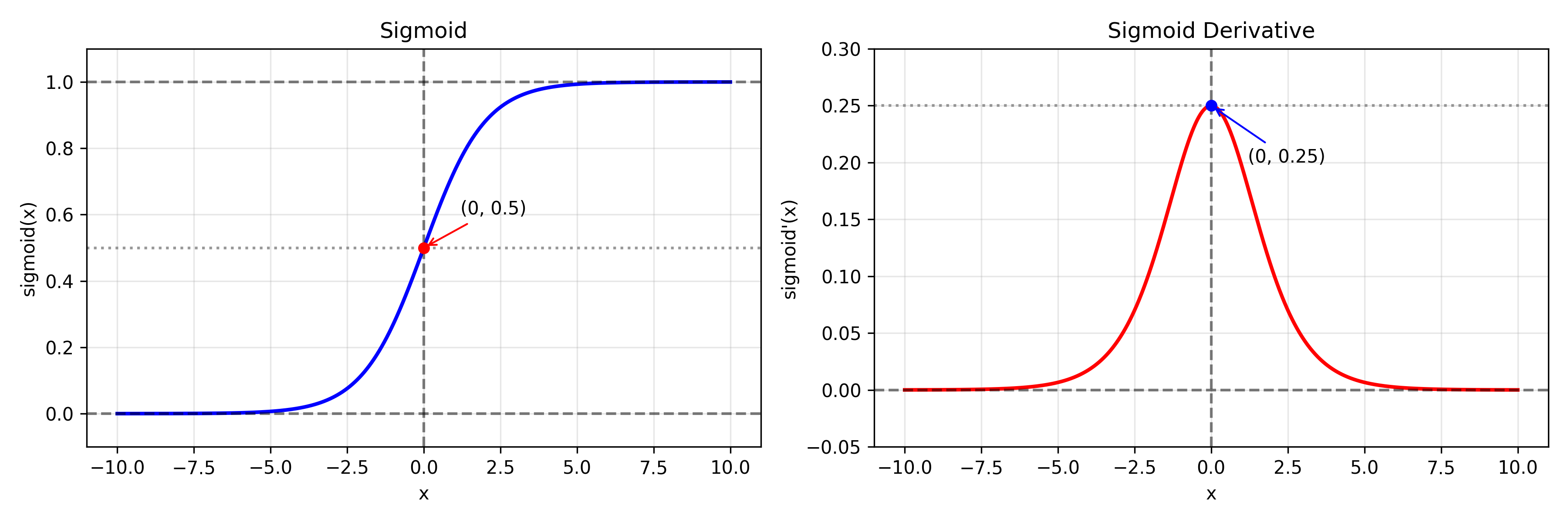
1. 好处

输出范围在 (0,1)，非常适合做：

• 概率建模（Logistic Regression）
• 二分类输出层

2. 坏处

导数 f ′ ( x ) f'(x) f′(x)最大值只有 0.25

-> 当 |x| 很大时，梯度趋近 0 ------ 直接导致深层网络训练困难

非零中心

-> 输出始终为正，导致梯度更新方向偏移, 收敛速度慢

饱和区问题

-> 当 x 很大或很小时，函数进入"饱和区"，梯度几乎为 0

3. 结论

Sigmoid 现在几乎只用于 输出层（概率），很少用于隐藏层

Tanh

f ( x ) = tanh ⁡ ( x ) f ′ ( x ) = 1 − tanh ⁡ 2 ( x ) f(x)=\tanh(x) \\ f'(x)=1-\tanh^2(x) f(x)=tanh(x)f′(x)=1−tanh2(x)

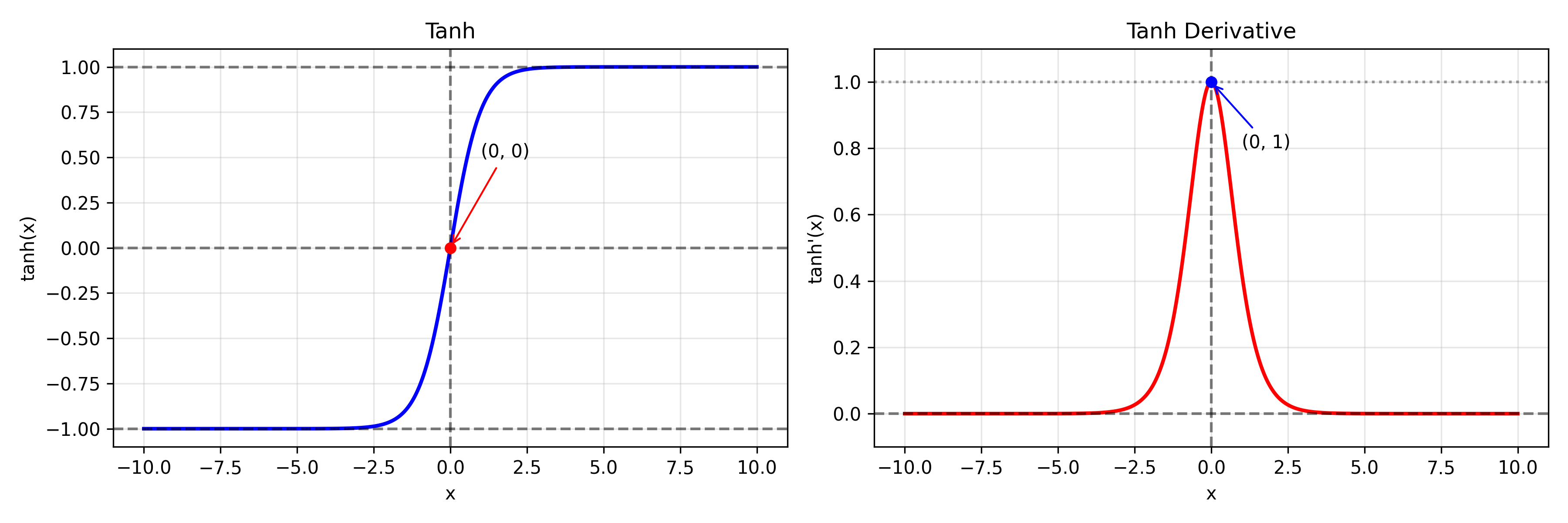
1. 好处

输出范围在 (-1,1)

• 零中心
  -> 梯度更新方向更加均衡，收敛速度比 Sigmoid 更快
• 梯度最大值为 1
  -> 比 Sigmoid 的 0.25 大

2. 坏处

依然存在梯度消失问题

-> 当 |x| 很大时仍进入饱和区, 深层网络训练依然困难

指数运算

-> 计算量相对较大

3. 结论

Tanh 比 Sigmoid 更适合隐藏层, 但在深层网络时代仍然不够理想, 在 ReLU 出现后逐渐被淘汰

Tanh - LeNet5

缩放版的 Tanh
f ( x ) = 1.7159 tanh ⁡ ( 2 3 x ) f ′ ( x ) = 1.7159 ⋅ 2 3 ( 1 − tanh ⁡ 2 ( 2 3 x ) ) f(x)=1.7159\tanh\left(\frac{2}{3}x\right) \\ f'(x) = 1.7159 \cdot \frac{2}{3} \left( 1-\tanh^2\left(\frac{2}{3}x\right) \right) f(x)=1.7159tanh(32x)f′(x)=1.7159⋅32(1−tanh2(32x))

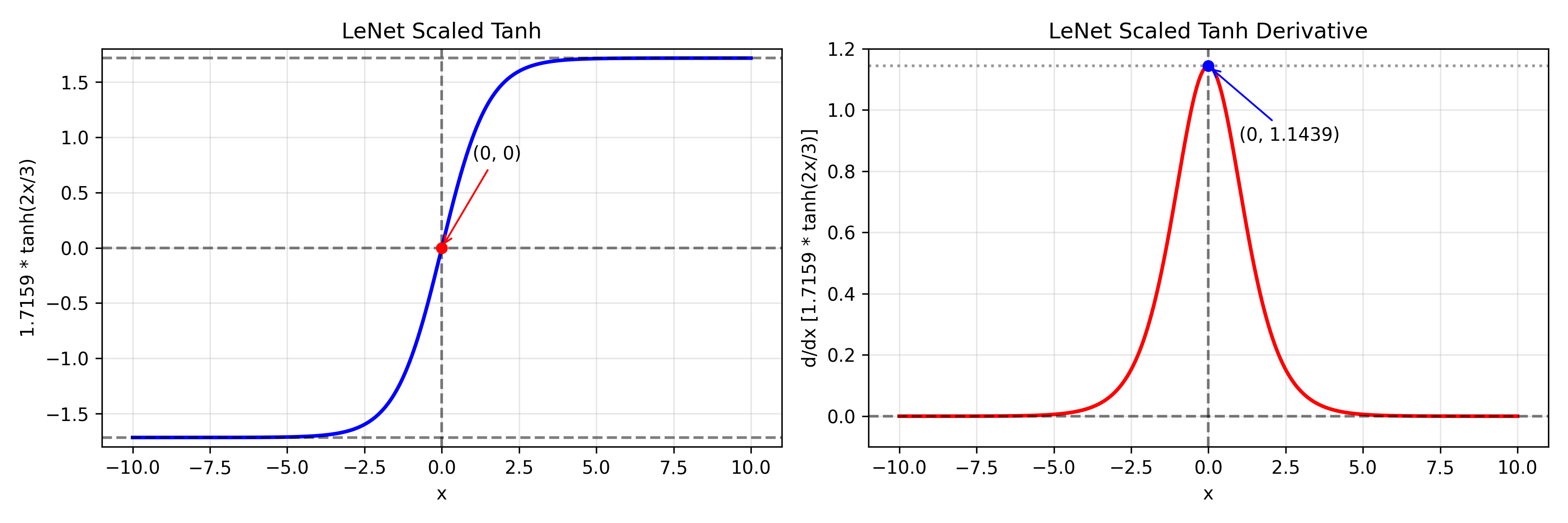
1. 好处

目的：

• 放大梯度
• 避免过早饱和
• 加速收敛

2. 坏处

本质仍然是 Tanh

-> 饱和问题依然存在

-> 深层网络依然难训练

3. 结论

属于"早期工程优化手段", 在 ReLU 出现后逐渐被淘汰

ReLU

f ( x ) = max ⁡ ( 0 , x ) f ′ ( x ) = { 1 x > 0 0 x ≤ 0 f(x)=\max(0,x) \\ f'(x)= \begin{cases} 1 & x>0\\ 0 & x\le0 \end{cases} f(x)=max(0,x)f′(x)={10x>0x≤0

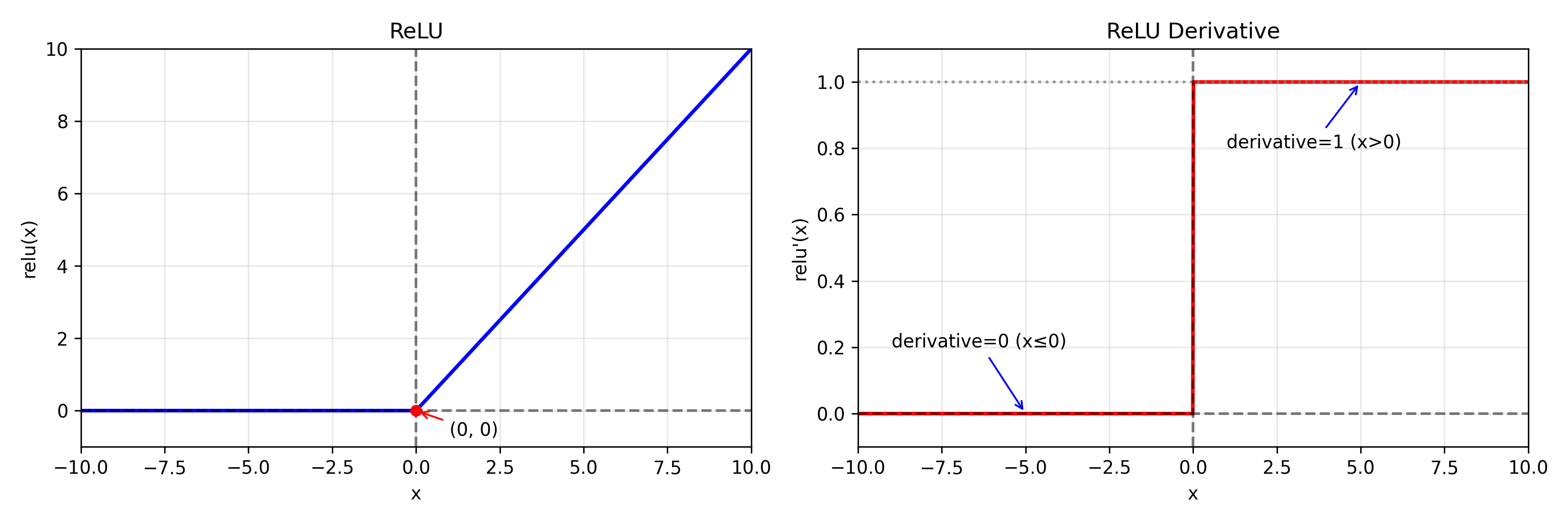
1. 好处

正区间梯度恒为 1

-> 大幅缓解梯度消失

计算简单

-> 不涉及指数运算

稀疏性

-> 负区间输出为 0，提高表达效率

2. 坏处

神经元死亡问题

-> 若权重更新后始终落在负区间

-> 梯度为 0，永久无法恢复

非零中心

-> 输出全部非负

3. 结论

ReLU 让深度网络真正可训练, 成为现代 CNN 默认激活函数

Leaky_ReLU

f ( x ) = { x x > 0 α x x ≤ 0 f ′ ( x ) = { 1 x > 0 α x < 0 f(x)= \begin{cases} x & x>0\\ \alpha x & x\le0 \end{cases} \\ f'(x)= \begin{cases} 1 & x>0\\ \alpha & x<0 \end{cases} f(x)={xαxx>0x≤0f′(x)={1αx>0x<0

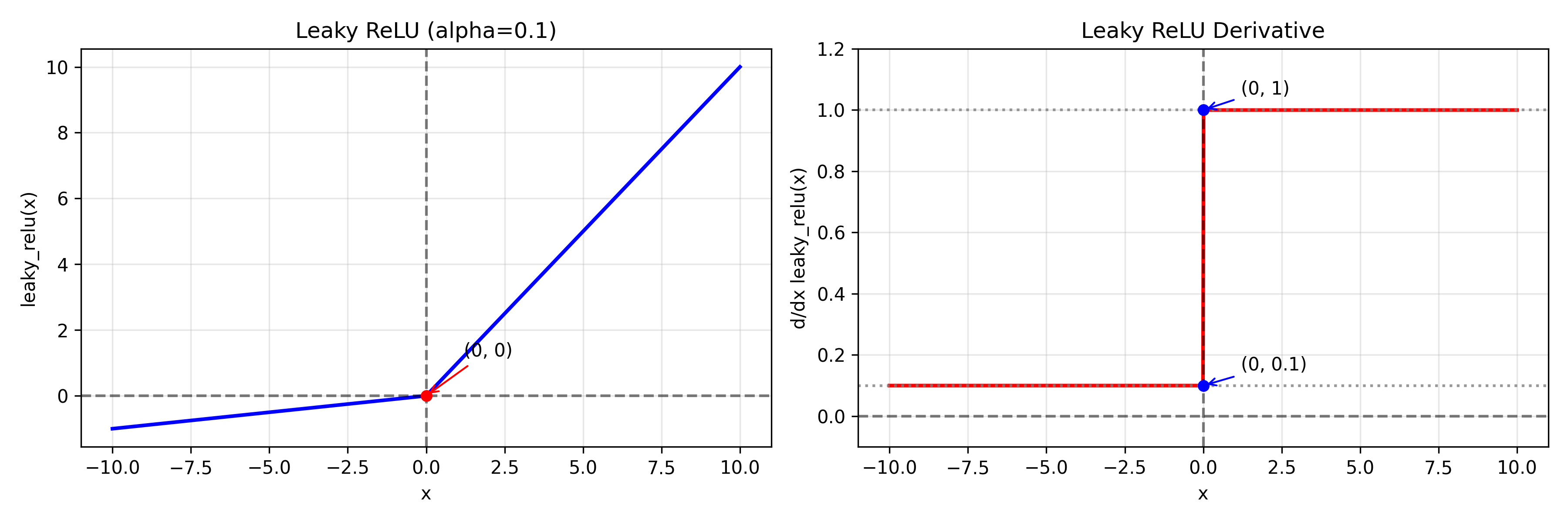
1. 好处

负区间保留小梯度

-> 避免"死亡神经元"

2. 坏处

α 需要人为设定

-> 不同任务最优值不同

仍然不是严格零中心

3. 结论

ReLU 的小改进版, 在一些任务中更稳定

PReLU

f ( x ) = max ⁡ ( 0 , x ) + a min ⁡ ( 0 , x ) ∂ f ∂ x = { 1 x > 0 a x < 0 ∂ f ∂ a = { 0 x > 0 x x < 0 f(x)=\max(0,x)+a\min(0,x) \\ \frac{\partial f}{\partial x} = \begin{cases} 1 & x>0\\ a & x<0 \end{cases} \quad\quad\quad \frac{\partial f}{\partial a} = \begin{cases} 0 & x>0\\ x & x<0 \end{cases} f(x)=max(0,x)+amin(0,x)∂x∂f={1ax>0x<0∂a∂f={0xx>0x<0

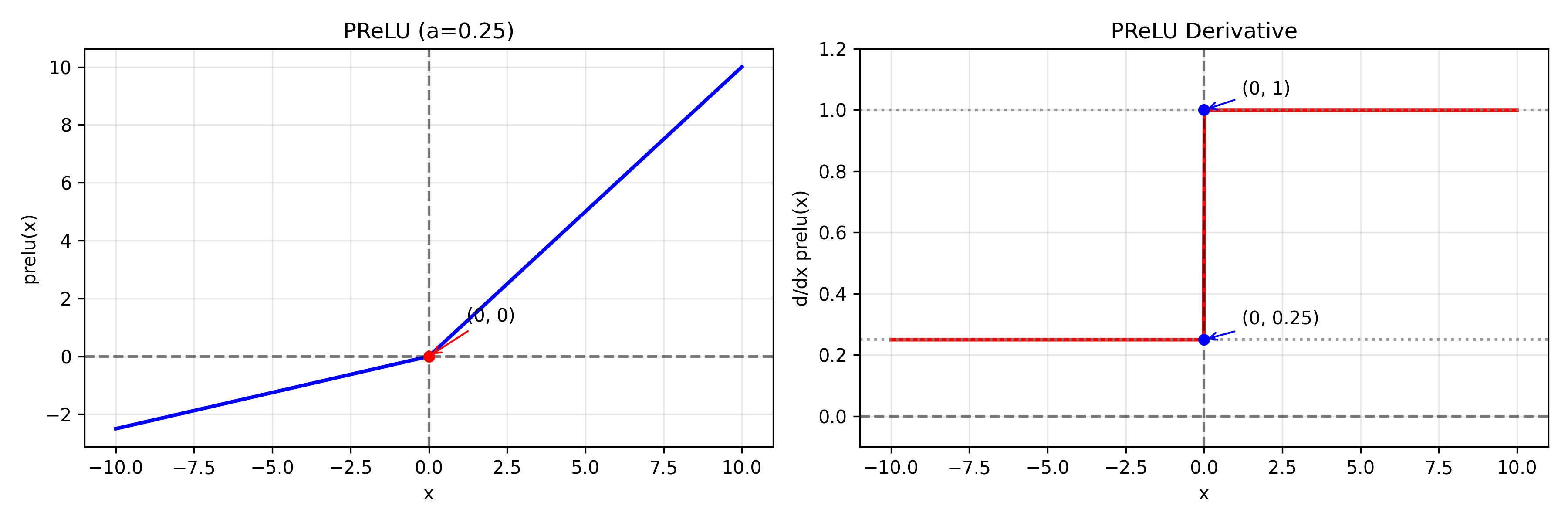
1. 好处

负区间斜率 a 可学习

-> 自适应调整

通常优于固定 Leaky ReLU

2. 坏处

• 增加参数量
• 小数据集可能过拟合
• 仍然是分段线性

3. 结论

更"智能"的 ReLU, 但主流依然是普通 ReLU

(在 ICCV 2015 中提出)

GeLU

f ( x ) = x Φ ( x ) f ′ ( x ) = Φ ( x ) + x ϕ ( x ) f(x)=x\Phi(x) \\ f'(x)=\Phi(x)+x\phi(x) f(x)=xΦ(x)f′(x)=Φ(x)+xϕ(x)

常用近似：
f ( x ) ≈ 0.5 x ( 1 + tanh ⁡ ( 2 π ( x + 0.044715 x 3 ) ) ) f ′ ( x ) ≈ 0.5 ( 1 + tanh ⁡ u ) + 0.5 x ( 1 − tanh ⁡ 2 u ) c ( 1 + 0.134145 x 2 ) 其中 { u = c ( x + 0.044715 x 3 ) c = 2 π f(x) \approx 0.5x\left(1+\tanh\left(\sqrt{\frac{2}{\pi}}\left(x+0.044715x^3\right)\right)\right) \\ f'(x) \approx 0.5(1+\tanh u) + 0.5x(1-\tanh^2 u) c(1+0.134145x^2) \\ \text{其中} \begin{cases} u=c(x+0.044715x^3) \\ c=\sqrt{\frac{2}{\pi}} \end{cases} f(x)≈0.5x(1+tanh(π2 (x+0.044715x3)))f′(x)≈0.5(1+tanhu)+0.5x(1−tanh2u)c(1+0.134145x2)其中{u=c(x+0.044715x3)c=π2

已知 d d x Φ ( x ) = ϕ ( x ) \frac{d}{dx}\Phi(x)=\phi(x) dxdΦ(x)=ϕ(x)

φ ( x ) φ(x) φ(x) 是标准正态分布 PDF: ϕ ( x ) = 1 2 π e − x 2 / 2 \phi(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2} ϕ(x)=2π 1e−x2/2

Φ ( x ) \Phi(x) Φ(x) 是累积分布函数 CDF: Φ ( x ) = ∫ − ∞ x ϕ ( t )   d t \Phi(x)=\int_{-\infty}^{x}\phi(t)\,dt Φ(x)=∫−∞xϕ(t)dt

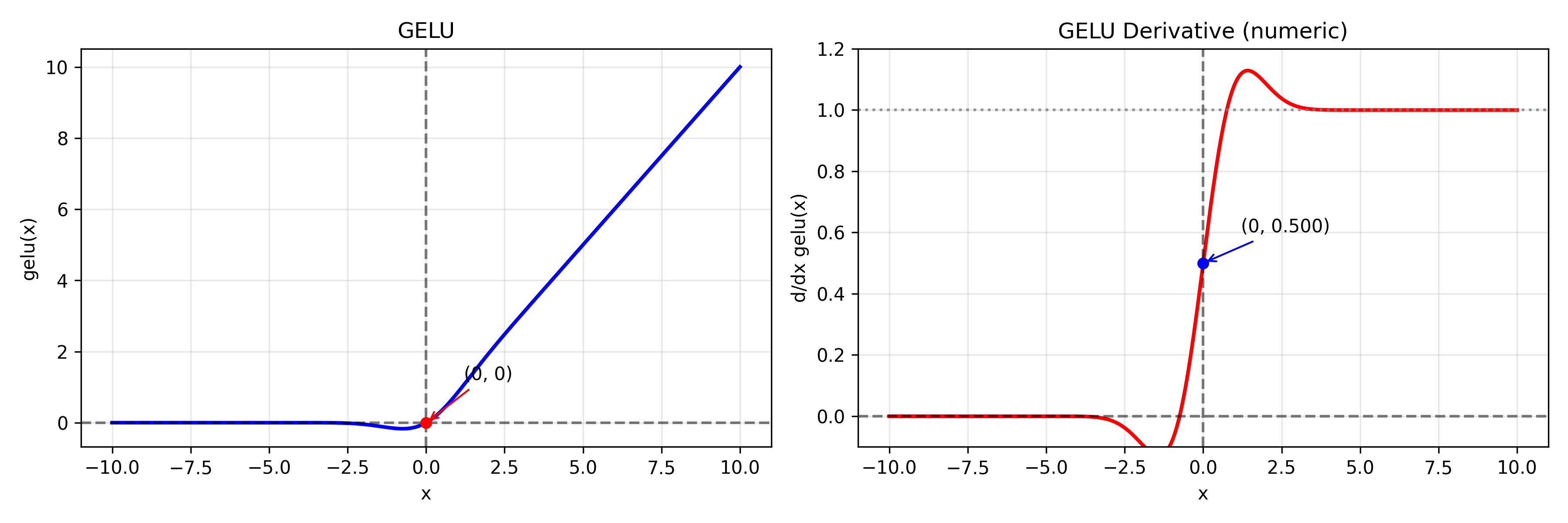
1. 好处

• 平滑
• 概率解释更自然
• 在 Transformer 中效果优于 ReLU

2. 坏处

• 计算复杂
• 推理速度略慢
• 在 CNN 中优势不明显

3. 结论

Transformer 时代主流激活函数, 更适合大模型

(被 BERT 等模型广泛采用)