TensorFlow 实现线性回归

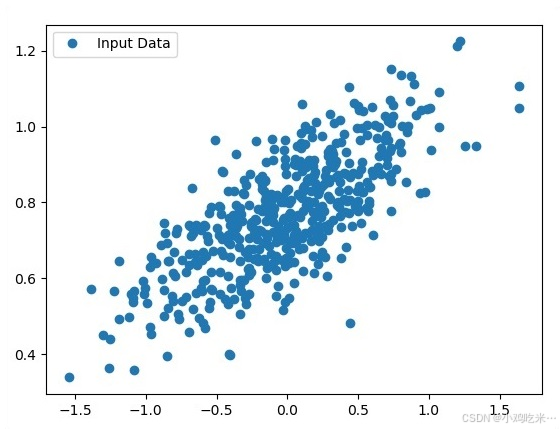
摘要：本文介绍了使用TensorFlow实现线性回归的基础方法。线性回归通过建立Y=Ax+b的线性关系模型，分析预测变量与自变量之间的关系。实现步骤包括：1）导入NumPy和Matplotlib库；2）设置参数生成500个模拟数据点；3）添加随机噪声构建数据集；4）可视化展示数据分布。最终生成的样本数据在x轴(-1.5,1.5)和y轴(0.4,1.2)范围内呈现线性分布，为后续训练线性回归模型提供基础数据。

[TensorFlow 实现线性回归](#TensorFlow 实现线性回归)

结果解读

设计线性回归算法的步骤

[步骤 1：导入必要模块](#步骤 1：导入必要模块)

[步骤 2：定义相关参数](#步骤 2：定义相关参数)

[步骤 3：生成模拟数据点](#步骤 3：生成模拟数据点)

[步骤 4：可视化生成的数据集](#步骤 4：可视化生成的数据集)

线性回归完整代码

TensorFlow 实现线性回归

在本章中，我们将介绍使用 TensorFlow 实现线性回归的基础示例。逻辑回归或线性回归是一种监督式机器学习方法，可用于对有序离散类别进行分类。本章的目标是构建一个模型，帮助用户预测预测变量与一个或多个自变量之间的关系。

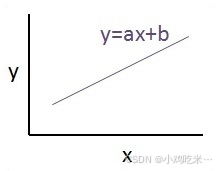
我们认为这两个变量之间存在线性关系。若将y设为因变量，x设为自变量，那么两个变量的线性回归关系可用如下公式表示：Y=Ax+b

我们将设计一个线性回归算法，通过该算法能理解以下两个核心概念：

代价函数
梯度下降算法

线性回归的示意图如下：

结果解读

y=ax+b中：

a为斜率
b为纵截距
r为相关系数
r2为决定系数

线性回归公式的可视化图形表示为y=ax+b，横轴为X。

设计线性回归算法的步骤

接下来我们学习设计线性回归算法的具体步骤。

步骤 1：导入必要模块

首先导入绘制线性回归图像所需的 Python 库，包括数值计算库 NumPy 和绘图库 Matplotlib：

python 复制代码

import numpy as np 
import matplotlib.pyplot as plt

步骤 2：定义相关参数

设定生成数据点的数量，并定义线性回归公式中的斜率和纵截距（原文此处笔误写为逻辑回归，实际为线性回归）：

python 复制代码

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

步骤 3：生成模拟数据点

通过循环，围绕线性回归公式Y=0.22x+0.78生成 500 个带随机噪声的模拟数据点：

python 复制代码

for i in range(number_of_points): 
    x = np.random.normal(0.0,0.5) 
    y = a*x + b + np.random.normal(0.0,0.1)
    x_point.append([x]) 
    y_point.append([y])

步骤 4：可视化生成的数据集

使用 Matplotlib 将生成的随机数据点绘制成图，直观展示数据分布：

python 复制代码

plt.plot(x_point,y_point, 'o', label = 'Input Data')
plt.legend()
plt.show()

线性回归完整代码

整合上述步骤，线性回归的完整实现代码如下：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78
for i in range(number_of_points): 
    x = np.random.normal(0.0, 0.5) 
    y = a*x + b + np.random.normal(0.0, 0.1)
    x_point.append([x]) 
    y_point.append([y]) 
   
plt.plot(x_point, y_point, 'o', label = 'Input Data')
plt.legend() 
plt.show()

上述代码中生成的 500 个数据点即为模型的输入数据，数据点的分布范围大致为：纵轴取值：0.4~1.2横轴取值：-1.5~1.5