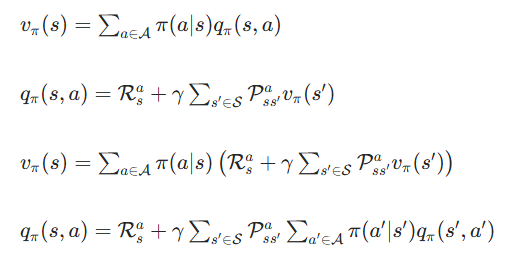前言
本博客是本人的学习笔记,不是教学或经验分享,全部资料基于北京邮电大学鲁鹏老师课程强化学习基础 (本科生课程) 北京邮电大学 鲁鹏_哔哩哔哩_bilibili,侵权即删。
一、前置知识回顾(强化学习基础)
本部分是理解 MDP 的前提,核心是明确强化学习的核心设定与智能体 - 环境的交互逻辑。
1. 强化学习的核心特点
1.无监督数据,仅依靠奖励信号学习
2.奖励存在延迟,非实时反馈
3.时间是核心影响因素,序列决策是核心问题
4.智能体当前动作会影响后续接收的观测与奖励
5.奖励假设:所有强化学习问题的目标,都可描述为最大化期望的累积奖励
2. 智能体与环境的交互流程
在每个时间步t,形成闭环交互:
智能体:接收环境的观测Ot、奖励Rt → 执行动作At
环境:接收智能体的动作At → 生成下一时刻观测Ot+1、奖励Rt+1
3. 历史与状态
历史Ht:观测、动作、奖励的完整序列,是截至t时刻的所有信息Ht=O1,R1,A1,O2,R2,A2,...,Ot,Rt
状态St:历史的函数St=f(Ht),是决定未来发生什么的核心信息,是对历史的充分统计。
4. 环境的可观测性
完全可观测:智能体可直接观测到全部环境状态(如围棋、象棋),天然满足马尔可夫性质
部分可观测:智能体仅能部分观测环境(如麻将、斗地主),需额外处理历史信息
5. 智能体的核心组件
强化学习智能体由以下 1 个或多个组件构成,是后续 MDP 的核心落地载体:

6. 强化学习的三大核心问题
|--------------|------------------------------------|
| 问题分类 | 核心定义 |
| 学习与规划 | 学习:环境未知,靠交互优化策略;规划:环境模型已知,靠计算优化策略 |
| 探索与利用 | 探索:放弃短期奖励,获取环境更多信息;利用:用已知信息最大化即时奖励 |
| 预测与控制 | 预测:给定策略,评估未来的奖励;控制:找到最优策略,最大化未来奖励 |
二、马尔可夫过程(MP, Markov Processes)
马尔可夫过程是所有后续模型的基础,核心是马尔可夫性质。
1. 核心:马尔可夫性质
通俗理解:未来只与现在有关,与过去无关。
数学定义: 即给定当前状态,未来与历史完全独立,当前状态是历史的充分统计。
即给定当前状态,未来与历史完全独立,当前状态是历史的充分统计。
2. 状态转移矩阵

3. 马尔可夫过程(马尔可夫链)的定义

4. 核心示例:学生的马尔可夫链
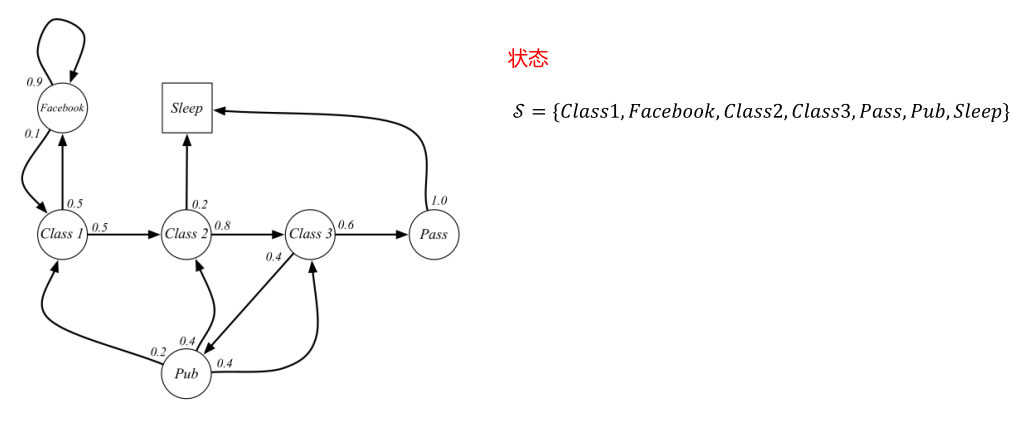
核心转移:Class1 以 0.5 概率到 Class2,0.5 概率到 Facebook;Sleep 为终止状态
分幕 (Episodes):从初始状态出发,到终止状态结束的状态序列,是马尔可夫链的采样结果示例幕:C1 → C2 → C3 → Pass → Sleep
三、马尔可夫奖励过程(MRP, Markov Reward Processes)
MRP 是带价值的马尔可夫链,在 MP 的基础上引入了奖励与折扣机制,是连接 MP 与 MDP 的关键桥梁。
1. MRP 的定义
2. 核心概念:回报 (Return)
定义:从t时刻状态S_t出发,到终止状态的衰减累积奖励,记为
折扣因子 γ 的核心作用(复习重点):
避免带环的马尔可夫过程出现无限大的回报
符合金融逻辑:即时奖励比延迟奖励价值更高
符合生物 / 人类行为对即时奖励的偏好
量化未来奖励的不确定性
极端情况:γ=0时,只关注眼前即时奖励;γ=1时,未来奖励与即时奖励等价
3. 核心概念:价值函数 (Value Function)
价值函数是强化学习的核心,用于量化一个状态的长期价值。
定义:一个状态的期望回报 
物理意义:输入一个状态,输出该状态下,智能体未来能获得的期望累积奖励,v(s)越大,说明该状态越 "好"。
关键特性:价值函数与折扣因子γ强相关,γ越大,越关注长期奖励,状态价值差异越明显。
4. 核心方程:MRP 的贝尔曼方程
贝尔曼方程是求解价值函数的核心,本质是将价值函数分解为「即时奖励」+「后继状态的折扣价值」。
(1)基础形式与推导
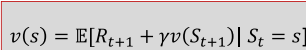

用s'表示当前状态s的所有可能后继状态,贝尔曼方程可展开为: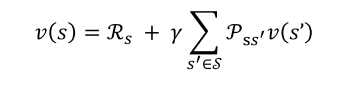
矩阵形式为:
(2)贝尔曼方程的求解
直接解析解:通过矩阵求逆求解,复杂度为O(|S|^3),仅适用于小型 MRPv=(I−γP)−1R
迭代求解方法(适用于大型 MRP,后续课程核心):动态规划 (DP)、蒙特卡洛评估 (MC)、时序差分学习 (TD)
四、马尔可夫决策过程(MDP, Markov Decision Processes)
MDP 是强化学习问题的数学理想化形式,几乎所有强化学习问题都可转化为 MDP,核心是在 MRP 的基础上引入了「动作」与「策略」,实现了智能体的决策能力。
1. MDP 的定义

2. 核心概念:策略 (Policy)


3. MDP 的价值函数
MDP 包含两类价值函数,是策略评估与优化的核心,二者存在明确的关联关系。
(1)状态价值函数

(2)动作价值函数

(3)两类价值函数的关联
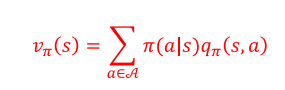
通俗理解:状态价值,是该状态下所有动作的动作价值,按策略概率加权的平均;动作价值,是执行该动作后的即时奖励,加之后继状态价值的折扣期望。
4. 贝尔曼期望方程
贝尔曼期望方程是 MDP 策略评估的核心,是 MRP 贝尔曼方程在 MDP 下的扩展,同样可分解为即时奖励 + 后继状态折扣价值。
(1)状态价值的贝尔曼期望方程
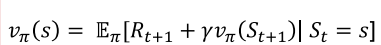
展开形式(结合价值函数关联关系):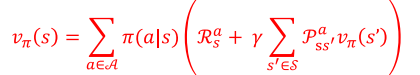
(2)动作价值的贝尔曼期望方程
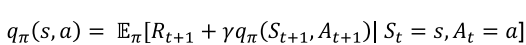
展开形式:

5. 最优价值函数与最优策略
强化学习的最终目标,是找到最优策略,实现累积奖励最大化。
(1)最优价值函数

核心意义:一旦求出最优价值函数,MDP 就被认为完成求解,最优价值函数明确了 MDP 能达到的最优表现。
(2)最优策略

核心特性:所有最优策略,都共享相同的最优状态价值函数和最优动作价值函数。
(3)最优策略的求解
最优策略可通过最大化最优动作价值函数直接得到,是确定性策略:当其他情况通俗理解:在每个状态s,直接选择能让q*(s,a)最大的动作,就是最优策略。
6. 贝尔曼最优方程
贝尔曼最优方程是求解最优价值函数的核心,本质是最优价值函数的自洽递推关系,是非线性方程,无直接解析解,需迭代求解。
(1)核心形式
基于最优价值函数的关联关系,得到两个核心方程:
(2)展开形式
最优状态价值的贝尔曼最优方程:
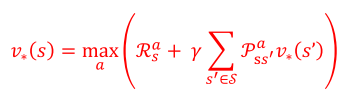
最优动作价值的贝尔曼最优方程:
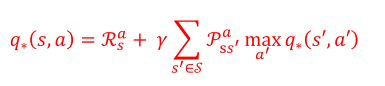
(3)求解方法
贝尔曼最优方程是非线性方程,无法直接矩阵求逆求解,核心迭代求解方法:
动态规划类:价值迭代 (Value Iteration)、策略迭代 (Policy Iteration)
无模型类:Q 学习 (Q-learning)、Sarsa
五、核心公式汇总(复习速查)
1. 基础定义公式
- 贝尔曼期望方程(策略评估)
- 贝尔曼最优方程(策略优化)
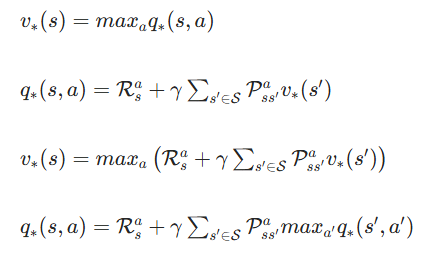
六、复习重点与易错点提示
核心递进关系:MP(状态 + 转移)→ MRP(+ 奖励 + 折扣)→ MDP(+ 动作 + 策略),三者的核心区别是元组的组成,需明确每个新增元素的物理意义。
易混淆概念:
状态价值v(s) vs 动作价值q(s,a):前者是状态的平均价值,后者是特定状态执行特定动作的价值
贝尔曼期望方程 vs 贝尔曼最优方程:前者针对给定策略,用于策略评估;后者针对最优策略,用于策略优化
策略评估 vs 策略优化:前者是 "给定策略,算价值",后者是 "优化策略,找最大价值"