子序列系列动态规划

子序列和子数组
最长递增子序列
- 题目描述
- 算法原理和实现
摆动序列
- 题目描述
- 算法原理和实现
最长递增子序列的个数
- 题目描述
- 算法原理和实现
最长数对链
- 题目描述
- 算法原理和实现
最长定差子序列
最长的斐波那契子序列的长度
- 题目描述
- 算法原理和实现
最长等差数列
- 题目描述
- 算法原理和实现
[等差数列划分 II - 子序列](#等差数列划分 II - 子序列)
- 题目描述
- 算法原理和实现

子序列和子数组

子序列是指从原序列中按顺序选取的元素组成的序列，不要求连续。例如，序列 [1, 2, 3] 的子序列包括 [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3] 等。

如此也是子序列，因此子序列的所有情况为2ⁿ。

子数组是原数组中连续的元素组成的片段。例如，数组 [1, 2, 3] 的子数组包括 [1], [2], [3], [1, 2], [2, 3], [1, 2, 3]，但不包括 [1, 3]。

如此便是子数组，因此子数组的所有情况为n²。

由此可见子序列问题应当比子数组问题更加复杂。

最长递增子序列

题目描述

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]

输出：4

解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]

输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]

输出：1

提示：

1 <= nums.length <= 2500
-104 <= nums[i] <= 104

进阶：

你能将算法的时间复杂度降低到 O(n log(n)) 吗?

算法原理和实现

动态规划

我们考虑经典的状态表示：

dp[i]为以i为结尾的所有子序列中最长的递增子序列的长度。

那么以i位置为结尾的最长递增子序列有两种情况：

长度为1，那就是i本身。
长度大于1，那么以i位置为结尾的子序列，倒数第二个元素就在[0,i-1]之间。意味着i与以[0,i-1]之间一个元素x结尾的递增子序列拼接在了一起，所以nums[i]>nums[x]。。

最终状态转移方程为：
d p [ i ] = m a x { d p [ x ] } 0 ≤ x < i & & n u m s [ x ] < n u m s [ i ] + 1 dp[i]=max\{dp[x]\}_{0≤x<i\&\&nums[x]<nums[i]}+1 dp[i]=max{dp[x]}0≤x<i&&nums[x]<nums[i]+1

最终实现：

cpp 复制代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size(),ret=1;
        vector<int>dp(n,1);
        for(int i=1;i<n;++i){
            for(int j=0;j<i;++j){
                if(nums[j]<nums[i]){
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
            ret=max(ret,dp[i]);
        }
        return ret;
    }
};

很显然我们的时间复杂度是O(n²)，空间复杂度是O(n)。

因为我们内层循环从头遍历了一遍前缀数组。

如果记前缀数组中最长递增子序列长度为ret，那么nums[i]其实就是拼接在前缀递增子序列长度在[0,ret]之间的子序列后面。

记录每个前缀递增子序列长度对应的元素，如果一个长度，有多个元素，我们取最小的元素。那么我们就能用二分查找的方式，快速找到最长的且末尾元素小于nums[i]的递增子序列。

具体实现：

cpp 复制代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        vector<int>tails(1,nums[0]);
        for(int i=1;i<n;++i){
            int left=0,right=tails.size()-1;
            while(left<=right){
                int mid=left+(right-left)/2;
                if(tails[mid]<nums[i]){
                    left=mid+1;
                }else{
                    right=mid-1;
                }
            }
            if(left==tails.size()){
                tails.push_back(nums[i]);
            }else{
                tails[left]=nums[i];
            }
        }
        return tails.size();
    }
};

时间复杂度O(nlogn)，空间复杂度O(n)。

摆动序列

题目描述

摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

示例 1：

输入：nums = [1,7,4,9,2,5]

输出：6

解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]

输出：7

解释：这个序列包含几个长度为 7 摆动序列。

其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]

输出：2

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
进阶：你能否用 O(n) 时间复杂度完成此题?

算法原理和实现

动态规划

这个和子数组系列的最长湍流子数组类似。不过我们这里考虑的是子序列。

在最长湍流子数组中，我们用一个字符标记上一个状态。现在子序列，我们就换一种双状态的动态表示。

up[i]表示以i位置结尾，且nums[i]大于倒数第二个元素的最长摆动序列的长度。

down[i]表示以i位置结尾，且nums[i]小于倒数第二个元素的最长摆动序列的长度。

所以具体实现就是：

cpp 复制代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size(),ret=1;
        vector<int>up(n,1),down(n,1);
        for(int i=1;i<n;++i){
            for(int j=0;j<i;++j){
                if(nums[i]>nums[j])up[i]=max(up[i],down[j]+1);
                else if(nums[i]<nums[j])down[i]=max(down[i],up[j]+1);
            }
            ret=max(down[i],up[i]);
        }
        return ret;
    }
};

时间复杂度O(n²)，空间复杂度O(n).

贪心

实际上我们可以记录前缀最长摆动序列长度，和前缀状态（大于或小于）。

当num[i]>nums[i-1]，且前缀状态是<时，我们可以将nums[i]拼接到摆动序列中。

看图就是：

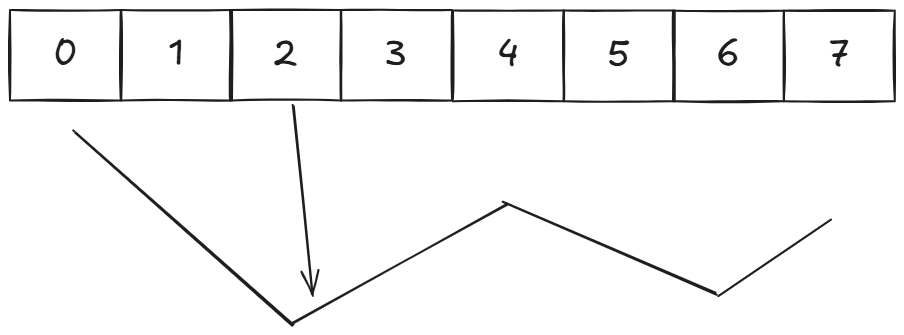
其实看图之后我们不难发现，最长摆动序列其实就是拐点数目。所以我们顺序统计拐点数目即可：

cpp 复制代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int ret=1,status=0,n=nums.size();
        for(int i=1;i<n;++i){
            if(nums[i]>nums[i-1]){
                if(status==2||!status)++ret;
                status=1;//1表示前缀状态是大于
            }else if(nums[i]<nums[i-1]){
                if(status==1||!status)++ret;
                status=2;//2表示前缀状态是小于
            }
        }
        return ret;
    }
};

时间复杂度O(n)，空间复杂度O(1)。

最长递增子序列的个数

题目描述

最长递增子序列的个数

给定一个未排序的整数数组 nums ，返回最长递增子序列的个数。

注意这个数列必须是严格递增的。

示例 1:

输入: [1,3,5,4,7]

输出: 2

解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

示例 2:

输入: [2,2,2,2,2]

输出: 5

解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。

提示:

1 <= nums.length <= 2000
-10⁶ <= nums[i] <= 10⁶

算法原理和实现

这里参考最长递增子序列的动态规划方式。我们长度就是拼接在前面的递增子序列中。但同时，我们还要记录以i位置为结尾的最长递增子序列的长度。

这个判断还是有点复杂的，以示例1来看：

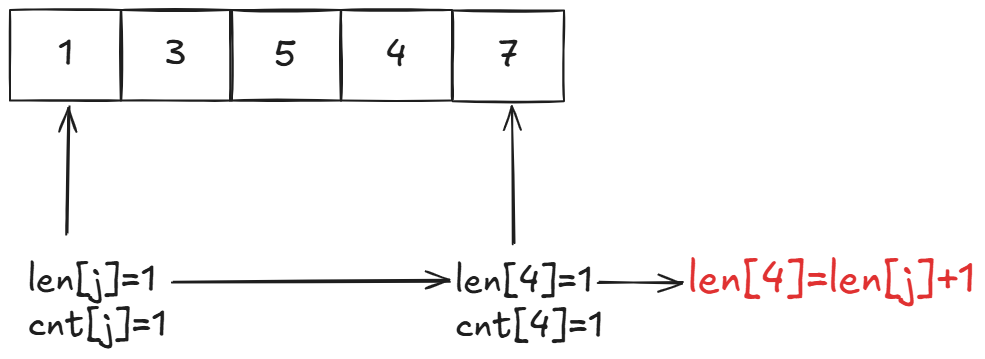
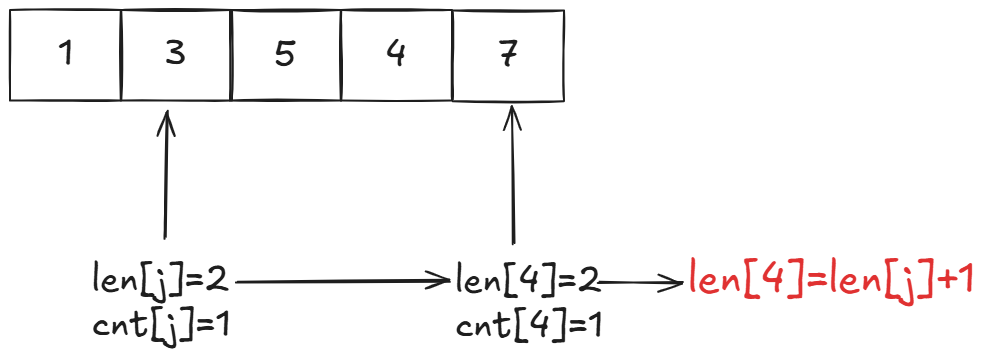
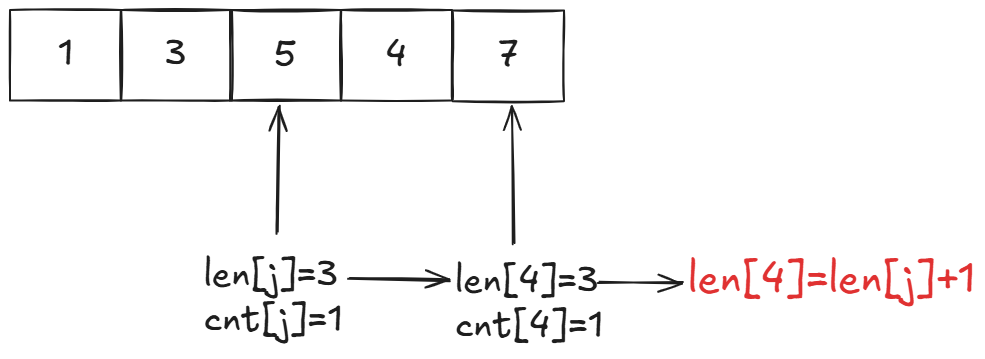
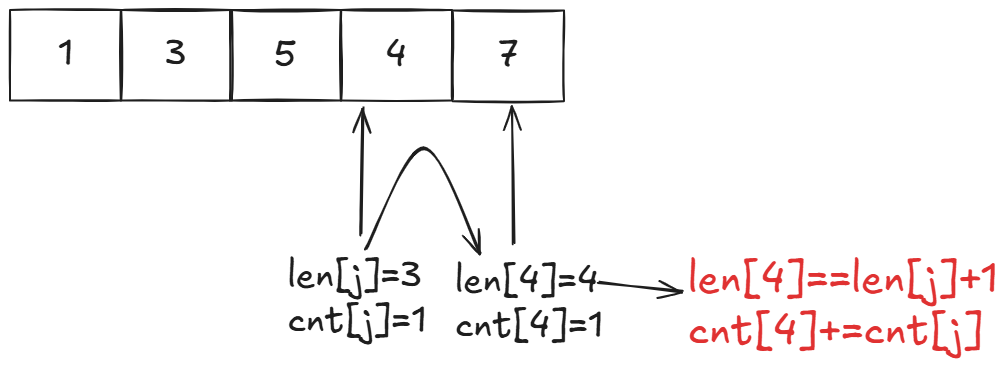
1,3,5,4,7\]的最长递增子序列是\[1, 3, 4, 7\] 和\[1, 3, 5, 7\]。 那么我们看len\[4\]和cnt\[4\]是如何更新的： ![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/4a208e2d03984f9d95bf3a7a8b70538a.png) ![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/adc6a6eccf1649fea0da7a752a03d099.png) ![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/2b23ad01c34f4a9da7713d765a2655f2.png) 最关键的地方来了： ![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/ba6d23a8f9734e90a130180ecf89b38c.png) 可以看到以下标4和下标3的最长递增子序列拼接之后还是等于目前下标4的最长递增子序列长度。我们就让下标4的最长递增子序列长度加上下标3的最长递增子序列长度。 所以后续判断都要围绕大于和等于两种情况进行： ```cpp class Solution { public: int findNumberOfLIS(vector& nums) { int n=nums.size(),maxlen=1,ret=1; vectorlen(n,1),cnt(n,1); for(int i=1;inums[j]){ if(len[j]+1>len[i]){ len[i]=len[j]+1; cnt[i]=cnt[j]; }else if(len[j]+1==len[i]){ cnt[i]+=cnt[j]; } } } if(len[i]>maxlen){ maxlen=len[i]; ret=cnt[i]; }else if(len[i]==maxlen){ ret+=cnt[i]; } } return ret; } }; ``` 时间复杂度O(n^2^)，空间复杂度O(n)。 延续第一问的最长递增子序列思路，我们也可以用二分查找的策略进行优化，我们依旧可以存储最长递增子序列长度对应的最小末尾元素。 同时我们要将相同长度的最长递增子序列依旧相应个数记录下来，方便后续统计个数（我这里图省事就用O（n）查找了），实际上可以整体二分记录。 具体实现： ```cpp class Solution { public: int findNumberOfLIS(vector& nums) { int n=nums.size(); vectortails(1,nums[0]); unordered_map>>hash;//长度，<元素大小，个数> hash[1].emplace_back(nums[0],1); for(int i=1;ia)cnt+=b; } if(!cnt)++cnt; hash[left+1].emplace_back(nums[i],cnt); } int cnt=0; for(auto [a,b]:hash[tails.size()]){ cnt+=b; } return cnt; } }; ``` 时间复杂度O(nlogn)，空间复杂度O(n)。 ## 最长数对链 ### 题目描述 [最长数对链](https://leetcode.cn/problems/maximum-length-of-pair-chain/description/) 给你一个由 n 个数对组成的数对数组 pairs ，其中 pairs\[i\] = \[lefti, righti\] 且 lefti \< righti 。 现在，我们定义一种 跟随 关系，当且仅当 b \< c 时，数对 p2 = \[c, d\] 才可以跟在 p1 = \[a, b\] 后面。我们用这种形式来构造 数对链 。 找出并返回能够形成的 最长数对链的长度 。 你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。 示例 1： > 输入：pairs = \[\[1,2\], \[2,3\], \[3,4\]

输出：2

解释：最长的数对链是 [1,2] -> [3,4] 。

示例 2：

输入：pairs = [[1,2],[7,8],[4,5]]

输出：3

解释：最长的数对链是 [1,2] -> [4,5] -> [7,8] 。

提示：

n == pairs.length
1 <= n <= 1000
-1000 <= lefti < righti <= 1000

算法原理和实现

动态规划

这题以第一个元素排序完之后就和最长递增子序列没什么区别，我们来实现二分优化版本：

cpp 复制代码

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) {
        int n=pairs.size();
        sort(pairs.begin(),pairs.end());
        vector<int>tails(1,pairs[0][1]);
        for(int i=1;i<n;++i){
            int left=0,right=tails.size()-1;
            while(left<=right){
                int mid=left+(right-left)/2;
                if(tails[mid]<pairs[i][0])left=mid+1;
                else right=mid-1;
            }
            if(left==tails.size()){
                tails.emplace_back(pairs[i][1]);
            }else{
                tails[left]=min(tails[left],pairs[i][1]);
            }
        }
        return tails.size();
    }
};

时间复杂度O(nlogn)，空间复杂度O(n)。

贪心

老实说，我都排完序了还动态规划显得有点楞。我们可以用第二个元素排序，然后记录前缀第二个元素最小值prev，当current的第一个元素大于prev时，current就加入到最长数对链中，然后更新prev。

具体实现：

cpp 复制代码

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) {
        sort(pairs.begin(),pairs.end(),[](vector<int>&a,vector<int>&b){
            return a[1]<b[1];
        });
        int prev=INT_MIN,ret=0,n=pairs.size();
        for(int i=0;i<n;++i){
            if(pairs[i][0]>prev){
                ++ret;
                prev=pairs[i][1];
            }
        }
        return ret;
    }
};

时间复杂度O(nlogn)，空间复杂度O(logn)->排序开销。

最长定差子序列

题目描述

最长定差子序列

给你一个整数数组 arr 和一个整数 difference，请你找出并返回 arr 中最长等差子序列的长度，该子序列中相邻元素之间的差等于 difference 。

子序列是指在不改变其余元素顺序的情况下，通过删除一些元素或不删除任何元素而从 arr 派生出来的序列。

示例 1：

输入：arr = [1,2,3,4], difference = 1

输出：4

解释：最长的等差子序列是 [1,2,3,4]。

示例 2：

输入：arr = [1,3,5,7], difference = 1

输出：1

解释：最长的等差子序列是任意单个元素。

示例 3：

输入：arr = [1,5,7,8,5,3,4,2,1], difference = -2

输出：4

解释：最长的等差子序列是 [7,5,3,1]。

提示：

1 <= arr.length <= 10⁵
-10⁴ <= arr[i], difference <= 10⁴

算法原理和实现

动态规划

首先我们还是依据最开始的最长递增子序列类似的思路。

我们定义dp[i]为以i结尾的左右子序列中最长的定差子序列长度。

那么i位置就遍历i以前的所有元素，如果nums[i]-nums[j]==difference就可以拼接在后面。

具体实现：

cpp 复制代码

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        int n=arr.size(),ret=1;
        vector<int>dp(n,1);
        for(int i=1;i<n;++i){
            for(int j=0;j<i;++j){
                if(arr[i]-arr[j]==difference){
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
            ret=max(dp[i],ret);
        }
        return ret;
    }
};

这样的时间复杂度是O(n²)。肯定会超时的，我们来讨论如何优化。

优化思路

仔细想想这个和递增子序列有什么不同，其实就是他的定差。

举个例子，如果是arr[i]==6,difference==2，那么和arr[i]拼接的定差子序列的倒数第二个元素一定是4，我们来看这种情况：

现在6的前缀有多个4，我该拼接哪一个呢？

实际上我们先考虑4拼接的是哪个2一切都会水落石出：

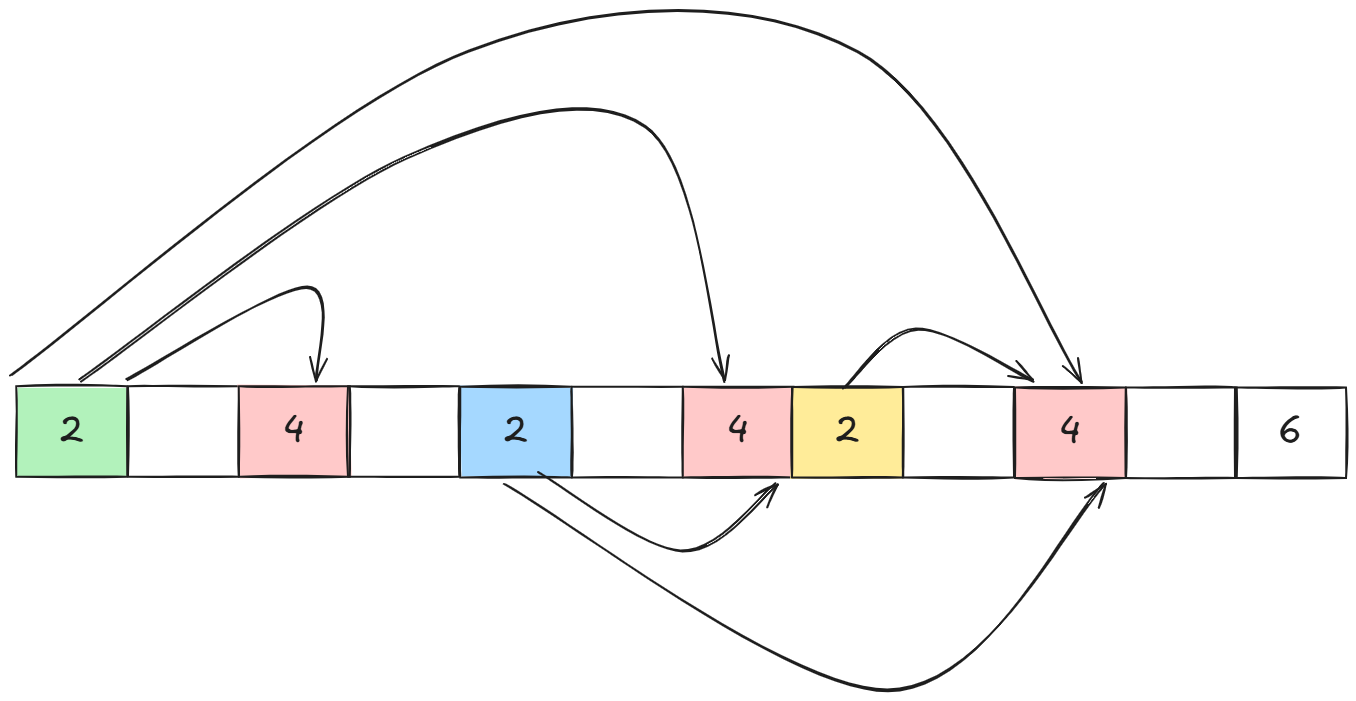
可以看到最前面的2一定和后续的4都匹配过，中间的2之和后面的两个4匹配过，最后一个2只和最后的4匹配过。

这意味着最后的4一定比前面的4拼接的定差子序列长。

所以我们只需要考虑离6最近的4即可。

所以优化思路就是倒着查询？

nonono，这样下来还是O(n²)，并没有质的飞跃。

实际上我们提过很重要的一点，6所拼接的前缀定差子序列的最后一个元素是固定的。

这意味着我们可以用一个哈希表来存储每个定差子序列最后一个元素以及其所对应的最大长度。

如此我们便能一次遍历完成：

时间复杂度是O(n)，空间复杂度也是O(n)。

此外，这题的数据是有范围的，这意味着我们可以用vector模拟哈希表，速度更胜一筹：

cpp 复制代码

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        const int OFFSET = 10000; // 把负数转为非负索引
        vector<int> dp(20001, 0); // 覆盖 [-10000, 10000]
        int ret = 1;
        
        for (int num : arr) {
            int curr = num + OFFSET;
            int prev = (num - difference) + OFFSET;
            
            if (prev >= 0 && prev <= 20000) {
                dp[curr] = dp[prev] + 1;
            } else {
                dp[curr] = 1;
            }
            
            ret = max(ret, dp[curr]);
        }
        return ret;
    }
};

最长的斐波那契子序列的长度

题目描述

最长的斐波那契子序列的长度

如果序列 x1, x2, ..., xn 满足下列条件，就说它是斐波那契式的：

n >= 3

对于所有 i + 2 <= n，都有 xi + xi+1 == xi+2

给定一个严格递增的正整数数组形成序列 arr ，找到 arr 中最长的斐波那契式的子序列的长度。如果不存在，返回 0 。

子序列是通过从另一个序列 arr 中删除任意数量的元素（包括删除 0 个元素）得到的，同时不改变剩余元素顺序。例如，[3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的子序列。

示例 1：

输入: arr = [1,2,3,4,5,6,7,8]

输出: 5

解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。

示例 2：

输入: arr = [1,3,7,11,12,14,18]

输出: 3

解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。

提示：

3 <= arr.length <= 1000
1 <= arr[i] < arr[i + 1] <= 10⁹

算法原理和实现

首先我们考虑基础的状态表示：

dp[i]为以i位置为结尾的最长斐波那契子序列的长度。但是我们发现dp[i+1]不容易求出，因为我们需要直到拼接i+1结尾的斐波那契子序列的倒数两个元素。

那么我们就需要记录两个结尾元素，因此状态表示修改为：

dp[i][j]以i，j结尾的最长斐波那契子序列长度，i<j

我们只需查看是否存在k<i使得,nums[k]+nums[i]==nums[j]，如果有dp[i][j]=dp[k][i]+1。

但是我们搜寻k的过程是比较缓慢的，如果遍历查找的话，时间复杂度就会来到O(n³)。但是原题的数组元素是递增的，因此我们可以用哈希表直接存储每个元素的下标，达到O(1)查找：

cpp 复制代码

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) {
        unordered_map<int,int>hash;
        int n=arr.size(),ret=0;
        vector<vector<int>>dp(n,vector<int>(n));
        for(int i=0;i<n;++i){
            hash[arr[i]]=i;
        }
        for(int j=2;j<n;++j){
            for(int i=1;i<j;++i){
                if(hash.count(arr[j]-arr[i])&&hash[arr[j]-arr[i]]<i)
                    dp[i][j]=max(dp[hash[arr[j]-arr[i]]][i]+1,3);
                ret=max(ret,dp[i][j]);
            }
        }
        return ret;
    }
};

时间复杂度O(n²)，空间复杂度O(n²)

最长等差数列

题目描述

最长等差数列

给你一个整数数组 nums，返回 nums 中最长等差子序列的长度。

回想一下，nums 的子序列是一个列表 nums[i1], nums[i2], ..., nums[ik] ，且 0 <= i1 < i2 < ... < ik <= nums.length - 1。并且如果 seq[i+1] - seq[i]( 0 <= i < seq.length - 1) 的值都相同，那么序列 seq 是等差的。

示例 1：

输入：nums = [3,6,9,12]

输出：4

解释：

整个数组是公差为 3 的等差数列。

示例 2：

输入：nums = [9,4,7,2,10]

输出：3

解释：

最长的等差子序列是 [4,7,10]。

示例 3：

输入：nums = [20,1,15,3,10,5,8]

输出：4

解释：

最长的等差子序列是 [20,15,10,5]。

提示：

2 <= nums.length <= 1000
0 <= nums[i] <= 500

算法原理和实现

这题考虑上一题的最长斐波那契序列，我们要记录最后两个值。同时为了查找快速，我们需要记录元素的下标到哈希表中。

但是这里的元素不是递增的，所以就不是唯一的。如果我们先存储到哈希表中，仍然可能会面临着大量相同元素，查找的复杂度退化到O(n)。

这时候又要考虑我们的最长定差子序列题目，根据那一题的分析，我们只需记录相同元素中最后一个元素的下标，这样能覆盖所有情况。

此外，我们还需要考虑固定倒数第一个元素还是倒数第二个元素。

上一题我们固定了最后一个元素，让倒数第二个元素移动。

这一题如果我们用同样的做法，我们就要维护倒数第二个元素的前缀元素下标，导致哈希表不断重置。这是相当不明智的。

因此这一题我们应当固定，倒数第二个元素，让倒数第一个元素移动，哈希表就无需重置。

此外，我们可以利用元素范围进一步优化哈希表：

cpp 复制代码

class Solution {
public:
    static int dp[1000][1000];
    static int hash[1501];
    int longestArithSeqLength(vector<int>& nums) {
        int n=nums.size(),ret=2; 
        for(int i=0;i<n;++i){
            int *dp_row=dp[i];
            for(int j=i+1;j<n;++j)dp_row[j]=2;
        }
        for(auto&e:hash)e=1001;
        for(int i=0;i<n;++i){
            for(int j=i+1;j<n;++j){
                int prev=2*nums[i]-nums[j];
                if(hash[prev+500]<i){
                    dp[i][j]=dp[hash[prev+500]][i]+1;
                }
                ret=max(ret,dp[i][j]);
            }
            hash[nums[i]+500]=i;
        }
        return ret;
    }
};
int Solution::dp[1000][1000];
int Solution::hash[1501];

时间复杂度O(n²)，空间复杂度O(n²)。其实也可以理解成O(1)毕竟是固定大小的。

如果想继续优化，可以考虑其他的状态标识，如遍历公差。也可以考虑根据公差提前终止循环。

等差数列划分 II - 子序列

题目描述

等差数列划分 II - 子序列

给你一个整数数组 nums ，返回 nums 中所有等差子序列的数目。

如果一个序列中至少有三个元素，并且任意两个相邻元素之差相同，则称该序列为等差序列。

例如，[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。

再例如，[1, 1, 2, 5, 7] 不是等差序列。

数组中的子序列是从数组中删除一些元素（也可能不删除）得到的一个序列。

例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

题目数据保证答案是一个 32-bit 整数。

示例 1：

输入：nums = [2,4,6,8,10]

输出：7

解释：所有的等差子序列为：
$2,4,6$ $4,6,8$ $6,8,10$ $2,4,6,8$ $4,6,8,10$ $2,4,6,8,10$ $2,6,10$

示例 2：

输入：nums = [7,7,7,7,7]

输出：16

解释：数组中的任意子序列都是等差子序列。

提示：

1 <= nums.length <= 1000
-2³¹ <= nums[i] <= 2³¹ - 1

算法原理和实现

这次我们只需要注意两个细节。

拼接前面等差子序列时，由于要求长度>=3，所以我们拼接完后最后三个元素是一个新的等差序列，所以要+1.
由于计算的是个数，我们这次不能只考虑最近的一个，而是要考虑所有元素。

用哈希表提前存储所有元素下标，具体实现：

cpp 复制代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n=nums.size(),ret=0;
        vector<vector<int>>dp(n,vector<int>(n));
        unordered_map<int,vector<int>>hash;
        for(int i=0;i<n;++i)hash[nums[i]].emplace_back(i);
        for(int j=2;j<n;++j){
            for(int i=1;i<j;++i){
                long long prev=2*(long long)nums[i]-nums[j];
                if(prev>=INT_MIN&&prev<=INT_MAX&&hash.count(prev)){
                    for(auto&e:hash[prev]){
                        if(e>=i)break;
                        dp[i][j]+=dp[e][i]+1;
                    }
                }
            }
        }
        for(auto&r:dp)
            for(auto&e:r)
                ret+=e;
        return ret;
    }
};

时间复杂度约为O(n²)，空间复杂度O(n²)。