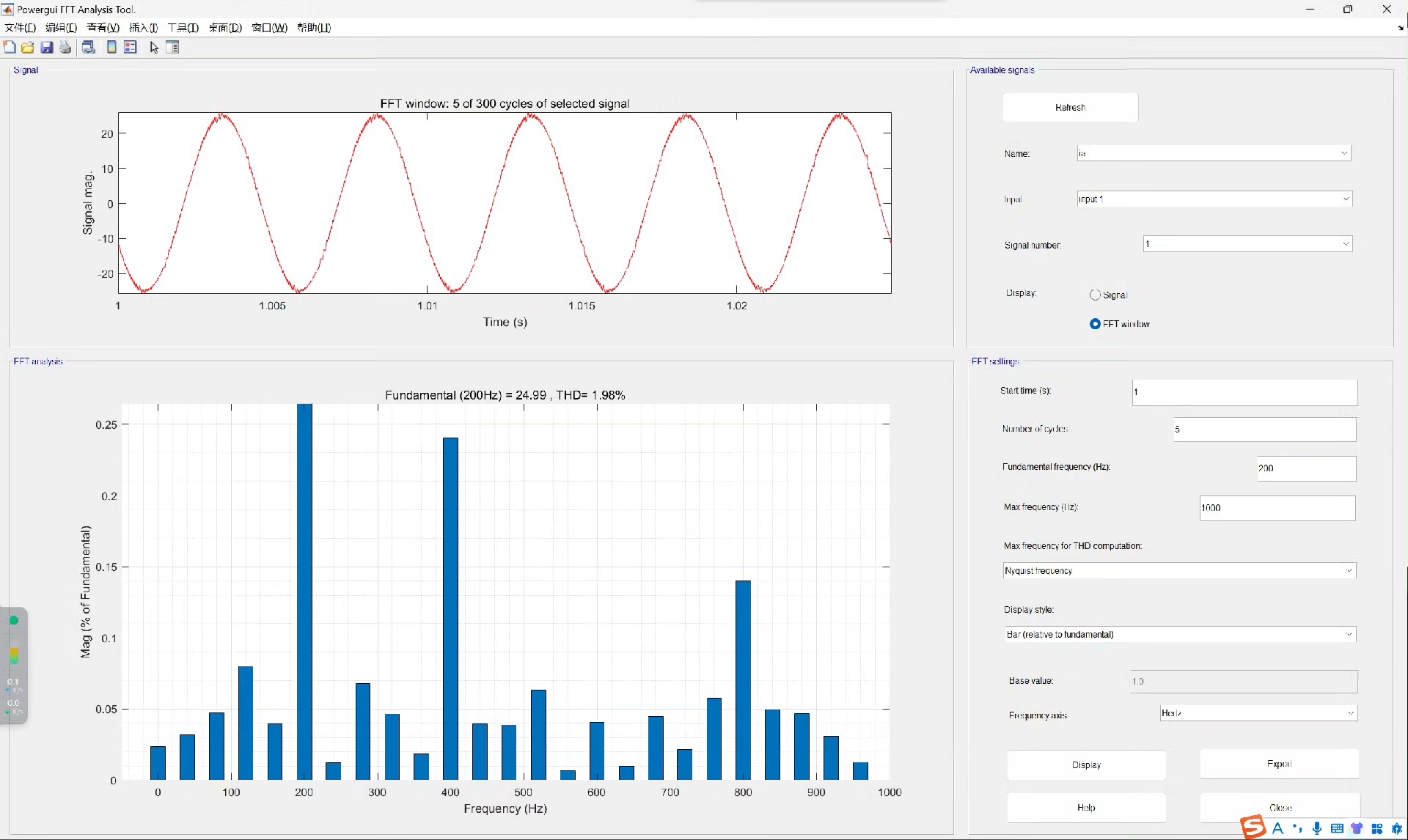
永磁同步模型转矩预测控制（三矢量）：消除权重系数策略的探索

永磁同步模型转矩预测控制(三矢量)_1 策略: 采用消除代价函数中的权重系数方法。电流谐波1.98%。含有对应的论文文献

在永磁同步电机控制领域，转矩预测控制一直是研究热点。今天咱聊聊采用消除代价函数中权重系数方法的永磁同步模型转矩预测控制（三矢量）策略。

为啥要消除权重系数

传统的转矩预测控制中，代价函数里的权重系数对控制效果影响重大。但这权重系数的选取往往得凭经验反复调试，既麻烦又可能不是最优。而采用消除权重系数的方法，就能有效规避这个难题，让控制过程更加简洁高效。

电流谐波表现

在采用这种策略后，电流谐波能控制在 1.98% 。较低的电流谐波意味着电机运行更平稳，损耗更小，效率更高。这一出色的电流谐波控制成果，证明了该策略在实际应用中的有效性。

代码实现思路及示例

python 复制代码

# 这里假设我们已经有了电机模型的相关参数
# 比如定子电阻Rs，电感Ld, Lq，永磁磁链lambda_f等
Rs = 0.5
Ld = 0.001
Lq = 0.002
lambda_f = 0.15

# 假设获取到的当前时刻电机状态
theta = 0.5  # 转子位置角
id = 0.1
iq = 0.2

# 预测下一时刻的电压矢量（简化示例，未包含完整计算）
def predict_voltage(id, iq, theta):
    # 这里简单用一些电机方程关系来计算预测电压
    vd = Rs * id - Lq * omega * iq
    vq = Rs * iq + Ld * omega * id + omega * lambda_f
    # 这里omega假设已知，实际可能需要通过其他算法获取
    omega = 10
    valpha = vd * np.cos(theta) - vq * np.sin(theta)
    vbeta = vd * np.sin(theta) + vq * np.cos(theta)
    return valpha, vbeta

# 获取预测电压矢量
valpha, vbeta = predict_voltage(id, iq, theta)

这段代码简单模拟了预测下一时刻电压矢量的过程。在实际的永磁同步电机转矩预测控制里，我们需要根据电机的数学模型，像上面代码里通过定子电阻、电感、永磁磁链以及当前的电流、转子位置角等参数来计算预测电压。虽然代码只是个简化示例，但核心思路就是通过这些参数关系去预估能满足控制目标的电压矢量。

对应论文文献支撑

这一策略可不是凭空而来，背后有相关论文文献作为坚实理论依据。通过研读相关论文，能更深入理解这种控制策略的原理、推导过程以及其在不同工况下的性能表现。论文从理论层面详细阐述了消除权重系数方法如何影响代价函数，进而提升永磁同步模型转矩预测控制的效果，为实际应用提供了可靠的理论指导。

永磁同步模型转矩预测控制(三矢量)_1 策略: 采用消除代价函数中的权重系数方法。电流谐波1.98%。含有对应的论文文献

永磁同步模型转矩预测控制（三矢量）中采用消除权重系数的策略，凭借其对电流谐波的良好控制以及摆脱权重系数调试困扰的优势，在永磁同步电机控制领域展现出了巨大的潜力。随着研究的不断深入，相信这一策略能在更多实际应用场景中大放异彩。