📖标题:Not All Preferences Are Created Equal: Stability-Aware and Gradient-Efficient Alignment for Reasoning Models
🌐来源:arXiv, 2602.01207v1
🌟摘要
基于偏好的对齐对于训练大型推理模型至关重要;然而,像直接偏好优化(DPO)这样的标准方法通常统一处理所有偏好对,忽略了训练实例的不断变化的效用。这种静态方法通常会导致低效或不稳定的优化,因为它浪费了对梯度可忽略不计的琐碎对的计算,并受到不确定决策边界附近样本引起的噪声的影响。面对这些挑战,我们提出了SAGE(稳定感知梯度效率),这是一个动态框架,旨在通过最大化策略更新的信噪比来增强对齐可靠性。具体而言,SAGE集成了基于模型能力的粗粒度课程机制和细粒度、稳定性感知评分功能,该功能优先考虑信息丰富、自信的错误,同时过滤掉不稳定的样本。多个数学推理基准的实验表明,SAGE显著加快了收敛速度,优于静态基线,突出了策略感知、稳定性感知数据选择在推理对齐中的关键作用。
🛎️文章简介
🔸研究问题:如何在推理模型的偏好对齐中避免静态数据选择导致的梯度低效与优化不稳定?
🔸主要贡献:论文提出SAGE框架,通过策略感知、稳定感知的动态偏好选择,显著提升对齐过程的收敛速度、稳定性和样本效率。
📝重点思路
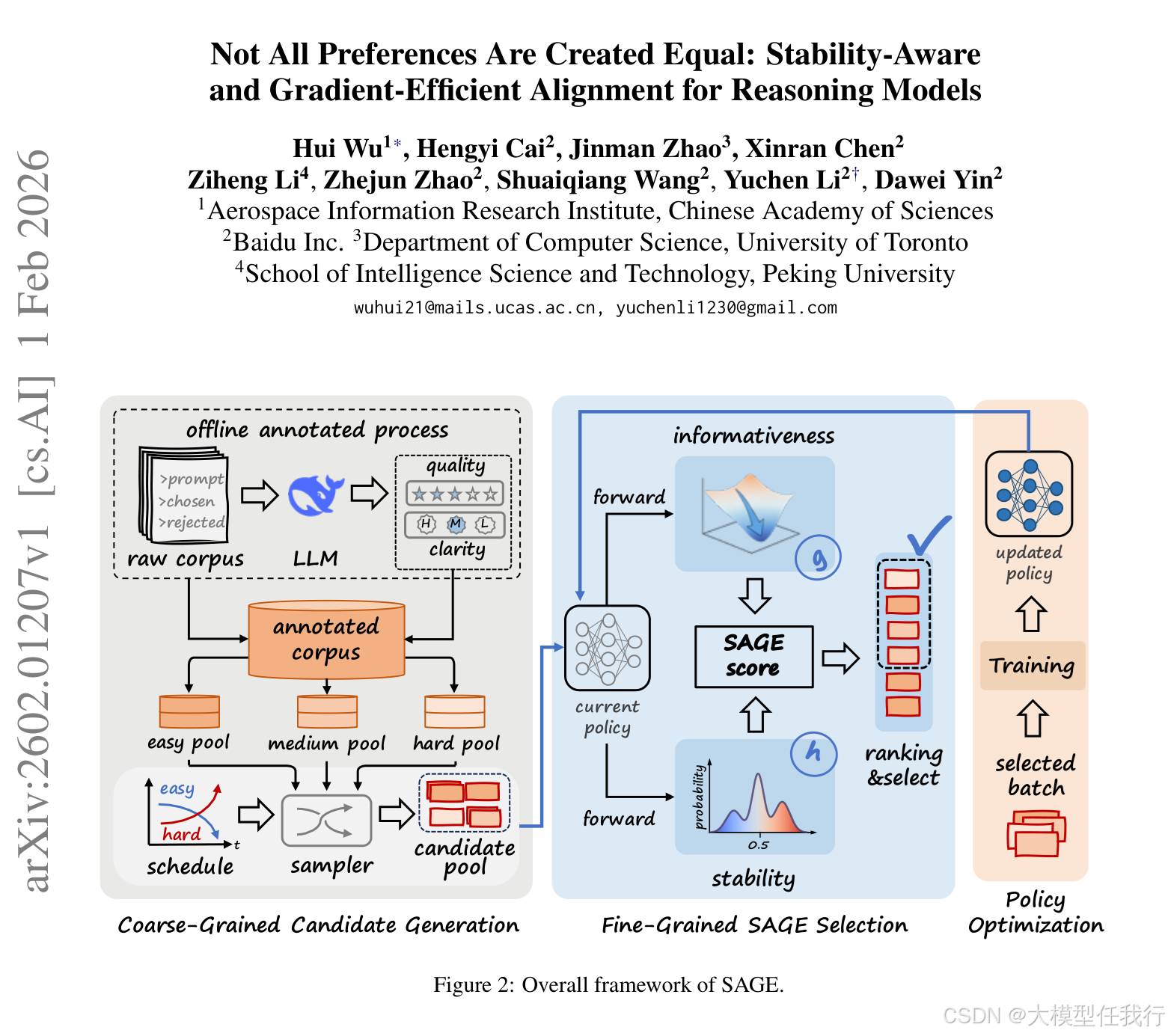
🔸设计粗粒度可刷新池机制,依据模型能力随训练阶段动态调整易/中/难样本池的混合比例,形成计算友好的课程学习。
🔸构建细粒度SAGE评分函数,以牛顿减量为灵感,联合建模梯度信号强度(1−p)²与局部曲率代理(p(1−p)),实现信噪比驱动的样本筛选。
🔸引入长度归一化与Tikhonov阻尼项,消除响应长度偏差并保障数值稳定性,使评分适用于长思维链场景。
🔸采用硬截断策略,仅保留Top-γ分数样本参与反向传播,物理剔除弱信号或高曲率噪声样本,而非软加权。
🔎分析总结
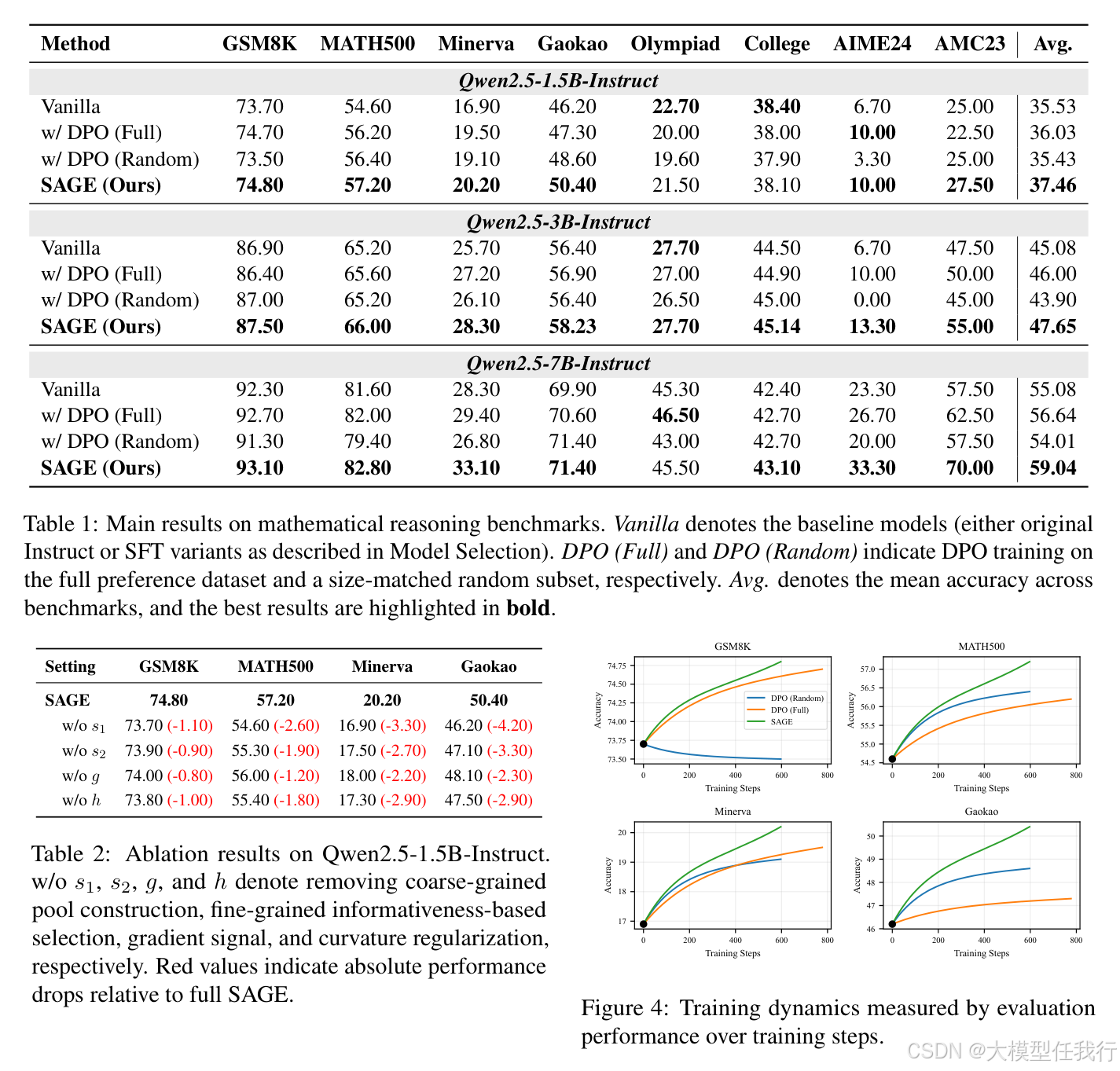
🔸SAGE在GSM8K至AIME24等8个数学推理基准上全面超越DPO全量/随机基线,平均准确率最高提升3.51%,验证其泛化有效性。
🔸梯度范数曲线显示SAGE显著降低梯度幅值与方差,训练更平滑,证实其通过曲率正则化缓解了高曲率区域的更新不稳定性。
🔸消融实验证明:移除曲率正则化(w/o h)导致Minerva等难题性能下降最剧烈,凸显稳定性对复杂推理的关键作用。
🔸SAGE在更少有效训练token下达到更高精度,且墙钟时间与基线相当,说明前向评分开销可控,反向传播更高效。
💡个人观点
论文将优化理论(牛顿减量)引入偏好对齐的数据选择,揭示推理任务中"样本效用动态耦合于模型状态+局部损失几何"的双重本质。
🧩附录