目录
一、什么是数据结构
数据结构是计算机中存储、组织数据的方式,旨在实现高效的数据访问和操作。它定义了数据元素之间的逻辑关系,以及对这些关系的操作(如插入、删除、搜索等)。数据结构的选择直接影响算法的性能和资源利用率。
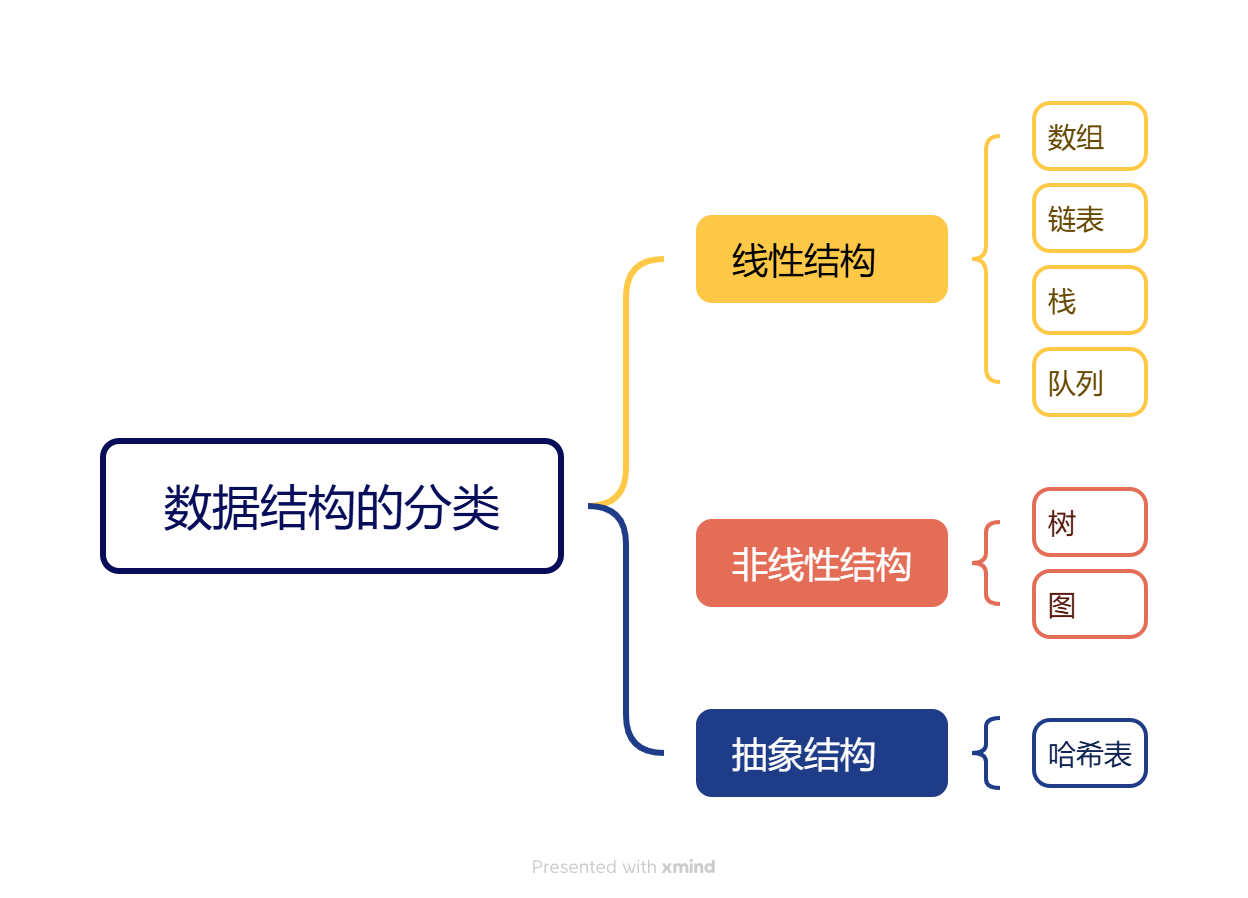
数据结构在Java中有具体的实现方式------集合类。在Java标准库中,提供了一些类,我们可以直接使用,有些集合类就是已经实现好的数据结构。我们要学好数据结构的理论功底,就能很好的使用这些集合类。
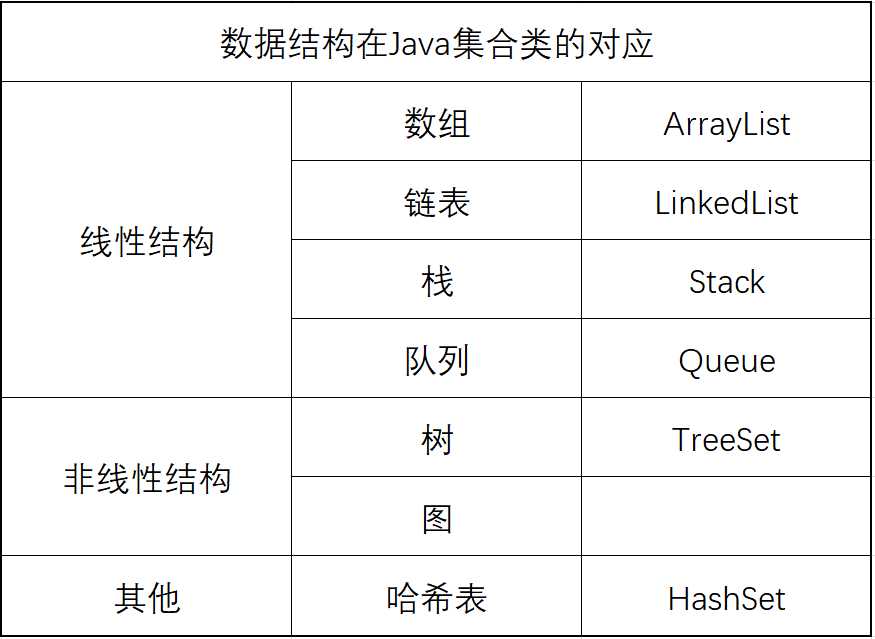
二、时间复杂度与空间复杂度
它们是衡量一段代码消耗资源开销多少的一种方式,衡量的时候只和代码有关,和使用的机器无关。
1.时间复杂度
站在数学的角度,我们使用问题规模N ,计算关键操作的次数与N之间的函数关系,在进行化简与近似,只取最高次项,把其他项忽略掉,把最高此项的系数也忽略掉,使用大O渐进表示法O()。
(1)计算func2的时间复杂度
java
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N; k++) {
count++;
}
int M = 10;
while ((M--) > 10) {
count++;
}
System.out.println(count);
}首先我们要先找这个代码的关键操作,count++,在for循环中的count++的循环次数为2N,而while中count++的循环次数为常数10,与N无关;故总的循环次数为2N+10,去掉常数与最高次项的系数,因此func2的时间复杂度为O(N)。
(2)计算func3的时间复杂度
java
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}这段代码的关键操作为count++,第一个for循环的循环次数为M,第二个循环的循环次数为N,故时间复杂度为O(M+N)。
(3)计算func4的时间复杂度
java
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}这段代码的关键操作为count++,for循环的循环次数为常数100,与问题规模N无关,无论N取多少,都不会影响count++,我们把这种代码的时间复杂度称为O(1)。
(4)计算bubblesort的时间复杂度
java
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}最坏时间复杂度 当输入数组完全逆序时,每次内层循环都需要执行完整的比较和交换操作。外层循环运行
n次(数组长度),内层循环运行次数从n-1逐步递减到1。总操作次数为: [ (n-1) + (n-2) +...... + 1 = (1+N)*N / 2 ] 因此最坏时间复杂度为 (O(n^2))。
(5)计算binarySearch的时间复杂度
java
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}这是一段取中间元素的代码,每循环一次,就是让区间范围缩小一半,假设我们的数组元素为8,循环次数为4,如果数组元素为16,循环次数为5,如果数组元素为32,循环次数为6,我们可以推断出数组元素为N时,2^(循环次数-1)=N,循环次数=log₂N+1,时间复杂度为O(log₂N)。
(6)计算factorial的时间复杂度
java
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}虽然没有循环,但是有递归,递归理论上都能转换为循环,假设N为1时,循环1次;假设N为2时,循环为2;N为3时,循环为3......我们可以得出N为几,就循环多少次。故时间复杂度为O(N)。
(7)计算fibonacci的时间复杂度
java
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}每执行一个方法,就能衍生出两个递归操作,每个递归又能衍生出两个递归操作......,一旦给N设置一个较大的值时,程序就会运行特别慢,时间复杂度为O(2N)
2.空间复杂度
空间复杂度就是衡量代码运行时消耗掉的临时空间
(1)计算bubblesort的空间复杂度
java
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}上述代码中,临时变量有int end,boolean sorted,int i,设数组元素为N,sorted与i都是创建了N次,但是都是销毁了前一个,才创建下一个,前一个与下一个都共用了同一个空间,实际上空间只需要固定3份。空间复杂度为O(1)
(2)计算fibonacci的空间复杂度
java
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}代码中的临时变量有long[] fibArray,int i,总共的空间为n+1+2,空间复杂度为O(n)。
(3)计算fibonacci的空间复杂度
java
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}代码中递归调用了N次,开辟了N个栈帧,空间复杂度为O(N)