Java 算法实践（四）：链表核心题型

在 Java 中，链表节点通常定义如下：

java 复制代码

public class ListNode {
    int val;
    ListNode next;
    ListNode(int x) { val = x; }
}

链表最大的特点是不支持随机访问 （No Random Access），查找时间复杂度为 O ( N ) O(N) O(N)，但插入和删除操作只需要 O ( 1 ) O(1) O(1)（前提是已知前驱节点）。

链表问题的核心难点在于：在操作 curr.next 时，很容易丢失 curr 后面的节点索引 。因此，链表解题的黄金法则是：在断开一根指针之前，先保存它的下一个节点。

一、核心基石：链表反转

这是链表操作中最基础、最高频的动作，也是后续解决"回文链表"、"K 个一组反转"等复杂问题的原子操作。

1.1 迭代反转法

题目链接 ：LeetCode 206. Reverse Linked List

题目描述：给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

核心难点 ：

链表不同于数组，无法通过下标访问。当我们改变当前节点 curr 的指向（curr.next = prev）时，原有指向下一个节点的连接就会断开。如果我们没有提前保存下一个节点，整条链表的后半部分就会丢失（内存泄漏，无法访问）。

核心逻辑 ：

需要三个指针来完成"局部反转"的操作，并在遍历过程中推进。

prev ：指向当前节点的前一个节点（反转后的"下一个"）。初始为 null。
curr ：当前正在处理的节点。初始为 head。
next ：临时保存当前节点的下一个节点（因为一旦修改 curr.next，原有的连接就会断开）。

Java 代码：

java 复制代码

public ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode curr = head;
    
    while (curr != null) {
        // 在修改引用之前，必须先暂存这一步的下一步
        // 否则一旦执行 curr.next = prev，就永远找不到原来的 next 了
        ListNode nextTemp = curr.next;
        
        // 修改引用指向前驱（核心反转步骤）
        curr.next = prev;
        
        // 指针整体平移
        prev = curr;
        curr = nextTemp;
    }
    
    // 循环结束时 curr 为 null，prev 指向原链表的尾部（新链表的头）
    return prev;
}

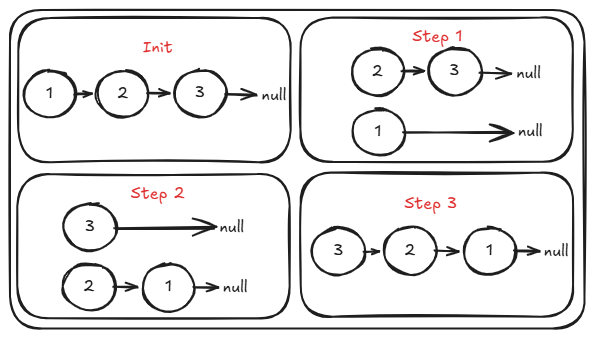
状态流转推演 ：

假设链表为 1 -> 2 -> 3 -> null。

步骤	curr	next (temp)	操作 (curr.next = prev)	状态变化	prev 更新	curr 更新
Init	1	-	-	`null`, `1->2->...`	`null`	`1`
1	1	2	`1.next = null`	`null <- 1`, `2->3`	`1`	`2`
2	2	3	`2.next = 1`	`null <- 1 <- 2`, `3`	`2`	`3`
3	3	null	`3.next = 2`	`null <- 1 <- 2 <- 3`	`3`	`null`
End	null	-	-	返回 `prev` (3)	-	-

1.2 递归反转法

虽然迭代法空间复杂度 O ( 1 ) O(1) O(1) 更优，但理解递归有助于解决后续"每 K 个一组反转"的问题。递归法在工程中不如迭代法常用（有栈溢出风险），但能够帮助理解链表结构。

复杂度对比：

迭代法 ：时间 O ( N ) O(N) O(N)，空间 O ( 1 ) O(1) O(1)。
递归法 ：时间 O ( N ) O(N) O(N)，空间 O ( N ) O(N) O(N)（递归栈的深度）。

逻辑：
reverseList(head) 的定义是：将以 head 为头的链表反转，并返回反转后的新头节点。

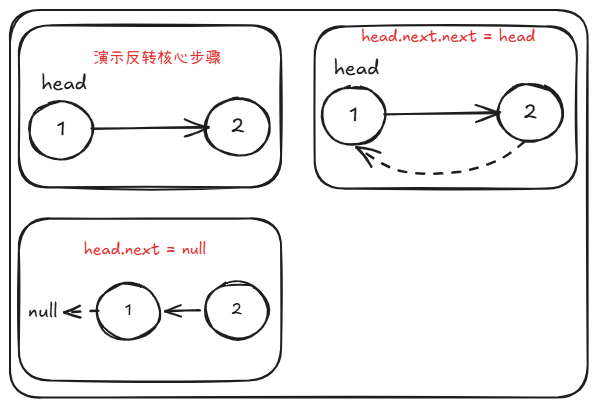
递归到最后一个节点，返回该节点作为新头 (newHead)。
在回溯过程中，让 head.next 指向 head（即 head.next.next = head）。
断开 head 原来的指向（head.next = null）。

Java 代码：

java 复制代码

public ListNode reverseList(ListNode head) {
    // 递归终止条件：如果链表为空，或者只有一个节点，无需反转，直接返回
    if (head == null || head.next == null) {
        return head;
    }
    
    // 递归过程：假设后面的链表已经反转好了
    ListNode newHead = reverseList(head.next);
    
    // 核心操作：将当前节点挂到后面链表的尾部
    // 此时 head.next 指向的是反转后链表的尾部
    head.next.next = head;
    
    // 断开防止成环
    head.next = null;
    
    return newHead;
}

核心逻辑解析 ：

对于 1 -> 2 -> 3 -> 4 -> 5，当前 head 是 1。

递（Calling）：调用 reverseList(2)。
归（Returning） ：假设递归成功返回，此时链表变成了：
- 剩余部分：5 -> 4 -> 3 -> 2 （反转好了）
- 当前连接 ：1 -> 2 （注意！1 的 next 依然指向 2，但 2 现在在反转链表的尾部）。
操作：需要把 1 放到 2 的后面。
- 利用原有的引用：head.next 就是 2。
- 代码逻辑：head.next.next = head ⇒ 2.next = 1。
收尾：head.next = null （防止 1 和 2 形成环 1 <-> 2）。

二、虚拟头节点：Dummy Node

适用场景 ：

在链表操作中，头节点 (Head) 是一个极其特殊的元素。很多算法逻辑（如删除、插入）对于"中间节点"和"头节点"的处理方式往往不同：

如果删除的是中间节点：prev.next = curr.next。
如果删除的是头节点：head = head.next。
这种差异会导致代码中充斥着大量的 if (head == null) 或 if (index == 0) 的边界判断。

引入 虚拟头节点 (Dummy Node/哨兵节点) 的核心目的是人为创建一个节点指向 head，使得原链表的所有节点（包括 head）都有了一个前驱节点。这样，所有的增删改查操作都可以统一为"对中间节点的操作逻辑"，从而消除边界判断。

简单来说：当链表的头节点（Head）有可能被删除、被移动或发生变化 时，引入一个虚拟的 dummy 节点指向 head，可以将所有节点的操作统一化，避免对头节点进行特殊的 if-else 判断。

核心模式：

java 复制代码

ListNode dummy = new ListNode(-1); // 值通常不重要
dummy.next = head;                 // 哨兵指向真正的头
ListNode curr = dummy;             // 操作指针从哨兵开始
// ... 执行统一逻辑 ...
return dummy.next;                 // 返回哨兵指向的下一个节点，即新链表的头

2.1 删除链表的倒数第 N 个节点

题目链接 ：LeetCode 19. Remove Nth Node From End of List

题目描述：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

思路解析 ：

要删除链表中的一个节点，必须拿到该节点的前驱节点 (Predecessor) 。

例如：A -> B -> C，要删除 B，我们需要站在 A 的位置执行 A.next = A.next.next。

挑战：如果倒数第 N 个节点恰好是 head，没有前驱怎么办？
解法：使用 Dummy Node。
双指针策略 ：
1. 让 fast 指针先走 n + 1 步
2. slow 和 fast 同时移动，直到 fast 指向 null。
3. 此时 slow 刚好位于倒数第 n + 1 个位置。
4. 执行 slow.next = slow.next.next。

关键点：为什么要让 fast 先走 n + 1 步？

利用快慢指针寻找倒数节点通常有两种移动策略，取决于目标是什么：
链表下标从零开始

目标是"找到"倒数第 N 个节点 ：
- 希望 slow 最终停在倒数第 N 个节点上。
- 如果链表长 L，slow 需要停在 L - n 的位置。
- 当 fast 指向 null (即位置 L) 时，slow 与 fast 的距离应为 n。
- 策略：fast 先走 n 步。
**目标是"删除"倒数第 N 个节点：
- 希望 slow 最终停在倒数第 N 个节点的前一个节点（即倒数第 N + 1 个节点）上，这样才能执行删除操作。
- 如果链表长 L，slow 需要停在 L - n - 1 的位置。
- 当 fast 指向 null (即位置 L) 时，slow 与 fast 的距离应为 n + 1。
- 策略：fast 必须先走 n + 1 步。

边界验证 ：

假如链表只有 1 个节点 [1]，删除倒数第 1 个（即删除 head）。

dummy -> 1 -> null。
n = 1，fast 先走 1 + 1 = 2 步，指向 null。
while 循环不执行。
slow 停在 dummy。
执行 dummy.next = dummy.next.next，即 dummy -> null。
返回 dummy.next (null)。逻辑完美闭环。

Java 代码：

java 复制代码

public ListNode removeNthFromEnd(ListNode head, int n) {
    // 初始化 Dummy 节点，规避删除 head 时的特殊判断
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    
    // slow 和 fast 都从 dummy 出发
    ListNode fast = dummy;
    ListNode slow = dummy;
    
    // 让 fast 领先 slow 正好 n + 1 步 
    // 这样当 fast 到达末尾(null)时，slow 正好在被删节点的前一个位置
    for (int i = 0; i <= n; i++) {
        fast = fast.next;
    }
    
    // 双指针同步移动，保持间隔不变，直到 fast 到达末尾
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    
    // 删除操作
    // slow 现在指向被删除节点的前一个节点
    slow.next = slow.next.next;
    
    return dummy.next;
}

2.2 合并两个有序链表

题目链接 ：LeetCode 21. Merge Two Sorted Lists

题目描述：将两个升序链表合并为一个新的升序链表并返回。

思路解析 ：

这是一道经典的拉链法题目。我们需要遍历两个链表，就像拉拉链一样，每次比较两边的节点值，将较小的那个接在新链表上。

引入 Dummy Node 的必要性 ：

在构建新链表之初，我们无法确定新链表的第一个节点 是 list1 的头还是 list2 的头。

不使用 Dummy ：必须先写一段逻辑比较 list1.val 和 list2.val 来初始化 head，还需要初始化一个 curr 指针。代码会有重复逻辑。
使用 Dummy ：直接创建一个虚拟头，curr 指针直接从 dummy 开始，进入 while 循环。所有节点的连接逻辑完全一致。

关键优化：O(1) 拼接

链表与数组最大的区别在于，当一个链表遍历完后，另一个链表剩余的部分不需要通过循环一个一个复制 。因为链表是通过指针连接的，我们只需要将 curr.next 直接指向剩余链表的头节点即可。这是一个 O ( 1 ) O(1) O(1) 的操作，极大地简化了代码。

Java 代码：

java 复制代码

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
    // 创建 Dummy 头节点作为新链表的哨兵节点
    ListNode dummy = new ListNode(-1);
    // curr 指针始终指向新链表的"尾部"，负责连接下一个较小的节点
    ListNode curr = dummy;
    
    // 循环比较，直到其中一个链表为空
    while (list1 != null && list2 != null) {
        if (list1.val <= list2.val) {
            curr.next = list1;      // 接上 list1
            list1 = list1.next;     // list1 指针后移
        } else {
            curr.next = list2;      // 接上 list2
            list2 = list2.next;     // list2 指针后移
        }
        // 新链表的尾指针后移，准备接下一个
        curr = curr.next;
    }
    
    // 处理剩余部分
    // 此时 list1 或 list2 中至多有一个不为空
    // 直接将剩余的一整串挂在 curr 后面即可
    if (list1 != null) {
        curr.next = list1;
    } else if (list2 != null) {
        curr.next = list2;
    }
    
    return dummy.next;
}

三、快慢指针进阶：中点与环入口

在链表问题中，快慢指针（Floyd 判圈算法）不仅能判断"是否存在环"，还能通过精确的步长控制，解决"中点定位"和"入环点定位"等几何问题。

3.1 寻找链表的中间节点

题目链接 ：LeetCode 876. Middle of the Linked List

题目描述：给定一个头结点为 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

思路解析 ：
距离原理 ：fast 速度是 slow 的 2 倍。当 fast 走完链表（达到 null）时，slow 走过的路程刚好是 fast 的一半，即到达中点。

边界条件控制 ：

链表长度的奇偶性决定了中点的定义，而 while 循环的终止条件决定了我们取的是哪一个中点。

假设链表：1 -> 2 -> 3 -> 4 -> 5 -> 6 (偶数长度 6)

目标：题目要求返回 4 (第二个中点)。
循环条件 ：while (fast != null && fast.next != null)
- Start: (1, 1)
- Step 1: slow=2, fast=3
- Step 2: slow=3, fast=5
- Step 3: slow=4, fast=null
- 终止：fast 为 null，循环结束，返回 slow (4)。符合预期。
变体思考 ：如果题目要求返回 3 (即偶数长度的前一个中点)，该怎么办？
- 需要让 slow 少走一步。可以通过修改循环条件为 while (fast.next != null && fast.next.next != null) 来实现，或者使用 Dummy Node 增加一个前置节点进行抵消。

Java 代码：

java 复制代码

public ListNode middleNode(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;
    
    // 核心循环条件解析：
    // 1. fast != null：防止链表长度为偶数时，fast 越界 (fast 最后停在 null)
    // 2. fast.next != null：防止链表长度为奇数时，fast 越界 (fast 最后停在最后一个节点)
    while (fast != null && fast.next != null) {
        slow = slow.next;       // 步长 1
        fast = fast.next.next;  // 步长 2
    }
    
    // 当循环结束时，slow 恰好停在中间位置（偶数长度则是第二个中点）
    return slow;
}

3.2 环形链表 II：寻找入环点

题目链接 ：LeetCode 142. Linked List Cycle II

题目描述：给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

思路解析（数学证明）：

这是一个经典的相遇问题。我们需要证明：当快慢指针相遇后，如果让其中一个指针回到起点，两者同速前进，它们必然会在入环点再次相遇。

变量定义：

a a a：从头节点 head 到 入环点 的距离。
b b b：从 入环点 到 首次相遇点 的距离。
c c c：从 首次相遇点 继续走回到 入环点 的剩余距离（即环长 L = b + c L = b + c L=b+c）。

推导过程：

相遇时刻的行程 ：
- slow 走的距离： S = a + b S = a + b S=a+b
- fast 走的距离： F = a + b + n ( b + c ) F = a + b + n(b + c) F=a+b+n(b+c) （其中 n ≥ 1 n \ge 1 n≥1，表示 fast 在环里转了 n n n 圈才追上 slow）。
速度倍率关系 ：
- 因为 V f a s t = 2 × V s l o w V_{fast} = 2 \times V_{slow} Vfast=2×Vslow，所以 F = 2 S F = 2S F=2S。
- 代入公式： a + b + n ( b + c ) = 2 ( a + b ) a + b + n(b + c) = 2(a + b) a+b+n(b+c)=2(a+b)
化简求值 ：
- a + b = n ( b + c ) a + b = n(b + c) a+b=n(b+c)
- 我们要求的是 a a a（起点的距离），所以移项得： a = n ( b + c ) − b a = n(b + c) - b a=n(b+c)−b
- 整理得： a = ( n − 1 ) ( b + c ) + c a = (n - 1)(b + c) + c a=(n−1)(b+c)+c
物理意义解读 ：
- ( b + c ) (b + c) (b+c) 就是环的长度 L L L。
- 公式 a = ( n − 1 ) L + c a = (n - 1)L + c a=(n−1)L+c 意味着：从头节点走到入环点的距离 a a a，等于从相遇点继续走 c c c 步，再加上 n − 1 n-1 n−1 圈的距离。
- 忽略圈数（因为在环里转圈最终还是回到原点），我们可以得出结论：距离 a a a 等效于距离 c c c。

算法执行流程：

判断环 ：先利用 slow (1 步) 和 fast (2 步) 确定是否相遇。如果不相遇则无环。
重置指针 ：相遇后，将 fast 指针重新指向链表头部 head。
同步推进 ：此时 slow 在相遇点，fast 在头部。让两者都以 1 步 的速度前进。
相遇即入口 ：根据上述推导 a = c a = c a=c，它们相遇的位置一定是入环点。

Java 代码：

java 复制代码

public ListNode detectCycle(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;
    
    // 第一阶段：判断是否有环
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        
        // 发生相遇，说明有环
        if (slow == fast) {
            // 第二阶段：寻找入环点
            // 将其中一个指针（如 fast）重置回链表头部
            fast = head;
            
            // 两个指针同速前进（步长均为 1）
            // 原理：Head到入口的距离 = 相遇点到入口的距离
            while (slow != fast) {
                slow = slow.next;
                fast = fast.next;
            }
            
            // 再次相遇点即为入环点
            return slow;
        }
    }
    
    return null;
}

四、进阶结构修改：分组反转与交换

在此类问题中，需要同时操作 3 到 4 个指针，且必须严格保证操作顺序。相较于全链表反转，局部反转需要处理"前驱节点连接新头"和"新尾连接后继节点"两个额外的衔接动作。

核心技巧：

哨兵节点（Dummy Node）：由于首组节点反转或交换后，链表的头节点（Head）会发生改变，使用虚拟头节点可以避免对"第一组"进行特殊判断。
多指针定位 ：在操作区间 [start, end] 之前，必须先持有 start 的前驱节点（pre）和 end 的后继节点（next），形成 pre -> [start ... end] -> next 的引用链保护。

4.1 两两交换链表中的节点

题目链接 ：LeetCode 24. Swap Nodes in Pairs

题目描述：给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

思路解析 ：

这是一道典型的迭代式指针修改 题目。我们需要在遍历过程中，将连续的两个节点 node1 和 node2 的位置互换。

指针操作细节 ：

假设当前链表状态为 prev -> node1 -> node2 -> nextStart。

我们的目标是将其变为 prev -> node2 -> node1 -> nextStart。

这涉及到三根指针的断开与重连：

前驱修正 ：prev.next 指向 node2（跳过 node1）。
内部反转 ：node2.next 指向 node1（原来的后面变前面）。
后继连接 ：node1.next 指向 nextStart（原来的前面变后面，并连接剩余部分）。

迭代维护 ：

完成交换后，原来的 node1 变成了当前组的尾部。为了处理下一组，需要将 prev 更新为 node1，curr 更新为 nextStart。

Java 代码：

java 复制代码

public ListNode swapPairs(ListNode head) {
    // 哨兵头节点处理头节点交换的情况
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    
    ListNode prev = dummy;
    ListNode curr = head;
    
    // 必须保证有两个节点才能交换
    while (curr != null && curr.next != null) {
    
	    // 定义本轮要交换的两个节点 + 暂存下一轮的起始节点
        ListNode first = curr;
        ListNode second = curr.next;
		ListNode nextStart = second.next;
		
		// 执行交换
		prev.next = second;          // 前一个节点指向交换对的第二个节点
		second.next = first;         // 第二个节点指向第一个节点
		first.next = nextStart;      // 第一个节点指向下一轮的起始节点
		
		// 移动指针，准备下一轮
		prev = first;                // prev 留在本轮交换后的尾节点（原第一个节点）
		curr = nextStart;            // curr 移动到下一轮的起始节点
    }
    
    return dummy.next;
}

4.2 K 个一组翻转链表

题目链接 ：LeetCode 25. Reverse Nodes in k-Group

题目描述：给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

思路解析 ：

这是链表反转类题目的递归解法典范。与迭代法相比，递归法利用系统调用栈天然地保留了"后续链表处理结果"的引用，代码结构往往更清晰。

算法宏观流程 ：

将问题分解为："处理当前 K 个节点" + "递归处理剩余所有节点"。

边界检查 ：
首先遍历链表的前 K 个节点。
- 如果节点数量不足 K 个（遇到 null），说明剩余部分不需要反转，直接返回当前的 head（保持原样）。
- 如果找到了第 K 个节点（groupEnd），说明当前组满足反转条件。
子问题递归 ：
在反转当前组之前，先递归调用函数 reverseKGroup(groupEnd.next, k)。
这个调用会返回后面所有节点处理完毕后的新头节点 。将这个结果直接挂在当前组反转后的尾部（即 head）。
当前组反转 ：
使用辅助函数 reverseList 将 [head, groupEnd) 区间的节点进行反转。反转后，原来的 groupEnd 成为新的头，原来的 head 成为新的尾。

Java 代码：

java 复制代码

public ListNode reverseKGroup(ListNode head, int k) {
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    
    ListNode groupPrev = dummy;
    
    while (true) {
        // 检查剩余节点是否有 k 个
        ListNode groupEnd = groupPrev;
        for (int i = 0; i < k; i++) {
            groupEnd = groupEnd.next;
            if (groupEnd == null) {
                return dummy.next; // 不足 k 个，保持原样返回，递归/循环终止
            }
        }
        
        // 核心递归逻辑
        // reverseList 将 [head, groupEnd] 区间反转，并返回新的头节点 (newNode)
	    ListNode newNode = reverseList(head, groupEnd);
	    
	    // 递归连接，head 变成了当前组的尾节点，它的 next 应该指向下一组递归处理的结果
        head.next = reverseKGroup(groupEnd, k);
        return newNode;
    }
}

// 链表反转函数变体（以支持区间反转）
private ListNode reverseList(ListNode head, ListNode node){
	ListNode pre = null;
    ListNode curr = head;
	while(curr != node){
		ListNode next = curr.next;
        curr.next = pre;
        pre = curr;
        curr = next;
    }
    return pre;
}

五、综合应用：回文链表

这道题是链表操作的综合应用，它同时考察了：快慢指针找中点 、链表反转 、多指针遍历比较。

题目链接 ：LeetCode 234. Palindrome Linked List

题目描述 ：给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。
要求：时间 O ( N ) O(N) O(N)，空间 O ( 1 ) O(1) O(1)。

思路解析 ：

若允许 O ( N ) O(N) O(N) 空间，可以直接将链表值复制到数组或栈中进行双向比较。但在 O ( 1 ) O(1) O(1) 空间限制下，无法使用额外的容器。由于单链表无法向后遍历，唯一的解决手段是修改链表结构。

核心策略：折半对比

回文的特性是左右对称。如果能找到链表的中间节点 ，将后半部分链表原地反转 ，那么原本指向"右边"的指针就会指向"左边"。

此时，只需要用两个指针，分别从"原本的头"和"反转后的尾"向中间遍历，逐一比对数值即可。

找中点 ：
使用快慢指针找到链表的中间位置。
- 注意：我们需要找到的是前半部分的尾节点。因为我们需要通过它来获取后半部分的入口，并在比对结束后重新连接链表。
反转后半部分 ：
将后半部分链表进行反转。例如 1->2->3->2->1，反转后变为 1->2->3 和 1->2（注意此时链表结构变为 Y 字形或断开，具体取决于实现）。
同步比对 ：
- 指针 P1 从 head 出发。
- 指针 P2 从反转后的后半部分头节点出发。
- 同步移动，一旦发现 val 不同立即返回 false。
状态复原（可选） ：
虽然题目没强制要求，但改变输入数据的结构是危险的。因此在返回结果前，建议再次反转后半部分，将链表恢复原状。

难点：奇偶长度的边界对齐

偶数长度 (1->2->2->1)：快慢指针策略会让 slow 停在第一个 2。后半部分是 2->1，反转后为 1->2。P1(1->2) 与 P2(1->2) 长度一致，完美匹配。
奇数长度 (1->2->3->2->1)：快慢指针策略会让 slow 停在 3。后半部分是 2->1 (3 的下一个)。反转后为 1->2。
- P1 从头走：1->2->3。
- P2 从尾走：1->2。
- 关键点 ：比对循环的终止条件应以 P2 (较短的半区) 为准。当 P2 走完时，P1 剩下的节点（中间节点）不需要比对，因为它自己肯定等于自己。

Java 代码：

java 复制代码

public boolean isPalindrome(ListNode head) {
    if (head == null || head.next == null) return true;

    // 寻找前半部分的尾节点 (即中点)
    // 这里的逻辑会让 slow 停在左中点 (对于偶数长度)
    // 例如：1->2->2->1，slow 指向第一个 2
    // 例如：1->2->3->2->1，slow 指向 3
    ListNode firstHalfEnd = endOfFirstHalf(head);
    
    // 反转后半部分
    ListNode secondHalfStart = reverseList(firstHalfEnd.next);

    // 判断是否回文，双指针同步比对
    ListNode p1 = head;
    ListNode p2 = secondHalfStart;
    boolean result = true;
    while (result && p2 != null) {
        if (p1.val != p2.val) {
            result = false;
        }
        p1 = p1.next;
        p2 = p2.next;
    }

    // 恢复链表 (可选，但建议加上)
    firstHalfEnd.next = reverseList(secondHalfStart);
    
    return result;
}

// 辅助函数：快慢指针找中点
private ListNode endOfFirstHalf(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;
    // 注意这里的条件，是为了让 slow 停在前半部分的最后一个节点
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow;
}

// 标准的链表反转函数
private ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode curr = head;
    while (curr != null) {
        ListNode nextTemp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

六、总结

链表题目在算法逻辑上通常属于"简单"或"中等"难度，但在实际面试中，其 Bug 率却极高。这主要是因为链表操作严重依赖于指针引用的精确控制 。稍有不慎，就会导致空指针异常 (NullPointerException) 或引用丢失（断链）。

5.1 核心解题模式回顾

在面对一道链表题目时，应首先判断其属于哪类标准模型：

结构变更类 ：
- 涉及反转、交换、重排。
- 对策：必须使用 三指针法 (prev, curr, next)，严格遵守"先保存 next，再修改引用"的操作顺序。
边界处理类 ：
- 涉及头节点的删除、插入，或链表合并。
- 对策：无条件引入 Dummy Node (虚拟头节点) ，将头节点的操作泛化为中间节点操作，消除 if (head == null) 分支。
位置查找类 ：
- 涉及找中点、找倒数第 K 个、判圈。
- 对策：使用 快慢指针 (Fast & Slow Pointers) 。利用步长差 ( v f a s t = 2 × v s l o w v_{fast} = 2 \times v_{slow} vfast=2×vslow) 在一次遍历中解决定位问题。

5.2 链表防御性编程

在代码提交或面试白板书写前，必须逐一核对以下检查点：

输入有效性检查 ：
- 代码能否正确处理 head == null 或 head.next == null（单节点）的情况？
- 建议：在函数开头统一处理 if (head == null) return ...。
断链保护机制 ：
- 在执行 curr.next = target 之前，是否已经确认 curr 后面的节点（原 curr.next）已经被其他变量保存？如果未保存，该部分链表将永久丢失（Memory Leak）。
循环终止条件的精确性 ：
- 全遍历 ：while (curr != null) ------ 用于访问每个节点。
- 停在尾节点 ：while (curr.next != null) ------ 用于需要操作尾节点（如连接新链表）。
- 快慢指针/偶数长度保护 ：while (fast != null && fast.next != null) ------ 防止 fast.next.next 抛出 NPE。

5.3 时空复杂度

时间复杂度 ：
- 标准：O ( N ) O(N) O(N)。绝大多数链表题都要求一次（或常数次）遍历。
- 警示：如果你的解法出现了嵌套循环（例如遍历每个节点，对每个节点再遍历寻找前驱），导致 O ( N 2 ) O(N^2) O(N2)，这通常可以使用双指针或哈希表的优化解法。
空间复杂度 ：
- 标准：O ( 1 ) O(1) O(1)。这是链表题最核心的考察点。
- 反模式 (Anti-Pattern) ：
  - 禁止使用 ArrayList 或 Stack 将链表元素全部存下来再操作。这违背了链表题考察"指针操作"的初衷。
  - 谨慎使用递归。虽然递归代码简洁（如反转链表），但递归调用栈的深度是 O ( N ) O(N) O(N)。在工程中，对于长链表可能会导致 StackOverflowError。因此，掌握迭代（Iterative）写法是必须的。

5.4 链表题型分类

题型分类	代表题目（LeetCode）	核心技巧	备注
基础反转	206（反转链表）	迭代三指针 / 递归	所有反转类题目的原子操作
局部反转	92（反转部分链表）、24（两两交换）、25（K 个一组翻转）	迭代 + 分段反转 + Dummy Node	25 是综合题，24 是热身
删除节点	19（删除倒数第 N 个）、83（删除排序链表重复）、82（删除排序链表全部重复）、203（移除指定值）	Dummy Node + 快慢指针 / 虚节点	头节点删除必用 Dummy
合并/重组	21（合并两个有序链表）、23（合并 K 个有序链表）、328（奇偶链表）	Dummy Node + 拉链法 / 多指针	21 是拉链法经典
位置查找	876（链表中间节点）、19（倒数第 N 个）	快慢指针	步长控制决定停在哪个位置
环检测	141（环形链表）、142（环形链表 II）	Floyd 快慢指针 + 数学推导（相遇后重置指针）	142 是进阶，必须懂证明
回文/对称	234（回文链表）	快慢指针找中点 + 反转后半部分 + 双指针比对	O(1) 空间综合题
相交/其他	160（相交链表）、2（两数相加）	双指针（浪漫相遇） / 模拟进位	160 是双指针经典应用

Java 算法实践（四）：链表核心题型

一、 核心基石：链表反转

1.1 迭代反转法

1.2 递归反转法

二、 虚拟头节点：Dummy Node

2.1 删除链表的倒数第 N 个节点

2.2 合并两个有序链表

三、 快慢指针进阶：中点与环入口

3.1 寻找链表的中间节点

3.2 环形链表 II：寻找入环点

四、 进阶结构修改：分组反转与交换

4.1 两两交换链表中的节点

4.2 K 个一组翻转链表

五、 综合应用：回文链表

六、 总结

5.1 核心解题模式回顾

5.2 链表防御性编程

5.3 时空复杂度

5.4 链表题型分类

一、核心基石：链表反转

二、虚拟头节点：Dummy Node

三、快慢指针进阶：中点与环入口

四、进阶结构修改：分组反转与交换

五、综合应用：回文链表

六、总结