文章目录
小编提醒:在动态规划问题中,将数组命名为f和dp都可以。
从记忆化搜索到动态规划
记忆化搜索
在搜索的过程中,如果搜索树中有很多重复的结点,此时可以通过⼀个 "备忘录",记录第⼀次搜索到 的结果。当下⼀次搜索到这个结点时,直接在 "备忘录" ⾥⾯找结果。其中,搜索树中的⼀个⼀个结点,也称为⼀个⼀个状态。 ⽐如经典的斐波那契数列问题:
cpp
int f[N]; // 备忘录
int fib(int n)
{
// 搜索之前先往备忘录⾥⾯瞅瞅
if(f[n] != -1) return f[n];
if(n == 0 || n == 1) return f[n] = n;
// 返回之前,把结果记录在备忘录中
f[n] = fib(n - 1) + fib(n - 2);
return f[n];
}递归改递推
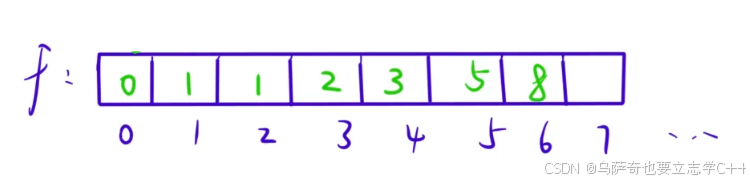
在⽤记忆化搜索解决斐波那契问题时,如果关注 "备忘录" 的填写过程,会发现它是从左往右依次填写 的。当位置前⾯的格⼦填写完毕之后,就可以根据格⼦⾥⾯的值计算出 位置的值。所以,整个 递归过程,我们也可以改写成循环的形式,也就是递推:
cpp
int f[N]; // f[i] 表⽰:第 i 个斐波那契数
int fib(int n)
{
// 初始化前两个格⼦
f[0] = 0; f[1] = 1;
// 按照递推公式计算后⾯的值
for(int i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
// 返回结果
return f[n];
}动态规划
动态规划(Dynamic Programming,简称DP)是⼀种⽤于解决多阶段决策问题的算法思想。它通过将复杂问题分解为更⼩的⼦问题,并存储⼦问题的解(通常称为"状态"),从⽽避免重复计算,提 ⾼效率。因此,动态规划⾥,蕴含着分治与剪枝思想。
上述通过记忆化搜索 以及递推解决斐波那契数列的⽅式,其实都是动态规划。
在递推形式的动态规划中,常⽤下⾯的专有名词来表述:
- 状态表⽰:指 f 数组中,每⼀个格⼦代表的含义。其中,这个数组也会称为 dp 数组,或者 dp 表。
- 状态转移⽅程:指 f 数组中,每⼀个格⼦是如何⽤其余的格⼦推导出来的。
- 初始化:在填表之前,根据题⽬中的默认条件或者问题的默认初始状态,将 f 数组中若⼲格⼦先 填上值。
其实递推形式的动态规划中的各种表述,是可以对应到递归形式的:
- 状态表⽰ <---> 递归函数的意义(如求出第n个斐波那契数是多少);
- 状态转移⽅程 <---> 递归函数的主函数体;
- 初始化 <---> 递归函数的递归出⼝。
如何利⽤动态规划解决问题第⼀种⽅式当然就是记忆化搜索了:
• 先⽤递归的思想去解决问题;
• 如果有重复⼦问题,就改成记忆化搜索的形式。
第⼆种⽅式,直接使⽤递推形式的动态规划解决:
- 定义状态表⽰: ⼀般情况下根据经验+递归函数的意义,赋予 dp 数组相应的含义。(其实还可以去蒙⼀个,如果 蒙的状态表⽰能解决问题,说明蒙对了。如果蒙错了,再换⼀个试~)
- 推导状态转移⽅程: 根据状态表⽰以及题意,在 dp 表中分析,当前格⼦如何通过其余格⼦推导出来。
- 初始化: 根据题意,先将显⽽易⻅的以及边界情况下的位置填上值。
- 确定填表顺序: 根据状态转移⽅程,确定按照什么顺序来填表。
- 确定最终结果: 根据题意,在表中找出最终结果。
下楼梯
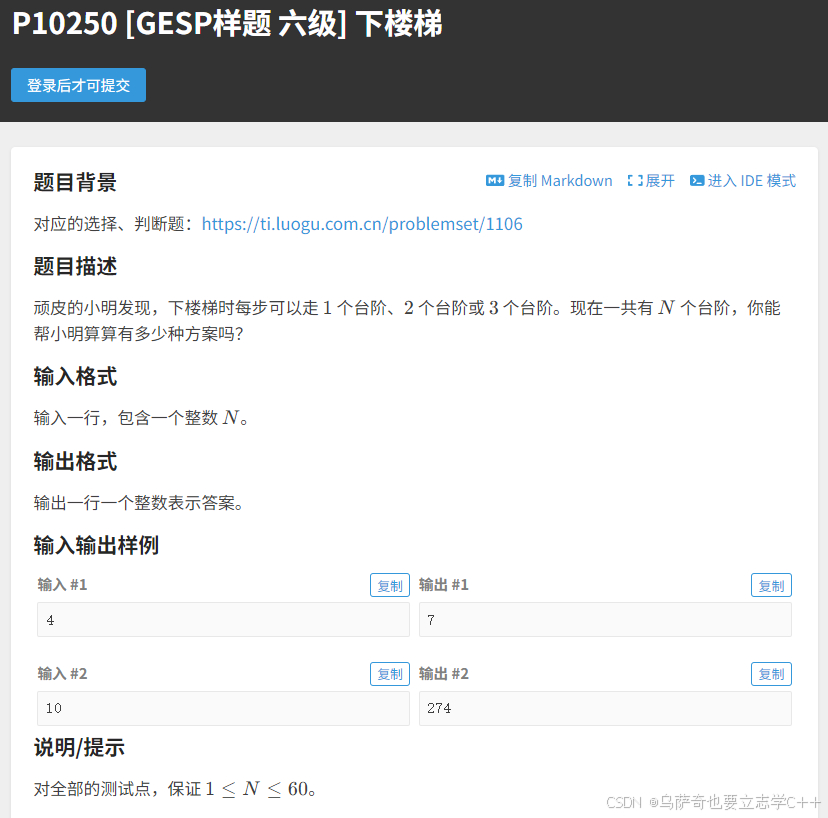
题目描述
题目解析
本题题意是研究从楼梯顶跳到楼梯底有多少种方法,我们可以转换一下思路,研究从楼梯底跳到楼梯顶有多少种方法,这样正向思路更容易思考。
1、状态表示我们先猜测f[i]表示跳到第i个台阶有多少种方法,f[0]表示地面。
2、状态转移方程
推导状态转移方程的一般思路是根据最后一步划分情况,我们利用本题来推导一下,最后一步有三种情况:
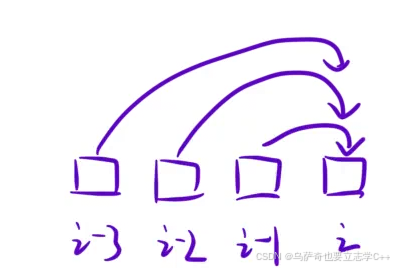
我们知道从i-1跳一步也就是往后跳一格就能走到i,那么如果跳到i-1有x种情况,也就是说从i-1跳到i有x种情况,
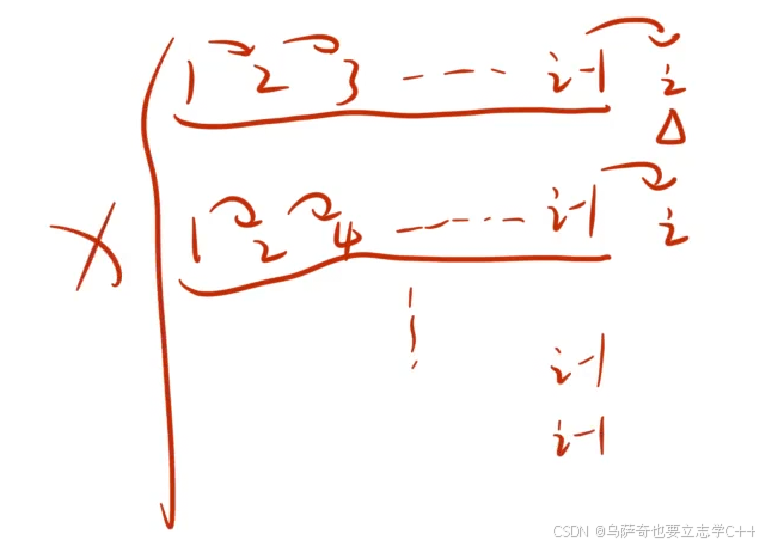
同理从i-1跳两步也就是往后跳两格就能走到i,那么如果跳到i-2有y种情况,也就是说从i-2跳到i有y种情况,那么如果跳到i-3有z种情况,也就是说从i-3跳到i有z种情况,那么跳到i一共就有x+y+z种情况,一句话总结,如果跳到i-1的情况确定了,跳到i的情况也就随之确定了。
所以本题的状态转移方程为f[i] = f[i -1] + f[i - 2] + f[i - 3]。
3、初始化首先我们要明确初始化有两个意义:
1、保证填表是正确性。
2、保证填表的时候不越界。
对于本题来说,利用状态转移方程填前三个格子的时候就会发生数组越界访问,所以需要对前三个格子进行初始化。
先看下标0格子,把它初始化为0和1都解释的通,所以对于这种模棱两可的格子,我们先不管,往后推几个格子再看,再看下标1格子,跳到下标1格子只有一种情况,对于下标2格子,跳到下标2格子有两种情况,对于下标3格子,有四种情况,所以为了满足状态转移方程,反推下标0格子应该填1。然后就从下标3格子开始往后递推。
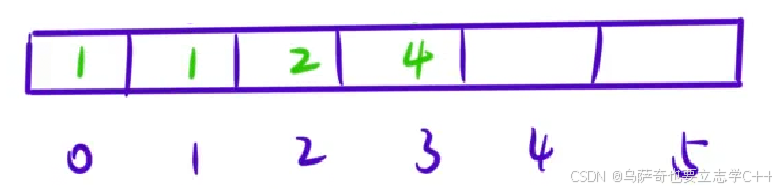
除了上面反推的方法,我们还可以完全忽略第一个格子,只初始化下标1、下标2、下标3这3个格子,从下标4开始往后递推。
4、确定填表顺序从左往右填表
5、最终结果f[n]即为结果
小编再说明一点,dp数组中下标0表示地面,1表示第一个台阶,依次类推,当题目n为3时表示一共有三个台阶,也就是需要拿到dp[3]的值,dp[3]包括dp[3]本身一共会有4个格子,也就是说开辟的格子总数始终会比n多1个。
本题小编再介绍一种空间优化的方法,利用滚动数组,方法如下:我们用未优化版本进行填表时,其实有很多空间是被浪费了的,比如在填下标6格子时,其实只用知道下标3、下标4、下标5的值就可以确定下标6格子的值,下标0、下标1、下标2的值是多余的,这三个格子的空间是没有存在的必要的,所以我们可以只开一个三个空间的小数组和一个临时变量t即可,小数组往后滚动即可完成递推,所以该优化方法叫做滚动数组,我们在此基础上再进一步优化可以将三个空间的小数组优化为3个整型变量,也就是开四个整型变量a b c t即可完成本题循环递推操作,它可以将O(n)的空间复杂度优化为O(1),如下图所示。
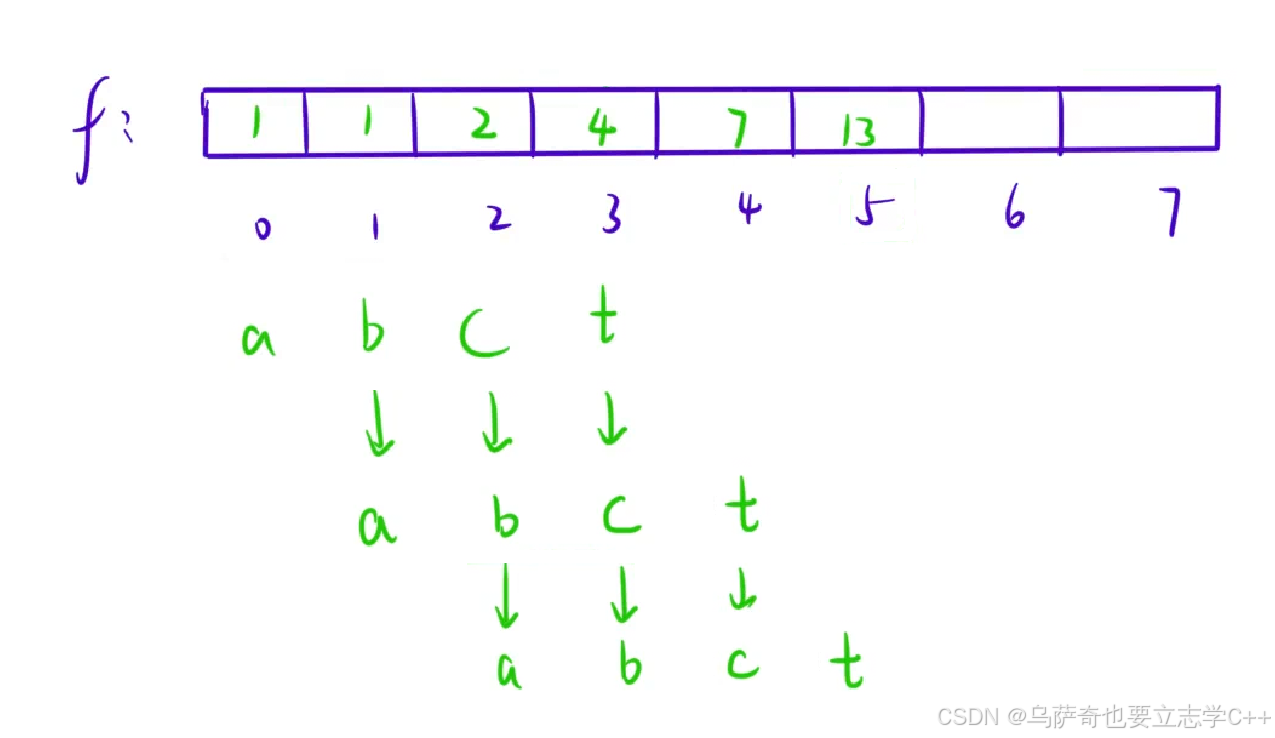
这里有两个注意事项:
1、变量的赋值顺序需要严格按照从左往右:a = b b = c c = t。
2、最后输出结果时需要判断台阶数n是否等于1,如果等于1表示还没有进行循环赋值,直接输出b,如果不等于1则输出c。
代码
注意本题dp数组元素范围是可能超过int的最大值的,所以dp数组的元素类型需要用long long。
cpp
//原始方法
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 70;
LL dp[N];
int main()
{
int n;
cin >> n;
//初始化
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
//根据状态转移方程递推填表
for (int i = 3; i <= n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
//输出结果
cout << dp[n] << endl;
return 0;
}
cpp
//利用滚动数组空间优化
#include <iostream>
using namespace std;
typedef long long LL;
int main()
{
int n;
cin >> n;
//初始化
LL a = 1, b = 1, c = 2, t = 0;
//往后滚动递推
for (int i = 3; i <= n; i++)
{
t = a + b + c;
a = b;
b = c;
c = t;
}
//输出结果
if (n == 1)
cout << b << endl;
else
cout << c << endl;
return 0;
}数字三角形
题目描述

题目解析
首先分析本题如何存储原始数据,如果用一个链式树形结构存储比较麻烦,所以我们可以参考题目输入示例用一个二维数组存储,如下图所示:
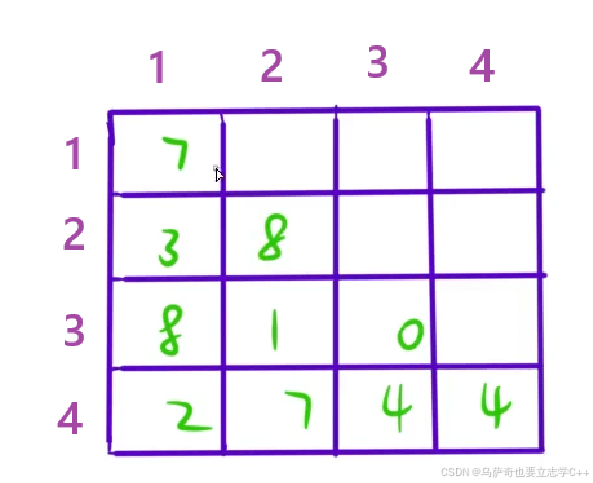
然后开始我们解决动态规划题目的5板斧:
1、状态表示 开一个二维数组dp,dp[i][j]表示从1 1走到i j的所有方案中的最大权值。
2、状态转移方程
推导状态转移方程需要根据最后一步划分情况,对于最后一个格子来说,最后一步可能来自两个格子的其中一个,一个是正上方,一个是左上方:
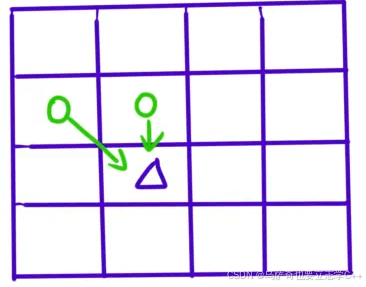
所以对于最后一个格子i j来说,它的最大权值dp[i][j]就是取正上方dp[i][j - 1]和左上方dp[i - 1][j - 1]格子权值的较大值,然后加上最后一个格子权值本身a[i][j],那么状态转移方程就是:
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - 1])+ a[i][j]
3、初始化因为本题计算格子最大权值需要拿格子正上方和左上方的格子最大权值,所以就会越界访问到非正常填表区域的格子,如下图所示绿色的最上面一行格子和最左边一列格子:
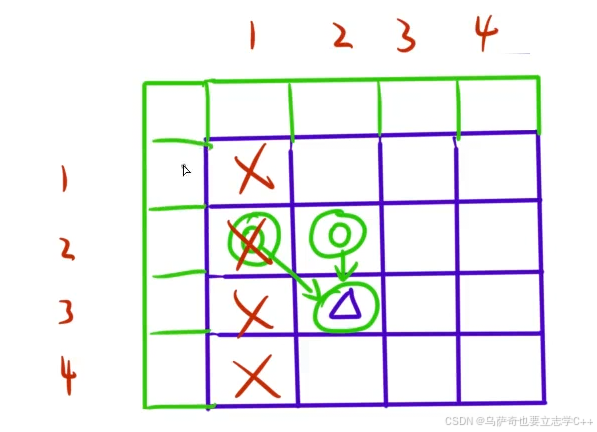
但是对于本题来说,因为我们只会填正方形给的左下半部分,所以只会越界访问到左边绿色一列。
解决方法就是在填表时访问到绿色格子时"装作没看到",就是在max二取一时只会取紫色格子,因为max是取较大值,并且本题的输入范围是 [0,100],所以只要将绿色格子初始化为0就可以保证只会取到紫色格子的值了。
4、填表顺序填表顺序仅需保证从上往下填即可,填同一行时无需关注左右顺序,因为填表时我们只关心上一行的值。 5、最终结果 dp数组最后一行的最大值
这里我们也可以对二维数组进行空间优化,将O(N^2)的空间复杂度优化为O(N),具体操作如下:对于本题来说,填格子是按行来填的,并且因为本题填格子时只关注正上方和左上方的格子,所以填一行格子时只关注上一行的格子情况,比如填第四行时只要有第三行的格子数据就足够了,第一行和第二行的格子是多余的,所以我们可以只开一个一维数组f,用数组f进行填表,方法如下图所示,f和f'本质是同一个数组的不同状态,f表示数组的原数据,f'表示更新后的数据,更新公式为:
f[i] = max(f[j],f[j - 1]) + a[i][j]
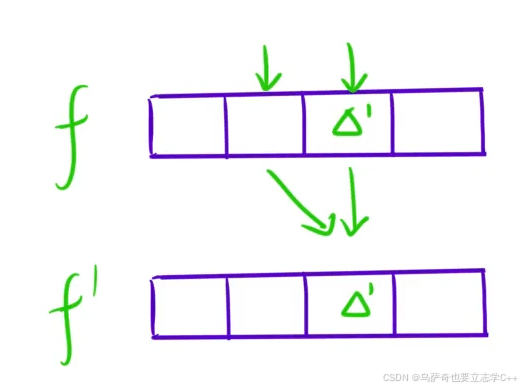
空间优化都需要注意填表顺序,本题更新一个位置格子数据时需要访问该位置原本的数据和该位置左边格子原本的数据,所以在更新一个位置格子数据时它左边的格子不能比它先更新,所以我们需要按照从右往左的顺序更新格子数据。
体现在代码中我们只用修改两个地方:
1、将二维dp数组改为一维,把二维数组的第一维删掉
2、修改每行格子的更新顺序
总结:对于二维转一维的空间优化我们只用关注两个地方,第一判断是否需要修改遍历更新顺序,第二在代码中只用将二维数组第一维删掉即可。
代码
cpp
//原始方法
#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N], dp[N][N];
int main()
{
int r;
cin >> r;
//处理输入
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= i; j++)
{
cin >> a[i][j];
}
}
//初始化,全局开辟的数组数据天然为0
//按序填表
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= i; j++)
{
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];
}
}
//输出结果
int ret = 0;
for (int i = 1; i <= r; i++)
{
ret = max(ret, dp[r][i]);
}
cout << ret << endl;
return 0;
}
cpp
//空间优化后代码
#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N], dp[N];
int main()
{
int r;
cin >> r;
//处理输入
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= i; j++)
{
cin >> a[i][j];
}
}
//初始化,全局开辟的数组数据天然为0
//按序填表
for (int i = 1; i <= r; i++)
{
for (int j = i; j >= 1; j--)
{
dp[j] = max(dp[j], dp[j - 1]) + a[i][j];
}
}
//输出结果
int ret = 0;
for (int i = 1; i <= r; i++)
{
ret = max(ret, dp[i]);
}
cout << ret << endl;
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
