项目篇----使用基数树对性能进行优化

卷卷的小趴菜学编程2026-02-17 10:43

1.为什么要使用基数树？

核心痛点：锁竞争

在高并发内存池中，页号到 Span 的映射 （MapObjectToSpan）是高频操作：

内存分配：需要找到合适的 Span 来切分小对象

内存释放：需要根据地址找到对应的 Span 来归还

而使用 unordered_map 或 map 的问题 ：

  1. 线程不安全：需要加锁保护，大量线程竞争导致性能瓶颈

  2. 结构不稳定：插入/删除时可能触发 rehash（哈希表）或旋转（红黑树），影响并发读

  3. 查找开销：哈希计算或树遍历有一定开销

基数树的优势：

O(1) 直接寻址：数组索引，无需哈希计算

结构稳定：写操作不改变树结构（预先分配节点），读操作无需加锁

读写分离：写时提前开好空间，读时直接访问

那说了半天，基数树是什么呢？

2.基数树

结构：直接用一个数组存储所有页号的映射

复制代码 
template <int BITS>
class TCMalloc_PageMap1 {
private:
    static const int LENGTH = 1 << BITS;  // 2^BITS 个槽位
    void** array_;  // 指针数组，每个位置存 Span*

public:
    void* get(Number k) const {
        if ((k >> BITS) > 0) return nullptr;
        return array_[k];  // O(1) 直接寻址
    }
    
    void set(Number k, void* v) {
        array_[k] = v;  // O(1) 直接写入
    }
};

这里只实现32位系统的，如果想实现64位的要写三层基数树

复制代码 
#pragma once
#include"Common.h"

// Single-level array
template <int BITS>
class TCMalloc_PageMap1 {
private:
	static const int LENGTH = 1 << BITS;
	void** array_;

public:
	typedef uintptr_t Number;

	//explicit TCMalloc_PageMap1(void* (*allocator)(size_t)) {
	explicit TCMalloc_PageMap1() {
		//array_ = reinterpret_cast<void**>((*allocator)(sizeof(void*) << BITS));
		size_t size = sizeof(void*) << BITS;
		size_t alignSize = SizeClass::_RoundUp(size, 1 << PAGE_SHIFT);
		array_ = (void**)SystemAlloc(alignSize >> PAGE_SHIFT);
		memset(array_, 0, sizeof(void*) << BITS);
	}

	// Return the current value for KEY.  Returns NULL if not yet set,
	// or if k is out of range.
	void* get(Number k) const {
		if ((k >> BITS) > 0) {
			return NULL;
		}
		return array_[k];
	}

	// REQUIRES "k" is in range "[0,2^BITS-1]".
	// REQUIRES "k" has been ensured before.
	//
	// Sets the value 'v' for key 'k'.
	void set(Number k, void* v) {
		array_[k] = v;
	}
};

// Two-level radix tree
template <int BITS>
class TCMalloc_PageMap2 {
private:
	// Put 32 entries in the root and (2^BITS)/32 entries in each leaf.
	static const int ROOT_BITS = 5;
	static const int ROOT_LENGTH = 1 << ROOT_BITS;

	static const int LEAF_BITS = BITS - ROOT_BITS;
	static const int LEAF_LENGTH = 1 << LEAF_BITS;

	// Leaf node
	struct Leaf {
		void* values[LEAF_LENGTH];
	};

	Leaf* root_[ROOT_LENGTH];             // Pointers to 32 child nodes
	void* (*allocator_)(size_t);          // Memory allocator

public:
	typedef uintptr_t Number;

	//explicit TCMalloc_PageMap2(void* (*allocator)(size_t)) {
	explicit TCMalloc_PageMap2() {
		//allocator_ = allocator;
		memset(root_, 0, sizeof(root_));

		PreallocateMoreMemory();
	}

	void* get(Number k) const {
		const Number i1 = k >> LEAF_BITS;
		const Number i2 = k & (LEAF_LENGTH - 1);
		if ((k >> BITS) > 0 || root_[i1] == NULL) {
			return NULL;
		}
		return root_[i1]->values[i2];
	}

	void set(Number k, void* v) {
		const Number i1 = k >> LEAF_BITS;
		const Number i2 = k & (LEAF_LENGTH - 1);
		ASSERT(i1 < ROOT_LENGTH);
		root_[i1]->values[i2] = v;
	}

	bool Ensure(Number start, size_t n) {
		for (Number key = start; key <= start + n - 1;) {
			const Number i1 = key >> LEAF_BITS;

			// Check for overflow
			if (i1 >= ROOT_LENGTH)
				return false;

			// Make 2nd level node if necessary
			if (root_[i1] == NULL) {
				//Leaf* leaf = reinterpret_cast<Leaf*>((*allocator_)(sizeof(Leaf)));
				//if (leaf == NULL) return false;
				static ObjectPool<Leaf>	leafPool;
				Leaf* leaf = (Leaf*)leafPool.New();

				memset(leaf, 0, sizeof(*leaf));
				root_[i1] = leaf;
			}

			// Advance key past whatever is covered by this leaf node
			key = ((key >> LEAF_BITS) + 1) << LEAF_BITS;
		}
		return true;
	}

	void PreallocateMoreMemory() {
		// Allocate enough to keep track of all possible pages
		Ensure(0, 1 << BITS);
	}
};

// Three-level radix tree
template <int BITS>
class TCMalloc_PageMap3 {
private:
	// How many bits should we consume at each interior level
	static const int INTERIOR_BITS = (BITS + 2) / 3; // Round-up
	static const int INTERIOR_LENGTH = 1 << INTERIOR_BITS;

	// How many bits should we consume at leaf level
	static const int LEAF_BITS = BITS - 2 * INTERIOR_BITS;
	static const int LEAF_LENGTH = 1 << LEAF_BITS;

	// Interior node
	struct Node {
		Node* ptrs[INTERIOR_LENGTH];
	};

	// Leaf node
	struct Leaf {
		void* values[LEAF_LENGTH];
	};

	Node* root_;                          // Root of radix tree
	void* (*allocator_)(size_t);          // Memory allocator

	Node* NewNode() {
		Node* result = reinterpret_cast<Node*>((*allocator_)(sizeof(Node)));
		if (result != NULL) {
			memset(result, 0, sizeof(*result));
		}
		return result;
	}

public:
	typedef uintptr_t Number;

	explicit TCMalloc_PageMap3(void* (*allocator)(size_t)) {
		allocator_ = allocator;
		root_ = NewNode();
	}

	void* get(Number k) const {
		const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);
		const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1);
		const Number i3 = k & (LEAF_LENGTH - 1);
		if ((k >> BITS) > 0 ||
			root_->ptrs[i1] == NULL || root_->ptrs[i1]->ptrs[i2] == NULL) {
			return NULL;
		}
		return reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3];
	}

	void set(Number k, void* v) {
		ASSERT(k >> BITS == 0);
		const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);
		const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1);
		const Number i3 = k & (LEAF_LENGTH - 1);
		reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3] = v;
	}

	bool Ensure(Number start, size_t n) {
		for (Number key = start; key <= start + n - 1;) {
			const Number i1 = key >> (LEAF_BITS + INTERIOR_BITS);
			const Number i2 = (key >> LEAF_BITS) & (INTERIOR_LENGTH - 1);

			// Check for overflow
			if (i1 >= INTERIOR_LENGTH || i2 >= INTERIOR_LENGTH)
				return false;

			// Make 2nd level node if necessary
			if (root_->ptrs[i1] == NULL) {
				Node* n = NewNode();
				if (n == NULL) return false;
				root_->ptrs[i1] = n;
			}

			// Make leaf node if necessary
			if (root_->ptrs[i1]->ptrs[i2] == NULL) {
				Leaf* leaf = reinterpret_cast<Leaf*>((*allocator_)(sizeof(Leaf)));
				if (leaf == NULL) return false;
				memset(leaf, 0, sizeof(*leaf));
				root_->ptrs[i1]->ptrs[i2] = reinterpret_cast<Node*>(leaf);
			}

			// Advance key past whatever is covered by this leaf node
			key = ((key >> LEAF_BITS) + 1) << LEAF_BITS;
		}
		return true;
	}

	void PreallocateMoreMemory() {
	}
};

3.性能测试

到这里我们的项目就基本上完成了，下面进行项目测试：

我们的测试内容为，多线程并发执行多轮次，对比tcmalloc 和malloc的效率差多少，比较二者时间！

测试聚焦小对象高频分配这一典型场景------在实际业务中，这种场景最为常见（如游戏服务器的消息对象、Web服务的请求上下文等）。固定分配16字节内存，通过4个线程并发执行，每线程进行10轮测试，每轮完成1000次分配与释放操作。

测试代码：

复制代码 
#include"ConcurrentAlloc.h"

// ntimes 一轮申请和释放内存的次数
// rounds 轮次
void BenchmarkMalloc(size_t ntimes, size_t nworks, size_t rounds)
{
	std::vector<std::thread> vthread(nworks);
	std::atomic<size_t> malloc_costtime = 0;
	std::atomic<size_t> free_costtime = 0;

	for (size_t k = 0; k < nworks; ++k)
	{
			vthread[k] = std::thread([&, k]() {
			std::vector<void*> v;
			v.reserve(ntimes);

			for (size_t j = 0; j < rounds; ++j)
			{
				size_t begin1 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					v.push_back(malloc(16));
					//v.push_back(malloc((16 + i) % 8192 + 1));
				}
				size_t end1 = clock();

				size_t begin2 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					free(v[i]); //malloc出来的函数  你在调用我们写的释放函数
				}
				size_t end2 = clock();
				v.clear();

				malloc_costtime += (end1 - begin1);
				free_costtime += (end2 - begin2);
			}
			});
	}

	for (auto& t : vthread)
	{
		t.join();
	}

	printf("%u个线程并发执行%u轮次，每轮次malloc %u次: 花费：%u ms\n",
		nworks, rounds, ntimes, malloc_costtime.load()); //这里是编译器变严格了导致的

	printf("%u个线程并发执行%u轮次，每轮次free %u次: 花费：%u ms\n",
		nworks, rounds, ntimes, free_costtime.load());

	printf("%u个线程并发malloc&free %u次，总计花费：%u ms\n",
		nworks, nworks * rounds * ntimes, malloc_costtime.load() + free_costtime.load());
}


// 单轮次申请释放次数 线程数 轮次
void BenchmarkConcurrentMalloc(size_t ntimes, size_t nworks, size_t rounds)
{
	std::vector<std::thread> vthread(nworks);
	std::atomic<size_t> malloc_costtime = 0;
	std::atomic<size_t> free_costtime = 0;

	//自己测试
	//vthread[0] = std::thread([&]() {
	//	std::vector<void*> v;
	//	v.reserve(ntimes);
	//	v.push_back(ConcurrentAlloc(16));
	//	ConcurrentFree(v[0]);
	//	v.clear(); 
	//	}

	for (size_t k = 0; k < nworks; ++k)
	{
		vthread[k] = std::thread([&]() {
			std::vector<void*> v;
			v.reserve(ntimes);

			for (size_t j = 0; j < rounds; ++j)
			{
				size_t begin1 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					v.push_back(ConcurrentAlloc(16));
					//v.push_back(ConcurrentAlloc((16 + i) % 8192 + 1));
				}
				
				size_t end1 = clock();

				size_t begin2 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					ConcurrentFree(v[i]);
				}
				
				size_t end2 = clock();
				v.clear();

				malloc_costtime += (end1 - begin1);
				free_costtime += (end2 - begin2);
			}
			});
	}
	

	for (auto& t : vthread)
	{
		t.join();
	}


	printf("%u个线程并发执行%u轮次，每轮次concurrent alloc %u次: 花费：%u ms\n",
		nworks, rounds, ntimes, malloc_costtime.load());

	printf("%u个线程并发执行%u轮次，每轮次concurrent dealloc %u次: 花费：%u ms\n",
		nworks, rounds, ntimes, free_costtime.load());

	printf("%u个线程并发concurrent alloc&dealloc %u次，总计花费：%u ms\n",
		nworks, nworks * rounds * ntimes, malloc_costtime.load() + free_costtime.load());

}


int main()
{
	size_t n = 1000;
	cout << "==========================================================" << endl;
	BenchmarkConcurrentMalloc(n, 4, 10);
	cout << endl << endl;

	BenchmarkMalloc(n,4 , 10); //测试不是这个哈
	cout << "==========================================================" << endl;

	return 0;
}

结果显示：

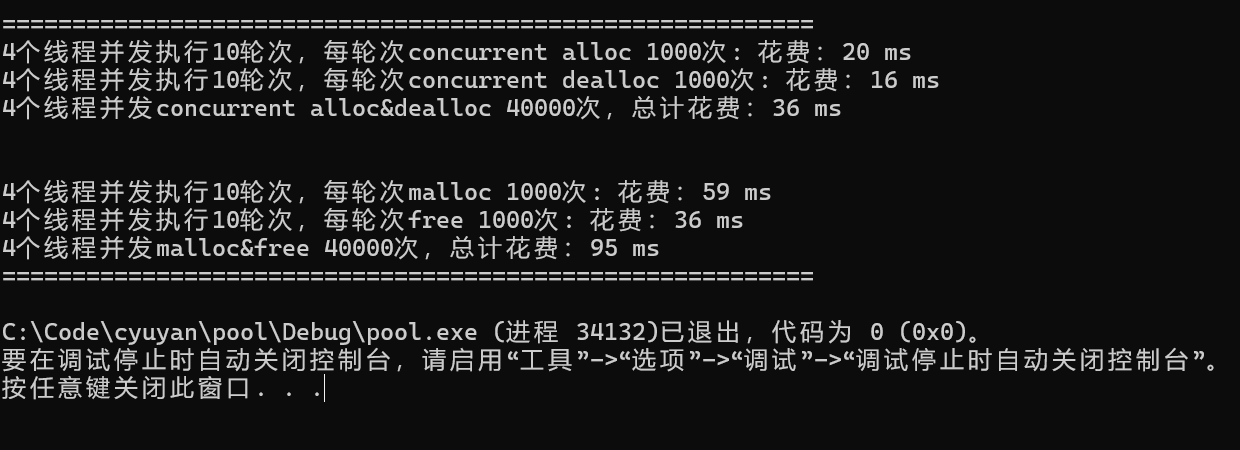
我们发现tcmalloc的性能确实快了不少！

好了本项目到此结束~

项目链接：

cyuyan: C语言的相关代码https://gitee.com/ren-zhihan/cyuyan/tree/master/pool/pool

项目技术总结：

第一层：ThreadCache（线程本地缓存）

核心机制

  • 线程隔离：每个线程拥有独立的内存缓存，通过TLS（线程本地存储）实现无锁访问

  • 208个自由链表：按对象大小分级管理，覆盖8B到256KB

  • 头插/头删策略：分配和释放都在链表头部操作，O(1)时间复杂度

关键计算公式

计算项 公式 说明
对齐后大小 ((size + align - 1) / align) × align 向上取整到对齐粒度
大小类索引 分段计算 + 累积偏移 根据5个区间分别映射到0-207
批量获取数量 min(当前maxSize, 理论计算值) 慢启动策略，逐步增长
慢启动增长 maxSize = maxSize + 1 每次满载后增加下次获取量

技术亮点

  • 慢启动批量获取：初始只获取1个对象，后续逐步增加，避免内存浪费

  • GC自动回收：当某个链表长度超过阈值，批量归还CentralCache

  • 无锁设计：TLS确保每个线程访问自己的缓存，无需任何同步原语

第二层：CentralCache（中央缓存）

核心机制

  • 桶锁细粒度并发：每个大小类独立加锁，减少锁竞争范围

  • Span管理单元：以连续页（Span）为单位组织内存，批量分配和回收

  • 双向循环链表：管理非空Span和空Span，支持O(1)插入删除

关键操作流程

获取对象（FetchRangeObj）：

  1. 加桶锁（锁定当前大小类）

  2. 查找非空Span（有可用对象的内存块）

  3. 从Span切分batchNum个对象

  4. 返回1个给ThreadCache，剩余缓存到ThreadCache

  5. 解锁

归还对象（ReleaseListToSpans）：

  1. 加桶锁

  2. 通过基数树查询每个对象所属的Span

  3. 头插法归还到对应Span的自由链表

  4. 若Span完全空闲（useCount=0），移出链表准备归还PageHeap

  5. 解锁

关键计算公式

计算项 公式 说明
切分对象数 Span总大小 / 对象大小 1页8KB切分16B对象得512个
Span使用计数 useCount += 实际分配数 跟踪Span内活跃对象
空闲判断 useCount == 0 表示Span可归还PageHeap

第三层：PageHeap（页堆）

核心机制

  • 128个空闲链表：按页数1-128分类管理Span

  • 大Span单独存储：超过128页的Span用有序集合管理

  • 伙伴系统合并：释放时尝试与前后相邻Span合并，减少碎片

  • 基数树映射：O(1)时间从地址查询所属Span

关键操作流程

申请Span（NewSpan）：

  1. 检查对应页数的空闲链表，有直接返回

  2. 无则查找更大页数的链表，分裂后返回所需部分

  3. 都无则向系统申请128页大Span，插入链表后重新分配

释放Span（ReleaseSpanToPageCache）：

  1. 向前合并：检查pageId-1是否为空闲Span，是则合并

  2. 向后合并：检查pageId+n是否为空闲Span，是则合并

  3. 合并后插入对应空闲链表

  4. 更新基数树映射（首尾页都映射）

关键计算公式

计算项 公式 说明
页号计算 pageId = address >> 13 8KB页，右移13位
地址还原 address = pageId << 13 页号转起始地址
分裂操作 k页给请求者，(n-k)页挂回n-k链表 大Span分裂利用
合并限制 合并后页数 ≤ 128 防止Span过大
基数树索引 直接数组寻址或分层索引 32位单层，64位三层

三层协作核心机制

对象分配流程

复制代码 
用户请求 → ThreadCache命中？→ 直接返回（无锁）
                ↓ 未命中
         CentralCache获取批量 → 填充ThreadCache后返回
                ↓ Central无Span
         PageHeap获取/分裂Span → 交给CentralCache切分
                ↓ PageHeap无Span
         系统调用申请内存 → 更新基数树

对象释放流程

复制代码 
用户释放 → ThreadCache缓存（头插法）
                ↓ 链表过长
         批量归还CentralCache → 分散到各Span
                ↓ Span完全空闲
         归还PageHeap → 尝试前后合并
                ↓ 空闲内存过多
         延迟归还给OS（madvise释放物理页）

关键技术亮点总结

技术点 作用 实现位置
TLS无锁访问 消除线程竞争 ThreadCache
慢启动批量 平衡内存占用与性能 ThreadCache ↔ CentralCache
桶锁细粒度 减少锁冲突 CentralCache
Span延迟归还 避免频繁系统调用 CentralCache
伙伴系统合并 减少外部碎片 PageHeap
基数树O(1)映射 快速地址到Span查询 PageHeap
分层基数树 适配32/64位地址空间 PageMap
大页对齐 适配HugePage，减少TLB miss SystemAlloc

性能优化核心思想

  1. 分层缓存：高频操作在最上层无锁处理，低频操作下沉到下层批量处理

  2. 空间换时间：ThreadCache的内存冗余换取分配速度

  3. 延迟计算：批量获取、延迟合并、后台GC，摊平开销

  4. 硬件亲和：缓存行对齐、HugePage、NUMA感知

  5. 确定性优先：牺牲极端最优，换取99%场景的稳定表现

相关推荐
CHANG_THE_WORLD2 小时前
深入指针4 - 学习笔记整理
笔记·学习·算法
菜鸡儿齐2 小时前
leetcode-最大子数组和
数据结构·算法·leetcode
小妖6662 小时前
js 实现插入排序算法（希尔排序算法）
java·算法·排序算法
星火开发设计2 小时前
标准模板库 STL：C++ 的利器 —— 容器、算法、迭代器
java·开发语言·数据结构·c++·算法·html
blackicexs2 小时前
第五周第一天
算法
MIngYaaa5202 小时前
2026寒假牛客 2.13
算法
大梦南柯2 小时前
第一次作业
算法
iAkuya2 小时前
(leetcode)力扣100 71字符串解码（栈（两种）||递归）
windows·算法·leetcode
重生之后端学习2 小时前
105. 从前序与中序遍历序列构造二叉树
java·数据结构·后端·算法·深度优先
热门推荐
01使用 1panel面板 部署 php网站02从零搭建一个 PHP 登录注册系统（含完整源码）03如何将 TRAE IDE 的插件市场源切换至 VS Code 官方市场04PHP Error: 常见错误及其解决方法05GitHub 镜像站点06openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南07Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services08BUUCTF[ACTF2020 新生赛]Include 1题解09Android Studio Panda 1 正式版来了：JDK 终于不用手动配了，内存泄漏也有原生方案了10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）