题解：P13722 [GCPC 2024] Geometric Gridlock

为了尽可能的少分类，我们尝试出最小能够构造出的可扩展的 k×5k \times 5k×5 的解。由于需要扩展，因此直接使用 IIIII\texttt{IIIII}IIIII 并不优。经过尝试，确定了 k=3k = 3k=3。因此本文以 n mod 3n \bmod 3nmod3 为分类对象进行阐述与构造。

首先来判断无解的情况。不失一般性地，令 n<mn < mn<m：

(n×m) mod 5≠0(n \times m) \bmod 5 \neq 0(n×m)mod5=0 由于每种都是五连块，显然最后总数应该为 555 的倍数。
n=1n = 1n=1 此时只能够用 IIIII\texttt{IIIII}IIIII 来填充，因此 m≠5m \neq 5m=5 时无解。
n=2n = 2n=2
- m=5m = 5m=5 此时只有 IIIII\texttt{IIIII}IIIII 可以填，不满足两个相邻五连块类型不同的条件，故无解。
- m=10m = 10m=10
  
  可以构造出以下解：
- m=15m = 15m=15
  
  可以构造出以下解：
- m>15m > 15m>15 由于以上两种情况在拼接时均不产生冲突，且 gcd⁡(10,15)=5\gcd (10,15) = 5gcd(10,15)=5，因此可以通过以上两种情况扩展出所有合法的 mmm。
n mod 3=0n \bmod 3 = 0nmod3=0

直接基于 3×53 \times 53×5 的块构造即可，每行复制 m5\frac{m}{5}5m 遍即可完成列扩展。但是都以 T 形积木块起始，会导致出现连通，因此在行的扩展时需要注意翻转。
n mod 3=1n \bmod 3 = 1nmod3=1

前面的部分与 n mod 3=0n \bmod 3 = 0nmod3=0 情况相同，在最后一个 4×54 \times 54×5 的块进行如下构造即可，每行复制 m5\frac{m}{5}5m 遍即可完成列扩展。
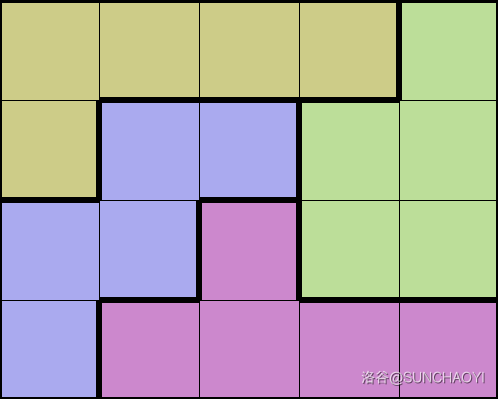
n mod 3=2n \bmod 3 = 2nmod3=2

同上所述，故只给出 5×55 \times 55×5 的基本方案，不做过多阐述。

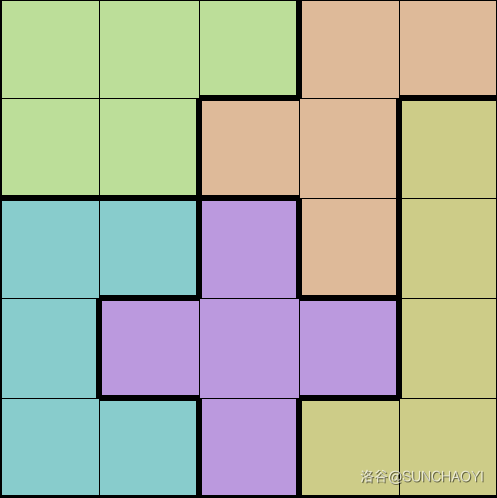
参考代码如下：

cpp 复制代码

vector <string> two_ten = {"LLLLNNNPPP","LIIIIINNPP"};
vector <string> two_fif = {"LIIIIINNYNNNPPP","LLLLNNNYYYYNNPP"};
vector <string> three_five = {"TLLLL","TTTYL","TYYYY"};
vector <string> four_five = {"LLLLP","LWWPP","WWYPP","WYYYY"};
vector <string> five_five = {"PPPFF","PPFFL","UUXFL","UXXXL","UUXLL"};
void solve ()
{
    int n = read (),m = read (),fl = 0;
    if (n * m % 5 != 0) {puts ("no");return;}
    if (n > m) fl ^= 1,swap (n,m);
    if (n > 2 && m % 5 != 0) fl ^= 1,swap (n,m);
    vector <vector <char>> ans (n + 1,vector <char> (m + 1));
    auto fill = [&] (int n,int st,vector <string> &chr,int bias = 0) -> void
    {
        for (int i = 1;i <= n;++i)
        {
            int pos = 0;
            for (auto v : chr[i - 1]) ans[i + bias][st + pos] = v,++pos;
        }
    };
    if (n == 1)
    {
        if (m != 5) {puts ("no");return;}
        for (int i = 1;i <= 5;++i) ans[1][i] = 'I';
    }
    else if (n == 2)
    {
        if (m == 5) {puts ("no");return;}
        int dx = 0,dy = 0;
        for (int i = 0;i <= m;++i)
            if (10 * i <= m && (m - 10 * i) % 15 == 0) {dx = i;dy = (m - 10 * i) / 15;break;}
        int pos = 1;
        while (dx--) fill (2,pos,two_ten),pos += 10;
        while (dy--) fill (2,pos,two_fif),pos += 15;
    }
    else 
    {
        for (int i = 1;i <= m;i += 5) fill (3,i,three_five);
        int delta = (3 + n % 3);
        if (delta == 3) delta = 0;
        for (int i = 4;i <= n - delta;i += 3)
        {
            for (int o = 0;o < 3;++o)
            {
                ans[i + o] = ans[i + o - 3];
                reverse (ans[i + o].begin () + 1,ans[i + o].end ());
            }
        }
        for (int i = 1;delta && i <= m;i += 5) fill (3 + n % 3,i,n % 3 == 0 ? three_five : (n % 3 == 1 ? four_five : five_five),n - (3 + n % 3));
    }
    puts ("yes");
    if (!fl)
    {
        for (int i = 1;i <= n;++i)
        {
            for (int j = 1;j <= m;++j) printf ("%c",ans[i][j]);
            puts ("");
        }
    }
    else
    {
        for (int j = 1;j <= m;++j)
        {
            for (int i = 1;i <= n;++i) printf ("%c",ans[i][j]);
            puts ("");
        }
    }
}