UVa1409/LA4019 Go to Class

题目链接
题意
分析
[AC 代码](#AC 代码)

题目链接

本题是2007年icpc亚洲区域赛成都赛区的G题

题意

给出一个校园，校园中有很多纵横道路，横的平行于 x 轴，竖的平行于 y 轴。横向道路有 n 条，纵向道路有 m 条（1≤n,m≤25）。道路是有宽度的，并且大小不一。道路之间是草坪。现给出所有道路以及宿舍和教室的坐标，求宿舍到教室且不经过草坪的最短距离。

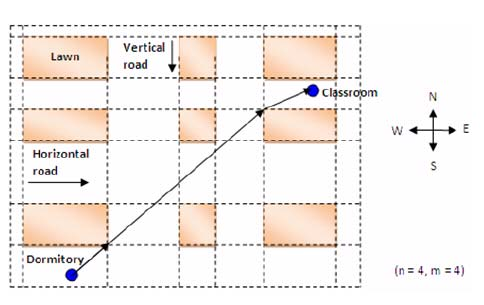
分析

需要用到一个结论：起点和终点需要走折线到达时，最优路线的那些转折点一定是纵横道路的交点。

先证明只有一条纵向道路和一条横向道路的简单情况，不妨设起点A在横向道路的北方，终点B在纵向道路的西方，见下图所示：

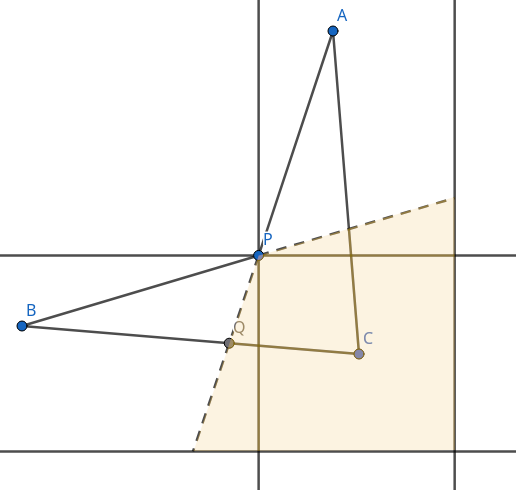
转折点只能在AP、BP的延长线和道路边界围起来的区域内选取，延长AP交BC于Q，则 { A C + C Q > A Q B Q + P Q > B P A Q = A P + P Q B C = B Q + C Q ⇒ A C + C Q + B Q + P Q > A P + P Q + B P ⇒ A C + B C + P Q > A P + P Q + B P ⇒ A C + B C > A P + B P \begin{align*}\\& \left\{\begin{matrix}AC+CQ>AQ\\BQ+PQ>BP\\AQ=AP+PQ\\BC=BQ+CQ\end{matrix}\right.\\& \Rightarrow AC+CQ+BQ+PQ>AP+PQ+BP\\& \Rightarrow AC+BC+PQ>AP+PQ+BP\\& \Rightarrow AC+BC>AP+BP \end{align*} ⎩ ⎨ ⎧AC+CQ>AQBQ+PQ>BPAQ=AP+PQBC=BQ+CQ⇒AC+CQ+BQ+PQ>AP+PQ+BP⇒AC+BC+PQ>AP+PQ+BP⇒AC+BC>AP+BP

可以将这个结论推广到有多条纵横道路的情况（用反证法），假设最优路线存在一个不是纵横道路交点的转折点C，如下图所示：

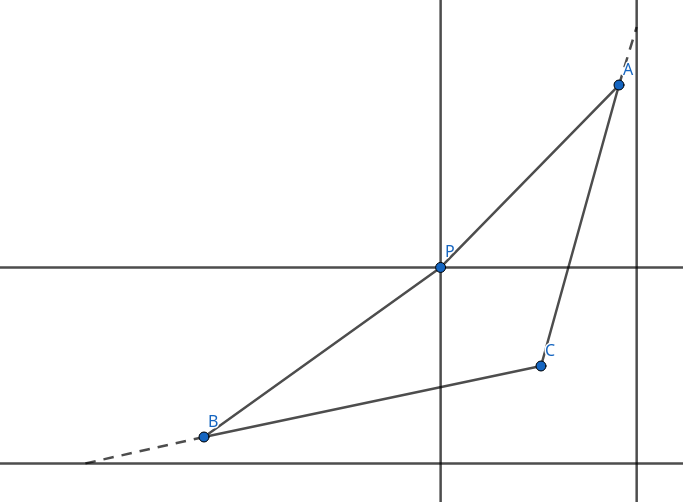
总是可以用纵横道路的交点P替换C从而更优。

至此，本题可以离散化处理后建图，用 dijkstra 求最短路即可。顶点集是起点、终点、各个纵横道路的交点，对直接可达的两点连边时有一个小难点：如何判断两个点直接可达？判断点 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) (x_1,y_1)、(x_2,y_2) (x1,y1)、(x2,y2) 是否直接可达可以按如下思路：

如果两点处在同一条横向道路（或者纵向道路）内，则直接可达；
否则
- 若x1==x2 || y1==y2，则不是直接可达；
- 否则，将两点所在线段按照纵向道路的 x 坐标离散化切割成若干小段
  - 不在纵向道路内的每一小段必须全部包含在某一条横向道路内（不能有露出的部分），则直接可达；
  - 否则不是直接可达；

判断是否直接可达的逻辑实现要注意各种细节，特别是数组越界检查。贴一份生成测试数据的 python 脚本：

python 复制代码

# coding=utf-8

from random import randint

# X, N = 100000, 25
X, N = 12, 4

def out(p, x, y):
    for i in range(0, len(x), 2):
        if p[0] >= x[i] and p[0] <= x[i+1]:
            return False
    for i in range(0, len(y), 2):
        if p[1] >= y[i] and p[1] <= y[i+1]:
            return False
    return True

def gen():
    n, m, y, x = randint(1, N), randint(1, N), [], []
    for i in range(2*n):
        f = True
        while f:
            f = False
            v = randint(-X, X)
            for j in range(i):
                if y[j] == v:
                    f = True
                    break
            if not f:
                y.append(v)
    for i in range(2*m):
        f = True
        while f:
            f = False
            v = randint(-X, X)
            for j in range(i):
                if x[j] == v:
                    f = True
                    break
            if not f:
                x.append(v)
    y.sort()
    x.sort()
    s, t = (randint(-X, X), randint(-X, X)), (randint(-X, X), randint(-X, X))
    while out(s, x, y):
        s = (randint(-X, X), randint(-X, X))
    while out(t, x, y):
        t = (randint(-X, X), randint(-X, X))
    return n, m, s, t, y, x

if __name__ == '__main__':
    with open('in.txt', 'w') as f:
        for _ in range(10):
            n, m, s, t, y, x = gen()
            f.write(f'{n} {m}\n{s[0]} {s[1]} {t[0]} {t[1]}\n{y[0]}')
            for i in range(1, 2*n):
                f.write(f' {y[i]}')
            f.write(f'\n{x[0]}')
            for i in range(1, 2*m):
                f.write(f' {x[i]}')
            f.write(f'\n')
        f.write('0 0\n')

AC 代码

cpp 复制代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;

#define M 2510
#define N 55
int x[N], y[N], xs, ys, xt, yt, n, m, t, kase = 0; double d[M]; bool f[M];
struct node {
    double d; int u;
    bool operator< (const node& rhs) const {
        return d > rhs.d;
    }
};

bool check(int x1, int y1, int x2, int y2) {
    int k = lower_bound(x, x+m, max(x1, x2)) - x;
    if (k < m && ((x1==x2 && x[k]==x1) || (k&1 && k == upper_bound(x, x+m, min(x1, x2)) - x))) return true;
    k = lower_bound(y, y+n, max(y1, y2)) - y;
    if (k < n && ((y1==y2 && y[k]==y1) || (k&1 && k == upper_bound(y, y+n, min(y1, y2)) - y))) return true;
    if (x1 == x2 || y1 == y2) return false;
    if (x1 > x2) swap(x1, x2), swap(y1, y2);
    long long d = x2 - x1;
    k = upper_bound(x, x+m, x1) - x;
    int a = k==0 ? x1 : max(x[k-1],x1), b = k==m ? x2 : x[k];
    if (y1 < y2) {
        for (int i=0; a<x2; a=b, b = ++k>=m ? x2 : min(x[k],x2)) if (k == m || ~k&1) {
            while (d*y[i] <= (a - x1)*(long long)y2 + (x2 - a)*(long long)y1) ++i;
            if (~i&1 || d*y[i] < (b - x1)*(long long)y2 + (x2 - b)*(long long)y1) return false;
        }
    } else for (int i=n-1; a<x2; a=b, b = ++k>=m ? x2 : min(x[k],x2)) if (k == m || ~k&1) {
        while (d*y[i] >= (a - x1)*(long long)y2 + (x2 - a)*(long long)y1) --i;
        if (i&1 || d*y[i] > (b - x1)*(long long)y2 + (x2 - b)*(long long)y1) return false;
    }
    return true;
}

double dis(int x1, int y1, int x2, int y2) {
    double dx = x1-x2, dy = y1-y2;
    return sqrt(dx*dx+dy*dy);
}

double solve() {
    cin >> xs >> ys >> xt >> yt; n <<= 1; m <<= 1; t = m*n;
    for (int i=0; i<n; ++i) cin >> y[i];
    for (int i=0; i<m; ++i) cin >> x[i];
    sort(x, x+m); sort(y, y+n);
    if (check(xs, ys, xt, yt)) return dis(xs, ys, xt, yt);
    priority_queue<node> q; d[t] = 1e30; f[t] = false;
    for (int i=0, k=0; i<m; ++i) for (int j=0; j<n; ++j, ++k) {
        if (check(xs, ys, x[i], y[j])) q.push({d[k] = dis(xs, ys, x[i], y[j]), k});
        else d[k] = 1e30;
        f[k] = false;
    }
    while (!q.empty()) {
        int u = q.top().u; q.pop();
        if (u == t) break;
        if (f[u]) continue;
        f[u] = 1;
        int x1 = x[u/n], y1 = y[u%n];
        if (check(x1, y1, xt, yt)) {
            double d1 = d[u] + dis(x1, y1, xt, yt);
            if (d[t] > d1) q.push({d[t] = d1, t});
        }
        for (int i=0, k=0; i<m; ++i) for (int j=0; j<n; ++j, ++k) if (!f[k] && check(x1, y1, x[i], y[j])) {
            double d1 = d[u] + dis(x1, y1, x[i], y[j]);
            if (d[k] > d1) q.push({d[k] = d1, k});
        }
    }
    return d[t];
}

int main() {
    cout << fixed << setprecision(4);
    while (cin >> n >> m && n) cout << "Case " << ++kase << ": " << solve() << endl;
    return 0;
}