深度学习的数学原理（七）—— 优化器：从SGD到Adam

在本专栏的前六篇内容中，我们已经逐步拆解了深度学习的核心数学基础：从梯度下降的核心逻辑（如何沿着梯度方向寻找损失最小值），到反向传播的链式法则（如何高效计算各层参数的梯度），再到激活函数的非线性本质与梯度特性（如何让深层网络具备拟合复杂数据的能力）。

而今天，我们将聚焦深度学习训练的"最后一公里"------优化器。在前文的例子中，我们一直沿用最基础的随机梯度下降（SGD）来更新参数，但在实际开发中，SGD的收敛慢、易震荡、对学习率敏感等问题，往往会影响模型训练效率。在本文中，我们将介绍实际开发中最常用的4类优化器，从数学原理层面拆解它们相较于SGD的核心优势，最后通过可直接复用的代码，详解各优化器的参数配置、输入输出及使用逻辑。

一、实际开发中常用的优化器：核心定位与适用场景

在深度学习工程实践中，优化器的选择直接决定模型的训练速度和最终性能。结合前文学到的梯度下降、反向传播知识，我们先梳理4类主流优化器的核心特点------它们覆盖了90%以上的深度学习场景，从简单线性模型到复杂Transformer大模型均有适配。

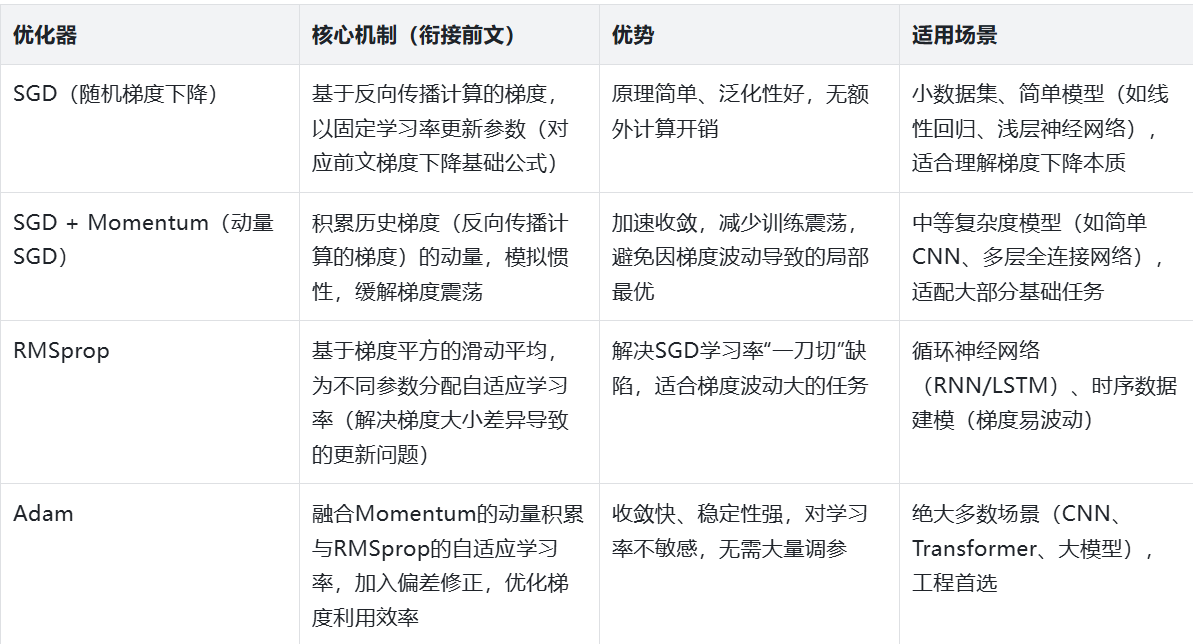
注：这4类优化器均基于"梯度下降"的核心逻辑（沿着梯度反方向更新参数），区别仅在于"如何利用梯度"------这也是我们接下来数学原理拆解的核心。

二、数学原理：进阶优化器为何优于SGD？

在前文"梯度下降"章节中，我们已经掌握了SGD的基础公式；结合"反向传播"章节，我们知道了如何计算各层参数的梯度（∇L(θt)\nabla L(\theta_t)∇L(θt)）。本节课，我们将从SGD的数学公式出发，逐步推导进阶优化器的改进逻辑，重点说明"如何通过数学改进，解决SGD的缺陷"。

2.1 基础回顾：SGD的数学公式与核心缺陷

SGD的参数更新公式极其简单：

θt+1=θt−η⋅∇L(θt)\theta_{t+1} = \theta_t - \eta \cdot \nabla L(\theta_t)θt+1=θt−η⋅∇L(θt)

其中各符号含义：

• θt\theta_tθt：第t步的模型参数（如权重w、偏置b，对应反向传播中需要更新的参数）；

• η\etaη：学习率（固定值，如0.01，控制参数更新幅度，前文已讲过其对训练的影响）；

• ∇L(θt)\nabla L(\theta_t)∇L(θt)：第t步损失函数对参数的梯度（通过反向传播的链式法则计算得出）。

结合前文学到的梯度、反向传播知识，我们很容易发现SGD的3个核心缺陷（也是进阶优化器需要解决的问题）：

1. 学习率固定：所有参数（无论梯度大小、更新需求）共用一个学习率，比如"梯度大的参数需要小学习率避免震荡，梯度小的参数需要大学习率加速更新"，SGD无法满足；

2. 仅依赖当前梯度：参数更新只看第t步的梯度，忽略历史梯度信息，容易被局部梯度波动影响（震荡），甚至陷入局部最优（比如梯度为0但不是全局最小值）；

3. 对学习率敏感：学习率太大，参数更新幅度过大，易震荡不收敛；学习率太小，收敛速度极慢，甚至无法收敛到最优解。

2.2 改进1：SGD + Momentum（引入动量，解决震荡与收敛慢）

Momentum（动量）的灵感来自物理中的"惯性"------物体运动时会积累速度，不会因瞬间的力而改变运动方向。对应到优化器中，就是让参数更新"记住"历史梯度的方向，结合当前梯度，减少震荡、加速收敛------本质是"对历史梯度进行加权平均，优化更新方向"。

数学公式

Momentum的参数更新分为两步，核心是"先计算动量（历史梯度+当前梯度），再用动量更新参数"：

第一步：计算动量（历史梯度的加权平均，模拟惯性）：

vt=γ⋅vt−1+η⋅∇L(θt)v_t = \gamma \cdot v_{t-1} + \eta \cdot \nabla L(\theta_t)vt=γ⋅vt−1+η⋅∇L(θt)

第二步：用动量更新参数（替代SGD中"直接用当前梯度更新"）：

θt+1=θt−vt\theta_{t+1} = \theta_t - v_tθt+1=θt−vt

新增符号说明：

• vtv_tvt：第t步的动量（可理解为"更新速度"），初始值v0=0v_0 = 0v0=0（刚开始训练，无历史梯度，动量为0）；

• γ\gammaγ：动量系数（通常取0.9），控制历史梯度的权重------γ\gammaγ越大，历史梯度的影响越强，惯性越明显。

优于SGD的核心数学逻辑

结合前文学到的梯度知识，我们从两个角度理解：

1. 加速收敛：如果连续多步的梯度方向一致（比如都指向损失函数的全局最小值），动量vtv_tvt会不断累加（γ⋅vt−1\gamma \cdot v_{t-1}γ⋅vt−1积累历史动量，加上当前梯度的贡献），参数更新速度会越来越快，大幅提升收敛效率；

2. 缓解震荡：如果梯度方向突然改变（比如局部最优附近的梯度波动，对应反向传播中梯度方向突变），动量的"惯性"（γ⋅vt−1\gamma \cdot v_{t-1}γ⋅vt−1）会抵消部分反向梯度的影响，减少参数更新的震荡幅度，避免在局部最优附近来回波动。

2.3 改进2：RMSprop（自适应学习率，解决学习率单一问题）

RMSprop的核心改进是"自适应学习率"------它通过计算"梯度平方的滑动平均"，判断每个参数的梯度波动程度，进而为不同参数分配不同的有效学习率：梯度大、波动大的参数，用小学习率（避免震荡）；梯度小、波动小的参数，用大学习率（加速更新）。

这里的"梯度平方"，本质是利用梯度的二阶信息（其实就是二阶偏导，可以简单理解为梯度的波动程度），弥补SGD仅用一阶梯度（更新方向）的不足。

数学公式

RMSprop的参数更新分为两步，核心是"先计算梯度平方的滑动平均，再自适应调整学习率"：

第一步：计算梯度平方的滑动平均（反映参数梯度的波动程度）：

st=β⋅st−1+(1−β)⋅(∇L(θt))2s_t = \beta \cdot s_{t-1} + (1 - \beta) \cdot (\nabla L(\theta_t))^2st=β⋅st−1+(1−β)⋅(∇L(θt))2

第二步：自适应更新参数（除以st+ϵ\sqrt{s_t} + \epsilonst +ϵ，调整学习率）：

θt+1=θt−η⋅∇L(θt)st+ϵ\theta_{t+1} = \theta_t - \eta \cdot \frac{\nabla L(\theta_t)}{\sqrt{s_t} + \epsilon}θt+1=θt−η⋅st +ϵ∇L(θt)

新增符号说明：

• sts_tst：第t步梯度平方的滑动平均，初始值s0=0s_0 = 0s0=0；

• β\betaβ：滑动平均系数（通常取0.99），控制历史梯度平方的权重；

• ϵ\epsilonϵ：极小值（通常取1e-8），核心作用是"防止分母为0"（当梯度为0时，sts_tst为0，加上ϵ\epsilonϵ可避免计算错误）。

优于SGD的核心数学逻辑

对比SGD的固定学习率，RMSprop的关键改进的是"有效学习率"：

SGD的有效学习率是固定的η\etaη，而RMSprop的有效学习率是ηst+ϵ\frac{\eta}{\sqrt{s_t} + \epsilon}st +ϵη------梯度越大，sts_tst越大，有效学习率越小；梯度越小，sts_tst越小，有效学习率越大。

这种自适应机制，完美解决了SGD"学习率一刀切"的缺陷，尤其适合梯度波动大的任务（如RNN训练）------这类任务中，不同时刻的梯度差异很大，SGD易震荡，而RMSprop可通过自适应学习率稳定训练。

2.4 改进3：Adam（融合动量+自适应学习率，工程首选）

Adam是目前工业界最常用的优化器，它的核心优势是"集大成者"------同时融合了Momentum的"动量积累"（利用历史梯度，加速收敛、缓解震荡）和RMSprop的"自适应学习率"（利用梯度平方，适配不同参数），还加入了"偏差修正"机制，解决初始阶段滑动平均估计偏差的问题，进一步提升训练稳定性。

数学公式

Adam的参数更新分为四步，每一步都对应着对SGD的改进，结合了Momentum和RMSprop的核心逻辑：

1. 计算一阶矩（动量，完全沿用Momentum的逻辑，积累历史梯度）：
   mt=β1⋅mt−1+(1−β1)⋅∇L(θt)m_t = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot \nabla L(\theta_t)mt=β1⋅mt−1+(1−β1)⋅∇L(θt)

2. 计算二阶矩（梯度平方的滑动平均，完全沿用RMSprop的逻辑，反映梯度波动）：
   vt=β2⋅vt−1+(1−β2)⋅(∇L(θt))2v_t = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot (\nabla L(\theta_t))^2vt=β2⋅vt−1+(1−β2)⋅(∇L(θt))2

3. 偏差修正（Adam的核心改进，解决初始阶段m_t、v_t接近0的偏差）：
   m^t=mt1−β1t,v^t=vt1−β2t\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}m^t=1−β1tmt,v^t=1−β2tvt

4. 更新参数（融合动量和自适应学习率）：
   θt+1=θt−η⋅m^tv^t+ϵ\theta_{t+1} = \theta_t - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}θt+1=θt−η⋅v^t +ϵm^t

默认超参数（工程中几乎无需调整，记牢即可）：

• β1=0.9\beta_1 = 0.9β1=0.9（一阶矩系数，对应Momentum的γ\gammaγ，控制动量积累）；

• β2=0.999\beta_2 = 0.999β2=0.999（二阶矩系数，对应RMSprop的β\betaβ，控制梯度平方的滑动平均）；

• ϵ=1e−8\epsilon = 1e-8ϵ=1e−8（防止分母为0）；

• η=0.01\eta = 0.01η=0.01（基础学习率，自适应机制会动态调整有效学习率）。

优于SGD的核心数学逻辑（综合优势）

Adam的优势是"三者兼顾"，完美解决SGD的所有核心缺陷：

1. 兼顾动量与自适应：既像Momentum一样，通过积累历史梯度加速收敛、缓解震荡；又像RMSprop一样，通过梯度平方的滑动平均，为不同参数分配自适应学习率；

2. 偏差修正：初始训练阶段（t较小时），m_t和v_t的值接近0，偏差修正可以放大初始梯度的影响，让训练初期的更新更稳定，避免收敛过慢；

3. 鲁棒性强：对基础学习率η\etaη不敏感，无需像SGD那样反复调试学习率，默认参数即可适配绝大多数模型和数据集。

三、代码实战：优化器的使用

结合前文学到的激活函数、神经网络结构知识，我们仍以"拟合非线性数据（y=x²+噪声）"为例，用PyTorch实现SGD、Momentum、RMSprop、Adam四种优化器，重点详解各优化器的参数配置、输入输出，以及训练效果对比。

3.1 环境准备与数据生成

我们沿用前文中"激活函数"章节的非线性数据，同时定义一个简单的非线性网络（2层全连接+ReLU激活），适配所有优化器的训练。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 设置matplotlib参数
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 12
plt.style.use('seaborn-v0_8')

# 设置中文字体显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 固定随机种子，保证结果可复现
torch.manual_seed(42)

# 1. 生成非线性数据（y = x² + 噪声）
x = torch.linspace(-3, 3, 100).unsqueeze(1)  # 输入：(100, 1)，适配网络输入维度
y = x**2 + torch.randn(100, 1) * 0.1         # 标签：(100, 1)，加入噪声模拟真实数据

# 2. 定义简单的非线性网络（2层全连接+ReLU激活）
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(1, 20)  # 输入层→隐藏层：1维输入，20个隐藏神经元
        self.fc2 = nn.Linear(20, 1)  # 隐藏层→输出层：20维输入，1维输出
        self.relu = nn.ReLU()        # 非线性激活函数（前文学过，保证网络非线性）
    
    def forward(self, x):
        # 前向传播流程：线性变换→ReLU激活→线性变换
        out = self.relu(self.fc1(x))
        out = self.fc2(out)
        return out

3.2 优化器初始化：参数详解与配置

所有优化器的核心输入的是"模型参数"和"学习率"，进阶优化器的额外参数均为前文数学公式中的超参数（如momentum、betas），我们逐一对应

# 初始化4个相同结构的模型（分别用不同优化器训练，保证对比公平）
model_sgd = SimpleNet()
model_momentum = SimpleNet()
model_rmsprop = SimpleNet()
model_adam = SimpleNet()

# 1. SGD优化器（基础版，对应前文数学公式）
# 核心参数：params=模型参数（必须，通过model.parameters()获取），lr=学习率（必须）
optimizer_sgd = torch.optim.SGD(model_sgd.parameters(), lr=0.01)

# 2. SGD + Momentum优化器（对应前文Momentum数学公式）
# 额外参数：momentum=动量系数（对应公式中的γ，默认0，通常设0.9）
optimizer_momentum = torch.optim.SGD(model_momentum.parameters(), lr=0.01, momentum=0.9)

# 3. RMSprop优化器（对应前文RMSprop数学公式）
# 核心参数：lr=学习率，alpha=滑动平均系数（对应公式中的β，默认0.99），eps=1e-8
optimizer_rmsprop = torch.optim.RMSprop(model_rmsprop.parameters(), lr=0.01, alpha=0.99, eps=1e-8)

# 4. Adam优化器（对应前文Adam数学公式）
# 核心参数：lr=学习率，betas=(β1, β2)（默认(0.9, 0.999)，对应公式中的两个系数），eps=1e-8
optimizer_adam = torch.optim.Adam(model_adam.parameters(), lr=0.01, betas=(0.9, 0.999), eps=1e-8)

# 统一损失函数：均方误差（MSE），适配回归任务（拟合y=x²）
criterion = nn.MSELoss()

# 存储各优化器的损失变化（用于后续对比收敛速度，衔接前文梯度下降的损失变化逻辑）
loss_history = {
    'SGD': [],
    'Momentum': [],
    'RMSprop': [],
    'Adam': []
}
# 打包模型、优化器、优化器名称，方便后续批量训练
models = [model_sgd, model_momentum, model_rmsprop, model_adam]
optimizers = [optimizer_sgd, optimizer_momentum, optimizer_rmsprop, optimizer_adam]
optimizer_names = ['SGD', 'Momentum', 'RMSprop', 'Adam']

3.3 训练过程：优化器的核心使用逻辑

无论哪种优化器，核心使用流程完全一致，重点记住三步：清空梯度→反向传播计算梯度→优化器更新参数，区别仅在于初始化时的参数配置。

# 训练次数：1000次（足够看到明显的收敛差异）
epochs = 1000

for epoch in range(epochs):
    # 批量训练4个模型（分别用4种优化器）
    for i, (model, optimizer, name) in enumerate(zip(models, optimizers, optimizer_names)):
        model.train()  # 开启训练模式（工程实操必备，确保 dropout、BN 等模块正常工作）
        # 1. 前向传播：输入x，得到模型预测值y_pred
        y_pred = model(x)
        # 2. 计算损失：对比预测值y_pred和真实值y，用MSE衡量误差
        loss = criterion(y_pred, y)
        # 3. 清空梯度（必须！否则梯度会累加，导致参数更新异常，衔接反向传播知识）
        optimizer.zero_grad()
        # 4. 反向传播：计算各层参数的梯度（前文重点讲解，PyTorch自动实现链式法则）
        loss.backward()
        # 5. 优化器更新参数（核心步骤：不同优化器的数学更新逻辑，在这一步自动实现）
        optimizer.step()
        # 记录当前epoch的损失，用于后续可视化
        loss_history[name].append(loss.item())
    
    # 每200次打印一次损失，观察训练进度（工程实操常用）
    if (epoch + 1) % 200 == 0:
        print(f"Epoch {epoch+1}/{epochs}")
        for name in optimizer_names:
            print(f"{name} 损失：{loss_history[name][-1]:.4f}")
        print("-" * 30)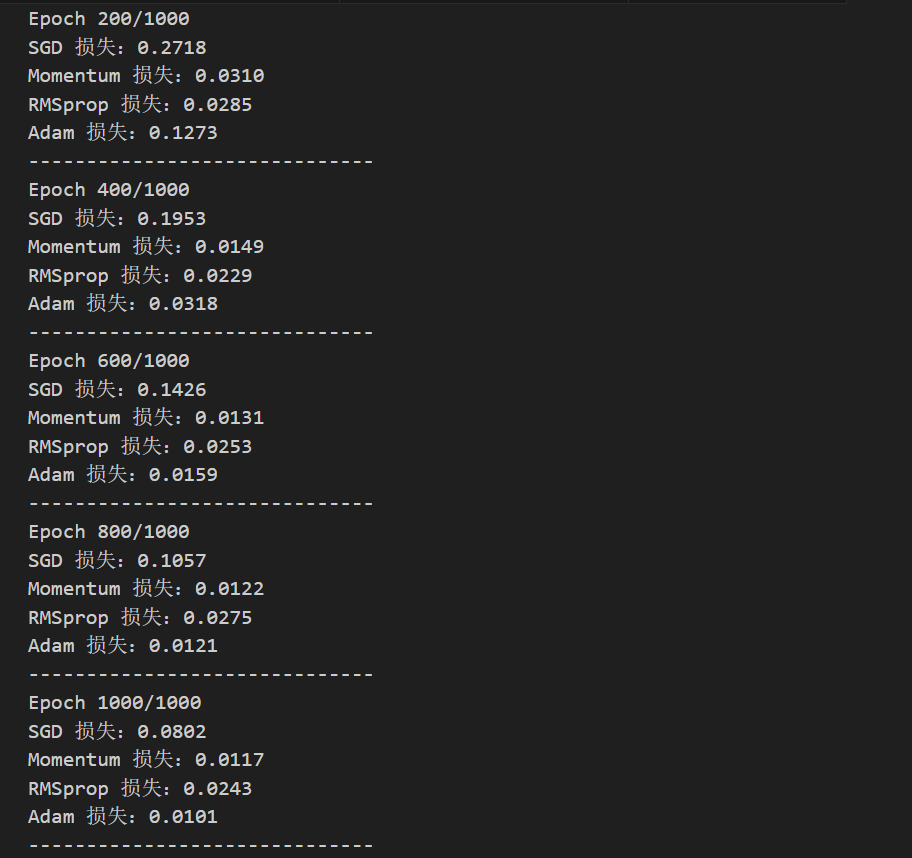

3.4 结果可视化：对比各优化器的收敛速度

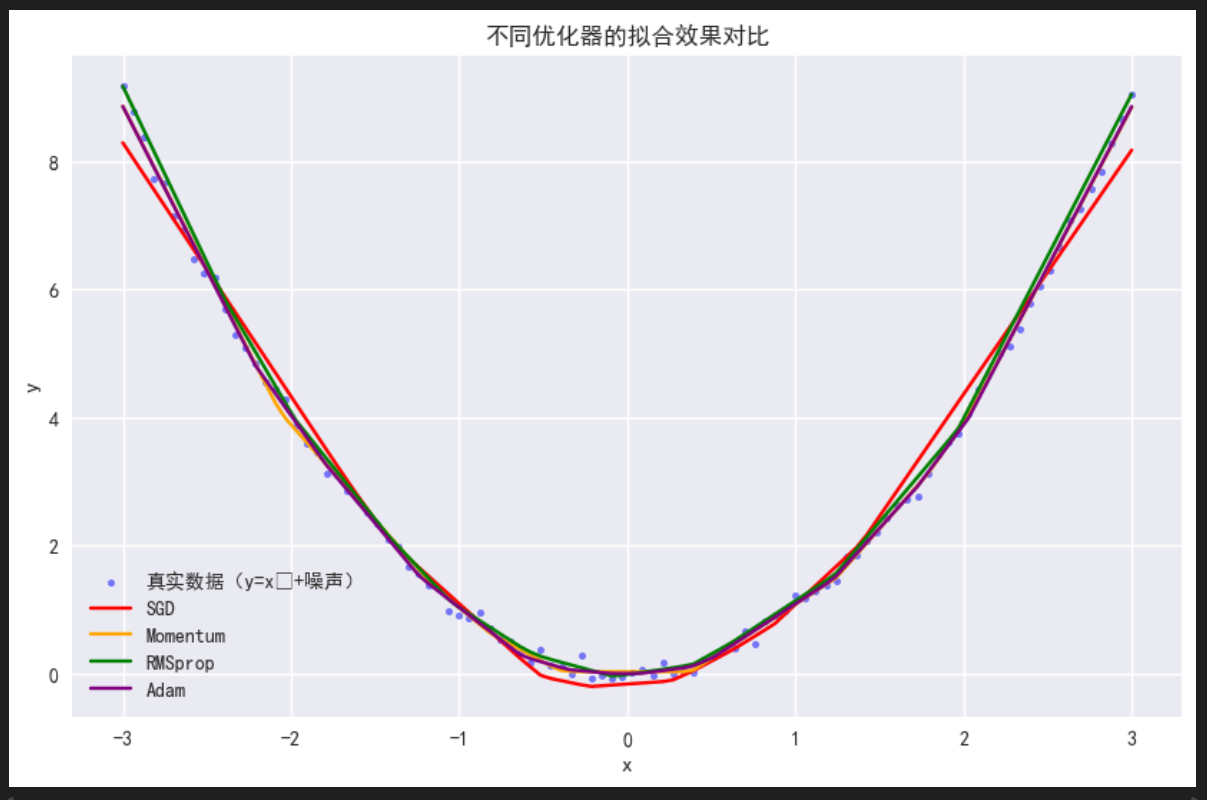
我们通过两个图对比：① 损失变化曲线（看收敛速度，对应数学原理中的"加速收敛"）；② 拟合效果曲线（看模型性能，对应前文激活函数的拟合能力）。

# 1. 绘制损失变化曲线（核心对比：收敛速度）
plt.figure(figsize=(10, 6))
for name in optimizer_names:
    plt.plot(loss_history[name], label=name)
plt.xlabel('训练步数（Epoch）')
plt.ylabel('损失值（MSE）')
plt.title('不同优化器的收敛速度对比（损失越小，拟合效果越好）')
plt.legend()
plt.grid(True, alpha=0.3)  # 添加网格，便于观察
plt.show()

# 2. 可视化各优化器的拟合效果（
plt.figure(figsize=(10, 6))
plt.scatter(x.numpy(), y.numpy(), s=10, color='blue', alpha=0.5, label='真实数据（y=x²+噪声）')

# 关闭梯度计算（预测时无需计算梯度，节省资源）
with torch.no_grad():
    y_pred_sgd = model_sgd(x)
    y_pred_momentum = model_momentum(x)
    y_pred_rmsprop = model_rmsprop(x)
    y_pred_adam = model_adam(x)

# 绘制各优化器的预测曲线
plt.plot(x.numpy(), y_pred_sgd.numpy(), color='red', label='SGD')
plt.plot(x.numpy(), y_pred_momentum.numpy(), color='orange', label='Momentum')
plt.plot(x.numpy(), y_pred_rmsprop.numpy(), color='green', label='RMSprop')
plt.plot(x.numpy(), y_pred_adam.numpy(), color='purple', label='Adam')

plt.xlabel('x')
plt.ylabel('y')
plt.title('不同优化器的拟合效果对比')
plt.legend()
plt.show()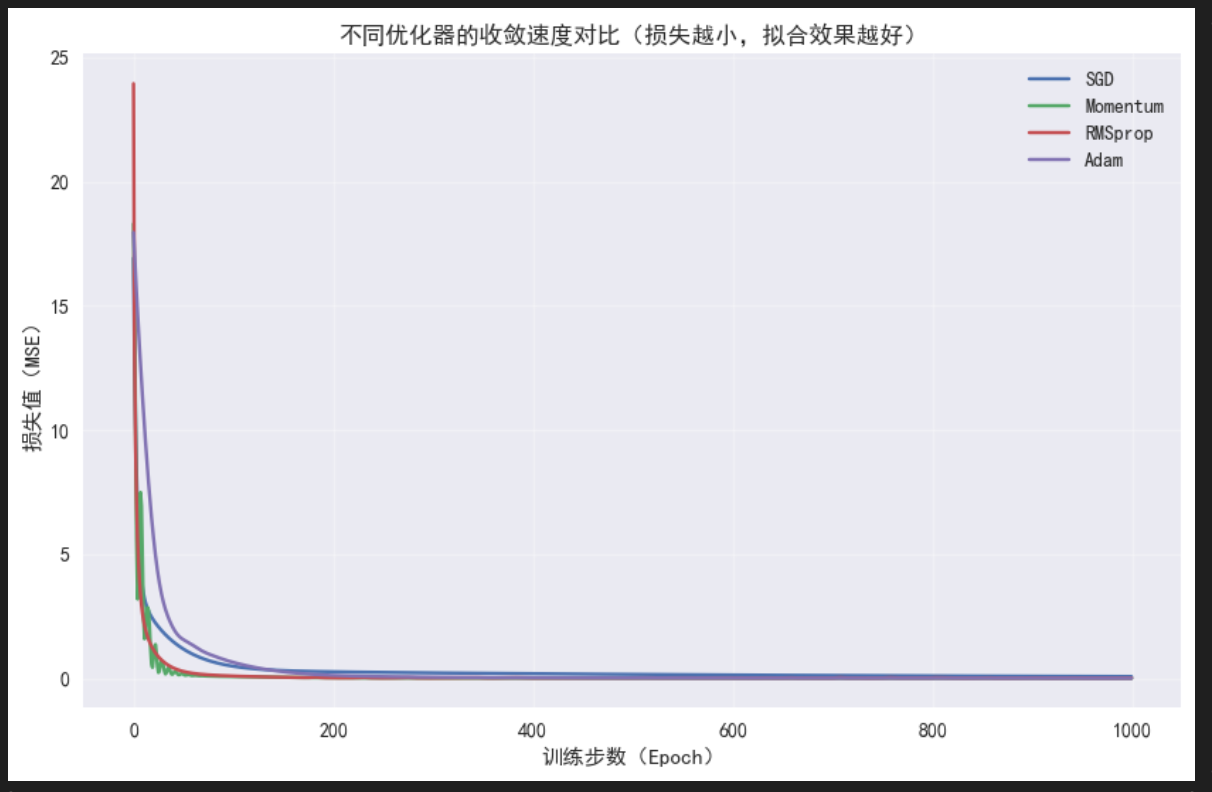

3.5 代码关键说明

结合前文学识和代码，重点说明3个核心点：

1. 优化器输入：

• 必选输入：params（模型参数，通过model.parameters()获取，是可迭代的参数列表，对应前文需要更新的权重w、偏置b）、lr（基础学习率，控制初始更新幅度）；

• 可选输入：所有可选参数均对应前文数学公式中的超参数（如momentum对应γ\gammaγ，betas对应β1\beta_1β1和β2\beta_2β2），默认值已适配绝大多数场景，无需刻意调整。

2. 优化器核心方法：

• zero_grad()：清空所有参数的梯度，必须在loss.backward()（反向传播）前调用，否则梯度会累加，导致参数更新异常；

• step()：执行参数更新，内部自动实现对应优化器的数学逻辑（如Adam的四步更新、Momentum的动量计算）；

• 输出：无返回值，直接修改模型的参数（model.parameters()），无需手动赋值。

3. 结果分析：

• 收敛速度：Adam ≈ RMSprop > Momentum > SGD，完美契合我们前文的数学推导------Adam融合了动量和自适应学习率，收敛最快；

• 拟合效果：Adam和RMSprop的预测曲线最贴合真实数据（当然该例子比较简单，Momentum 拟合的也很好，实际上比RMSprop还要好一些），SGD的曲线震荡最明显，说明进阶优化器的改进有效解决了SGD的缺陷。

四、总结

本节课是专栏"深度学习的数学原理"的第七篇内容，我们衔接前文的梯度下降、反向传播、激活函数知识，完成了"参数更新"的闭环------从"如何计算梯度"（反向传播），到"如何利用梯度更新参数"（优化器），彻底打通了深度学习训练的核心逻辑。

核心总结：

1. 进阶优化器的核心逻辑：均基于SGD的梯度下降思想，通过"利用历史梯度（动量）""自适应学习率""偏差修正"等数学改进，解决SGD的收敛慢、易震荡、对学习率敏感的缺陷；

2. 数学与实操的对应：Momentum的核心是"动量积累"（vtv_tvt），RMSprop的核心是"梯度平方的滑动平均"（sts_tst），Adam的核心是"融合两者+偏差修正"，代码中的参数与数学公式一一对应；

3. 优先使用Adam（适配绝大多数场景，无需大量调参），实际上，优化器在目前封装的非常好，Adam效果也比较不错，在大部分情况下都可以直接使用