【大模型思维链】Reasoning with Language Model is Planning with World Model

Reasoning with Language Model is Planning with World Model

语言模型推理即世界模型规划。

摘要

大语言模型（LLMs）已展现出卓越的推理能力，尤其是在思维链（CoT）提示的引导下。然而，LLMs有时仍会难以解决对人类而言相对简单的问题，例如在特定环境中生成实现给定目标的行动方案，或执行复杂的数学与逻辑推理。这一缺陷源于一个关键事实：LLMs缺乏内部世界模型来预测世界状态（如环境状态、中间变量值）并模拟行动的长期结果。这使得LLMs无法执行类似人类大脑的审慎规划，即探索替代推理路径、预测未来状态与回报，并对现有推理步骤进行迭代优化。

为了突破这些限制，我们提出了一种新的LLM推理框架------规划驱动推理（RAP）。RAP将LLM重新定位为世界模型与推理智能体的双重角色，并整合了基于蒙特卡洛树搜索的原则性规划算法，以在广阔的推理空间中进行策略性探索。在推理过程中，LLM（作为智能体）在LLM（作为世界模型）与奖励信号的引导下逐步构建推理树，并通过在探索与利用间取得适当平衡，高效获得高奖励的推理路径。我们将RAP应用于多种具挑战性的推理问题，包括规划生成、数学推理与逻辑推断，并验证了其相对于现有强基线的优越性。采用LLaMA-33B的RAP模型甚至在规划生成任务中超越了使用GPT-4的CoT方法，实现了33%的相对性能提升。

代码

1.引言

大语言模型在多种任务中展现出涌现的推理能力（Brown等人，2020；Chowdhery等人，2022;OpenAI，2023）。最新研究通过提示大语言模型生成中间推理步骤（例如思维链，简称CoT）（Wei等人，2022）或回答一系列子问题（例如最少到最多提示法）（Zhou等人，2022），进一步提升了其能力。然而，对于人类感到简单的任务，大语言模型仍然面临困难。例如，在制定将积木移动到目标状态的动作计划时，GPT-3（Brown等人，2020）的成功率仅为1%，而人类的成功率高达78%（Valmeekam等人，2022）；这些模型在需要多步骤数学、逻辑或常识推理的复杂任务上也表现欠佳（Huang和Chang，2022；Mialon等人，2023）。

人类拥有一个内部世界模型，即对环境的心理表征（JohnsonLaird, 1983, 2010; Gentner and Stevens, 2014），该模型使人类能够模拟行动及其对世界状态的影响，从而为运动控制、想象、推理和决策等复杂任务进行审慎规划（Tolman, 1948; Briscoe, 2011; Schulkin, 2012; LeCun, 2022）。例如，为制定实现目标的行动计划，基于世界模型的规划涉及探索多种备选行动方案，通过推演可能的未来情景来评估其可能结果，并基于评估迭代优化计划（Huys et al., 2012; Gasparski and Orel, 2014; Ho et al., 2021）。这与当前大语言模型（LLM）的推理方式形成鲜明对比，后者是本能地以自回归方式生成推理轨迹。具体而言，我们指出了当前LLM推理的几个关键局限，包括：（1）缺乏内部世界模型来模拟世界状态（例如积木的摆放、中间变量的值），而这正是人类规划的基础；（2）缺少评估推理过程并将其导向期望状态的奖励机制；以及由上述两者共同导致的（3）无法平衡探索与利用，以高效探索广阔的推理空间。

为克服上述局限，本研究提出了一种新框架------规划式推理（RAP），使大语言模型能够以接近人类有意识规划的方式进行推理。RAP通过引入世界模型增强大语言模型，并采用基于原则的规划方法（具体为蒙特卡洛树搜索，MCTS）在高效探索后生成高奖励值的推理轨迹（见图1）。值得注意的是，我们通过使用特定提示词对大语言模型自身进行功能重构来获取世界模型。在推理过程中，大语言模型通过迭代考量最具潜力的推理步骤（行动），并运用世界模型（同一经重构的大语言模型）前瞻未来结果，从而战略性地构建推理树。随后，系统将预估的未来奖励值反向传播，以更新大语言模型对当前推理步骤的认知，引导其通过探索更优方案来完善推理过程。我们基于MCTS的规划方法有效维持了探索（未访问的推理轨迹）与利用（当前已识别的最优推理步骤）之间的动态平衡。

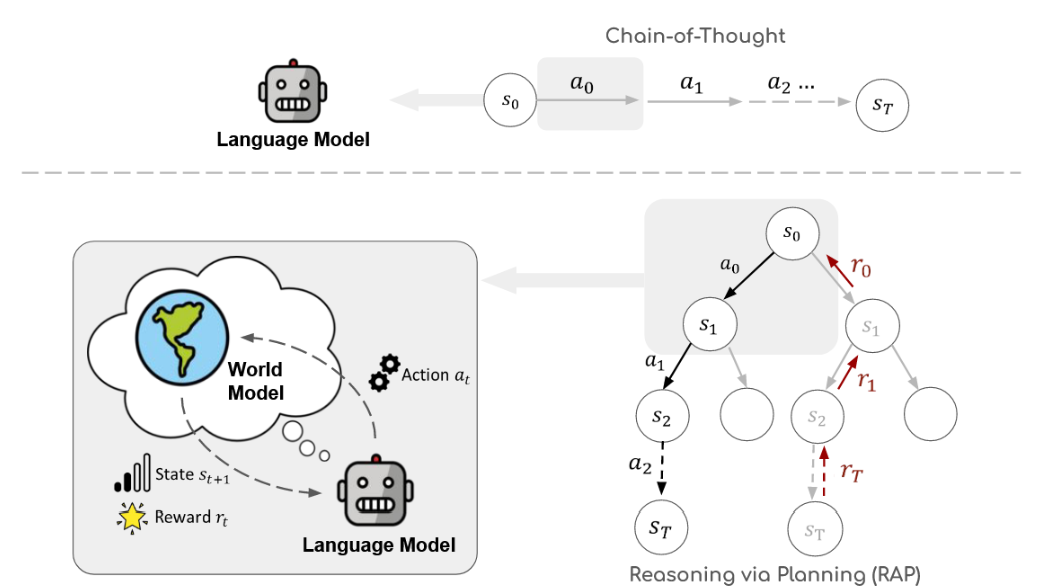
图1：规划推理（RAP）概述。与先前的大型语言模型推理方法（如思维链；Wei等人，2022）相比，我们通过世界模型（由语言模型改造而成）显式地对世界状态进行建模，并利用先进的规划算法来解决推理问题。

研究表明，递归抽象规划（RAP）是一个通用框架，适用于多种复杂问题，并在近期主流大语言模型推理方法基础上实现了显著提升。在规划生成任务中，尤其是Blocksworld（Valmeekam等人，2023）的2/4/6步问题上，RAP取得了64%的平均成功率，而思维链（CoT）方法几乎完全失败。此外，搭载RAP的LLaMA-33B模型相比采用CoT的GPT-4实现了33%的相对性能提升。在数学推理（如GSM8K，Cobbe等人，2021）和逻辑推理（以PrOntoQA为例，Saparov和He，2022）领域，RAP同样持续优于包括CoT、从简到难提示学习及其自洽性变体在内的多种强基线方法。

2.相关工作

基于大语言模型的推理

大语言模型推理通常涉及将复杂问题分解为连续的中间步骤（即推理链）再生成最终答案，其典型代表是思维链提示及其变体（Wei等人，2022；Kojima等人，2022）。基础思维链一次性生成完整推理链，随着步骤增加可能引入额外错误。自洽性方法（Wang等人，2022）通过采样多条推理链并采用多数投票选择最佳答案。循序渐进提示（Zhou等人，2022）将问题拆解为更简单的子问题并依序解答。与我们的奖励机制构建相似，近期研究探索了通过自我评估方法为中间步骤提供反馈（Welleck等人，2022；Shinn等人，2023；Paul等人，2023）。与我们状态构建思路一致，Li等人（2022）将潜在"情境"融入大语言模型，指代上下文实体的状态。更相关的是，近期研究开始探索由搜索算法引导的复杂推理结构。例如CoRe（Zhu等人，2022）通过蒙特卡洛树搜索微调解码过程中的推理步骤生成器与验证器以解决数学应用题。与我们研究同期，Yao等人（2023）应用基于启发式搜索，例如深度/广度优先搜索，以寻找更优的推理路径。然而，上述方法均未正式引入世界模型，亦未将奖励与状态实例化至统一框架中。与这些搜索引导的方法相比，RAP是一个更为原则性的框架，它通过高级规划将世界模型与奖励机制有机结合。

基于大语言模型的规划

规划作为智能体的一项核心能力，指为达成特定目标而生成一系列行动的过程（McCarthy, 1963; Bylander, 1994）。经典规划方法已在机器人及具身环境中得到广泛应用（Camacho and Alba, 2013; Jiang et al., 2019）。近期，直接引导大语言模型进行规划的方法受到关注并展现出潜力（Huang et al., 2022; Singh et al., 2022; Ding et al., 2023）。此外，基于大语言模型强大的编程能力（Lyu et al., 2023; Jojic et al., 2023; Liu et al., 2023），近期研究首先将自然语言指令转化为可执行的规划描述语言（如PDDL），随后运行经典规划算法，例如LLM+P（Liu et al., 2023）。然而，基于代码的规划受限于其狭窄的领域和环境，而RAP能够处理开放领域问题，例如数学与逻辑推理。更多关于世界模型与规划的相关工作将在附录D中讨论。

3.基于规划的推理（RAP）

本节我们将提出"规划式推理"（Reasoning via Planning, RAP）框架，该框架使大语言模型能够通过战略性规划，为广泛类型的推理任务构建连贯的推理轨迹。我们首先通过提示工程对大语言模型进行改造以构建世界模型（第3.1节）。该世界模型为审慎规划奠定基础，使得大语言模型能够进行前瞻性规划并探寻未来的预期结果。随后，我们在第3.2节引入了用于评估推理过程中各状态的奖励机制。在世界模型与奖励机制的引导下，基于蒙特卡洛树搜索的规划方法能够高效探索广阔的推理空间，并寻找到最优推理轨迹（第3.3节）。最后，当规划过程中获得多个具有潜力的推理轨迹时，我们在第3.4节进一步提出一种聚合方法，通过集成结果进一步提升推理性能。

3.1 语言模型作为世界模型

一般而言，世界模型能够预测对当前状态施加行动后的下一个推理状态（Ha与Schmidhuber，2018b；Matsuo等人，2022）。RAP使我们能够根据不同推理问题的具体需求，以多种方式实例化状态和行动这两个通用概念（图2）。例如，在积木世界中，很自然地将状态定义为积木的配置（用自然语言描述），并将行动定义为移动积木的行为（例如"拿起橙色积木"）。在数学推理问题中，我们用状态表示中间变量的取值，并将行动设置为驱动推理以推导出新值的子问题。在逻辑推理中，状态是我们当前关注的事实，行动则是为下一步演绎选择规则。

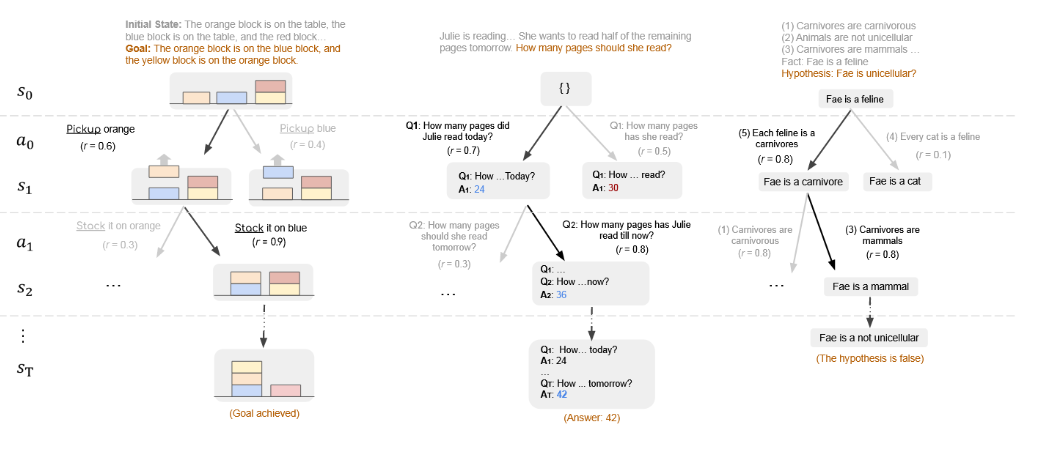
图2：Blocksworld领域中的规划生成（左）、GSM8K中的数学推理（中）以及PrOntoQA中的逻辑推理（右）的RAP。

在定义了状态与动作后，推理过程可形式化为马尔可夫决策过程（MDP）：给定当前状态 s t s_t st（t=0,1,...,T，例如初始状态 s 0 s_0 s0），大语言模型（作为推理智能体）通过从其生成分布中采样来产生动作空间 a t ∼ p ( a ∣ s t , c ) a_t ∼ p(a|s_t, c) at∼p(a∣st,c)，其中 c 为恰当的提示（例如上下文示例）。选定动作后，世界模型将预测推理的下一状态 s t + 1 s_{t+1} st+1。具体而言，我们复用同一大语言模型来获取状态转移分布 p ( s t + 1 ∣ s t , a t , c ′ ) p(s_{t+1}|s_t, a_t, c') p(st+1∣st,at,c′)，其中 c ′ c' c′ 是引导大语言模型生成状态的另一提示。例如在积木世界中，给定先前状态 s t s_t st 与动作 a t a_t at，大语言模型（作为世界模型）将生成文本 s t + 1 s_{t+1} st+1 来描述积木的新排列状态。

继续这一过程会生成一个推理轨迹，该轨迹由交替出现的状态和动作序列构成（ s 0 , a 0 , s 1 , . . . , a T − 1 , s T ）（s_0, a_0, s_1, ..., a_{T−1}, s_T）（s0,a0,s1,...,aT−1,sT）。这与先前的推理方法（如思维链（Wei等人，2022））不同，后者的中间推理步骤仅包含动作序列，例如（ a 0 a_0 a0 = "拿起红色积木"， a 1 a_1 a1 = "堆叠到黄色积木上"，...）（对比参见图1）。通过加入（预测的）世界状态来增强推理过程，有助于大语言模型进行更接地气、更连贯的推断。需要注意的是，完整的推理轨迹由大语言模型自身模拟（作为一个拥有内部世界模型的推理智能体），而无需与外部真实环境交互。这类似于人类在脑海中构思可能计划的过程。通过引入世界模型来模拟未来状态的能力，使我们能够整合原则性规划算法，从而高效探索广阔的推理空间，如第3.3节所述。

3.2 奖励设计

在推理过程中，我们需要评估每个推理步骤的可行性与合意性，并基于评估结果引导推理（第3.3节）。每个推理步骤（即将动作 a t a_t at应用于状态 s t s_t st）的评估由奖励函数 r t = r ( s t , a t ) ∈ R r_t = r(s_t, a_t) ∈ R rt=r(st,at)∈R执行。与状态和动作类似，奖励函数可以通过不同方式指定，以适应针对目标推理问题的任何先验知识或偏好。在此，我们介绍几种适用于不同任务的常见奖励函数，这些函数在我们的实验中被证明是有效的。

行动的可能性。当大型语言模型根据上下文演示及当前状态生成一个行动时，该特定行动的概率反映了模型的偏好。因此，我们可以将行动的对数概率作为奖励进行整合。这一奖励反映了大型语言模型作为智能体的"本能"，亦可作为探索行动选择的先验依据。

状态置信度。在某些问题中，状态预测并非易事，例如在数学推理中（图2，中间部分），给定一个动作（即子问题），世界模型通过回答该子问题来预测下一状态。我们将状态（在此情境下即答案）的置信度作为一种奖励纳入考量。具体而言，我们从世界模型中抽取多个答案样本，并以最频繁答案的出现比例作为置信度。更高的置信度表明状态预测与大型语言模型的世界知识更为一致（Hao et al., 2023b），这通常意味着推理步骤更为可靠。

大语言模型的自我评估。有时识别推理错误比预先避免生成这些错误更为容易。因此，允许大语言模型通过"这个推理步骤正确吗？"这一问题进行自我批判，并使用"是"这一词符的下一词概率作为奖励，是有益的。该奖励评估了大语言模型自身对推理正确性的估计。需注意，用于自我评估的具体问题可能因任务而异。

任务特定启发式方法。RAP还允许我们在奖励函数中灵活地融入其他任务特定的启发式规则。例如，在Blocksworld的规划生成中，我们会将预测的当前积木状态与目标进行比较，以此计算奖励（第4.1节）。这种奖励机制旨在激励移动规划积极地朝向目标推进。

3.3 基于蒙特卡洛树搜索的规划

在获得世界模型（第3.1节）与奖励函数（第3.2节）后，大型语言模型便可结合任意规划算法进行推理。我们采用蒙特卡洛树搜索（MCTS）（Kocsis与Szepesvári，2006；Coulom，2007）------一种强大的规划算法，它能对推理树空间进行战略性探索，并在探索与利用之间取得恰当平衡，从而高效地找出高奖励值的推理轨迹。

具体而言，蒙特卡洛树搜索（MCTS）通过迭代方式构建一棵推理树，其中每个节点代表一个状态，每条边代表一个动作及执行该动作后从当前状态转移到下一状态的过程（图1）。该方法用于引导大语言模型智能体为扩展并探索树中最具潜力的节点，该算法维护一个状态-动作价值函数 Q ： S × A → R Q：S × A → R Q：S×A→R，其中 Q ( s , a ) Q(s, a) Q(s,a) 用于估计在状态 s 下采取动作 a 的预期未来奖励。图3展示了每次迭代中扩展树与更新 Q 值的四个操作。该过程持续进行直至达到指定的计算预算（例如迭代次数），并从树中获取最终生成的轨迹。规划算法的更多细节及伪代码详见附录A与算法1。

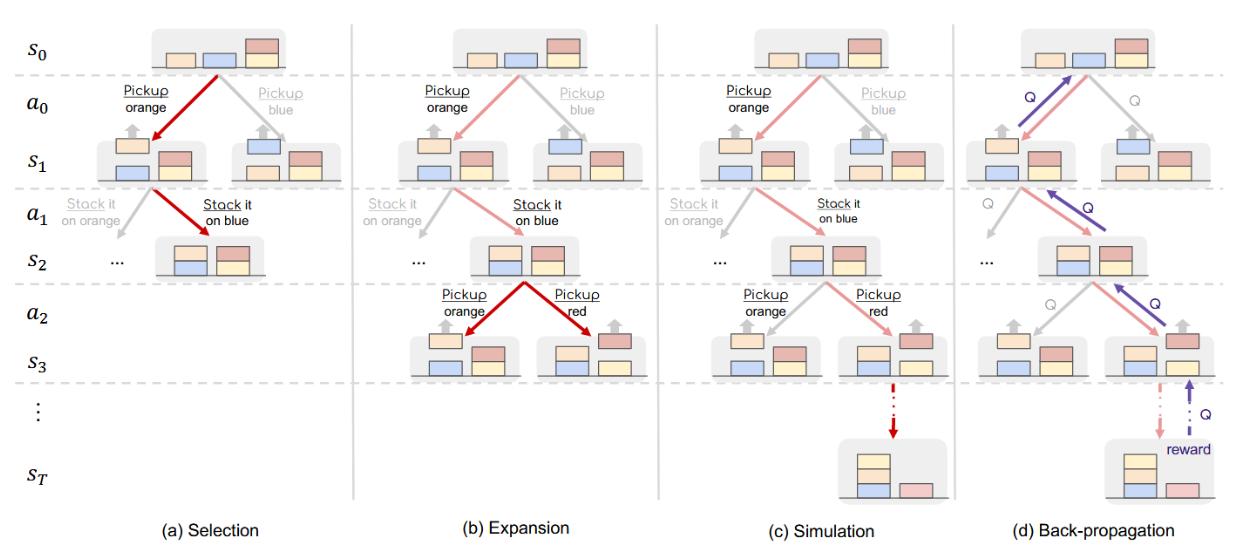
图3：MCTS规划中单次迭代四个阶段的示意图（第3.3节）。

选择阶段。第一阶段从现有树中选取最具备扩展潜力的部分，以便在下一阶段进行拓展。算法从根节点（即初始状态 s 0 s_0 s0）开始，在树的每一层级选择一个子节点作为下一节点。当抵达当前树的叶节点时，该阶段结束。图 3(a) 将所选路径以红色高亮显示。为了在探索（访问较少的节点）和利用（访问高价值节点）之间取得平衡，我们采用学术界广为使用的应用于树的置信上界方法（UCT，Kocsis 和 Szepesvári，2006）来选择每个子节点。具体而言，在节点 s 处，我们通过综合考虑 Q 值（用于利用）和不确定性（用于探索）来选择树中的动作：

a ∗ = arg ⁡ max ⁡ a ∈ A ( s ) [ Q ( s , a ) + w ln ⁡ N ( s ) N ( c ( s , a ) ) ] , ( 1 ) a^*=\arg\max_{a\in A(s)}\left[Q(s,a)+w\sqrt{\frac{\ln N(s)}{N(c(s,a))}}\right],\quad(1) a∗=arga∈A(s)max[Q(s,a)+wN(c(s,a))lnN(s) ],(1)

其中 N(s) 表示节点 s 在先前迭代中被访问的次数， c ( s , a ) c(s, a) c(s,a) 表示在状态 s 下应用动作 a 所对应的子节点。某子节点先前被访问的次数越少（即对该子节点的认知不确定性越高），公式中第二项的值就越大。权重 w 用于控制探索与利用之间的平衡。

扩展阶段。此阶段通过向上述选定的叶节点添加新的子节点来扩展树。根据叶节点的状态，我们使用LLM（作为智能体）采样d个可能动作（例如数学推理中的子问题），再利用LLM（作为世界模型）预测对应的后续状态，从而生成d个子节点。需注意：若上述选定的叶节点本身已是终止节点（推理链终点），则跳过扩展阶段，直接进入反向传播步骤。

仿真。为估算预期的未来奖励（Q值），此阶段利用世界模型对当前节点的未来情境进行推演。从上述当前节点出发，在每一节点s处，我们依据滚动策略生成动作，并使用世界模型预测下一状态。该滚动过程将持续进行直至抵达终止状态。滚动策略可通过多种方式定义（例如添加不同随机性）。在实验中，为简化流程并降低噪声干扰，我们采用与前述扩展阶段类似的流程，即生成d个候选动作并选取局部奖励最高的动作 a ′ = m a x a ′ r ( s , a ) a' = max_{a'} r(s, a) a′=maxa′r(s,a)。实际应用中，出于效率考量，我们舍弃了r函数中计算成本较高的部分（例如需要多次采样答案的状态置信度奖励），转而使用简化的轻量级奖励函数进行仿真阶段的行为选择。

反向传播。在上述阶段抵达终止状态后，我们获得了一条从根节点到终止节点的推理路径。此时，我们将路径上的奖励进行反向传播，以更新路径上每个状态-动作对的 Q 值。具体而言，我们通过聚合节点 s 之后所有未来步骤的奖励来更新 Q(s, a)。

当达到预定的蒙特卡洛树搜索（MCTS）迭代次数后，我们终止算法，并从构建的树中选择最终推理轨迹进行评估。选择方式有多种：一种是从根节点开始，迭代选择具有最高Q值的动作，直至到达终端节点；另一种是直接选择在迭代中获得最高奖励的路径，或者选择被访问次数最多的叶节点（及其对应的根到叶路径）。在实际应用中，我们观察到第二种策略通常能产生最佳结果。

3.4 RAP 聚合

对于仅需最终答案的问题，例如数学推理（第4.2节），RAP能够通过不同的MCTS迭代生成多条推理轨迹和多个答案，这些结果将被汇总以产生最终答案。我们将此机制称为RAP聚合。需注意，对于计划生成或逻辑推理这类需要输出完整推理轨迹的问题，则不会应用RAP聚合。

4.实验

在本节中，我们将RAP框架应用于一系列广泛的问题，以展示其灵活性和有效性，包括具身环境中的计划生成（4.1）、解决数学文字问题的数学推理（4.2）以及验证假设的逻辑推理（4.3）。后续章节将阐述RAP中的世界模型表述如何实现对状态和行动的多样化设计，从而适应不同的推理场景。

我们主要将RAP与思维链（CoT）（Wei等人，2022）及其变体（如由简至繁提示）（Zhou等人，2022）作为基线进行比较。若适用，我们也会考虑集成多推理路径的方法（亦称为自洽性方法（Wang等人，2022））。此外，在计算资源允许的情况下，我们还将RAP与GPT-4（OpenAI，2023）进行对比。默认情况下，我们使用LLaMA-33B模型（Touvron等人，2023a）作为我们方法与基线的基础大语言模型，采样温度为0.8。所有提示词均列于附录C中。

4.1 计划生成

规划生成任务旨在生成一系列行动序列以实现既定目标，并可能包含附加约束条件。生成规划的能力对于具身智能体至关重要，例如家庭服务机器人（Puig et al., 2018）。

任务配置。为探究RAP框架在计划生成任务中的适用性，我们在Blocksworld基准测试（Valmeekam等人，2022）中调整并评估了RAP。该任务要求智能体按特定顺序将积木重新堆叠排列。我们将状态定义为积木的当前摆放方式，将动作定义为移动积木的指令。具体而言，每个动作由4个动词（即STACK、UNSTACK、PUT和PICKUP）之一及被操作对象组成。在动作空间中，我们根据动作的领域限制及积木当前状态生成当前有效的动作。为实现状态转移，我们获取当前动作并查询大语言模型，预测相关积木的状态变化，随后通过添加新的积木状态条件并移除不再成立的条件来更新当前状态。当某个状态满足目标中的所有条件，或达到树的深度限制时，我们终止对应节点的搜索。

为评估该领域内行动的质量，我们采用两种独立的奖励机制。首先，我们向大语言模型提供若干示例测试用例及其解决方案，随后计算给定当前状态下行动的对数概率（即第3.2节中的"行动似然"奖励），记为r1。此项奖励反映了作为推理智能体的大语言模型的直觉判断。当距离目标仅剩少量步骤时，该奖励通常具有指示性，而对于远期目标则可靠性较低。此外，我们会在执行行动后将新状态与目标进行比较，并根据满足条件的数量提供奖励r2（即"任务特定启发式"奖励）。具体而言，当所有条件均被满足时，我们会分配一个极大值奖励，以确保该方案被选作最终解。

结果。我们采用Blocksworld数据集（Valmeekam等人，2023年）中的测试案例，并按所需最少操作步数进行分组，得到30个可在2步内解决的案例，57个在4步内解决的案例，以及114个在6步内解决的案例。每个测试案例最多包含5个积木。作为基准方法，我们向大语言模型提供4个带有对应解决方案的测试案例，并要求其生成一个为新问题制定计划。此设置与Valmeekam等人（2022）中所述相同，我们将其表示为思维链（CoT），因为解决方案是逐步生成的。对于RAP，则展示相同的提示以帮助大语言模型计算r1。

如表1所示，采用LLaMA-33B的思维链（CoT）方法仅能对少数2步问题生成有效规划，且在更复杂问题上完全失效。递归性推理规划（RAP）相比CoT有显著提升，几乎能解决所有4步以内的问题及部分6步问题，平均成功率可达64%。值得注意的是，6步问题的搜索空间可达5的6次方量级，而我们的算法在20次迭代内仍有42%的概率能找到有效规划。更突出的是，我们的框架使LLaMA-33B实现了相对于GPT-4的33%相对性能提升，而后者已知具备更强的推理能力（Bubeck et al., 2023）。

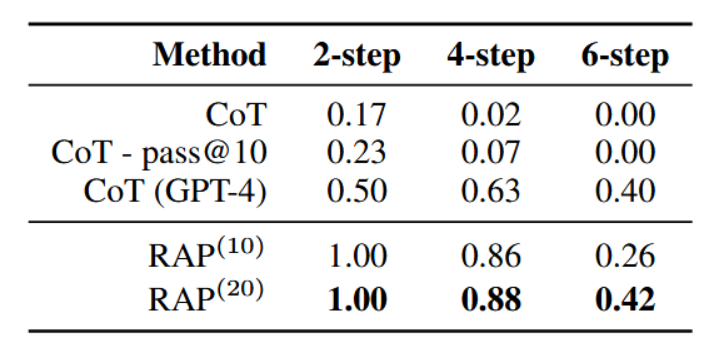
表1：Blocksworld实验结果。RAP(10)和RAP(20)分别指代我们的方法中迭代次数设置为10和20的情况。"pass@10"表示每个测试用例采样10个计划，只要至少有一个计划正确，该测试用例即视为被解决。包括RAP在内的所有其他设置均仅评估单一计划。

案例研究。我们在图4中对比了CoT与RAP的推理路径。现将性能提升的原因总结如下：（1）通过在推理过程中维持世界状态，RAP能够识别当前状态下的有效动作，避免生成无效计划。（2）当大语言模型的初步直觉无效时，RAP能够回溯并尝试其他解决方案。具体而言，CoT试图先实现第二个目标（即"将橙色置于红色之上"），并计划在前两步达成该目标。然而，优先完成第二个目标会导致第一个目标无法实现。相反，尽管RAP在最初几次迭代中犯了相同错误，我们的框架能引导智能体探索其他可能路径（如第3.3节所述），最终生成成功计划。（3）在计算奖励值rt时，我们仅将当前状态输入大语言模型并隐藏历史信息。例如在图4场景中，为计算动作a2的奖励，大语言模型会接收到一个以状态s2为初始状态的"新"测试案例。这显著降低了后续步骤的决策难度，从而为前几步更困难的决策节省了迭代资源。

图4：在积木世界中对比思维链（左）与推理动作规划（右）的推理轨迹。

4.2 数学推理

任务设置。数学推理任务（如GSM8k（Cobbe等人，2021））通常包含一段描述和一个最终问题。为得出最终问题的答案，需要依据问题背景进行多步骤数学计算。因此，将最终问题分解为一连串更小的子问题（图2右）是自然思路。我们将状态定义为中间变量的值，将动作定义为针对未知中间变量提出渐进的子问题。世界模型随后利用中间变量和问题描述对子问题给出响应，并将新的中间变量值加入下一状态。我们通过加权几何平均数 r t = r t , 1 α ∗ r t , 2 1 − α r_t=r_{t,1}^\alpha*r_{t,2}^{1-\alpha} rt=rt,1α∗rt,21−α，结合大语言模型对帮助程度的自我评估 r t , 1 r_{t,1} rt,1与状态置信度 r t , 2 r_{t,2} rt,2，作为奖励函数。该奖励机制旨在鼓励提出更相关、更有用的子问题。为兼顾为探究推理路径长度对奖励的影响，我们采用未来多步平均奖励的最大值来计算Q值。

Q ∗ ( s t , a t ) = max ⁡ s t , a t , r t , . . . , s l , a l , r l , s l + 1 a v g ( r t , . . . , r l ) . ( 2 ) Q^*(s_t,a_t)=\max_{s_t,a_t,r_t,...,s_l,a_l,r_l,s_{l+1}}\mathrm{avg}(r_t,...,r_l).\quad(2) Q∗(st,at)=st,at,rt,...,sl,al,rl,sl+1maxavg(rt,...,rl).(2)

作为一项相关研究，最小到最多提示法（Zhou等人，2022）在子问题分解方面与我们思路相似，但其一次性生成所有子问题。相反，RAP根据当前状态st来考虑每一个动作at，从而能够做出更具信息依据的决策。

结果。我们在GSM8k（一个小学数学应用题数据集）上评估我们的框架。同时，我们以思维链提示（Wei等人，2022）、Least-to-Most提示（Zhou等人，2022）及其自洽性（Wang等人，2022）变体作为基线，评估了基础模型。所有方法均使用相同的4个示例演示。

如表2所示，我们的RAP框架正确解决了48.8%的问题，其表现优于思维链提示法和带有自我一致性的最小到最多提示法。值得注意的是，该结果是RAP仅根据奖励选择单一推理轨迹时取得的。RAP-Aggregate机制的引入进一步将准确率提升了约3%。我们还计算了在不同蒙特卡洛树搜索迭代次数和基线方法中不同自我一致性样本数量下的准确率，在图5中，我们发现，在所有迭代次数/样本量的条件下，RAP聚合方法均持续优于基线模型。这表明当仅允许少量迭代/采样时，在奖励机制的引导下，我们的框架能够显著更有效地找到可靠的推理路径。

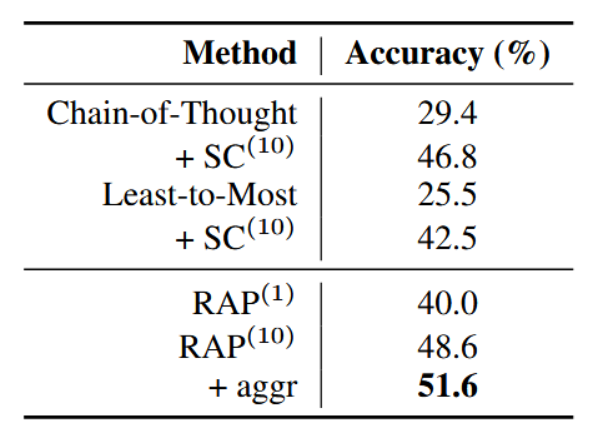
表2：GSM8k数据集上的结果。上标数字表示样本数或迭代次数。

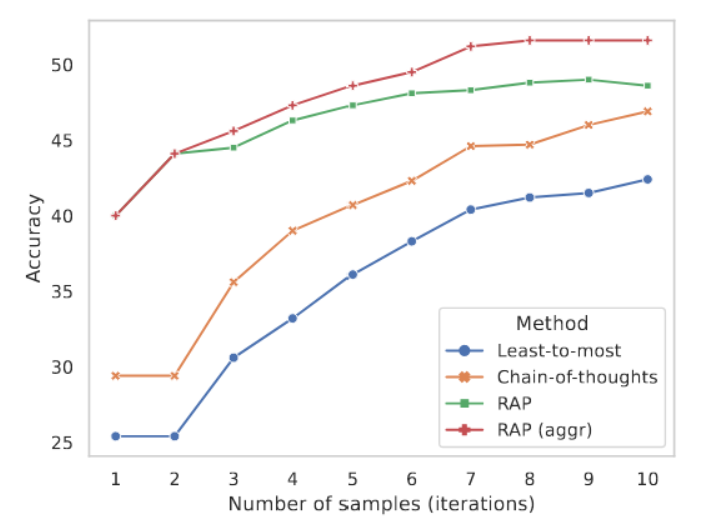
图5：GSM-8K数据集上，采用不同数量的采样路径或迭代次数的结果。

4.3 逻辑推理

任务设定。逻辑推理任务（例如PrOntoQA（Saparov和He，2022））通常提供一组事实和逻辑规则，要求模型通过将逻辑规则应用于给定事实来验证某一假设事实的真伪，如图2所示。这类任务不仅要求得出正确最终答案（真/假），还需要提供展示推理结果的详细证明。为应用我们的框架，我们将状态定义为当前关注的焦点事实，类似于人类推理时的工作记忆（Baddeley, 1992）。动作定义为从事实集中选择一条规则。世界模型执行单步推理以得到新事实作为下一状态。奖励通过自我评估计算（第3.2节），具体做法是向大语言模型提供少量带标注的示例，以帮助其更好地理解推理步骤的质量。我们使用后续步骤的平均奖励更新Q函数，这与GSM8k任务中的公式（2）方法一致。

结果。我们在PrOntoQA（Saparov and He，2022）上评估RAP框架的性能，并沿用其设定的"真实"本体（使用现实世界知识）和"随机"规则排序。我们将需要3、4、5个推理步跃才能完成正确证明的示例混合，以防止大语言模型记忆何时结束推理。我们从Saparov和He（2022）发布的生成脚本中随机抽取500个示例。我们同时比较最终答案的预测准确率和整个证明的准确率。蒙特卡洛树搜索进行20次迭代，自洽性采样采取20个样本。

如表3所示，我们的框架实现了94.2%的答案正确率和78.8%的证明准确率，其证明准确率较思维链基线高出14%，预测准确率较自洽思维链基线高出4.4%。这一显著提升充分表明在PrOntoQA中，RAP有效解决了逻辑推理问题，其功效得以验证。如图2案例所示，RAP能够准确识别推理链何时陷入僵局，并将信号回溯至早期推理步骤，其规划算法使其能够探索先前步骤的替代方案。自我评估奖励机制进一步帮助RAP识别潜在的错误推理步骤，促使智能体在后续迭代中避免此类错误。

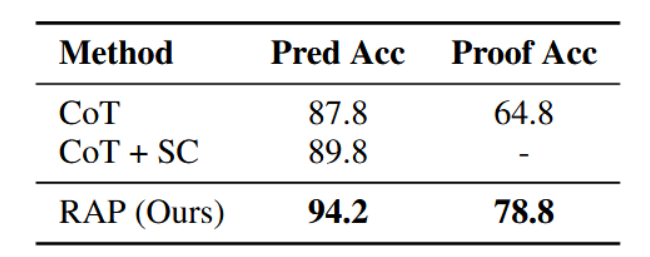
表3：ProntoQA数据集上的结果。

5.分析

5.1 复杂问题

为进一步研究RAP能否帮助更强大的大语言模型解决更复杂的问题，我们在完整的Blocksworld（Valmeekam等人，2023年）数据集上使用性能更强的Llama-2 70B模型（Touvron等人，2023b）进行了实验。

完整版Blocksworld（Valmeekam等人，2023）包含602个测试用例。我们根据每个测试用例所需的最少动作数对其进行分组。我们的实验在两种不同设置下进行：简单设置与困难设置。

在简单设置中，我们预先知晓每个用例所需的最少动作数。利用这一信息，我们选用与测试用例具有相同最少动作数的示例用例。对于每组用例，我们随机选取10个案例构建示例池，其余案例则作为测试集。在推理过程中，我们从该池中随机抽取4个示例案例，并用其构建提示。

在困难设置中，我们从完整数据集中随机选取10个案例构成全局示例池，并将这些案例从测试集中排除。在推理过程中，无论测试用例所需的最少动作数如何，我们都从该全局池中随机抽取4个示例案例。

我们采用思维链提示（Wei等人，2022）作为基线，并通过改进的提示技术（附录E）评估我们的RAP(10)（进行10次迭代）。实验结果总结于表4中。无论在简单还是困难设置下，RAP均以显著优势超越CoT的表现。值得注意的是，当测试案例需要更多步骤（六步或以上）才能解决时，CoT的成功率会出现严重下降，而RAP则能保持相对较高的成功率。结合第4.1节的实验结果，我们进一步得出结论：RAP是一个能够增强大语言模型推理能力的通用框架，且其效果不受模型内在能力的限制。

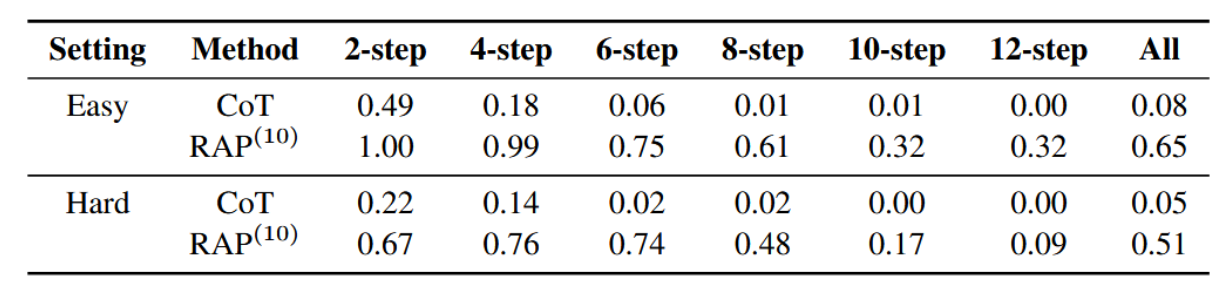
表4：基于Llama-2 70B的完整积木世界测试结果。

5.2 奖励选择

在我们的主要实验中，我们根据启发式规则和探索性实验的结果，选择了当前实验中的奖励组合方案。为理解奖励选择对大型语言模型推理的影响，我们补充了关于规划生成（表5）与数学推理（表6）奖励机制的全面实验。

通常，多种奖励的组合有助于提升性能。然而，奖励的效果取决于任务的性质。例如，行动可能性奖励对于计划生成至关重要，但对数学推理帮助不大。更多讨论详见附录F。

6 结论

本文提出"规划驱动推理"（RAP），一种新颖的大语言模型推理框架，它赋予大语言模型类人战略规划式的推理能力。该框架将大语言模型重新定位，使其同时充当世界模型和推理代理，能够模拟世界状态并预测行动结果，且通过蒙特卡洛树搜索实现探索与利用的有效平衡。在多种复杂推理问题上的大量实验表明，RAP优于多种当前基于思维链的推理方法，甚至在特定设定下超越了先进的GPT-4。

在本研究中，我们主要关注利用冻结的大型语言模型，其能力可能受限于预训练阶段。未来值得探索如何通过微调使大型语言模型更好地进行推理并作为世界模型发挥作用（Xiang et al., 2023），以及如何将外部工具（Hao et al., 2023a; Schick et al., 2023）与RAP相结合，以解决更复杂的现实世界问题。

7.引用文献

附录

A 蒙特卡洛树搜索规划

我们对MCTS算法进行改进，以搜索最优推理路径（算法1）。与传统MCTS应用相比，我们面临巨大的推理空间和LLM高昂的计算成本。因此，我们在实现中对经典MCTS做了如下修改：（1）对于开放域问题（如数学问题），无法枚举所有可能行动（子问题），因此我们通过从LLM中采样固定数量的潜在行动来缩减行动空间，采样条件基于当前状态的提示词和上下文示例。（2）在选择阶段，若存在尚未探索的行动，我们使用轻量级局部奖励（如自我评估奖励）估算其Q值，再通过UCT准则选择行动。这为探索过程提供了先验知识，鉴于有限的迭代预算，这一点至关重要。

B 实验设置

B.1 语言模型解码

我们采用温度为0.8的随机采样方法。生成过程在达到最大长度2048或遇到换行符标记时终止。

B.2 计算资源

我们所有的实验均在4台显存为24GB的NVIDIA A5000 GPU上运行。

C 提示词

C.1 计划生成

以下展示了为RAP计算行动似然性的提示词，该提示词同样应用于思维链基线中。<init_state>与<goals>将根据待解决的问题进行实例化。

复制代码

我正在操作一套积木，需要将积木排列成堆。以下是我可以执行的操作：
拾起一块积木
从另一块积木顶部移开一块积木
放下手中的积木
将一块积木堆叠在另一块积木顶部

我的操作受到以下限制：
每次只能拾起或移开一块积木。
只有当手为空时才能拾起或移开积木。
只有当积木位于桌面上且处于清空状态时才能拾起。
清空状态指积木顶部没有其他积木且未被拾起。
只有当被移开的积木确实位于另一块积木顶部时，才能执行移开操作。
只有当被移开的积木处于清空状态时，才能执行移开操作。
拾起或移开积木后，该积木即被手持。
只能放下当前手持的积木。
只有当手持待堆叠的积木时，才能将其堆叠到另一块积木上。
只有当目标积木处于清空状态时，才能将积木堆叠到其顶部。
放下或堆叠积木后，手部变为空置状态。

[初始状态]
红色积木处于清空状态，黄色积木处于清空状态，手部为空置状态，
红色积木位于蓝色积木顶部，黄色积木位于橙色积木顶部，
蓝色积木置于桌面，橙色积木置于桌面。
我的目标是达成：橙色积木位于红色积木顶部。

[执行计划]
从橙色积木顶部移开黄色积木
放下黄色积木
拾起橙色积木
将橙色积木堆叠在红色积木上方 
[计划结束]

[陈述] 初始条件为：橙色积木顶部是空的，黄色积木顶部是空的，手是空的，蓝色积木在红色积木之上，橙色积木在蓝色积木之上，红色积木在桌子上，黄色积木在桌子上。我的目标是：蓝色积木在红色积木之上，且黄色积木在橙色积木之上。我的计划如下：
[计划] 拿起黄色积木，将黄色积木堆叠在橙色积木之上。
[计划结束]

[陈述] 初始条件为：红色积木顶部是空的，蓝色积木顶部是空的，橙色积木顶部是空的，手是空的，蓝色积木在黄色积木之上，红色积木在桌子上，橙色积木在桌子上，黄色积木在桌子上。我的目标是：蓝色积木在橙色积木之上，且黄色积木在红色积木之上。我的计划如下：
[计划] 将蓝色积木从黄色积木上取下，将蓝色积木堆叠在橙色积木之上，拿起黄色积木，将黄色积木堆叠在红色积木之上。
[计划结束]

[陈述] 初始条件为：红色积木顶部是空的，蓝色积木顶部是空的，黄色积木顶部是空的，手是空的，黄色积木在橙色积木之上，红色积木在桌子上，蓝色积木在桌子上，橙色积木在桌子上。我的目标是：橙色积木在蓝色积木之上，且黄色积木在红色积木之上。我的计划如下：
[计划] 将黄色积木从橙色积木上取下，将黄色积木堆叠在红色积木之上，拿起橙色积木，将橙色积木堆叠在蓝色积木之上。
[计划结束]

[陈述] 初始条件为：<初始状态>。我的目标是：<目标状态>。我的计划如下：
[计划]
对于使用世界模型进行的下一个状态预测，我们应用以最后一个动作为条件的提示。这里我们以"拿起"动作后更新状态的提示为例。同样，<状态>和<动作>将用当前状态和动作实例化。
我正在玩一组积木，需要将积木排列成堆。以下是我可以执行的动作：
拿起一块积木
将一块积木从另一块积木上取下
放下手中的积木
将一块积木堆叠在另一块积木之上
我的动作有以下限制：一次只能拿起或取下一块积木。
只有当我的手是空的时，我才能拿起或取下一块积木。
只有当积木在桌子上且其顶部是空的时，我才能拿起它。一块积木顶部是空的，意味着它上面没有其他积木，并且它没有被拿在手中。
只有当我要取下的积木确实在另一块积木之上时，我才能将其从该积木上取下。
只有当我要取下的积木顶部是空的时，我才能将其从另一块积木上取下。
一旦我拿起或取下了一块积木，我就持有了该积木。
我只能放下我正持有的积木。
只有当我持有要堆叠的积木时，我才能将其堆叠在另一块积木之上。
只有当我要堆叠的目标积木顶部是空的时，我才能将一块积木堆叠在其上。
一旦我放下或堆叠了一块积木，我的手就变为空的。
在给定一个初始状态和一个动作后，给出执行该动作后的新状态。

[场景一] 
[状态0] 当前状态为：白色积木顶部空闲，青色积木顶部空闲，棕色积木顶部空闲，机械手为空闲，白色积木置于紫色积木之上，紫色积木置于桌面上，青色积木置于桌面上，棕色积木置于桌面上。
[动作] 拾取棕色积木。
[状态变化] 机械手由空闲变为持有棕色积木，棕色积木由桌面上变为在机械手中，且棕色积木不再顶部空闲。
[状态1] 当前状态为：白色积木顶部空闲，青色积木顶部空闲，棕色积木在机械手中，机械手持有棕色积木，白色积木置于紫色积木之上，紫色积木置于桌面上，青色积木置于桌面上。

[场景二] 
[状态0] 当前状态为：紫色积木顶部空闲，青色积木顶部空闲，白色积木顶部空闲，机械手为空闲，白色积木置于棕色积木之上，紫色积木置于桌面上，青色积木置于桌面上，棕色积木置于桌面上。
[动作] 拾取青色积木。
[状态变化] 机械手由空闲变为持有青色积木，青色积木由桌面上变为在机械手中，且青色积木不再顶部空闲。
[状态1] 当前状态为：青色积木在机械手中，白色积木顶部空闲，紫色积木顶部空闲，机械手持有青色积木，白色积木置于棕色积木之上，紫色积木置于桌面上，棕色积木置于桌面上。

[场景三] [状态0] <状态> [动作] <动作> [状态变化]

算法1 RAP-MCTS

输入：初始状态 s 0 s_0 s0、状态转移概率函数 p θ p_\theta pθ、奖励函数 r θ r_\theta rθ、动作生成器 p φ p_\varphi pφ、生成动作数量 d d d、深度限制 L L L、模拟次数 N N N、探索权重 w w w

1: 初始化动作记忆 A : S ↦ A A: S \mapsto A A:S↦A，子节点映射 c : S × A ↦ S c: S \times A \mapsto S c:S×A↦S 与奖励映射 r : S × A ↦ R r: S \times A \mapsto R r:S×A↦R

2: 初始化状态-动作价值函数 Q : S × A ↦ R Q: S \times A \mapsto R Q:S×A↦R 与访问计数器 N : S ↦ N N: S \mapsto \mathbb{N} N:S↦N

3: for n ← 0 , ... , N − 1 n \leftarrow 0, \dots, N-1 n←0,...,N−1 do

4: t ← 0 t \leftarrow 0 t←0

5: while N ( s t ) > 0 N(s_t) > 0 N(st)>0 do ▷ 选择阶段

6: N ( s t ) ← N ( s t ) + 1 N(s_t) \leftarrow N(s_t) + 1 N(st)←N(st)+1

7: a t ← arg ⁡ max ⁡ a ∈ A ( s t ) [ Q ( s t , a ) + w ln ⁡ N ( s t ) N ( c ( s t , a ) ) ] a_t \leftarrow \arg\max_{a \in A(s_t)} \left[ Q(s_t, a) + w \sqrt{\frac{\ln N(s_t)}{N(c(s_t, a))}} \right] at←argmaxa∈A(st)[Q(st,a)+wN(c(st,a))lnN(st) ]

8: r t = r ( s t , a t ) , s t + 1 ← c ( s t , a t ) r_t = r(s_t, a_t), \quad s_{t+1} \leftarrow c(s_t, a_t) rt=r(st,at),st+1←c(st,at)

9: t ← t + 1 t \leftarrow t + 1 t←t+1

10: end while

11: while s t s_t st 非终止状态 ∧ t ≤ L \land t \leq L ∧t≤L do

12: for i ← 1 , ... , d i \leftarrow 1, \dots, d i←1,...,d do ▷ 扩展阶段

13: 采样 a t ( i ) ∼ p φ ( a ∣ s t ) a^{(i)}t \sim p\varphi(a \mid s_t) at(i)∼pφ(a∣st), s t + 1 ( i ) ∼ p θ ( s t , a t ( i ) ) s^{(i)}{t+1} \sim p\theta(s_t, a^{(i)}_t) st+1(i)∼pθ(st,at(i)), r t ( i ) ∼ r θ ( s t , a t ( i ) ) r^{(i)}t \sim r\theta(s_t, a^{(i)}_t) rt(i)∼rθ(st,at(i))

14: 更新 A ( s t ) ← { a t ( i ) } i = 1 d A(s_t) \leftarrow \{a^{(i)}t\}{i=1}^d A(st)←{at(i)}i=1d, c ( s t , a t ( i ) ) ← s t + 1 ( i ) c(s_t, a^{(i)}t) \leftarrow s^{(i)}{t+1} c(st,at(i))←st+1(i), r ( s t , a t ) ← r t ( i ) r(s_t, a_t) \leftarrow r^{(i)}_t r(st,at)←rt(i)

15: end for

16: a t + 1 ← arg ⁡ max ⁡ a ∈ A ( s t ) r ( s t , a t ) a_{t+1} \leftarrow \arg\max_{a \in A(s_t)} r(s_t, a_t) at+1←argmaxa∈A(st)r(st,at) ▷ 模拟阶段

17: r t ← r ( s t , a t ) , s t + 1 ← c ( s t , a t ) r_t \leftarrow r(s_t, a_t), \quad s_{t+1} \leftarrow c(s_t, a_t) rt←r(st,at),st+1←c(st,at)

18: t ← t + 1 t \leftarrow t + 1 t←t+1

19: end while

20: for t ′ ← t , ... , 0 t' \leftarrow t, \dots, 0 t′←t,...,0 do ▷ 反向传播

21: 根据 { r t ′ , r t ′ + 1 , ... , r t } \{r_{t'}, r_{t'+1}, \dots, r_t\} {rt′,rt′+1,...,rt} 更新 Q ( s t ′ , a t ′ ) Q(s_{t'}, a_{t'}) Q(st′,at′)

22: end for

23: end for

C.2 数学推理

以下展示数学推理中RAP方法的提示词结构。该提示词同时用于动作提议和下一状态预测。在实例化<问题>后，我们在提示词前添加"Question 5.1"前缀，从而能够通过大语言模型采样第一个动作。后续动作的采样方式类似，区别在于需要按照上下文示例的格式，将所有已生成的子问题和子答案追加到提示词中。下一状态预测（即回答子问题）也采用相同的工作流程。

复制代码

给定一个问题，请将其分解为若干子问题。针对每个子问题，请用完整句子回答，并以"答案是"结尾。当原始问题可被回答时，请以"现在我们可以回答原问题："开始该子问题。

问题1：四年前，科迪的年龄只有穆罕默德的一半。如果穆罕默德目前的年龄是30岁的两倍，那么科迪现在多大？
问题1.1：穆罕默德现在多大？
答案1.1：他目前是30 * 2 = 60岁。答案是60。
问题1.2：四年前穆罕默德多大？
答案1.2：四年前，他应该是60 - 4 = 56岁。答案是56。
问题1.3：四年前科迪多大？
答案1.3：四年前科迪的年龄是穆罕默德的一半。因此，科迪当时是56 / 2 = 28岁。答案是28。
问题1.4：现在我们可以回答原问题：科迪现在多大？
答案1.4：她现在应该是28 + 4 = 32岁。答案是32。

问题2：在一个没有月亮的夜晚，三只萤火虫在晚风中飞舞。随后，有比一打少四只的萤火虫加入了它们，之后又有两只萤火虫飞走了。还剩下多少只萤火虫？
问题2.1：有多少只萤火虫加入了？
答案2.1：加入的萤火虫数量比一打少四只，即12 - 4 = 8只萤火虫。答案是8。
问题2.2：现在我们可以回答原问题：还剩下多少只萤火虫？
答案2.2：最初有三只萤火虫在飞舞。加入了8只萤火虫后，有两只飞走了。所以剩下3 + 8 - 2 = 9只。答案是9。

问题3：阿里在詹姆斯先生的农场工作后，攒下了四张10美元纸币和六张20美元纸币。阿里将总钱数的一半给了妹妹，并用剩余钱数的3/5购买了晚餐。计算他在购买晚餐后还剩下多少钱。
问题3.1：阿里总共有多少钱？
答案3.1：阿里有四张10美元纸币和六张20美元纸币。所以他共有4 * 10 + 6 * 20 = 160美元。答案是160。
问题3.2：阿里给了妹妹多少钱？
答案3.2：阿里将总钱数的一半给了妹妹。所以他给了妹妹160 / 2 = 80美元。答案是80。
问题3.3：阿里给妹妹钱后还剩下多少钱？
答案3.3：给妹妹钱后，阿里还剩下160 - 80 = 80美元。答案是80。
问题3.4：阿里用多少钱购买晚餐？
答案3.4：阿里用剩余钱数的3/5购买晚餐。所以他用了80 * 3/5 = 48美元购买晚餐。答案是48。
问题3.5：现在我们可以回答原问题：阿里购买晚餐后还剩下多少钱？
答案3.5：购买晚餐后，阿里还剩下80 - 48 = 32美元。答案是32。

问题4：一辆汽车正在一条多弯的隧道中行驶。一段时间后，汽车必须穿过一个需要总共右转4次的环形路段。第一次转弯后，它行驶了5米。第二次转弯后，它行驶了8米。第三次转弯后，它又行驶了一段距离，而在第四次转弯后，它立即驶出了隧道。如果汽车在环形路段总共行驶了23米，那么它在第三次转弯后需要行驶多远？
问题4.1：除了第三次转弯后的路段，汽车行驶了多远？
答案4.1：第一次转弯后行驶5米，第二次转弯后行驶8米，第四次转弯后行驶0米。总计5 + 8 + 0 = 13米。答案是13。
问题4.2：现在我们可以回答原问题：汽车在第三次转弯后需要行驶多远？
答案4.2：汽车在环形路段总共行驶了23米。除了第三次转弯后的路段，它行驶了13米。所以它在第三次转弯后需要行驶23 - 13 = 10米。答案是10。

问题5：<question>

C.3 逻辑推理

我们展示了行动提议、行动可能性计算及下一状态预测的提示模板。<fact>与<query>将根据具体问题实例化。

复制代码

给定一组事实和一个当前主张，输出一个可能的事实作为下一步。请务必复制事实中的确切句子。不要改动任何措辞。不要自行创造词语。

事实1：
每个鳞翅目都是昆虫。
每个节肢动物都是原口动物。
每个动物都是多细胞的。
原口动物是无脊椎动物。
每个鲸鱼都有骨骼。
每只红蛱蝶都是蝴蝶。
无脊椎动物是动物。
蝴蝶是鳞翅目。
每个昆虫都有六条腿。
每个昆虫都是节肢动物。
节肢动物没有骨骼。

查询1：
真或假：莎莉没有骨骼。
主张1.1：莎莉是一种昆虫。
下一步1.1：每个昆虫都有六条腿。
主张1.2：莎莉是一只蝴蝶。
下一步1.2：蝴蝶是鳞翅目。
主张1.3：莎莉是鳞翅目。
下一步1.3：每个鳞翅目都是昆虫。
主张1.4：莎莉没有骨骼。
下一步1.4：完成。
主张1.5：莎莉是节肢动物。
下一步1.5：节肢动物没有骨骼。
主张1.6：莎莉是一只红蛱蝶。
下一步1.6：每只红蛱蝶都是蝴蝶。

事实2：
质数是自然数。
每个梅森质数都不是合数。
虚数不是实数。
每个实数都是数。
自然数是整数。
每个实数都是实数。
每个梅森质数都是质数。
自然数是正数。
质数不是合数。
整数是实数。

查询2：
真或假：127不是实数。
主张2.1：127是实数。
下一步2.1：完成。
主张2.1：127是一个自然数。
下一步2.1：自然数是整数。
主张2.2：127是一个质数。
下一步2.2：质数是自然数。
主张2.3：127是一个实数。
下一步2.3：每个实数都是实数。
主张2.4：127是一个梅森质数。
下一步2.4：每个梅森质数都是质数。
主张2.5：127是一个整数。
下一步2.5：整数是实数。

事实3：鳞翅目是昆虫。所有动物都是多细胞的。每种昆虫都是节肢动物。每个无脊椎动物都是动物。昆虫有六足。节肢动物体型小。节肢动物是无脊椎动物。每只蝴蝶都属于鳞翅目。鲸鱼体型不小。
查询3：真或假：波莉体型不小。
主张3.1：波莉是节肢动物。下一步3.1：节肢动物体型小。
主张3.2：波莉是昆虫。下一步3.2：每种昆虫都是节肢动物。
主张3.3：波莉体型小。下一步3.3：完成。
主张3.4：波莉是鳞翅目昆虫。下一步3.4：鳞翅目是昆虫。

事实4：所有猫科动物都是猫。哺乳动物是脊椎动物。两侧对称动物是动物。脊椎动物是脊索动物。食肉动物是哺乳动物。哺乳动物不是冷血动物。每个脊索动物都是两侧对称动物。每个猫科动物都是食肉动物。蛇是冷血动物。动物不是单细胞生物。所有食肉动物都不是草食动物。
查询4：判断真假：法伊不是冷血动物。
主张4.1：法伊是猫科动物。
后续4.1：每个猫科动物都是食肉动物。
主张4.2：法伊不是冷血动物。
后续4.2：结束。
主张4.2：法伊是哺乳动物。
后续4.2：哺乳动物不是冷血动物。
主张4.3：法伊是猫。
后续4.3：所有猫都是猫科动物。
主张4.4：法伊是食肉动物。
后续4.4：食肉动物是哺乳动物。

事实5：素数为素数。实数为数。每个整数都是实数。实数不是虚数。梅森素数是素数。复数为虚数。每个素数都是自然数。自然数为正数。每个梅森素数都是素数。每个自然数都是整数。
查询5：真或假：7是虚数。
主张5.1：7不是虚数。
下一步5.1：完成。
主张5.1：7是自然数。
下一步5.1：每个自然数都是整数。
主张5.2：7是素数。
下一步5.2：每个素数都是自然数。
主张5.3：7是实数。
下一步5.3：实数不是虚数。
主张5.4：7是整数。
下一步5.4：每个整数都是实数。

事实6：蜘蛛并非六足。昆虫为六足。昆虫属于节肢动物。所有动物皆非单细胞生物。无脊椎动物属于动物。鳞翅目昆虫属于昆虫。所有节肢动物皆分节。节肢动物属于无脊椎动物。所有蝴蝶皆属鳞翅目。斯特拉是一只蝴蝶。
查询6：真或假：斯特拉是六足的。
主张6.1：斯特拉是一种昆虫。
下一步6.1：昆虫是六足的。
主张6.2：斯特拉是一种鳞翅目昆虫。
下一步6.2：鳞翅目昆虫属于昆虫。
主张6.3：斯特拉是一只蝴蝶。
下一步6.3：所有蝴蝶皆属鳞翅目。
主张6.4：斯特拉是六足的。
下一步6.4：完成。

事实7：<事实>查询7：<查询>

D 相关工作：世界模型与规划

近年来,规划算法已取得一系列成功应用(如AlphaZero、MuZero等)。这类算法通常基于树结构搜索,旨在有效维持探索与利用的平衡。转移动态知识是规划的前提,近期基于模型的强化学习研究提出通过学习世界模型(或称动态模型)来规划或辅助策略学习。为提升样本效率,已有研究尝试从离线轨迹中学习世界模型,并直接在世界模型中学习策略。通过在世界模型中进行潜在想象,可训练智能体解决长时序任务。此外,世界模型也被证明有助于物理机器人学习。本文采用大语言模型作为世界模型,并应用规划算法搜索推理路径,其思想内核与模型预测控制一脉相承。相较前人研究,本框架采用通用大语言模型作为世界模型,具备广泛的适应能力在一系列开放域推理任务中。Xiang等人（2023）提出通过训练大语言模型结合外部世界模型以获取具身体验，而RAP则专注于推理阶段，且兼容任何训练方法。

E 自适应提示词

通过初步实验，我们观察到大语言模型的性能会受到演示案例与测试案例间难度差异的影响。在RAP方法中，当预测出新状态时，我们会将剩余任务重新表述为一个以预测新状态初始化的新测试案例。这个新测试案例所需的最小行动步骤数将减少，从而导致演示案例与新案例的分布产生差异。为缓解此问题，我们预先计算了演示案例的中间状态。在推理过程中，我们在每次迭代中根据新状态从起始处截断演示轨迹，随着搜索树的加深，这降低了演示案例所需的最小行动步骤数。该技术显著提升了RAP的性能，特别是对于更复杂、更容易受到分布失配影响的问题。

F奖励选项

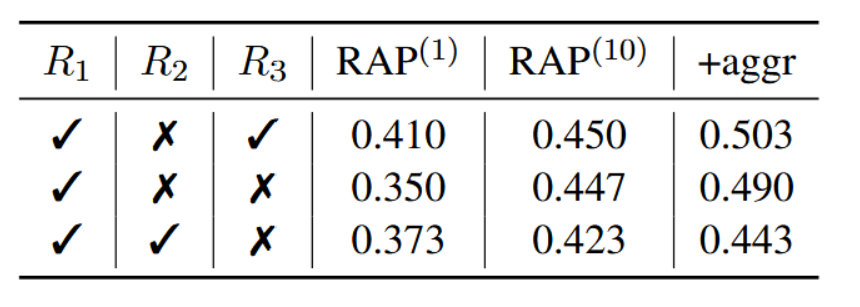
结果。我们在计划生成（表5）与数学推理（表6）的奖励机制上进行了全面实验。需注意，两表中的首行均代表我们在主要实验中所采用的设置。如表5所示，行动似然与任务特定奖励的组合（第1行）能显著优于单一奖励基线（第3、4、5行）。有趣的是，加入自我评估奖励可进一步小幅提升性能（第2行）。此外，根据表6中GSM8k前300个样本的结果可见，在置信度奖励（第2行）基础上增加行动似然奖励（第3行）或自我评估奖励（第1行），均能在单次迭代中提升仅使用置信度奖励（第1行）的RAP性能，但行动似然奖励在迭代次数增加时会降低准确率。整体而言，自我评估奖励能达成最佳性能。这表明自我评估奖励作为一种高效且计算成本低的探索先验信息，在引导推理过程中具有重要作用。

自我评估与行动似然。自我评估与行动似然所对应的奖励机制尤其值得关注，因为它们可广泛应用于多种推理任务。通常，其最佳使用方式以及与其他奖励的结合，需要基于对任务性质的实证设计与理解，且其有效性在不同任务间可能存在显著差异。此处，我们阐述这些奖励选择背后的若干直观考量：

（a）对于推理步骤简短且结构清晰的问题，行动似然具有较强指示性；反之，它可能受无关标记干扰而变得不可靠。例如，在Blocksworld领域中，单个步骤通常遵循特定模式（如PICK/PUT/STACK积木...），使得行动似然具有指示性。然而，在数学领域中，推理步骤以自然语言句子表达，自由度更高，可能引入噪声。

（b）对于某些在生成过程中难以避免错误、但在事后相对容易识别错误的问题，自我评估成为一种有助于提升推理准确性的机制。在数学推理中，大语言模型可能难以首先生成正确的推理步骤，但检测计算或逻辑错误则更为可行。而在Blocksworld中，评估候选动作的质量并不直观，仍需多步推理。这一特性降低了自我评估奖励的准确性，使其作用有限------尤其是考虑到似然本身已能为搜索提供良好的直观指引。

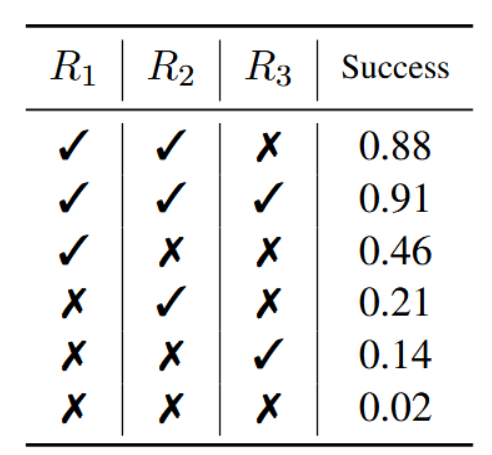
表5：Blocksworld消融实验。R1为行动似然奖励，R2为任务特定奖励，R3为自评估奖励。

表6：基于GSM8k前300个样本的消融研究。R1代表状态转移置信度奖励，R2代表动作似然奖励，R3代表自我评估奖励。