考研408--数据结构--day12--查找&二叉排序树

元亓亓亓2026-02-18 10:22

（以下内容全部出自上述课程）

目录

  • 查找
    • [1. 基本概念](#1. 基本概念)
    • [2. 常见操作](#2. 常见操作)
    • [3. 评价指标](#3. 评价指标)
    • [4. 小结](#4. 小结)
  • 顺序查找
    • [1. 算法思想](#1. 算法思想)
    • [2. 算法实现](#2. 算法实现)
      • [2.1 普通实现](#2.1 普通实现)
      • [2.2 哨兵实现](#2.2 哨兵实现)
    • [3. 算法优化](#3. 算法优化)
      • [3.1 有序排列](#3.1 有序排列)
      • [3.2 被查概率不同--排序](#3.2 被查概率不同--排序)
    • [4. 小结](#4. 小结)
  • 折半查找
    • [1. 算法思想](#1. 算法思想)
      • [1.1 查找33](#1.1 查找33)
      • [1.2 查找12](#1.2 查找12)
    • [2. 算法实现](#2. 算法实现)
    • [3. 查找判定树](#3. 查找判定树)
      • [3.1 奇数个元素](#3.1 奇数个元素)
      • [3.2 偶数个元素](#3.2 偶数个元素)
    • [4. 查找效率](#4. 查找效率)
    • [5. 小结](#5. 小结)
    • [6. 拓展思考](#6. 拓展思考)
  • 分块查找
    • [1. 算法思想](#1. 算法思想)
      • [1.1 顺序查找索引表](#1.1 顺序查找索引表)
      • [1.2 折半查找索引表](#1.2 折半查找索引表)
    • [2. 查找效率分析（ASL）](#2. 查找效率分析（ASL）)
    • [3. 小结](#3. 小结)
    • [4. 拓展思考](#4. 拓展思考)
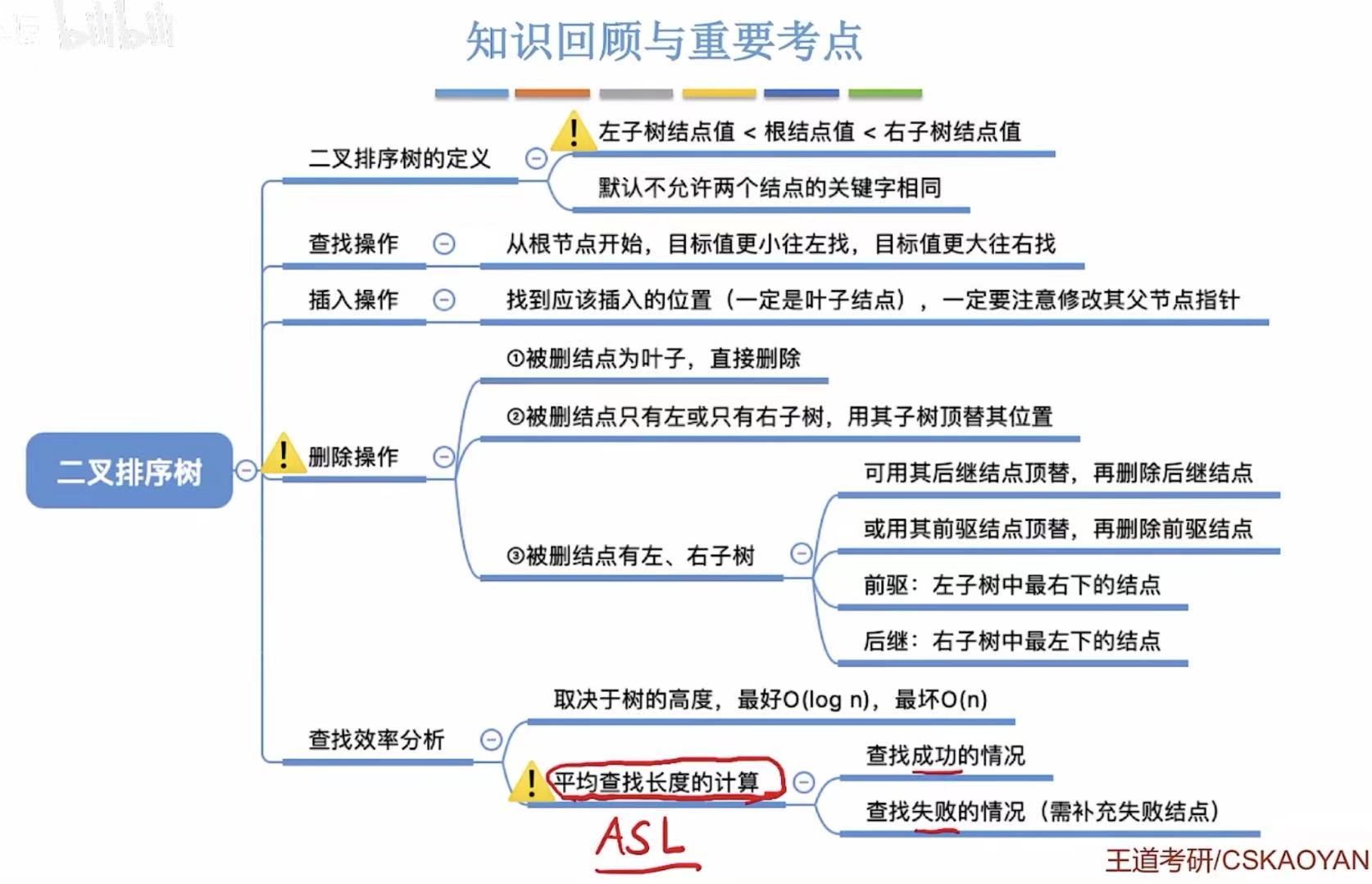
  • 二叉排序树
    • [1. 定义](#1. 定义)
    • [2. 操作](#2. 操作)
      • [2.1 查找操作](#2.1 查找操作)
      • [2.2 插入操作](#2.2 插入操作)
      • [2.3 删除操作](#2.3 删除操作)
    • [3. 查找效率分析](#3. 查找效率分析)
    • [4. 小结](#4. 小结)

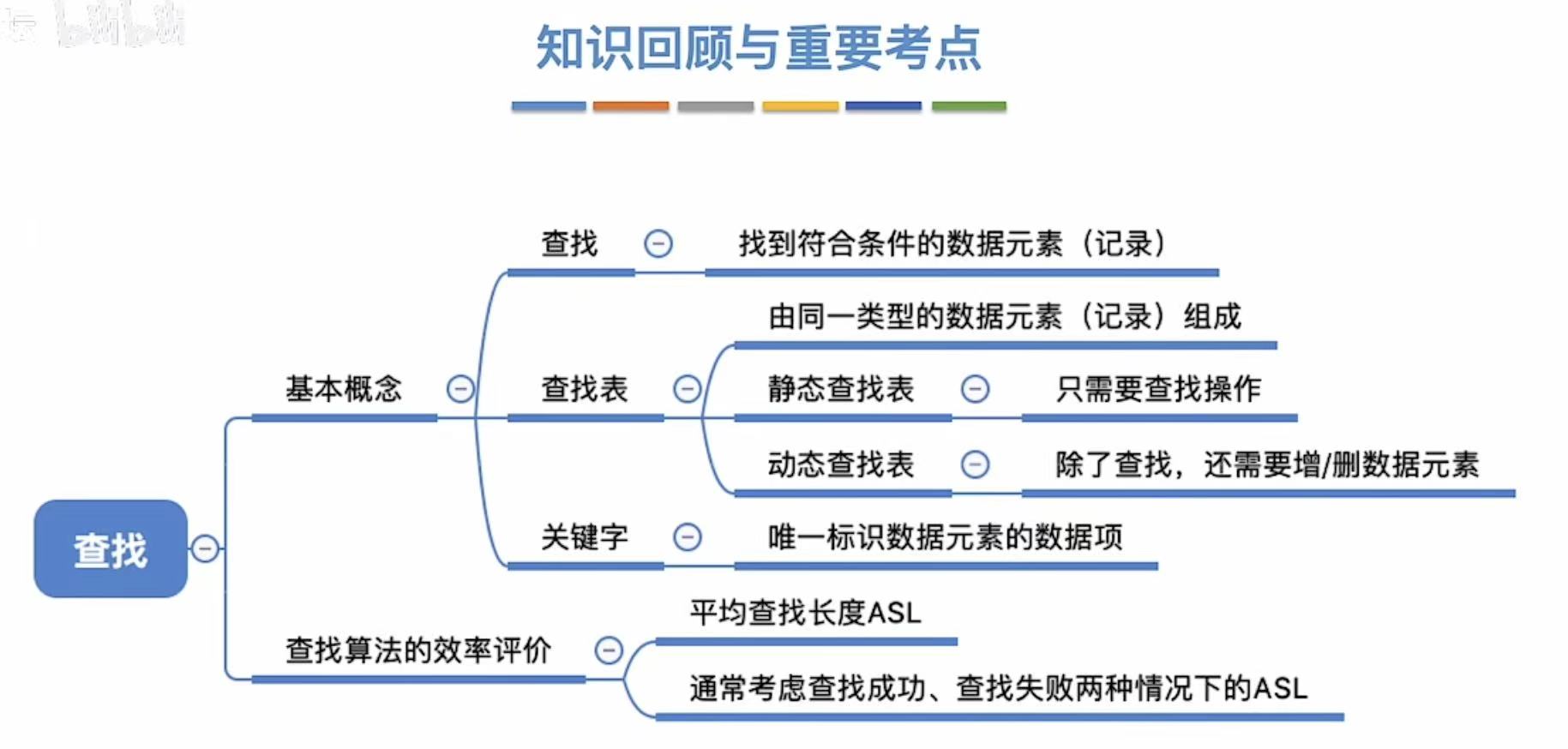
查找

1. 基本概念

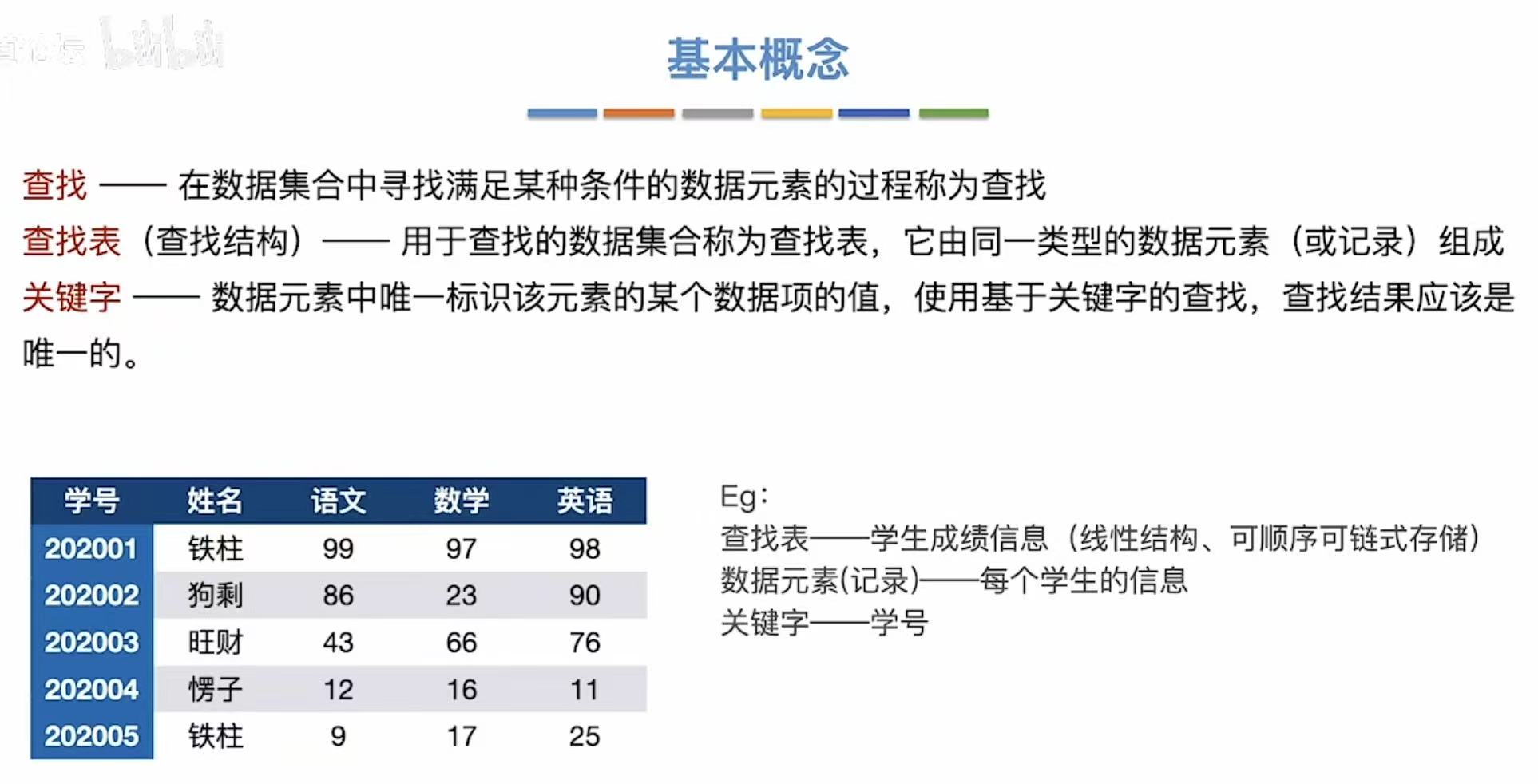
  • 查找：在XX中，找满足XX的XX的过程。
  • 查找表：在XX中的XX。
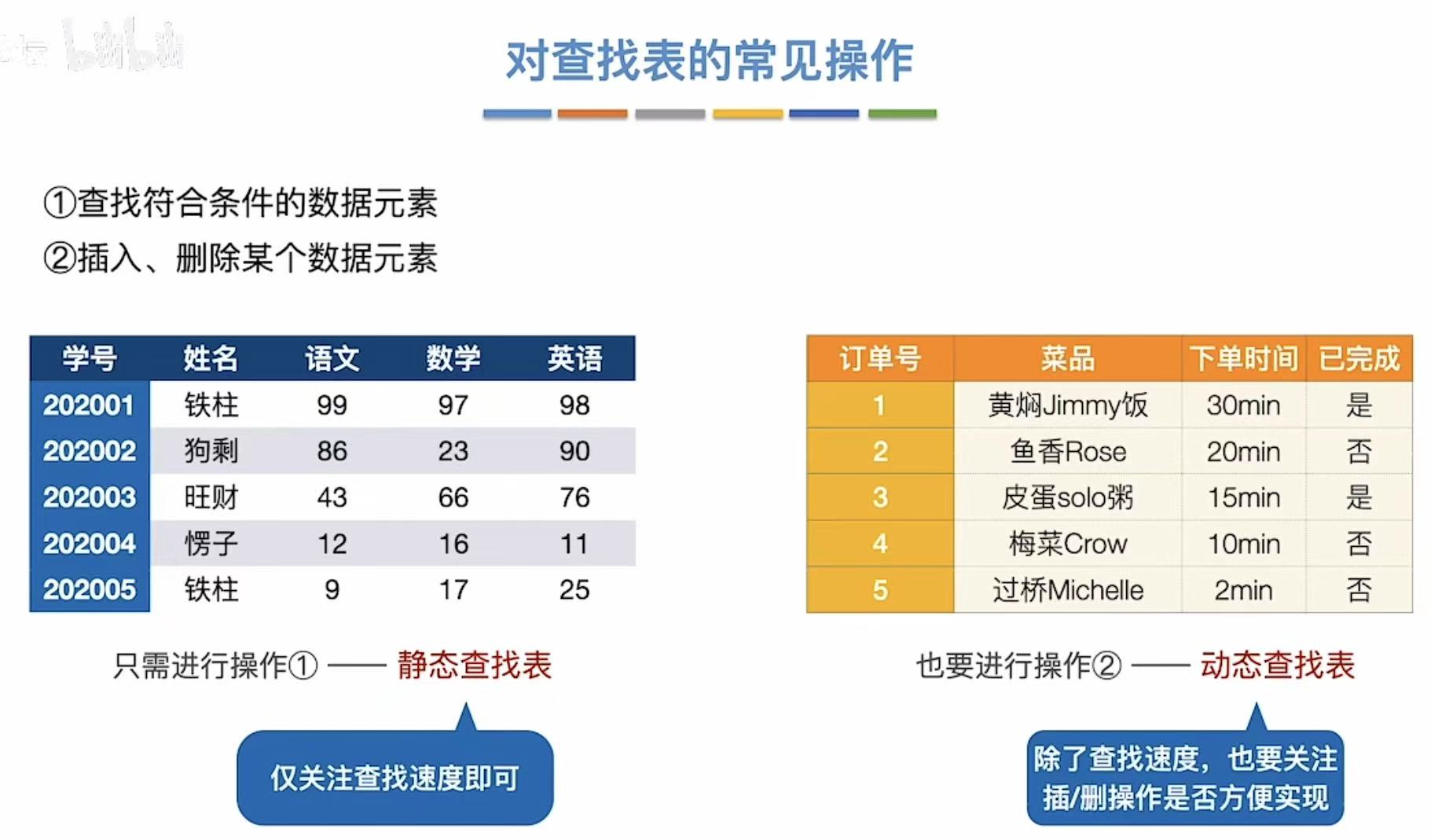
  • 关键字：唯一标识。比如下面例子中的学号，其他都可能重复，但是学号不可能重复。

查找表可以是下图中的表格形式：

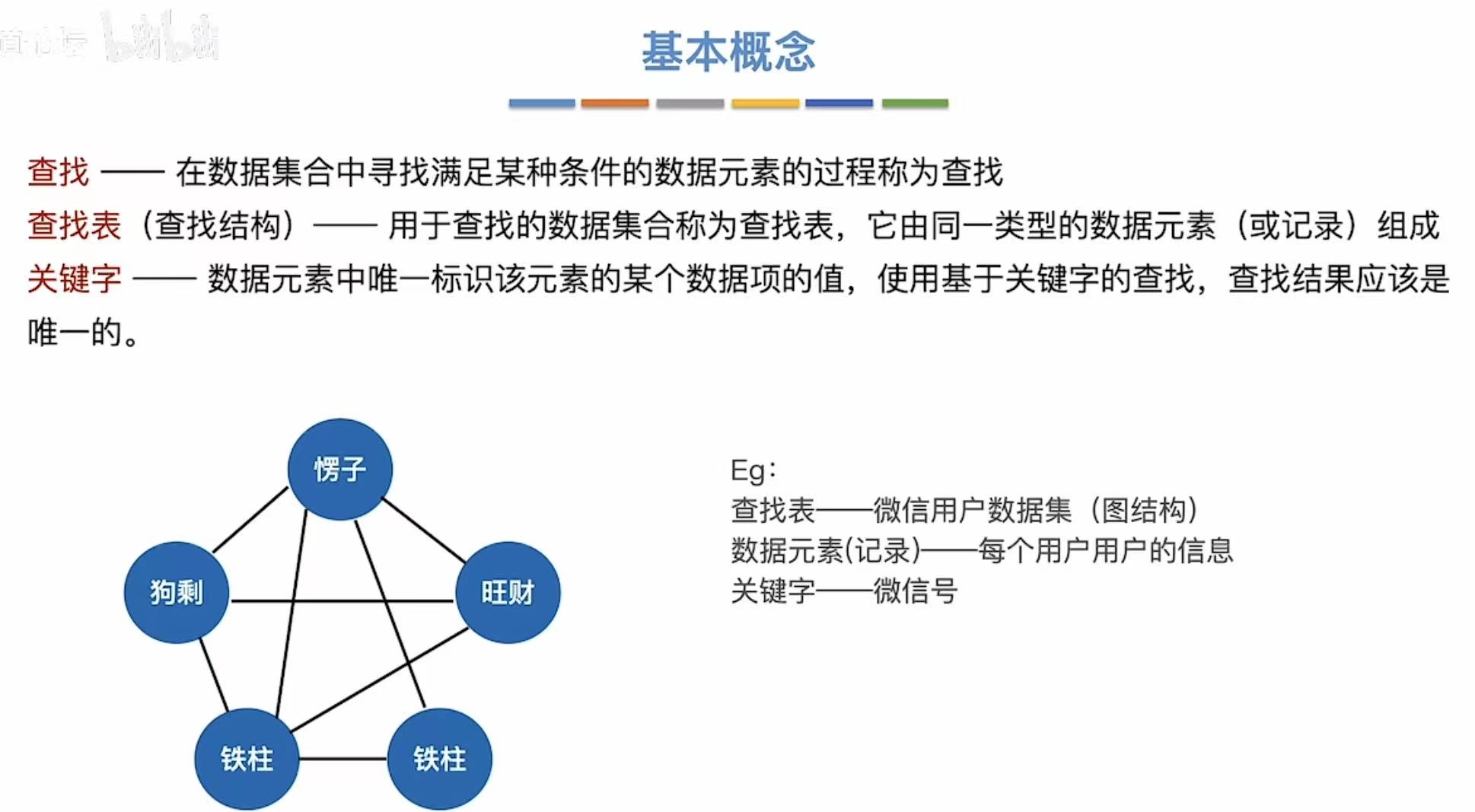
也可以是下图中的图的形式：

2. 常见操作

  • 静态查找表：只进行查找操作。
  • 动态查找表 ：查找+插入+删除

3. 评价指标

  • 查找长度：对比次数。---->和关键字对比
  • 平均查找长度 ：对比次数的平均值。---->和关键字对比

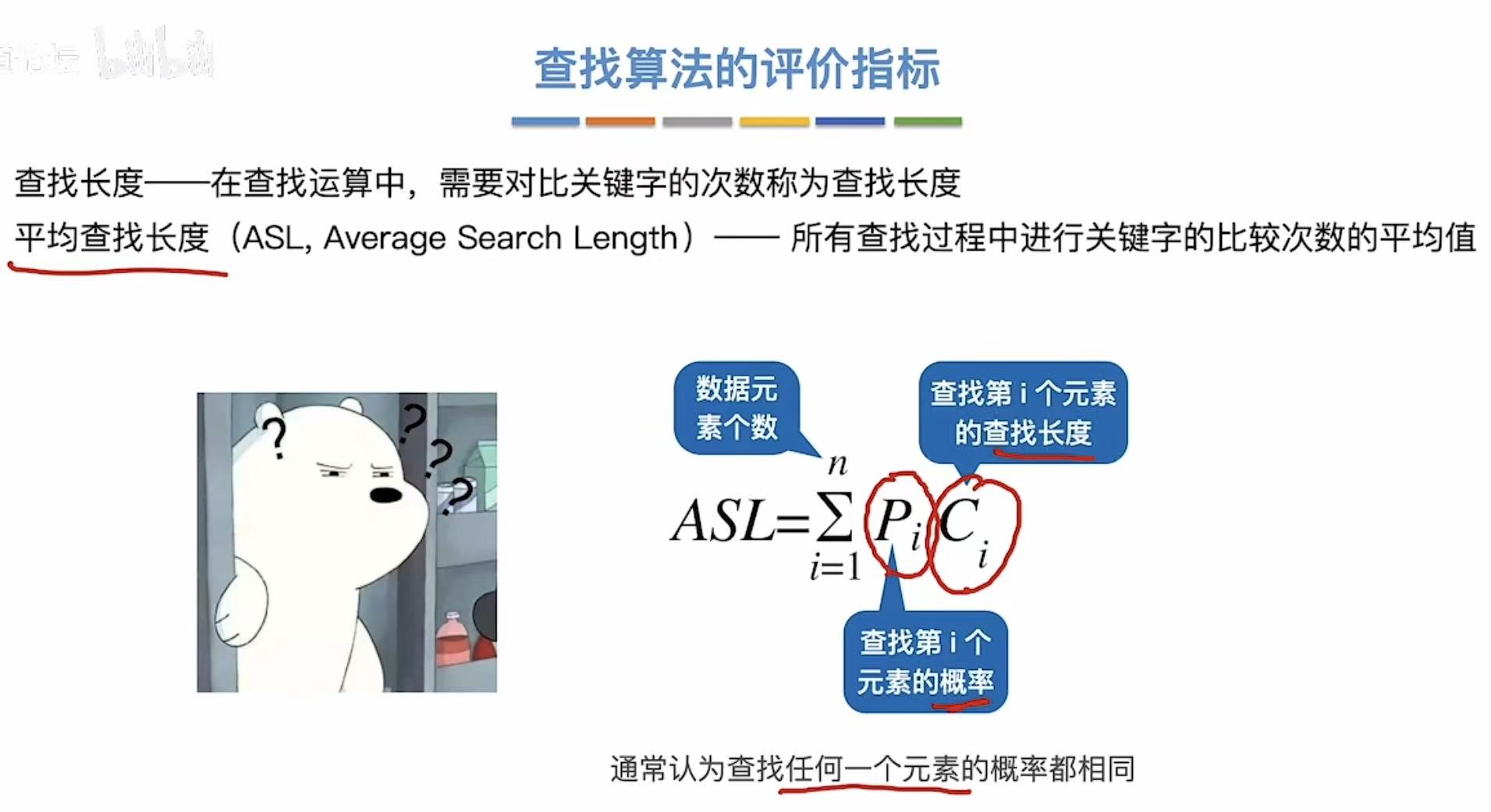
    查找成功-->树上刚好有的数字-->层数*当前层数的数字个数的和 ；因为要平均值，所以还要除以全部的数字个数
  • 左侧ASL：第一层11；第二层2 2；第三层34；第四层41；-->前一个数字是层数，后一个数字是个数
  • 右侧ASL：同上，前一个数字是层数，后一个数字是个数

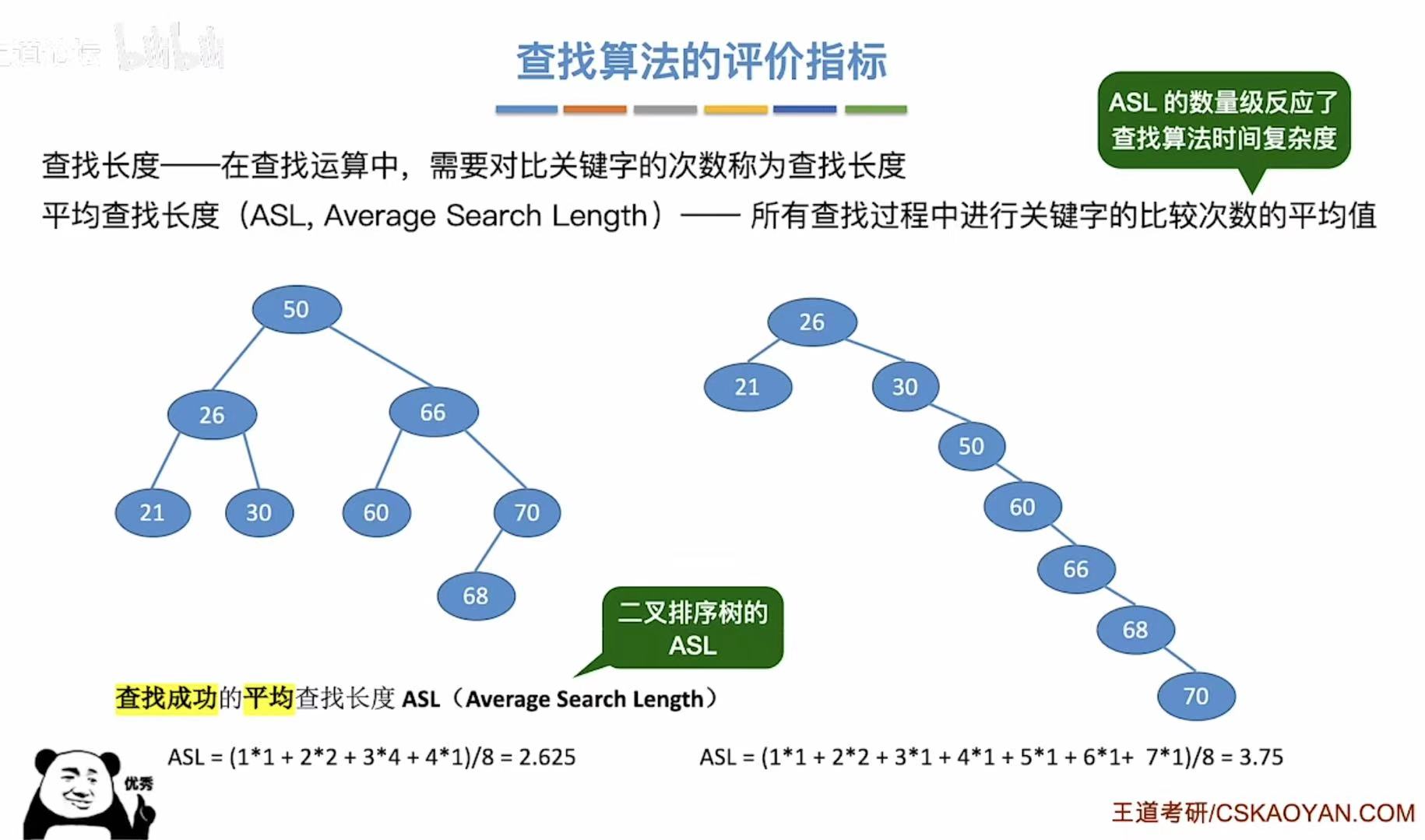
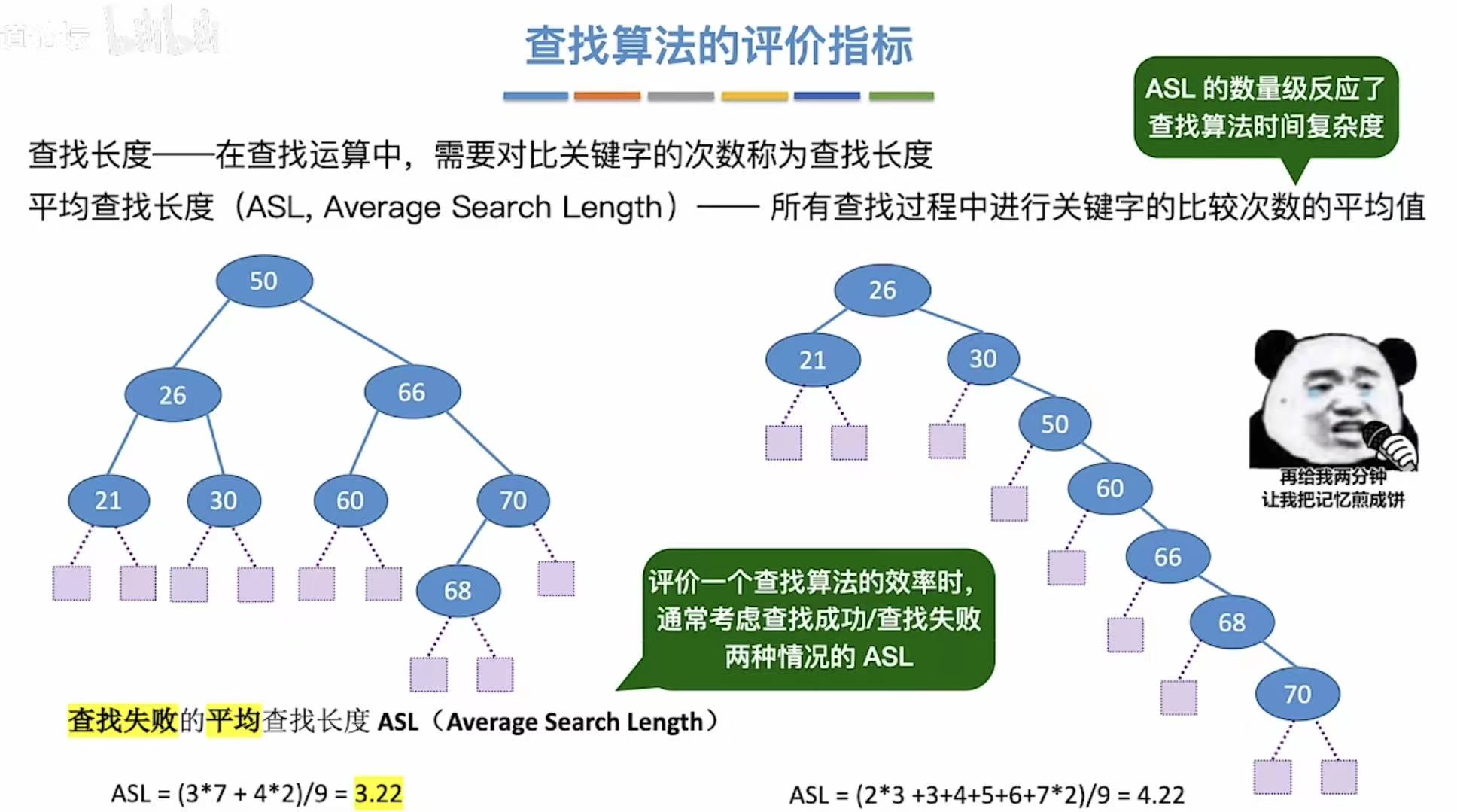
    查找失败-->树上没有的数字-->就是每个数字下面的空叶子节点（图中紫色方框）
  • 左侧ASL：第三层37；第四层4 2；-->因为是对比关键字，所以层数以树中有的数字 为标准

4. 小结

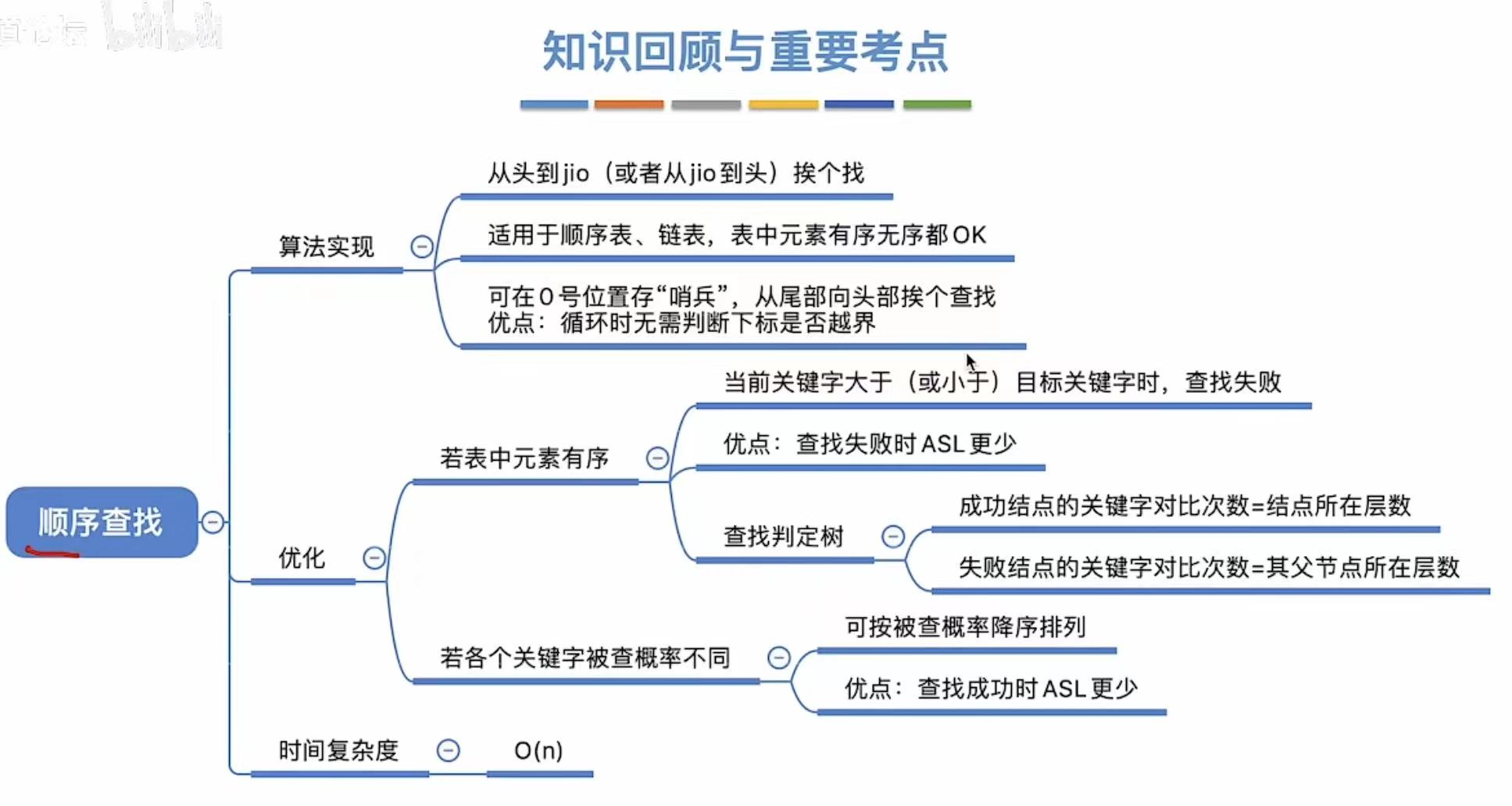
顺序查找

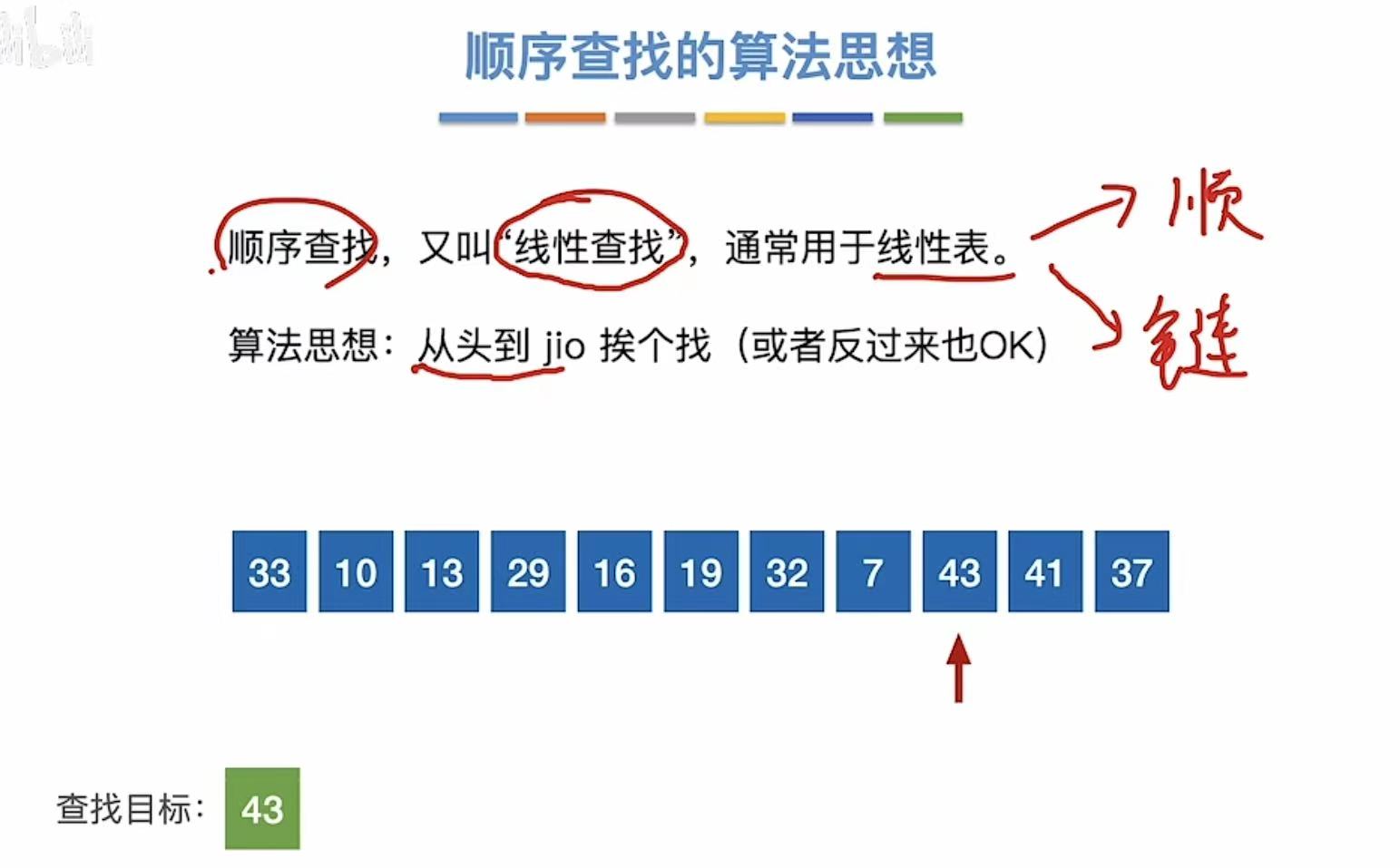
1. 算法思想

其实就是从头找到尾，从左找到右，毫无技巧，就是硬找。

2. 算法实现

2.1 普通实现

java 复制代码 
// 定义顺序表的数据结构（静态或动态数组）
typedef struct {
    ElemType *elem;       // 指向动态数组的基地址（存储实际元素）
    int TableLen;         // 表中当前元素的个数（长度）
} SSTable;                // SSTable：顺序查找表（Sequential Search Table）

// 顺序查找函数：在顺序表 ST 中查找关键字 key
// 返回值：若找到，返回元素下标；否则返回 -1
int Search_Seq(SSTable ST, ElemType key) {
    int i;                 // 循环变量，用于遍历表中的元素

    // 从第一个元素开始，依次比较每个元素与 key
    // 条件：i < ST.TableLen 且 ST.elem[i] != key
    // 即：只要还没到表尾，并且当前元素不等于 key，就继续往后找
    for (i = 0; i < ST.TableLen && ST.elem[i] != key; ++i);

    // 查找结束后判断结果：
    // 如果 i == ST.TableLen，说明遍历完所有元素都没找到 → 失败
    // 否则 i 是找到的位置 → 成功
    return i == ST.TableLen ? -1 : i;
}


2.2 哨兵实现

就是在下标为0的数组中存入自己需要查找的数字。

  • 成功：从后往前遍历，没遍历到0的时候就找到自己要找的数字就是成功了。
  • 失败：从后往前遍历，遍历到0才找到自己要找的数字，因为这个还是自己存的，所以直接失败。
java 复制代码 
// 定义顺序表的数据结构（静态或动态数组）
typedef struct {
    ElemType *elem;       // 指向动态数组的基地址（存储实际元素）
    int TableLen;         // 表中当前元素的个数（长度）
} SSTable;                // SSTable：顺序查找表（Sequential Search Table）

// 哨兵优化的顺序查找函数
// 通过在表头设置"哨兵"，避免每次循环判断是否越界
int Search_Seq(SSTable ST, ElemType key) {
    // 将要查找的关键字 key 放入表头位置（即 elem[0]），作为"哨兵"
    // 这样可以保证一定能找到 key，从而简化循环条件
    ST.elem[0] = key;     // 🔹 "哨兵"设置：把目标值放在开头

    int i;                 // 循环变量，用于从后往前遍历

    // 从最后一个元素开始，向前查找，直到遇到 key
    // 因为已经设置了哨兵，所以一定能在某个位置找到 key
    // 不需要再判断 i >= 0，直接用 ST.elem[i] != key 即可
    for (i = ST.TableLen; ST.elem[i] != key; --i);

    // 返回下标：如果原表中有 key，则返回正确下标；
    // 如果没有，则由于哨兵存在，会返回 0（但原表中没有 key，所以返回 0 是错误的？）
    return i;
}

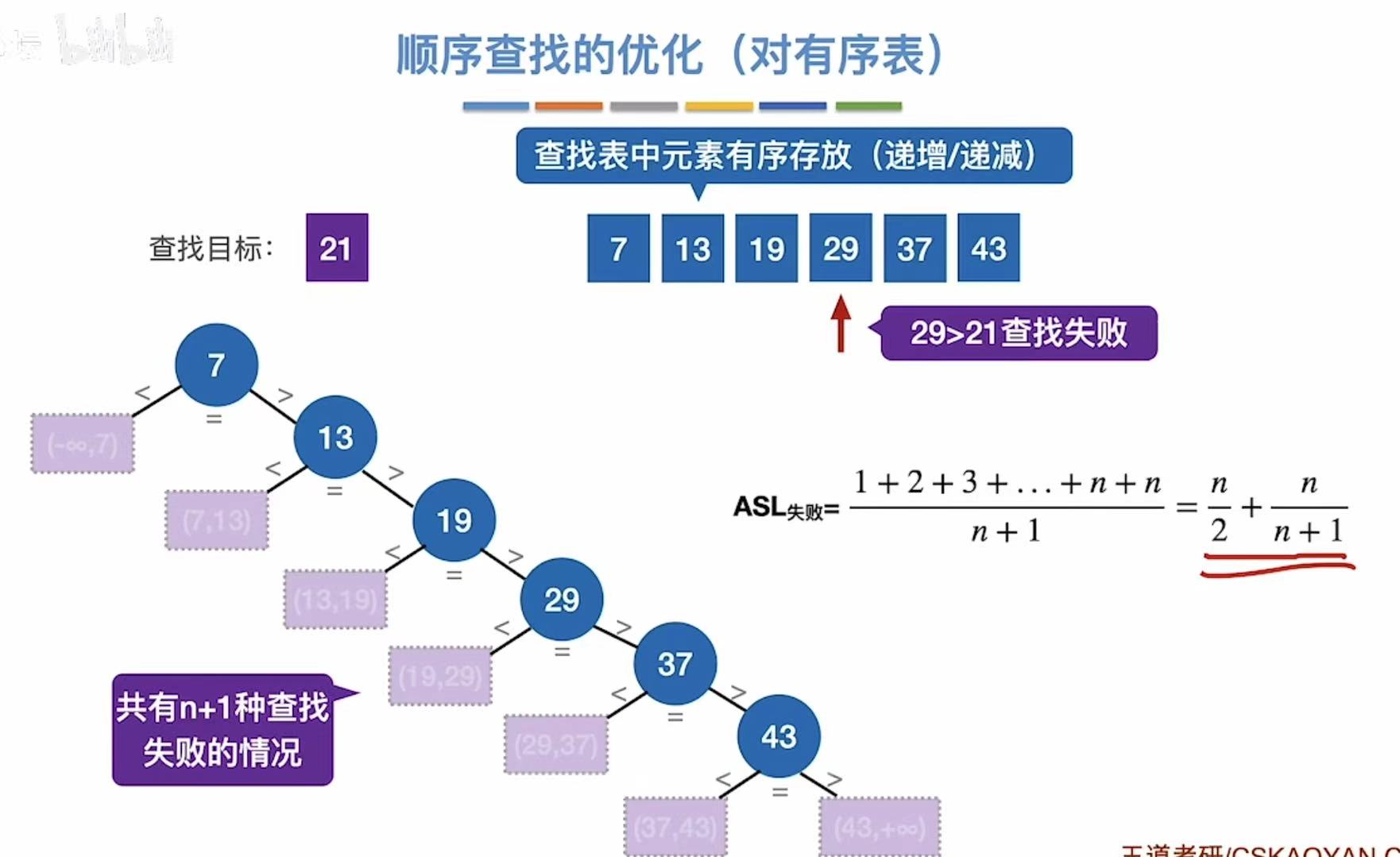
3. 算法优化

  • 成功ASL：可能1次成功、2次成功...n次成功，然后取平均值
  • 失败ASL：遍历到下标为0的数组，就是n+1次对照，就是失败了

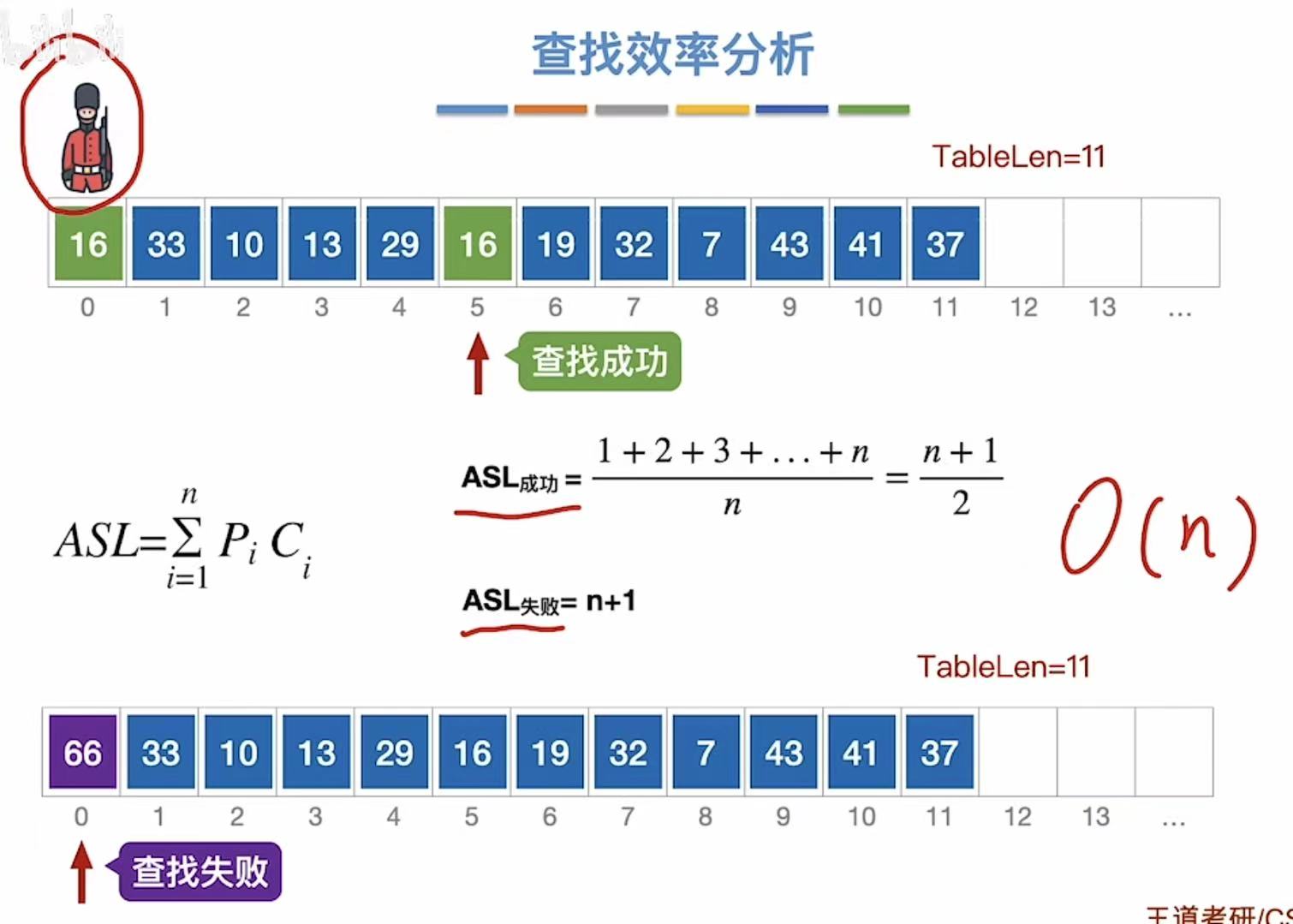
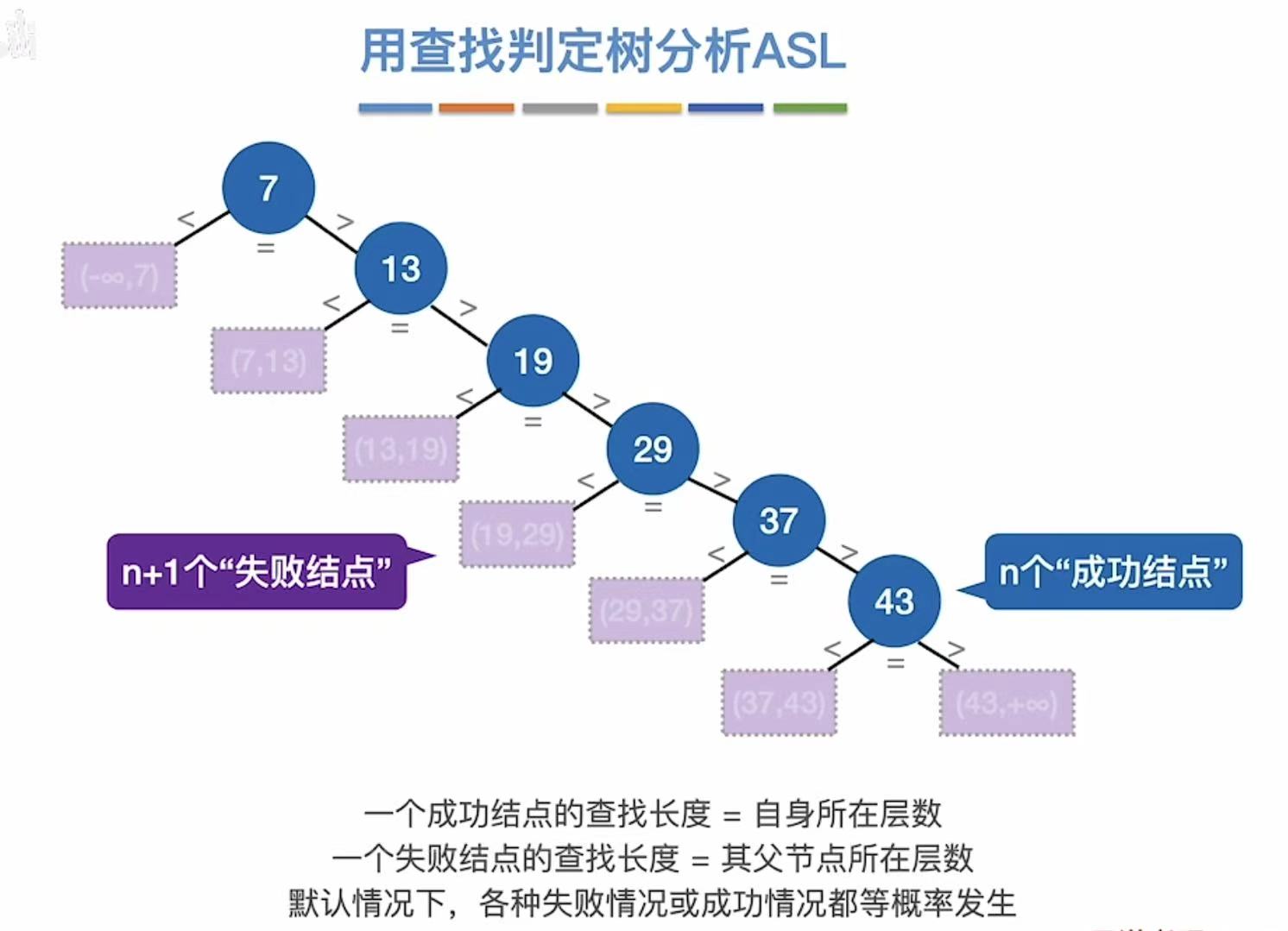
3.1 有序排列

优化：把乱序的数字有序排列，变成查找判定树，因为有序就知道自己数字的大小，避免全部遍历

失败ASL：

  • 分子：比如想找6，刚遍历到7，遍历一次就知道没有这个数，查找失败；以此类推，得到分子；
  • 分母：一共有n+1种失败情况

    小总结：

3.2 被查概率不同--排序

如果有的数字被查找的概率高，有的很低，就可以把概率高的数字排在前面，便于经常查找

4. 小结

折半查找

1. 算法思想

用于有序表的查找。

  • low：指向下标最小的数
  • high：指向下标最大的数
  • mid：指向(low+high)/2的下标的数（奇数除二，小数取低：11/2=5.5，取5）

1.1 查找33

查找33：

  • mid和33对比，mid小
  • low指向mid+1
  • mid继续(low+high)/2
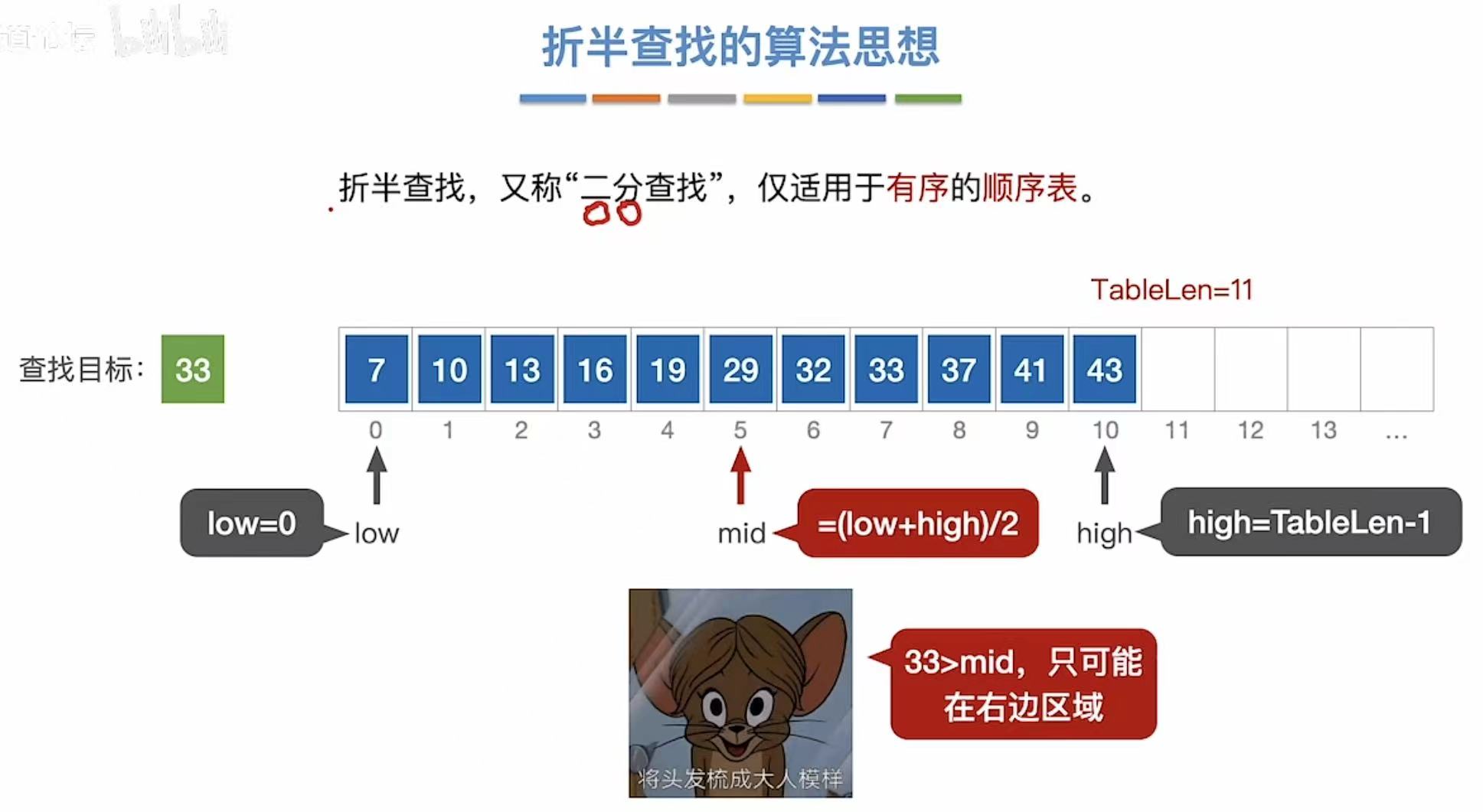
  • mid和33对比，mid大
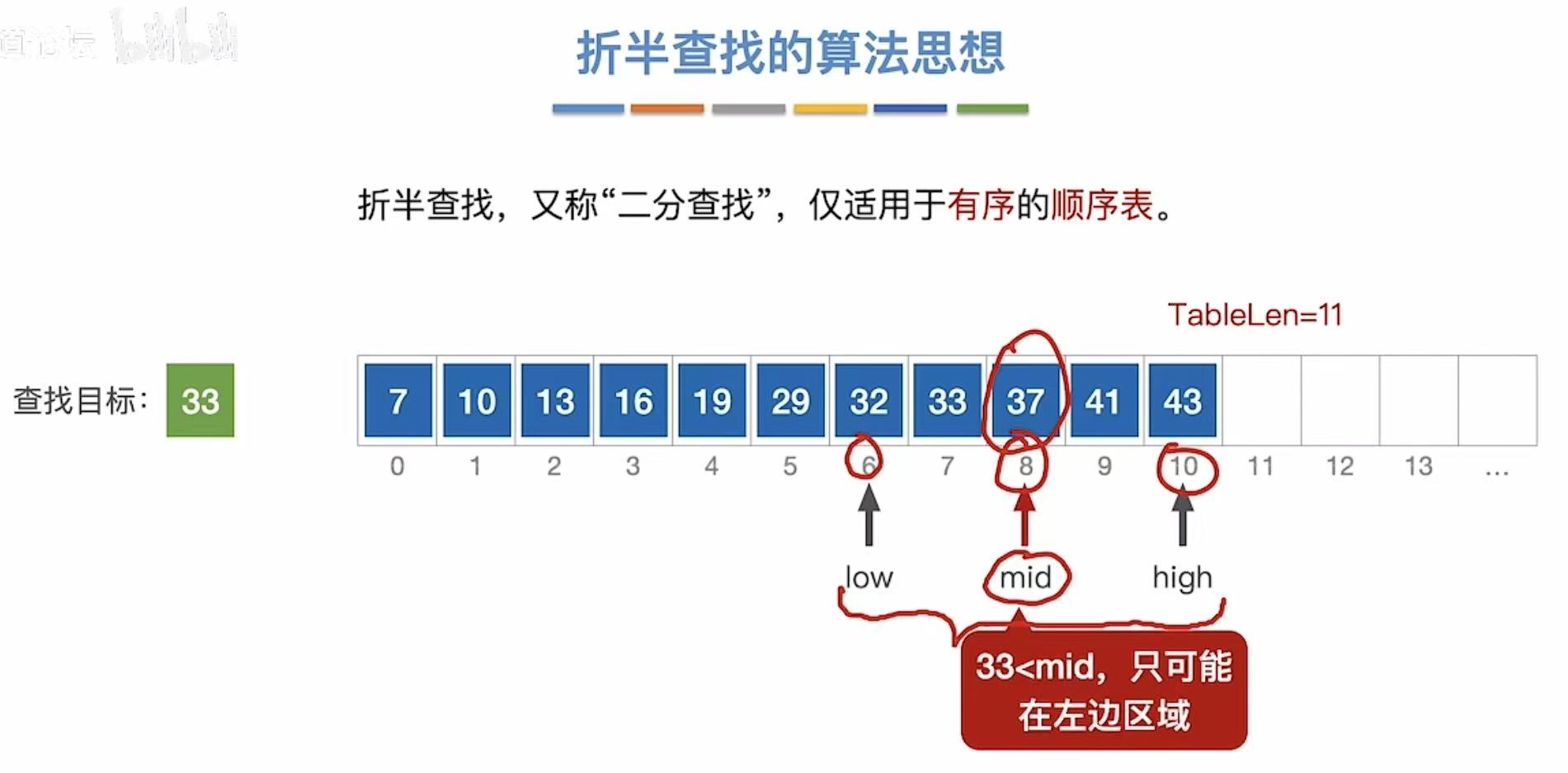
  • high指向mid-1
  • mid继续(low+high)/2-->(6+7)/2=6.5，取6
  • mid和33对比，mid小
  • low指向mid+1
  • mid继续(low+high)/2
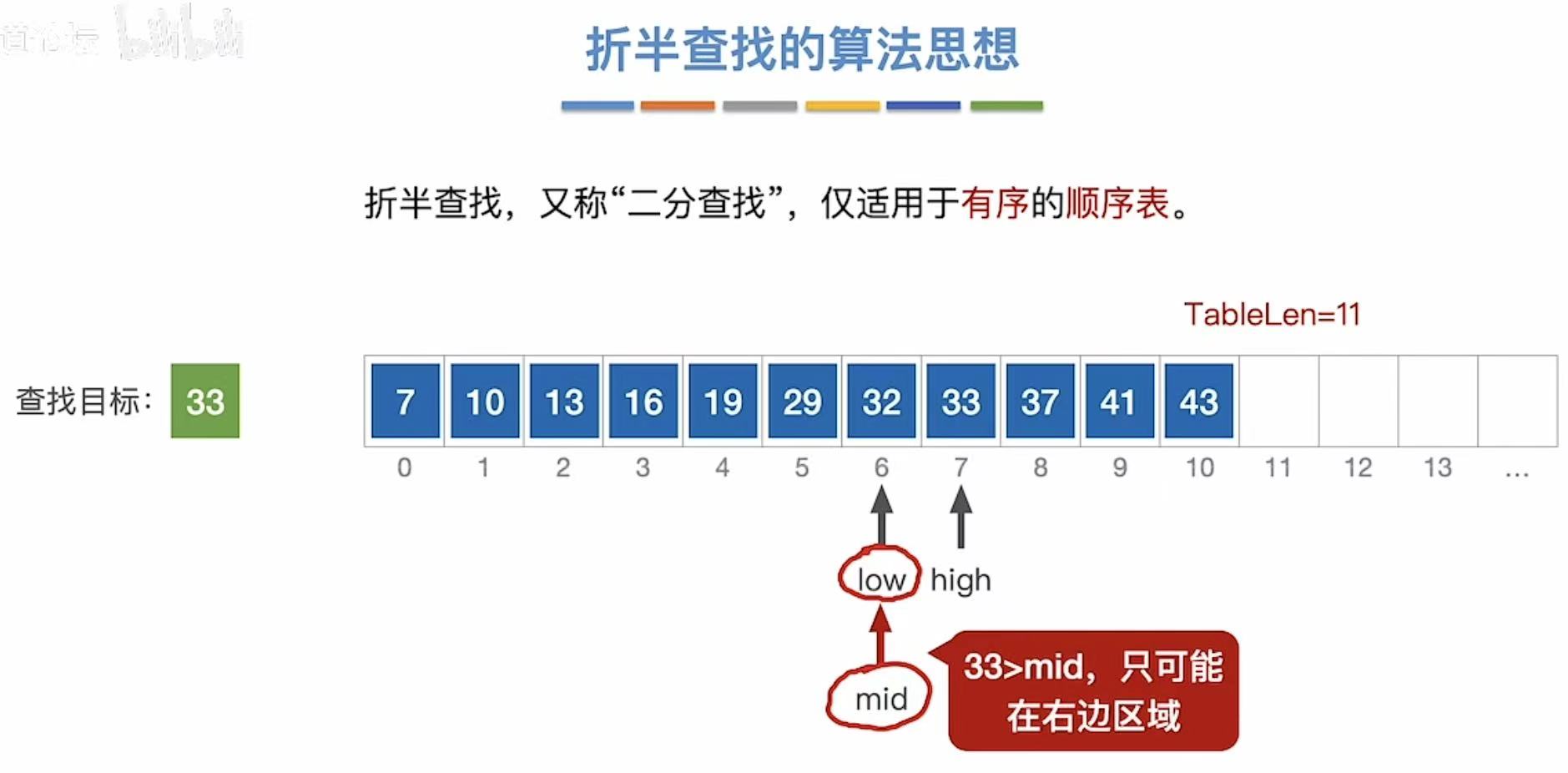
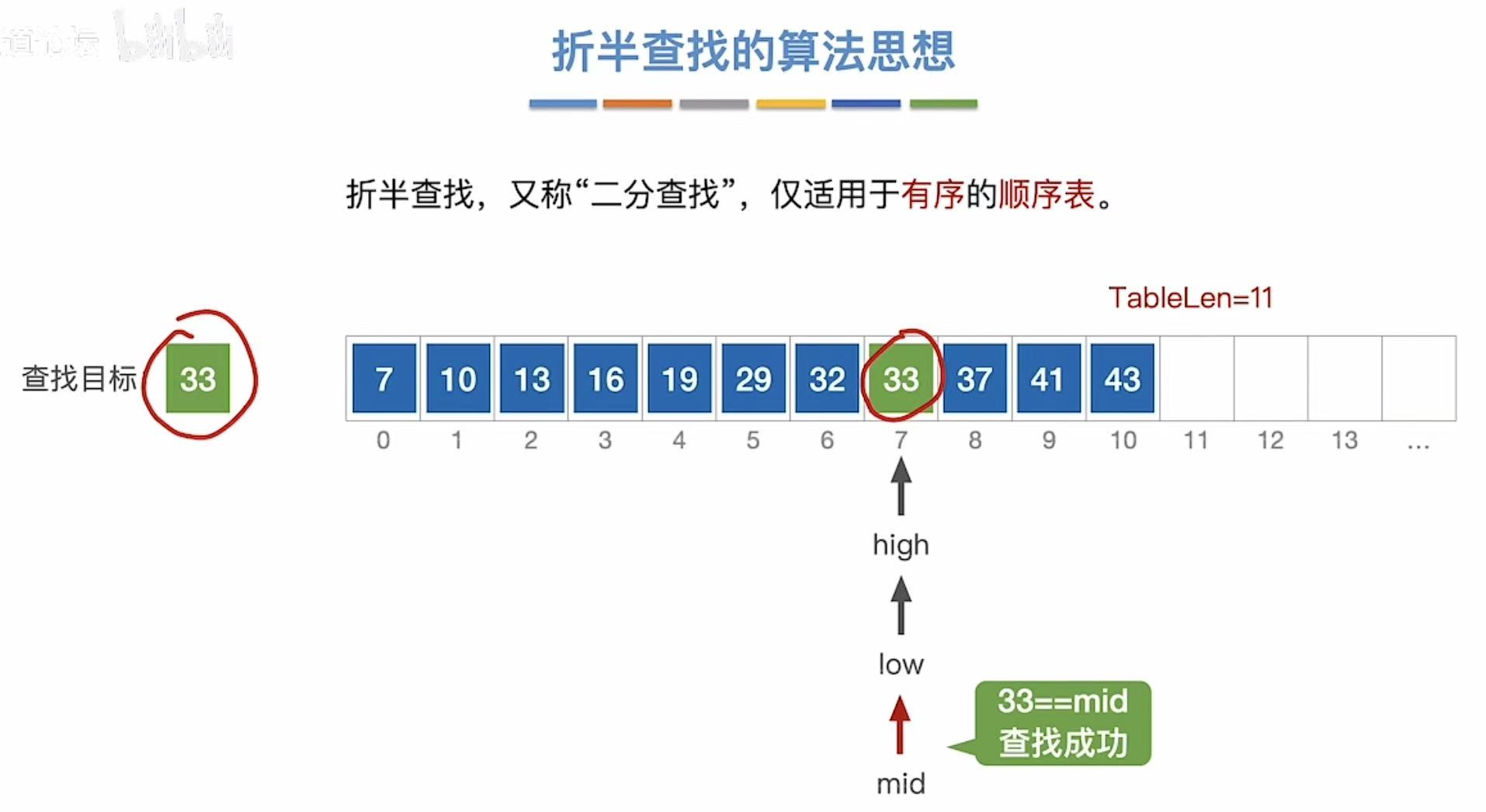
  • 最后三个指针同时指向下标7
  • 和33比，正好相等，查找成功

1.2 查找12





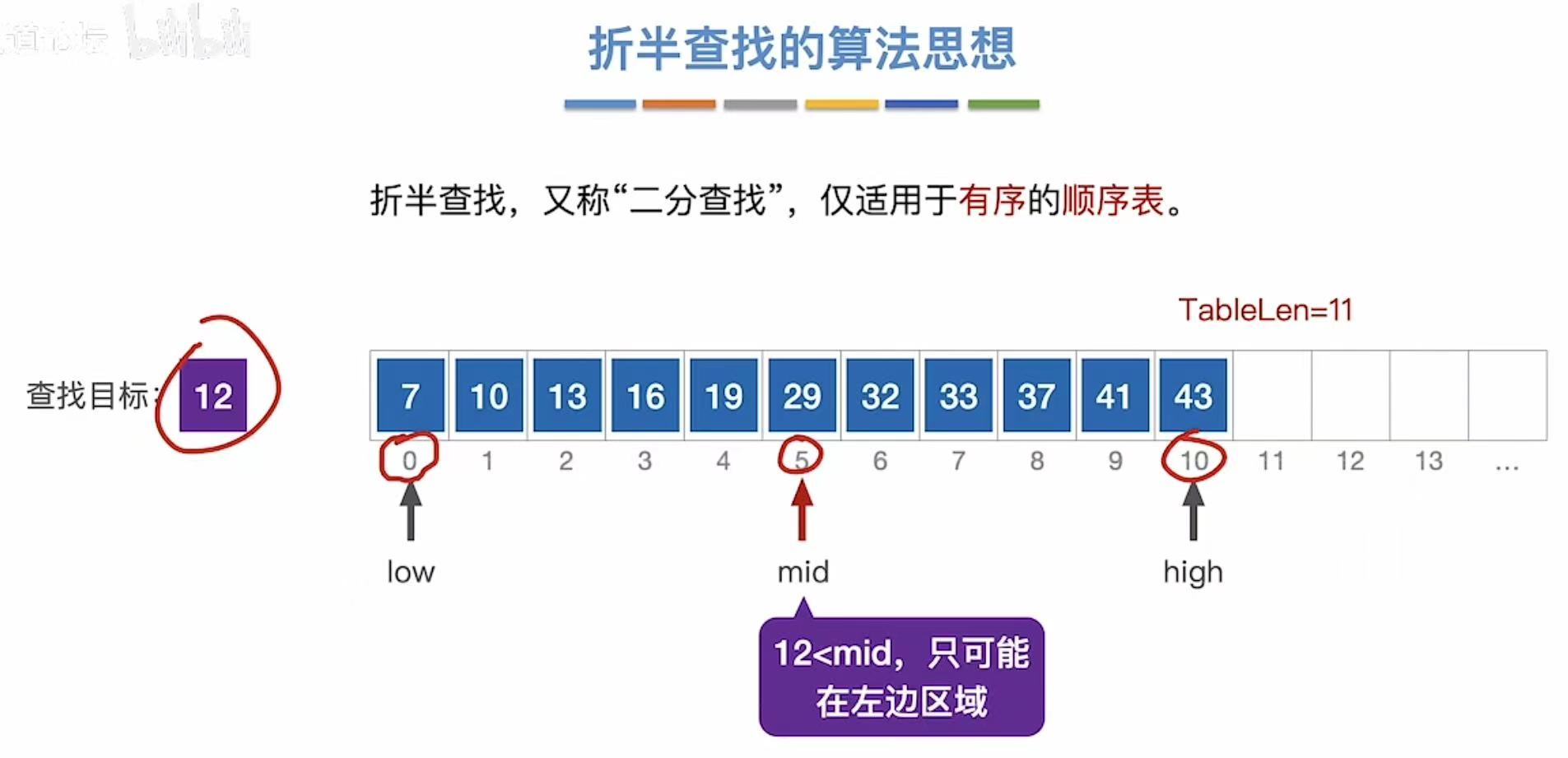
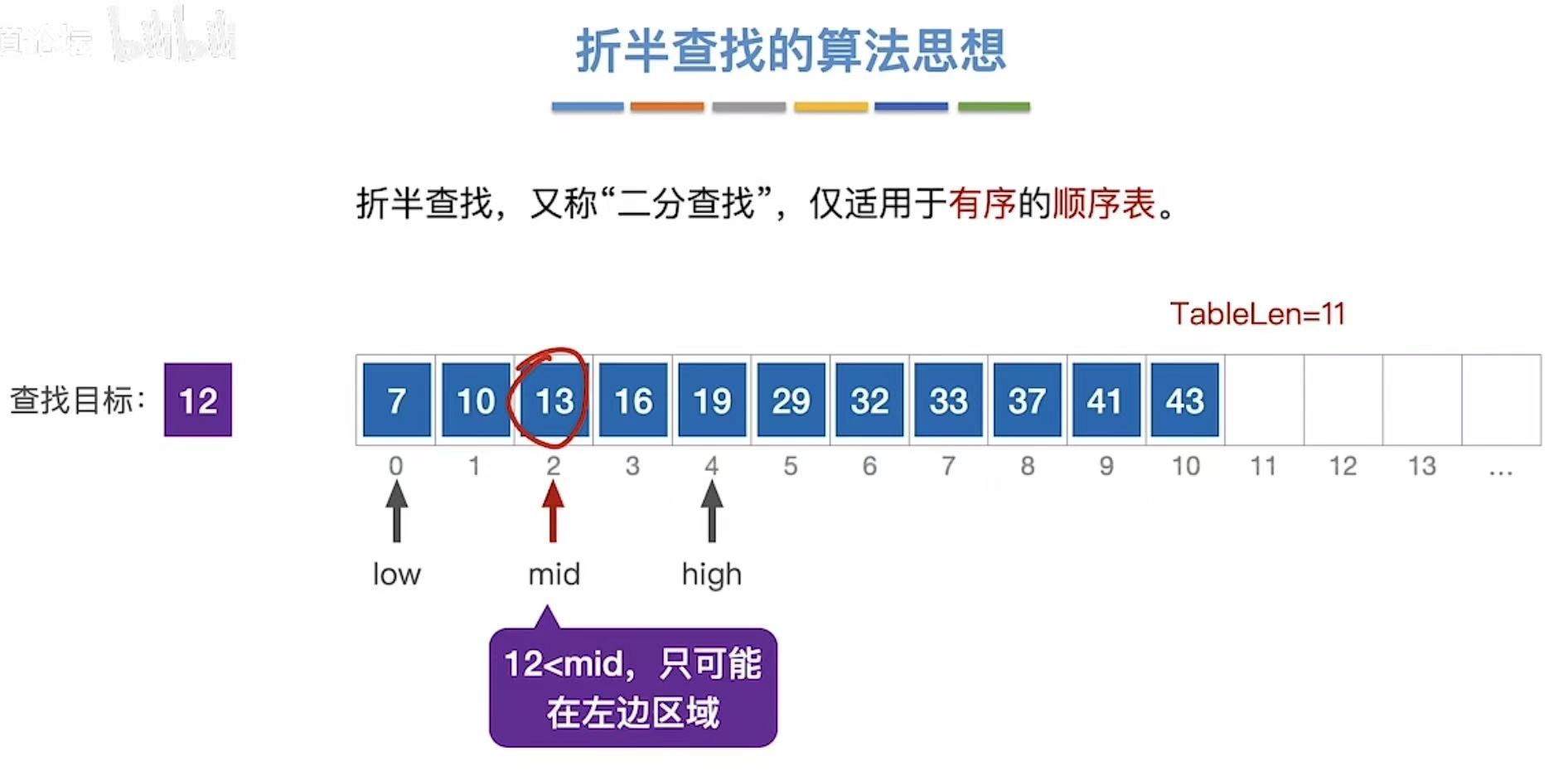
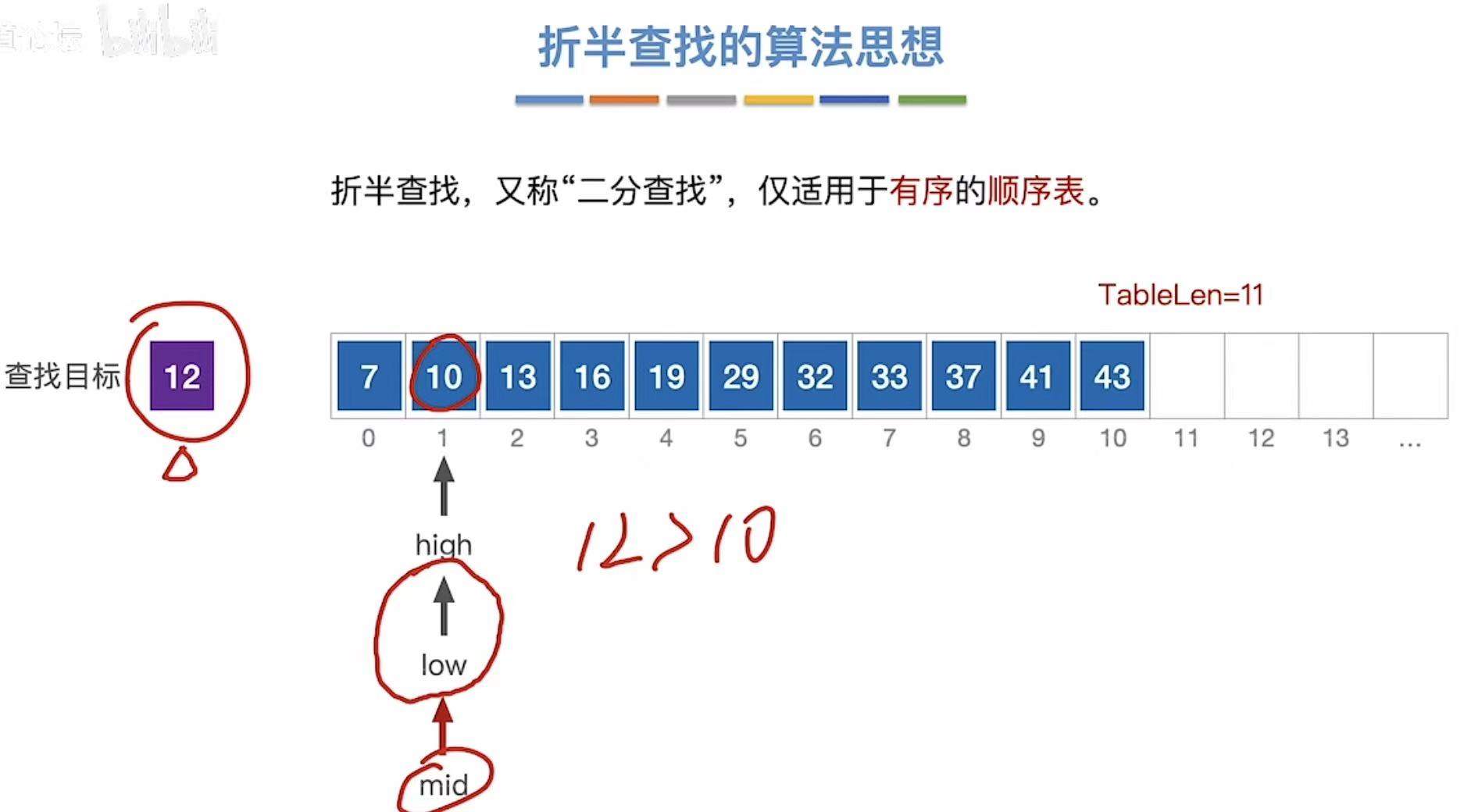
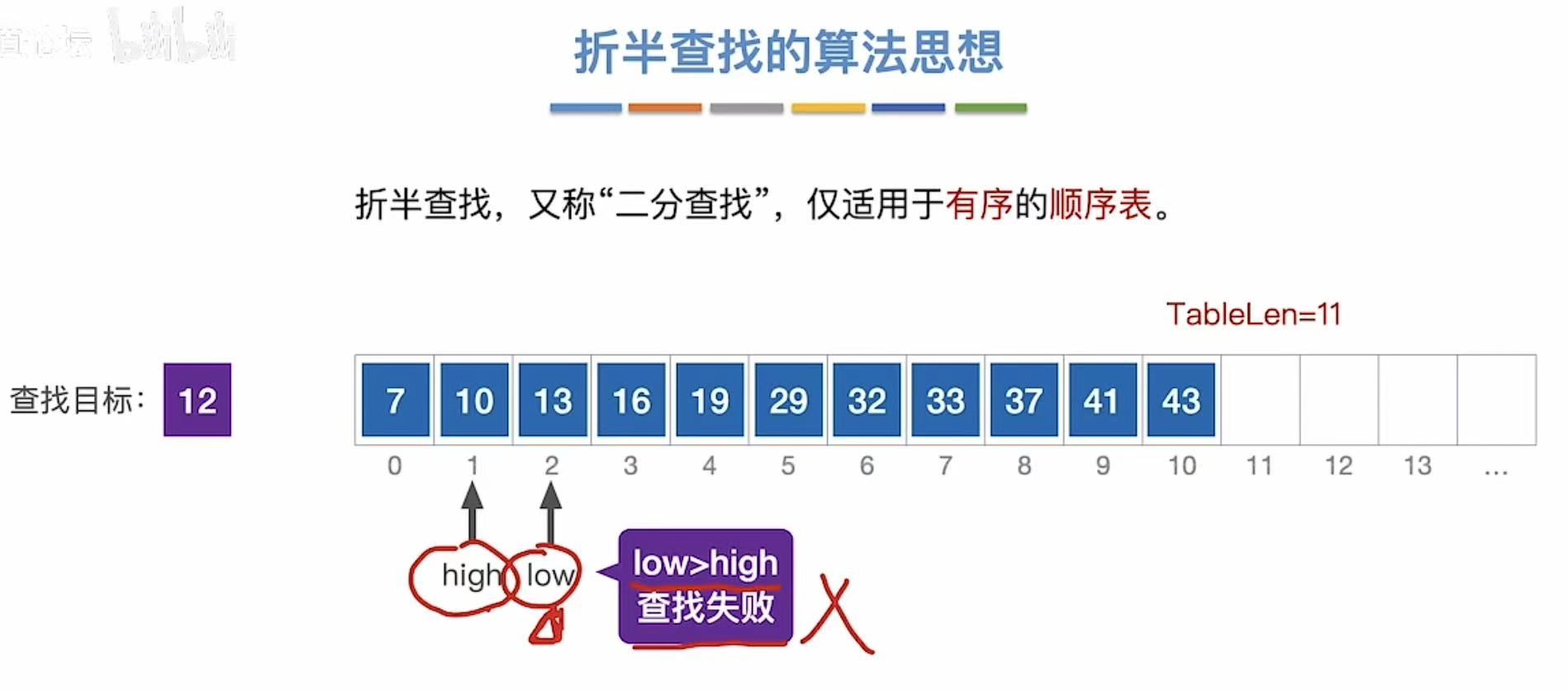
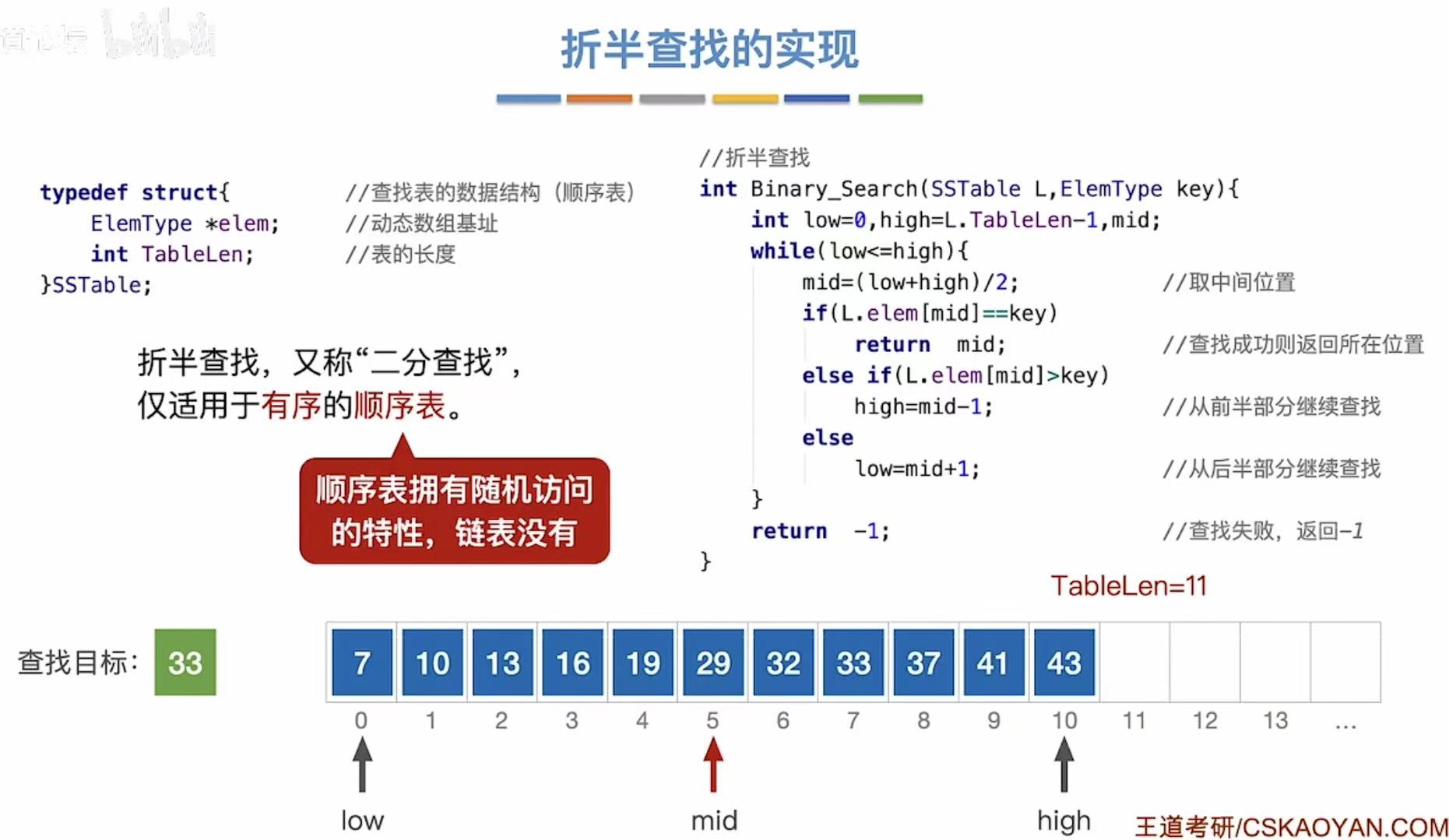
2. 算法实现

java 复制代码 
// 定义顺序表的数据结构（静态或动态数组）
typedef struct {
    ElemType *elem;       // 指向动态数组的基地址（存储实际元素）
    int TableLen;         // 表中当前元素的个数（长度）
} SSTable;                // SSTable：顺序查找表（Sequential Search Table）

// 折半查找函数：在有序顺序表 L 中查找关键字 key
// 返回值：若找到，返回元素下标；否则返回 -1
int Binary_Search(SSTable L, ElemType key) {
    int low = 0;           // 左边界：初始为第一个元素的下标
    int high = L.TableLen - 1; // 右边界：初始为最后一个元素的下标
    int mid;               // 中间位置的下标

    // 当左边界 <= 右边界时，继续查找（区间非空）
    while (low <= high) {
        mid = (low + high) / 2;  // 计算中间位置（向下取整）

        // 如果中间元素等于目标值，查找成功
        if (L.elem[mid] == key) {
            return mid;           // 返回该元素的下标
        }
        // 如果中间元素大于目标值，说明目标在左半部分
        else if (L.elem[mid] > key) {
            high = mid - 1;       // 调整右边界为 mid-1
        }
        // 如果中间元素小于目标值，说明目标在右半部分
        else {
            low = mid + 1;        // 调整左边界为 mid+1
        }
    }

    // 循环结束说明未找到目标值，返回 -1
    return -1;
}


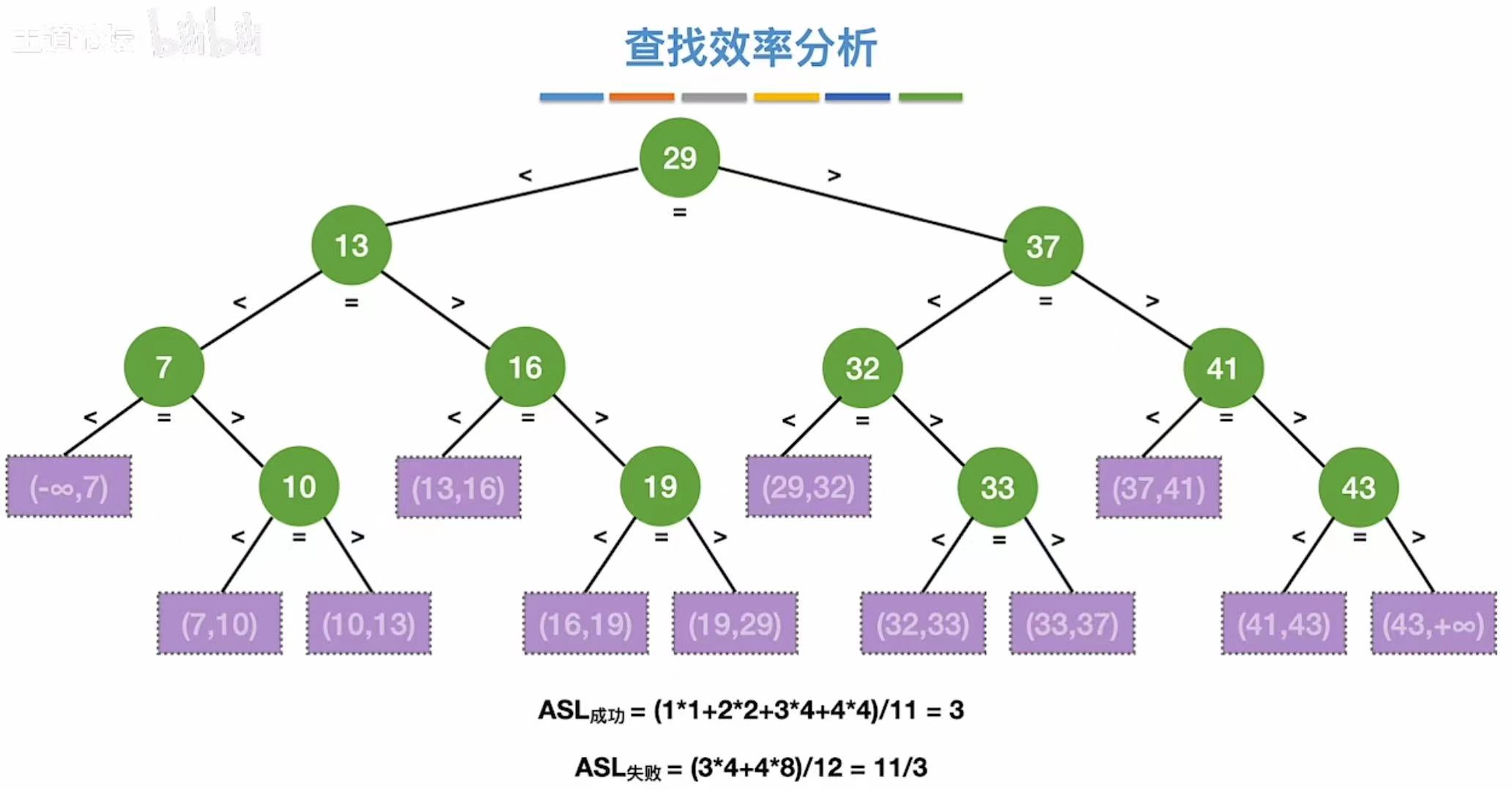
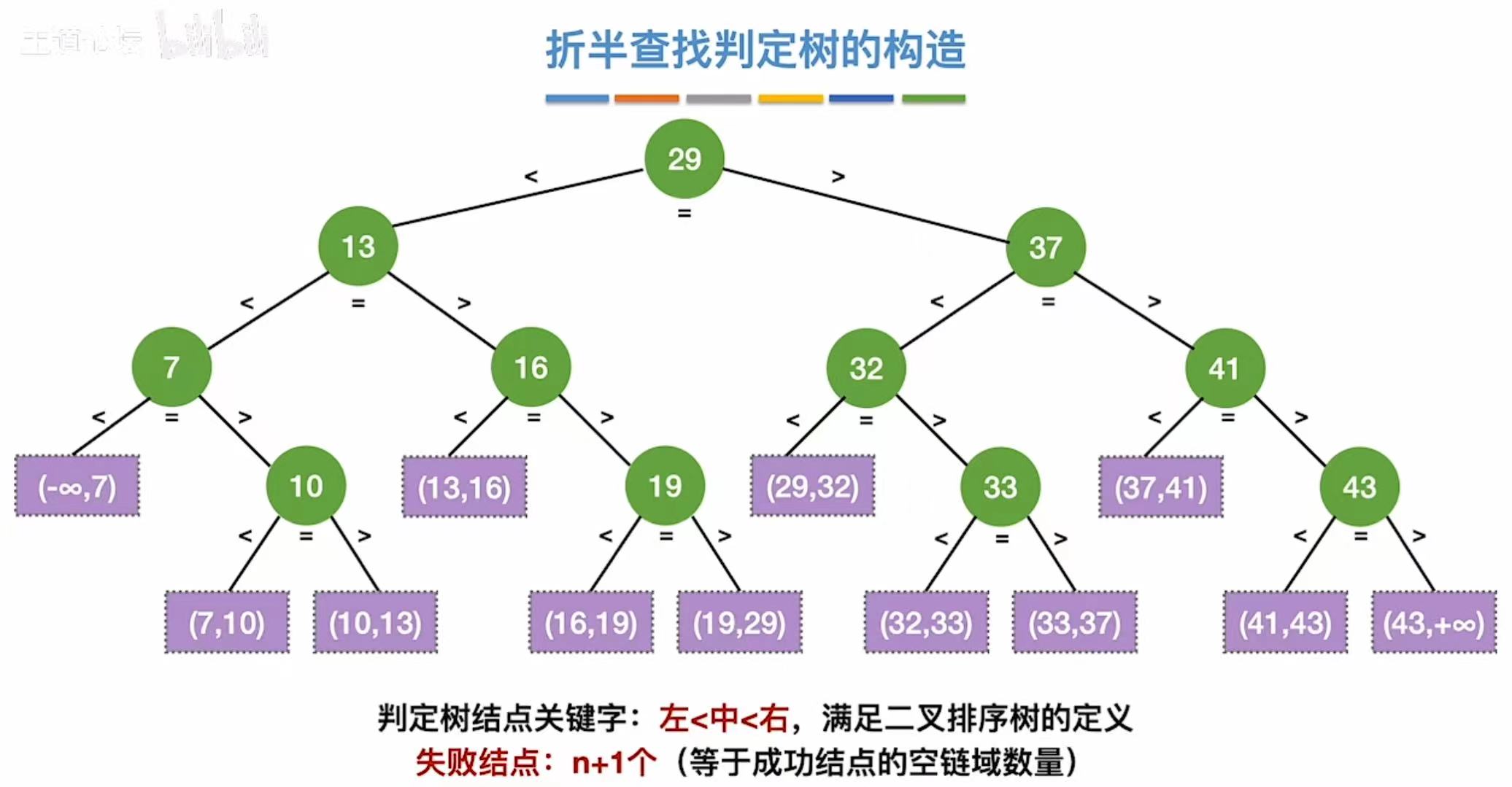
3. 查找判定树

3.1 奇数个元素

正常情况下：

奇数个（因为有下标0），所以除2正好能平分

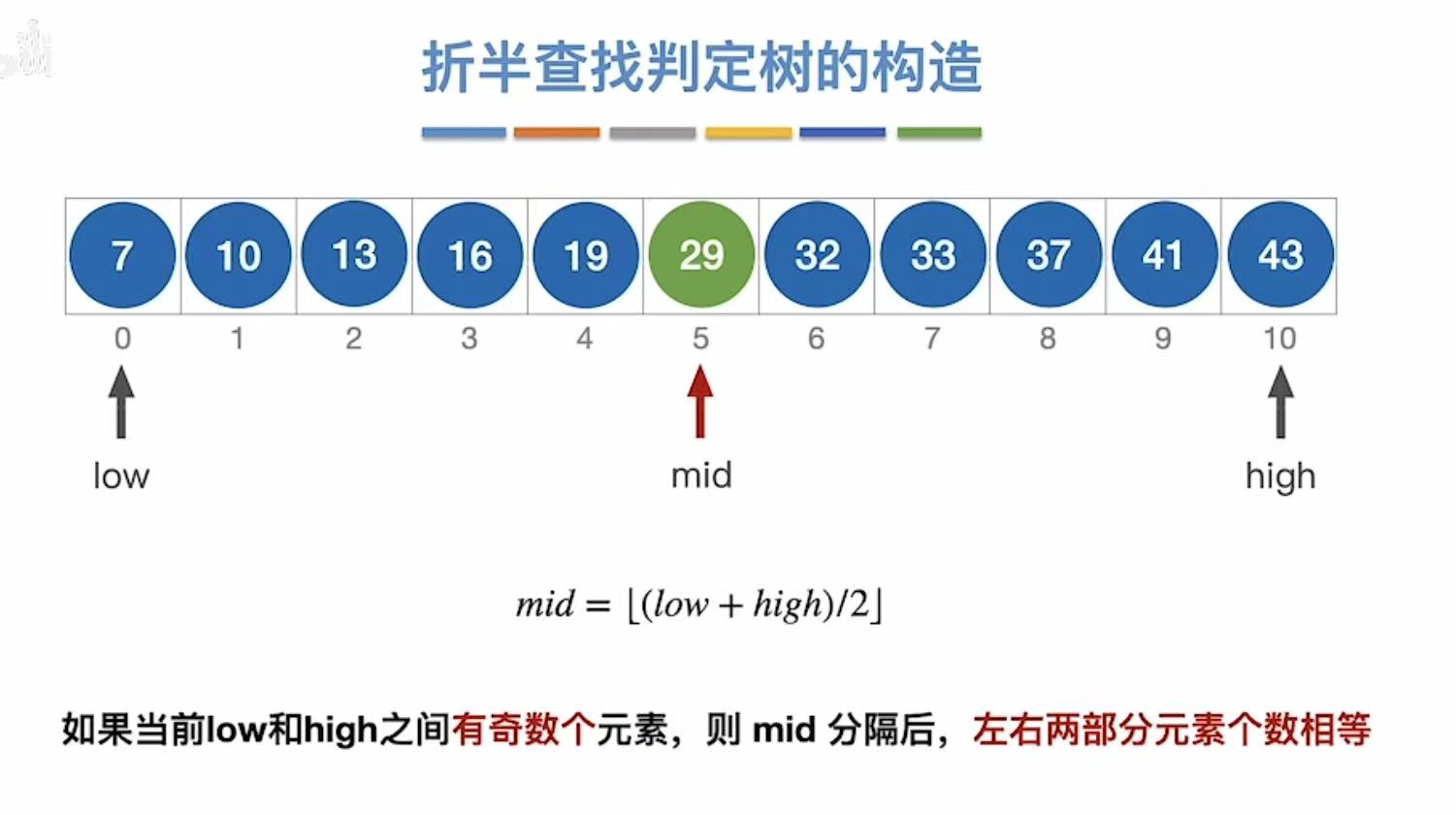
暂时可以分成这样：

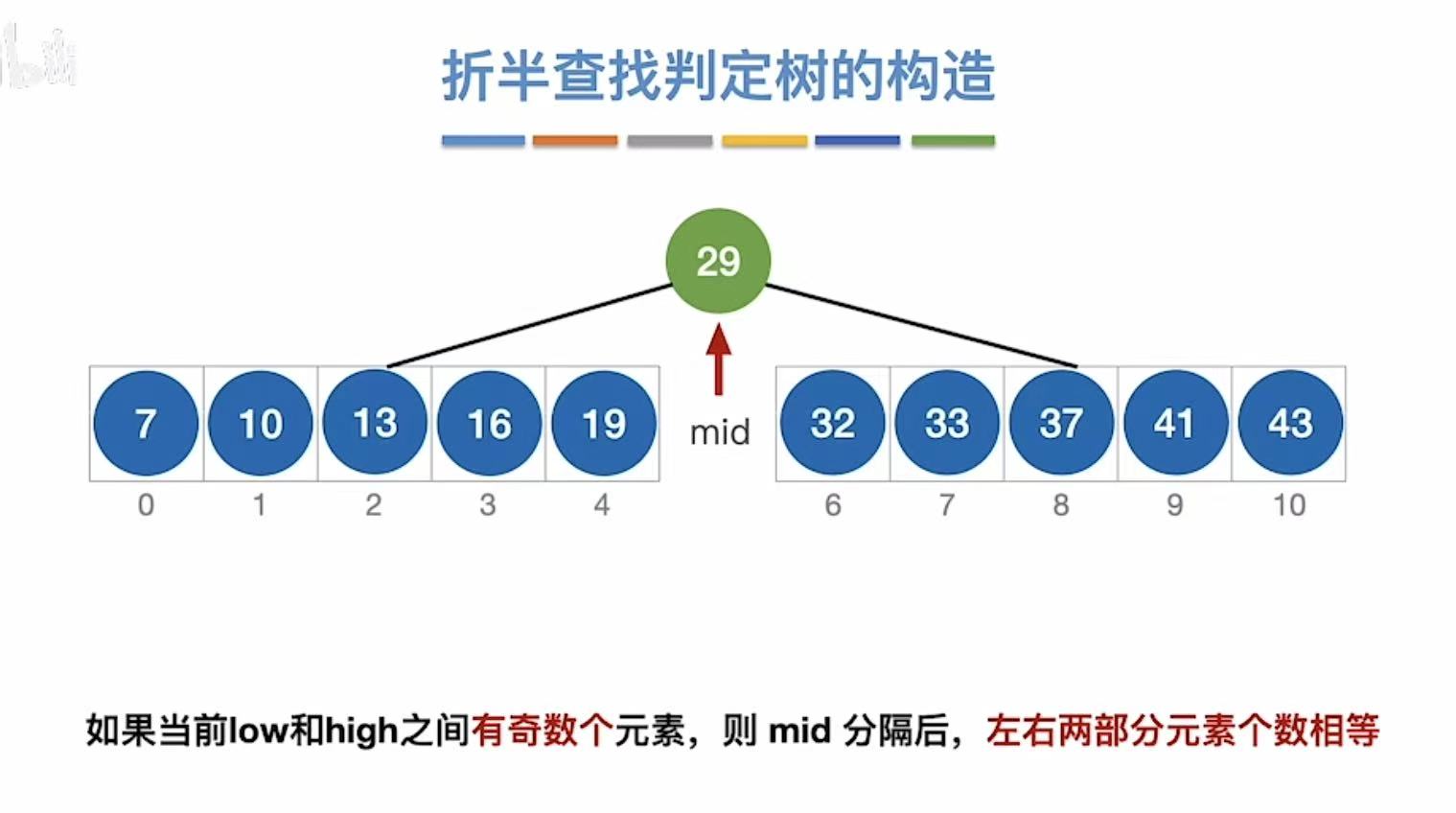
3.2 偶数个元素

偶数个的话，因为我们取低，所以左边的元素会比右边的元素少

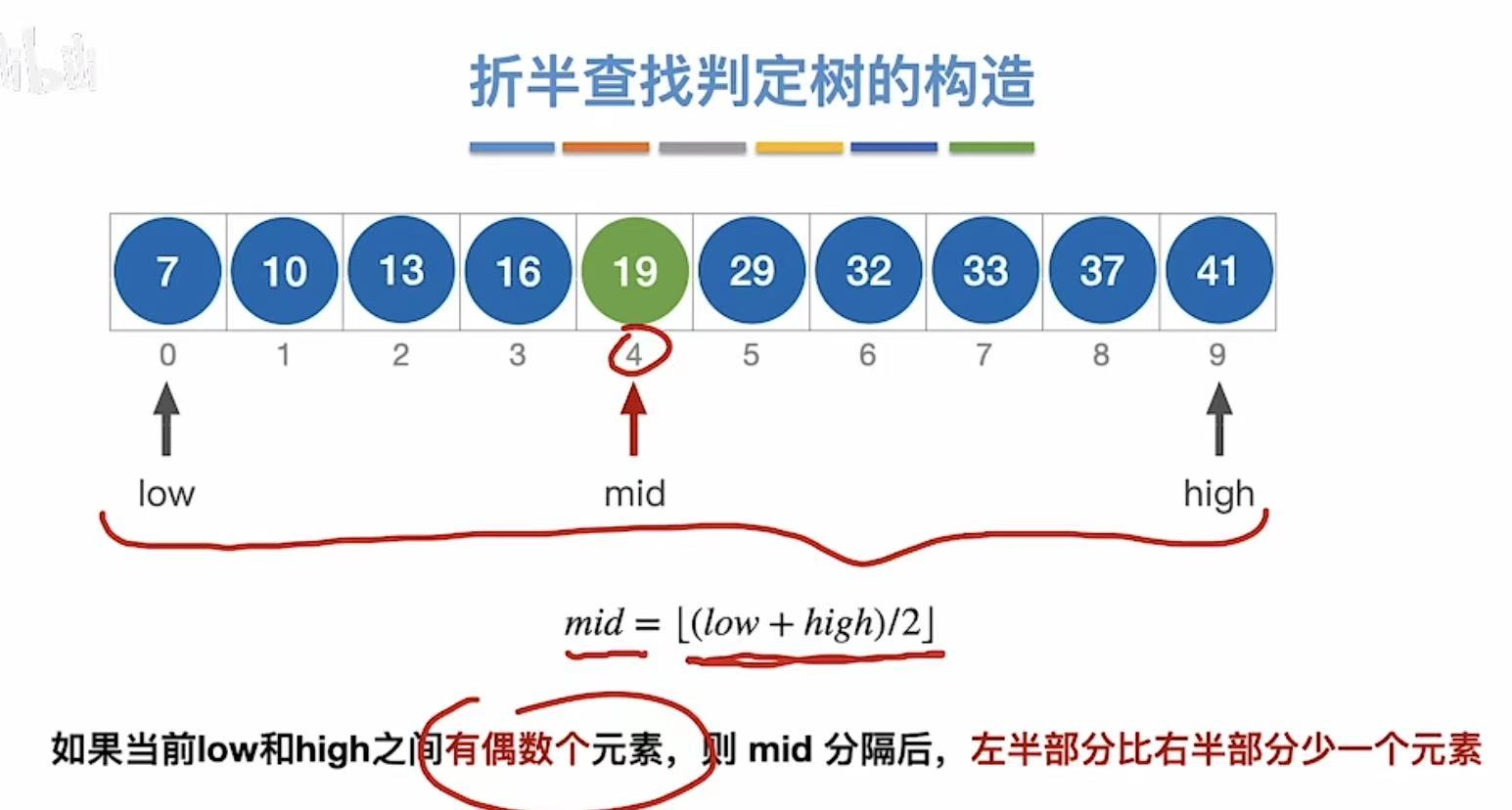
暂时可以分成这样

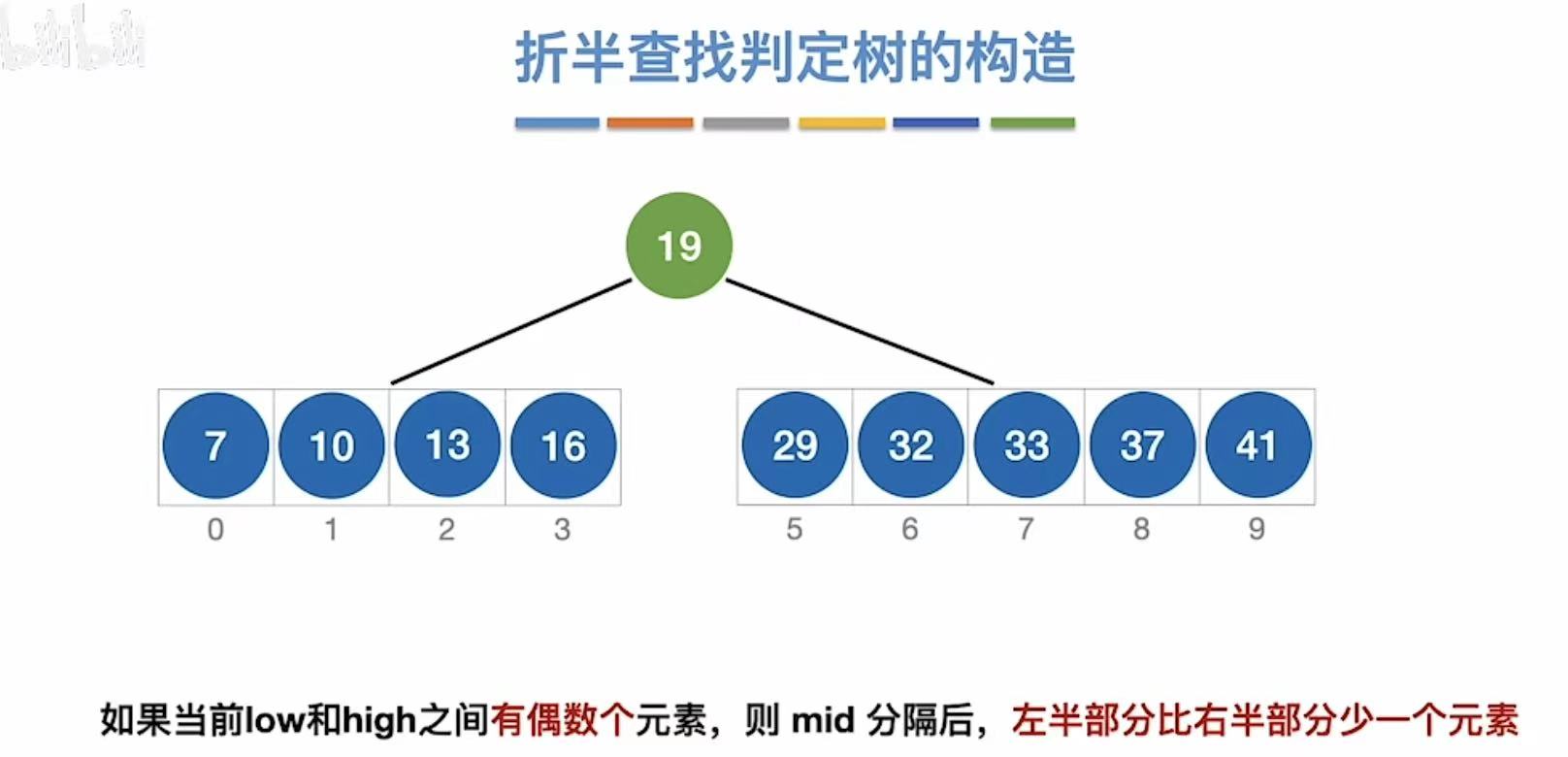
然后继续左右子树划分，得到第二层的结点：

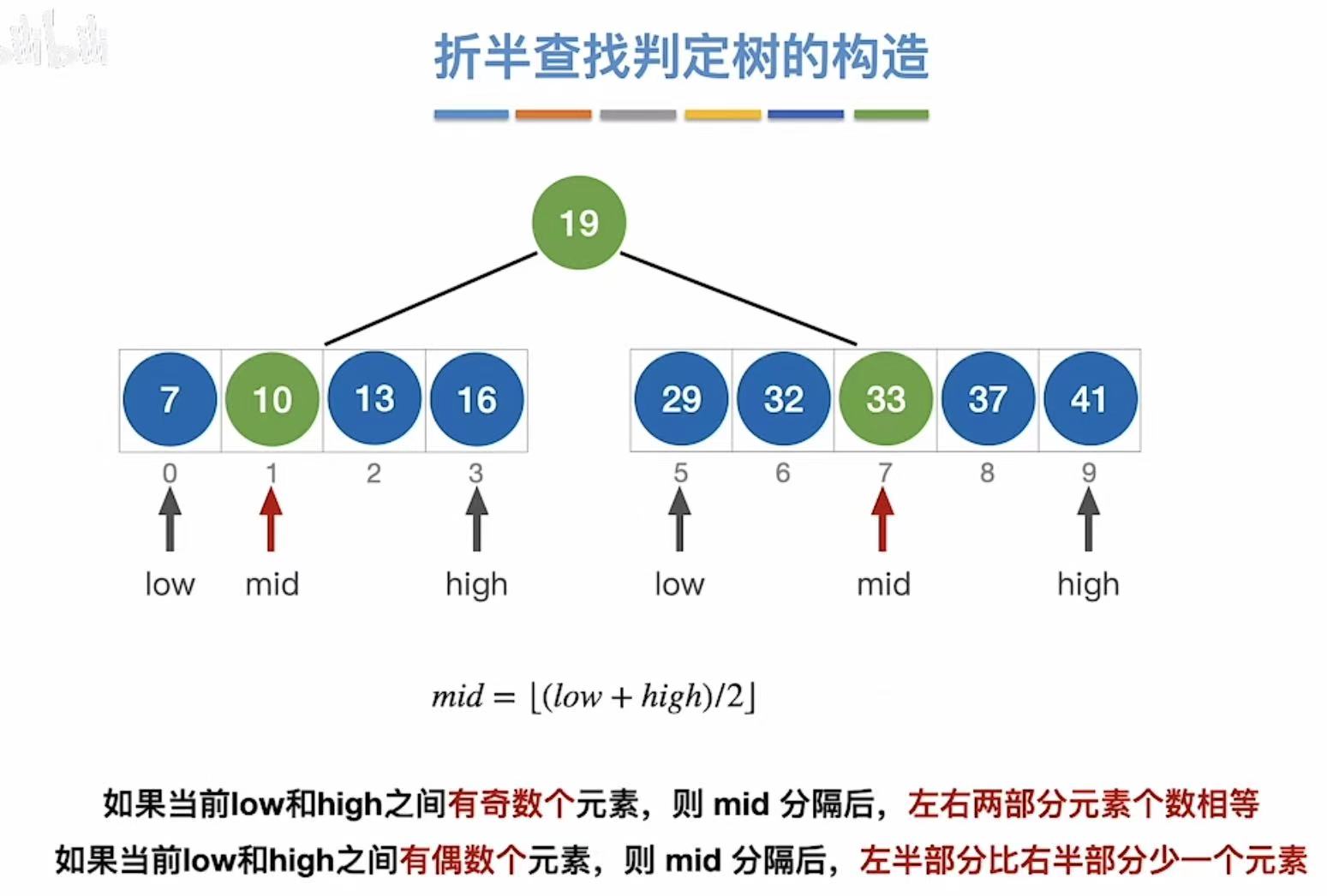
继续划分，得到第三层：

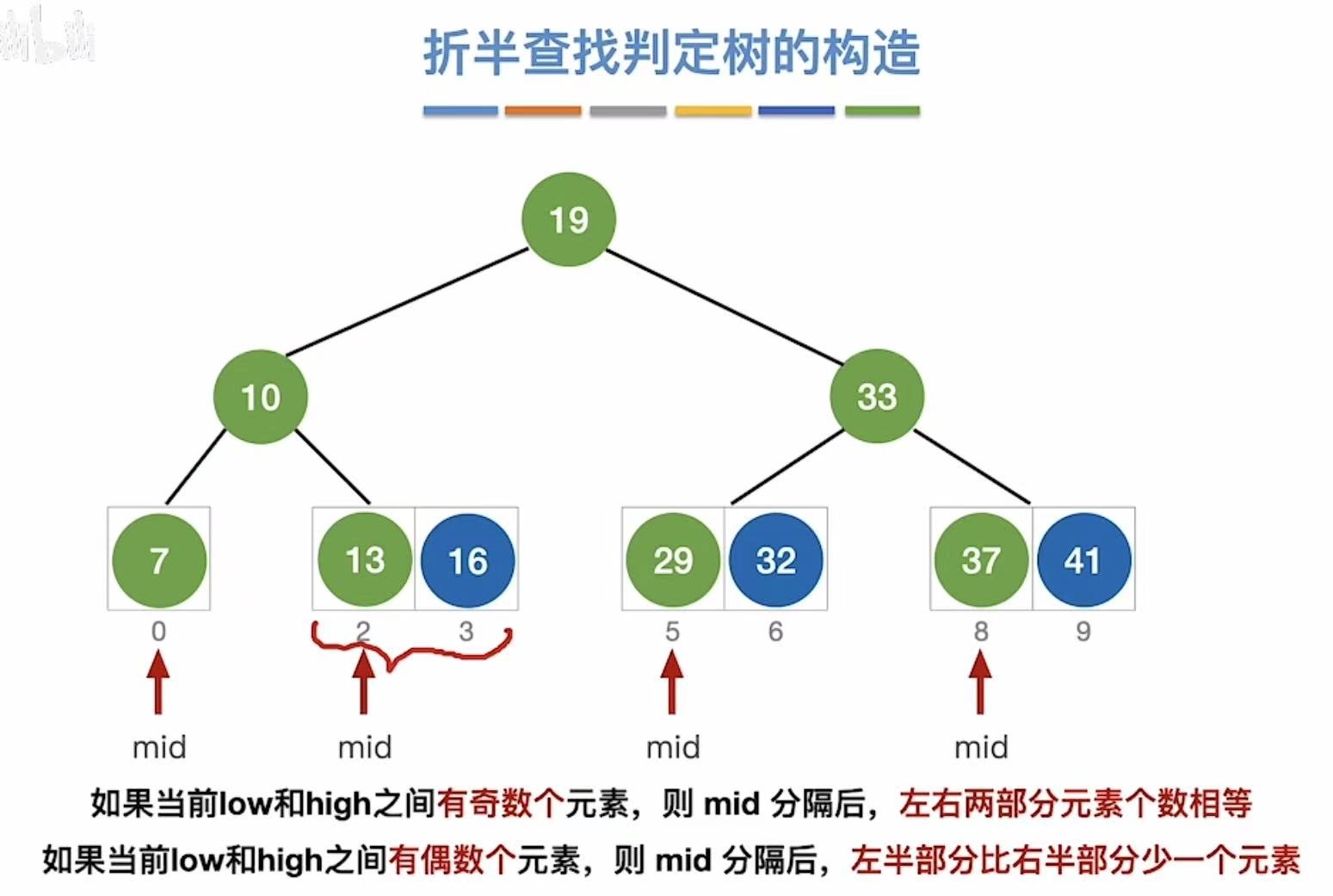
最后就变成了这样：

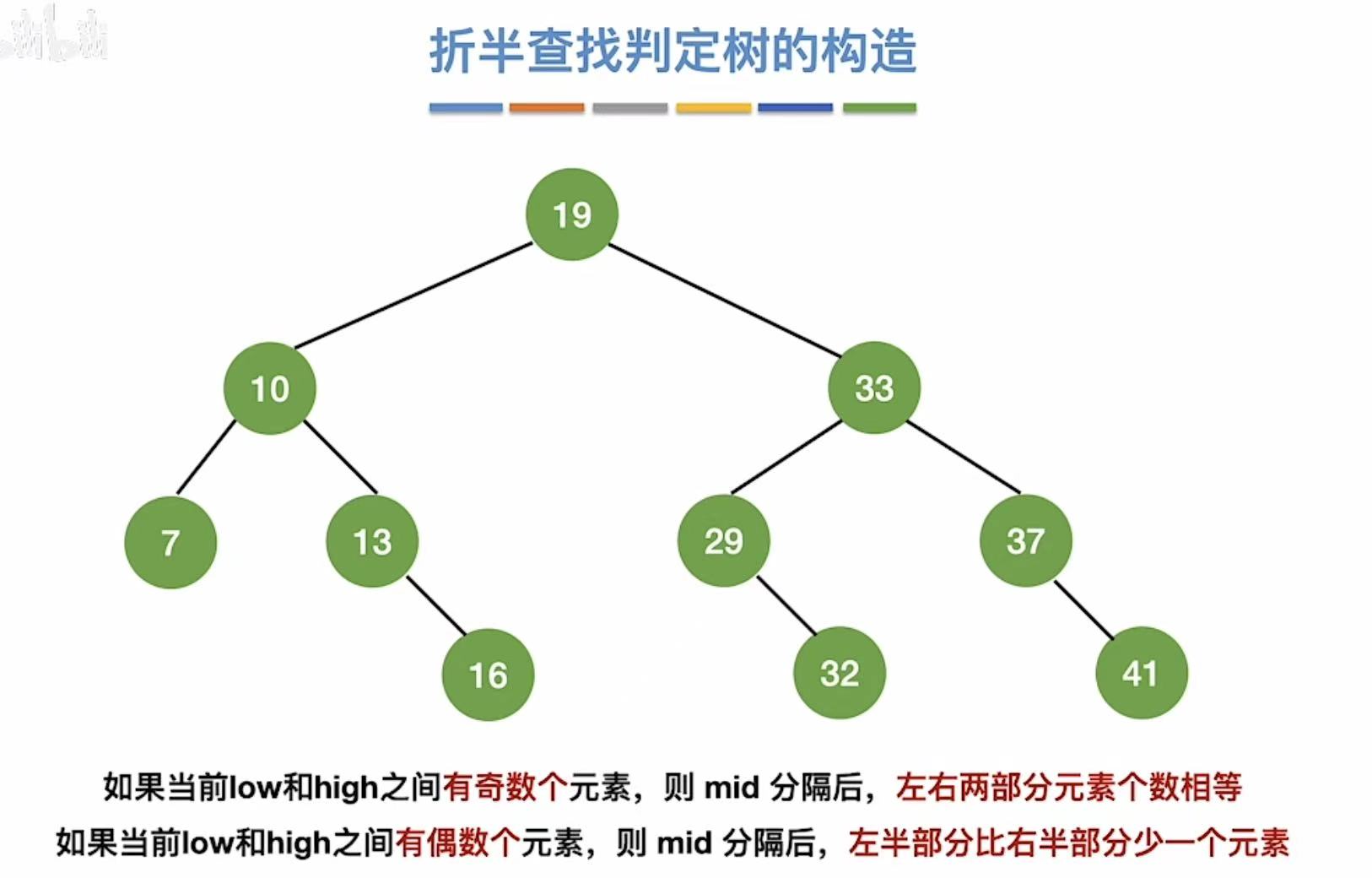
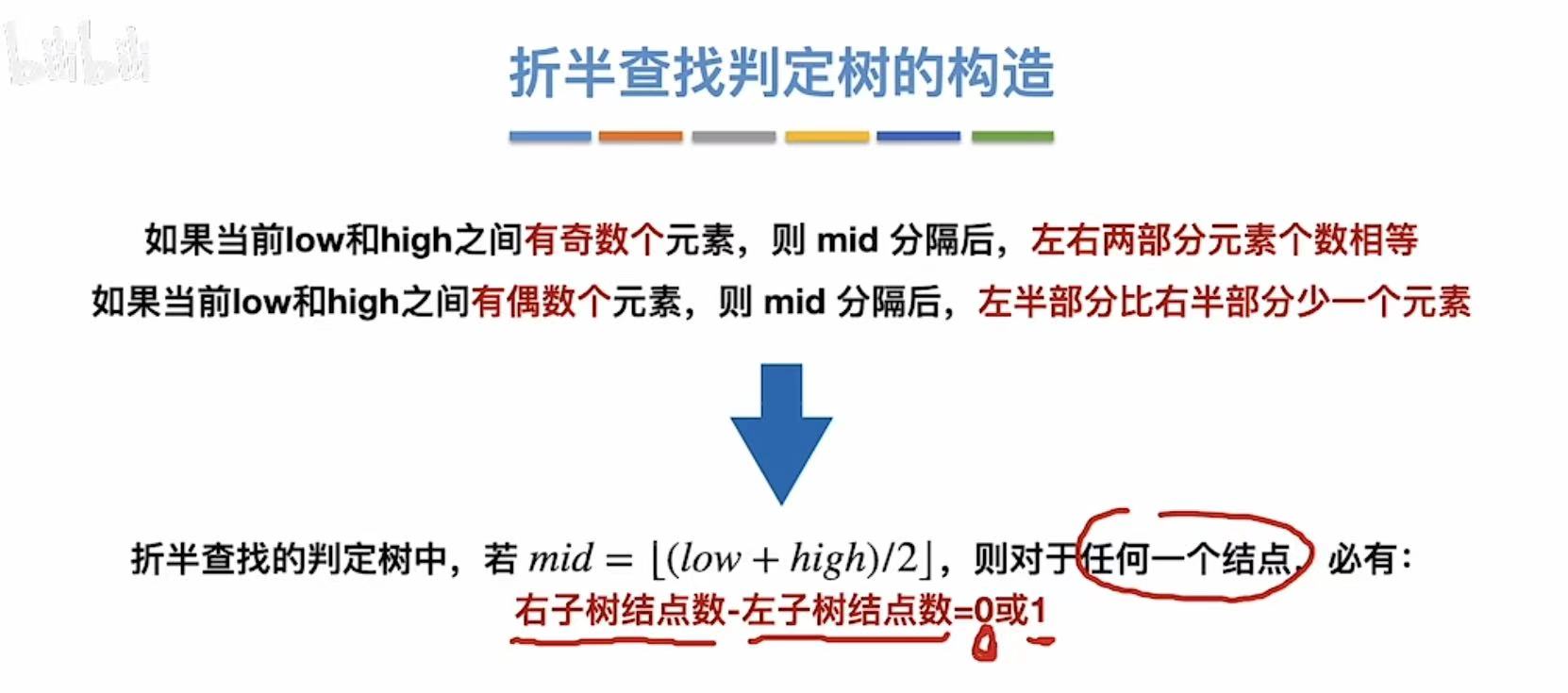
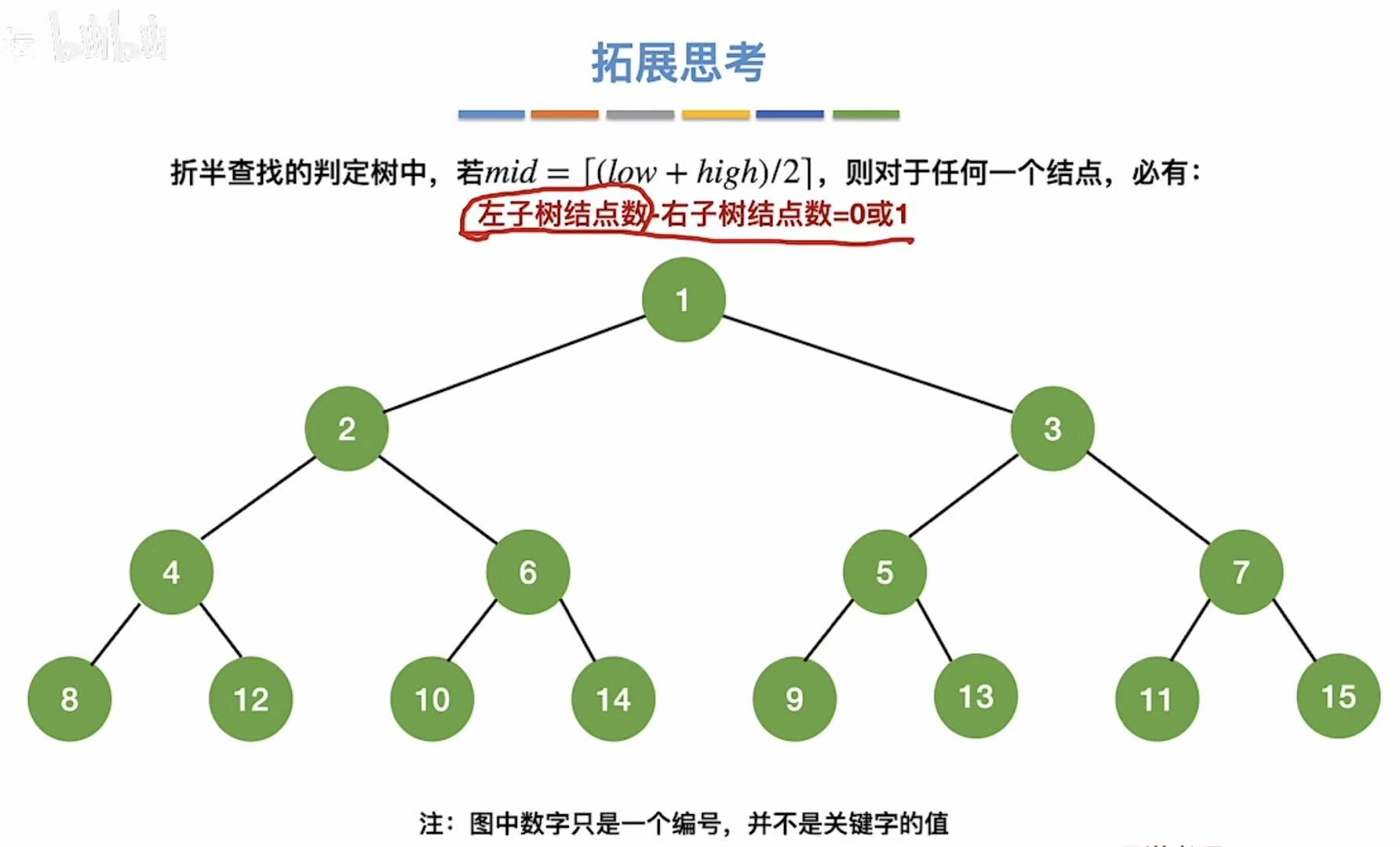
按照取低的标准，我们就可以得到：右-左=1or0

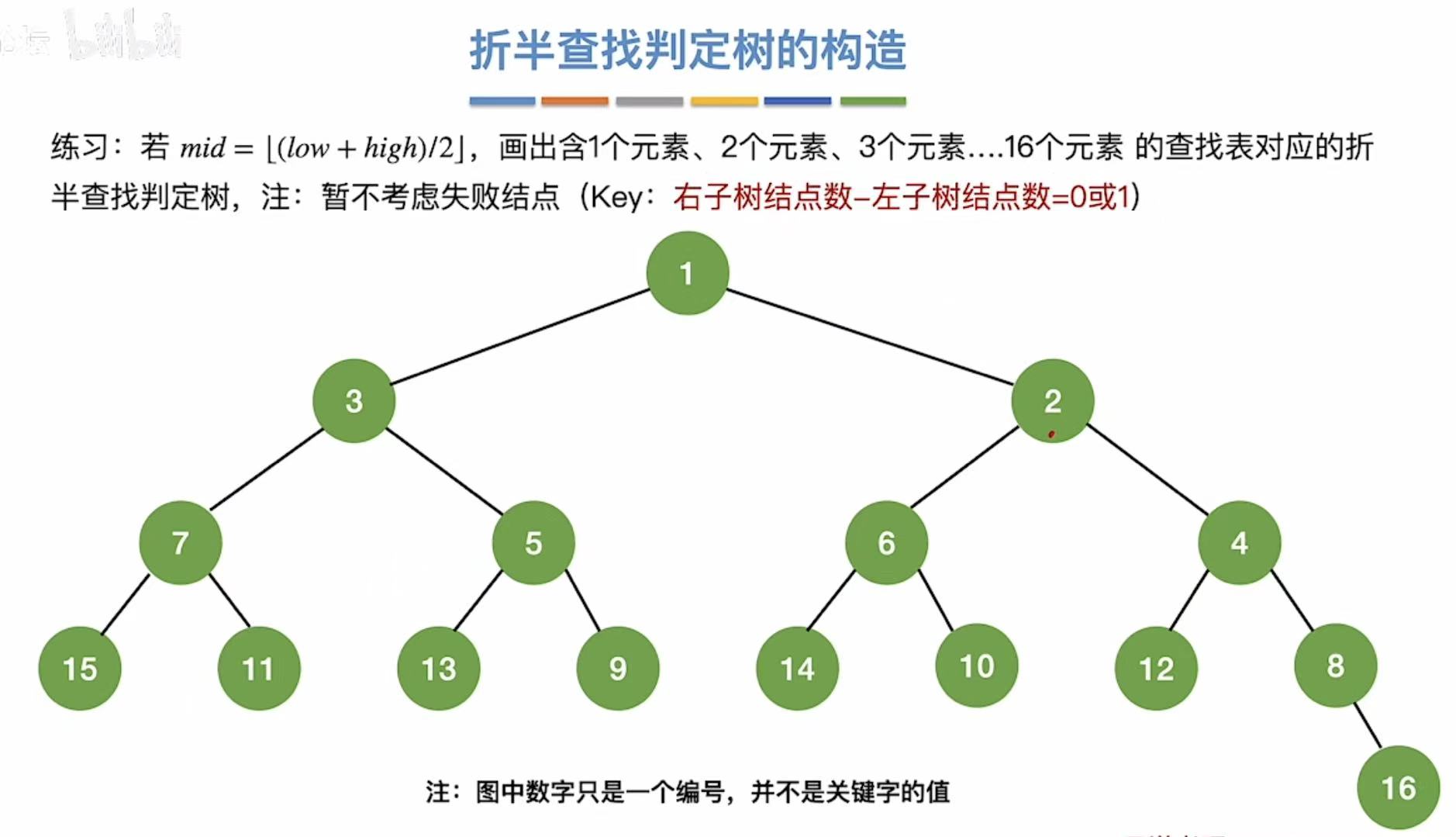
我们就可以根据这个规律，画出各种各样的折半查找判定树：

  • 图中数字只是编号
  • 比如，只保留1，就是含一个元素的判定树；只保留1、2，就是含两个元素的判定树；以此类推...

    完全二叉树可见：完全二叉树

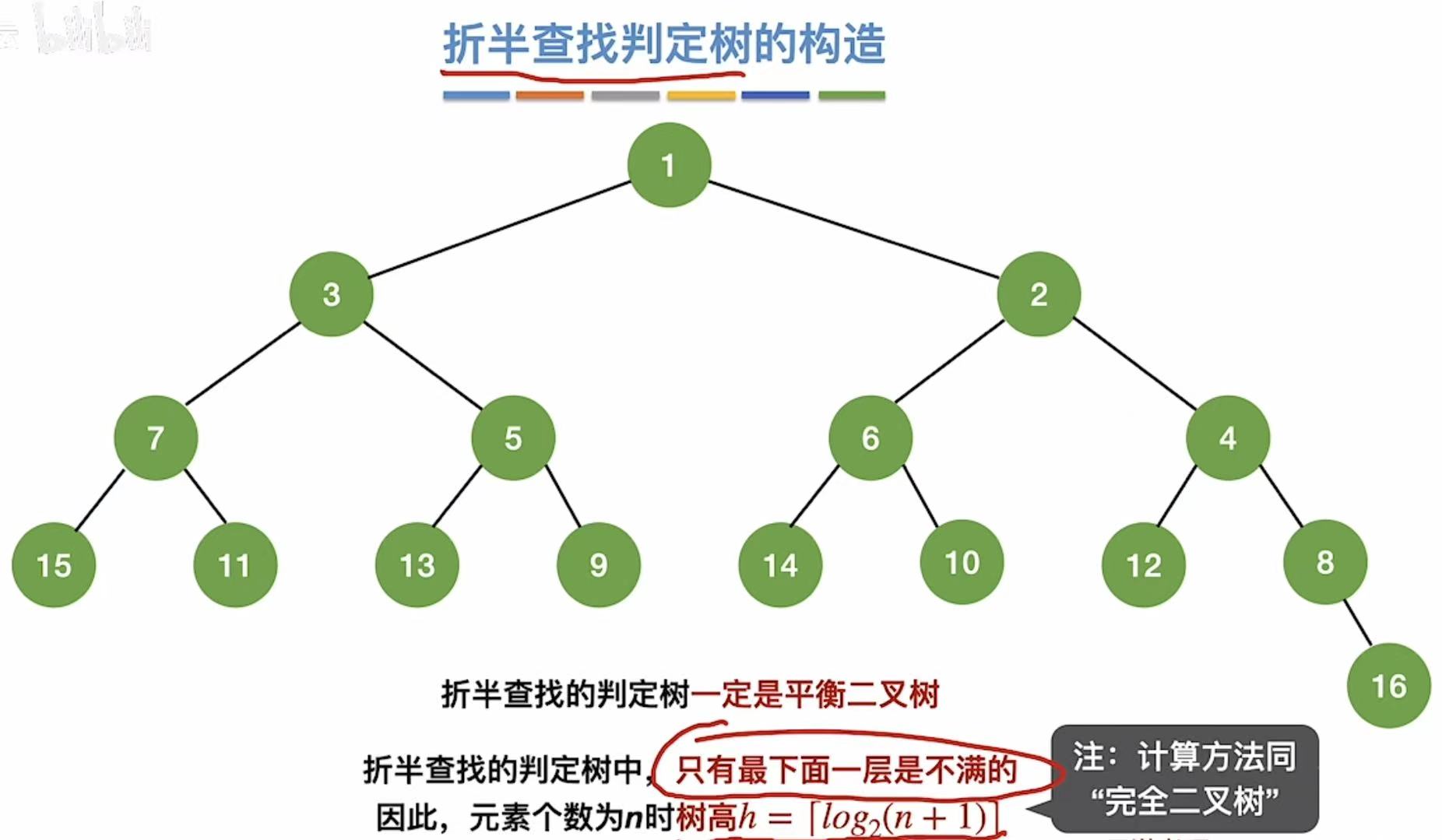
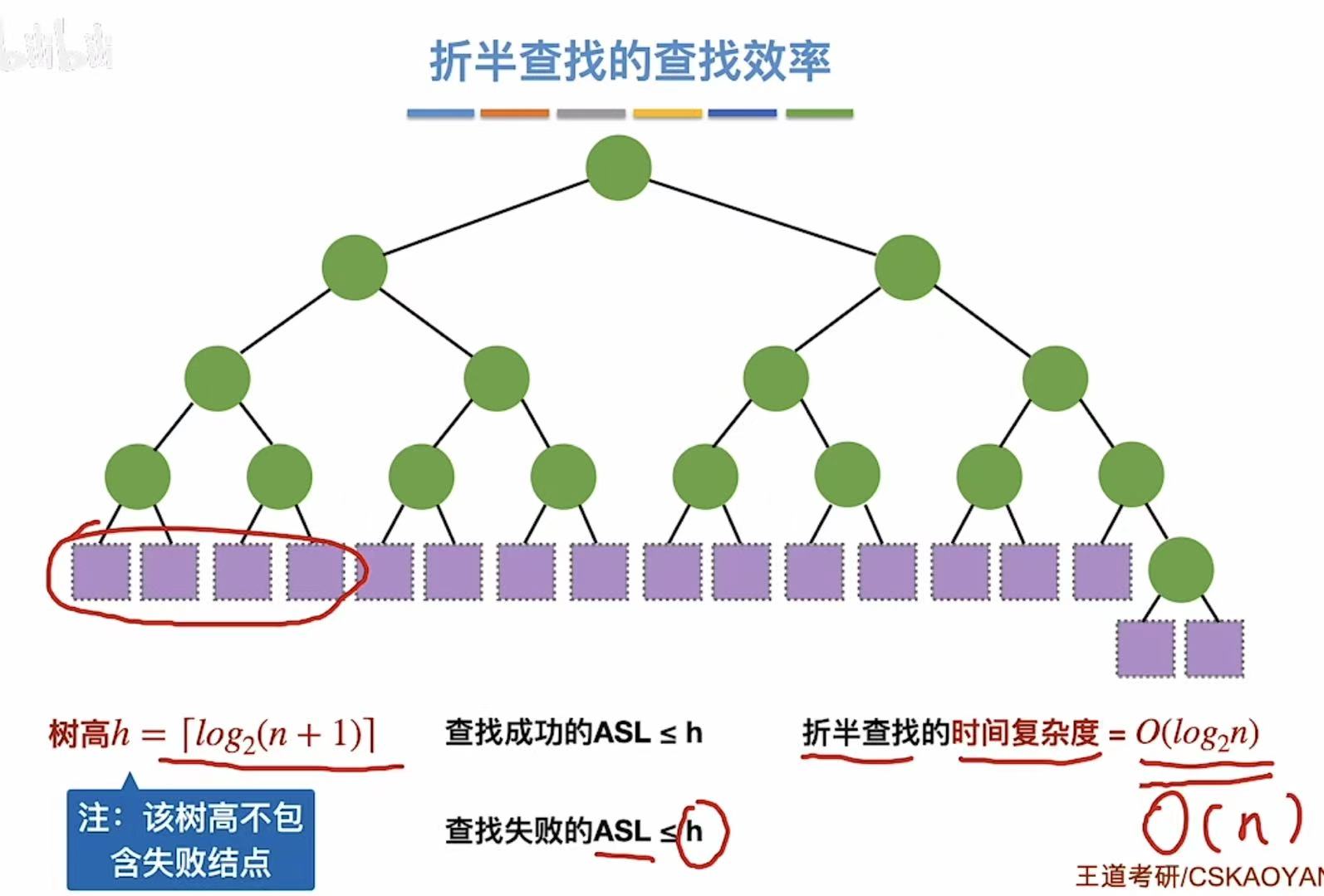
4. 查找效率

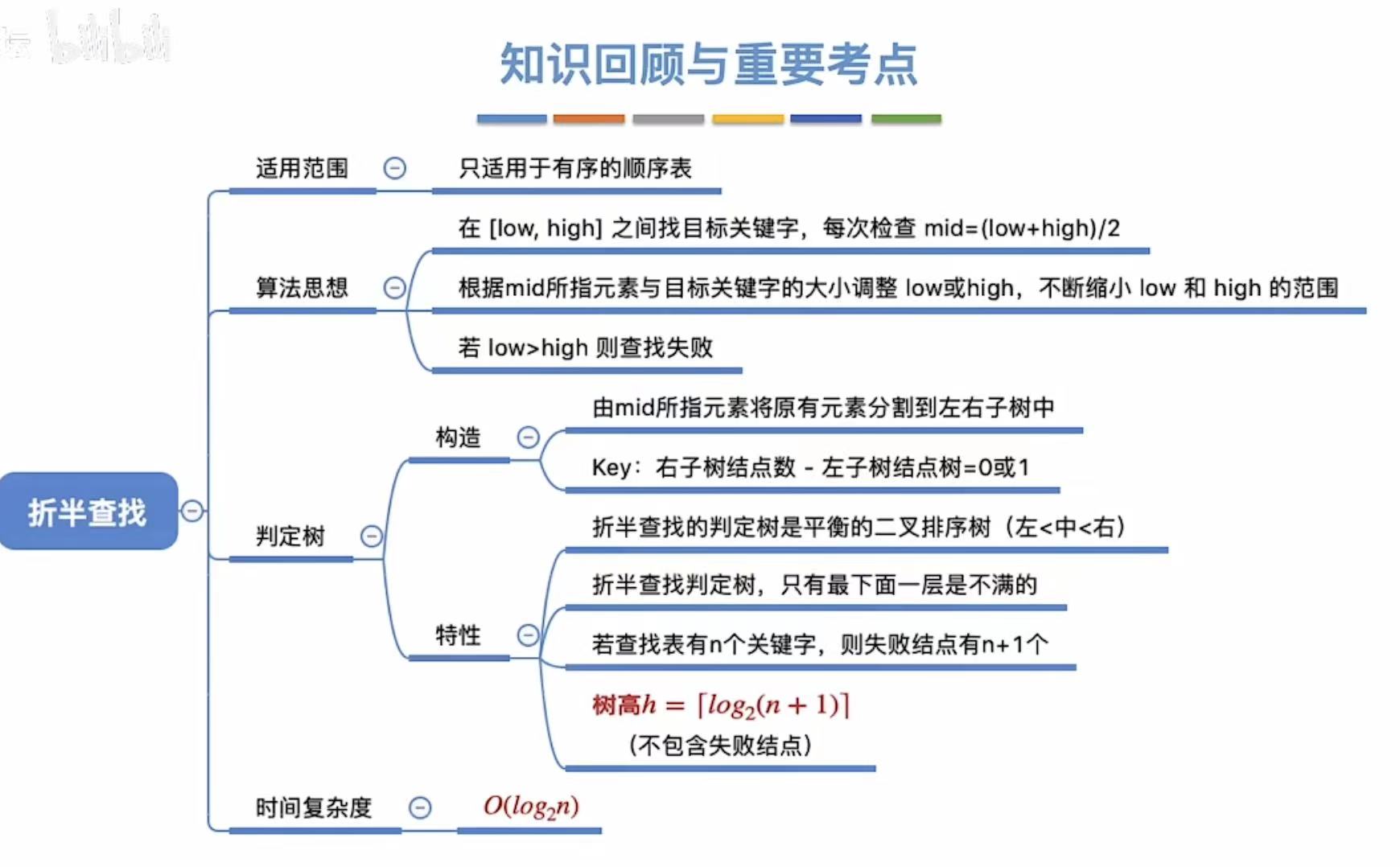
5. 小结

6. 拓展思考

折半不一定比顺序查找更快，比如找7，顺序直接找到，折半还要从中间找。

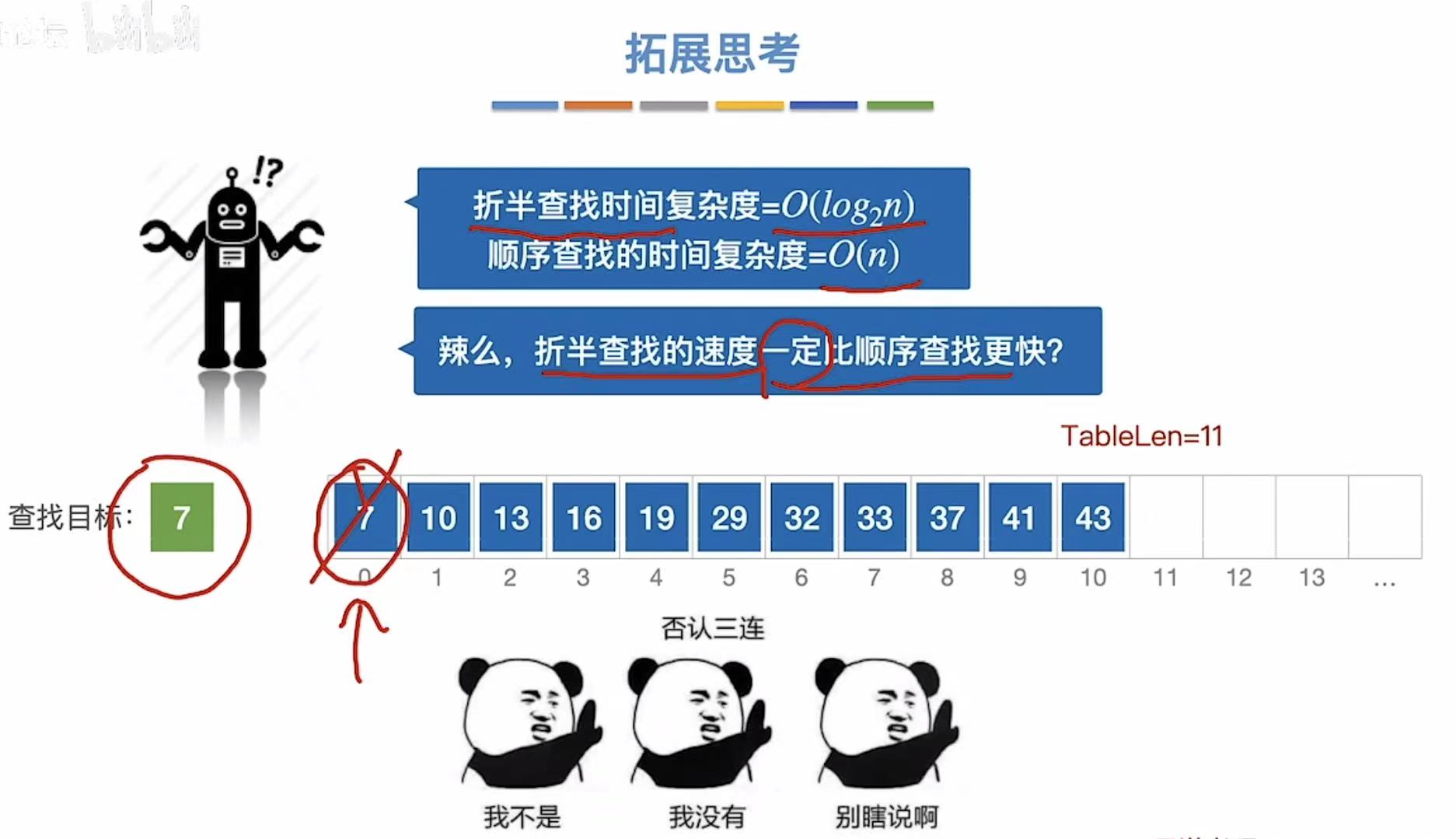
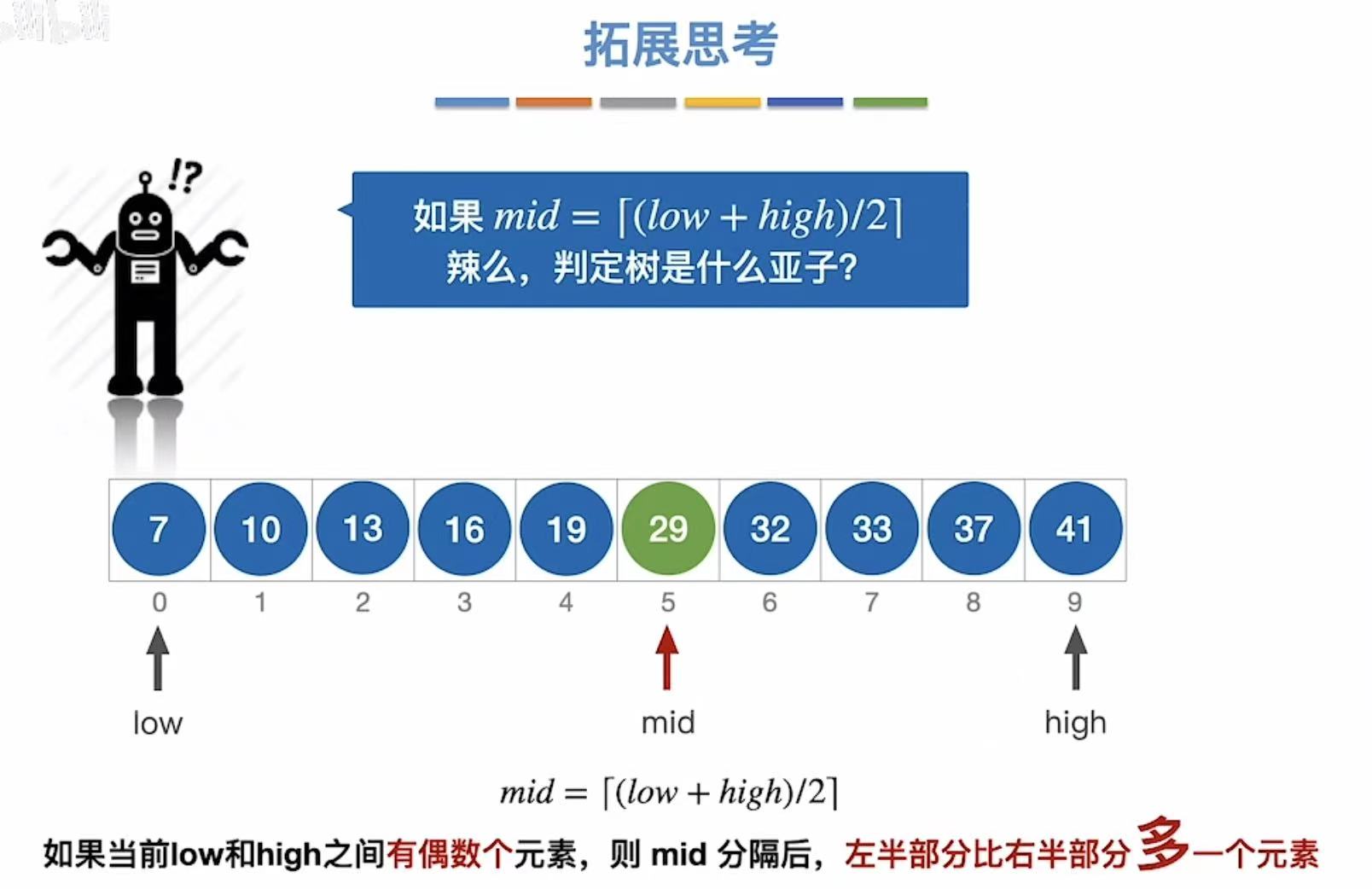
上面全部都是在取低的标准下进行的，那么如果我们取高呢？

取高的话，就和上面反过来，右面比左面少一个元素：

分块查找

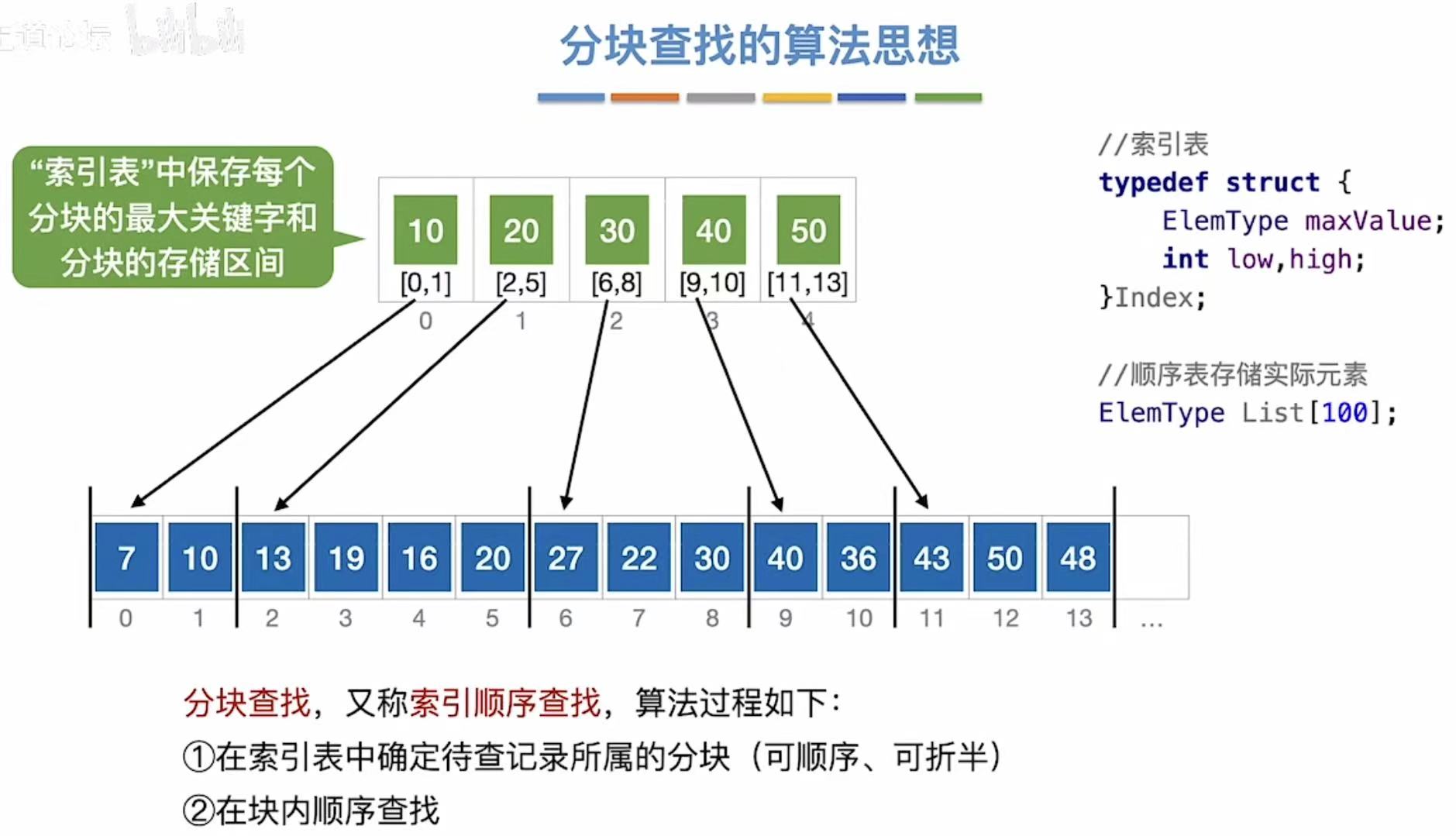
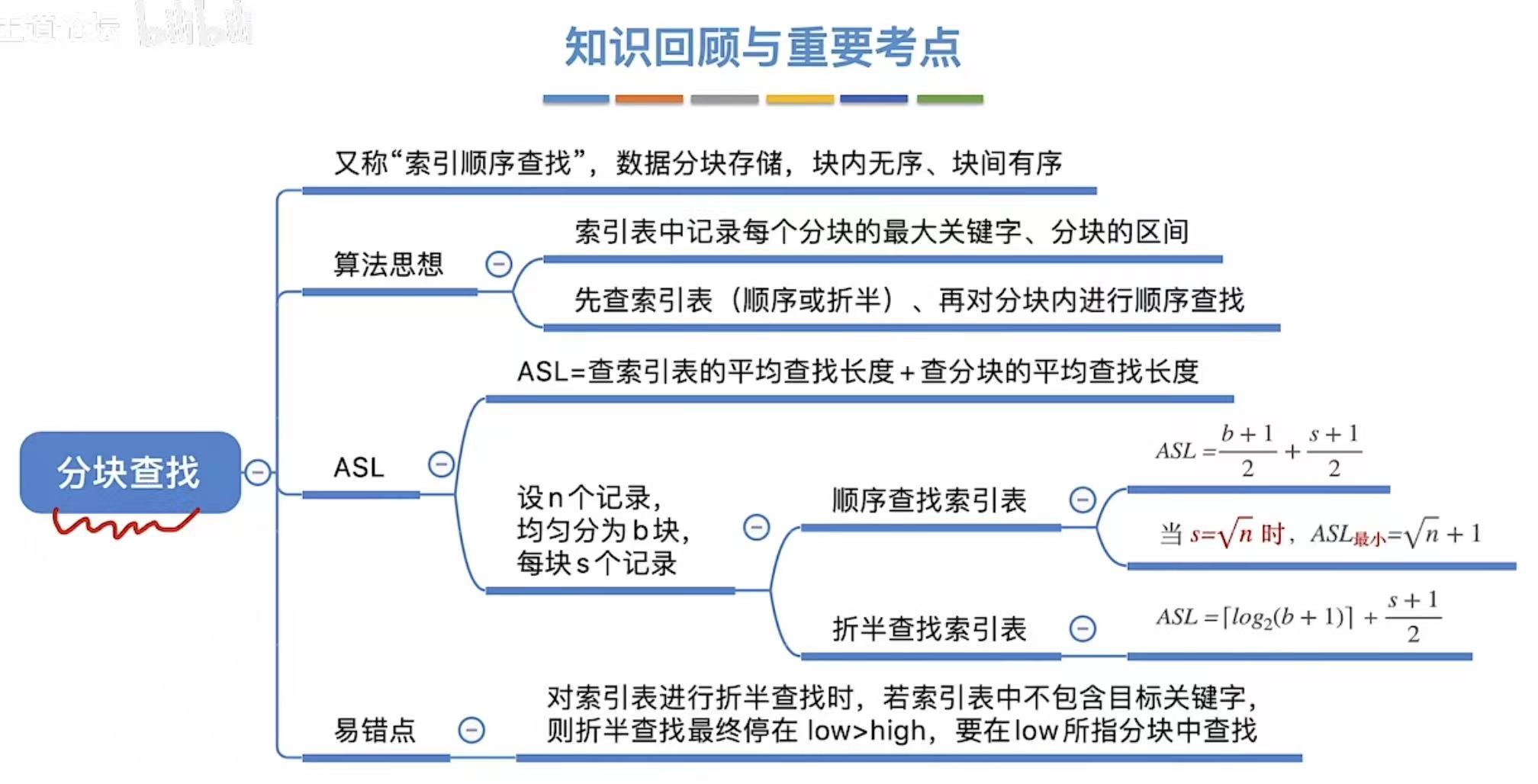
1. 算法思想

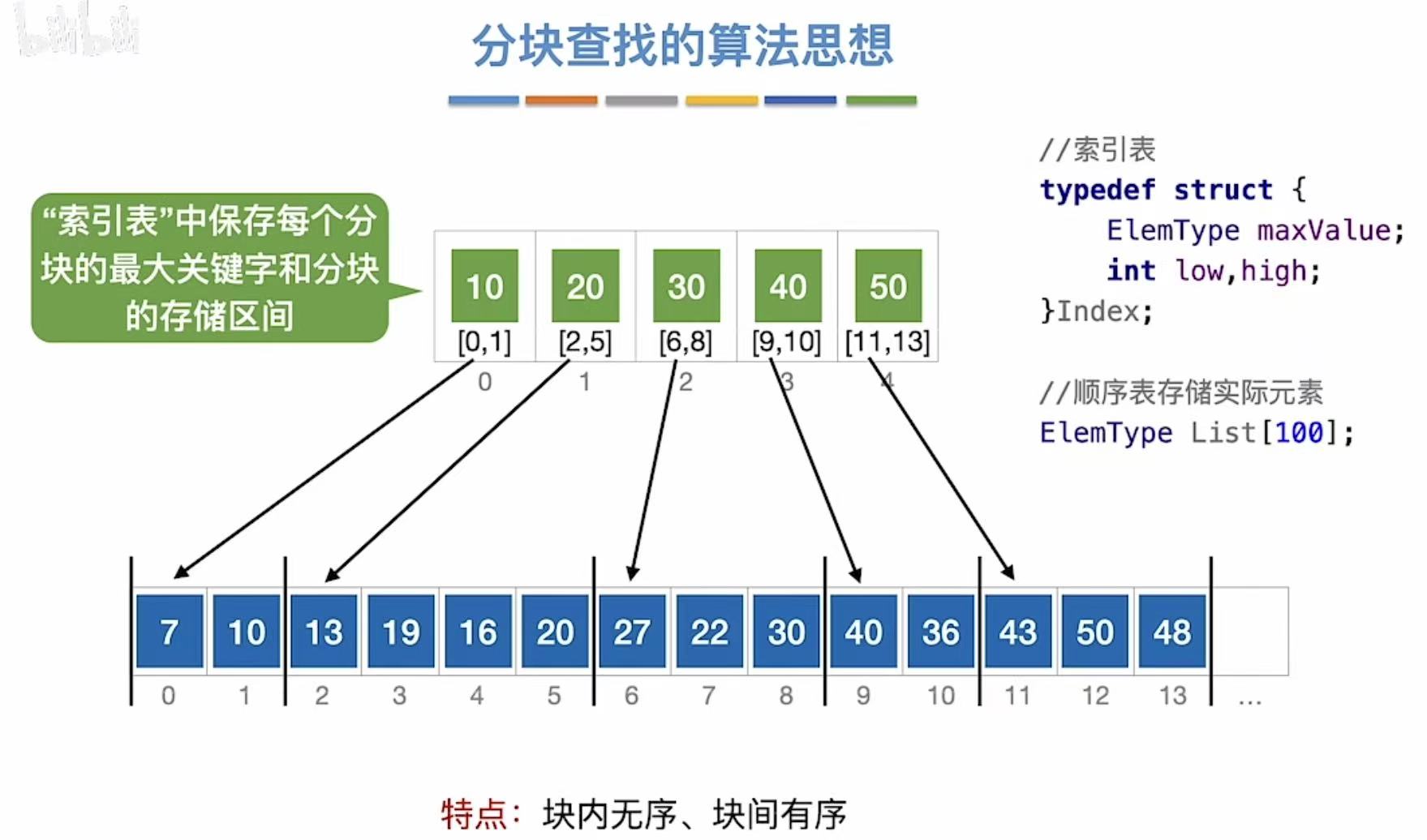
其实就是多加了一个索引表，先查索引再查表

1.1 顺序查找索引表

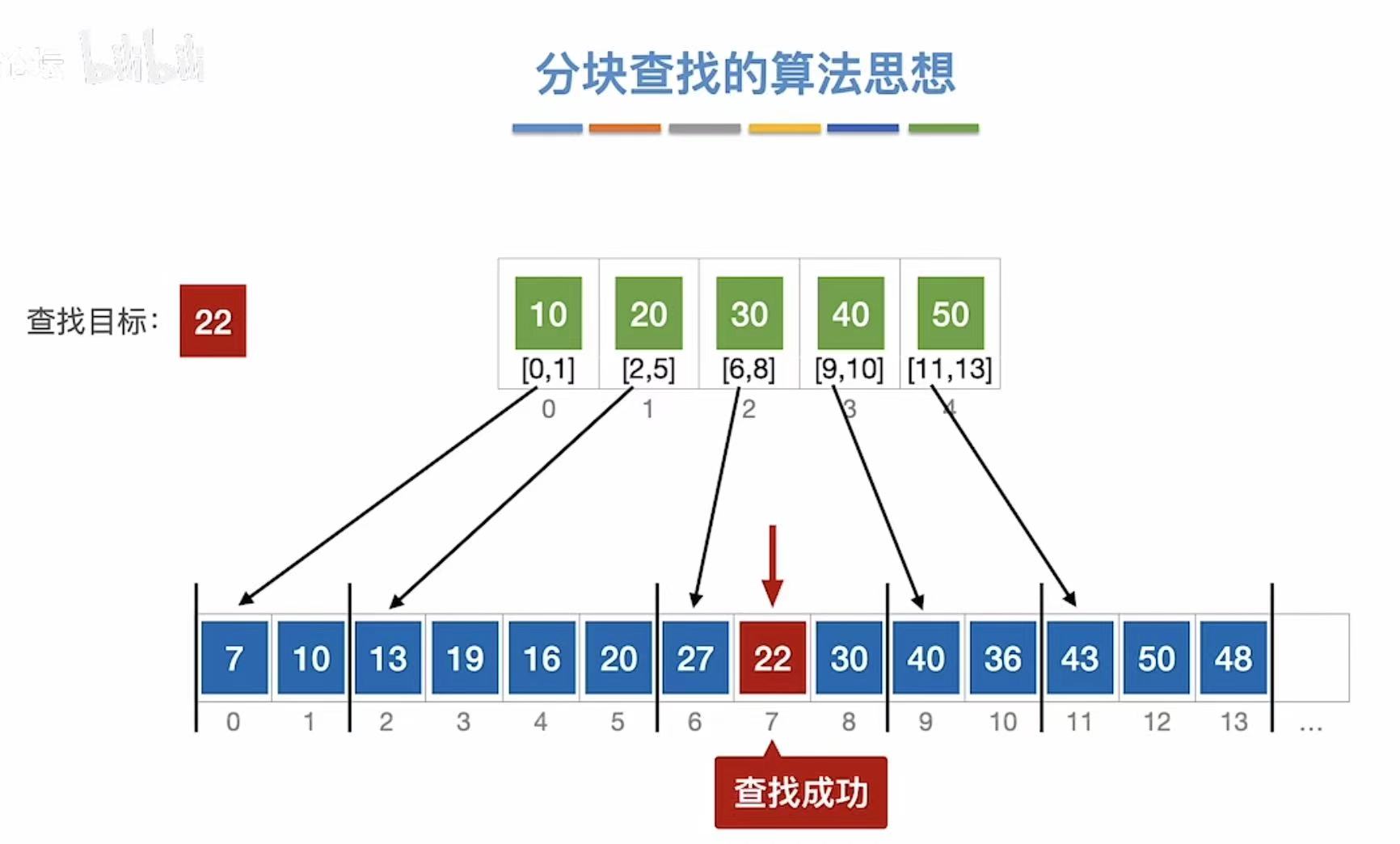
找22：

  • 先查索引表-->最大为10、pass；最大为20、pass；最大为30、√
  • 看索引30对应的是下标6至8
  • 就去数组中顺序查找
  • 27？×
  • 22？对-->查找成功

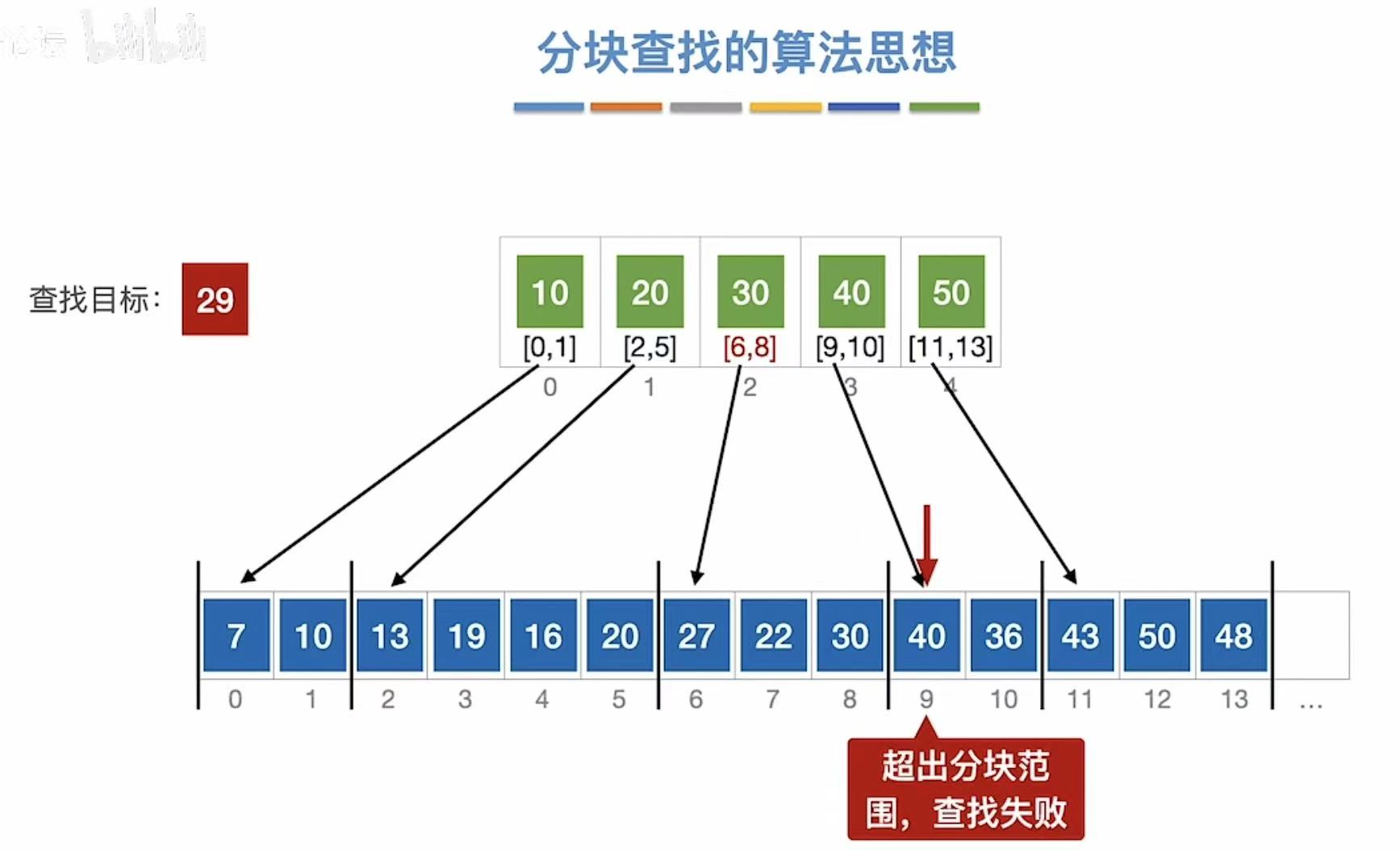
    找29：
  • 先查索引表-->最大为10、pass；最大为20、pass；最大为30、√
  • 看索引30对应的是下标6至8
  • 就去数组中顺序查找
  • 27？×
  • 22？×
  • 30？×
  • 40？×-->超出分块范围，查找失败

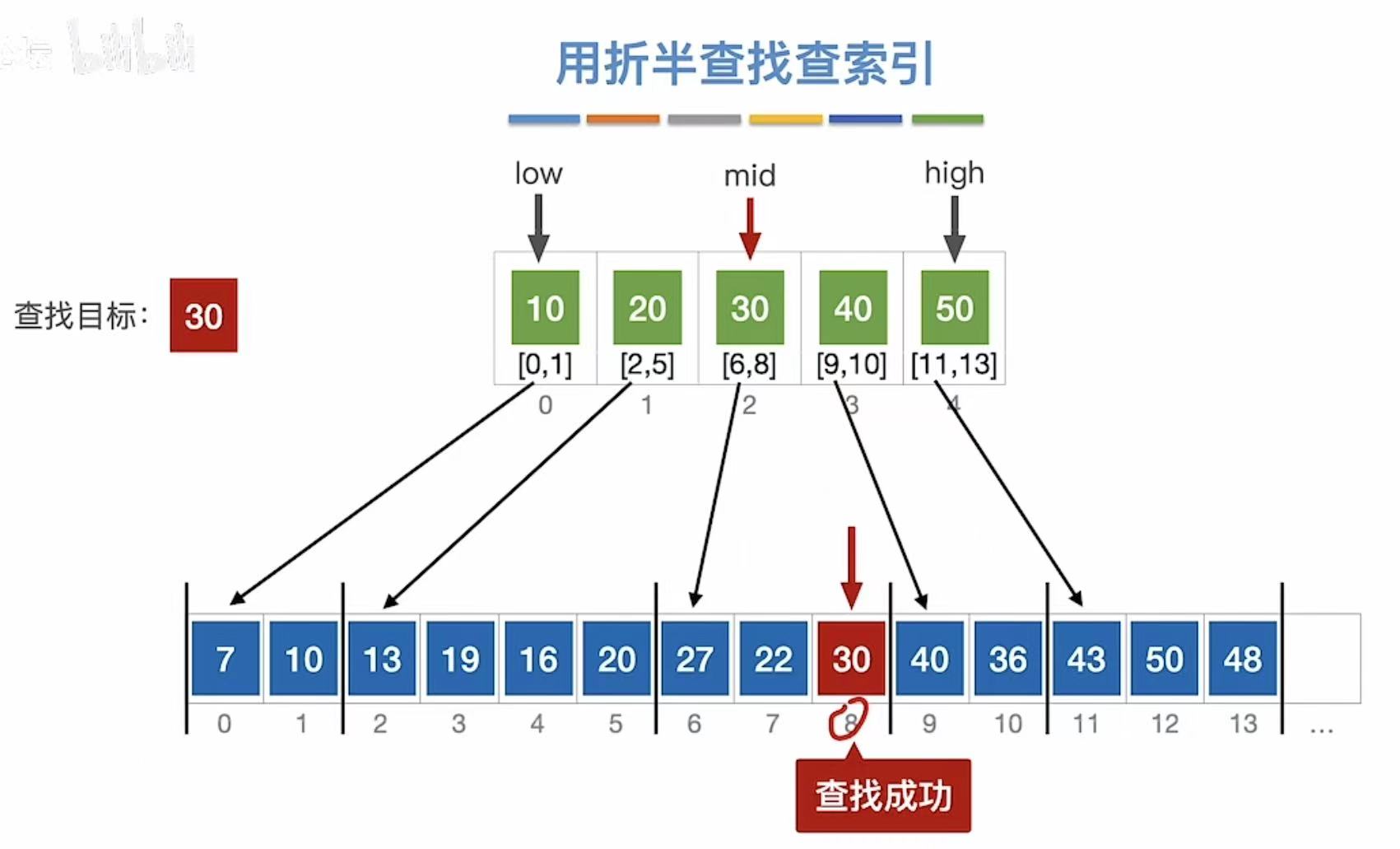
1.2 折半查找索引表

找30：

  • 先查索引表-->mid和30比较-->直接比对正确
  • 看索引30对应的是下标6至8
  • 就去数组中顺序查找
  • 27？×
  • 22？×
  • 30？√-->查找成功

    找19：
  • 先查索引表
  • 索引表因为是分块的整数数字
  • 所以想要继续往下查找
  • 就必须在low所指的分块中继续查找

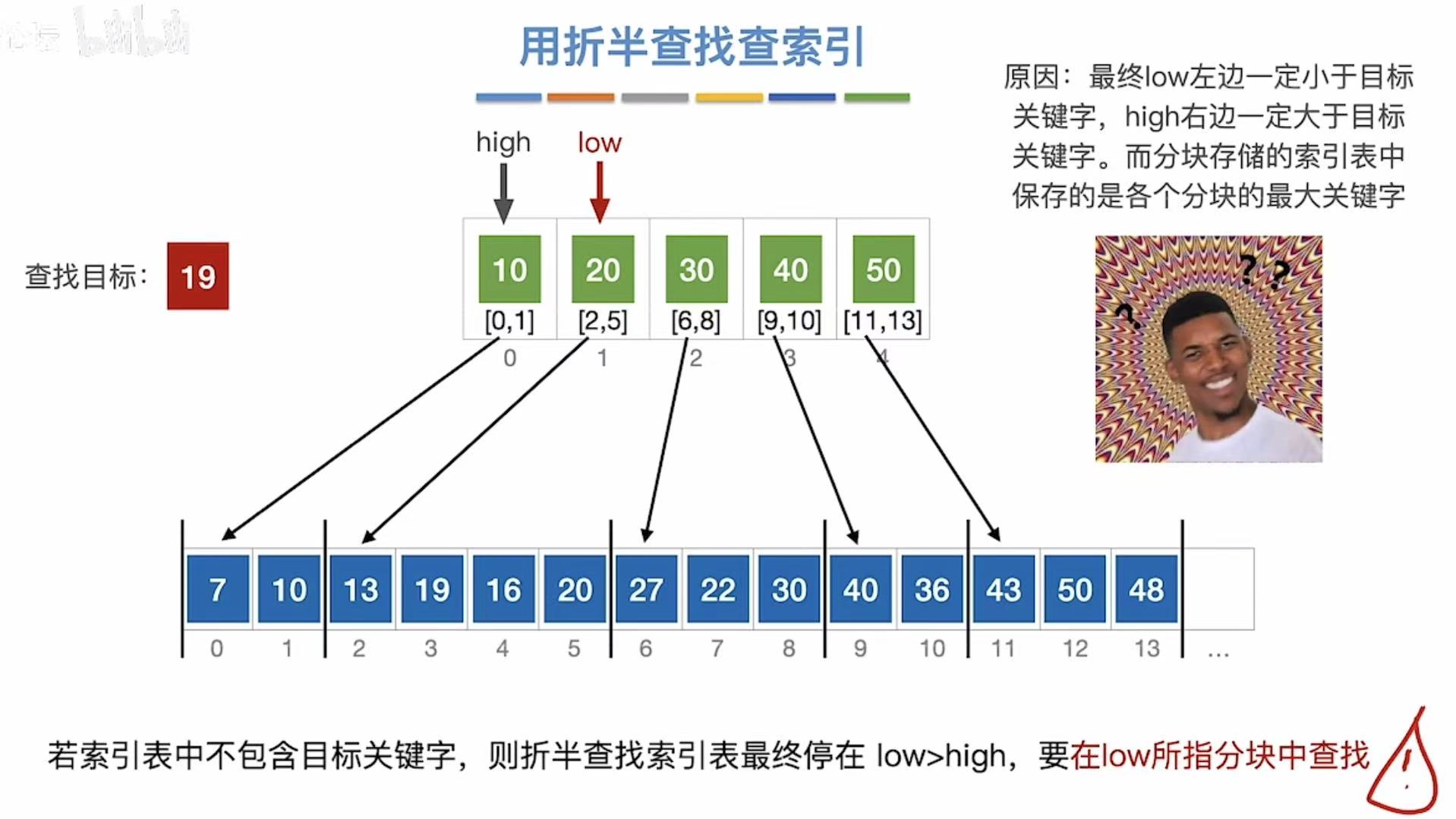
    找19：
  • 先查索引表-->low指向20所在的分块
  • 看索引20对应的是下标2至5
  • 就去数组中顺序查找
  • 13？×
  • 19？对-->查找成功

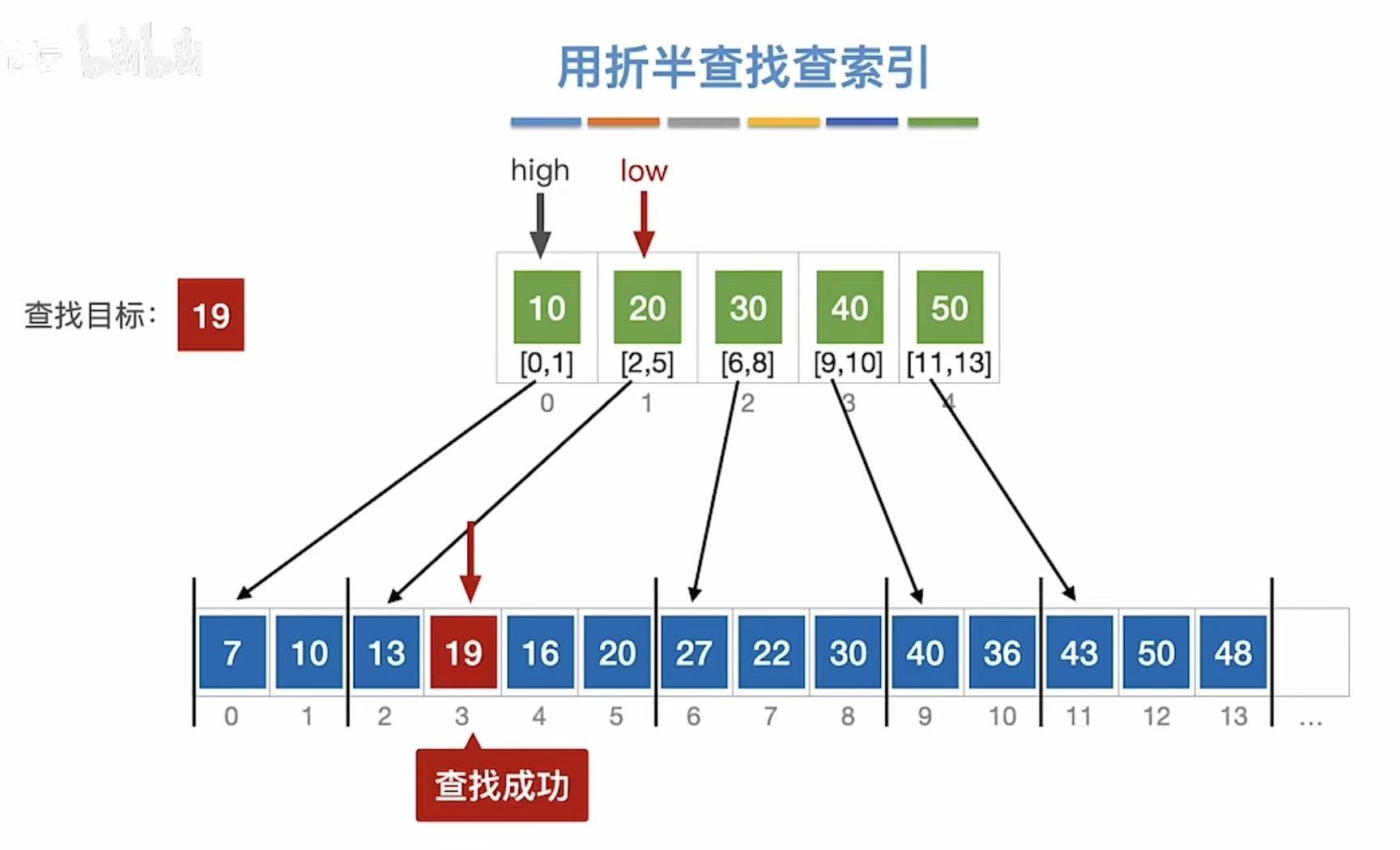
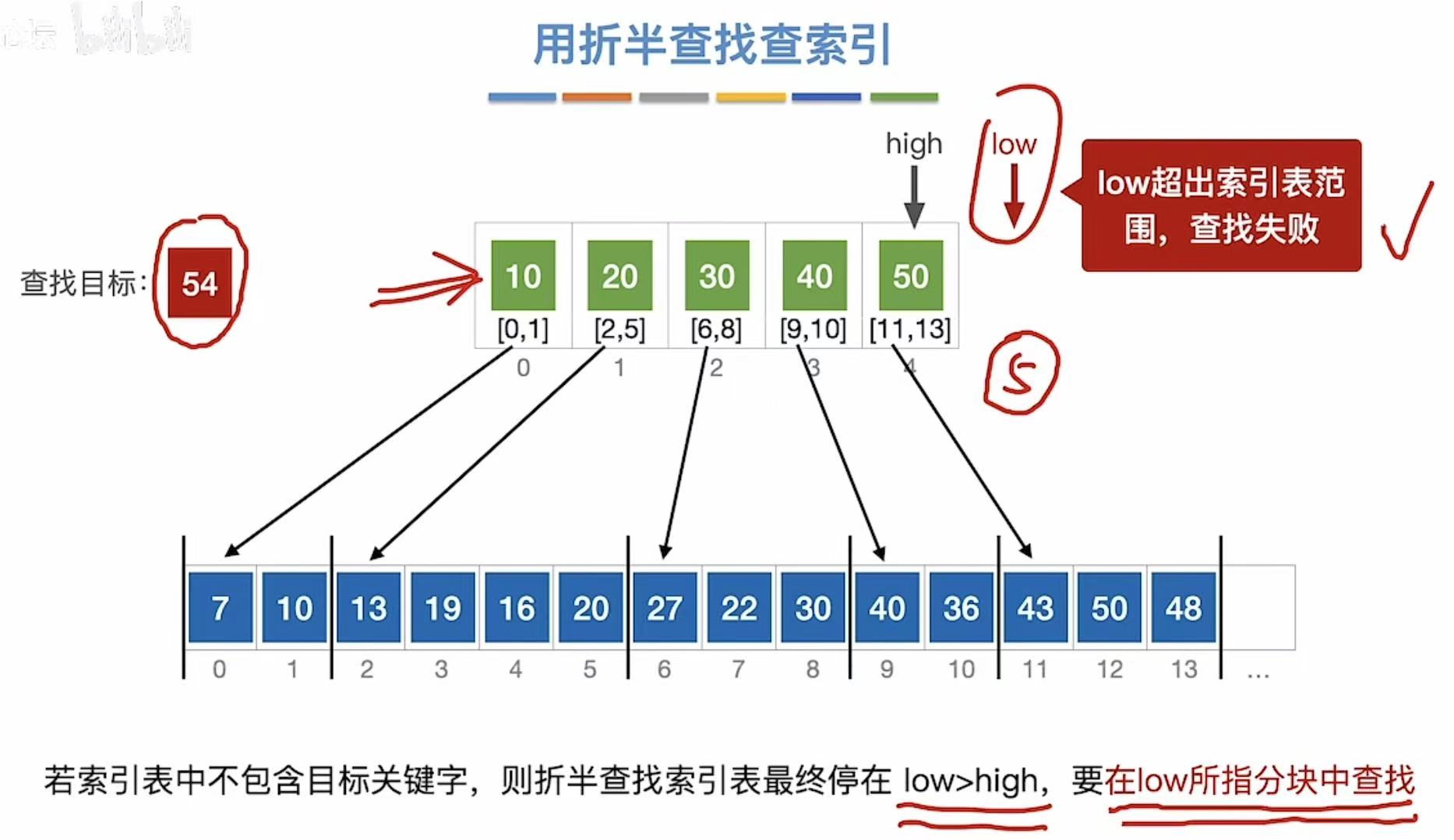
    找54：
  • 先查索引表-->low超出索引表范围
  • 直接查找失败

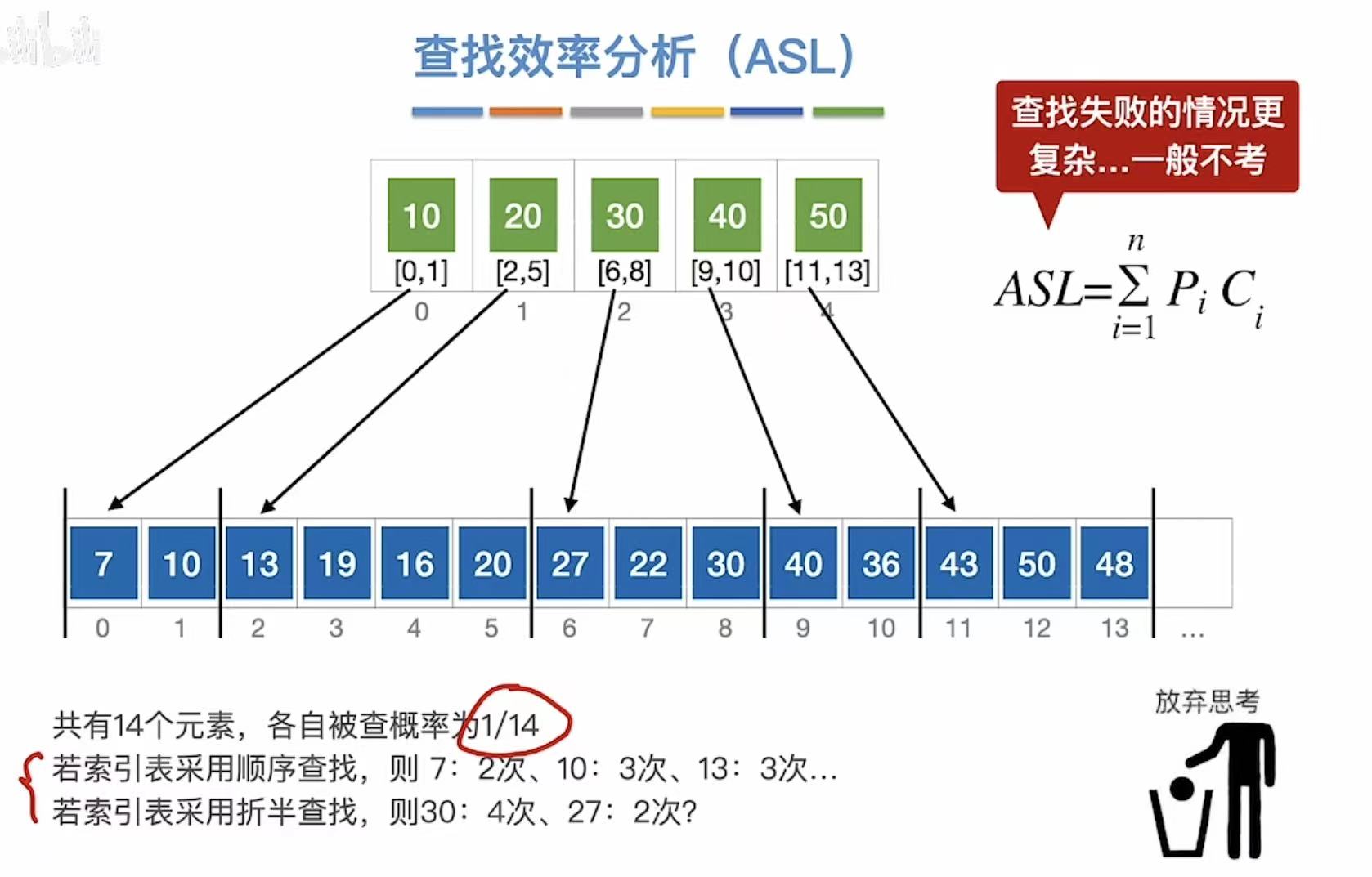
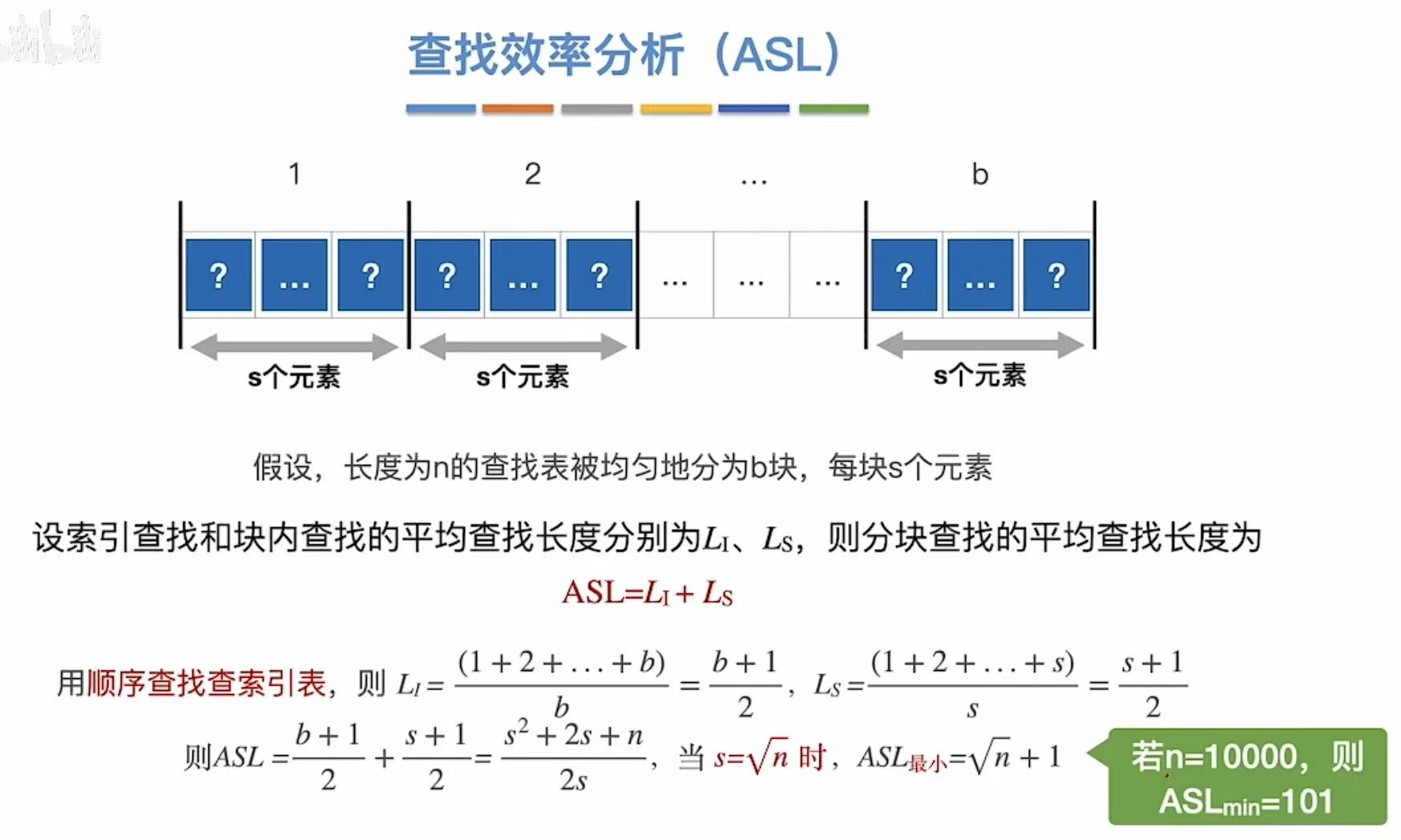
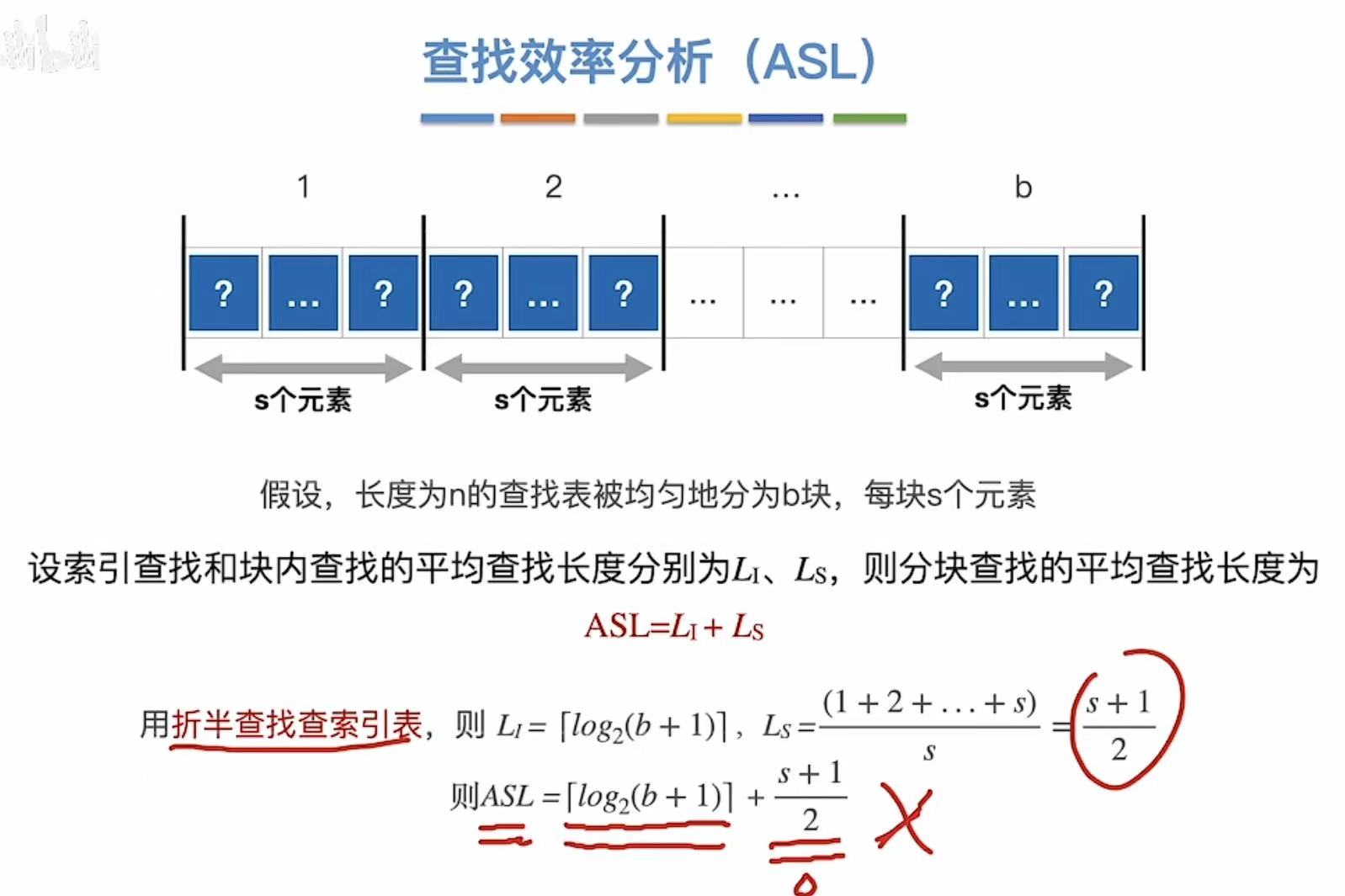
2. 查找效率分析（ASL）

基本不考：


3. 小结

4. 拓展思考

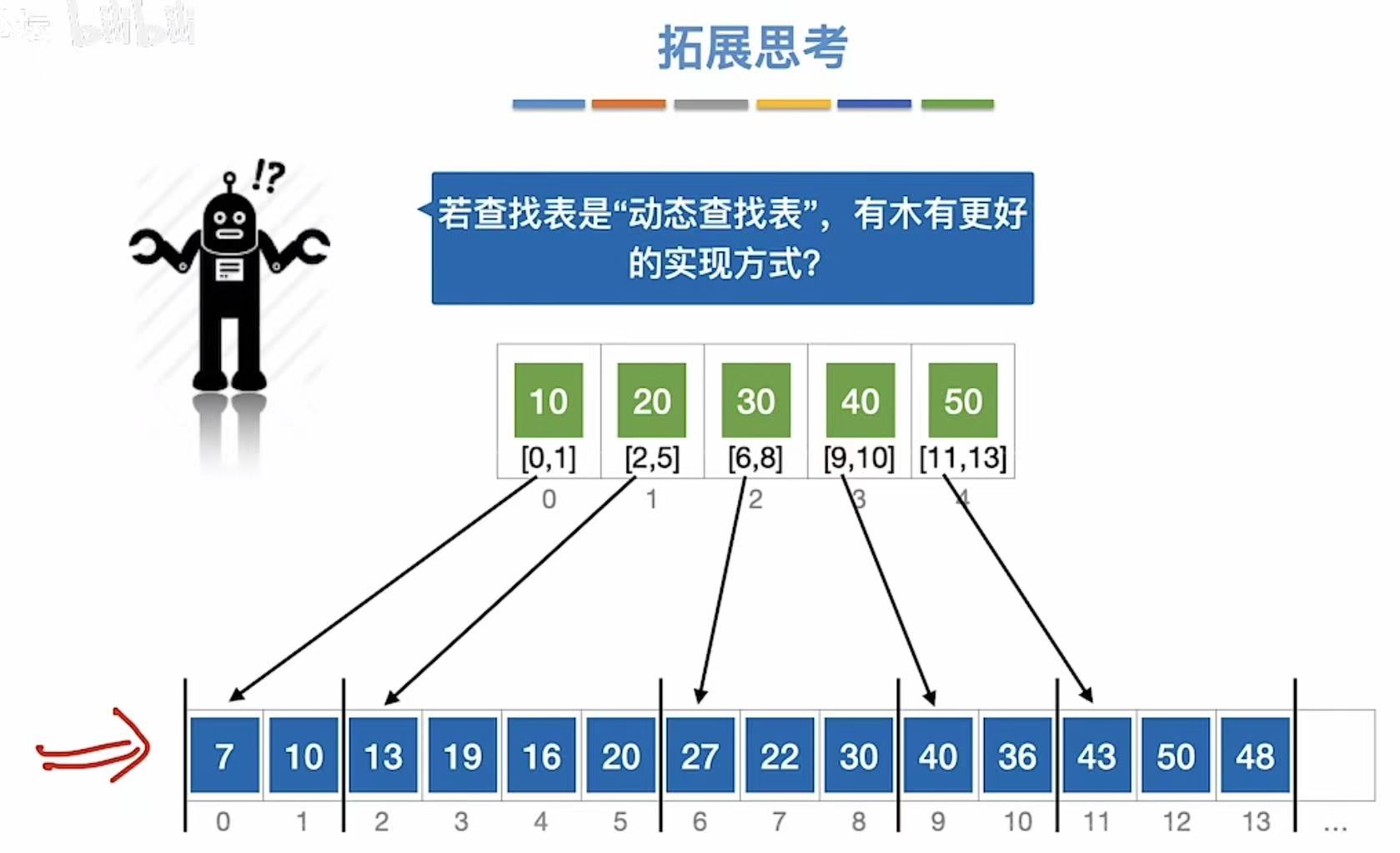
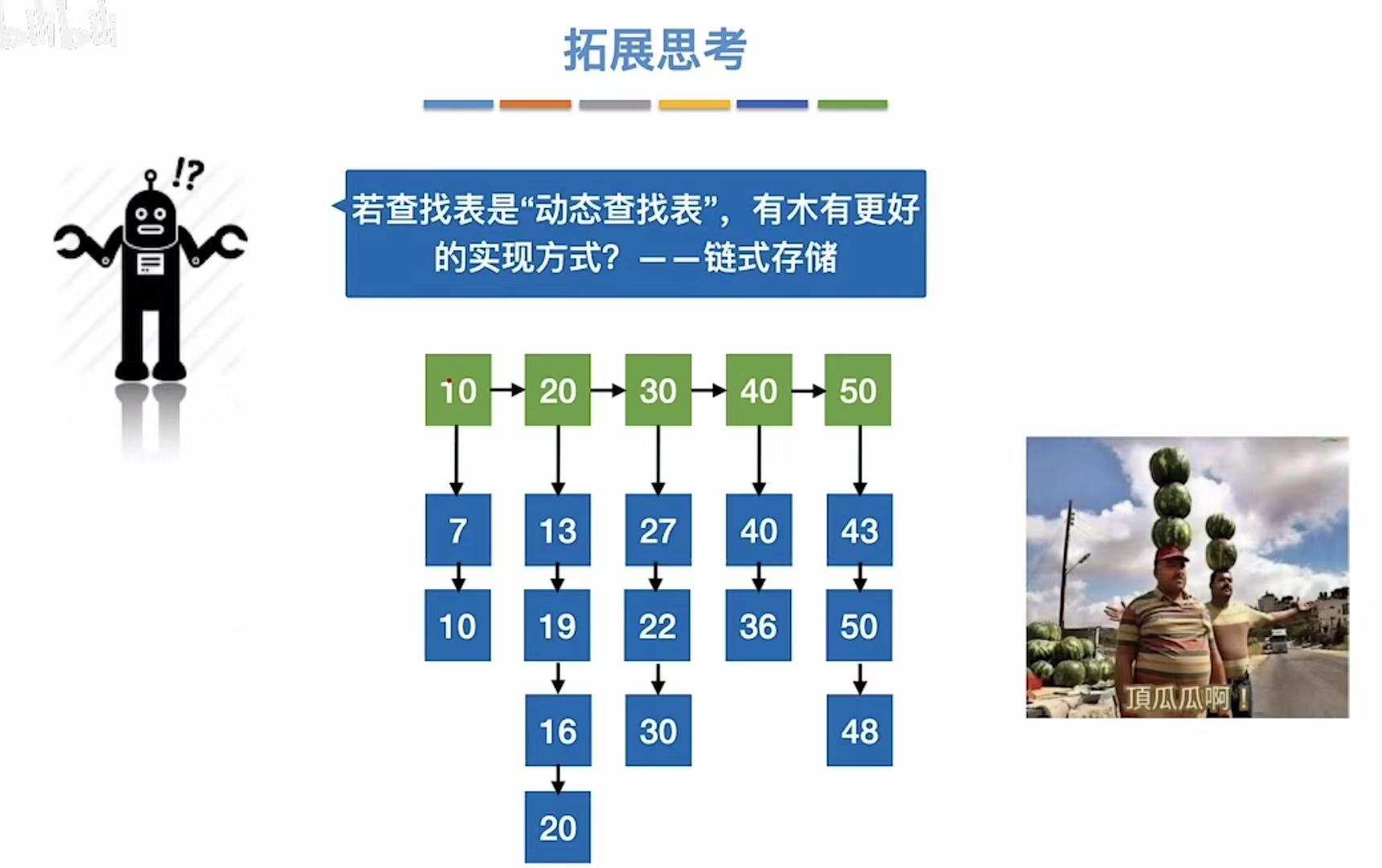
如果查找表是动态查找表，就可以使用链式存储。

二叉排序树

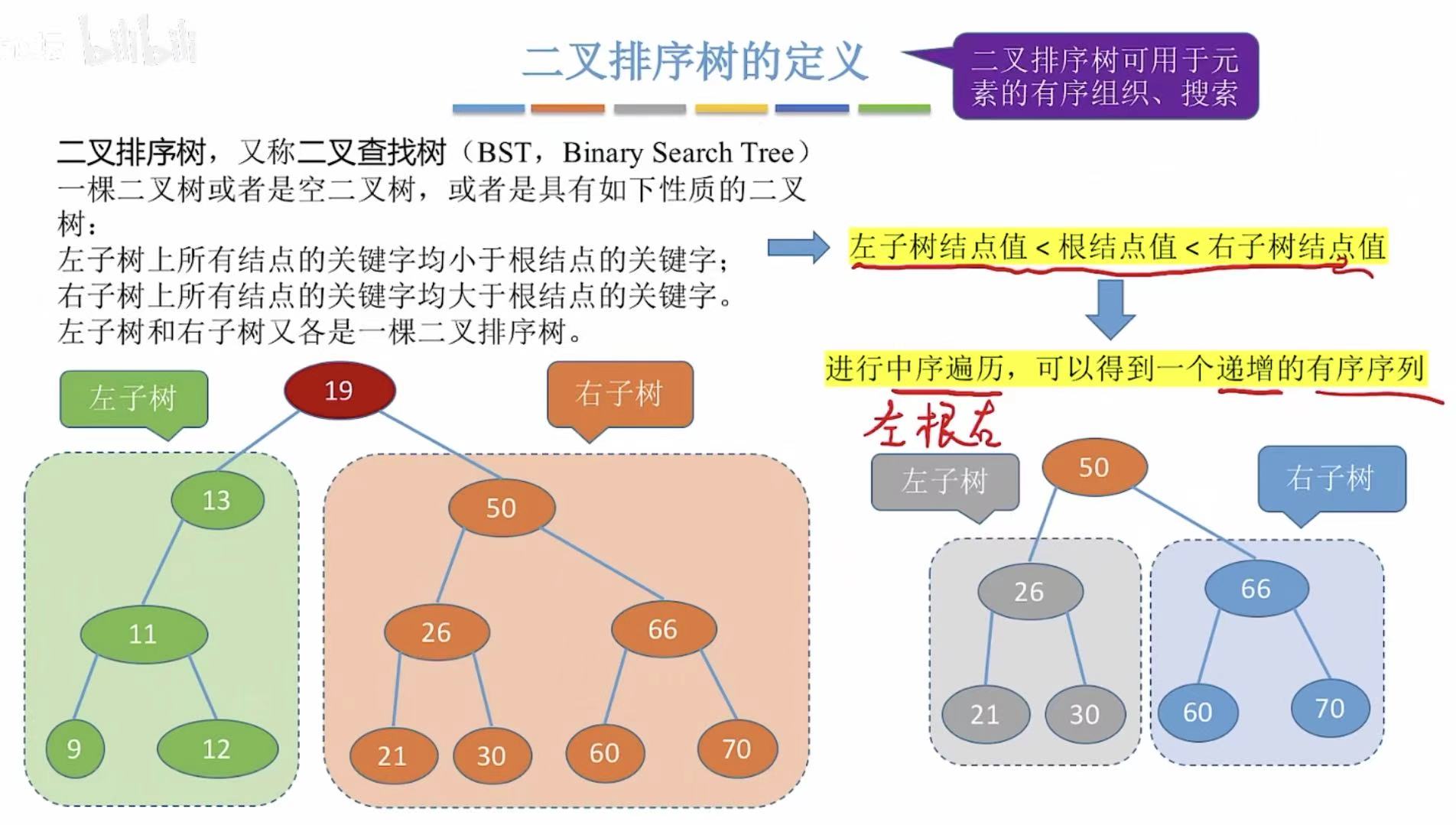
1. 定义

因为是用来查找的，肯定就会根据某种规则排序：

值大小：左<根<右

2. 操作

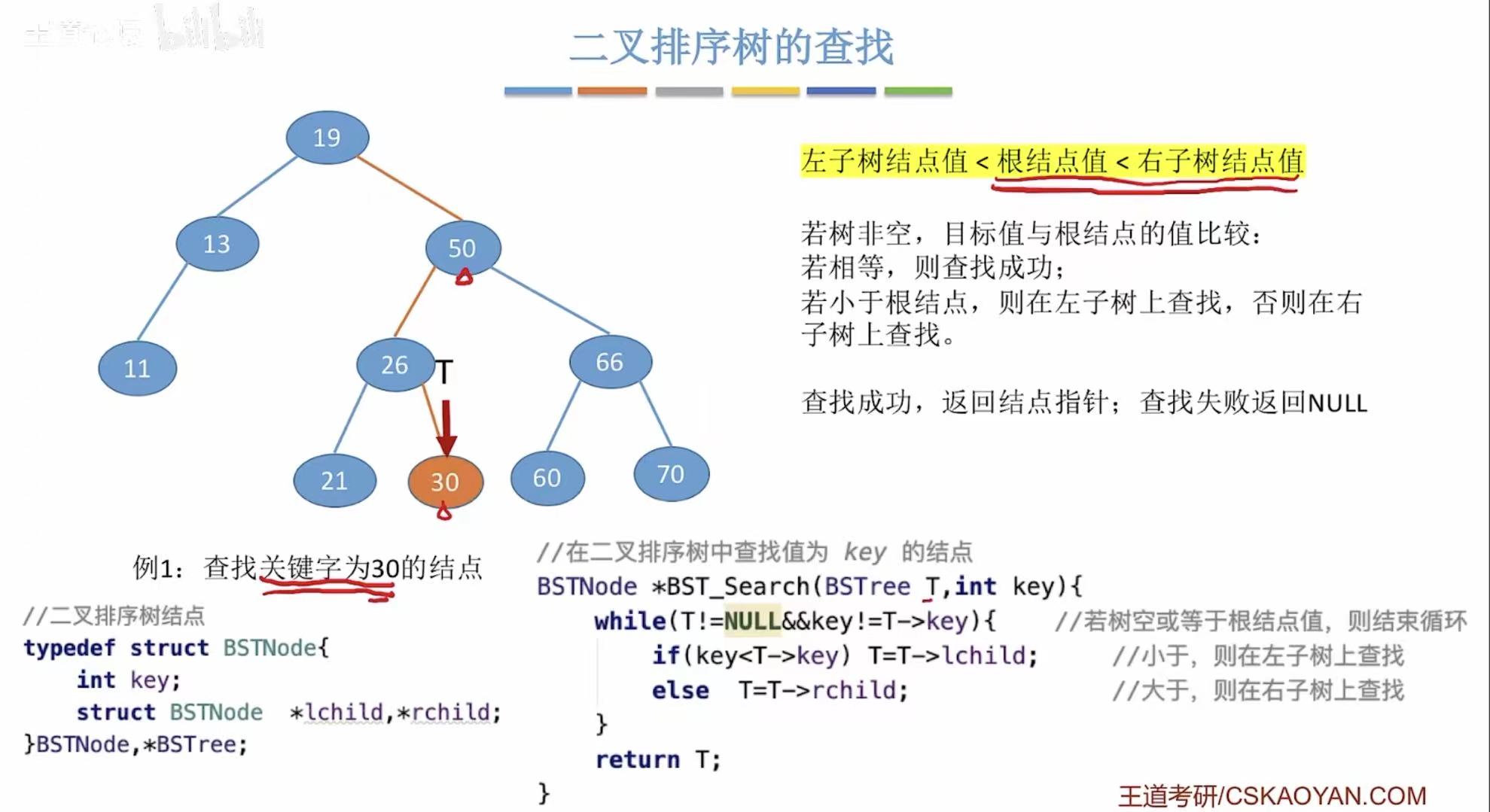
2.1 查找操作

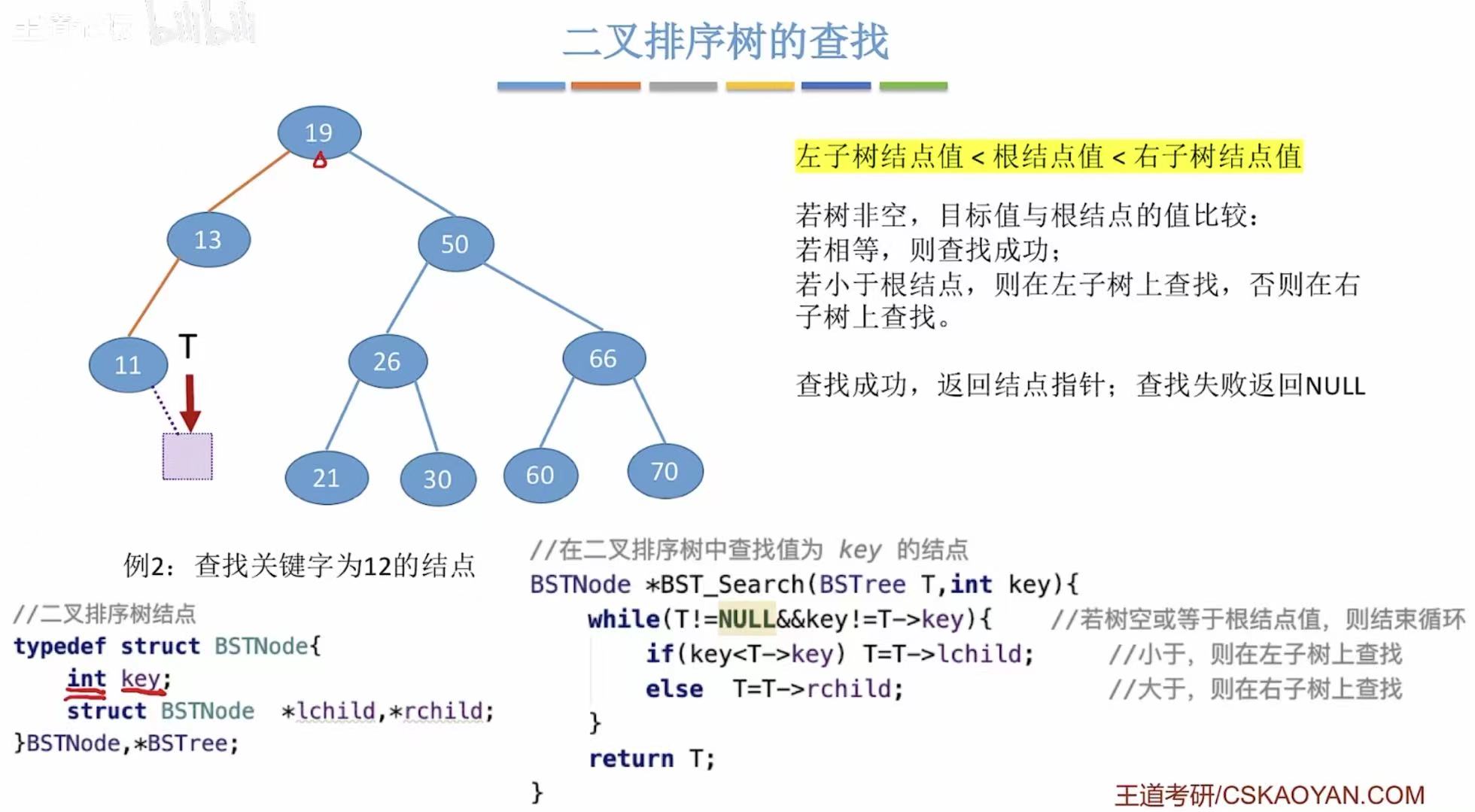
找30：

  • 30>19，去19的右子树
  • 30<50，去50的左子树
  • 30>26，去26的右子树
  • 30=30，查找成功

    找12：
  • 12<19，去19的左子树
  • 12<13，去13的左子树
  • 12>11，去11的右子树
  • 11的右子树为空，查找失败

    迭代实现（非递归）
java 复制代码 
// 在二叉排序树 T 中查找关键字 key 的结点（迭代实现）
BSTNode *BST_Search(BSTree T, int key) {
    // 循环条件：只要树不为空且当前结点的值不等于 key，就继续查找
    while (T != NULL && key != T->key) {
        // 如果 key 小于当前结点的值，则在左子树中查找
        if (key < T->key)
            T = T->lchild;   // 移动到左孩子

        // 如果 key 大于当前结点的值，则在右子树中查找
        else
            T = T->rchild;   // 移动到右孩子
    }

    // 循环结束时，T 要么是 NULL（未找到），要么是目标结点（找到了）
    return T;
}

递归实现

java 复制代码 
// 在二叉排序树 T 中查找关键字 key 的结点（递归实现）
BSTNode *BSTSearch(BSTree T, int key) {
    // 若树为空，说明查找失败
    if (T == NULL)
        return NULL;

    // 若当前结点的值等于 key，查找成功
    if (key == T->key)
        return T;

    // 若 key 小于当前结点的值，在左子树中递归查找
    else if (key < T->key)
        return BSTSearch(T->lchild, key);

    // 若 key 大于当前结点的值，在右子树中递归查找
    else
        return BSTSearch(T->rchild, key);
}

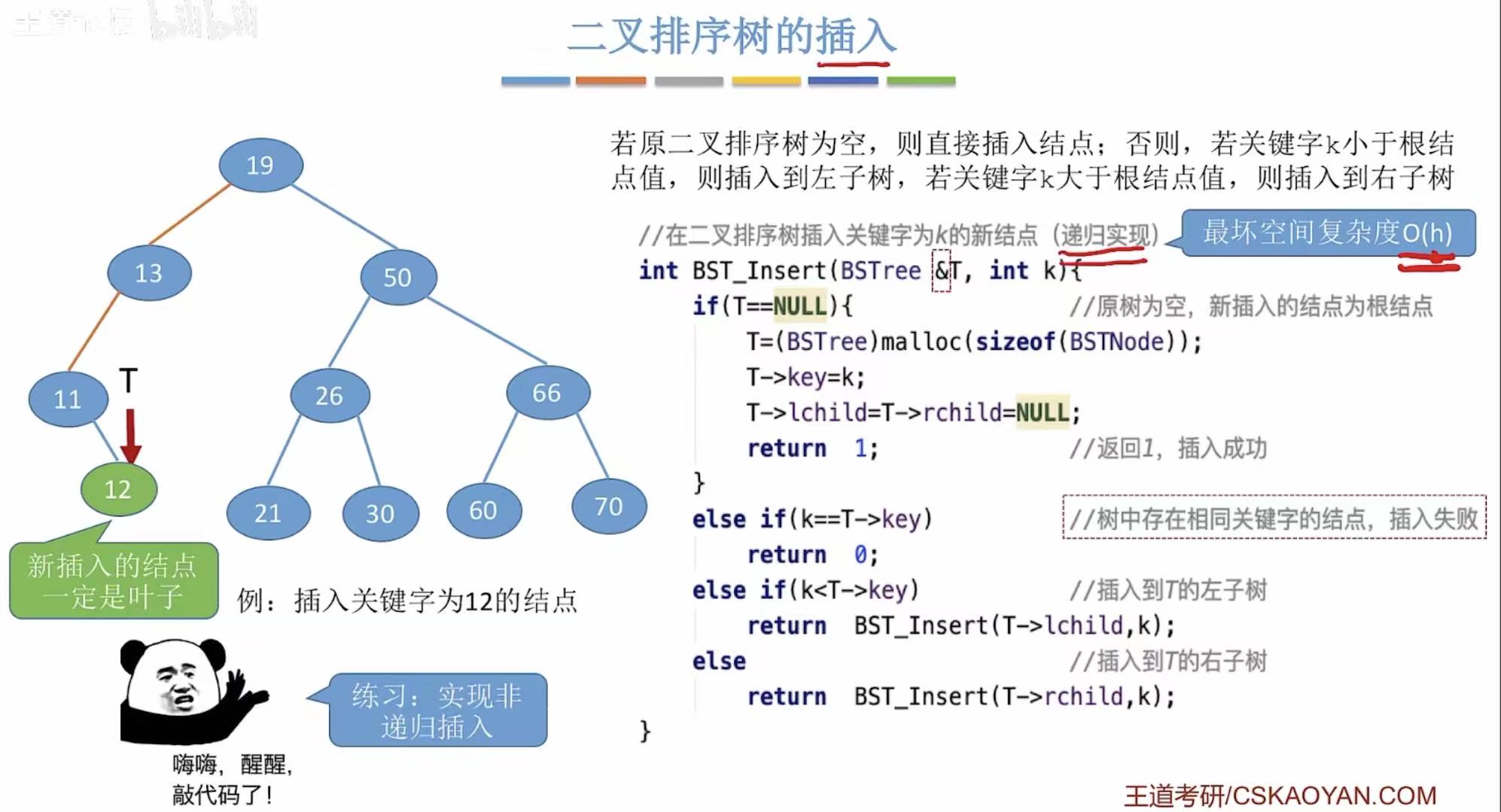
2.2 插入操作

递归插入：

java 复制代码 
// 在二叉排序树 T 中插入关键字为 k 的新结点（递归实现）
int BST_Insert(BSTree T, int k) {
    // 若原树为空，则创建新结点作为根
    if (T == NULL) {
        T = (BSTree)malloc(sizeof(BSTNode));   // 动态分配内存
        T->key = k;                            // 设置键值
        T->lchild = T->rchild = NULL;          // 左右子树为空
        return 1;                              // 插入成功，返回 1
    }

    // 若树中已存在相同关键字的结点，插入失败
    else if (k == T->key)
        return 0;

    // 若 k < 当前结点值，则在左子树中递归插入
    else if (k < T->key)
        return BST_Insert(T->lchild, k);

    // 若 k > 当前结点值，则在右子树中递归插入
    else
        return BST_Insert(T->rchild, k);
}

非递归插入：

java 复制代码 
// 非递归插入：在 BST 中插入关键字 k
// 返回值：1 表示成功，0 表示失败（已存在）
int BST_Insert_NonRec(BSTree *T, int k) {
    BSTree p = *T;           // p 指向当前结点
    BSTree parent = NULL;    // parent 指向 p 的父结点

    // 从根开始向下查找插入位置
    while (p != NULL) {
        if (k == p->key) {
            return 0;         // 关键字已存在，插入失败
        }
        parent = p;           // 记录父结点
        if (k < p->key) {
            p = p->lchild;    // 向左子树移动
        } else {
            p = p->rchild;    // 向右子树移动
        }
    }

    // 此时 p == NULL，找到了插入位置
    // 创建新结点
    BSTree newNode = (BSTree)malloc(sizeof(BSTNode));
    newNode->key = k;
    newNode->lchild = newNode->rchild = NULL;

    // 根据 parent 的 key 值决定插入到左还是右
    if (k < parent->key) {
        parent->lchild = newNode;
    } else {
        parent->rchild = newNode;
    }

    return 1; // 插入成功
}

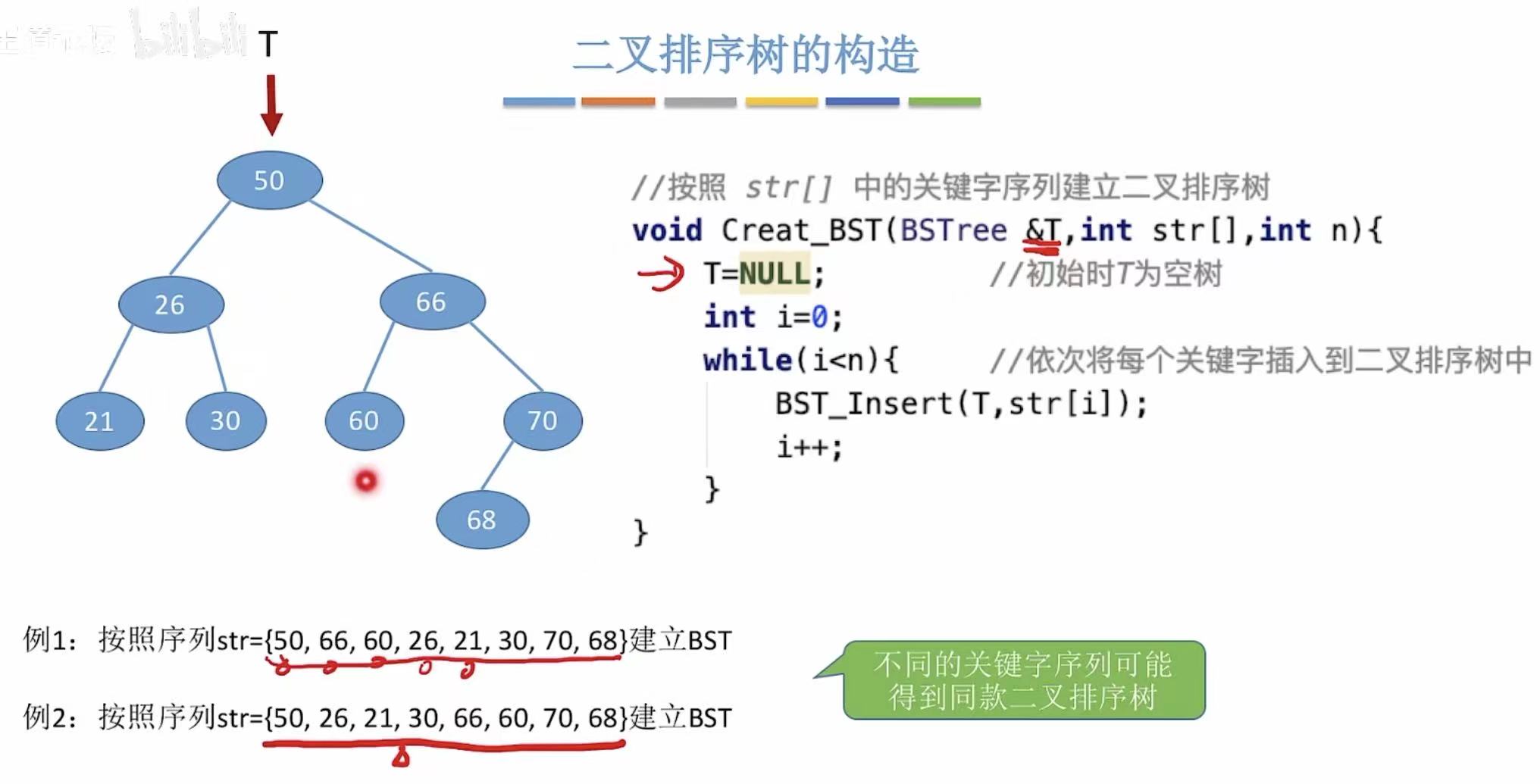
不同的关键字序列可能会得到同款二叉排序树。

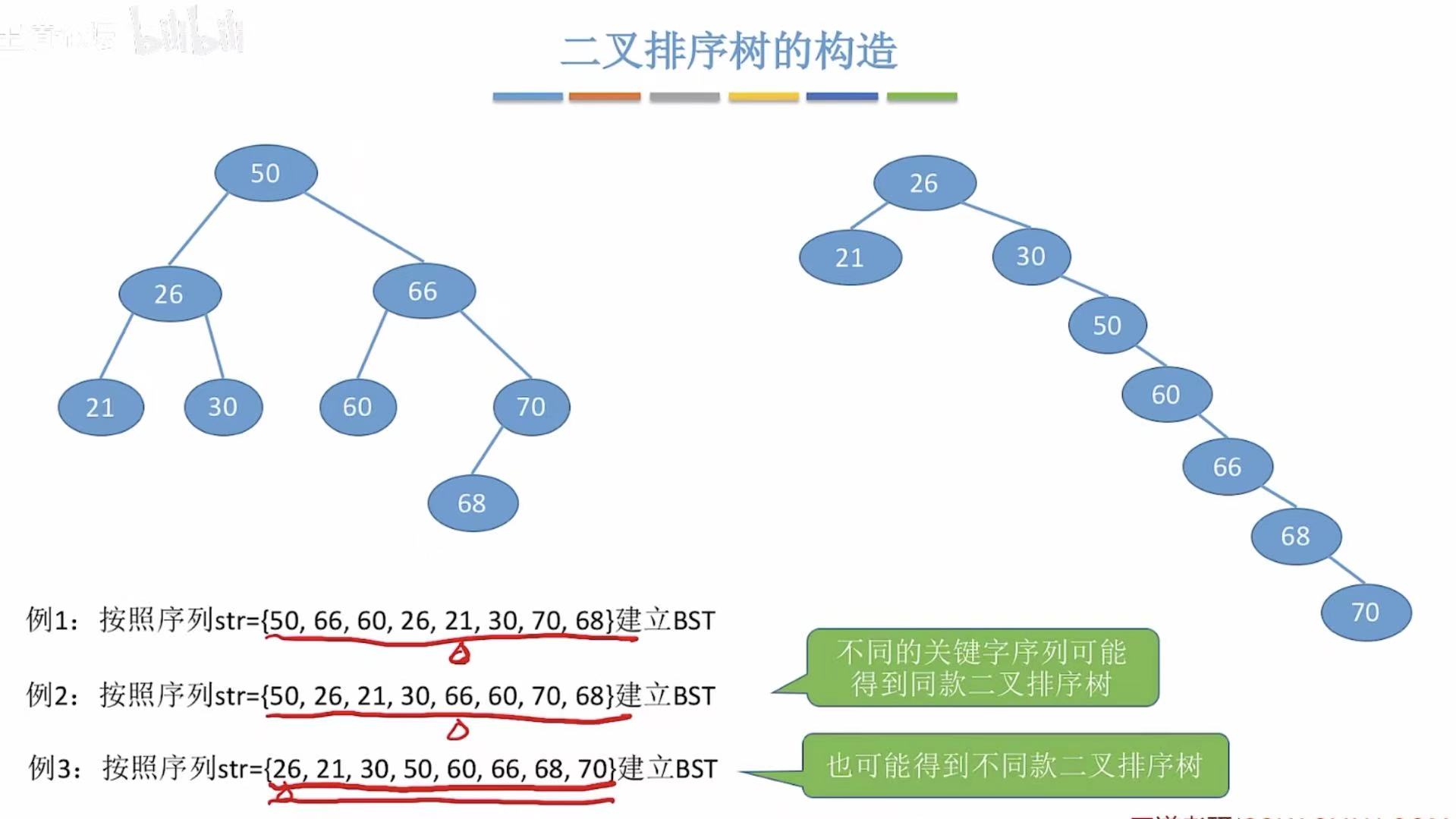
也可能得到不同款的二叉排序树。

2.3 删除操作

  1. 叶节点直接删除
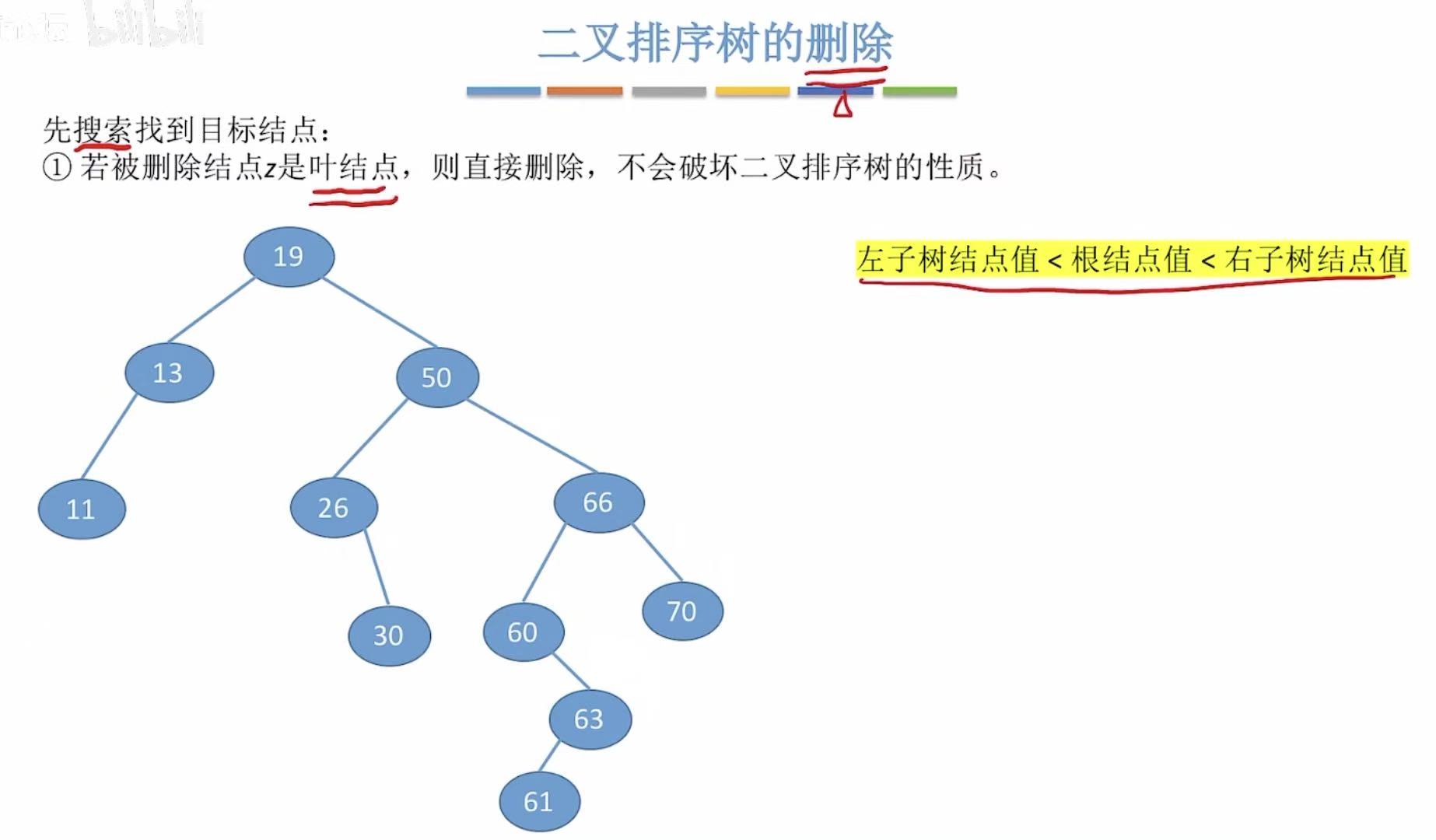
  2. 只有一个儿子，就让儿子代替自己的位置
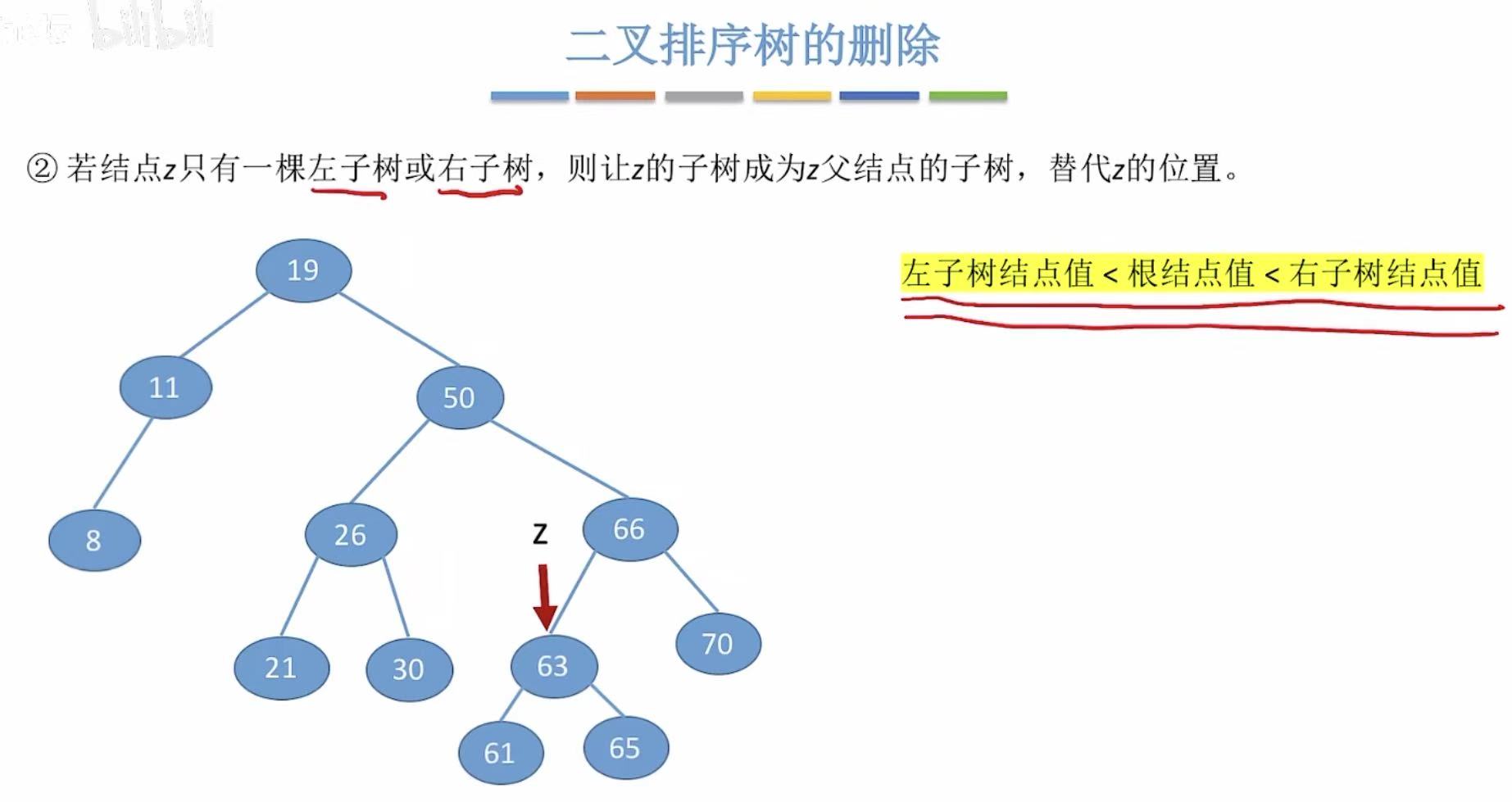
  3. 有两个儿子，就用自己合适的后代代替自己的位置（右左左）。
    比如要删除50，就用它右子树的左孩子来代替自己的位置。

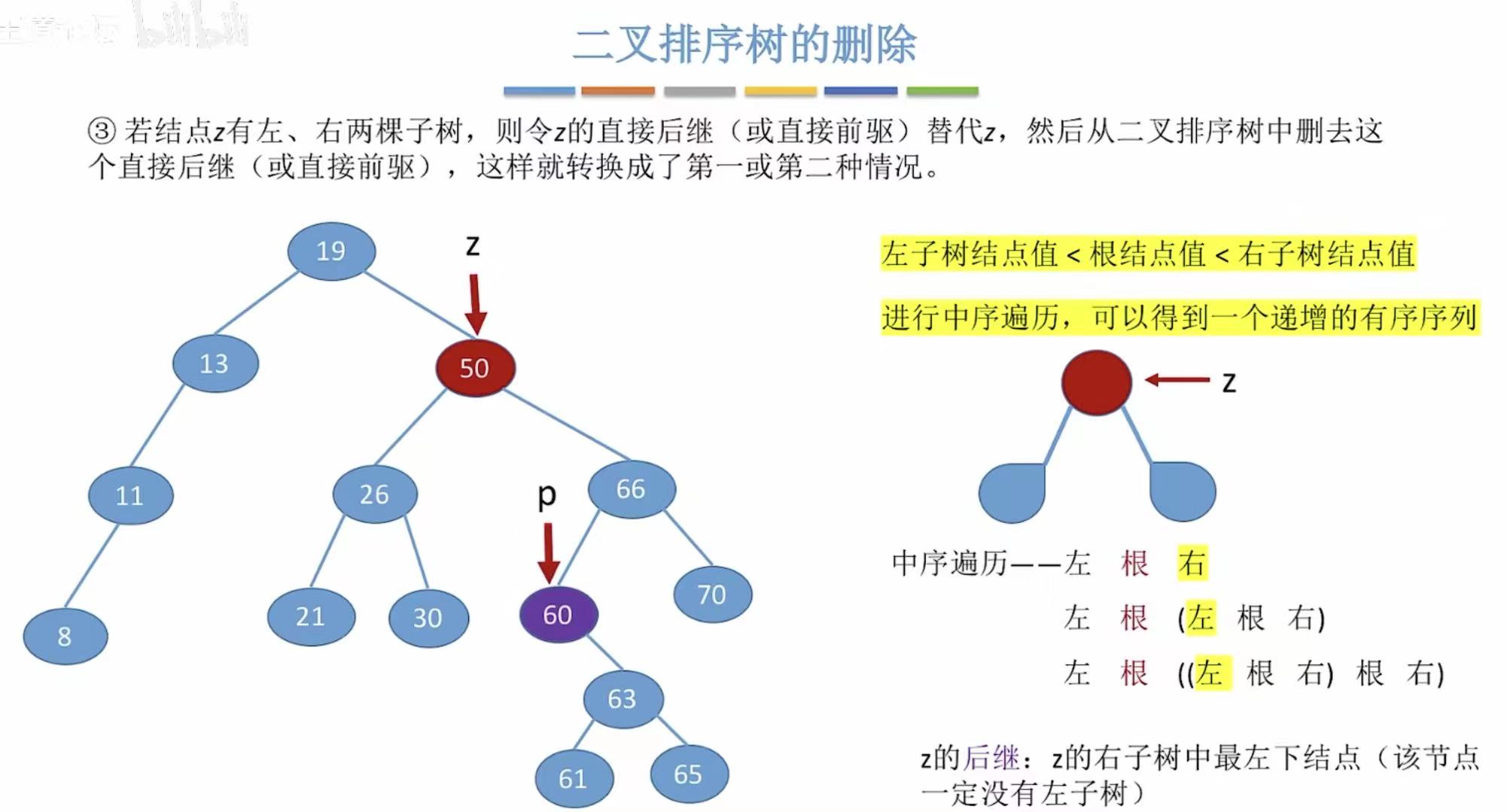
    60直接代替50的位置：
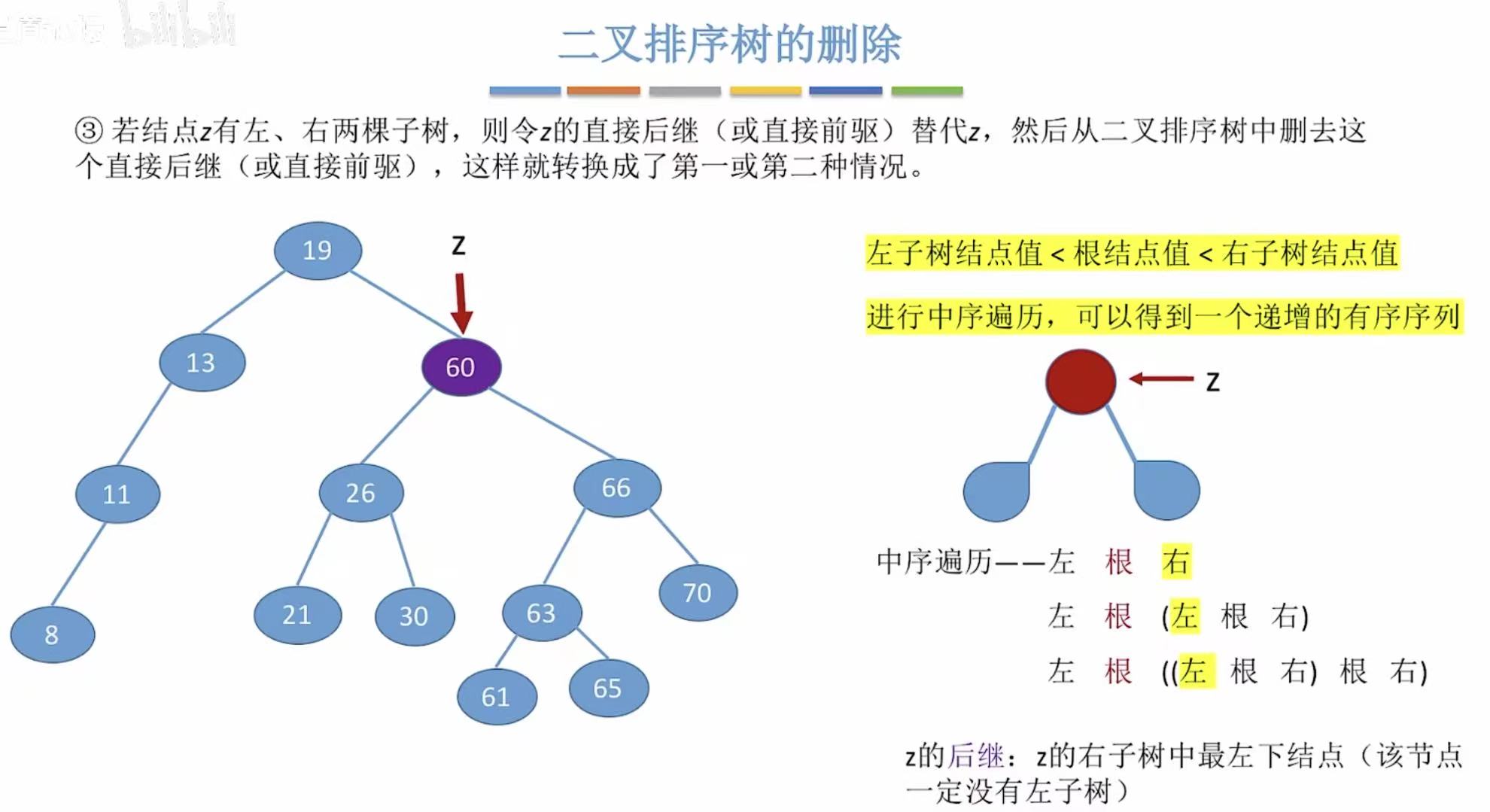
  4. 有两个儿子，就用自己合适的后代代替自己的位置（左右右）。
    比如要删除50，就用它左子树的右孩子来代替自己的位置。

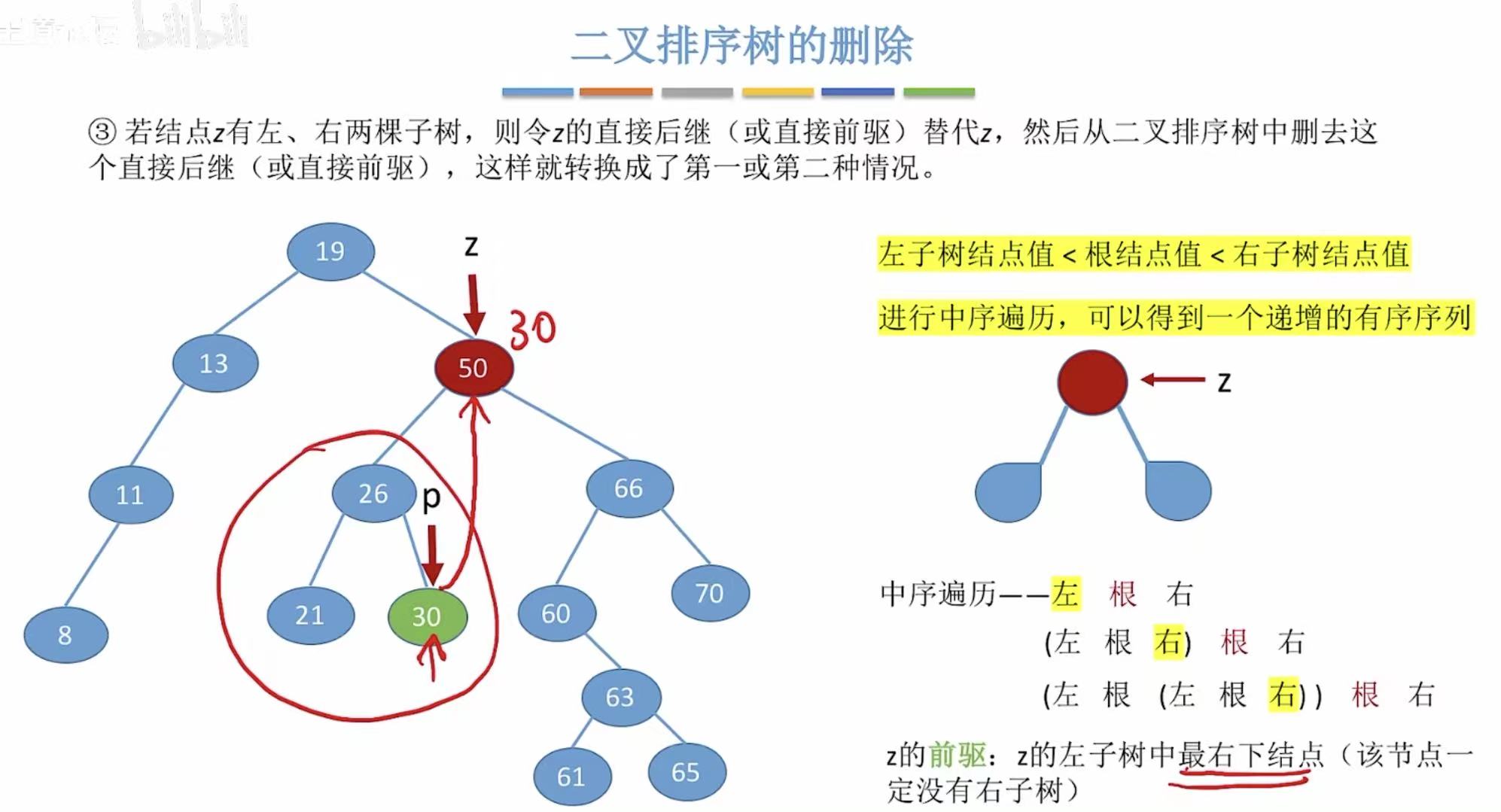
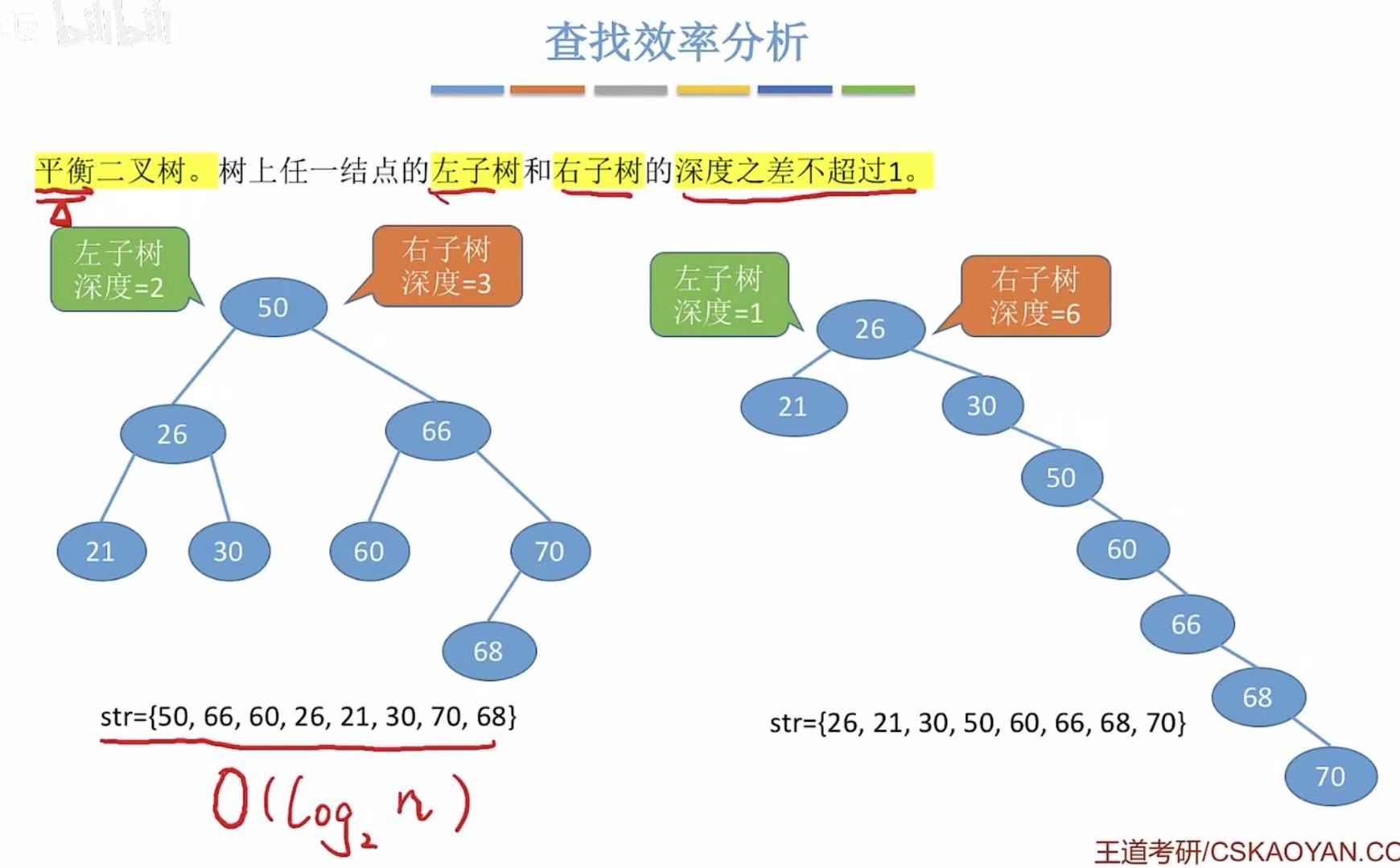
3. 查找效率分析


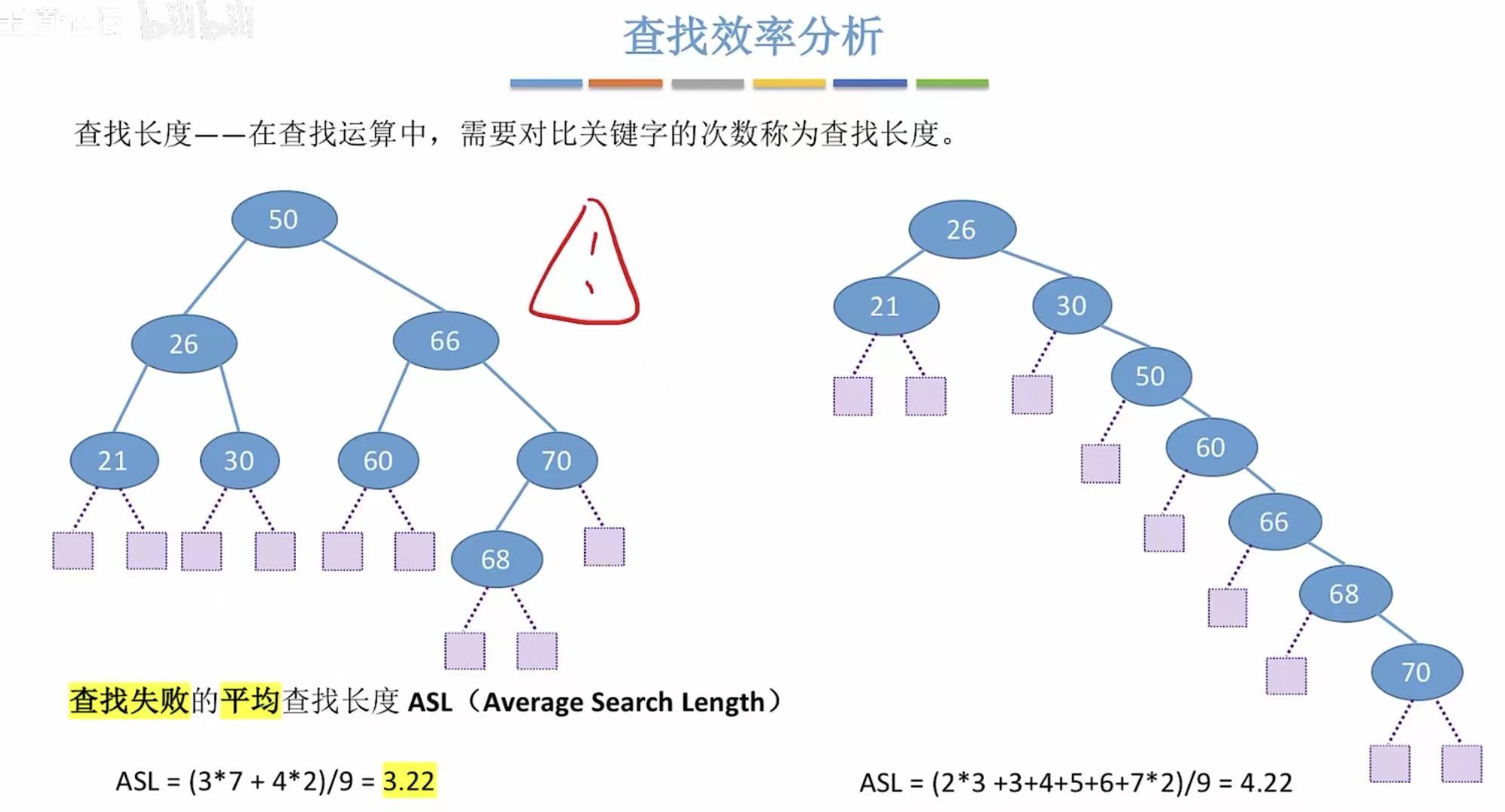
4. 小结

相关推荐
lifallen1 小时前
CDQ 分治 (CDQ Divide and Conquer)
java·数据结构·算法
洛豳枭薰2 小时前
Redis 基础数据结构
数据结构·redis
ValhallaCoder2 小时前
hot100-二分查找
数据结构·python·算法·二分查找
m0_531237172 小时前
C语言-指针,结构体
c语言·数据结构·算法
丰海洋2 小时前
leetcode-hot100-1.两数之和
数据结构·算法·leetcode
苦藤新鸡2 小时前
58 单词搜索
数据结构·算法
RelishCoding2 小时前
02-二分查找
数据结构
im_AMBER3 小时前
Leetcode 123 二叉树的层平均值 | 二叉树的右视图 | 二叉树的层序遍历
数据结构·学习·算法·leetcode·二叉树
样例过了就是过了3 小时前
LeetCode热题100 轮转数组
数据结构·算法·leetcode
热门推荐
01从零搭建一个 PHP 登录注册系统（含完整源码）02使用 1panel面板 部署 php网站03GitHub 镜像站点04AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot05PHP Error: 常见错误及其解决方法06Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services07MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法08如何将 TRAE IDE 的插件市场源切换至 VS Code 官方市场09openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）