FA :formulas and algorithm,PC :planning and control,PRM:Probabilistic Roadmap Method
一、PRM 核心原理与数学基础
1. 核心定义
概率路图法(Probabilistic Roadmap Method)是一种基于采样的离线路径规划算法,核心思想是:
- 先在机器人的构型空间(C 空间) 中随机采样大量无碰撞的节点(构型);
- 将这些节点连接成一个连通的图(路图),仅保留无碰撞的边;
- 当需要规划路径时,只需在预先生成的路图上用图搜索算法(如 Dijkstra、A*)找起点到终点的路径。
2. 关键数学概念
- 构型空间(C 空间) :描述机器人所有可能姿态的空间,2D 平面移动机器人的 C 空间是(x,y)(x,y)(x,y),记为C⊆R2C⊆R^2C⊆R2;
- 自由空间(CfreeC_{free}Cfree) :C 空间中无碰撞的区域,Cfree=q∈C∣q无碰撞C_{free}={q∈C∣q 无碰撞}Cfree=q∈C∣q无碰撞;
- 障碍空间(CobsC_{obs}Cobs) :C 空间中有碰撞的区域,Cobs=C∖CfreeC_{obs}=C∖C_{free}Cobs=C∖Cfree;
- 邻域半径(rrr):每个采样节点仅连接其邻域内的其他节点,避免全连接导致的计算爆炸;
- 采样概率 :PRM 通过随机采样覆盖Cfree,采样点满足均匀分布q∼Uniform(CfreeC_{free}Cfree)。
3. 算法推导(核心公式)
PRM 的目标是构建路图G=(V,E)G=(V,E)G=(V,E),其中:
- 节点集V⊆CfreeV⊆C_{free}V⊆Cfree,满足∀q∈V,q∈/Cobs∀q∈V,q∈/C_{obs}∀q∈V,q∈/Cobs;
- 边集 E=(qi,qj)∣qi,qj∈VE={(q_i,q_j)∣q_i,q_j∈V}E=(qi,qj)∣qi,qj∈V,线段 qiqj⊆Cfree,∥qi−qj∥≤r{q_iq_j⊆C_{free},∥q_i−q_j∥≤r}qiqj⊆Cfree,∥qi−qj∥≤r;
路径规划阶段,需将起点qstartq_{start}qstart和终点qgoalq_{goal}qgoal加入路图,再求解最短路径:
Path=argminP∈P(qstart,qgoal)∑(qi,qj)∈P∥qi−qj∥Path=arg min_{P∈P(q_{start},q_{goal})} \sum_{(q_i,q_j)∈P}∥q_i−q_j∥Path=argminP∈P(qstart,qgoal)∑(qi,qj)∈P∥qi−qj∥
其中P(qstart,qgoal)P(q_{start},q_{goal})P(qstart,qgoal)是路图中从起点到终点的所有可行路径集合。
二、PRM 操作步骤(标准流程)
PRM 分为离线建图 和在线查询两个阶段,具体步骤如下:
阶段 1:离线构建概率路图
- 初始化:设定采样点数N、邻域半径r,初始化空路图G=(V,E);
- 随机采样:在 C 空间中随机生成N个采样点,过滤掉落在障碍空间Cobs的点,将剩余无碰撞点加入节点集V;
- 邻域搜索:对每个节点qi∈V,找到所有满足∥qi−qj∥≤r的节点qj∈V;
- 碰撞检测:对每对邻域节点(qi,qj),检查连接它们的线段是否与障碍物碰撞,无碰撞则将边(qi,qj)加入边集E;
- 保存路图:完成所有节点和边的构建,保存路图G。
阶段 2:在线路径查询
- 加入起止点 :将起点qstartq_{start}qstart和终点qgoalq_{goal}qgoal加入节点集VVV,并分别与邻域内的节点建立无碰撞边;
- 图搜索 :用 Dijkstra 或 A * 算法在路图G 中搜索从qstartq_{start}qstart到qgoalq_{goal}qgoal的最短路径;
- 输出路径:若找到路径则返回,否则返回 "无可行路径"。
三、Python 代码示例(2D 平面 PRM 实现)
下面是一个可直接运行的 2D 平面 PRM 实现,包含采样、建图、路径搜索全流程,注释详细且易理解。
示例一
前置依赖
先安装必要库:
bash
pip install numpy matplotlib networkx完整代码
bash
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from math import sqrt
class PRMPlanner:
def __init__(self, obstacle_list, sample_n=200, radius=1.0):
"""
初始化PRM规划器
:param obstacle_list: 障碍物列表,每个障碍物为(x, y, 半径)
:param sample_n: 采样节点数量
:param radius: 邻域搜索半径
"""
self.obstacle_list = obstacle_list # 障碍物集合
self.sample_n = sample_n # 采样点数
self.radius = radius # 邻域半径
self.graph = nx.Graph() # 概率路图(用networkx存储)
def random_sample(self):
"""随机采样无碰撞节点,返回采样点列表"""
sample_points = []
while len(sample_points) < self.sample_n:
# 在[0, 10]x[0, 10]的2D空间中随机采样
x = np.random.uniform(0, 10)
y = np.random.uniform(0, 10)
point = (x, y)
# 检查采样点是否与障碍物碰撞
if not self.is_collision(point, None):
sample_points.append(point)
return sample_points
def is_collision(self, point1, point2):
"""
碰撞检测:
- 若point2为None:检查point1是否在障碍物内
- 若point2不为None:检查point1到point2的线段是否与障碍物碰撞
"""
# 检查点碰撞
if point2 is None:
x, y = point1
for (ox, oy, r) in self.obstacle_list:
if sqrt((x - ox)**2 + (y - oy)**2) <= r:
return True # 碰撞
return False
# 检查线段碰撞(点1到点2)
x1, y1 = point1
x2, y2 = point2
for (ox, oy, r) in self.obstacle_list:
# 计算线段到障碍物中心的最短距离
dx = x2 - x1
dy = y2 - y1
a = dx**2 + dy**2
b = 2 * (dx*(x1 - ox) + dy*(y1 - oy))
c = (x1 - ox)**2 + (y1 - oy)**2 - r**2
discriminant = b**2 - 4*a*c
if discriminant < 0:
continue # 无交点
t1 = (-b - sqrt(discriminant)) / (2*a)
t2 = (-b + sqrt(discriminant)) / (2*a)
# 检查交点是否在线段上(t∈[0,1])
if (0 <= t1 <= 1) or (0 <= t2 <= 1):
return True # 碰撞
return False
def build_roadmap(self):
"""构建概率路图"""
# 1. 随机采样无碰撞节点
sample_points = self.random_sample()
# 2. 将采样点加入图中(节点用索引标识,属性存储坐标)
for i, point in enumerate(sample_points):
self.graph.add_node(i, pos=point)
# 3. 邻域搜索并添加无碰撞边
for i in range(len(sample_points)):
p1 = sample_points[i]
for j in range(i+1, len(sample_points)):
p2 = sample_points[j]
# 检查距离是否在邻域半径内
dist = sqrt((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)
if dist <= self.radius:
# 检查线段是否碰撞
if not self.is_collision(p1, p2):
# 添加边,权重为距离
self.graph.add_edge(i, j, weight=dist)
return sample_points
def plan(self, start, goal):
"""
路径规划:将起止点加入路图,搜索最短路径
:param start: 起点坐标 (x,y)
:param goal: 终点坐标 (x,y)
:return: 可行路径列表(坐标点),若无则返回None
"""
# 检查起止点是否在障碍物内
if self.is_collision(start, None) or self.is_collision(goal, None):
print("起点/终点在障碍物内,无可行路径")
return None
# 1. 将起止点加入图中
sample_points = list(nx.get_node_attributes(self.graph, 'pos').values())
start_idx = len(sample_points)
goal_idx = len(sample_points) + 1
self.graph.add_node(start_idx, pos=start)
self.graph.add_node(goal_idx, pos=goal)
# 2. 连接起止点与邻域内的节点
for i, p in enumerate(sample_points):
# 连接起点
dist_start = sqrt((start[0]-p[0])**2 + (start[1]-p[1])**2)
if dist_start <= self.radius and not self.is_collision(start, p):
self.graph.add_edge(start_idx, i, weight=dist_start)
# 连接终点
dist_goal = sqrt((goal[0]-p[0])**2 + (goal[1]-p[1])**2)
if dist_goal <= self.radius and not self.is_collision(goal, p):
self.graph.add_edge(goal_idx, i, weight=dist_goal)
# 3. Dijkstra算法搜索最短路径
try:
path_idx = nx.dijkstra_path(self.graph, start_idx, goal_idx, weight='weight')
except nx.NetworkXNoPath:
print("未找到可行路径")
return None
# 4. 将索引转换为坐标
path = [self.graph.nodes[idx]['pos'] for idx in path_idx]
return path
def plot_result(self, start, goal, path):
"""可视化结果"""
plt.figure(figsize=(8, 8))
# 绘制障碍物
for (ox, oy, r) in self.obstacle_list:
circle = plt.Circle((ox, oy), r, color='gray', alpha=0.5)
plt.gca().add_patch(circle)
# 绘制路图节点
node_pos = nx.get_node_attributes(self.graph, 'pos')
nx.draw_networkx_nodes(self.graph, node_pos, node_size=10, node_color='blue')
# 绘制路图边
nx.draw_networkx_edges(self.graph, node_pos, edge_color='lightblue', alpha=0.3)
# 绘制路径
if path is not None:
path_x = [p[0] for p in path]
path_y = [p[1] for p in path]
plt.plot(path_x, path_y, color='red', linewidth=2, label='Path')
# 绘制起止点
plt.scatter(start[0], start[1], color='green', s=100, label='Start')
plt.scatter(goal[0], goal[1], color='orange', s=100, label='Goal')
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.grid(True)
plt.legend()
plt.title('PRM Path Planning')
plt.show()
# ---------------------- 测试代码 ----------------------
if __name__ == "__main__":
# 定义障碍物(x, y, 半径)
obstacles = [
(2, 2, 1),
(5, 5, 1.5),
(8, 2, 1),
(4, 8, 1)
]
# 初始化PRM规划器
prm = PRMPlanner(obstacle_list=obstacles, sample_n=200, radius=1.5)
# 构建路图
prm.build_roadmap()
# 定义起止点
start_point = (1, 1)
goal_point = (9, 9)
# 路径规划
path = prm.plan(start_point, goal_point)
# 可视化
prm.plot_result(start_point, goal_point, path)
# 输出路径坐标
if path is not None:
print("规划路径坐标:")
for i, p in enumerate(path):
print(f"点{i}: {p}")代码关键部分解释
- 碰撞检测函数(is_collision) :
- 点碰撞:判断采样点是否在障碍物圆形区域内;
- 线段碰撞:通过求解线段与圆的交点,判断是否有交点且交点在线段上。
- 路图构建(build_roadmap):
- 用 networkx 存储图结构,节点存储坐标,边存储距离权重;
- 仅连接邻域内无碰撞的节点,避免全连接。
- 路径搜索(plan):
- 将起止点加入路图并连接邻域节点;
- 调用 networkx 的 Dijkstra 算法找最短路径。
- 可视化(plot_result):
- 绘制障碍物、路图、起止点和规划路径,直观展示结果。
运行结果说明
运行代码后会弹出可视化窗口,蓝色小点是采样节点,浅蓝色线是路图边,红色线是规划的路径;
绿色点是起点,橙色点是终点,灰色圆形是障碍物;
控制台会输出路径的坐标点列表。示例二
bash
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
from celluloid import Camera # 保存动图时用,pip install celluloid
import time
# ==================== PRM核心参数(优化版)====================
N_SAMPLE = 2000 # 采样点数量
N_KNN = 30 # 邻域点个数
MAX_EDGE_LEN = 30.0 # 最大边长度
ROBOT_RADIUS = 1.5 # 机器人半径
show_animation = True
ANIMATION_INTERVAL = 20 # 动画间隔(毫秒)
PLOT_PAUSE_TIME = 0.001 # 绘图暂停时间
# 强制设置matplotlib后端(解决动画显示问题)
plt.switch_backend('TkAgg')
# 设置matplotlib参数
plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'Arial']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.figsize'] = (12, 10)
plt.rcParams['animation.html'] = 'jshtml'
class Node:
"""Dijkstra搜索节点类"""
def __init__(self, x, y, cost, parent_index):
self.x = x
self.y = y
self.cost = cost
self.parent_index = parent_index
def __str__(self):
return f"{self.x:.1f},{self.y:.1f},{self.cost:.1f},{self.parent_index}"
def prm_planning(start_x, start_y, goal_x, goal_y, obstacle_x_list, obstacle_y_list, robot_radius, *, ax=None, camera=None, rng=None):
"""PRM主规划函数:采样→建路网→Dijkstra搜索"""
print(f"\n📊 PRM参数:采样点={N_SAMPLE}, 邻域数={N_KNN}, 最大边长度={MAX_EDGE_LEN}, 机器人半径={robot_radius}")
# 构建障碍物KD树
obstacle_kd_tree = KDTree(np.vstack((obstacle_x_list, obstacle_y_list)).T)
# 1. 生成无碰撞采样点集
print("🔄 正在生成采样点...")
sample_x, sample_y = sample_points(
start_x, start_y, goal_x, goal_y,
robot_radius, obstacle_x_list, obstacle_y_list,
obstacle_kd_tree, rng
)
print(f"✅ 生成采样点数量:{len(sample_x)} (包含起点终点)")
if show_animation and ax is not None:
ax.plot(sample_x, sample_y, ".b", markersize=2, alpha=0.6, label="Sample Points")
plt.pause(PLOT_PAUSE_TIME)
if camera:
camera.snap()
# 2. 生成概率路图
print("🔄 正在构建概率路网...")
road_map = generate_road_map(sample_x, sample_y, robot_radius, obstacle_kd_tree, ax, camera)
# 统计路网连通性
total_edges = sum(len(edges) for edges in road_map)
print(f"✅ 路网构建完成,总边数:{total_edges}")
# 3. Dijkstra算法搜索最短路径
print("🔄 正在搜索最优路径...")
rx, ry = dijkstra_planning(
start_x, start_y, goal_x, goal_y,
road_map, sample_x, sample_y, ax, camera
)
return rx, ry
def is_collision(sx, sy, gx, gy, rr, obstacle_kd_tree):
"""优化的碰撞检测函数"""
dx = gx - sx
dy = gy - sy
d = math.hypot(dx, dy)
# 最大边长度放宽限制
if d > MAX_EDGE_LEN:
return True
# 优化的分段检测
step = max(1.0, rr / 2)
n_step = max(1, int(d / step))
yaw = math.atan2(dy, dx)
for i in range(n_step + 1):
x = sx + step * i * math.cos(yaw)
y = sy + step * i * math.sin(yaw)
dist, _ = obstacle_kd_tree.query([x, y])
if dist <= rr * 0.9:
return True
# 终点检测
dist, _ = obstacle_kd_tree.query([gx, gy])
if dist <= rr * 0.9:
return True
return False
def generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree, ax, camera):
"""优化的路网生成函数"""
road_map = []
n_sample = len(sample_x)
sample_kd_tree = KDTree(np.vstack((sample_x, sample_y)).T)
# 为每个采样点找更多邻域点
for i in range(n_sample):
ix, iy = sample_x[i], sample_y[i]
# 查询更多邻域点
k = min(N_KNN * 2, n_sample - 1)
dists, indexes = sample_kd_tree.query([ix, iy], k=k)
edge_ids = []
# 筛选无碰撞邻域点
for ii in range(1, len(indexes)):
nx = sample_x[indexes[ii]]
ny = sample_y[indexes[ii]]
if not is_collision(ix, iy, nx, ny, rr, obstacle_kd_tree):
edge_ids.append(indexes[ii])
if len(edge_ids) >= N_KNN:
break
road_map.append(edge_ids)
# 可视化路网构建过程
if show_animation and ax is not None and i % 50 == 0:
for neighbor_id in edge_ids:
ax.plot(
[sample_x[i], sample_x[neighbor_id]],
[sample_y[i], sample_y[neighbor_id]],
"-k", linewidth=0.3, alpha=0.2
)
plt.pause(PLOT_PAUSE_TIME)
if camera:
camera.snap()
return road_map
def dijkstra_planning(sx, sy, gx, gy, road_map, sample_x, sample_y, ax, camera):
"""优化的Dijkstra搜索函数"""
start_node = Node(sx, sy, 0.0, -1)
goal_node = Node(gx, gy, 0.0, -1)
open_set, closed_set = dict(), dict()
# 起点和终点索引
start_idx = len(road_map) - 2
goal_idx = len(road_map) - 1
open_set[start_idx] = start_node
# 打印起点终点信息
print(f"\n🎯 起点坐标: ({sx:.1f}, {sy:.1f}) (索引: {start_idx})")
print(f"🎯 终点坐标: ({gx:.1f}, {gy:.1f}) (索引: {goal_idx})")
path_found = True
search_count = 0
while True:
search_count += 1
# 无可行节点
if not open_set:
print("\n❌ 未找到可行路径!原因分析:")
print(f" - 搜索迭代次数: {search_count}")
print(f" - 起点邻域数: {len(road_map[start_idx])}")
print(f" - 终点邻域数: {len(road_map[goal_idx])}")
path_found = False
break
# 选择代价最小节点
current_id = min(open_set, key=lambda o: open_set[o].cost)
current_node = open_set[current_id]
# 每20步打印一次搜索状态
if search_count % 20 == 0:
print(f"🔍 搜索中 - 当前节点: ({current_node.x:.1f}, {current_node.y:.1f}), "
f"代价: {current_node.cost:.1f}, Open集大小: {len(open_set)}")
# 可视化搜索过程
if show_animation and ax is not None and search_count % 5 == 0:
ax.plot(current_node.x, current_node.y, "xg", markersize=5, alpha=0.8)
plt.pause(PLOT_PAUSE_TIME)
if camera:
camera.snap()
# 到达终点
if current_id == goal_idx:
print(f"\n✅ 找到目标点!总搜索步数: {search_count}")
goal_node.parent_index = current_node.parent_index
goal_node.cost = current_node.cost
break
# 移动节点
del open_set[current_id]
closed_set[current_id] = current_node
# 扩展邻域节点
for neighbor_id in road_map[current_id]:
nx = sample_x[neighbor_id]
ny = sample_y[neighbor_id]
cost = current_node.cost + math.hypot(nx - current_node.x, ny - current_node.y)
neighbor_node = Node(nx, ny, cost, current_id)
if neighbor_id in closed_set:
continue
if neighbor_id in open_set:
if open_set[neighbor_id].cost > cost:
open_set[neighbor_id].cost = cost
open_set[neighbor_id].parent_index = current_id
else:
open_set[neighbor_id] = neighbor_node
# 路径回溯
if not path_found:
return [], []
print("🔄 正在回溯路径...")
rx, ry = [goal_node.x], [goal_node.y]
parent_idx = goal_node.parent_index
path_length = 0
while parent_idx != -1:
if parent_idx in closed_set:
node = closed_set[parent_idx]
rx.append(node.x)
ry.append(node.y)
path_length += math.hypot(rx[-1]-rx[-2], ry[-1]-ry[-2])
parent_idx = node.parent_index
else:
print("⚠️ 路径回溯中断,父节点不存在")
break
# 关键修复:反转路径,使其从起点到终点
rx.reverse()
ry.reverse()
print(f"✅ 路径生成完成,路径长度: {path_length:.1f}, 路径点数: {len(rx)}")
# 立即绘制路径(确保路径被绘制)
if show_animation and ax is not None and rx:
ax.plot(rx, ry, "-r", linewidth=4, alpha=0.8, label="Planned Path", zorder=10)
ax.plot(rx, ry, "-w", linewidth=2, alpha=0.8, zorder=9) # 白色描边增强视觉效果
plt.pause(PLOT_PAUSE_TIME)
if camera:
camera.snap()
return rx, ry
def sample_points(sx, sy, gx, gy, rr, ox, oy, obstacle_kd_tree, rng):
"""优化的采样函数"""
max_x = max(ox) if ox else 100.0
max_y = max(oy) if oy else 100.0
min_x = min(ox) if ox else 0.0
min_y = min(oy) if oy else 0.0
sample_x, sample_y = [], []
if rng is None:
rng = np.random.default_rng()
# 增加采样效率
sample_attempts = 0
max_attempts = N_SAMPLE * 10
while len(sample_x) < N_SAMPLE and sample_attempts < max_attempts:
sample_attempts += 1
tx = rng.uniform(min_x + 5, max_x - 5)
ty = rng.uniform(min_y + 5, max_y - 5)
dist, _ = obstacle_kd_tree.query([tx, ty])
if dist >= rr * 0.8:
sample_x.append(tx)
sample_y.append(ty)
if len(sample_x) % 200 == 0:
print(f" 已采样: {len(sample_x)}/{N_SAMPLE}")
# 强制加入起点和终点
sample_x.append(sx)
sample_y.append(sy)
sample_x.append(gx)
sample_y.append(gy)
if sample_attempts >= max_attempts:
print(f"⚠️ 采样达到最大尝试次数 {max_attempts}")
return sample_x, sample_y
def create_complex_9area_obstacles():
"""构建9区域复杂障碍物场景"""
ox, oy = [], []
# 1. 外边界
for i in range(101):
ox.append(i), oy.append(0.0)
ox.append(i), oy.append(100.0)
ox.append(0.0), oy.append(i)
ox.append(100.0), oy.append(i)
# 2. 横向挡板(留更大缺口)
# 横向挡板1(y=30):x=0~15 + x=45~75
for i in range(0, 16):
ox.append(i), oy.append(30.0)
for i in range(45, 76):
ox.append(i), oy.append(30.0)
# 横向挡板2(y=70):x=25~55 + x=85~100
for i in range(25, 56):
ox.append(i), oy.append(70.0)
for i in range(85, 101):
ox.append(i), oy.append(70.0)
# 3. 纵向挡板(留更大缺口)
# 纵向挡板1(x=30):y=0~35 + y=65~100
for i in range(0, 36):
ox.append(30.0), oy.append(i)
for i in range(65, 101):
ox.append(30.0), oy.append(i)
# 纵向挡板2(x=70):y=25~45 + y=75~85
for i in range(25, 46):
ox.append(70.0), oy.append(i)
for i in range(75, 86):
ox.append(70.0), oy.append(i)
# 4. 额外障碍物(减小尺寸)
# 区域1:更小的矩形
for i in range(8, 12):
ox.append(i), oy.append(12.0)
ox.append(i), oy.append(18.0)
for i in range(12, 18):
ox.append(8.0), oy.append(i)
ox.append(12.0), oy.append(i)
# 区域5:更小的圆形
for theta in np.linspace(0, 2*math.pi, 50):
ox.append(50 + 6*math.cos(theta))
oy.append(50 + 6*math.sin(theta))
# 区域9:更短的斜向障碍
for i in range(85, 92):
ox.append(i), oy.append(82 + (i-85)*0.8)
ox.append(i), oy.append(88 + (i-85)*0.8)
return ox, oy
def main(rng=None):
print("="*60)
print("🚀 PRM Path Planning Algorithm (9-area Complex Scene)")
print("="*60)
# 创建图形和坐标轴
fig, ax = plt.subplots(1, 1, figsize=(12, 10))
camera = Camera(fig) if show_animation else None
# 设置坐标轴
ax.set_xlim(-5, 105)
ax.set_ylim(-5, 105)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title("PRM Algorithm - 9-area Complex Scene", fontsize=14, pad=20)
# 起点/终点
sx, sy = 10.0, 10.0 # 左上区域
gx, gy = 90.0, 90.0 # 右下区域
# 构建障碍物
ox, oy = create_complex_9area_obstacles()
# 初始化可视化
if show_animation:
# 绘制障碍物、起点、终点
ax.plot(ox, oy, ".k", markersize=1, label="Obstacles", zorder=1)
ax.plot(sx, sy, "^r", markersize=15, label="Start", zorder=7)
ax.plot(gx, gy, "^g", markersize=15, label="Goal", zorder=7)
# 添加图例
ax.legend(loc="upper right", fontsize=12, framealpha=0.9)
# 刷新显示
plt.pause(1.0) # 初始暂停1秒,让用户看清初始画面
if camera:
camera.snap()
# 执行PRM规划
start_time = time.time()
rx, ry = prm_planning(
sx, sy, gx, gy, ox, oy, ROBOT_RADIUS,
ax=ax, camera=camera, rng=rng
)
end_time = time.time()
print(f"\n⏱️ 总执行时间: {end_time - start_time:.2f} 秒")
# ========== 关键修复:确保最终路径绘制 ==========
if show_animation:
# 清除原有路径(避免重复)
for line in ax.get_lines():
if line.get_label() == "Planned Path":
line.remove()
# 重新绘制最终路径(确保显示)
if rx and ry and len(rx) > 1:
# 主路径 - 红色粗线
path_line = ax.plot(rx, ry, "-r", linewidth=5, alpha=0.9,
label="Final Path", zorder=8)[0]
# 路径描边 - 白色细线,增强视觉效果
ax.plot(rx, ry, "-w", linewidth=2, alpha=0.9, zorder=7)
# 高亮路径节点
ax.plot(rx, ry, "or", markersize=4, alpha=0.8, zorder=6)
# 更新标题和图例
ax.set_title("PRM Algorithm - Path Planning Successful!",
fontsize=16, color="darkgreen", pad=20)
ax.legend(loc="upper right", fontsize=12, framealpha=0.9)
print("\n🎉 最终路径已绘制完成!")
print(f"📏 路径详情:起点({sx:.1f},{sy:.1f}) → 终点({gx:.1f},{gy:.1f})")
print(f"📈 路径包含 {len(rx)} 个节点,总长度 {math.hypot(rx[-1]-rx[0], ry[-1]-ry[0]):.1f}")
else:
ax.set_title("PRM Algorithm - No Feasible Path Found",
fontsize=16, color="darkred", pad=20)
print("\n❌ 无法绘制路径:未找到可行路径")
# 强制刷新绘图
plt.draw()
plt.pause(2.0) # 暂停2秒查看结果
# 保存动图
if camera:
try:
print("\n📸 正在生成动画...")
animation = camera.animate(interval=ANIMATION_INTERVAL, repeat=True, repeat_delay=2000)
animation.save('prm_9area_animation.gif', writer='pillow', fps=20, dpi=120)
print("✅ 动画已保存为 prm_9area_animation.gif")
except Exception as e:
print(f"⚠️ 动画保存失败: {e}")
# 保存高清静态图
plt.savefig("prm_9area_final_result.png", dpi=200, bbox_inches="tight", facecolor='white')
print("✅ 最终结果图已保存为 prm_9area_final_result.png")
# 保持图形窗口打开
print("\n📺 路径规划完成!按关闭窗口退出程序...")
plt.show(block=True)
print("\n" + "="*60)
print("🏁 PRM algorithm execution completed")
print("="*60)
if __name__ == '__main__':
# 确保在主线程运行
import matplotlib
matplotlib.use('TkAgg')
main()运行结果
在整个区域内,抛洒概率点:
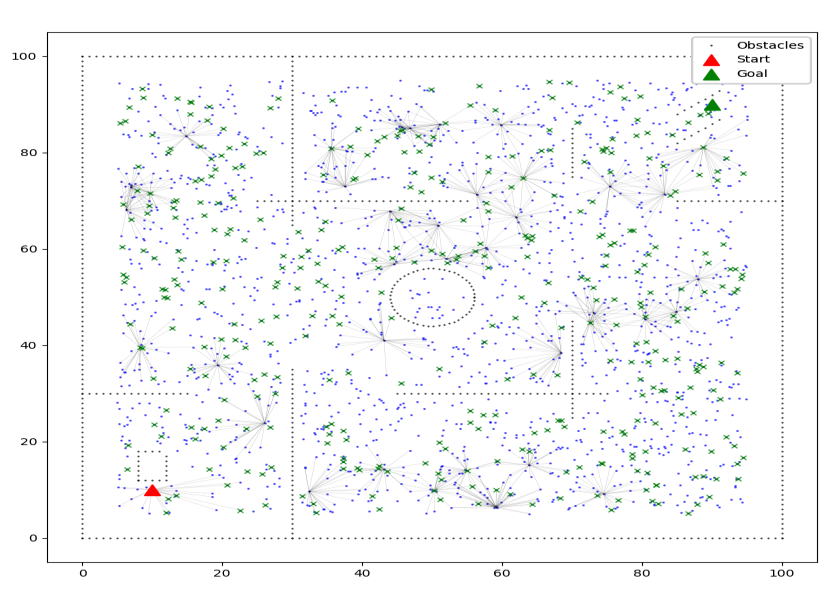
运行后的结果: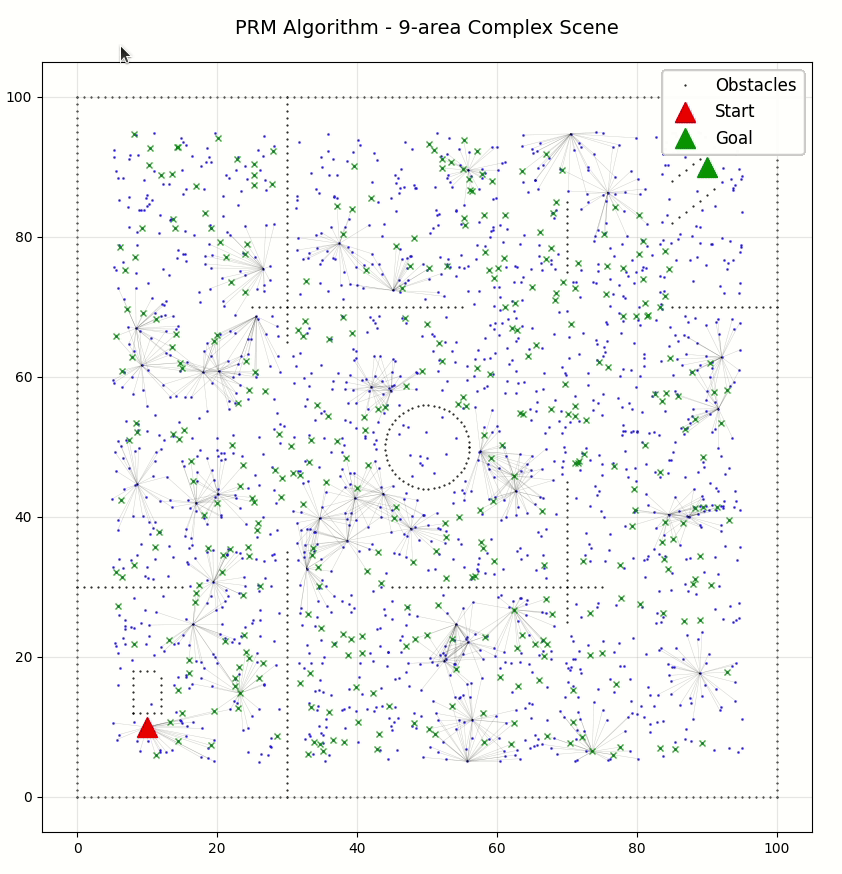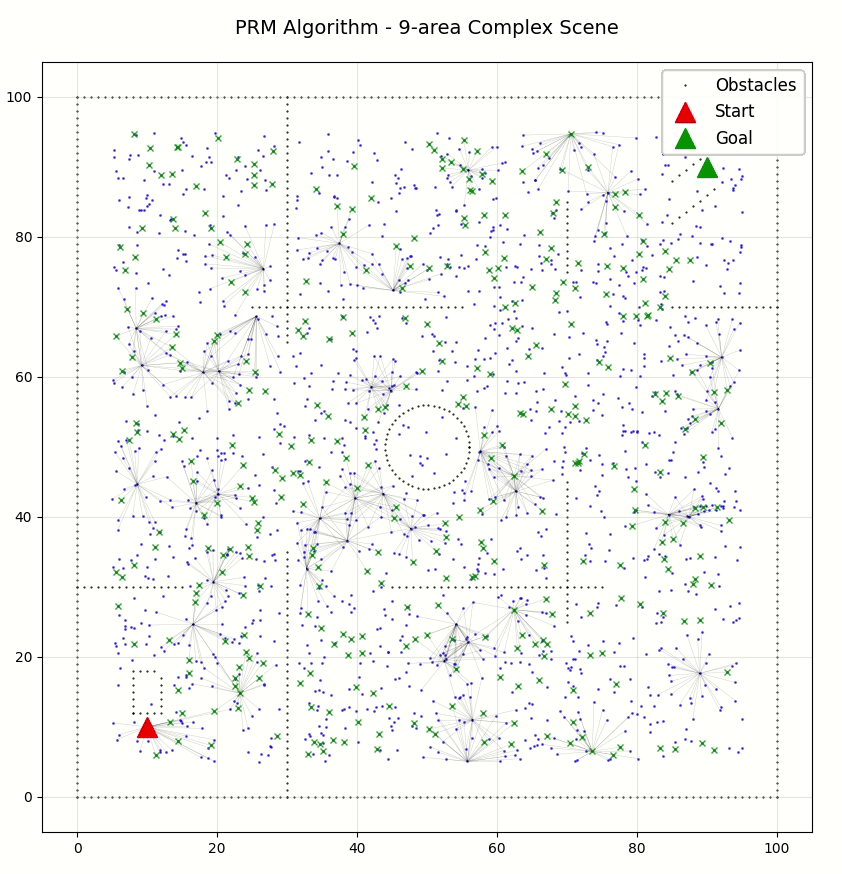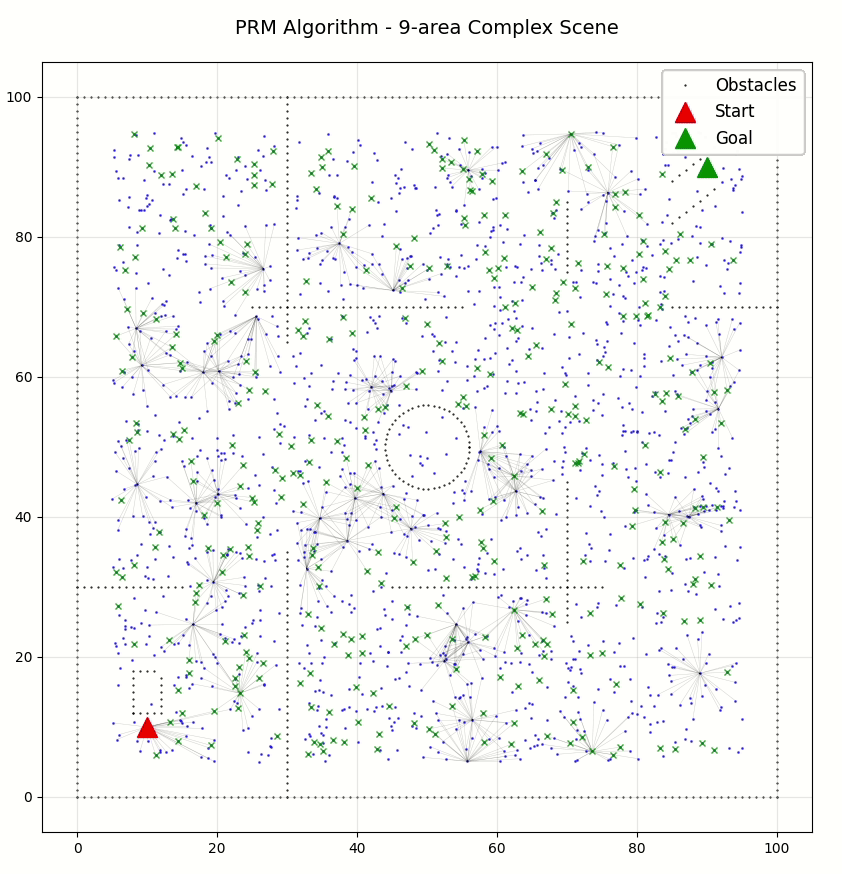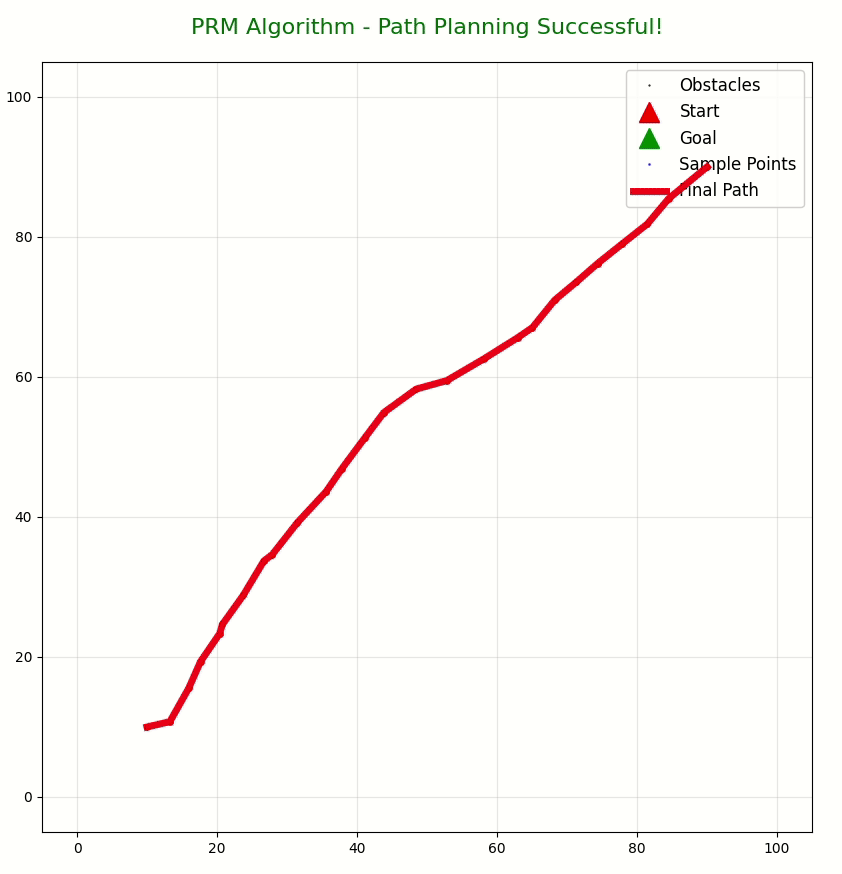
四、结束语
- 核心逻辑:PRM 先离线在自由空间采样建图,再在线通过图搜索找路径,适合高维空间、复杂静态环境;
- 关键参数:采样点数越多、邻域半径越大,路图连通性越好,但计算量也越大;
- 优缺点 :
- 优点:离线建图后在线查询速度快,适合多次查询的场景;
- 缺点:对窄通道环境采样覆盖差,可能找不到路径,且无法处理动态障碍物。