队列-双端队列【Queue2】

一工作就3个月没更新了哈哈，更新一下知识库的知识点~

话说守望先锋的哈基米真可爱~

1、什么是双端队列

双端队列，简称 Deque，是一种具有队列和栈性质的抽象数据类型。与普通队列（Queue）只能在队尾添加元素、在队头移除元素不同，双端队列允许在两端进行元素的插入和删除操作。

你可以把它想象成一个"两头通"的桥，人们既可以从队头加入/离开，也可以从队尾加入/离开。这种灵活性使得 Deque 成为一种非常强大的数据结构，可以同时高效地实现队列和栈的操作。

2、双端队列 vs 普通队列 vs 栈

数据结构	插入位置	删除位置	操作原则	灵活性
栈(Stack)	顶部	顶部	LIFO(后进先出)	⭐⭐
队列(Queue)	队尾	队首	FIFO(先进先出)	⭐⭐
双端队列(Deque)	两端任意	两端任意	灵活组合	⭐⭐⭐⭐⭐

3、为什么需要 Deque？

栈（Stack 类 / Deque 模拟栈） ：Java 的Stack类（或用Deque模拟栈）仅支持从栈顶（Top）执行push（入栈）、pop（出栈）、peek（查看栈顶）操作，无法直接访问栈底元素，也不能随机访问栈中任意位置的元素，操作灵活性极低。
队列（Queue 接口） ：Java 的Queue接口（典型实现如LinkedList）严格遵循先进先出（FIFO）规则，仅能从队尾（offer）添加元素、队头（poll）移除元素，无法灵活地在队头 / 队尾之外的位置操作，也不支持反向遍历或修改。
静态数组（如 int []、String []）：Java 静态数组长度固定，且在数组中间位置插入 / 删除元素时，需手动遍历并移动后续所有元素，时间复杂度为 O (n)，效率极低。
链表（LinkedList 底层实现） ：Java 无原生链表类，但LinkedList底层是双向链表结构，其随机访问（通过索引get(int index)）需从头节点或尾节点遍历到目标位置，时间复杂度 O (n)，远不如数组的 O (1) 随机访问性能。

Java 的ArrayList是最常用的动态数组实现，其底层基于可变长度的连续内存块（会自动扩容），核心操作的性能特征直接受限于连续内存布局：

尾部操作 ：add(E e)（尾部添加）、remove(size()-1)（尾部删除）的时间复杂度为 O (1)（均摊）。因为ArrayList会预分配额外的内存空间（默认扩容因子 1.5 倍），尾部操作无需移动其他元素，仅需修改元素计数和对应位置的值。
头部操作 ：add(0, E e)（头部插入）、remove(0)（头部删除）的时间复杂度为 O (n)。为了保持内存的连续性，头部插入时需要将数组中所有元素向右移动一位；头部删除时需要将所有元素向左移动一位，元素数量越多，移动耗时越长，这是ArrayList最关键的性能瓶颈。

Deque 的优势

Deque 被设计出来就是为了解决这个问题。它通过一种非连续的内存布局，保证了在两端的添加和删除操作都具有**O(1)**的平均时间复杂度。

4、Deque 的底层实现原理

要理解 Deque 为何如此高效，我们需要探究其内部结构。一种经典且高效的实现方式是采用：块状双向链表

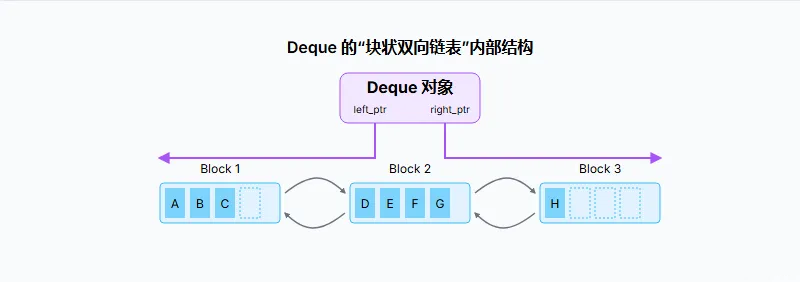
这种结构是如何工作的？

数据块: Deque 内部维护了一系列固定大小的数组（例如，每个数组容量为64），我们称之为"数据块"。
双向链表: 这些数据块通过指针连接成一个双向链表。每个块都知道它的前一个块和后一个块是谁。
头尾指针: Deque 对象本身持有指向最左边块（头部）和最右边块（尾部）的指针，以及块内具体元素的偏移量。

当在 Deque 的一端添加元素时：

如果该端的块还有空间，直接在块内的数组中添加元素即可。这是一个 O(1) 操作。
如果该端的块已满，只需创建一个新的空块，通过链表指针将其连接到当前端块的旁边，然后将新元素放入新块中。这个过程只涉及指针操作和内存分配，与 Deque 中已有元素的数量无关，因此也是 O(1) 操作。

删除操作的逻辑完全对称，同样高效。这种设计巧妙地规避了动态数组那样大规模的数据迁移问题。

:::info
为什么不用纯粹的双向链表？

纯粹的双向链表（每个节点存一个元素）虽然也能实现 O(1) 的两端操作，但有两个主要缺点：

内存开销大：每个元素都需要额外存储两个指针。
缓存性能差：元素在内存中是零散分布的，CPU 无法有效利用缓存进行预读，导致访问速度慢。而 Deque 的"块状"结构，使得一个块内的元素是连续存储的，大大提高了缓存命中率，实现了空间和时间的双重优化。

:::

随机访问的代价

这种设计的唯一缺点是随机访问 deque[i] 的性能。对于靠近两端的元素访问很快，通常是 O(1) 操作，但越靠近中间，速度越慢，是O(n)操作，这点就不如list了。

5、双端队列的实现

5.1、Java的Deque接口

优先使用性能更优的ArrayDeque实现

plain 复制代码

package duilie;

import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;

/**
 * @Author Stringzhua
 * @Date 2025/12/18 17:51
 * description:
 */
public class DequeExample {

    // deque的rotate操作 右旋转n位
    public static <T> void rotate(Deque<T> deque, int n) {
        if (deque.isEmpty() || n == 0) {
            return;
        }
        // 处理旋转步数超过队列长度的情况（取模），兼容负数左旋转
        int rotateSteps = n % deque.size();
        if (rotateSteps < 0) {
            rotateSteps += deque.size();
        }
        // 右旋转逻辑：每次将最后一个元素移到头部，循环n次
        for (int i = 0; i < rotateSteps; i++) {
            T lastElement = deque.removeLast();
            deque.addFirst(lastElement);
        }
    }

    // 自定义有限长度Deque
    static class LimitedDeque<T> extends ArrayDeque<T> {
        private final int maxLen;

        public LimitedDeque(int maxLen) {
            super(maxLen);
            this.maxLen = maxLen;
        }

        @Override
        public void addLast(T t) {
            if (size() == maxLen) {
                this.removeFirst(); // 超过最大长度，移除头部元素
            }
            super.addLast(t); // 调用父类的addLast（返回void）
        }

        // 兼容offerLast（Java 8中offerLast返回boolean）
        @Override
        public boolean offerLast(T t) {
            if (size() == maxLen) {
                this.removeFirst();
            }
            super.addLast(t);
            return true;
        }

        // 重写toString
        @Override
        public String toString() {
            StringBuilder sb = new StringBuilder();
            sb.append("deque([");
            if (!isEmpty()) {
                Object[] elements = this.toArray();
                for (int i = 0; i < elements.length; i++) {
                    sb.append(elements[i]);
                    if (i < elements.length - 1) {
                        sb.append(", ");
                    }
                }
            }
            sb.append("])");
            sb.append(", maxlen=").append(maxLen);
            return sb.toString();
        }
    }

    // 辅助方法：格式化普通Deque的输出
    public static <T> String formatDeque(Deque<T> deque) {
        StringBuilder sb = new StringBuilder();
        sb.append("deque([");
        if (!deque.isEmpty()) {
            Object[] elements = deque.toArray();
            for (int i = 0; i < elements.length; i++) {
                sb.append(elements[i]);
                if (i < elements.length - 1) {
                    sb.append(", ");
                }
            }
        }
        sb.append("])");
        return sb.toString();
    }

    public static void main(String[] args) {
        // 1. 创建一个 deque
        Deque<String> d = new ArrayDeque<>(Arrays.asList("c", "d", "e"));
        System.out.printf("初始 deque: %s%n", formatDeque(d));

        // 2. 在右侧添加元素
        d.addLast("f");
        System.out.printf("append('f'): %s%n", formatDeque(d));

        // 3. 在左侧添加元素
        d.addFirst("b");
        System.out.printf("appendleft('b'): %s%n", formatDeque(d));

        // 4. 从右侧移除元素
        String rightItem = d.removeLast();
        System.out.printf("pop() -> '%s', deque: %s%n", rightItem, formatDeque(d));

        // 5. 从左侧移除元素
        String leftItem = d.removeFirst();
        System.out.printf("popleft() -> '%s', deque: %s%n", leftItem, formatDeque(d));

        // 6. 旋转元素
        rotate(d, 1);
        System.out.printf("rotate(1): %s%n", formatDeque(d));

        // 7. 创建一个有最大长度限制的 deque
        LimitedDeque<Integer> dLimited = new LimitedDeque<>(3);
        dLimited.addLast(1);
        dLimited.addLast(2);
        dLimited.addLast(3);
        System.out.printf("有限长度 deque (满): %s%n", dLimited);
        dLimited.addLast(4);
        System.out.printf("添加 4 后: %s%n", dLimited);
    }
}

运行结果：

plain 复制代码

初始 deque: deque([c, d, e])
append('f'): deque([c, d, e, f])
appendleft('b'): deque([b, c, d, e, f])
pop() -> 'f', deque: deque([b, c, d, e])
popleft() -> 'b', deque: deque([c, d, e])
rotate(1): deque([e, c, d])
有限长度 deque (满): deque([1, 2, 3]), maxlen=3
添加 4 后: deque([2, 3, 4]), maxlen=3

5.2、基于双向链表的实现

plain 复制代码

package duilie;

/**
 * 基于双向链表的双端队列 Java 实现
 * @author Stringzhua
 */
public class DequeDemo {

    // 双向链表节点类
    static class Node {
        Object data;
        Node prev; // 前驱指针
        Node next; // 后继指针

        public Node(Object data) {
            this.data = data;
            this.prev = null;
            this.next = null;
        }
    }

    // 基于双向链表的双端队列实现
    static class Deque {
        private Node head; // 哨兵头节点
        private Node tail; // 哨兵尾节点
        private int size;  // 队列元素个数

        public Deque() {
            // 初始化哑头/哑尾节点，简化边界处理
            head = new Node(null);
            tail = new Node(null);
            head.next = tail;
            tail.prev = head;
            size = 0;
        }

        /**
         * 在两个节点之间插入新节点
         * @param data 插入的元素
         * @param predecessor 前驱节点
         * @param successor 后继节点
         */
        private void addBetween(Object data, Node predecessor, Node successor) {
            Node newNode = new Node(data);
            newNode.prev = predecessor;
            newNode.next = successor;
            predecessor.next = newNode;
            successor.prev = newNode;
            size++;
        }

        /**
         * 删除指定节点
         * @param node 要删除的节点
         * @return 被删除节点的元素
         */
        private Object removeNode(Node node) {
            if (size == 0) {
                throw new IndexOutOfBoundsException("双端队列为空");
            }

            Object data = node.data;
            Node predecessor = node.prev;
            Node successor = node.next;
            predecessor.next = successor;
            successor.prev = predecessor;
            size--;
            return data;
        }

        /**
         * 在左端添加元素
         * @param data 要添加的元素
         */
        public void appendLeft(Object data) {
            addBetween(data, head, head.next);
        }

        /**
         * 在右端添加元素
         * @param data 要添加的元素
         */
        public void appendRight(Object data) {
            addBetween(data, tail.prev, tail);
        }

        /**
         * 从左端删除并返回元素
         * @return 左端的元素
         */
        public Object popLeft() {
            return removeNode(head.next);
        }

        /**
         * 从右端删除并返回元素
         * @return 右端的元素
         */
        public Object popRight() {
            return removeNode(tail.prev);
        }

        /**
         * 查看左端元素
         * @return 左端的元素
         */
        public Object peekLeft() {
            if (size == 0) {
                throw new IndexOutOfBoundsException("双端队列为空");
            }
            return head.next.data;
        }

        /**
         * 查看右端元素
         * @return 右端的元素
         */
        public Object peekRight() {
            if (size == 0) {
                throw new IndexOutOfBoundsException("双端队列为空");
            }
            return tail.prev.data;
        }

        /**
         * 检查队列是否为空
         * @return 空返回true，否则返回false
         */
        public boolean isEmpty() {
            return size == 0;
        }

        /**
         * 获取队列长度
         * @return 元素个数
         */
        public int size() {
            return size;
        }

        /**
         * 重写toString
         * @return 队列的字符串表示
         */
        @Override
        public String toString() {
            if (isEmpty()) {
                return "Deque([])";
            }

            StringBuilder elements = new StringBuilder();
            Node current = head.next;
            while (current != tail) {
                elements.append(current.data);
                if (current.next != tail) {
                    elements.append(" ↔ ");
                }
                current = current.next;
            }
            return String.format("Deque([%s])", elements.toString());
        }
    }

    public static void main(String[] args) {
        // 创建双端队列实例
        Deque dq = new Deque();

        // 1. 基本操作演示
        System.out.println("=== 双端队列基本操作演示 ===");
        System.out.printf("初始状态: %s%n", dq); // Deque([])

        // 左端添加元素
        dq.appendLeft("A");
        dq.appendLeft("B");
        System.out.printf("左端添加A,B后: %s%n", dq); // Deque([B ↔ A])

        // 右端添加元素
        dq.appendRight("C");
        dq.appendRight("D");
        System.out.printf("右端添加C,D后: %s%n", dq); // Deque([B ↔ A ↔ C ↔ D])

        // 2. 查看操作
        System.out.println("\n=== 查看操作 ===");
        System.out.printf("左端元素: %s%n", dq.peekLeft()); // B
        System.out.printf("右端元素: %s%n", dq.peekRight()); // D
        System.out.printf("队列长度: %d%n", dq.size()); // 4

        // 3. 删除操作
        System.out.println("\n=== 删除操作 ===");
        Object leftItem = dq.popLeft();
        System.out.printf("从左端删除: %s%n", leftItem); // B
        System.out.printf("删除后状态: %s%n", dq); // Deque([A ↔ C ↔ D])

        Object rightItem = dq.popRight();
        System.out.printf("从右端删除: %s%n", rightItem); // D
        System.out.printf("删除后状态: %s%n", dq); // Deque([A ↔ C])

        // 4. 作为栈使用（LIFO）
        System.out.println("\n=== 作为栈使用 ===");
        Deque stackDq = new Deque();
        // 入栈（右端进入）
        for (int i = 1; i <= 3; i++) {
            stackDq.appendRight(i);
            System.out.printf("入栈 %d: %s%n", i, stackDq);
        }

        // 出栈（右端出来）
        while (!stackDq.isEmpty()) {
            Object item = stackDq.popRight();
            System.out.printf("出栈 %s: %s%n", item, stackDq);
        }

        // 5. 作为队列使用（FIFO）
        System.out.println("\n=== 作为队列使用 ===");
        Deque queueDq = new Deque();
        // 入队（右端进入）
        String[] queueItems = {"first", "second", "third"};
        for (String item : queueItems) {
            queueDq.appendRight(item);
            System.out.printf("入队 %s: %s%n", item, queueDq);
        }

        // 出队（左端出来）
        while (!queueDq.isEmpty()) {
            Object item = queueDq.popLeft();
            System.out.printf("出队 %s: %s%n", item, queueDq);
        }
    }
}

运行结果：

plain 复制代码

=== 双端队列基本操作演示 ===
初始状态: Deque([])
左端添加A,B后: Deque([B ↔ A])
右端添加C,D后: Deque([B ↔ A ↔ C ↔ D])

=== 查看操作 ===
左端元素: B
右端元素: D
队列长度: 4

=== 删除操作 ===
从左端删除: B
删除后状态: Deque([A ↔ C ↔ D])
从右端删除: D
删除后状态: Deque([A ↔ C])

=== 作为栈使用 ===
入栈 1: Deque([1])
入栈 2: Deque([1 ↔ 2])
入栈 3: Deque([1 ↔ 2 ↔ 3])
出栈 3: Deque([1 ↔ 2])
出栈 2: Deque([1])
出栈 1: Deque([])

=== 作为队列使用 ===
入队 first: Deque([first])
入队 second: Deque([first ↔ second])
入队 third: Deque([first ↔ second ↔ third])
出队 first: Deque([second ↔ third])
出队 second: Deque([third])
出队 third: Deque([])

5.3、基于环形数组实现的队列

环形数组能够做到所有操作都是O(1)操作，其核心本质：

1. 数学原理：模运算

(front - 1 + capacity) % capacity- 左端位置计算
(front + size) % capacity- 右端位置计算
模运算是CPU原生支持的操作，时间复杂度O(1)

2. 内存原理：随机访问

数组元素在内存中连续存储
地址计算公式：address = base_address + index × element_size
无论访问哪个索引，计算时间都是常数

3. 算法原理：避免数据移动

传统数组插入需要移动后续所有元素
环形数组通过指针重定向避免数据移动
空间复用，逻辑连续但物理不连续

plain 复制代码

package duilie;

/**
 * @Author Stringzhua
 * @Date 2026/1/5 14:28
 * description:
 * 基于循环数组的双端队列实现
 * <p>
 * 核心设计原理：
 * 1. 使用固定大小的数组作为底层存储
 * 2. 通过front指针标记第一个元素的位置
 * 3. 通过size记录当前元素个数
 * 4. 通过模运算实现环形访问
 * <p>
 * 时间复杂度分析：所有操作都是O(1)，因为只需要简单的指针计算
 */

public class CircularArrayDeque<T> {
    private T[] data;          // 底层数组
    private int capacity;      // 数组容量
    private int front;         // 第一个元素的索引
    private int size;          // 当前元素个数

    /**
     * 初始化 - 时间复杂度: O(1)
     *
     * @param capacity 初始容量
     */
    @SuppressWarnings("unchecked")
    public CircularArrayDeque(int capacity) {
        this.capacity = capacity;
        // Java不支持直接创建泛型数组，需要类型转换
        this.data = (T[]) new Object[capacity];
        this.front = 0;
        this.size = 0;
    }

    /**
     * 无参构造函数，默认容量8
     */
    public CircularArrayDeque() {
        this(8);
    }

    /**
     * 左端添加 - O(1)摊销复杂度
     * <p>
     * 为什么是O(1)？
     * 1. 指针计算: (front-1+capacity)%capacity - O(1)
     * 2. 数组赋值: data[index] = value - O(1)
     * 3. 计数器: size += 1 - O(1)
     *
     * @param element 要添加的元素
     */
    public void appendLeft(T element) {
        if (size == capacity) {
            resize(); // 扩容，摊销后O(1)
        }

        // 关键：模运算实现环形左端插入
        front = (front - 1 + capacity) % capacity;
        data[front] = element;
        size++;
    }

    /**
     * 右端添加 - O(1)摊销复杂度
     *
     * @param element 要添加的元素
     */
    public void appendRight(T element) {
        if (size == capacity) {
            resize();
        }

        int rear = (front + size) % capacity; // O(1)计算
        data[rear] = element;
        size++;
    }

    /**
     * 左端删除 - 严格的O(1)
     *
     * @return 删除的元素
     * @throws IllegalStateException 队列为空时抛出
     */
    public T popLeft() {
        if (size == 0) {
            throw new IllegalStateException("双端队列为空");
        }

        T element = data[front]; // O(1)数组访问
        data[front] = null;      // 清理引用，帮助GC
        front = (front + 1) % capacity; // O(1)指针移动
        size--;
        return element;
    }

    /**
     * 右端删除 - 严格的O(1)
     * <p>
     * 为什么是O(1)？
     * 1. 计算尾部位置: (front+size-1)%capacity - O(1)
     * 2. 数组访问: data[rear] - O(1)
     * 3. 清理和计数: O(1)
     *
     * @return 删除的元素
     * @throws IllegalStateException 队列为空时抛出
     */
    public T popRight() {
        if (size == 0) {
            throw new IllegalStateException("双端队列为空");
        }

        int rear = (front + size - 1) % capacity; // O(1)计算尾部
        T element = data[rear];                  // O(1)数组访问
        data[rear] = null;                       // 清理引用，帮助GC
        size--;
        return element;
    }

    /**
     * 查看左端元素 - O(1)
     *
     * @return 左端元素
     * @throws IllegalStateException 队列为空时抛出
     */
    public T peekLeft() {
        if (size == 0) {
            throw new IllegalStateException("双端队列为空");
        }
        return data[front]; // 直接访问，O(1)
    }

    /**
     * 查看右端元素 - O(1)
     *
     * @return 右端元素
     * @throws IllegalStateException 队列为空时抛出
     */
    public T peekRight() {
        if (size == 0) {
            throw new IllegalStateException("双端队列为空");
        }
        int rear = (front + size - 1) % capacity;
        return data[rear];
    }

    /**
     * 扩容操作 - 摊销O(1)
     * <p>
     * 为什么扩容是摊销O(1)？
     * 1. 每次扩容都将容量翻倍
     * 2. 触发扩容需要插入capacity个元素
     * 3. 复制n个元素的成本被分摊到n次插入中
     * 4. 均摊下来每次插入的扩容成本是O(1)
     */
    @SuppressWarnings("unchecked")
    private void resize() {
        T[] oldData = data;
        int oldCapacity = capacity;

        // 新容量翻倍
        capacity = oldCapacity * 2;
        data = (T[]) new Object[capacity];

        // 重新排列数据，消除环形结构
        for (int i = 0; i < size; i++) {
            int oldIndex = (front + i) % oldCapacity;
            data[i] = oldData[oldIndex];
        }

        front = 0; // 重置front指针
    }

    /**
     * 检查是否为空 - O(1)
     *
     * @return 空返回true，否则false
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 返回元素个数 - O(1)
     *
     * @return 元素个数
     */
    public int size() {
        return size;
    }

    /**
     * 获取逻辑顺序（用于调试和可视化）
     *
     * @return 逻辑顺序的数组
     */
    public Object[] getLogicalOrder() {
        Object[] result = new Object[size];
        for (int i = 0; i < size; i++) {
            int index = (front + i) % capacity;
            result[i] = data[index];
        }
        return result;
    }

    /**
     * 字符串表示
     *
     * @return 格式化的字符串
     */
    @Override
    public String toString() {
        if (isEmpty()) {
            return "CircularArrayDeque([])";
        }

        StringBuilder sb = new StringBuilder();
        sb.append("CircularArrayDeque([");
        Object[] logicalOrder = getLogicalOrder();
        for (int i = 0; i < logicalOrder.length; i++) {
            sb.append(logicalOrder[i]);
            if (i != logicalOrder.length - 1) {
                sb.append(", ");
            }
        }
        sb.append("])");
        return sb.toString();
    }

    // 主方法：功能演示
    public static void main(String[] args) {
        // 创建循环数组双端队列实例，初始容量为4
        CircularArrayDeque<String> circularDq = new CircularArrayDeque<>(4);

        // 1. 基本操作演示 - 每个操作都是O(1)
        System.out.println("=== 循环数组双端队列演示 ===");
        System.out.printf("初始容量: %d, 当前大小: %d%n", 4, circularDq.size());
        System.out.println("初始数组状态: " + java.util.Arrays.toString(circularDq.data));

        // 演示左端插入的O(1)过程
        System.out.println("\n--- 左端插入O(1)演示 ---");
        System.out.printf("插入前: front=%d, size=%d%n", 0, circularDq.size());
        circularDq.appendLeft("A"); // O(1): 只需(front-1+capacity)%capacity计算
        System.out.printf("插入A后: front=%d, size=%d%n", circularDq.front, circularDq.size());
        System.out.println("数组状态: " + java.util.Arrays.toString(circularDq.data));
        System.out.println("逻辑顺序: " + java.util.Arrays.toString(circularDq.getLogicalOrder()));

        circularDq.appendLeft("B"); // 再次O(1)插入
        System.out.printf("插入B后: front=%d, 逻辑顺序: %s%n",
                circularDq.front, java.util.Arrays.toString(circularDq.getLogicalOrder()));

        // 演示右端插入的O(1)过程
        System.out.println("\n--- 右端插入O(1)演示 ---");
        circularDq.appendRight("C"); // O(1): 只需(front+size)%capacity计算
        System.out.println("插入C后: 逻辑顺序: " + java.util.Arrays.toString(circularDq.getLogicalOrder()));
        System.out.println("数组状态: " + java.util.Arrays.toString(circularDq.data));

        circularDq.appendRight("D");
        System.out.println("插入D后: 逻辑顺序: " + java.util.Arrays.toString(circularDq.getLogicalOrder()));
        System.out.printf("当前容量已满: %d/%d%n", circularDq.size(), 4);

        // 2. 自动扩容演示 - 摊销O(1)
        System.out.println("\n--- 自动扩容演示 ---");
        System.out.printf("扩容前容量: %d, 数据: %s%n", 4, java.util.Arrays.toString(circularDq.data));
        circularDq.appendRight("E"); // 这会触发扩容
        System.out.printf("扩容后容量: %d, 新front: %d%n", circularDq.capacity, circularDq.front);

        // 打印扩容后有效数据
        Object[] validData = new Object[circularDq.size()];
        System.arraycopy(circularDq.data, 0, validData, 0, circularDq.size());
        System.out.println("扩容后数据: " + java.util.Arrays.toString(validData));

        System.out.println("逻辑顺序保持: " + java.util.Arrays.toString(circularDq.getLogicalOrder()));

        // 3. 删除操作演示 - 每个都是O(1)
        System.out.println("\n--- 删除操作演示 ---");
        while (circularDq.size() > 0) {
            if (circularDq.size() % 2 == 1) {
                // 左端删除 - O(1)
                String item = circularDq.popLeft();
                System.out.printf("左端删除: %s, 剩余: %s, front=%d%n",
                        item, java.util.Arrays.toString(circularDq.getLogicalOrder()), circularDq.front);
            } else {
                // 右端删除 - O(1)
                String item = circularDq.popRight();
                System.out.printf("右端删除: %s, 剩余: %s%n",
                        item, java.util.Arrays.toString(circularDq.getLogicalOrder()));
            }
        }
    }
}

运行结果：

plain 复制代码

=== 循环数组双端队列演示 ===
初始容量: 4, 当前大小: 0
初始数组状态: [null, null, null, null]

--- 左端插入O(1)演示 ---
插入前: front=0, size=0
插入A后: front=3, size=1
数组状态: [null, null, null, A]
逻辑顺序: [A]
插入B后: front=2, 逻辑顺序: [B, A]

--- 右端插入O(1)演示 ---
插入C后: 逻辑顺序: [B, A, C]
数组状态: [C, null, B, A]
插入D后: 逻辑顺序: [B, A, C, D]
当前容量已满: 4/4

--- 自动扩容演示 ---
扩容前容量: 4, 数据: [C, D, B, A]
扩容后容量: 8, 新front: 0
扩容后数据: [B, A, C, D, E]
逻辑顺序保持: [B, A, C, D, E]

--- 删除操作演示 ---
左端删除: B, 剩余: [A, C, D, E], front=1
右端删除: E, 剩余: [A, C, D]
左端删除: A, 剩余: [C, D], front=2
右端删除: D, 剩余: [C]
左端删除: C, 剩余: [], front=3

双端队列示例1：集成 Java 8+ Stream API + 迭代器（Iterable 接口）

plain 复制代码

import java.util.Iterator;
import java.util.Spliterator;
import java.util.Spliterators;
import java.util.function.Consumer;
import java.util.stream.Stream;
import java.util.stream.StreamSupport;

/**
 * 支持Stream和迭代的双端队列（体现Java 8+ Stream API、Iterable接口特性）
 */
public class IterableCircularDeque<T> implements Iterable<T> {
    private T[] data;
    private int capacity;
    private int front;
    private int size;

    @SuppressWarnings("unchecked")
    public IterableCircularDeque(int capacity) {
        this.capacity = capacity;
        this.data = (T[]) new Object[capacity];
        this.front = 0;
        this.size = 0;
    }

    public IterableCircularDeque() {
        this(8);
    }

    // 核心操作：左端添加（保留原逻辑）
    public void appendLeft(T element) {
        if (size == capacity) resize();
        front = (front - 1 + capacity) % capacity;
        data[front] = element;
        size++;
    }

    // 核心操作：右端添加（保留原逻辑）
    public void appendRight(T element) {
        if (size == capacity) resize();
        int rear = (front + size) % capacity;
        data[rear] = element;
        size++;
    }

    // 核心操作：左端删除（保留原逻辑）
    public T popLeft() {
        if (size == 0) throw new IllegalStateException("队列为空");
        T element = data[front];
        data[front] = null;
        front = (front + 1) % capacity;
        size--;
        return element;
    }

    // 核心操作：右端删除（保留原逻辑）
    public T popRight() {
        if (size == 0) throw new IllegalStateException("队列为空");
        int rear = (front + size - 1) % capacity;
        T element = data[rear];
        data[rear] = null;
        size--;
        return element;
    }

    // 扩容逻辑（保留原逻辑）
    @SuppressWarnings("unchecked")
    private void resize() {
        T[] oldData = data;
        capacity *= 2;
        data = (T[]) new Object[capacity];
        for (int i = 0; i < size; i++) {
            int oldIndex = (front + i) % oldData.length;
            data[i] = oldData[oldIndex];
        }
        front = 0;
    }

    // ========== Java特性：实现Iterable接口，支持foreach遍历 ==========
    @Override
    public Iterator<T> iterator() {
        return new Iterator<>() {
            private int current = 0; // 遍历计数器

            @Override
            public boolean hasNext() {
                return current < size;
            }

            @Override
            public T next() {
                int index = (front + current) % capacity;
                current++;
                return data[index];
            }
        };
    }

    // ========== Java特性：支持Stream流操作 ==========
    public Stream<T> stream() {
        // 将迭代器转换为Spliterator，再包装为Stream
        return StreamSupport.stream(
                Spliterators.spliterator(
                        iterator(), size, Spliterator.ORDERED),
                false // 非并行流
        );
    }

    // ========== Java特性：forEach默认方法（Iterable接口） ==========
    @Override
    public void forEach(Consumer<? super T> action) {
        // 自定义高效实现，避免迭代器开销
        for (int i = 0; i < size; i++) {
            int index = (front + i) % capacity;
            action.accept(data[index]);
        }
    }

    // 获取大小
    public int size() {
        return size;
    }

    // 测试示例
    public static void main(String[] args) {
        IterableCircularDeque<String> deque = new IterableCircularDeque<>(4);
        deque.appendLeft("A");
        deque.appendLeft("B");
        deque.appendRight("C");
        deque.appendRight("D");

        // 特性1：foreach遍历（Iterable接口）
        System.out.println("=== foreach遍历 ===");
        for (String s : deque) {
            System.out.print(s + " "); // 输出：B A C D
        }
        System.out.println();

        // 特性2：Stream API操作
        System.out.println("\n=== Stream流操作 ===");
        deque.stream()
                .filter(s -> s.compareTo("B") > 0) // 过滤大于"B"的元素
                .map(String::toLowerCase)          // 转小写
                .forEach(s -> System.out.print(s + " ")); // 输出：a c d
        System.out.println();

        // 特性3：forEach方法（Lambda）
        System.out.println("\n=== forEach Lambda ===");
        deque.forEach(s -> System.out.println("元素：" + s));
    }
}

双端队列示例2：泛型边界 + 自动资源释放（AutoCloseable）

plain 复制代码

/**
 * 带资源管理的双端队列（体现Java泛型边界、AutoCloseable特性）
 * @param <T> 元素类型，必须实现AutoCloseable（支持资源释放）
 */
public class ResourceDeque<T extends AutoCloseable> implements AutoCloseable {
    private T[] data;
    private int capacity;
    private int front;
    private int size;

    @SuppressWarnings("unchecked")
    public ResourceDeque(int capacity) {
        this.capacity = capacity;
        this.data = (T[]) new AutoCloseable[capacity]; // 泛型边界限定
        this.front = 0;
        this.size = 0;
    }

    // 核心操作：右端添加
    public void append(T element) {
        if (size == capacity) resize();
        int rear = (front + size) % capacity;
        data[rear] = element;
        size++;
    }

    // 核心操作：左端删除
    public T take() {
        if (size == 0) throw new IllegalStateException("队列为空");
        T element = data[front];
        data[front] = null;
        front = (front + 1) % capacity;
        size--;
        return element;
    }

    // 扩容逻辑
    @SuppressWarnings("unchecked")
    private void resize() {
        T[] oldData = data;
        capacity *= 2;
        data = (T[]) new AutoCloseable[capacity];
        for (int i = 0; i < size; i++) {
            int oldIndex = (front + i) % oldData.length;
            data[i] = oldData[oldIndex];
        }
        front = 0;
    }

    // ========== Java特性：AutoCloseable，自动释放所有资源 ==========
    @Override
    public void close() throws Exception {
        System.out.println("开始释放队列中所有资源...");
        // 遍历并关闭所有元素的资源
        for (int i = 0; i < size; i++) {
            int index = (front + i) % capacity;
            if (data[index] != null) {
                data[index].close(); // 调用元素的close方法
                data[index] = null;
            }
        }
        size = 0;
        System.out.println("所有资源释放完成");
    }

    // 测试示例：模拟管理可关闭的资源（如文件）
    static class MockResource implements AutoCloseable {
        private final String name;
        public MockResource(String name) {
            this.name = name;
            System.out.println("创建资源：" + name);
        }

        @Override
        public void close() {
            System.out.println("释放资源：" + name);
        }

        @Override
        public String toString() {
            return name;
        }
    }

    // 测试main方法
    public static void main(String[] args) {
        // 特性1：try-with-resources自动释放资源
        try (ResourceDeque<MockResource> deque = new ResourceDeque<>(2)) {
            deque.append(new MockResource("文件1.txt"));
            deque.append(new MockResource("数据库连接1"));
            
            MockResource res = deque.take();
            System.out.println("取出资源：" + res);
        } catch (Exception e) {
            e.printStackTrace();
        }
        // 执行完try块后，会自动调用deque.close()，释放剩余资源
    }
}

双端队列示例3：接口抽象 + 默认方法（Java 8+）

plain 复制代码

/**
 * 双端队列接口（体现Java接口抽象、默认方法特性）
 */
interface Deque<T> {
    // 抽象方法：核心操作
    void appendLeft(T element);
    void appendRight(T element);
    T popLeft();
    T popRight();
    int size();
    boolean isEmpty();

    // ========== Java特性：默认方法（接口自带实现） ==========
    // 默认方法：批量添加元素
    default void addAll(Iterable<T> elements) {
        for (T e : elements) {
            appendRight(e); // 复用已有方法
        }
    }

    // 默认方法：清空队列
    default void clear() {
        while (!isEmpty()) {
            popLeft(); // 复用已有方法
        }
    }

    // 默认方法：反转队列（通用逻辑）
    default void reverse() {
        if (size() <= 1) return;
        int n = size();
        for (int i = 0; i < n / 2; i++) {
            T left = popLeft();
            T right = popRight();
            appendLeft(right);
            appendRight(left);
        }
    }
}

/**
 * 基于循环数组的Deque实现（实现接口，复用默认方法）
 */
class ArrayDequeImpl<T> implements Deque<T> {
    private T[] data;
    private int capacity;
    private int front;
    private int size;

    @SuppressWarnings("unchecked")
    public ArrayDequeImpl(int capacity) {
        this.capacity = capacity;
        this.data = (T[]) new Object[capacity];
        this.front = 0;
        this.size = 0;
    }

    // 实现接口的抽象方法
    @Override
    public void appendLeft(T element) {
        if (size == capacity) resize();
        front = (front - 1 + capacity) % capacity;
        data[front] = element;
        size++;
    }

    @Override
    public void appendRight(T element) {
        if (size == capacity) resize();
        int rear = (front + size) % capacity;
        data[rear] = element;
        size++;
    }

    @Override
    public T popLeft() {
        if (isEmpty()) throw new IllegalStateException("队列为空");
        T element = data[front];
        data[front] = null;
        front = (front + 1) % capacity;
        size--;
        return element;
    }

    @Override
    public T popRight() {
        if (isEmpty()) throw new IllegalStateException("队列为空");
        int rear = (front + size - 1) % capacity;
        T element = data[rear];
        data[rear] = null;
        size--;
        return element;
    }

    @Override
    public int size() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    // 扩容逻辑
    @SuppressWarnings("unchecked")
    private void resize() {
        T[] oldData = data;
        capacity *= 2;
        data = (T[]) new Object[capacity];
        for (int i = 0; i < size; i++) {
            int oldIndex = (front + i) % oldData.length;
            data[i] = oldData[oldIndex];
        }
        front = 0;
    }

    // 辅助方法：打印队列
    public void print() {
        for (int i = 0; i < size; i++) {
            int index = (front + i) % capacity;
            System.out.print(data[index] + " ");
        }
        System.out.println();
    }

    // 测试示例
    public static void main(String[] args) {
        Deque<Integer> deque = new ArrayDequeImpl<>(4);

        // 1. 调用接口默认方法：addAll
        deque.addAll(java.util.Arrays.asList(1, 2, 3, 4));
        System.out.println("初始队列：");
        ((ArrayDequeImpl<Integer>) deque).print(); // 输出：1 2 3 4

        // 2. 调用接口默认方法：reverse
        deque.reverse();
        System.out.println("反转后队列：");
        ((ArrayDequeImpl<Integer>) deque).print(); // 输出：4 3 2 1

        // 3. 调用接口默认方法：clear
        deque.clear();
        System.out.println("清空后大小：" + deque.size()); // 输出：0
    }
}

6、时间复杂度分析

操作	双向链表（Java对应结构）	动态数组（Java对应结构）	循环数组（Java对应结构）	Python deque（Java替代方案）
左端插入	O(1) （Java用`LinkedList`，直接操作头尾节点）	O(n) （Java用`ArrayList`，需整体后移元素）	O(1) （Java用`ArrayDeque`，模运算定位）	O(1) （Java用`ArrayDeque`替代）
右端插入	O(1) （`LinkedList`直接操作尾节点）	O(1)摊销（`ArrayList`满容量时扩容复制）	O(1) （`ArrayDeque`模运算定位）	O(1) （`ArrayDeque`支持）
左端删除	O(1) （`LinkedList`直接操作头节点）	O(n) （`ArrayList`需整体前移元素）	O(1) （`ArrayDeque`仅移动front指针）	O(1) （`ArrayDeque`支持）
右端删除	O(1) （`LinkedList`直接操作尾节点）	O(1) （`ArrayList`仅修改size）	O(1) （`ArrayDeque`仅修改size）	O(1) （`ArrayDeque`支持）
随机访问	O(n) （`LinkedList`需遍历查找）	O(1) （`ArrayList`下标直接访问）	O(1) （`ArrayDeque`通过`(front+index)%capacity`计算）	O(n) （`LinkedList`对应此特性）
空间开销	高（`LinkedList`每个节点存prev/next指针）	中（`ArrayList`扩容预留冗余空间）	低（`ArrayDeque`无额外指针，仅用数组）	中（`ArrayDeque`分块平衡开销）

以下是Java的双端队列API对比表，清晰展示不同实现类的方法、复杂度和适用场景：

Java 双端队列（Deque）核心API对比表

功能场景	ArrayDeque（循环数组）	LinkedList（双向链表）	时间复杂度	核心特点
左端插入	addFirst(E e) / offerFirst(E e)	addFirst(E e) / offerFirst(E e)	O(1)	offerFirst返回boolean，addFirst抛异常
右端插入	addLast(E e) / offerLast(E e)	addLast(E e) / offerLast(E e)	O(1)（ArrayDeque摊销）	ArrayDeque扩容时批量复制，摊销后O(1)
左端删除	removeFirst() / pollFirst()	removeFirst() / pollFirst()	O(1)	pollFirst为空返回null，removeFirst抛异常
右端删除	removeLast() / pollLast()	removeLast() / pollLast()	O(1)	LinkedList需定位尾节点前驱，逻辑O(1)
查看左端元素	getFirst() / peekFirst()	getFirst() / peekFirst()	O(1)	peekFirst为空返回null，getFirst抛异常
查看右端元素	getLast() / peekLast()	getLast() / peekLast()	O(1)	直接访问头尾指针，无遍历开销
判断是否为空	isEmpty()	isEmpty()	O(1)	均通过size字段直接判断
获取元素个数	size()	size()	O(1)	维护独立size字段，无需计算
清空队列	clear()	clear()	O(1) / O(n)	ArrayDeque重置指针；LinkedList需遍历置空节点
随机访问（第n个元素）	无原生方法（需手动计算：(front + n) % capacity）	get(int index)	O(1) / O(n)	ArrayDeque手动计算下标O(1)；LinkedList遍历O(n)
批量添加	addAll(Collection<? extends E> c)	addAll(Collection<? extends E> c)	O(k)（k为元素数）	均从右端批量添加
包含元素检查	contains(Object o)	contains(Object o)	O(n) / O(n)	均需遍历所有元素
删除指定元素	remove(Object o)	remove(Object o)	O(n) / O(n)	找到元素后删除操作O(1)，查找O(n)

补充特性对比（非API）

特性维度	ArrayDeque（循环数组）	LinkedList（双向链表）
空间开销	低（仅数组+少量指针，扩容预留冗余）	高（每个节点含prev/next指针，额外内存占用）
缓存友好性	高（数组连续内存，CPU缓存命中率高）	低（节点分散存储，缓存命中率低）
适用场景	高频双端操作、随机访问（手动计算下标）	频繁中间插入/删除、需序列化存储
线程安全性	非线程安全	非线程安全
空元素支持	不支持（存储null会抛出异常）	支持（可存储null元素）

总结

API层面 ：ArrayDeque和LinkedList实现了相同的Deque接口，核心双端操作方法完全一致，仅异常处理和返回值规则相同。
性能层面 ：ArrayDeque在绝大多数场景下性能更优（缓存友好、空间开销低），是Java双端队列的首选。
场景选择 ：仅当需要在队列中间频繁插入/删除，或需存储null元素时，才选择LinkedList。

7、可视化

juejin

8、双端队列的典型应用场景

广度优先搜索 (BFS): 性能远超 list.pop(0)。
滑动窗口: 高效地从两端添加和删除元素来维护窗口。
任务调度 (如轮转调度): 完美匹配任务队列的需求。
撤销/重做功能 : 使用两个 Deque 分别模拟历史和未来操作。
历史记录: 可以非常方便地实现自动淘汰旧记录的容器。

9、总结

双端队列是一种非常灵活和高效的数据结构，它的核心价值在于：

**灵活性：**可以在两端进行O(1)操作，适应多种算法需求
**实用性：**在滑动窗口、回文检测、历史记录等场景中发挥重要作用
**高效性：**相比数组和普通队列，提供了更好的操作效率