滑动窗口算法通关指南：从模板到实战，搞定LeetCode高频题

滑动窗口算法通关指南：从模板到实战，搞定LeetCode高频题

滑动窗口（Sliding Window）是算法领域解决「子串/子数组」类问题的最优解之一 ，核心思想是通过双指针维护一个动态的「窗口」区间，避免暴力枚举所有子串/子数组，将时间复杂度从 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2) 降至 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ) O(n) </math>O(n) 。本文将从通用模板出发，结合LeetCode高频真题，拆解滑动窗口的核心逻辑、易错点和适用场景，帮你彻底掌握这一算法。

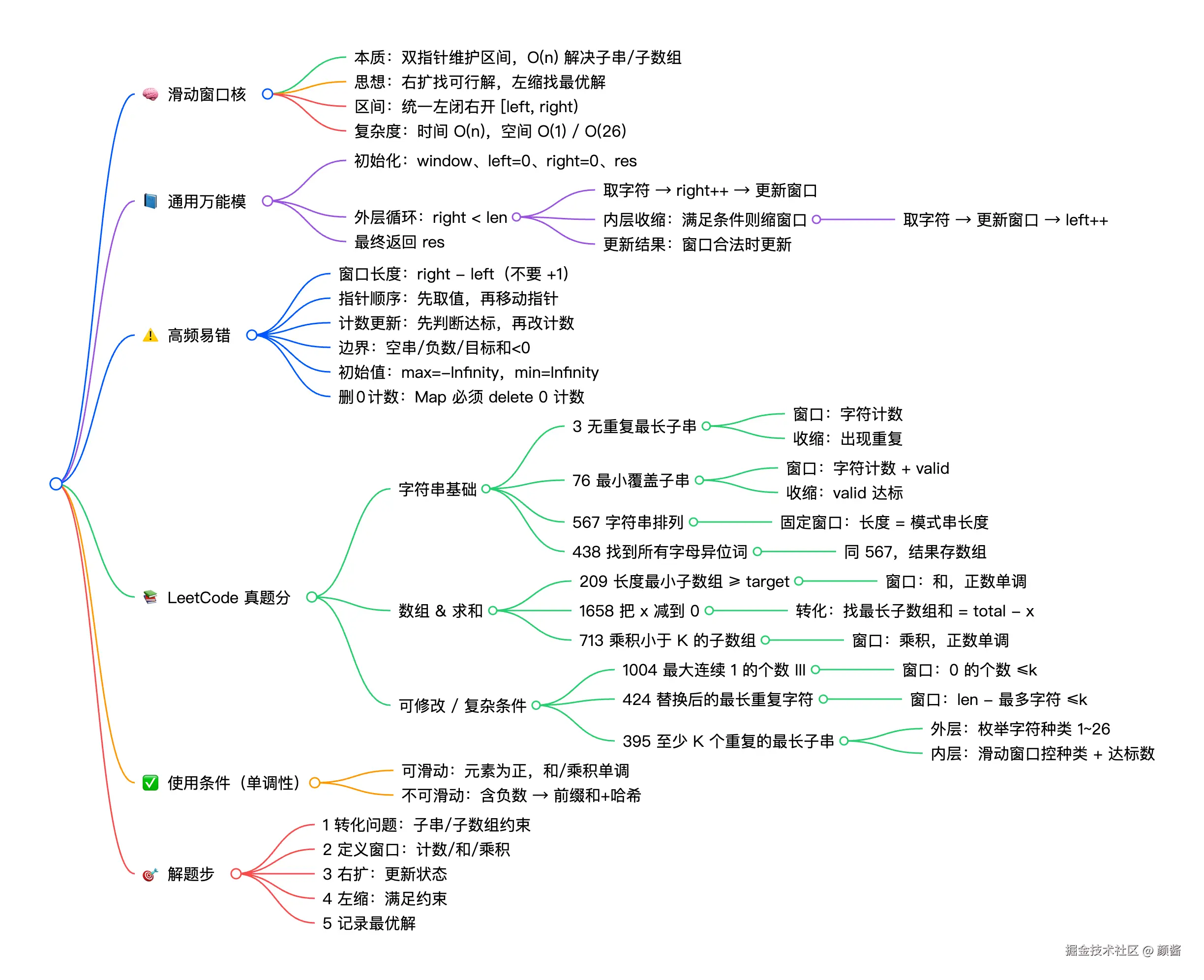
一、滑动窗口核心思想与通用模板

1. 核心原理

滑动窗口通过「右指针扩展窗口找可行解，左指针收缩窗口找最优解」的思路，在一次遍历中完成子串/子数组的条件筛选。根据窗口长度是否固定，可分为：

• 固定窗口：窗口长度固定（如找字符串的排列），只需控制窗口不越界；

• 可变窗口：窗口长度动态调整（如最小覆盖子串），需根据条件收缩/扩展。

2. 通用模板（左闭右开）

滑动窗口的核心是「左闭右开」区间（[left, right)），这是最易记、最不易出错的写法，所有操作都遵循「先取值，再移指针」的规则：

function slide(s){
  let window; // 存储窗口内的统计信息（计数/和/乘积等）
  let left = 0; // 左指针（闭区间）
  let right = 0; // 右指针（开区间）
  let res; // 存储最终结果（长度/数量/子串等）

  while(right < s.length){
    // 1. 扩展窗口：取右指针字符 → 移指针 → 更新窗口状态
    const rStr = s[right];
    right++;
    // 处理窗口数据（计数/和/乘积等）

    // 2. 收缩窗口：满足收缩条件时，左指针右移
    while(/* 收缩条件 */){
      const lStr = s[left];
      // 处理窗口数据（更新统计信息）
      left++; // 先处理数据，再移指针
    }

    // 3. 更新结果（仅在窗口满足条件时）
  }

  return res;
}

3. 核心规则（必记）

• 右指针：先取值，再移动 （保证窗口是 [left, right)）；

• 左指针：先处理数据，再移动（避免漏更窗口状态）；

• 窗口长度：right - left（左闭右开无需+1）；

• 收缩条件：仅当窗口不满足「核心约束」时触发（如和超标、字符重复、种类数超限）。

二、经典真题实战：从易到难拆解

1. 基础题：无重复字符的最长子串（LeetCode 3）

题目描述

给定一个字符串 s，找出其中不含有重复字符的最长子串的长度。

核心思路

右指针扩窗口，遇到重复字符时左指针收缩到「重复字符的下一位」，全程记录最长无重复窗口长度。

/**
 * LeetCode 3 无重复字符的最长子串 - 滑动窗口解法（自定义易记版）
 * 核心思路：右指针扩窗口，遇到重复字符时左指针收缩到「重复字符的下一位」，全程记录最长无重复窗口长度
 * @param {string} s - 输入字符串（需找无重复字符的最长子串）
 * @return {number} 无重复字符的最长子串长度
 */
var lengthOfLongestSubstring = function(s) {
  // ========== 滑动窗口核心变量定义 ==========
  // window：记录当前窗口内每个字符的出现次数（用于快速判断字符是否重复）
  let window = new Map() 
  // left：窗口左指针（左闭），指向当前窗口的起始位置
  let left = 0 
  // right：窗口右指针（右开），指向当前要加入窗口的字符的下一个位置
  // 窗口区间为 [left, right) → 左闭右开，长度 = right - left
  let right = 0 
  // maxLen：记录遍历过程中找到的最长无重复子串长度（初始为0，兼容空字符串）
  let maxLen = 0

  // ========== 核心：右指针扩大窗口（遍历整个字符串） ==========
  while(right < s.length){
    // 步骤1：取出当前右指针指向的字符（要加入窗口的字符）
    const rStr = s[right];
    // 步骤2：右指针右移 → 窗口区间变为 [left, right)（【易错点1】先取值再移指针，保证左闭右开）
    right++

    // 步骤3：更新窗口内当前字符的计数
    // before：当前字符在窗口内已有的次数（无则默认0）
    const before = window.get(rStr) || 0;
    // newCount：当前字符加入后的新次数
    const newCount = before + 1; 
    // 更新window中该字符的计数
    window.set(rStr, newCount);

    // ========== 核心：收缩窗口（仅当当前字符重复时） ==========
    // 【易错点2】收缩条件：当前加入的字符rStr在窗口内重复（计数>1），而非s[right]！
    // 原因：right已右移，s[right]是下一个要处理的字符，rStr才是刚加入的字符
    while(window.get(rStr) > 1){
      // 步骤1：取出左指针指向的字符（要移出窗口的字符）
      const lStr = s[left];
      // 步骤2：获取该字符在窗口内的当前计数
      const before = window.get(lStr);
      // 步骤3：窗口内该字符计数减1（移出窗口）
      window.set(lStr, before - 1);
      // 步骤4：左指针右移 → 收缩窗口（【易错点3】先处理字符再移指针，避免漏更计数）
      left++
      // 收缩逻辑：直到当前重复的rStr在窗口内计数≤1（无重复）为止
    }

    // ========== 更新最长无重复子串长度 ==========
    // 【易错点4】必须在收缩窗口后更新！此时窗口[left, right)内无重复字符
    // 窗口长度 = right - left（左闭右开，无需+1）
    maxLen = Math.max(maxLen, right - left);
  }

  // ========== 返回结果 ==========
  // maxLen始终记录最长长度，直接返回即可（空字符串返回0，单字符返回1）
  return maxLen;
};

优化点

若题目明确字符是「ASCII 字符」，可将 Map 换成数组（访问更快），逻辑完全一致：

var lengthOfLongestSubstring = function(s) {
  const window = new Array(128).fill(0); // ASCII 字符集
  let left = 0, right = 0, maxLen = 0;
  while (right < s.length) {
    const rCode = s.charCodeAt(right);
    right++;
    window[rCode]++;

    while (window[rCode] > 1) { // 收缩条件不变
      const lCode = s.charCodeAt(left);
      window[lCode]--;
      left++;
    }
    maxLen = Math.max(maxLen, right - left);
  }
  return maxLen;
};

2. 进阶题：最小覆盖子串（LeetCode 76）

题目描述

给你一个字符串 s、一个字符串 t，返回 s 中涵盖 t 所有字符的最小子串。若不存在则返回空字符串 ""。

核心思路

右指针扩窗口找满足条件的子串 → 左指针缩窗口找最短子串，通过 validCount 统计「数量达标」的字符种类数。

/**
 * LeetCode 76 最小覆盖子串 - 滑动窗口解法（自定义易记版）
 * 核心思路：右指针扩窗口找满足条件的子串 → 左指针缩窗口找最短子串
 * @param {string} s - 源字符串（要找子串的字符串）
 * @param {string} t - 目标字符串（需要包含的所有字符）
 * @return {string} 满足条件的最短子串，无则返回空
 */
var minWindow = function(s, t) {
  // ========== 1. 初始化：统计目标字符串t的字符需求 ==========
  const tMap = new Map()
  for(let letter of t){
    tMap.set(letter, (tMap.get(letter) || 0) + 1)
  }

  // ========== 2. 滑动窗口核心变量定义 ==========
  const sLen = s.length; // 源字符串长度，控制右指针边界
  let left = 0; // 窗口左指针（左闭）
  let right = 0; // 窗口右指针（右开）→ 窗口区间 [left, right)
  const window = new Map(); // 记录窗口内t中字符的出现次数
  let validCount = 0; // 窗口中「数量达标」的字符种类数（不是总数！）

  // ========== 3. 结果存储变量 ==========
  let shortLeftIndex = 0; // 最短子串的起始索引
  let minStrLen = Infinity; // 最短子串长度（初始无穷大，方便找最小值）

  // ========== 4. 核心：右指针扩大窗口（找满足条件的子串） ==========
  while(right < sLen){
    // 扩窗口：取出当前右指针指向的字符
    const curLetter = s[right];
    // 指针往前移动 → 窗口变为 [left, right)（【易错点1】右指针先取值再移动，保证左闭右开）
    right++;

    // 只处理t中存在的字符（优化：避免无效字符干扰统计）
    if(tMap.has(curLetter)){
      // 更新窗口内该字符的数量
      const newCount = (window.get(curLetter) || 0) + 1;
      window.set(curLetter, newCount);
      // 【易错点2】只有数量「刚好达标」时，validCount才+1（多一个不算）
      // 比如t需要2个A，窗口有3个A时，这里不会重复+1
      if(tMap.get(curLetter) === newCount){
        validCount++;
      }
    }

    // ========== 5. 核心：左指针收缩窗口（找最短的满足条件子串） ==========
    // 当窗口包含t所有字符（达标种类数 = t的字符种类数），开始收缩
    while(validCount === tMap.size){
      // 步骤1：更新最短子串信息
      const curLen = right - left; // 【易错点3】左闭右开区间，长度=右-左（不用+1）
      const isShorter = curLen < minStrLen;
      // 是目前最短的，更新结果存储变量
      if(isShorter){
        shortLeftIndex = left;
        minStrLen = curLen;
      }

      // 步骤2：移出左指针指向的字符，收缩窗口
      const curLeftStr = s[left];
      // 只处理t中存在的字符（无效字符直接跳过更新）
      if(tMap.has(curLeftStr)){
        // 【易错点4】先记录「移出前的数量」！这是判断validCount是否减1的关键
        const beforeCount = window.get(curLeftStr);
        // 窗口内该字符数量减1
        window.set(curLeftStr, beforeCount - 1);
        // 【易错点5】只有「移出前刚好达标」，移出后才不达标，validCount才-1
        // 比如t需要2个A，移出前窗口有2个A → 移出后剩1个，validCount-1
        if(tMap.get(curLeftStr) === beforeCount){
          validCount--;
        }
      }

      // 左指针往前移动 → 窗口收缩（【易错点6】先处理字符再移动，避免漏更）
      left++;
    }
  }

  // ========== 6. 返回结果 ==========
  // 若minStrLen仍为无穷大，说明无满足条件的子串；否则截取最短子串
  // 【易错点7】slice是左闭右开，结束位置=起始索引+长度
  return minStrLen === Infinity ? '' : s.slice(shortLeftIndex, shortLeftIndex + minStrLen);
};

3. 固定窗口题：字符串的排列（LeetCode 567）

题目描述

判断 s2 是否包含 s1 的排列（即 s1 的排列之一是 s2 的子串）。

核心思路

固定窗口长度为 s1.length，滑动窗口判断是否匹配 s1 的字符计数。

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
/**
 * LeetCode 567 字符串的排列 - 滑动窗口解法（自定义易记版）
 * 核心思路：固定窗口长度为short.length，滑动窗口判断是否匹配short的字符排列
 * @param {string} short - 短字符串（要找排列的目标串）
 * @param {string} long - 长字符串（要在其中找子串）
 * @return {boolean} 是否存在short的排列子串
 */
var checkInclusion = function(short, long) {
  // ========== 1. 初始化：统计短字符串的字符需求 ==========
  const shortMap = new Map()
  for(const l of short){
    const before = shortMap.get(l) || 0
    shortMap.set(l, before + 1)
  }

  // ========== 2. 滑动窗口核心变量 ==========
  let window = new Map() // 窗口内字符计数
  let validCount = 0 // 窗口中「数量达标」的字符种类数
  let left = 0 // 窗口左指针（左闭）
  let right = 0 // 窗口右指针（右开）→ 窗口区间 [left, right)
  // 备注：res变量可省略，找到符合条件的直接return true，最终返回false即可

  // ========== 3. 核心：右指针扩大窗口 ==========
  while(right < long.length){
    // 扩窗口：取出当前右指针字符，右指针右移（左闭右开）
    const rStr = long[right]
    right++

    // 仅处理short中存在的字符（过滤无效字符）
    if(shortMap.has(rStr)){
      const before = window.get(rStr) || 0
      const newCount = before + 1 // 拆分变量，更易读
      window.set(rStr, newCount)
      // 【易错点1】只有数量「刚好达标」时，validCount才+1（多一个不算）
      if(newCount === shortMap.get(rStr)){
        validCount++
      }
    }

    // ========== 4. 核心：收缩窗口（固定窗口长度=short.length） ==========
    // 窗口长度≥short.length时，开始收缩（保证窗口长度不超过目标）
    while(right - left >= short.length){
      // 【核心判断】窗口长度等于short.length + 所有字符数量达标 → 找到排列
      // （你的代码这里逻辑正确，是解题关键）
      if(right - left === short.length && validCount === shortMap.size){
        return true // 找到直接返回，无需继续遍历
      }

      // 移出左指针字符，收缩窗口
      const lStr = long[left]
      if(shortMap.has(lStr)){
        const before = window.get(lStr) || 0
        // 【易错点2】先判断「移出前是否达标」，再更新计数（顺序不能反）
        if(before === shortMap.get(lStr)){
          validCount--
        }
        window.set(lStr, before - 1)
      }

      // 左指针右移（【易错点3】先处理字符再移动，保证左闭右开）
      left++
    }
  }

  // 遍历完未找到，返回false
  return false
};

4. 转化问题题：将 x 减到 0 的最小操作数（LeetCode 1658）

题目描述

移除数组最左/最右元素，使元素和等于 x，求最小操作数；无法满足则返回 -1。

核心思路

问题转化 ：找「和为 sum(nums)-x 的最长子数组」，最少操作数 = 数组长度 - 最长子数组长度。

/**
 * LeetCode 1658 将数组和减到x的最少操作数 - 滑动窗口通用框架版
 * 核心思路：转化为找「和为 sum(nums)-x 的最长子数组」，最少操作数 = 数组长度 - 最长子数组长度
 * 通用思维框架：扩窗口（只收集）→ 缩窗口（只调整）→ 判结果（只校验）
 * @param {number[]} nums - 输入整数数组
 * @param {number} x - 目标删除元素的和
 * @return {number} 最少操作数，无法满足返回-1
 */
var minOperations = function(nums, x) {
  // ========== 1. 问题转化 + 初始化基础变量 ==========
  // 计算数组总和（reduce初始值为0，兼容空数组）
  const totalSum = nums.reduce((acc, cur) => acc + cur, 0);
  // 核心转化：找和为 targetSum 的最长子数组 → 操作数 = 数组长度 - 子数组长度
  const targetSum = totalSum - x;
  const numsLen = nums.length; // 数组长度，后续多次使用，提前存储

  // ========== 2. 前置边界处理（【易错点1】提前终止无效逻辑） ==========
  // 场景1：目标和为0 → 需删除所有元素，操作数=数组长度
  if (targetSum === 0) return numsLen;
  // 场景2：目标和为负 → 总和<x，无法满足，直接返回-1（避免后续无效遍历）
  if (targetSum < 0) return -1;

  // ========== 3. 滑动窗口核心变量初始化 ==========
  let windowSum = 0; // 窗口内元素和（仅记录当前窗口的和，不存储其他状态）
  let left = 0; // 窗口左指针（左闭），指向窗口起始位置
  let right = 0; // 窗口右指针（右开），指向窗口下一个要加入的元素
  // 【易错点2】初始化为-1，区分「无符合条件子数组」和「子数组长度为0」
  // 若初始化为0，会把「无结果」和「子数组长度为0」混淆，导致返回错误值
  let maxSubLen = -1;

  // ========== 4. 核心阶段1：扩窗口（只收集元素，不做任何结果判断） ==========
  while (right < numsLen) {
    // 步骤1：取出当前右指针指向的元素（要加入窗口的元素）
    const curRightNum = nums[right];
    // 步骤2：右指针右移 → 窗口区间变为 [left, right)（左闭右开）
    // 【易错点3】先取值再移指针，保证左闭右开的窗口规则，避免漏取/错取元素
    right++;
    // 步骤3：更新窗口状态（仅累加和，无其他操作）
    windowSum += curRightNum;

    // ========== 5. 核心阶段2：缩窗口（只调整窗口，不做结果判断） ==========
    // 收缩条件：窗口和超过目标和（仅处理「超标」情况，职责单一）
    // 【易错点4】收缩条件是 > 而非 >=，仅处理超标，等于的情况留到后续判断
    while (windowSum > targetSum) {
      // 步骤1：取出当前左指针指向的元素（要移出窗口的元素）
      const curLeftNum = nums[left];
      // 步骤2：更新窗口状态（仅减去和，无其他操作）
      windowSum -= curLeftNum;
      // 步骤3：左指针右移 → 收缩窗口
      // 【易错点5】先更新窗口和再移指针，保证窗口状态和指针位置一致
      left++;
    }

    // ========== 6. 核心阶段3：判结果（收缩完成后，统一校验） ==========
    // 此时窗口和 ≤ targetSum，仅判断是否等于目标和，更新最长子数组长度
    // 【易错点6】必须在收缩后判断，避免统计「超标窗口」的长度
    if (windowSum === targetSum) {
      // 窗口长度 = right - left（左闭右开，无需+1）
      // 【易错点7】窗口长度计算错误会导致结果偏大/偏小
      maxSubLen = Math.max(maxSubLen, right - left);
    }
  }

  // ========== 7. 结果转换与返回 ==========
  // 若maxSubLen仍为-1 → 无符合条件的子数组 → 返回-1
  // 否则 → 最少操作数 = 数组长度 - 最长子数组长度
  // 【易错点8】返回逻辑搞反（比如返回maxSubLen - numsLen）会导致结果错误
  return maxSubLen === -1 ? -1 : numsLen - maxSubLen;
};

5. 复杂条件题：至少有 K 个重复字符的最长子串（LeetCode 395）

题目描述

找到字符串中每个字符出现次数都≥k 的最长子串长度。

核心思路

拆分问题：枚举「子串的目标字符种类数」（1~26），对每个种类数用滑动窗口找最优解。

/**
 * @param {string} s 输入字符串（仅包含小写字母）
 * @param {number} k 子串中每个字符的最小出现次数要求
 * @return {number} 满足条件的最长子串长度（无则返回0）
 * 核心解题思路：
 * 1. 拆分问题：枚举「子串的目标字符种类数」（1~字符串实际字符种类数），把复杂问题拆成多个简单问题；
 * 2. 滑动窗口：对每个目标种类数，用左闭右开滑动窗口找「恰好该种类数、且所有字符出现次数≥k」的最长子串；
 * 3. 全局更新：取所有枚举结果的最大值，即为最终答案。
 * 时间复杂度：O(m*n)（m=字符串实际字符种类数≤26，n=字符串长度）→ 简化为O(n)
 * 空间复杂度：O(1)（最多存储26种字符的计数，属于常数空间）
 */
var longestSubstring = function(s, k) {
  const len = s.length;
  // 【易错点1】边界处理：空字符串直接返回0，避免后续逻辑出错
  if (len === 0) return 0;

  // 步骤1：统计字符串中实际存在的字符种类数（优化点：只枚举实际种类数，减少循环次数）
  const charSet = new Set([...s]);
  const totalType = charSet.size; // 实际字符种类数（比如"aaabb"的totalType=2）
  
  let maxLen = -Infinity; // 初始化最长长度为无穷小（后续取最大值）

  // 步骤2：外层枚举「子串的目标字符种类数」（1 ~ 实际字符种类数）
  for (let targetType = 1; targetType <= totalType; targetType++) {
    // 窗口核心统计变量
    let validType = 0; // 窗口内「出现次数≥k」的字符种类数（达标种类数）
    const charCountMap = new Map(); // 窗口内字符→出现次数的映射（仅存非0计数的字符）
    let left = 0, right = 0; // 滑动窗口指针：左闭右开 [left, right)

    // 步骤3：内层滑动窗口遍历字符串（左闭右开逻辑）
    while (right < len) {
      // ===== 扩展窗口：右指针右移，加入当前字符 =====
      const curChar = s[right]; // 取当前右指针指向的字符（未自增前）
      right++; // 右指针右移，窗口变为 [left, right)

      // 更新当前字符的计数
      const prevCount = charCountMap.get(curChar) || 0; // 之前的计数（默认0）
      const newCount = prevCount + 1; // 新计数
      charCountMap.set(curChar, newCount);

      // 【易错点2】仅当「计数首次达到k」时，达标种类数+1（避免重复计数，比如k=3，计数从3→4时不重复加）
      if (newCount === k) {
        validType++;
      }

      // ===== 收缩窗口：窗口内字符种类数超过目标值时 =====
      // 【易错点3】收缩条件是charCountMap.size > targetType（保证窗口内字符种类数≤目标值）
      while (charCountMap.size > targetType) {
        const leftChar = s[left]; // 取当前左指针指向的字符
        const prevCount = charCountMap.get(leftChar); // 左边界字符的当前计数

        // 【核心易错点4】先判断「减之前的计数是否等于k」（减之后会失达标），再更新计数
        // 原因：如果prevCount===k，减1后计数变为k-1，该字符不再达标，需提前减少达标种类数
        if (prevCount === k) {
          validType--;
        }

        // 更新左边界字符的计数
        const newCount = prevCount - 1;
        charCountMap.set(leftChar, newCount);

        // 【易错点5】计数减到0时，必须从Map中删除该字符（保证charCountMap.size是真实的字符种类数）
        // 否则Map中残留计数为0的字符，会导致charCountMap.size统计错误
        if (newCount === 0) {
          charCountMap.delete(leftChar);
        }

        left++; // 左指针右移，收缩窗口
      }

      // ===== 更新最长长度：仅当窗口满足「字符种类数=目标值 且 所有字符都达标」时 =====
      // 条件解读：
      // 1. charCountMap.size === targetType → 窗口内恰好是目标种类数的字符
      // 2. targetType === validType → 所有目标种类数的字符都达标（出现次数≥k）
      if (charCountMap.size === targetType && targetType === validType) {
        // 【易错点6】窗口长度计算：right-left（左闭右开），切勿写成right-left+1
        maxLen = Math.max(maxLen, right - left);
      }
    }
  }

  // 步骤4：最终结果处理
  // 【易错点7】若maxLen仍为- Infinity，说明无满足条件的子串，返回0；否则返回maxLen
  return maxLen === -Infinity ? 0 : maxLen;
};

// ===================== 易错点汇总（单独提取，方便记忆） =====================
/**
 * 易错点1：未处理空字符串边界，直接进入循环；
 * 易错点2：计数超过k时重复增加validType（比如k=3，计数从3→4时仍加1）；
 * 易错点3：收缩条件写错（比如写成charCountMap.size >= targetType）；
 * 易错点4：收缩窗口时先更新计数再判断是否失达标（导致validType统计错误）；
 * 易错点5：计数为0时未删除字符，导致charCountMap.size统计错误；
 * 易错点6：窗口长度计算错误（左闭右开应为right-left，而非right-left+1）；
 * 易错点7：未判断maxLen是否为初始值，直接返回maxLen（无满足条件时返回- Infinity）。
 */

// ===================== 测试用例（可直接运行验证） =====================
// console.log(longestSubstring("aaabb", 3)); // 预期输出：3（子串"aaa"）
// console.log(longestSubstring("ababbc", 2)); // 预期输出：5（子串"ababb"）
// console.log(longestSubstring("a", 1)); // 预期输出：1（单字符达标）
// console.log(longestSubstring("abc", 2)); // 预期输出：0（无达标子串）
// console.log(longestSubstring("aaaa", 2)); // 预期输出：4（全串达标）

三、滑动窗口适用场景与避坑指南

1. 适用场景

滑动窗口仅适用于「连续子串/子数组 + 区间约束 」问题，且需满足「单调性」：

• 正数数组的和/乘积：加入元素→和/乘积增大，移出元素→和/乘积减小；

• 字符计数：加入元素→计数+1，移出元素→计数-1；

• 若包含负数/0，需改用「前缀和+哈希表」（如LeetCode 560）。

2. 高频易错点（必记）

易错点	错误表现	正确做法
窗口长度计算	写成 right-left+1	左闭右开区间长度= right-left
指针移动顺序	先移指针再取值	右指针：先取值，再移动；左指针：先处理数据，再移动
计数更新顺序	收缩窗口时先更计数再判断	先判断「移出前是否达标」，再更新计数
边界处理	未处理空字符串/空数组	提前判断空输入，返回0/-1等
初始值设置	最大长度初始化为0	最大长度初始化为-Infinity，最小长度初始化为Infinity

3. 解题步骤总结

1. 问题转化：将目标问题转化为「找满足XX条件的子串/子数组」；

2. 定义窗口：确定窗口的统计变量（计数/和/乘积）和收缩条件；

3. 扩展窗口：右指针遍历，更新窗口状态；

4. 收缩窗口：满足收缩条件时，左指针右移，更新窗口状态；

5. 更新结果：在窗口满足条件时，记录最优解。

四、总结

滑动窗口是解决子串/子数组问题的「银弹」，核心是左闭右开的双指针规则 和单调性约束。掌握本文的通用模板和易错点，能解决LeetCode 80%以上的滑动窗口真题。

关键要记住：滑动窗口的本质是「用空间换时间」，通过维护窗口内的统计信息，避免重复遍历，将暴力解法的 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2) 复杂度降至线性 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ) O(n) </math>O(n) 。只要理解「扩窗口找可行解，缩窗口找最优解」的核心逻辑，就能灵活应对各类变体问题。