递归搜索入门

• 个人对递归的理解
• • 两两交换链表中的节点
  • 全排列
• 汉诺塔问题
• • 题目描述
  • 算法原理和实现
• 合并两个有序链表
• • 题目描述
  • 算法原理和实现
• 反转链表
• • 题目描述
  • 算法原理和实现
• [Pow(x, n)](#Pow(x, n))
• • 题目描述
  • 算法原理和实现
  • 快速幂

个人对递归的理解

如果读者已经阅读过我的动态规划相关的文章，特别是两个数组的动态规划这篇。你们会发现动态规划和递归非常的相似，甚至可以说动态规划就是递归的迭代实现。

当然这个说法是不太准确的，这要求问题必须有最优子结构，才能动态规划。

言归正传，在我看来递归的本质就缩小规模。对于一些问题，规模较小的时候我们能直接处理。规模大了就很难处理，那么递归就是我们只处理一部分，剩下部分交给递归处理。

干说有点晦涩，我们举两个实际的例子

两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

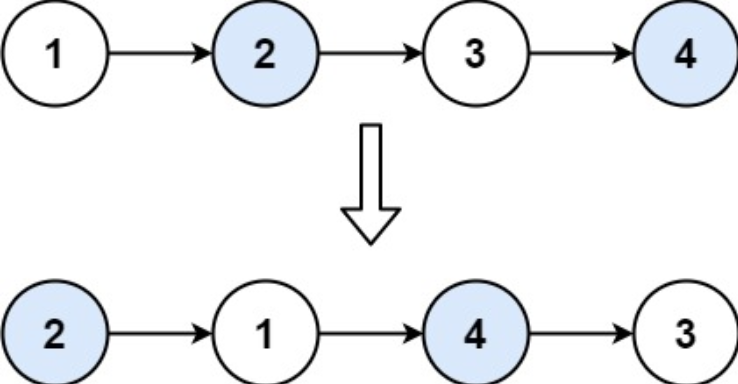
这个题目就非常符合我们缩减规模的思路，不管他给的链表多长，我们就只反转前两个结点，剩下部分就交给递归处理：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head||!head->next)return head;

        ListNode*next=head->next;
        head->next=swapPairs(next->next);//交给递归处理
        next->next=head;//只反转头两个
        return next;
    }
};

知道为什么我们递归一定能实现吗。因为我们设置了一个规模最小值的出口。这里是链表为空或者只有一个结点就无需翻转。然后我们对原问题一直缩减规模，他最终一定会变成最小规模，然后解决。

这里就是我们递归设计的本质:

⑴ 边界条件：确定递归到何时终止；

⑵ 递归模式：大问题是如何分解为小问题的。

我们再看另一种形式的缩小规模。

全排列

给定一个不含重复数字的整数数组 nums ，返回其 所有可能的全排列 。可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

例如我们要寻找1，2，3，4四个元素的全排列。直接求是比较困难的，但我们可以只做一部分工作，比如只确定排列的开头是哪个元素：

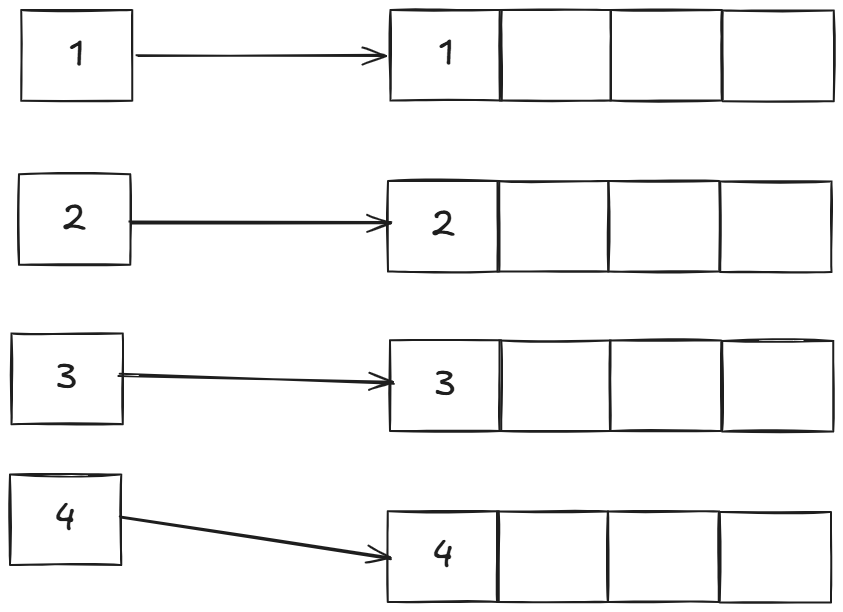
实际上就四种情况，我们确定好了哪个元素开头，再递归处理剩下三个元素的全排列即可。

这样我们就做到了缩小问题规模。

实际上实现要复杂一点，我们要标记已经排列好的元素，让他不能再后续出现。

具体实现：

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        int n=nums.size();
        vector<bool>vis(n);
        vector<vector<int>>ret;
        vector<int>arrange(n);
        function<void(int)>dfs=[&](int pos){//从哪个位置开始排列，即排列pos后的剩余元素
            if(pos==n){//已经排列完所有元素，是其中一种结果
                ret.emplace_back(arrange);
                return;
            }
            for(int i=0;i<n;++i){
                if(!vis[i]){//检测元素是否没被用过
                    arrange[pos]=nums[i];//1.没用过就当作首元素
                    vis[i]=true;
                    dfs(pos+1);//2.递归处理剩余排列
                    vis[i]=false;
                }
            }
        };
        dfs(0);
        return ret;
    }
};

值得注意的是，这就是所谓的回溯算法。

汉诺塔问题

题目描述

汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:

(1) 每次只能移动一个盘子;

(2) 盘子只能从柱子顶端滑出移到下一根柱子;

(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1：

输入：A = [2, 1, 0], B = [], C = []

输出：C = [2, 1, 0]

示例 2：

输入：A = [1, 0], B = [], C = []

输出：C = [1, 0]

提示：

• A 中盘子的数目不大于 14 个。

算法原理和实现

根据我最开始的理论，我们可以缩小问题规模来解决问题。

首先只有一个盘子的情况我们是非常清晰的，直接挪过去就行了。

那多个盘子呢？

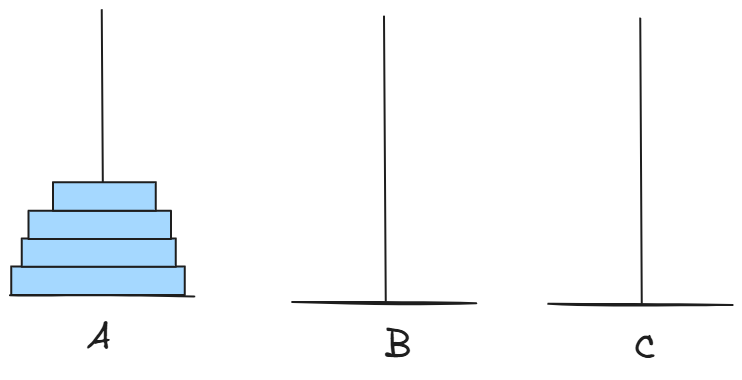
模糊其中过程，关键步骤无非就是：

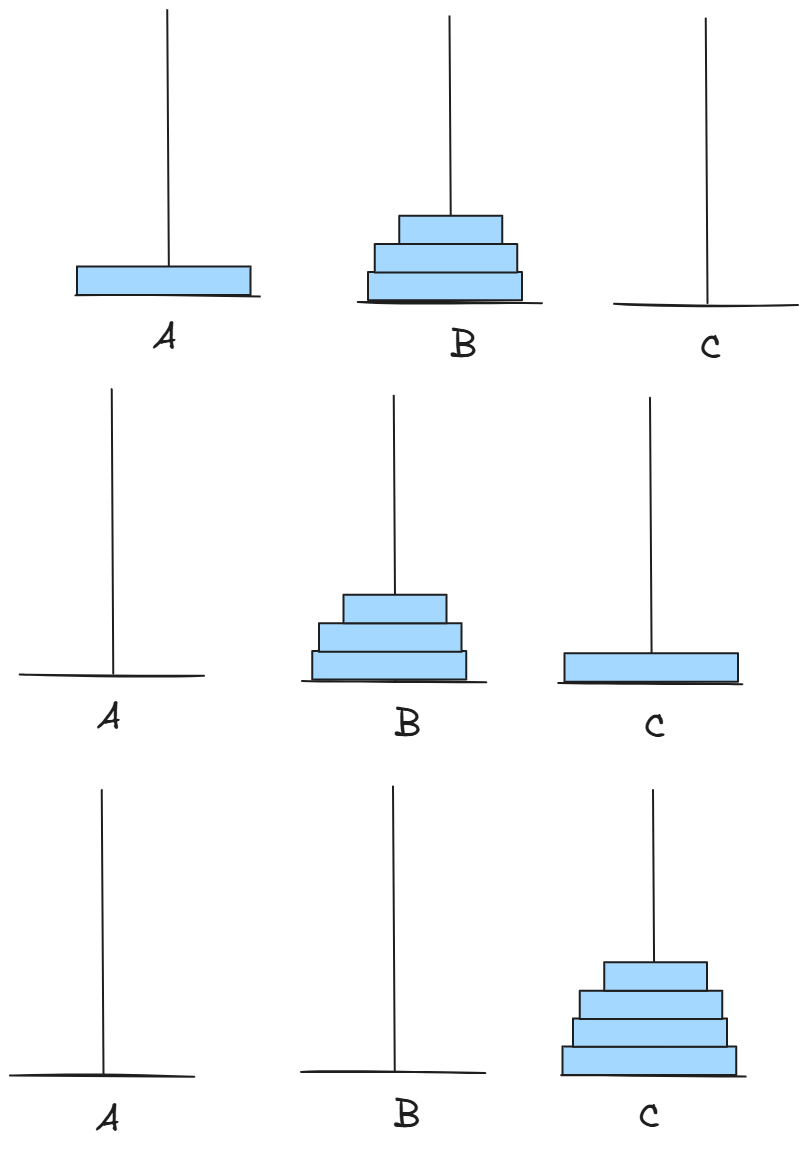
我们先将上面n-1个盘子移动到中间柱子，然后把剩下盘子挪到最后一个柱子，最后把中间的柱子上的盘子挪到最后一个柱子。

那么我们是不是就将问题从n缩减到n-1规模。

这里缩减规模和前面全排列缩减规模区别无非就是，全排列是先解决小规模问题，再处理递归缩小规模问题。

这里是先处理递归缩小规模的问题，在处理小规模问题。

那么具体实现：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        move(A.size(),A,B,C);
    }
    void move(int n,vector<int>& A, vector<int>& B, vector<int>& C){
        if(!n)return;//没盘子了，无需移动
        move(n-1,A,C,B);//将A上n-1盘子放到B
        C.push_back(A.back());//将A的最后一个盘子放到C
        A.pop_back();
        move(n-1,B,A,C);//将B上的盘子挪到C
    }
};

实际上这题如果想要跑的快，我们直接将AC交换即可：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        swap(A,C);
    }
};

合并两个有序链表

题目描述

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]

输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []

输出：[]

示例 3：

输入：l1 = [], l2 = [0]

输出：[0]

提示：

• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列

算法原理和实现

有了前面的缩减规模的经验，读者是不是已经猜到了我们要怎么做了？没错，我们这次一次合并一个结点，剩下交给递归处理。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* dfs(ListNode* list1, ListNode* list2){
        if(!list1)return list2;//如果list1空，直接合并list2
        if(!list2)return list1;//同理
        ListNode*ret;
        if(list1->val>list2->val)swap(list1,list2);//首元素选择较小的一个
        ret=list1;
        ret->next=dfs(list1->next,list2);
        return ret;
    }
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode*dummy=new ListNode(),*ret;//哨兵位
        dummy->next=dfs(list1,list2);
        ret=dummy->next;
        delete dummy;
        return ret;
    }
};

我们这里添加哨兵位 是为了避免边界判断，不管list1和list2是不是空，都是一套逻辑。这是链表类问题的通常做法。

当然我这样只是为了演示链表问题解法，递归更简略的解法如下：

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(!list1)return list2;
        if(!list2)return list1;
        if(list1->val>list2->val)swap(list1,list2);
        list1->next=mergeTwoLists(list1->next,list2);
        return list1;
    }
};

反转链表

题目描述

反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

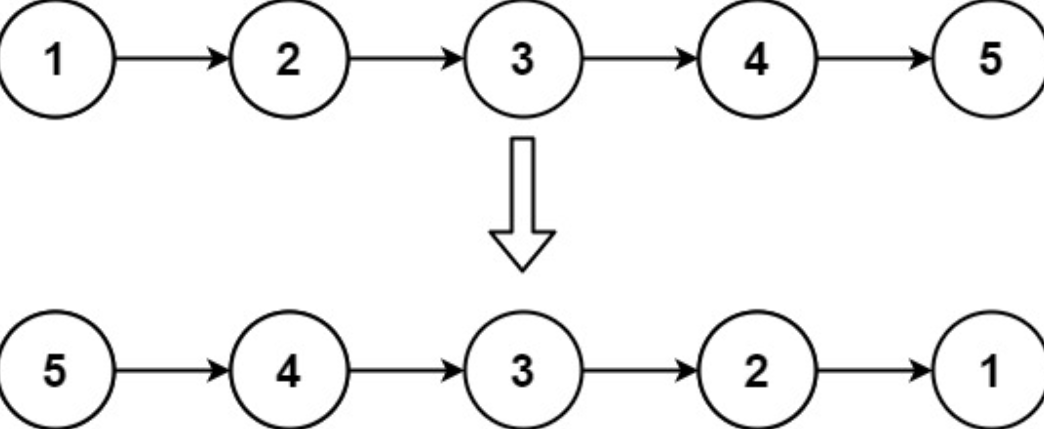
输入：head = [1,2,3,4,5]

输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]

输出：[2,1]

示例 3：

输入：head = []

输出：[]

提示：

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

算法原理和实现

我们缩减规模的思路就是，先逆序首元素的后续结点，然后让首元素的后续结点指向首元素，最后返回末尾结点：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode *dfs(ListNode* head){
        if(!head->next)return head;
        head->next=dfs(head->next);
        head->next->next=head;
        head->next=nullptr;
        return head;
    }
    ListNode* reverseList(ListNode* head) {
        if(!head)return nullptr;
        ListNode*ret=head;
        while(ret->next)ret=ret->next;
        dfs(head);
        return ret;
    }
};

实际上我们能直接合并这个过程：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head||!head->next)return head;
        ListNode*ret=reverseList(head->next);//逆序后续结点，并记录返回值
        head->next->next=head;//逆序当前结点
        head->next=nullptr;
        return ret;
    }
};

Pow(x, n)

题目描述

Pow(x, n)

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10

输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3

输出：9.26100

示例 3：

输入：x = 2.00000, n = -2

输出：0.25000

解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -2³¹ <= n <= 2³¹-1
• n 是一个整数
• 要么 x 不为零，要么 n > 0 。
• -10⁴ <= xⁿ <= 104

算法原理和实现

这个根据上述题目的经验，我们很容易知道这次缩减规模就是，只乘一次，然后返回剩余结果。

不过要注意这里有负数幂，我们可以转化为整数幂，比如Pow(3,-2)=Pow(1/3,2)。

问题是这里n的取值是可能为INT_MIN，如果直接取-n是会越界的，因此我们最好是这样Pow(x,n)=1/x*Pow(1/x,-1-n).

class Solution {
public:
    double myPow(double x, int n) {
        if(n==0)return 1;
        else if(n<0)return 1/x*myPow(1/x,-1-n);
        else return x*myPow(x,n-1);
    }
};

不出意外，我们的代码栈溢出了：

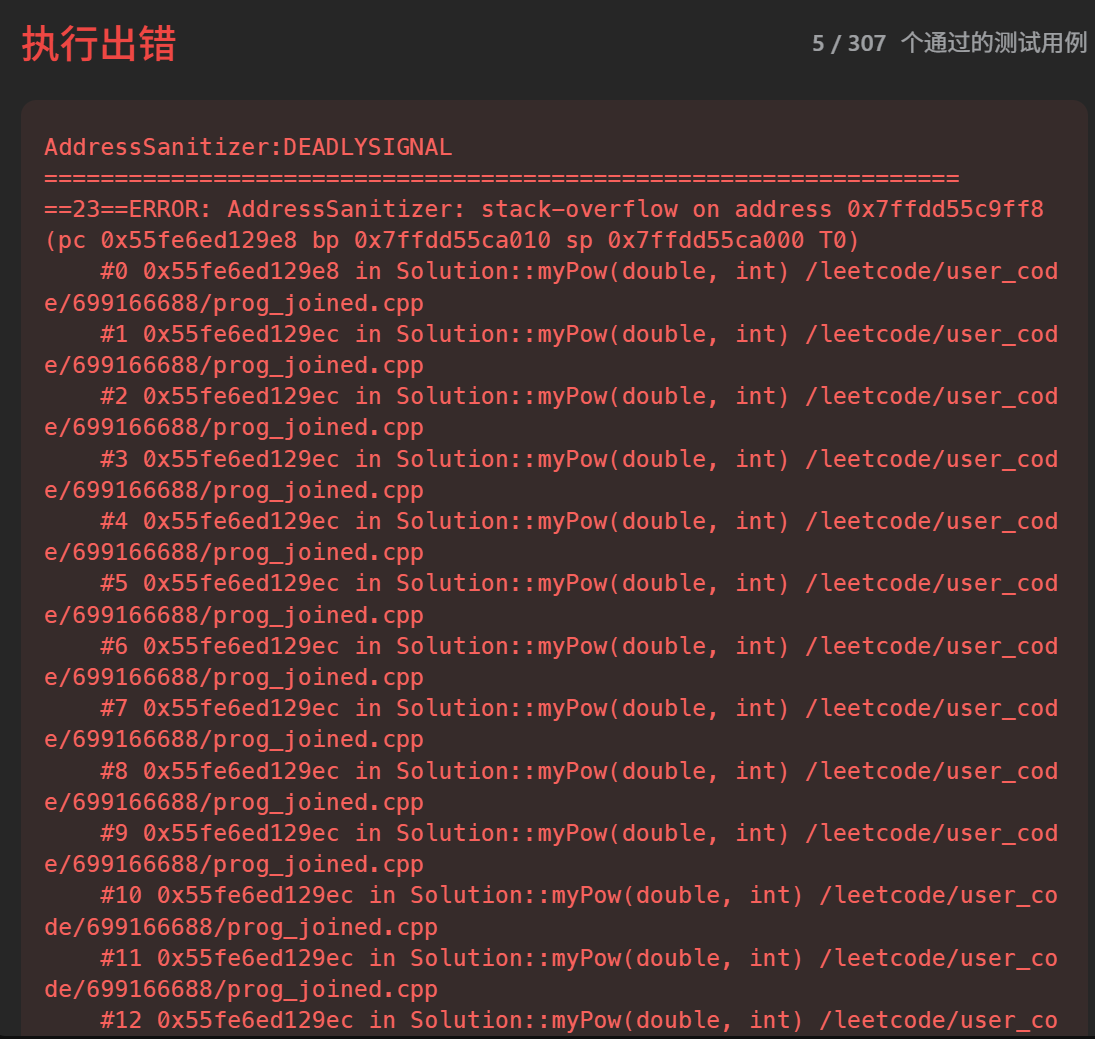
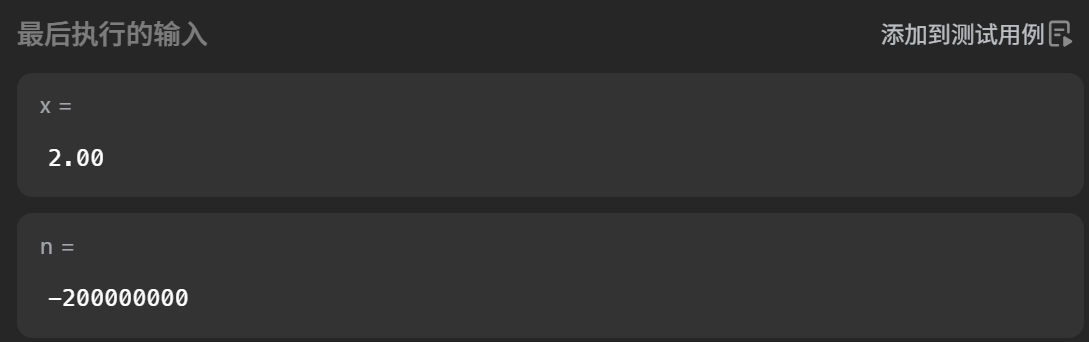
快速幂

因为我们一次次减少可以是可以，但是太慢了。

我们能不能直接取得Pow(x,n/2)，然后返回Pow(x,n/2)*Pow(x,n/2)呢

当然可以了，但是注意我们n是可能为奇数，所以正确返回应该是Pow(x,n/2)*Pow(x,(n+1)/2)

class Solution {
public:
    double myPow(double x, int n) {
        if(n==0)return 1;
        else if(n==1)return x;
        else if(n<0)return 1/x*myPow(1/x,-1-n);
        else return myPow(x,n/2)*myPow(x,(n+1)/2);
    }
};

注意这里要加上n==1的判断，因为n为1时(n+1)/2==1，如果不加就会死循环的。

那么问题来了，我们这个做法就能过了吗？

答案是不能：

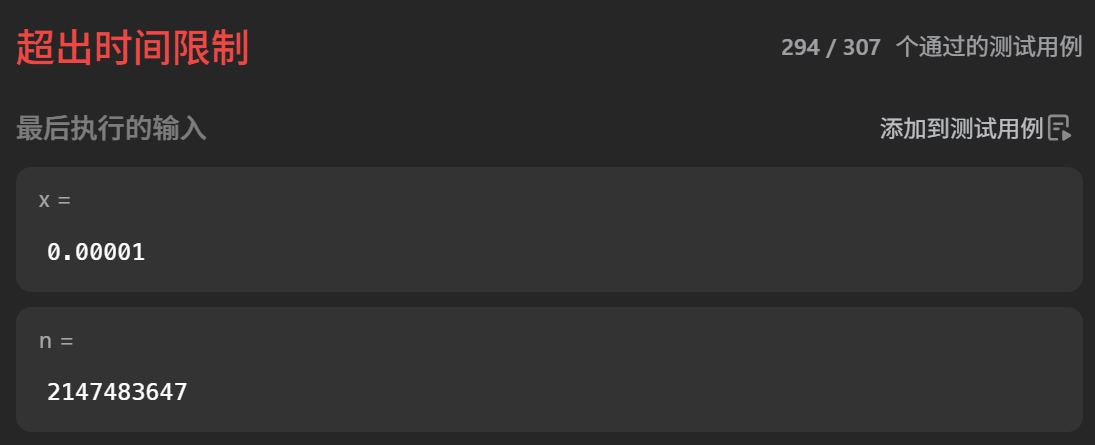
直接超出时间限制了，这是为什么呢？

仔细想想我们执行Pow(3,4)的过程：

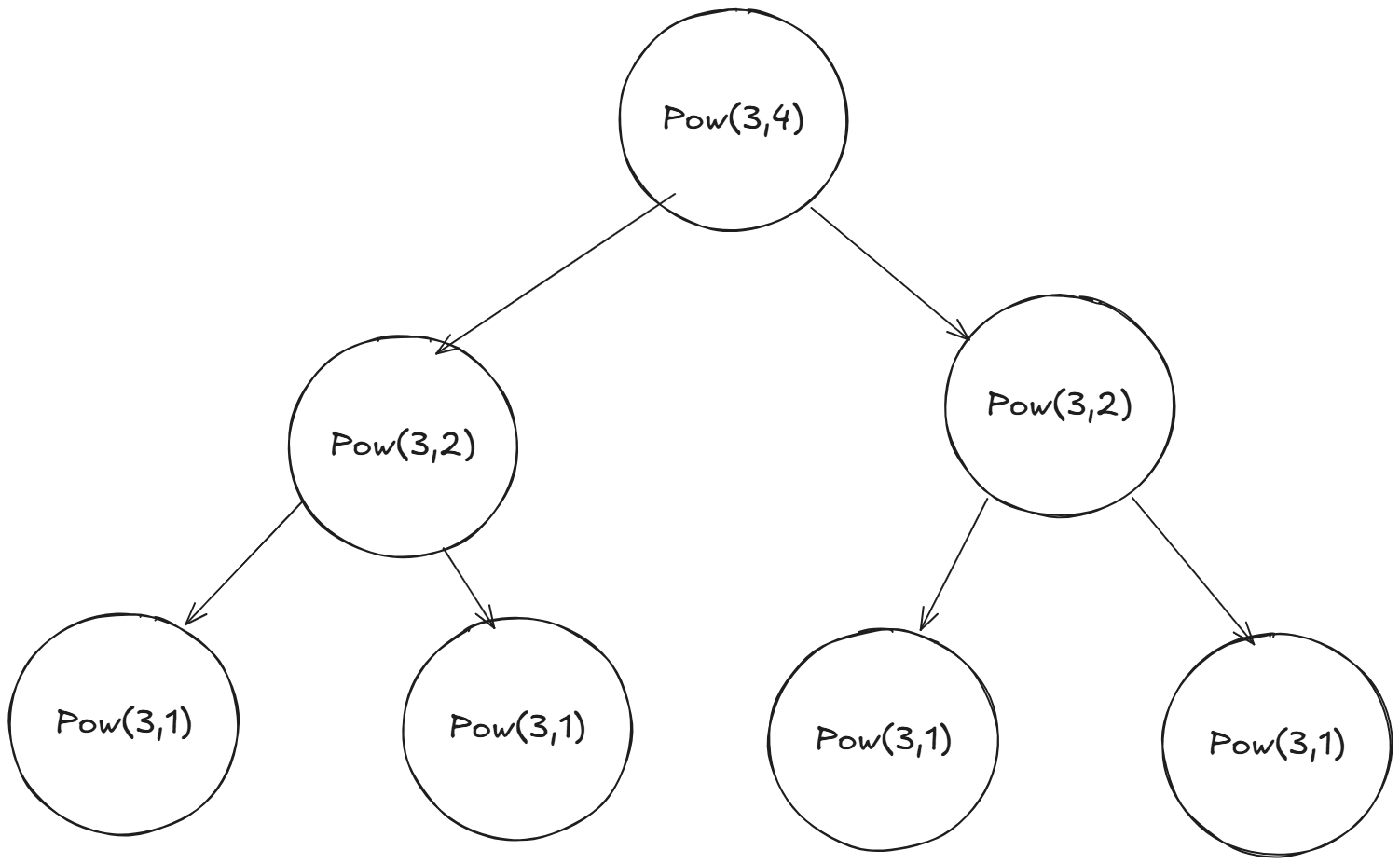
是的，我们执行了整个二叉树的过程，树高是log n，我们就执行了2^logn也就是n次。跟原来比没有优化，只不过我们及时弹栈，所以没有栈溢出了。

这是因为我们左右子树根本就是相同（或者相差一个x），但我们却重复执行，像一个失忆症患者。

所以我们这次要记录下左子树的结果，这也就是最基本的记忆化搜索。

class Solution {
public:
    double myPow(double x, int n) {
        if(n==0)return 1;
        else if(n<0)return 1/x*myPow(1/x,-1-n);
        else{
            double ret=myPow(x,n/2);
            ret*=ret;
            if(n%2)ret*=x;
            return ret;
        }
    }
};

这次我们就成功实现了，时间复杂度是O(logn)