文章目录
- 线索栏
- 笔记栏
-
- [1. 补码的定义与解释](#1. 补码的定义与解释)
- [2. 补码的表示范围与唯一性](#2. 补码的表示范围与唯一性)
- [3. 关键数值与位模式(图2-14总结)](#3. 关键数值与位模式(图2-14总结))
- [4. C语言实现与可移植性](#4. C语言实现与可移植性)
- [5. 旁注精要](#5. 旁注精要)
- 6.练习题
- 总结栏
线索栏
- 补码编码的数学定义是什么?公式 B 2 T w B2T_w B2Tw如何解释?
- 在补码中,最高有效位(符号位)的权重是多少?它如何决定数值的正负?
- 给定一个位向量,如何手动计算其补码值?(请以 [1011]为例)
- w位补码能表示的范围是多少? T M i n w TMin_w TMinw和 T M a x w TMax_w TMaxw的位模式与数值是什么?为什么范围是不对称的?
- 函数 B 2 T w B2T_w B2Tw是否也是双射?其反函数是什么?
- 对于不同的字长(w=8,16, 32, 64),关键的数值(UMax, TMin, TMax, -1, 0)是多少?它们的十六进制和二进制模式有何规律?
- (旁注)为什么需要 stdint.h中的 intN_t类型?如何正确打印这些类型的值?
- (旁注)除了补码,有符号数还有哪两种表示方法?它们的定义和主要缺点是什么?
笔记栏
1. 补码的定义与解释
1)数学定义
对于位向量 x ⃗ = [ x w − 1 , x w − 2 , . . . , x 0 ] \vec{x}=[x_{w−1},x_{w−2},...,x_0] x =[xw−1,xw−2,...,x0],其表示的补码值为: B 2 T w ( x ⃗ ) ≐ − x w − 1 ⋅ 2 w − 1 + i = ∑ i = 0 w − 2 x i ⋅ 2 i B2T_w (\vec{x})\doteq−x_{w−1} \cdot2^{w−1}+i=\sum_{i=0}^{w-2} x_{i} \cdot2i B2Tw(x )≐−xw−1⋅2w−1+i=i=0∑w−2xi⋅2i
2)核心思想
最高有效位(MSB) x w − 1 x_{w−1} xw−1作为符号位,权重为 − 2 w − 1 −2^{w−1} −2w−1(负权重)。其余位权重为正,与无符号编码相同。
(1)符号位 = 0:值为非负(0∼ 2 w − 1 2^{w−1} 2w−1−1)。
(2)符号位 = 1:值为负( − 2 w − 1 −2^w−1 −2w−1∼−1)。
3)计算示例(w=4)
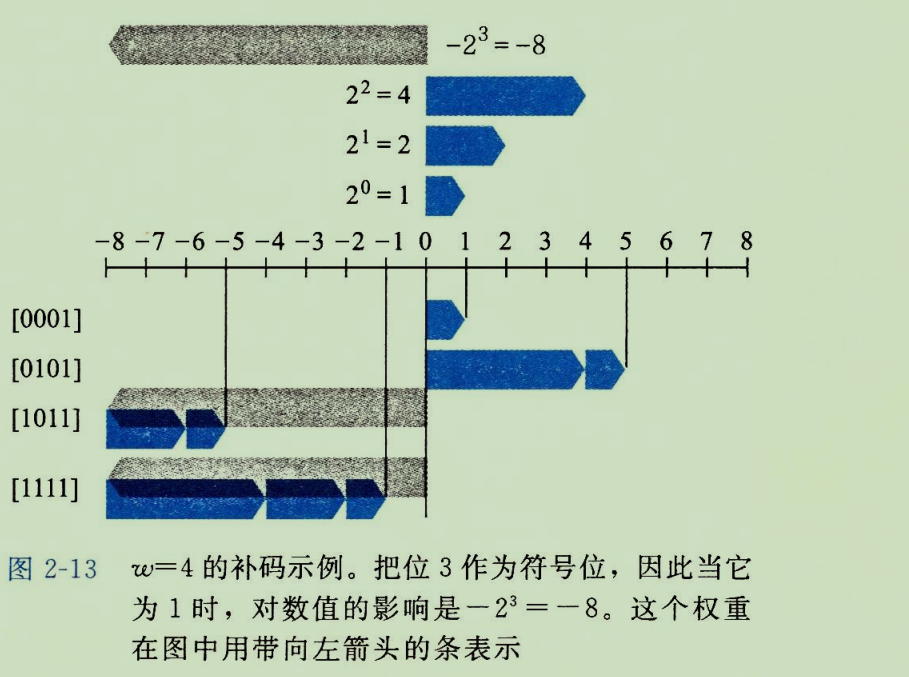
B 2 T 4 B2T_4 B2T4([0001]) = 0*(-8) + 0 * 4 + 0 * 2 + 1 * 1 = 1
B 2 T 4 B2T_4 B2T4([0101]) = 0*(-8) + 1 * 4 + 0 * 2 + 1 * 1 = 5
B 2 T 4 B2T_4 B2T4([1011]) = 1*(-8) + 0 * 4 + 1 * 2 + 1 * 1 = -5
B 2 T 4 B2T_4 B2T4([1111]) = 1*(-8) + 1 * 4 + 1 * 2 + 1 * 1 = -1
2. 补码的表示范围与唯一性
1)取值范围
(1)最小值 T M i n w TMin_w TMinw:位模式 [10...0],值为 − 2 w − 1 −2^{w−1} −2w−1。
(2)最大值 T M a x w TMax_w TMaxw:位模式 [01...1],值为 2 w − 1 2^{w−1} 2w−1−1。
(3)示例 (w=4): T M i n 4 TMin_4 TMin4 = -8([1000]), T M a x 4 TMax_4 TMax4 = 7([0111])。
2)不对称性
∣ T M i n w TMin_w TMinw∣=∣ T M a x w TMax_w TMaxw∣+1。因为0占用了非负数的一个编码,导致负数比正数多一个。
3)唯一性(双射)
函数 B 2 T w B2T_w B2Tw 是位模式到区间 [ T M i n w TMin_w TMinw, T M a x w TMax_w TMaxw]的一一映射。其反函数记为 T 2 B w T2B_w T2Bw 。
3. 关键数值与位模式(图2-14总结)
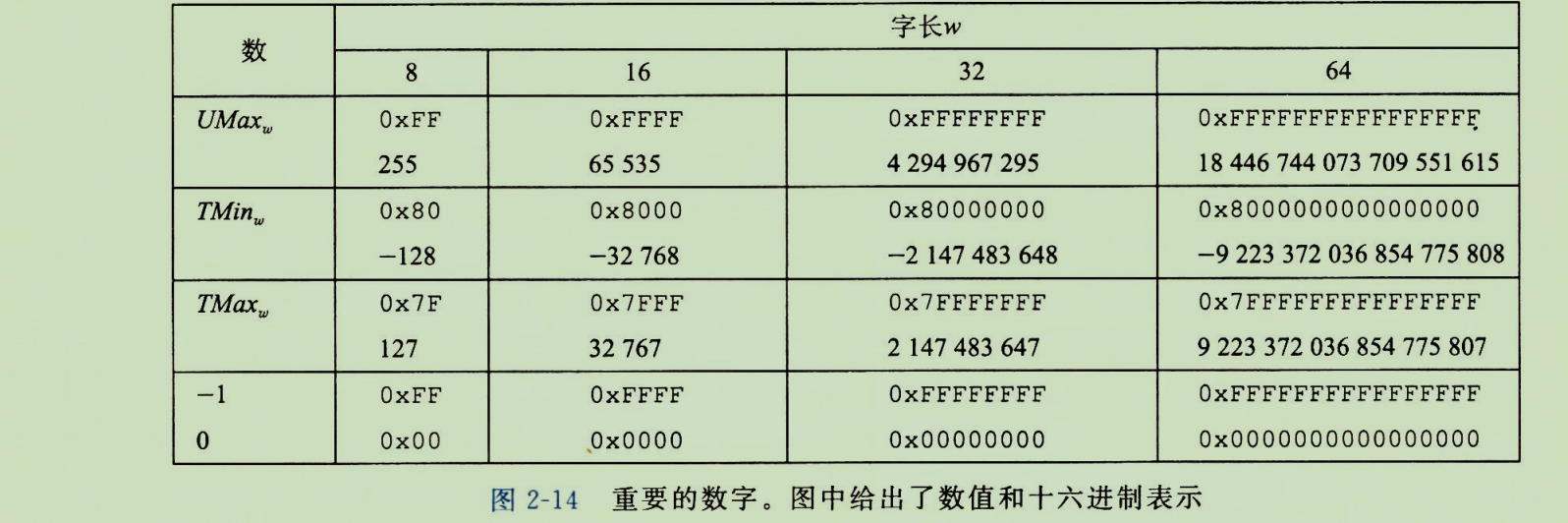
(1)TMin和 TMax的十六进制模式互补:TMin是最高位为1,其余为0;TMax是最高位为0,其余为1。
(2)-1 的位模式是全1,这与无符号数的最大值 UMax相同。这为类型转换埋下伏笔。
(3)UMax = 2 * TMax + 1。
4. C语言实现与可移植性
(1)几乎通用:几乎所有机器都用补码表示有符号整数。
(2)可移植性警告:C标准不强制要求补码。要编写最大可移植的代码,应仅依赖 <limits.h>定义的常量(如 INT_MAX),而非假设特定范围或表示。
(3)典型假设:多数程序假设补码和典型取值范围,这在实际中可广泛移植。
5. 旁注精要
1)确定大小的整数类型(<stdint.h>)
(1)类型:intN_t(有符号), uintN_t(无符号),N通常为8, 16, 32, 64。
(2)用途:确保精确位宽,对网络协议、二进制文件格式等至关重要。
(3)打印:使用宏(如 PRId32, PRIu64)生成正确的 printf格式串,保证跨编译环境正确。
2)Java的规定
强制使用补码,且各整数类型位宽严格固定(如 byte为8位)。
3)其他有符号表示法
(1)反码:符号位权重为 − ( 2 w − 1 − 1 ) −(2^{w−1}−1) −(2w−1−1)。缺点:存在 +0([00...0]) 和 -0([11...1])。
(2)原码:最高位仅表示符号(0正1负),其余位表示绝对值。缺点:同样存在 +0和 -0。现代机器基本不用,但浮点数阶码部分使用。
6.练习题
练习题2.17
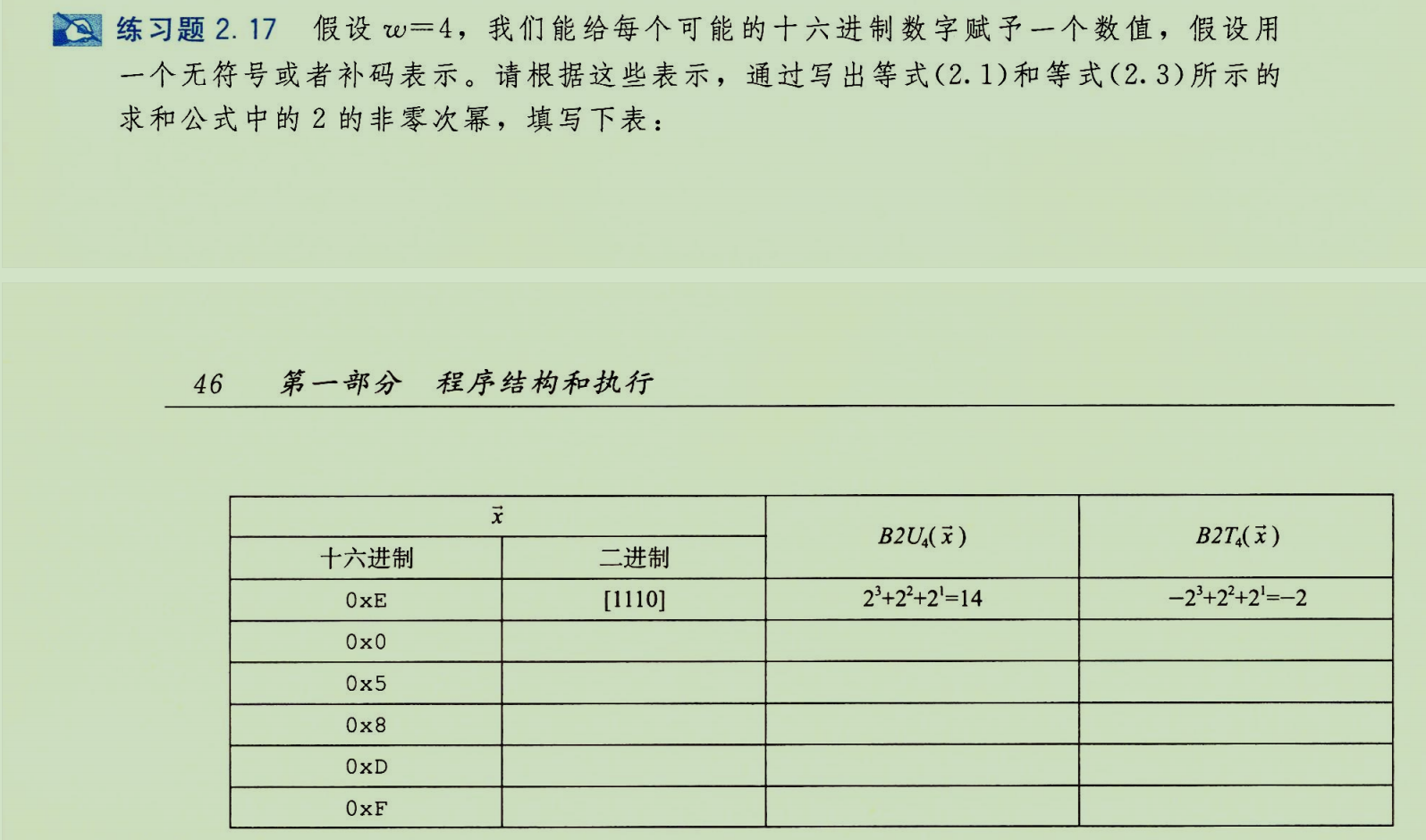
练习将十六进制数字解释为无符号数和补码数,并手动计算其十进制值。核心是理解同一串位,在不同解释(上下文)下,值不同。
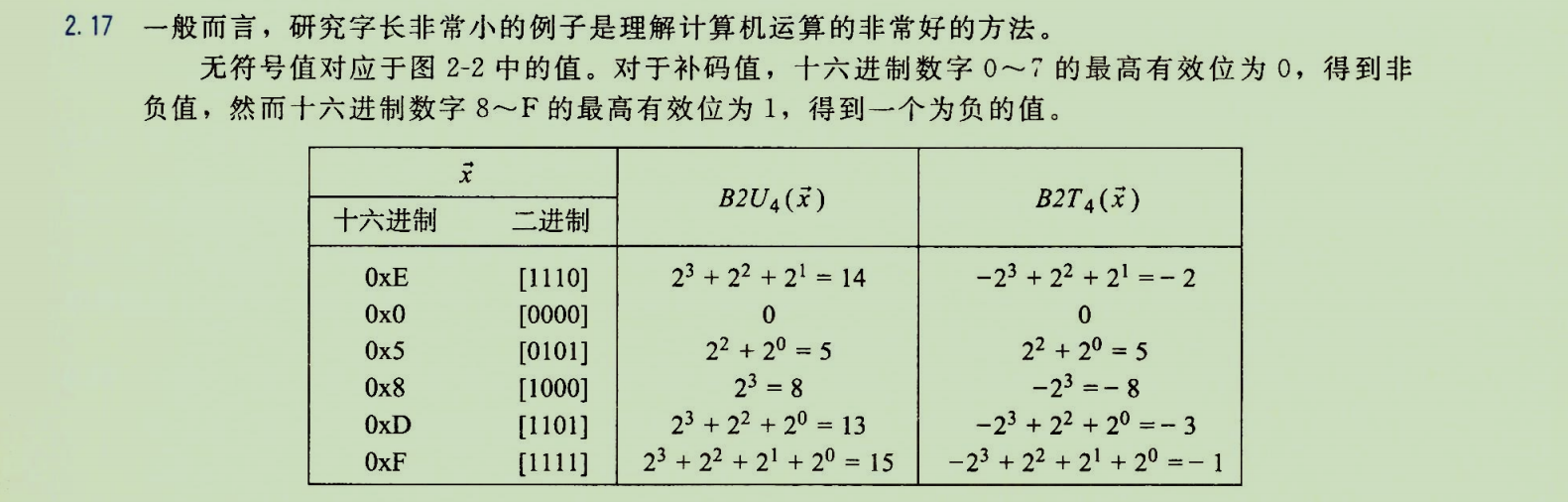
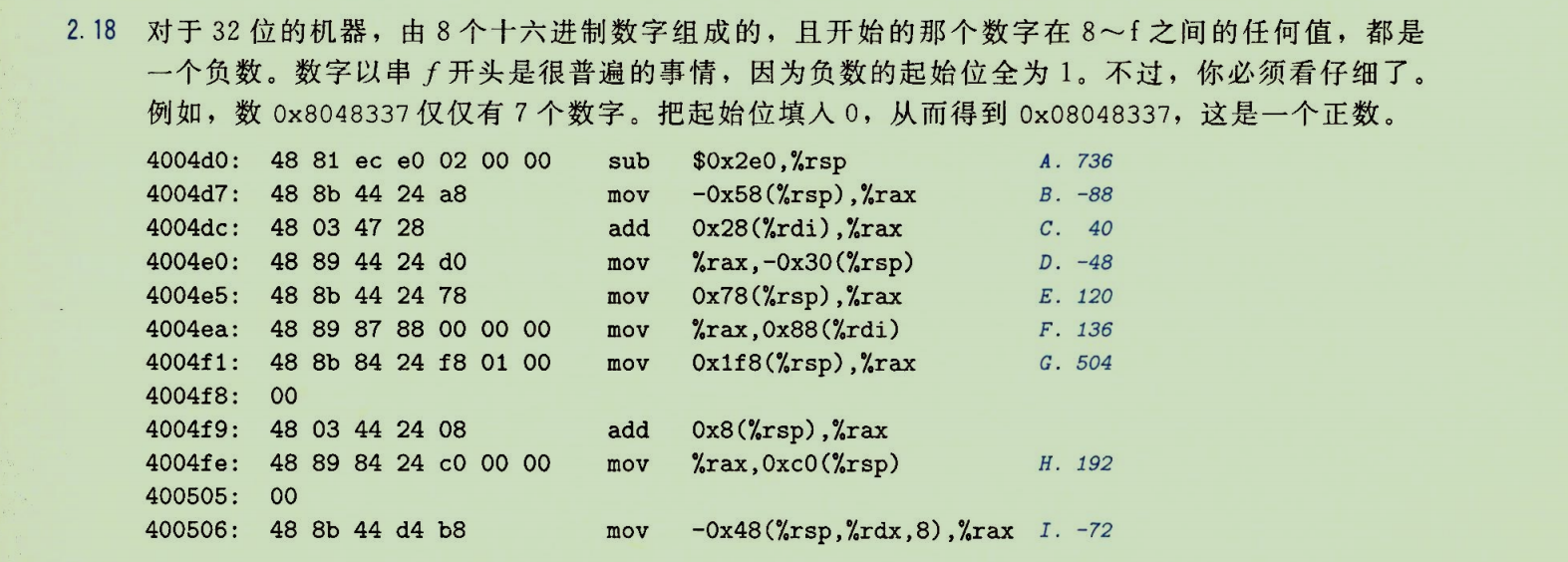
练习题2.18
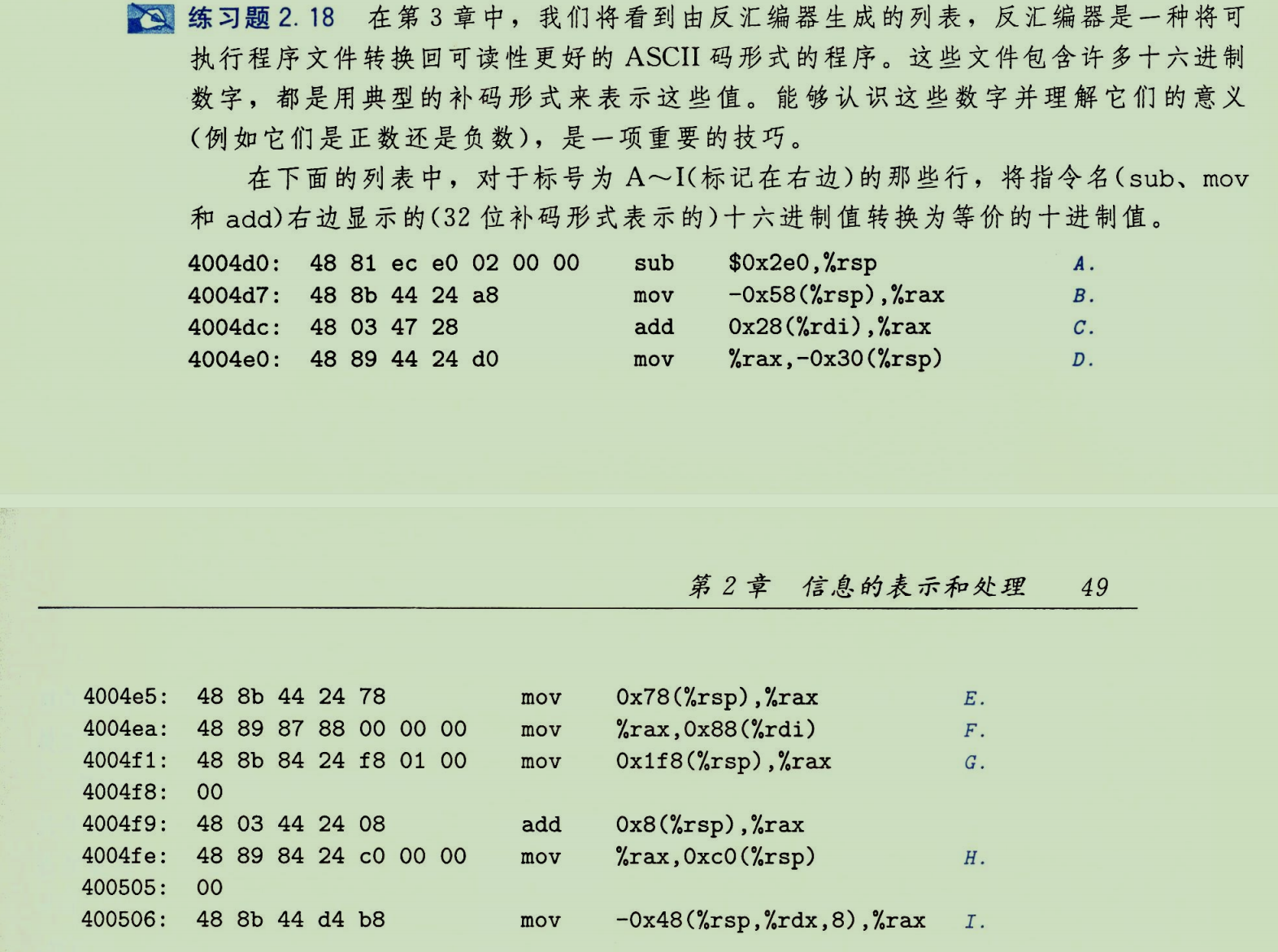
进一步练习根据补码编码公式 B 2 T w B2T_w B2Tw,将十六进制机器代码值转换为程序员可读的十进制值。这是理解机器级代码的基础。
总结栏
本节深入探讨了计算机表示有符号整数的标准方式------补码编码。
- 核心公式: B 2 T w ( x ) = − x w − 1 ∗ 2 w − 1 + Σ x i ∗ 2 i B2T_w(x) = -x_{w-1} * 2^{w-1} + Σ x_i *2^i B2Tw(x)=−xw−1∗2w−1+Σxi∗2i。其精髓在于赋予最高有效位负权重( − 2 w − 1 -2^{w-1} −2w−1),从而统一了正负数的表示。
- 关键范围:
(1) T M i n w = − 2 w − 1 TMin_w = -2^{w-1} TMinw=−2w−1(模式:1后跟w-1个0)
(2) T M a x w = 2 w − 1 − 1 TMax_w = 2^{w-1} - 1 TMaxw=2w−1−1 (模式:0后跟w-1个1)
(3) 范围不对称(|TMin| =|TMax| + 1),这是由0的表示唯一性导致的。 - 重要模式:-1 表示为全1,0表示为全0。TMin和TMax的位模式互为"互补"。
- 唯一性:补码编码也是双射,保证了数值和位模式的一一对应。
- 编程实践:虽然补码无处不在,但C标准未强制规定,编写可移植代码应使用 <limits.h>和 <stdint.h>。Java则明确强制使用固定位宽的补码。
理解补码是理解整数运算、溢出和类型转换的基础。其设计巧妙之处在于,使用相同的加法器电路即可处理无符号数和有符号数(补码)的加法。