
(以下内容全部出自上述课程)
目录
- 平衡二叉树
-
- [1. 定义](#1. 定义)
- [2. 插入操作](#2. 插入操作)
- [3. 插入新结点后如何解决不平衡问题](#3. 插入新结点后如何解决不平衡问题)
-
- [3.1 LL](#3.1 LL)
- [3.2 RR](#3.2 RR)
- [3.3 LR](#3.3 LR)
- [3.4 RL](#3.4 RL)
- [3.5 小结](#3.5 小结)
- [4. 填个坑](#4. 填个坑)
- [5. 练习](#5. 练习)
-
- [5.1 RR型](#5.1 RR型)
- [5.2 RL型](#5.2 RL型)
- [5.3 LR型](#5.3 LR型)
- [6. 查找效率分析](#6. 查找效率分析)
- [8. 小结](#8. 小结)
- 平衡二叉树的删除
-
- [1. 删除](#1. 删除)
- [2. 删除操作实例](#2. 删除操作实例)
-
- [2.1 例1-删9](#2.1 例1-删9)
- [2.2 例2-删55](#2.2 例2-删55)
- [2.3 例3-删32](#2.3 例3-删32)
- [2.4 例4-删32](#2.4 例4-删32)
- [2.5 例5-删75](#2.5 例5-删75)
- [2.6 例6-删75](#2.6 例6-删75)
- [3. 小结](#3. 小结)
- 红黑树的定义和性质
-
- [1. 定义](#1. 定义)
- [2. 练习:是否符合红黑树要求?](#2. 练习:是否符合红黑树要求?)
- [3. 黑高](#3. 黑高)
- [4. 性质](#4. 性质)
- [5. 查找](#5. 查找)
- 红黑树的插入
-
- [1. 概述](#1. 概述)
- [2. 练习](#2. 练习)
- [3. 小结](#3. 小结)
- 红黑树的删除
平衡二叉树
1. 定义
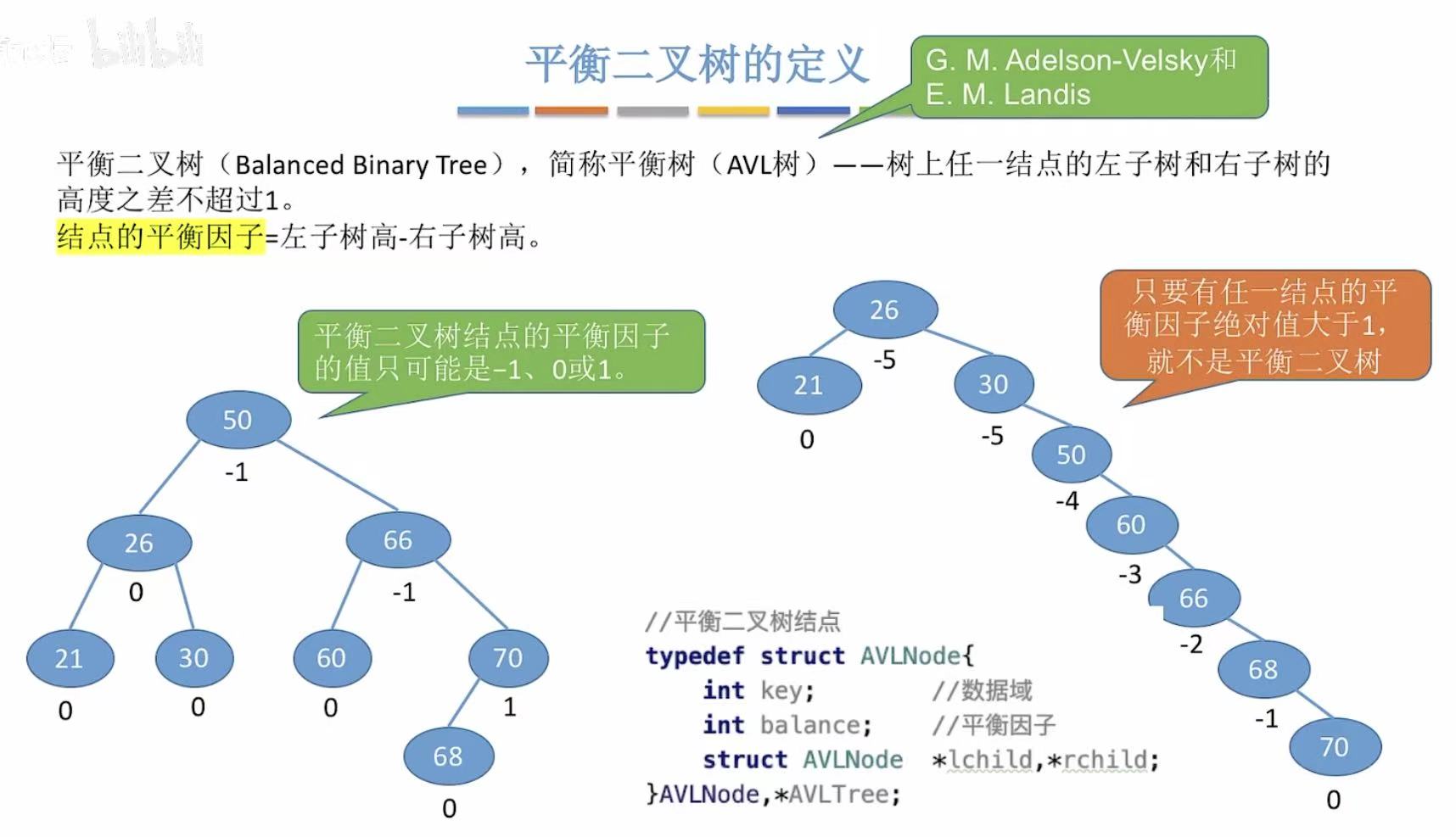
就是两边高度看着差不多,不会出现一条腿特别长另一条腿特别短的情况。
- 结点的平衡因子=左子树高-右子树高
- 平衡二叉树:树上任一结点的平衡因子为-1、0、1.
2. 插入操作
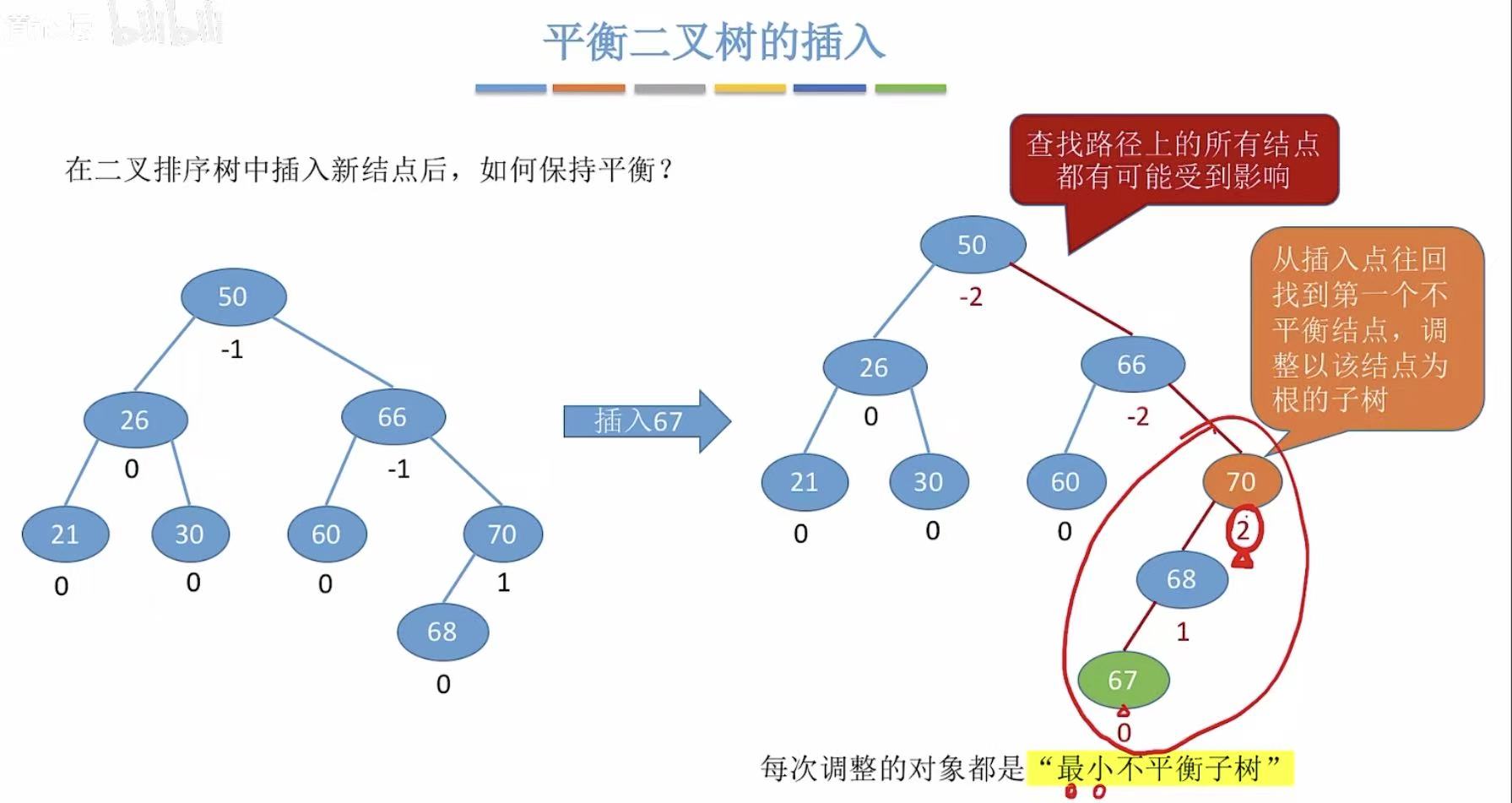
当我们对平衡二叉树进行插入操作 的时候,很容易会把这棵树变得不平衡 ,那么我们该怎么办呢?
我们需要顺着插入的结点向上寻找,找到第一个不平衡的结点 ,调节该结点为根的子树。
比如:右图中我们插入67 导致二叉树不平衡,我们就算出每个结点的平衡因子,当平衡因子为-2 的时候,就代表这个结点不平衡 ,也就是从70 开始向上的结点都不平衡,我们就要调整以70为根的子树 ,这个子树就是最小不平衡树 。
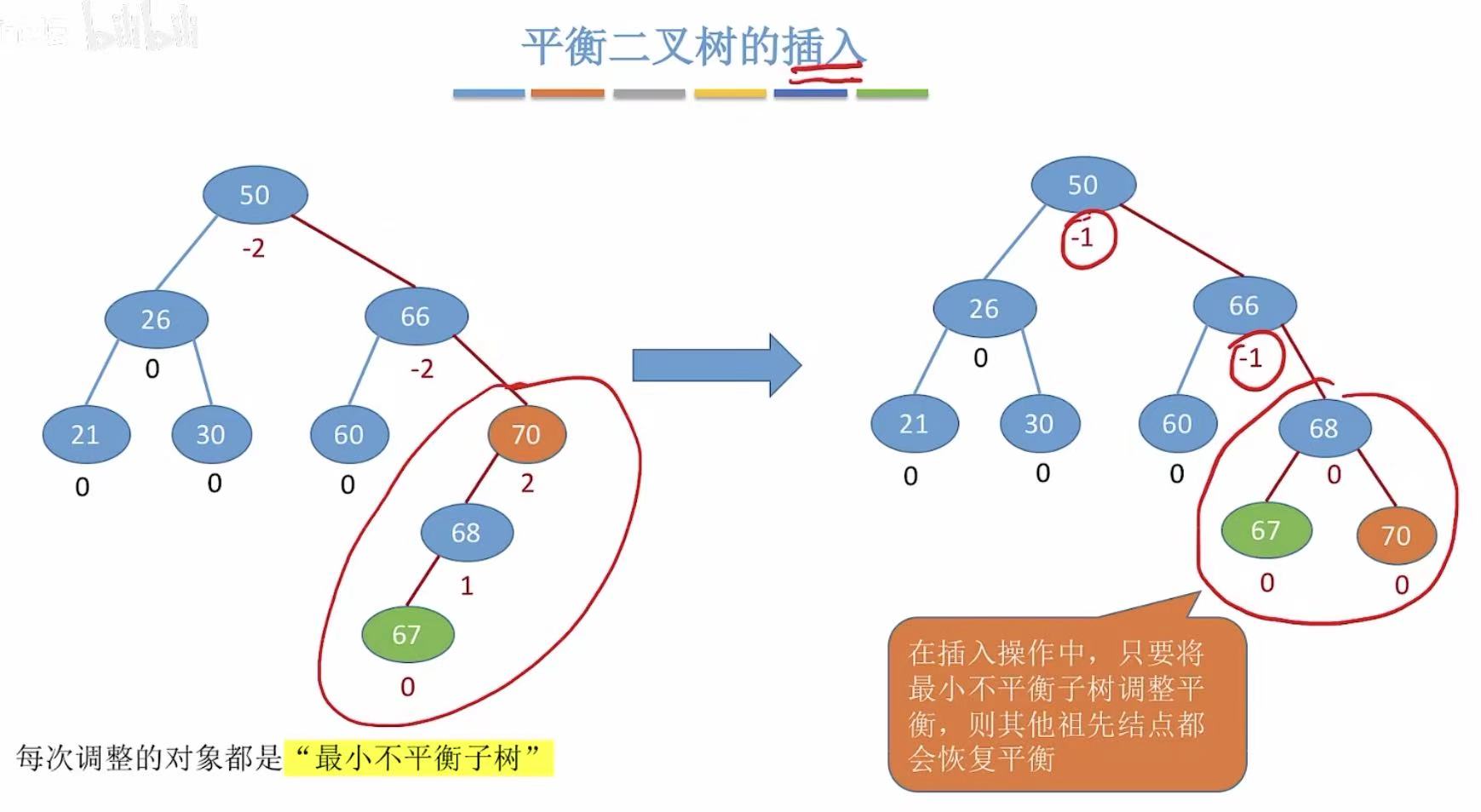
当我们调整了这个最小不平衡树,上面原本不平衡的结点,也会随着它的调整逐渐平衡。
3. 插入新结点后如何解决不平衡问题
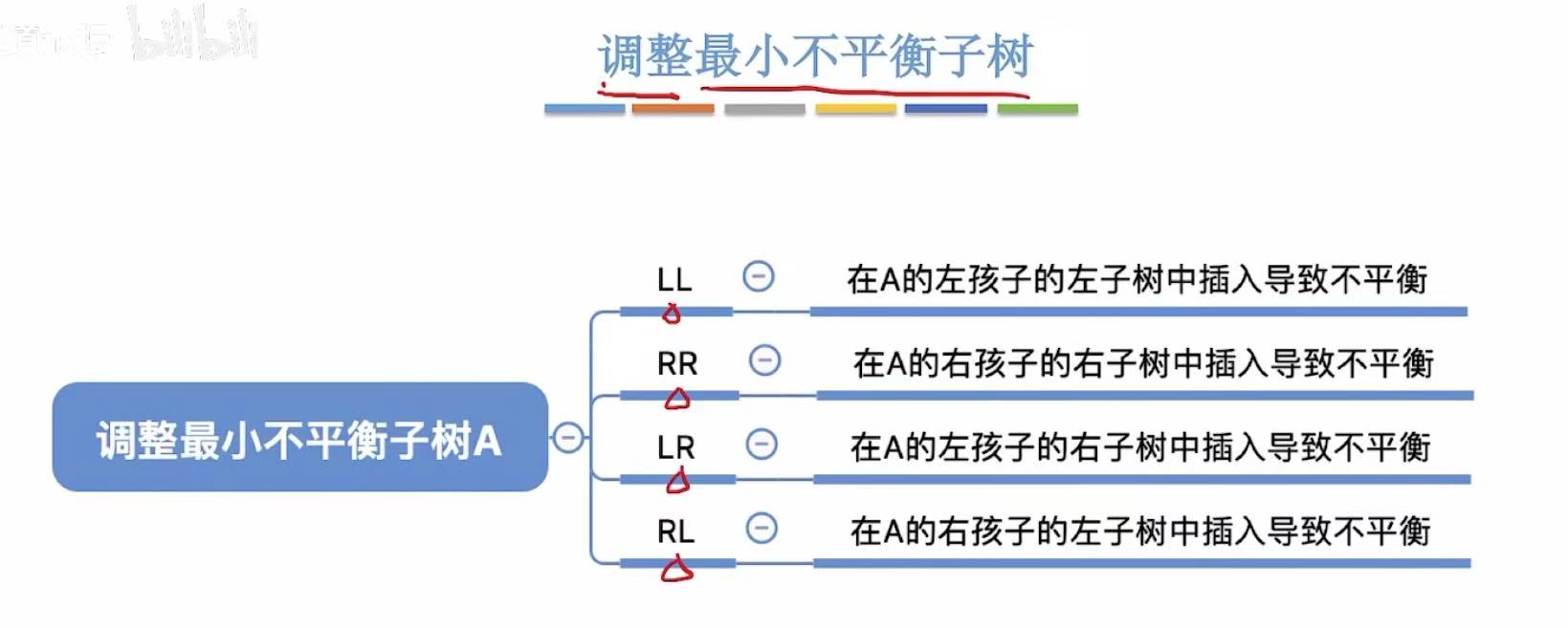
3.1 LL
- LL:在左孩子的左子树上插入了新的结点。
- 右单旋转 :B上A下,因为A下来变成了B结点的右孩子,BR就多出来了,就让给A带。
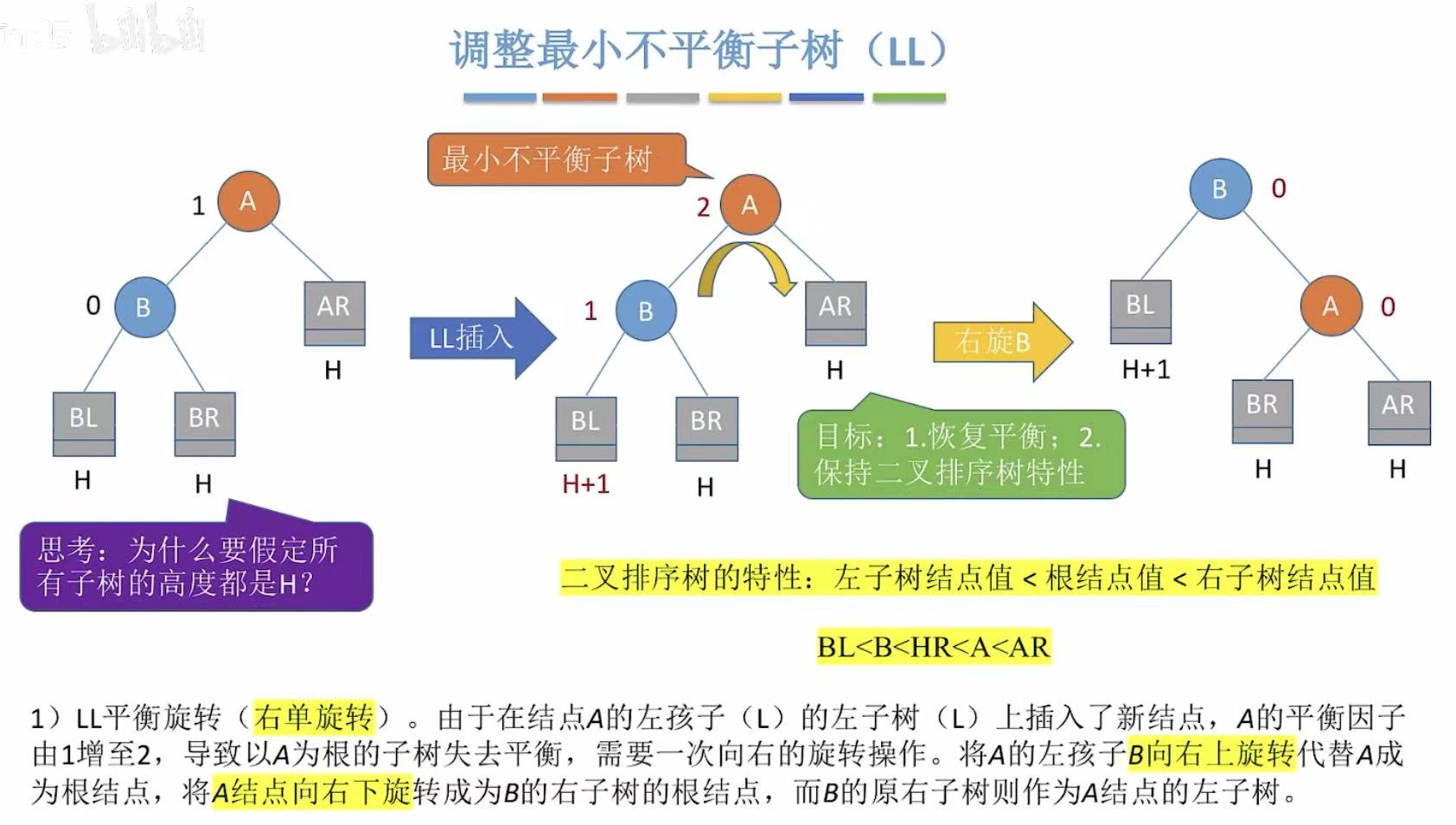
3.2 RR
- RR:在右孩子的右子树上插入了新的结点。
- 左单旋转:B上A下,因为A下来变成了B结点的右孩子,BL就多出来了,就让给A带。
- 往哪边儿旋转,哪边儿的孩子就被抛弃。
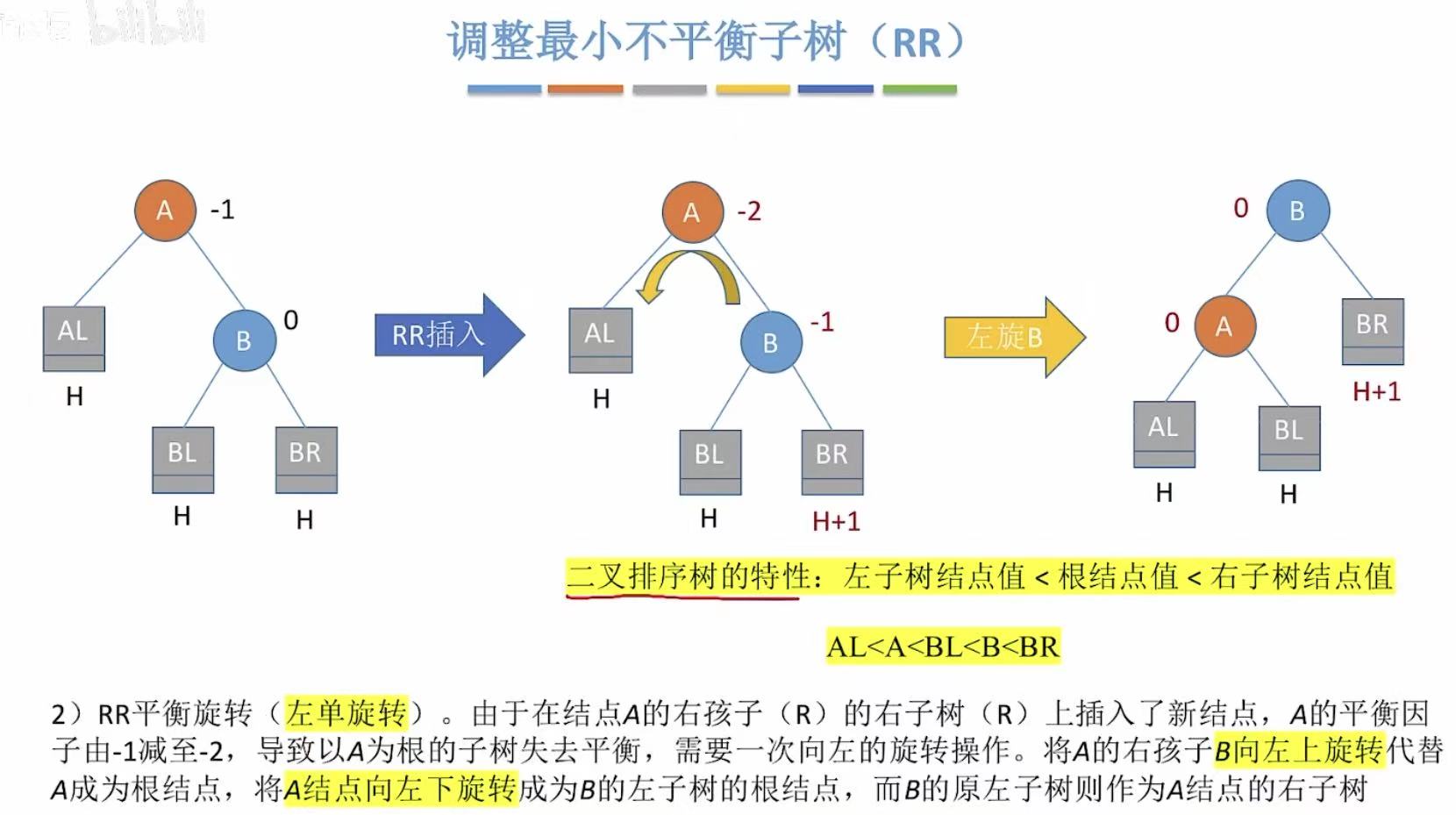
代码思路:就是指明谁代替了谁,成为了什么。
右单旋转:
- p的右孩子成为了f的左孩子
- f成为了p的右孩子
- p成为了根节点
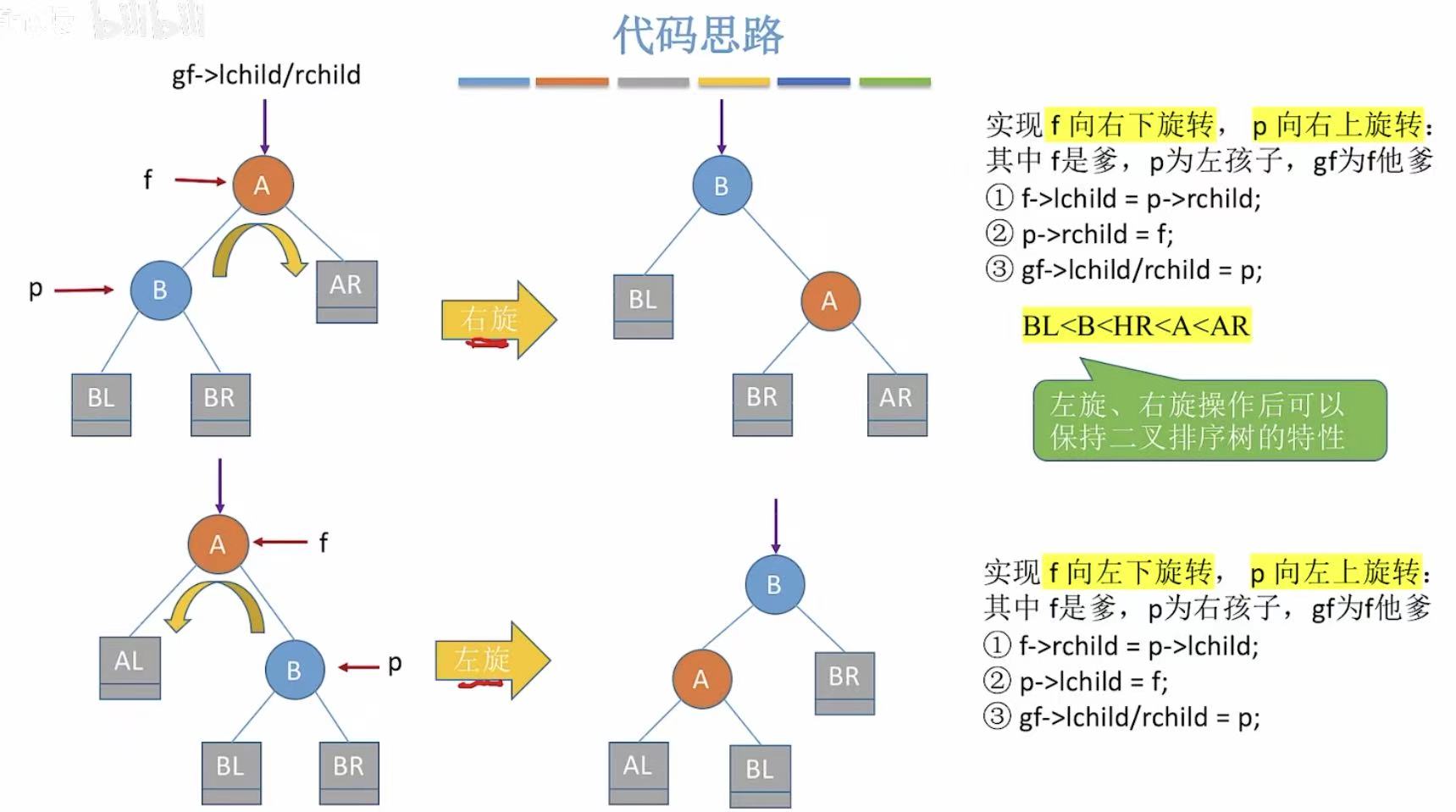
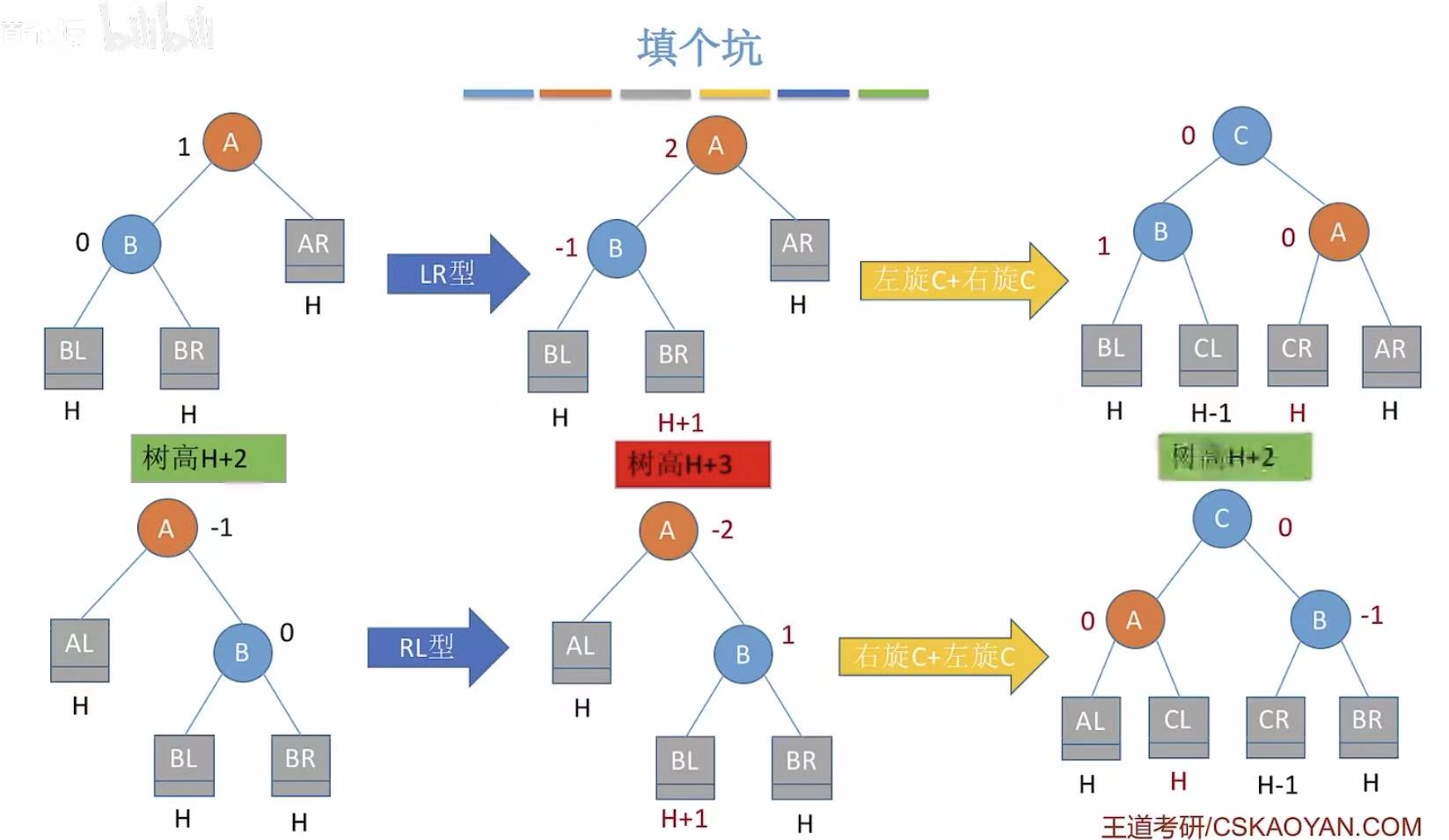
3.3 LR
- LR :在左孩子的右子树上插入了新的结点。
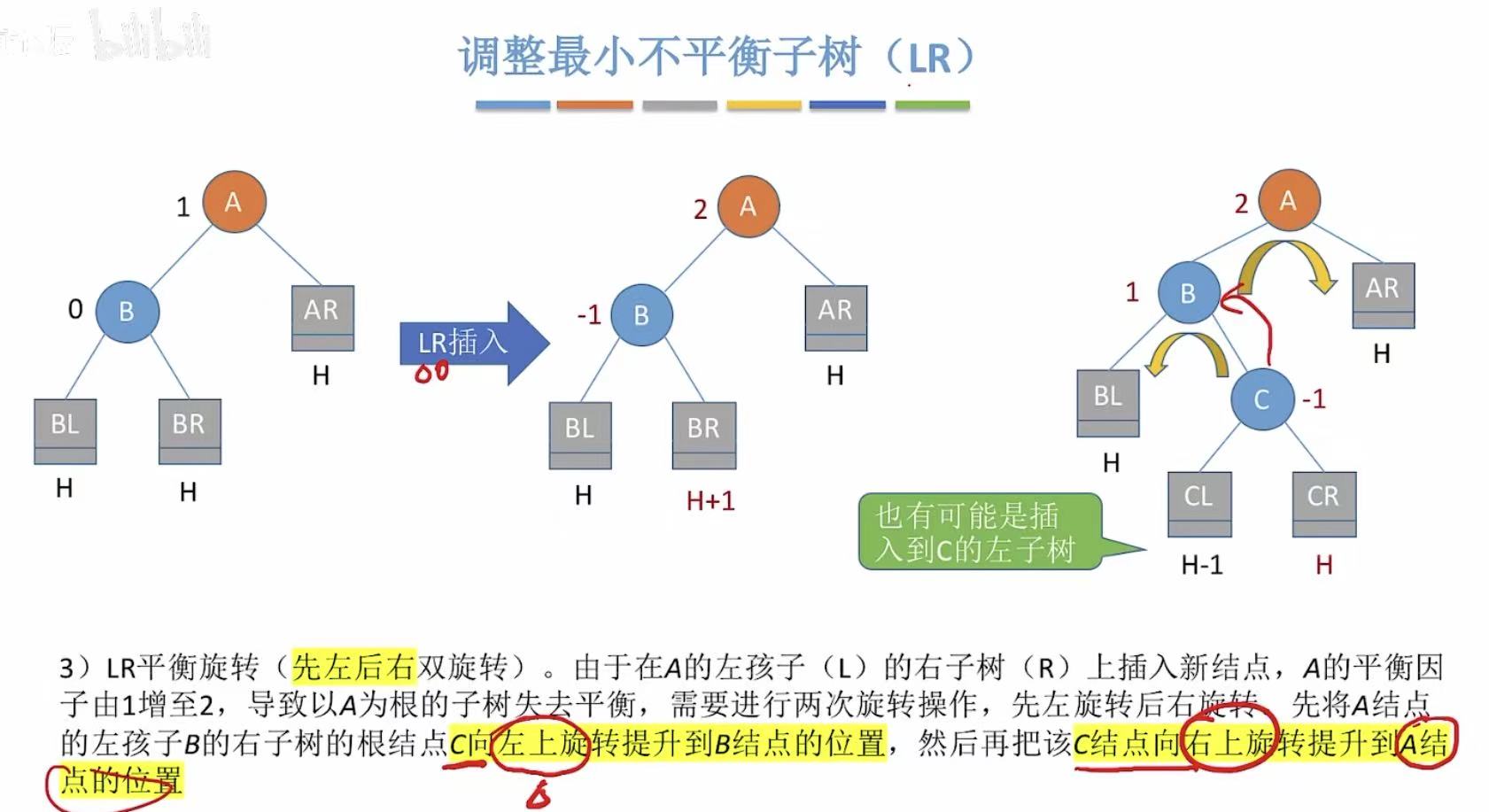
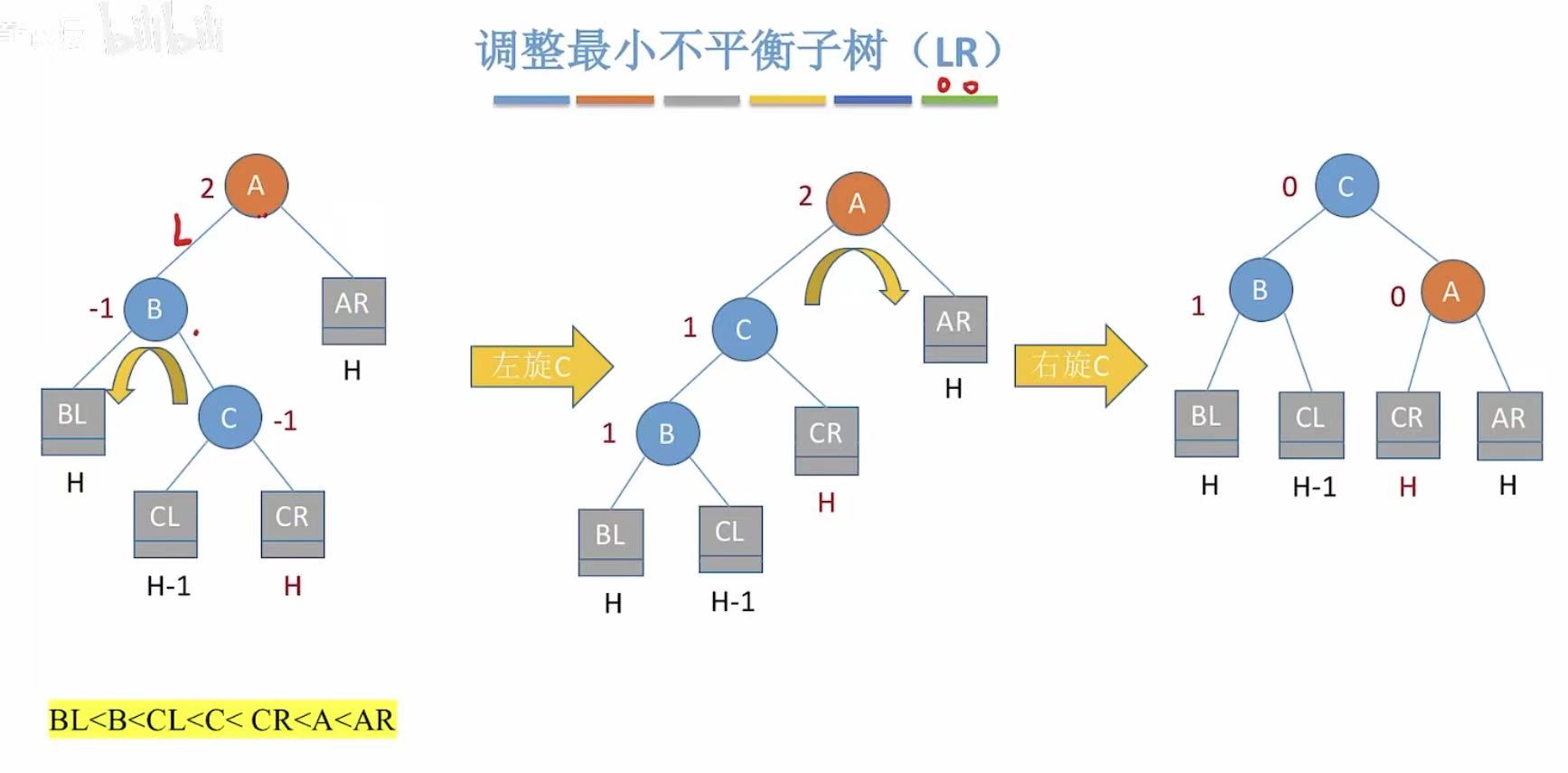
- 先左后右 :C最后是根节点,因为左旋和B换,所以C的左孩子让给B;因为右旋和A换,所以C的右孩子让给A。
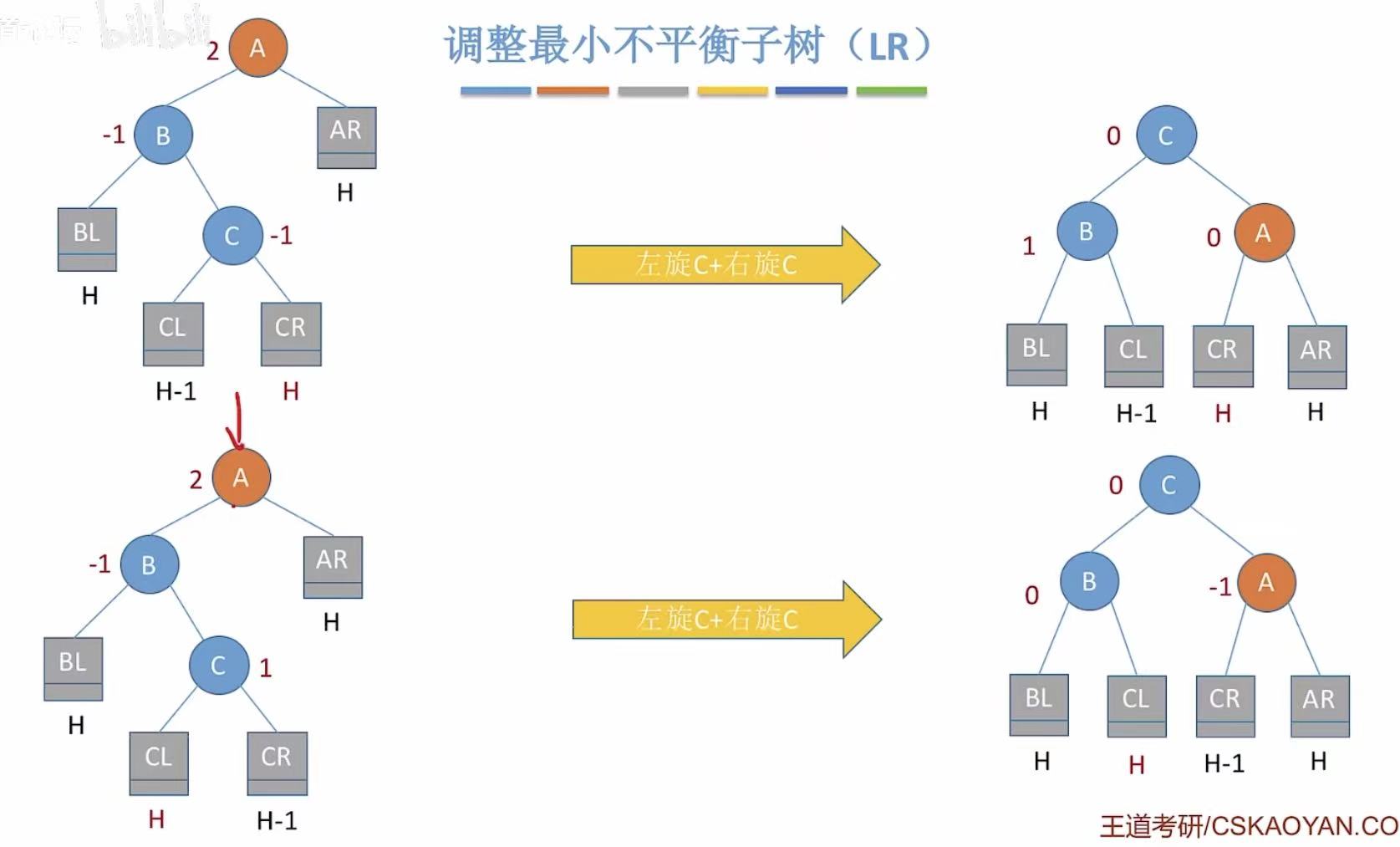
3.4 RL
- RL :在右孩子的左子树上插入了新的结点。
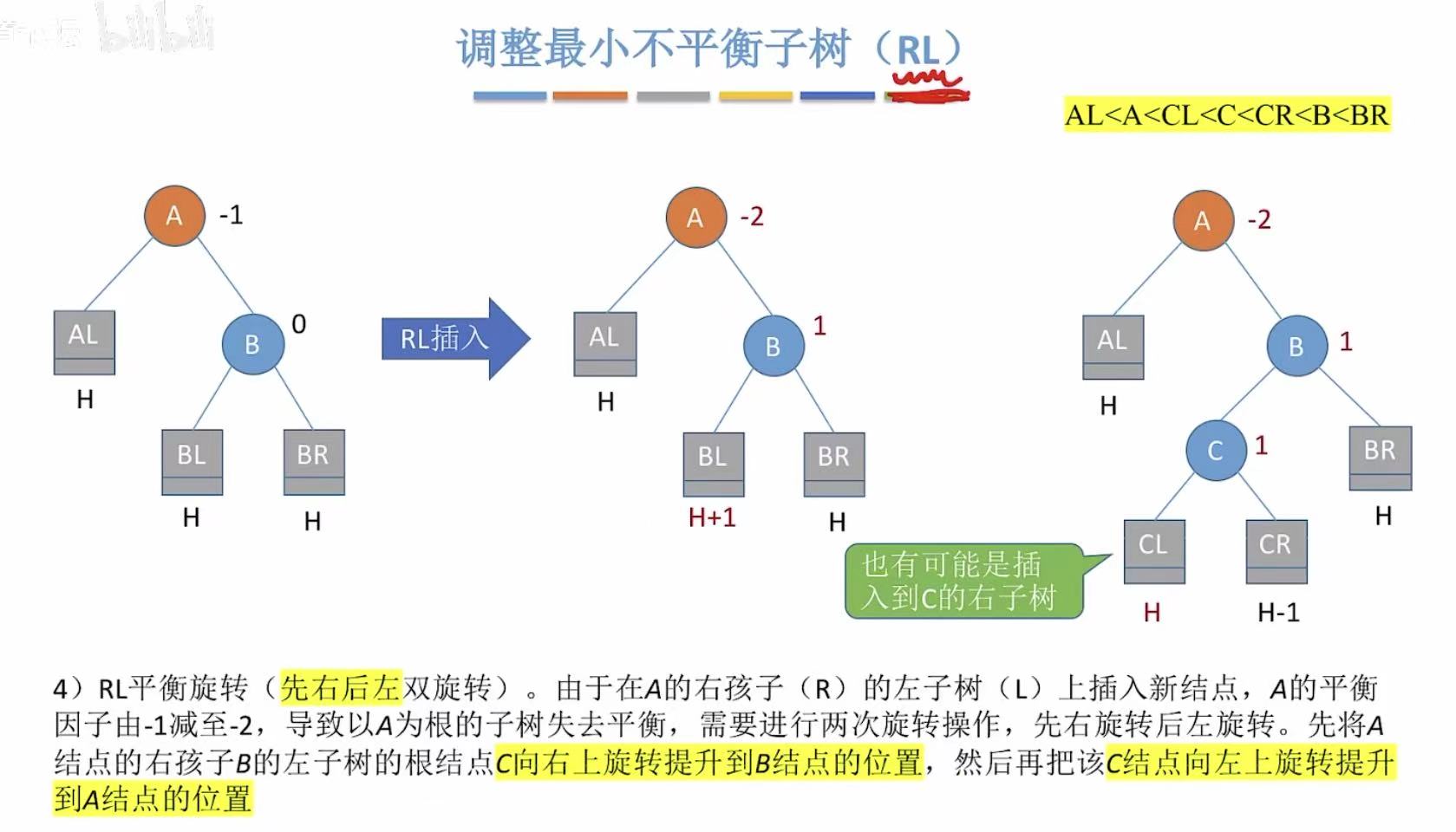
- 先右后左 :C最后是根节点,因为右旋和B换,所以C的右孩子让给B;因为左旋和A换,所以C的左孩子让给A。
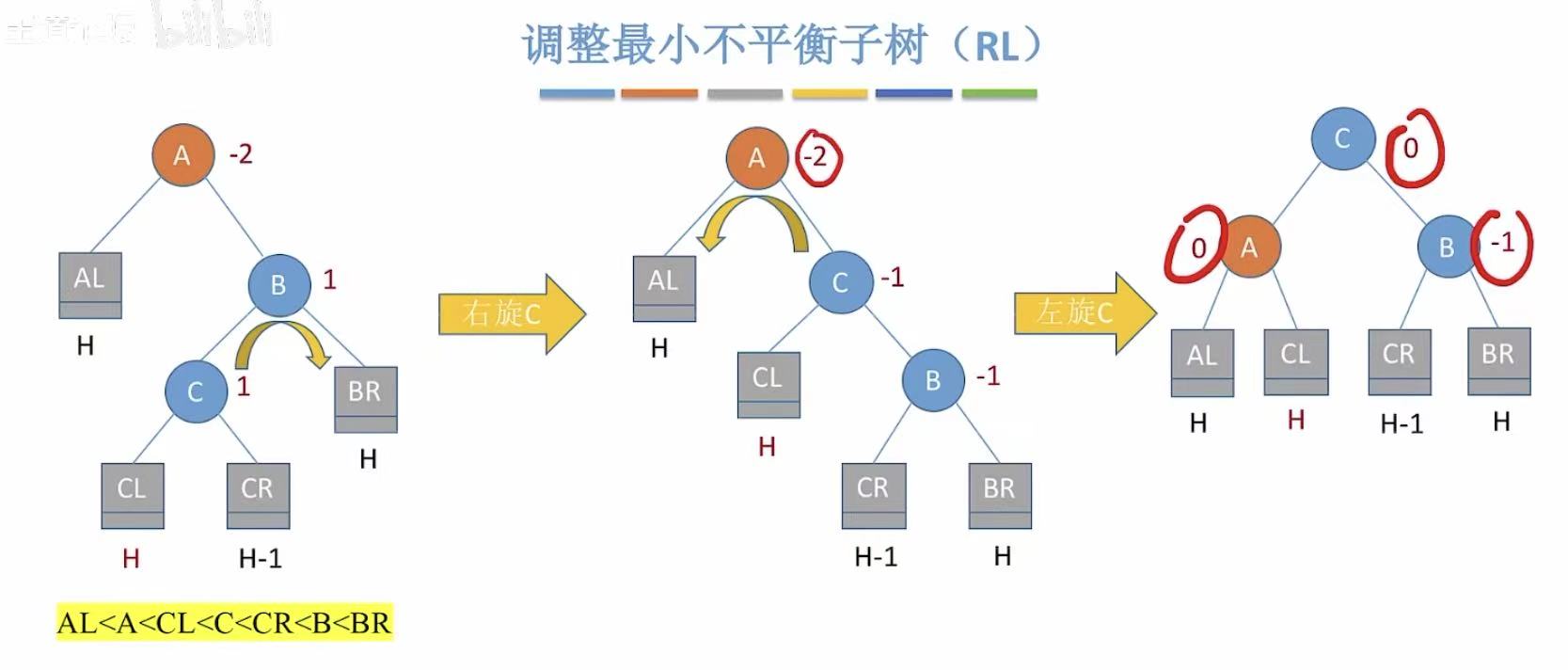
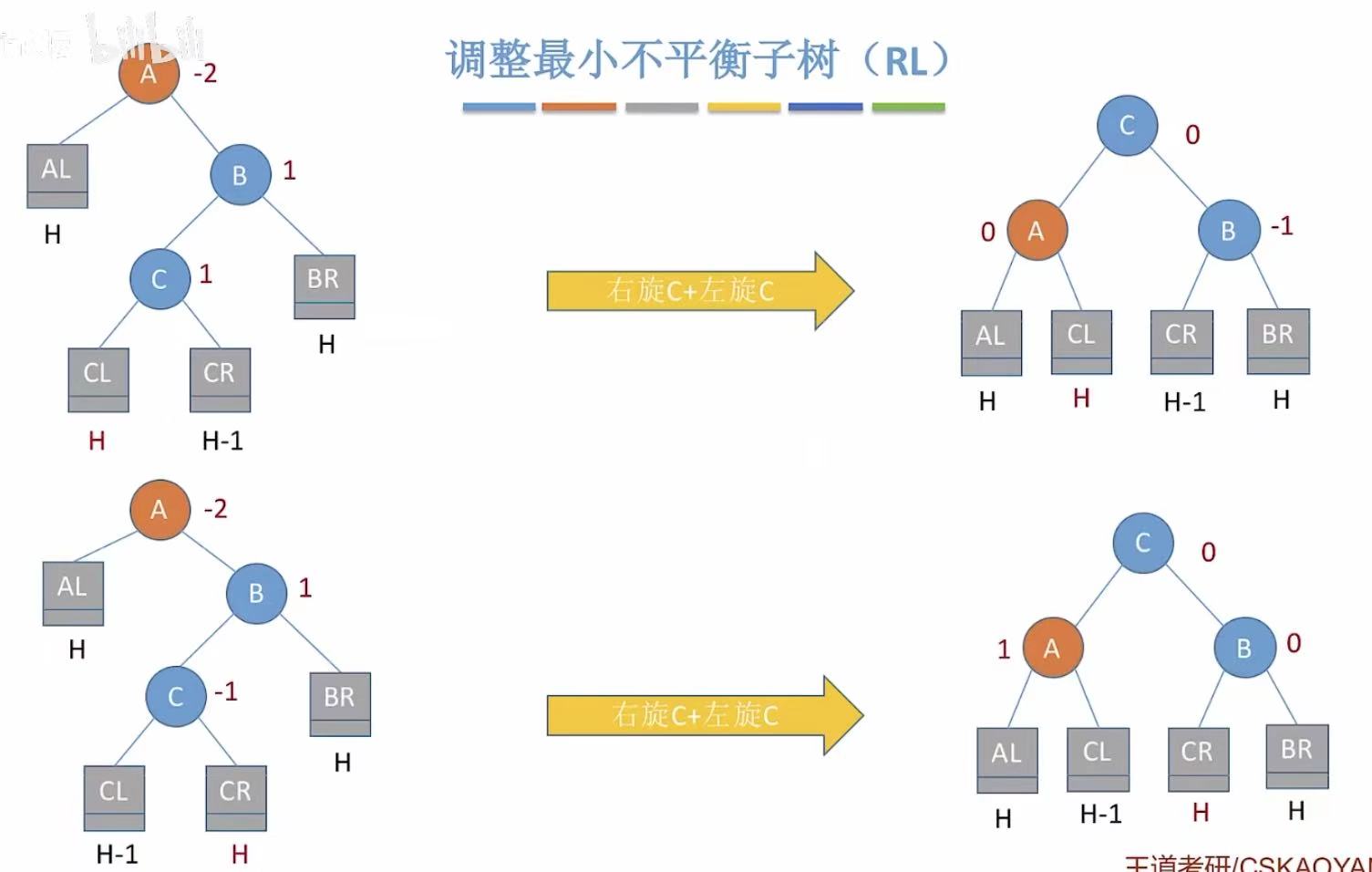
3.5 小结

4. 填个坑
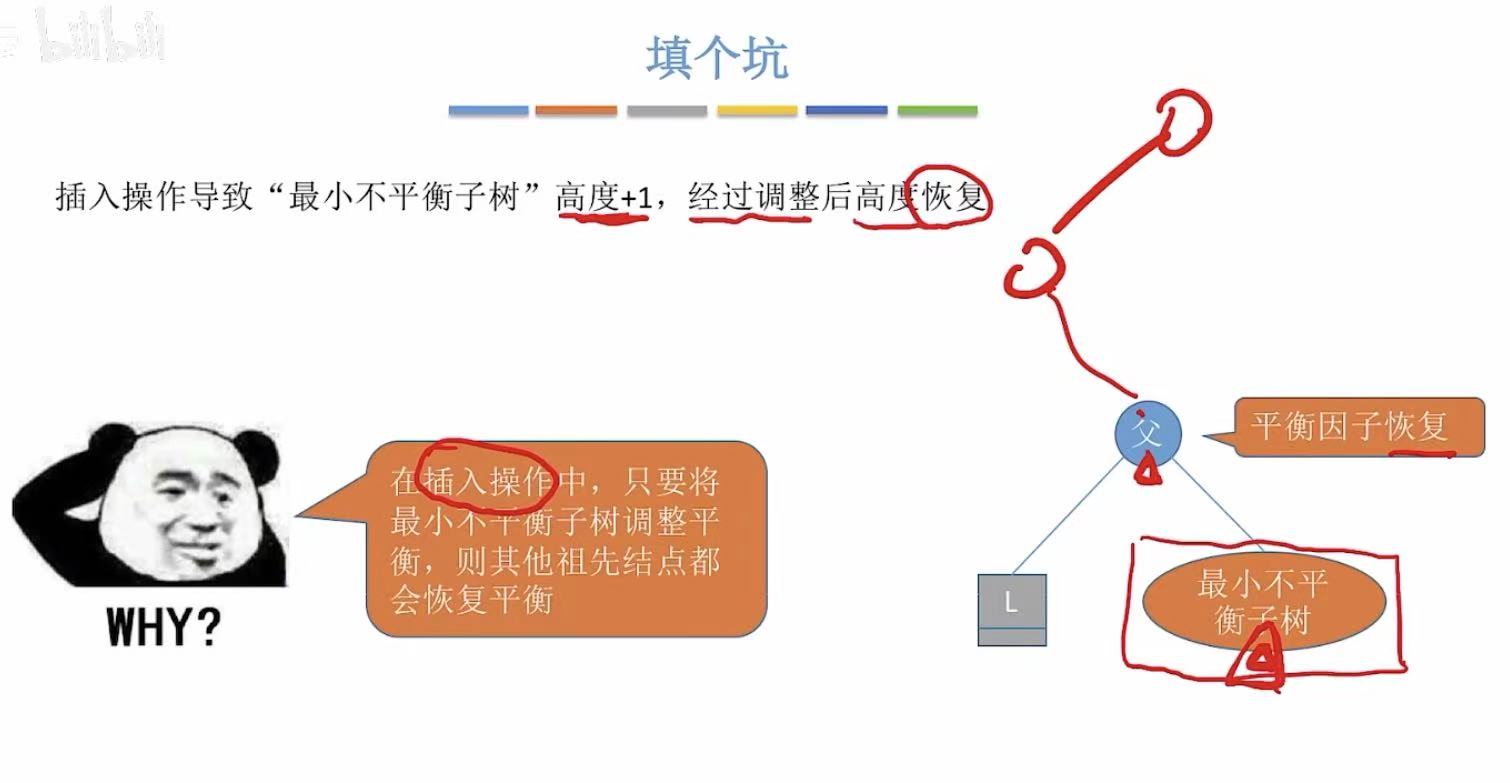
我们之前说想让插入后的不平衡的二叉树重新平衡,只需要调整最小不平衡子树,那么为什么呢?
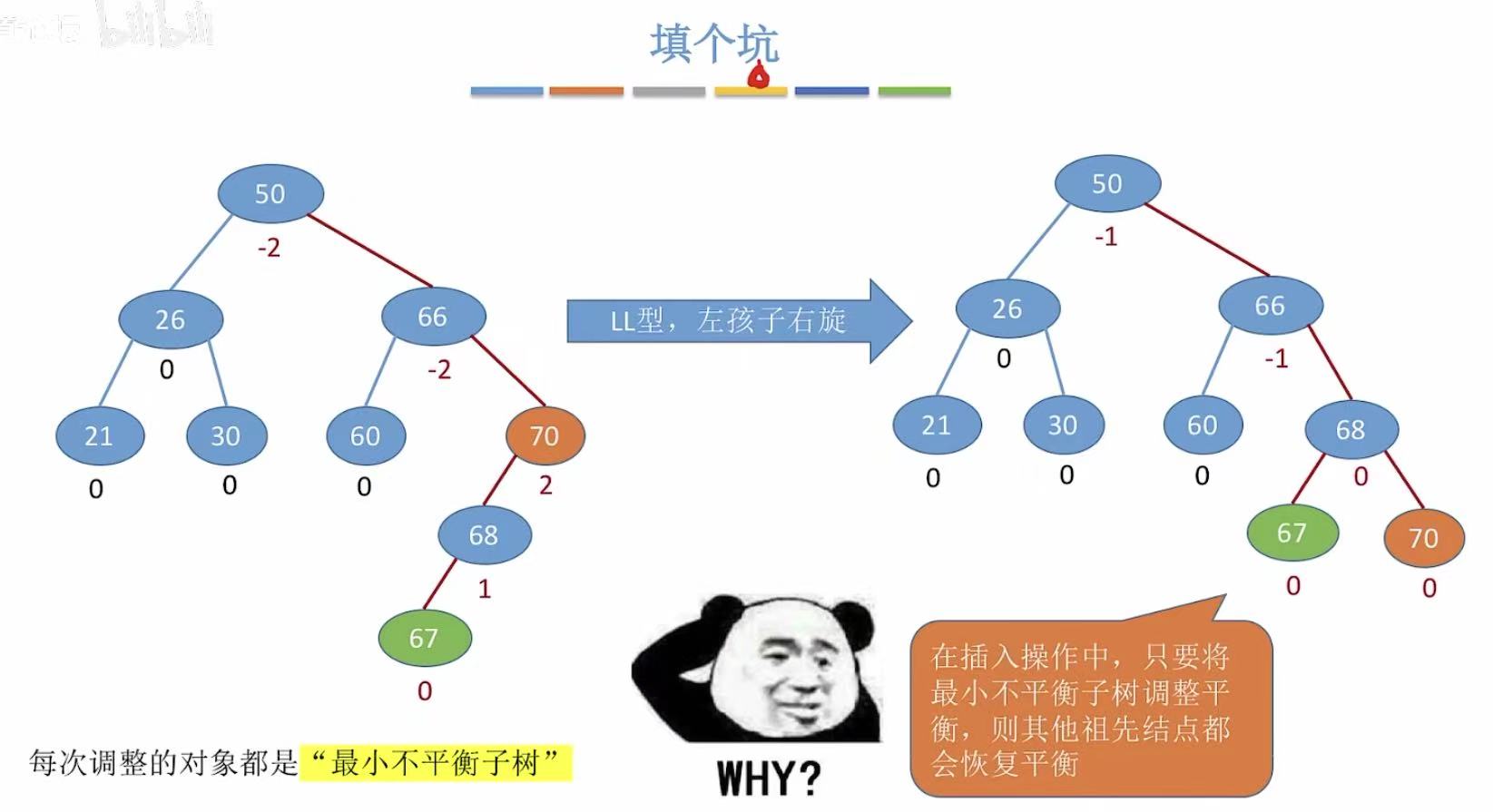
实际上,在 AVL 插入操作中,旋转后 的最小不平衡子树的高度 会恢复为插入前的高度 。
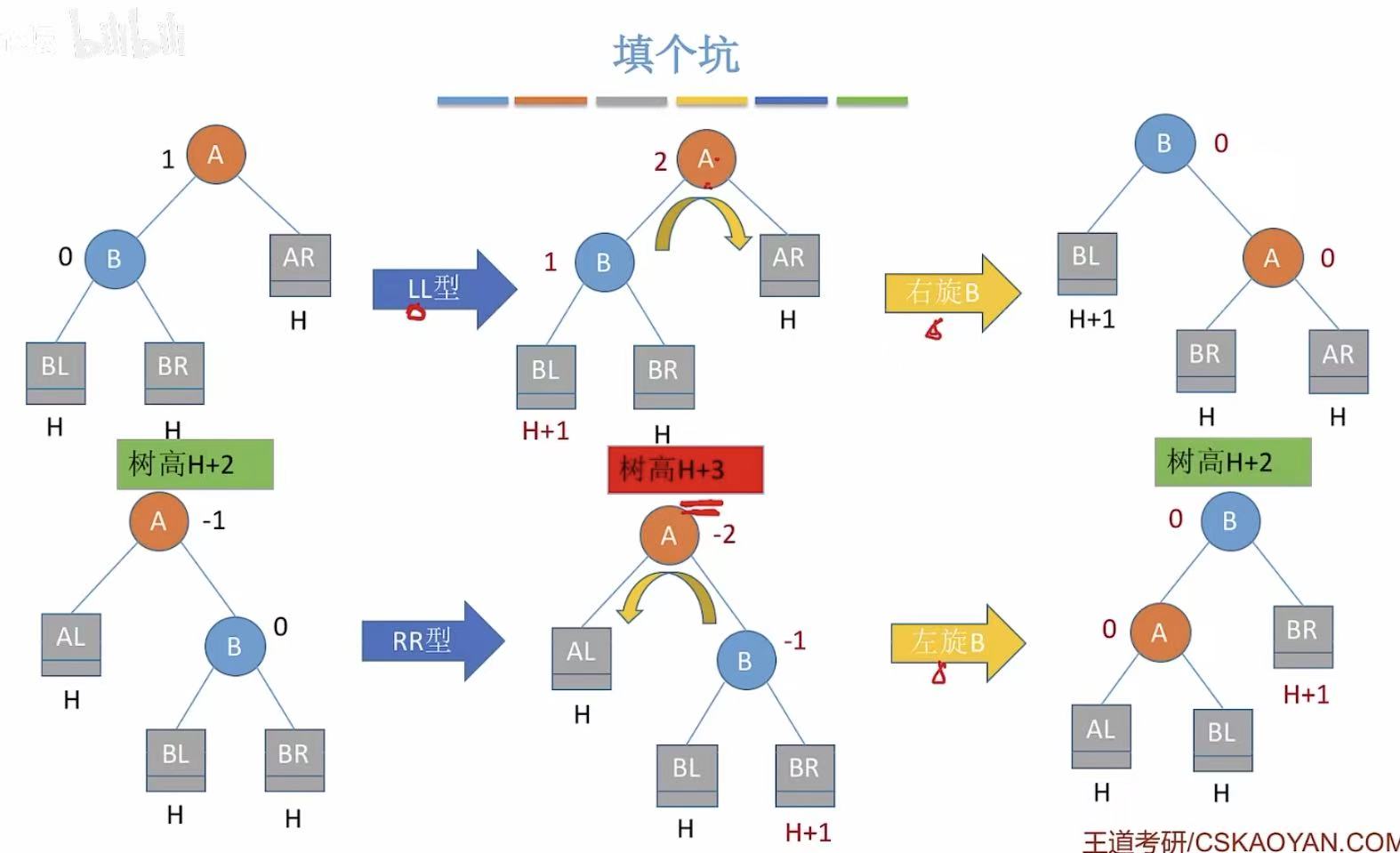
因为高度没变:
- 它的父节点的 左右子树高度差没有改变;
- 所以父节点的平衡因子不变;
- 祖先节点的平衡因子也都不变;
- 整棵树除了这个局部区域外,其他部分仍然满足 AVL 性质
因此,只需调整最小不平衡子树一次,整棵树就重新平衡了。
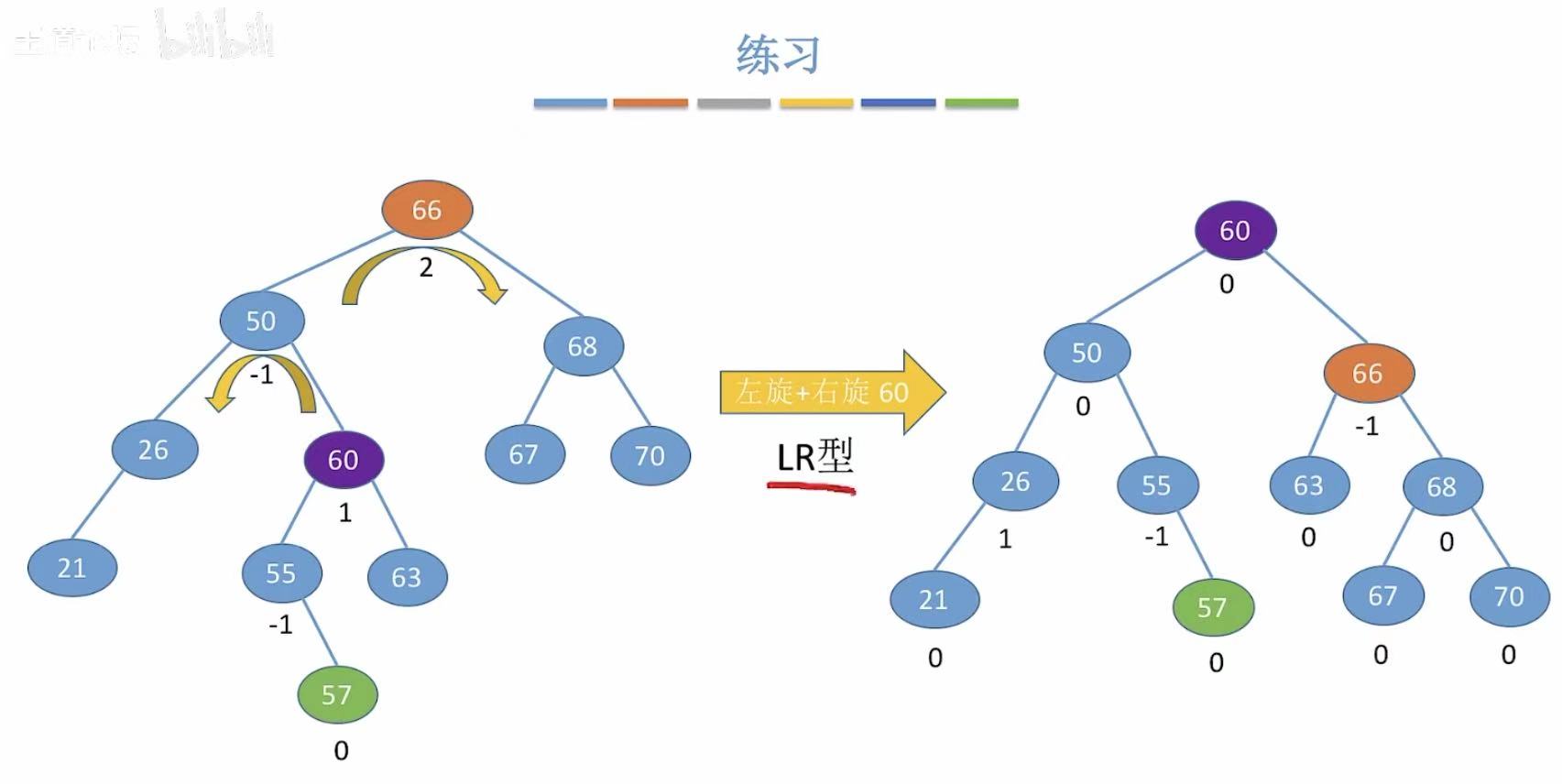
5. 练习
5.1 RR型
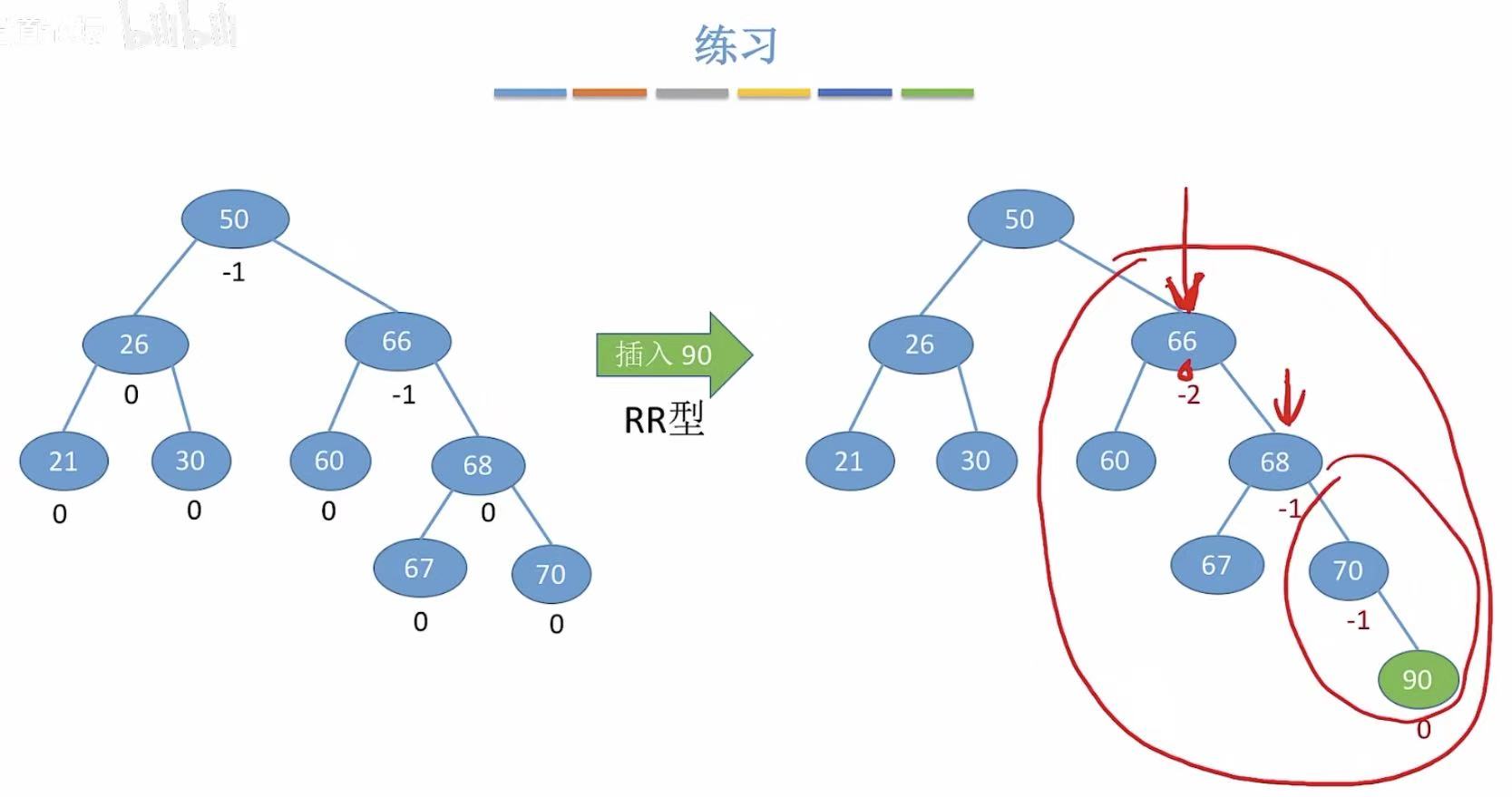
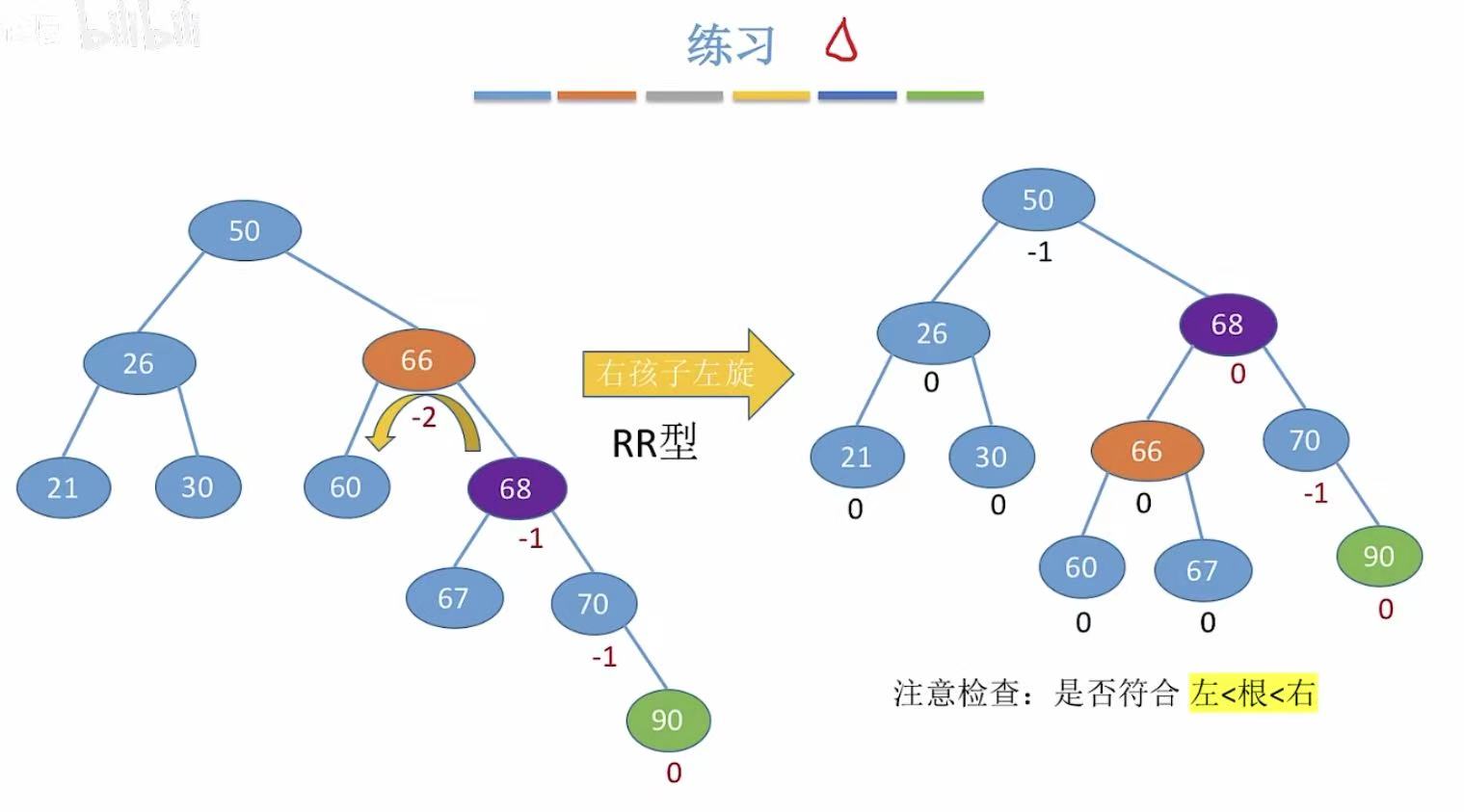
5.2 RL型
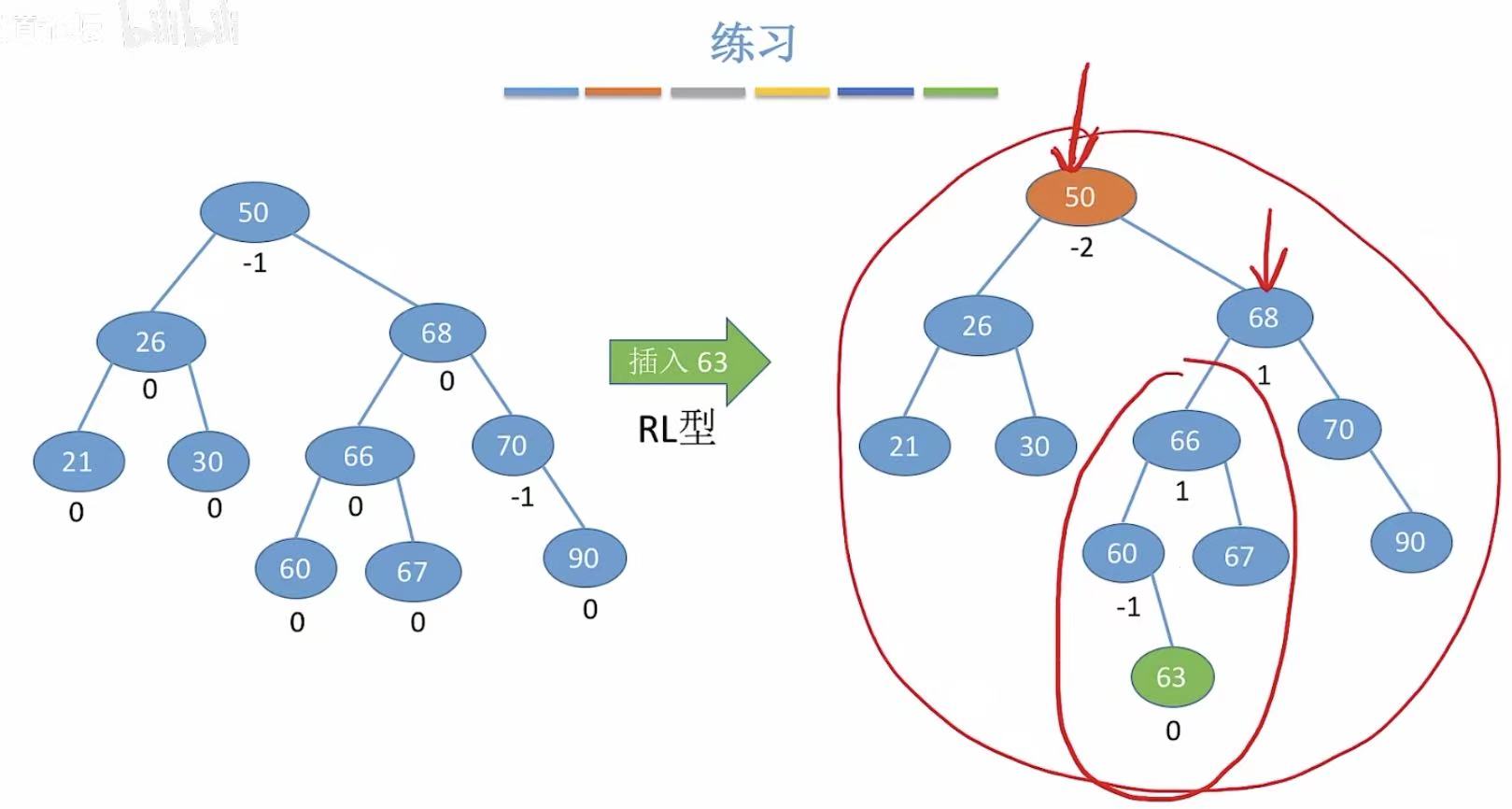
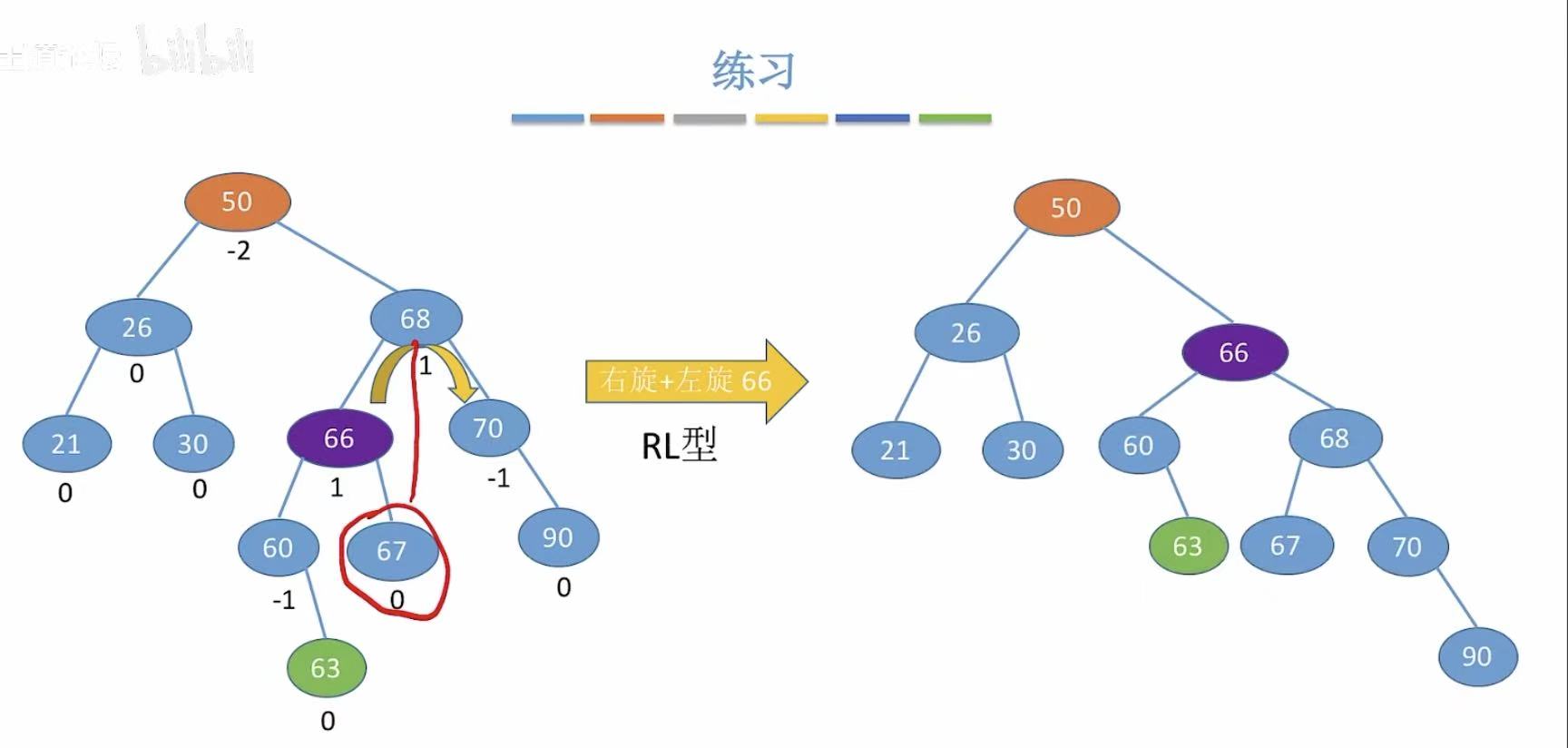
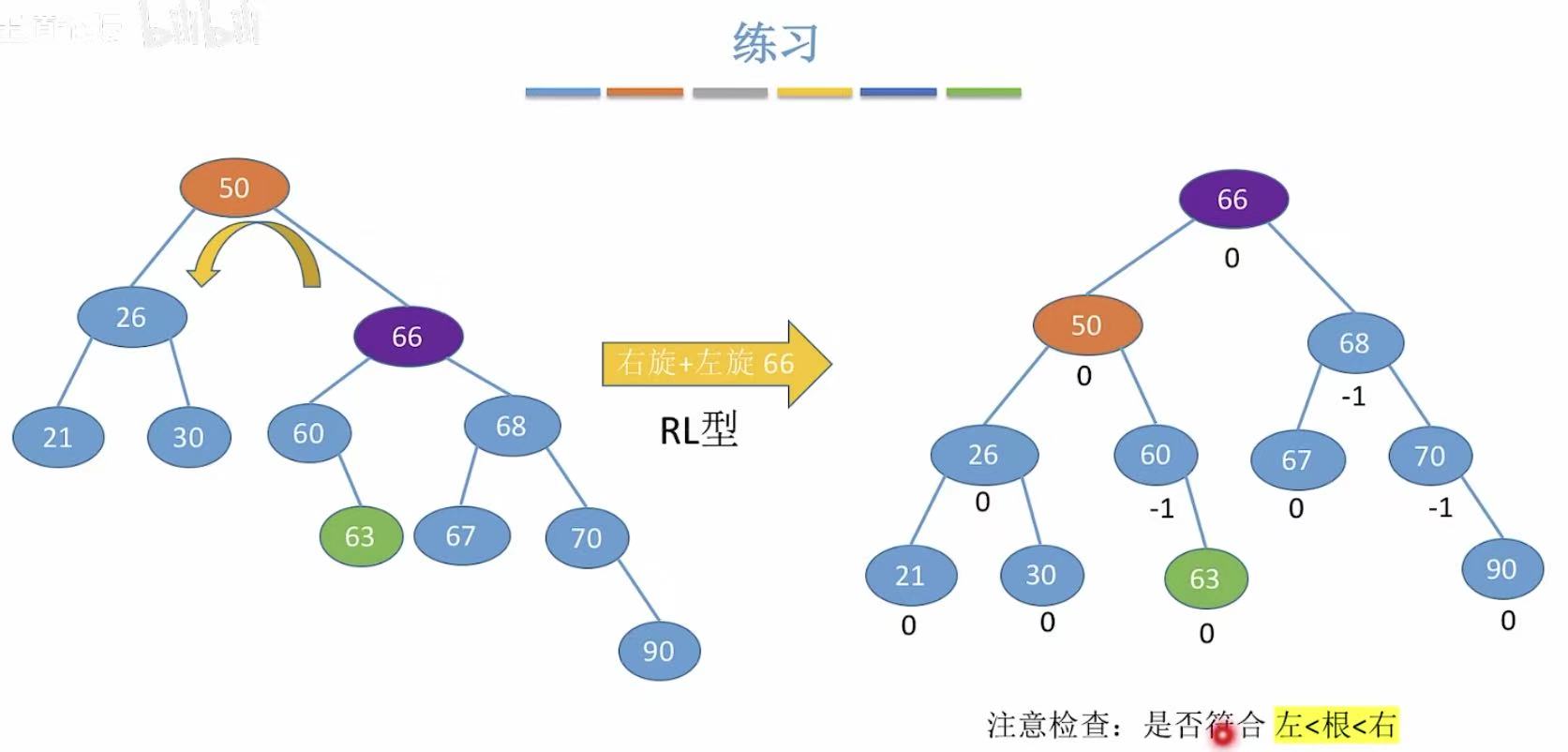
5.3 LR型
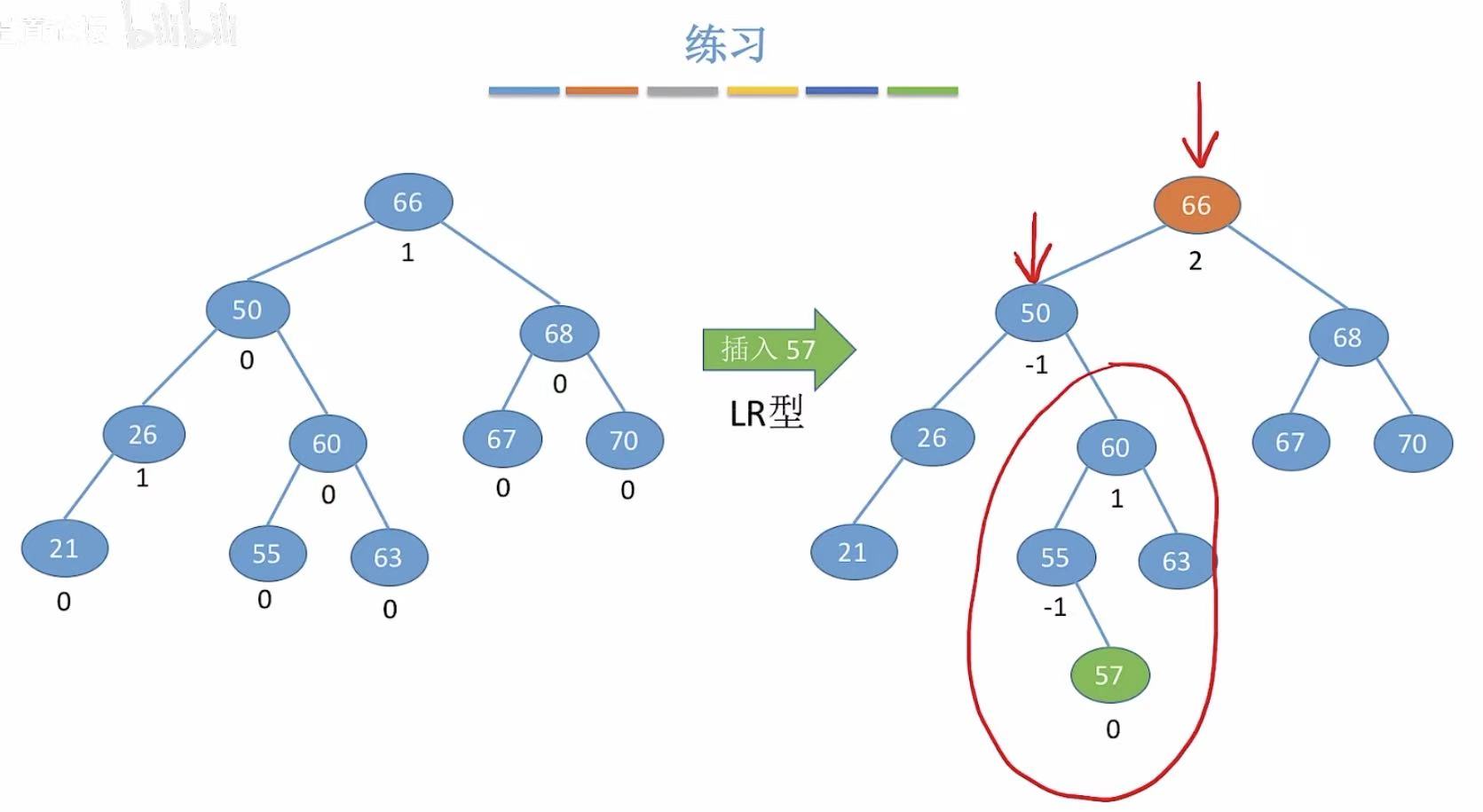
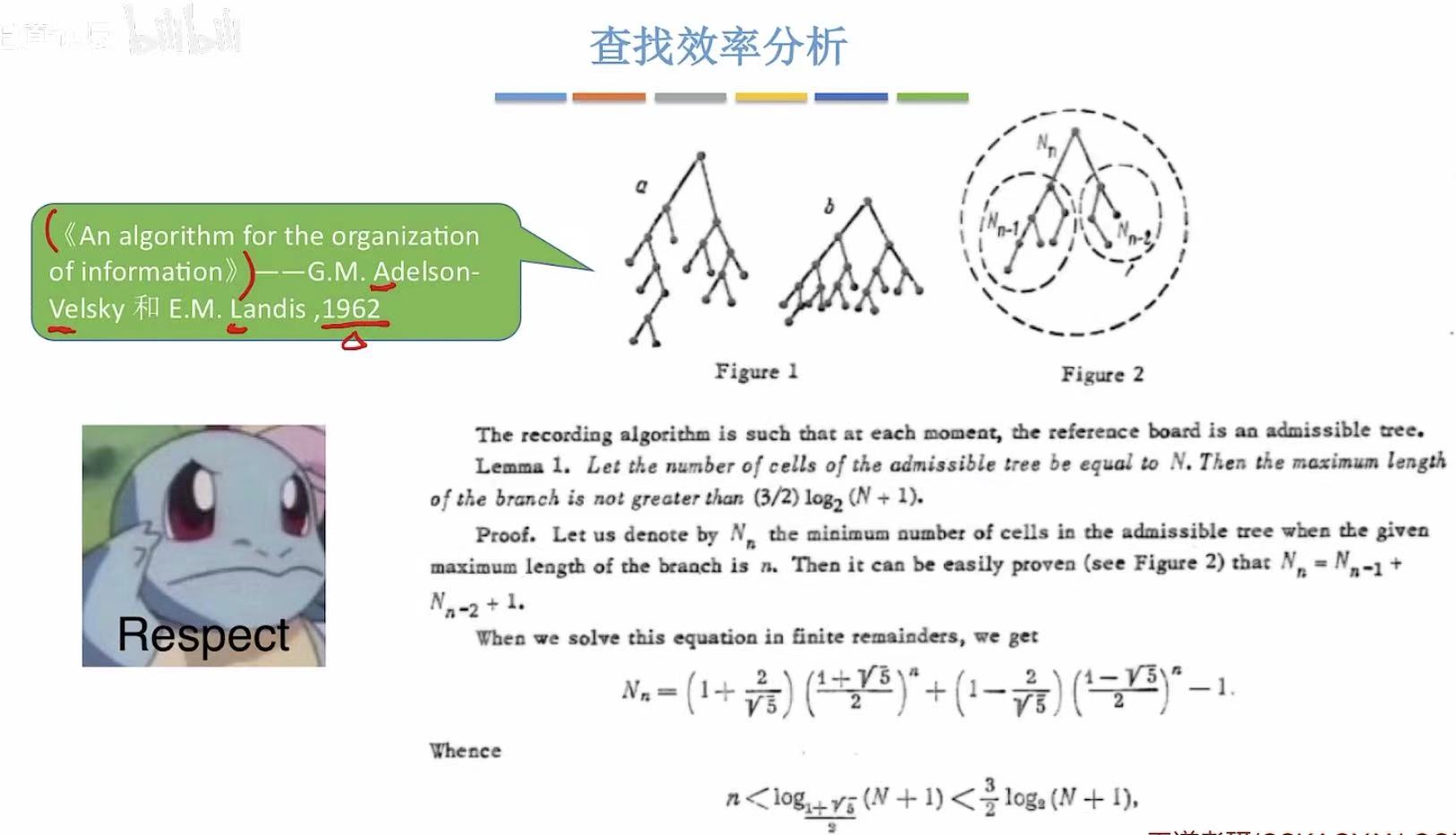
6. 查找效率分析

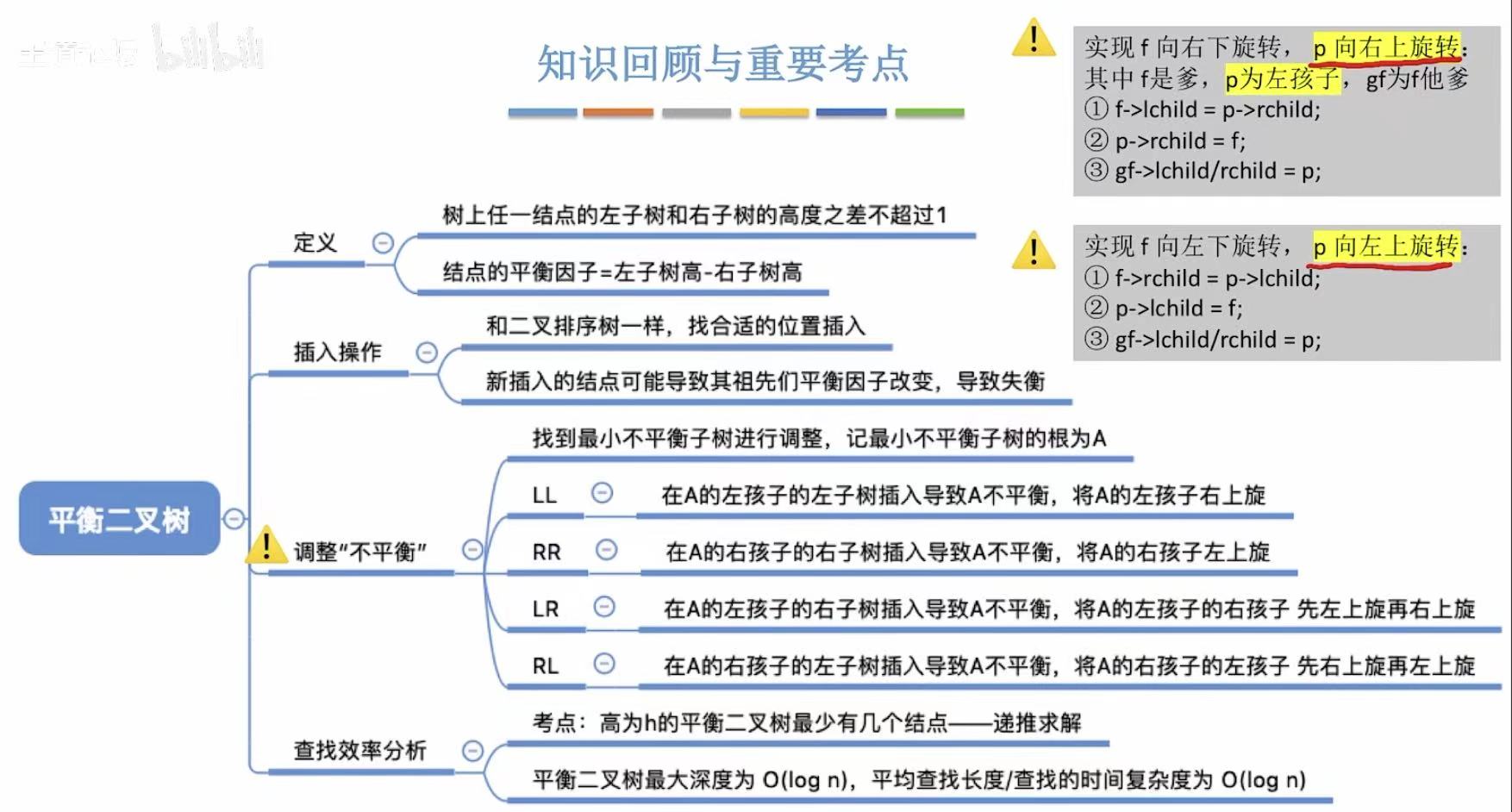
8. 小结
平衡二叉树的删除
1. 删除
删除操作和插入操作相同,都会使得二叉树不平衡,所以关键点都是需要将二叉树最后恢复平衡状态。
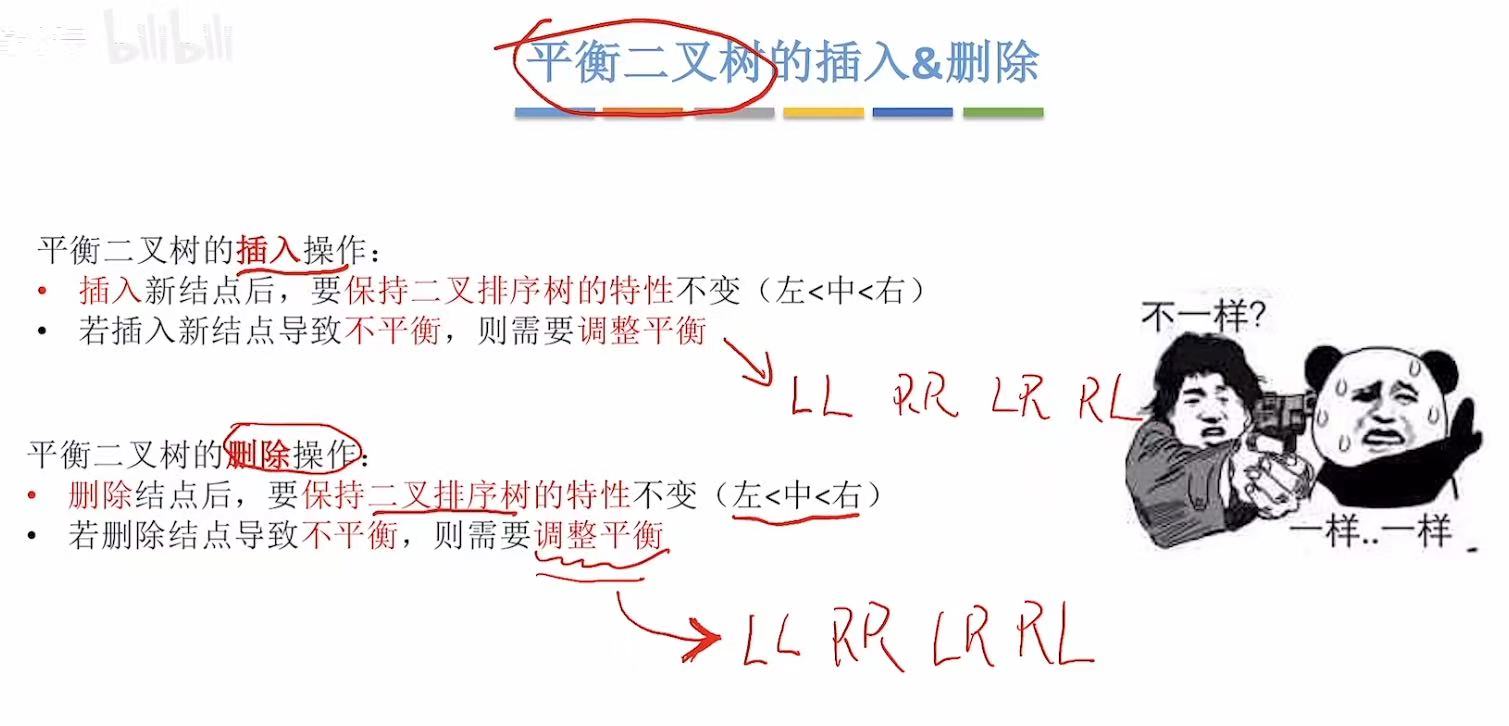
具体调整方法和插入方法相同。

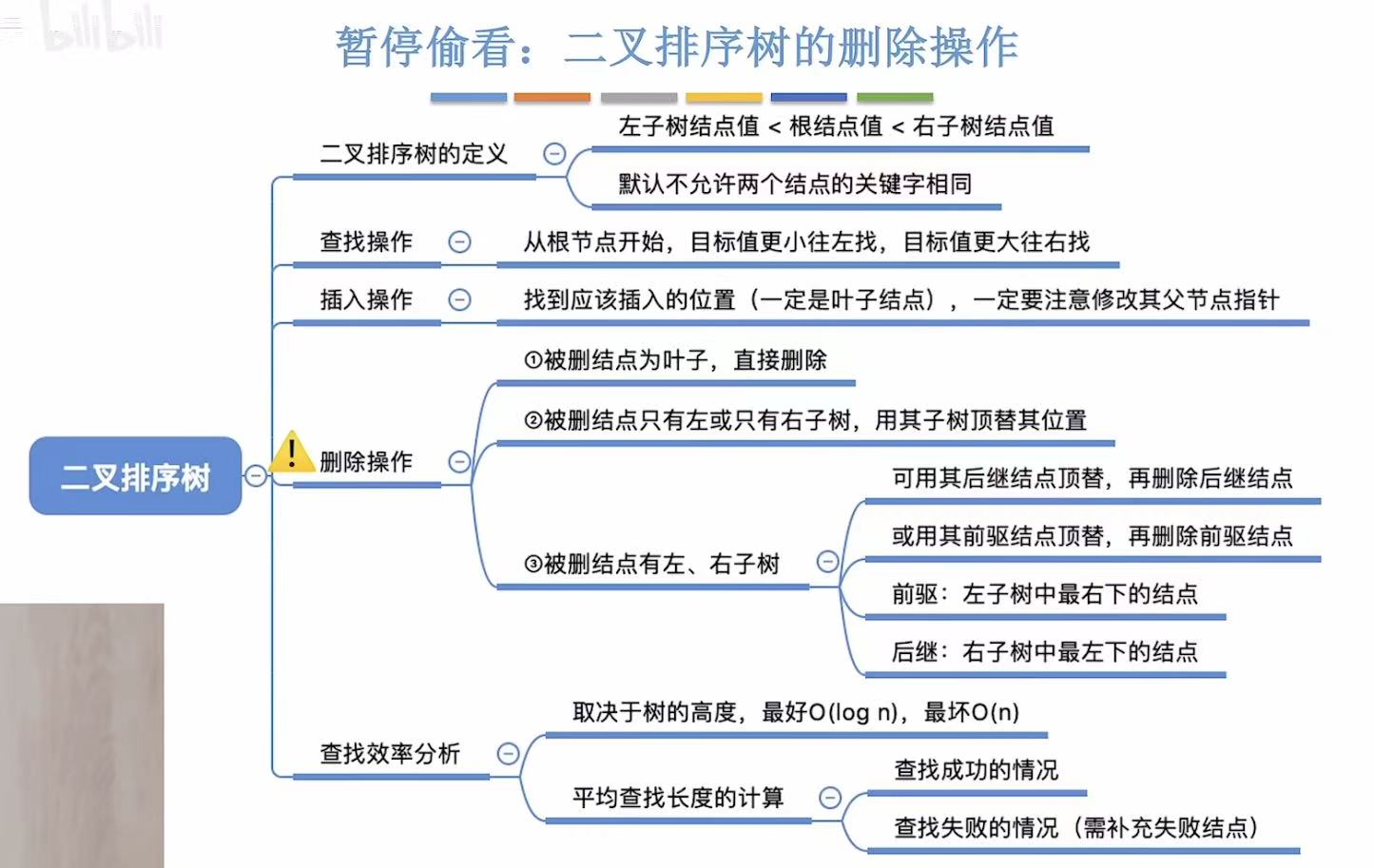
具体删除方法和二叉排序树相同。
二叉排序树具体可见:二叉排序树
2. 删除操作实例
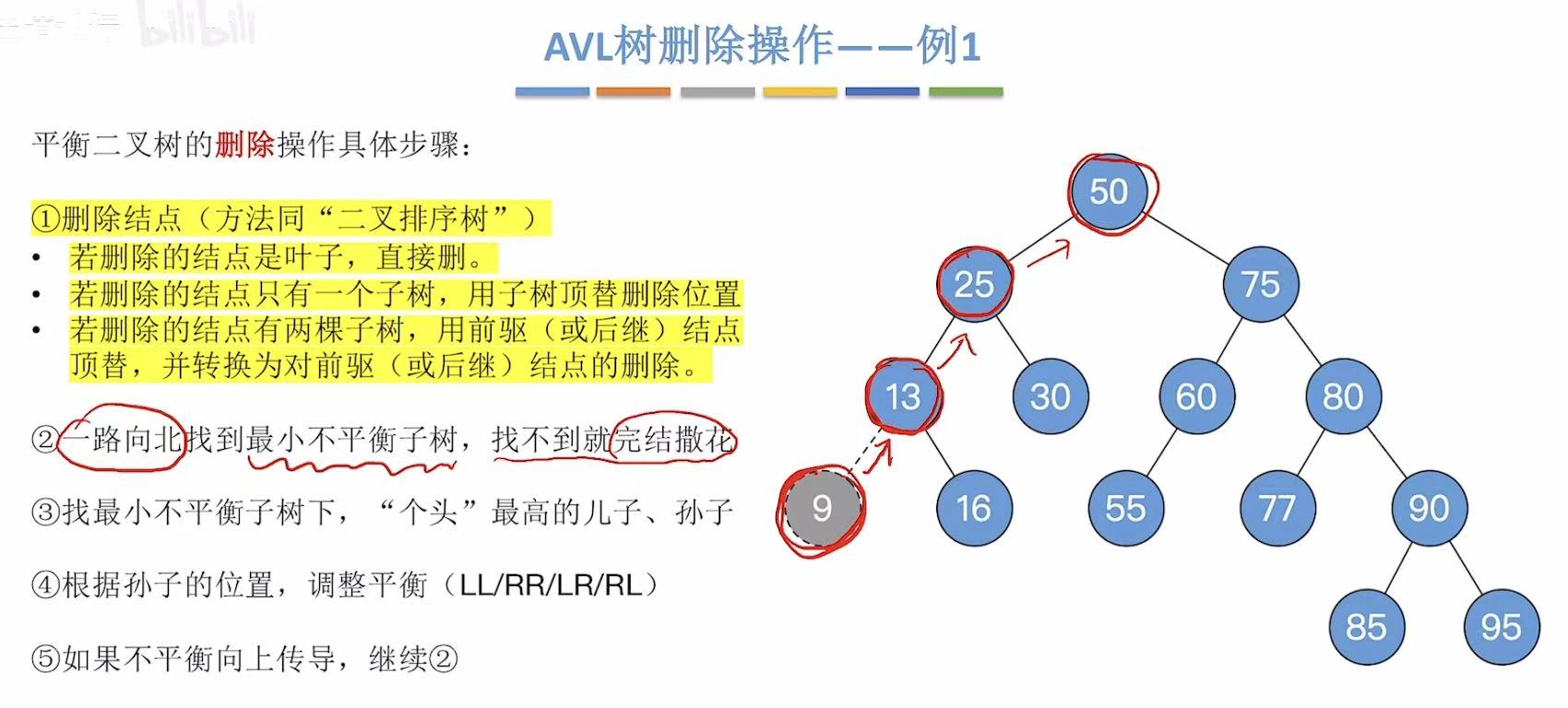
2.1 例1-删9
叶子节点直接删。
2.2 例2-删55
一路向北找到最小不平衡子树
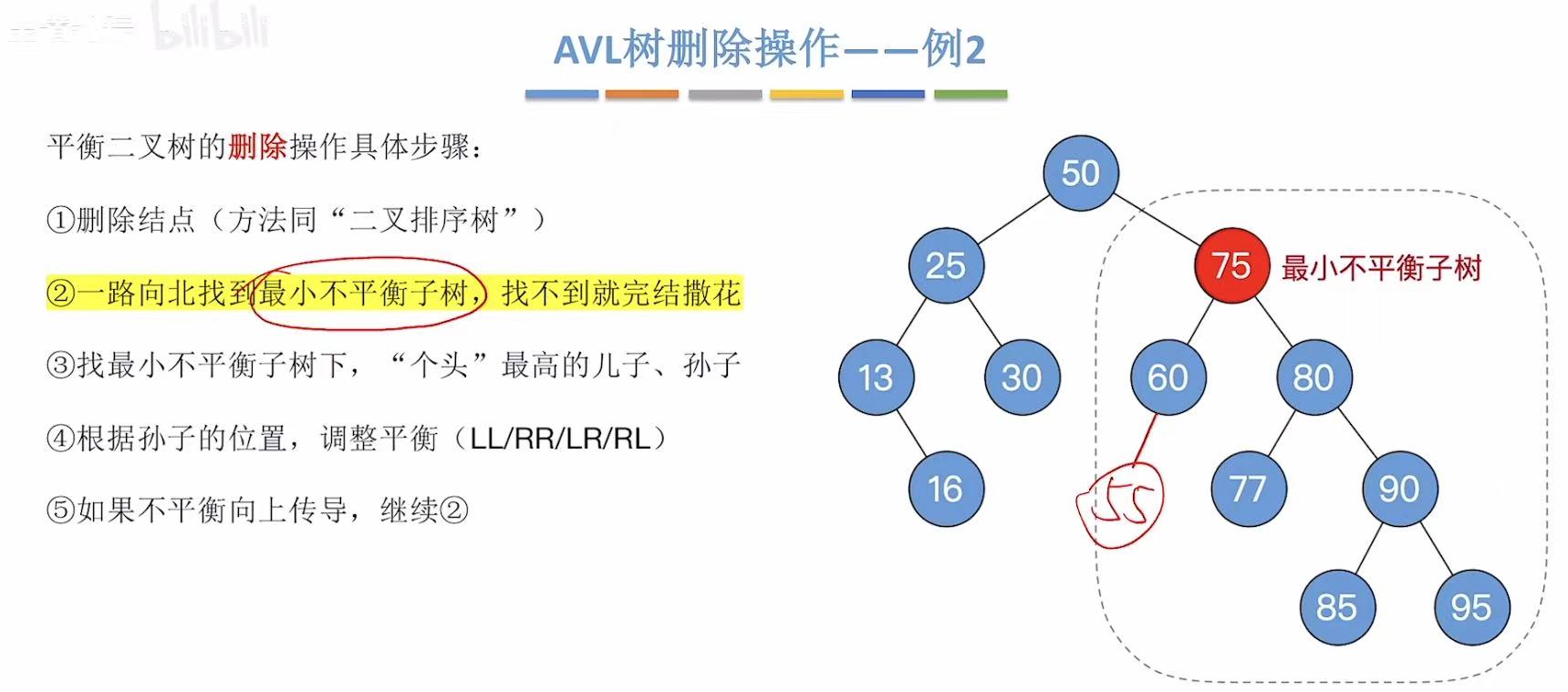
然后就可以找到个头最高的儿子 和个头最高的孙子 。
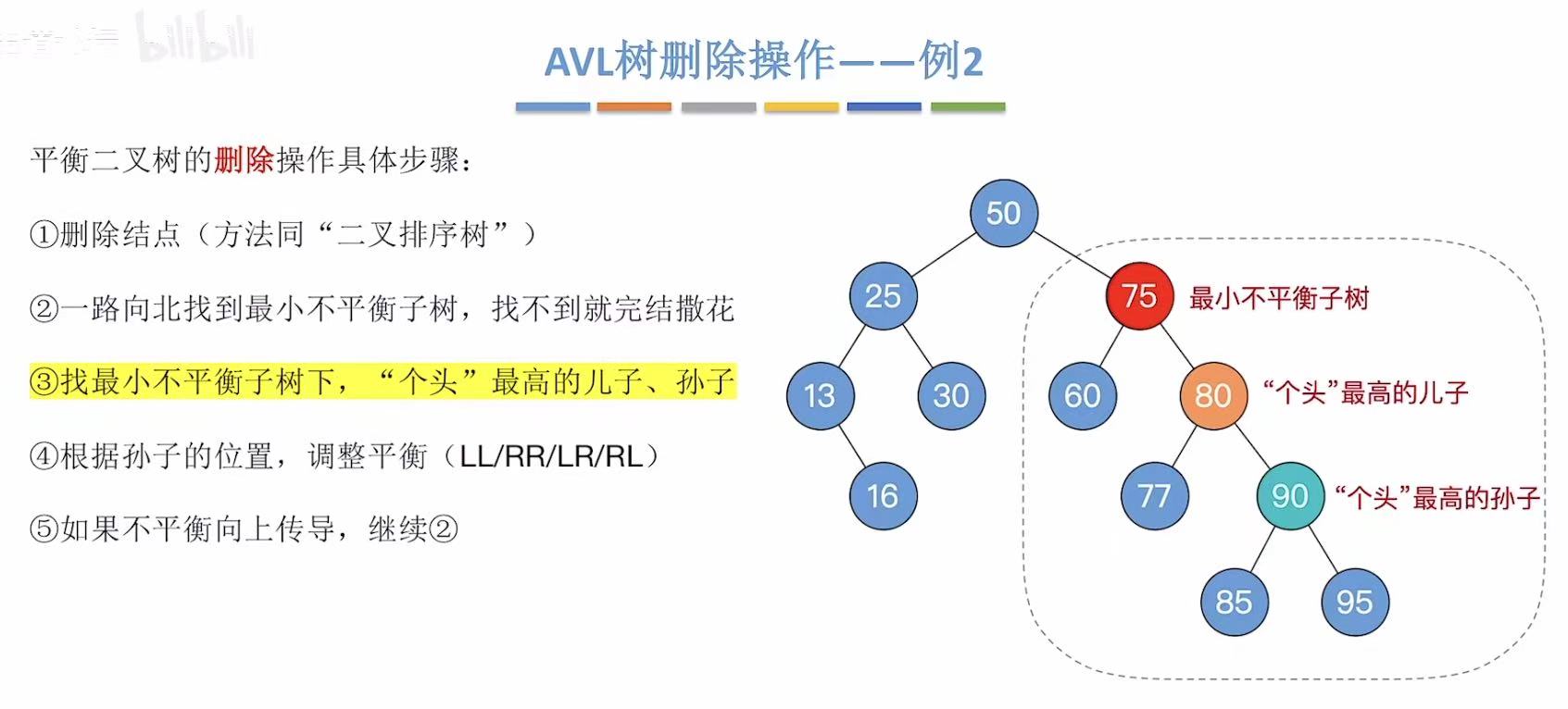
孙子右孩子的右子树上,即RR
所以采取左单旋转 ,调整平衡。
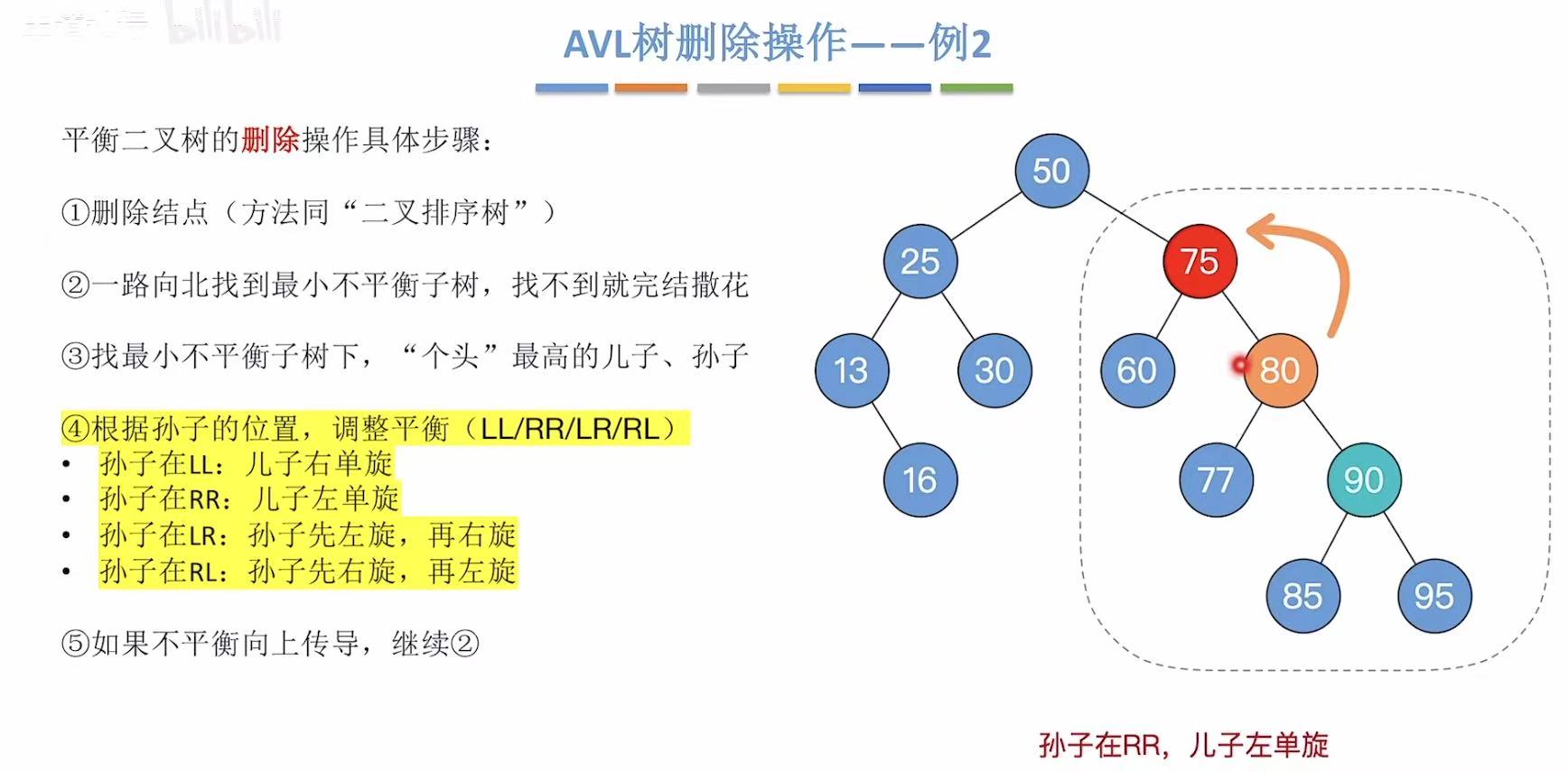
旋转后:
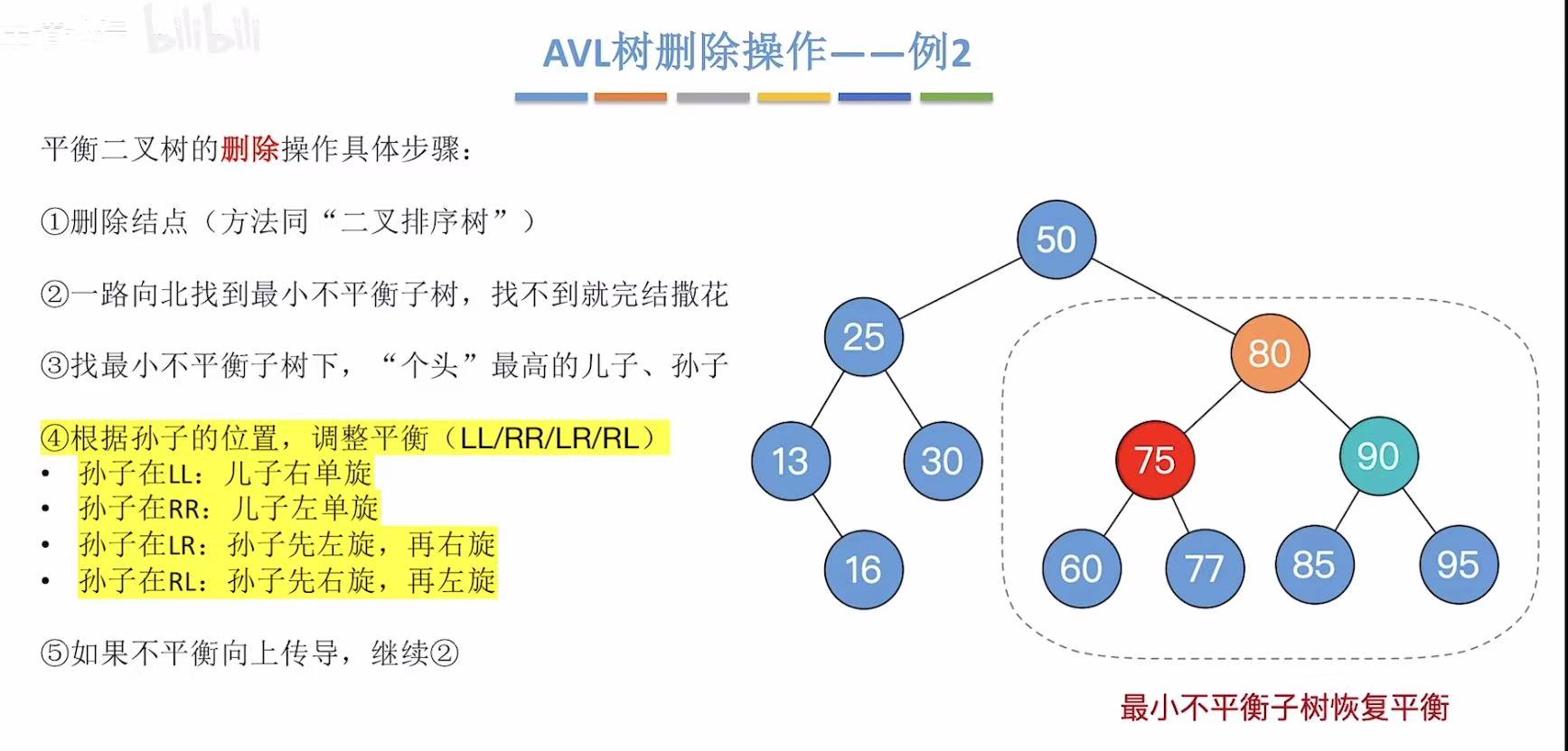
此时已经是平衡的了,所以第五步直接跳过
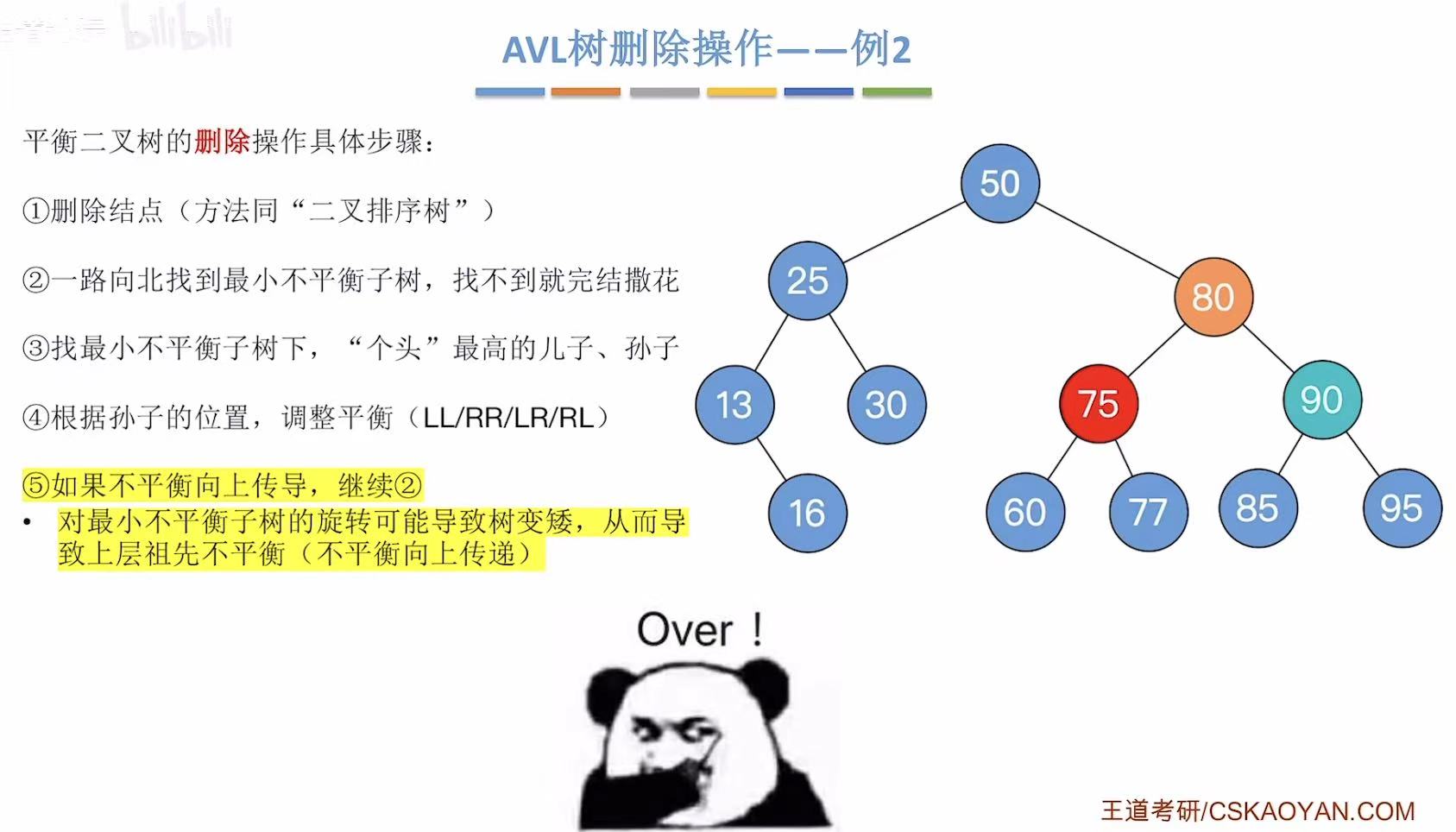
2.3 例3-删32
叶子节点直接删除
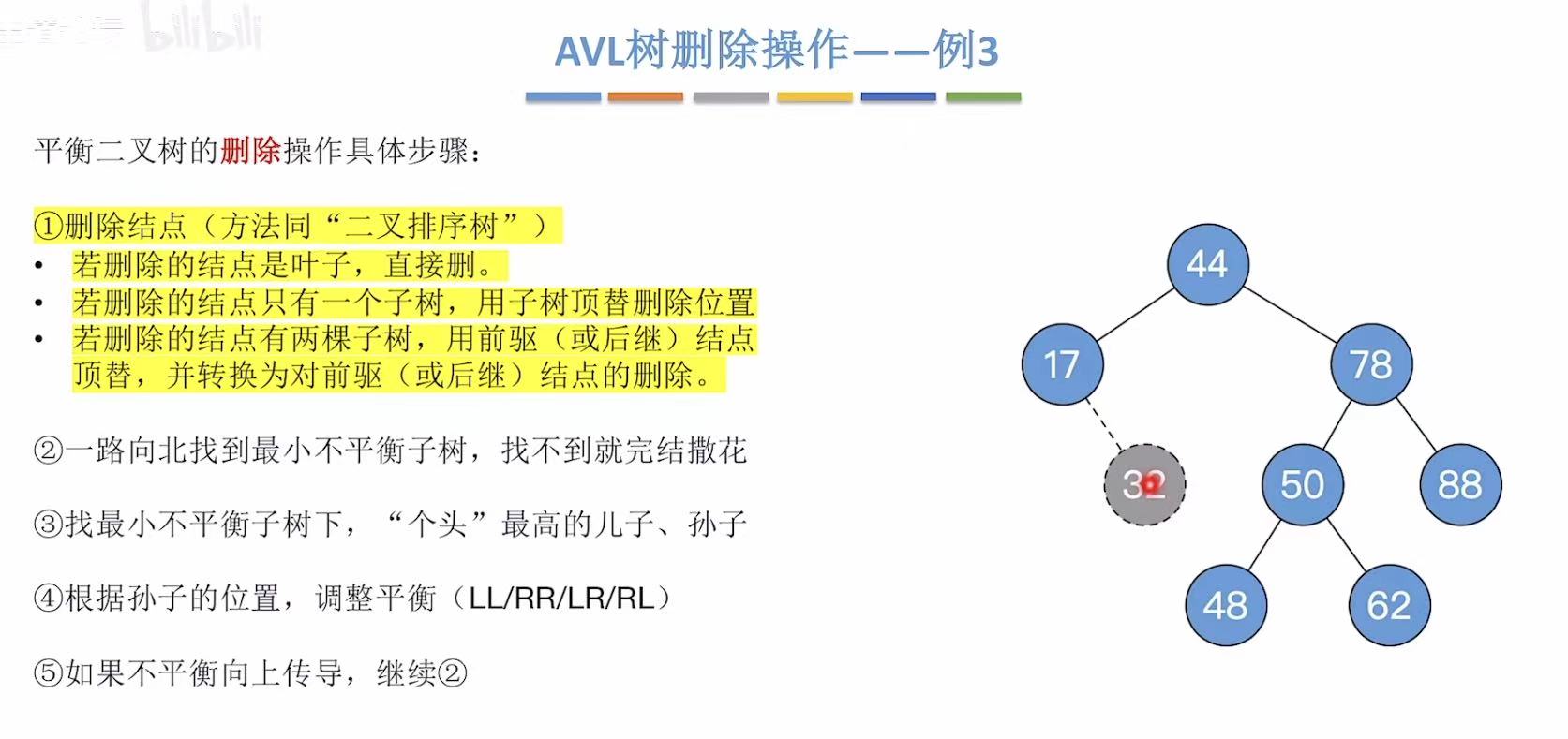
找到最小不平衡树
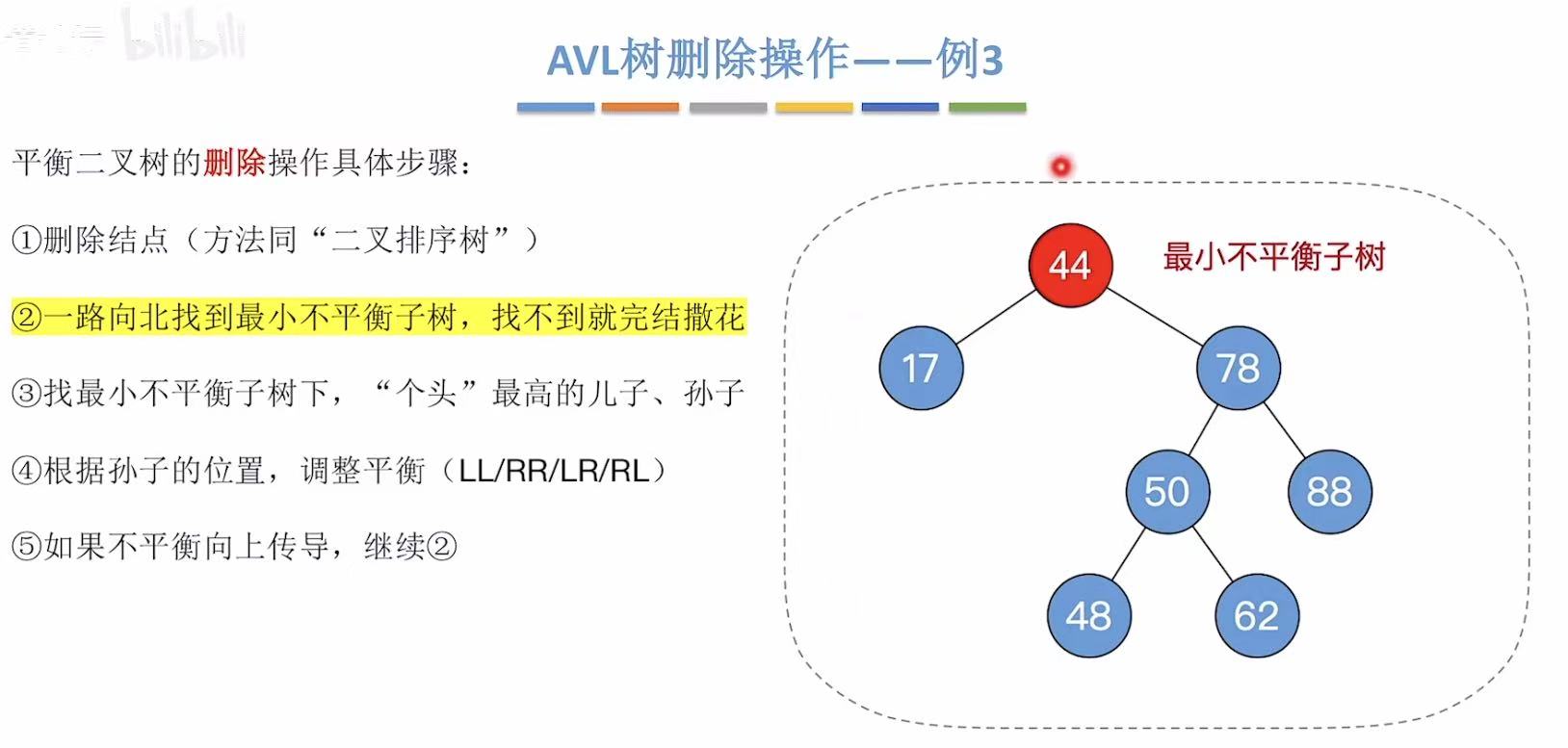
找到个头最高的儿子和孙子
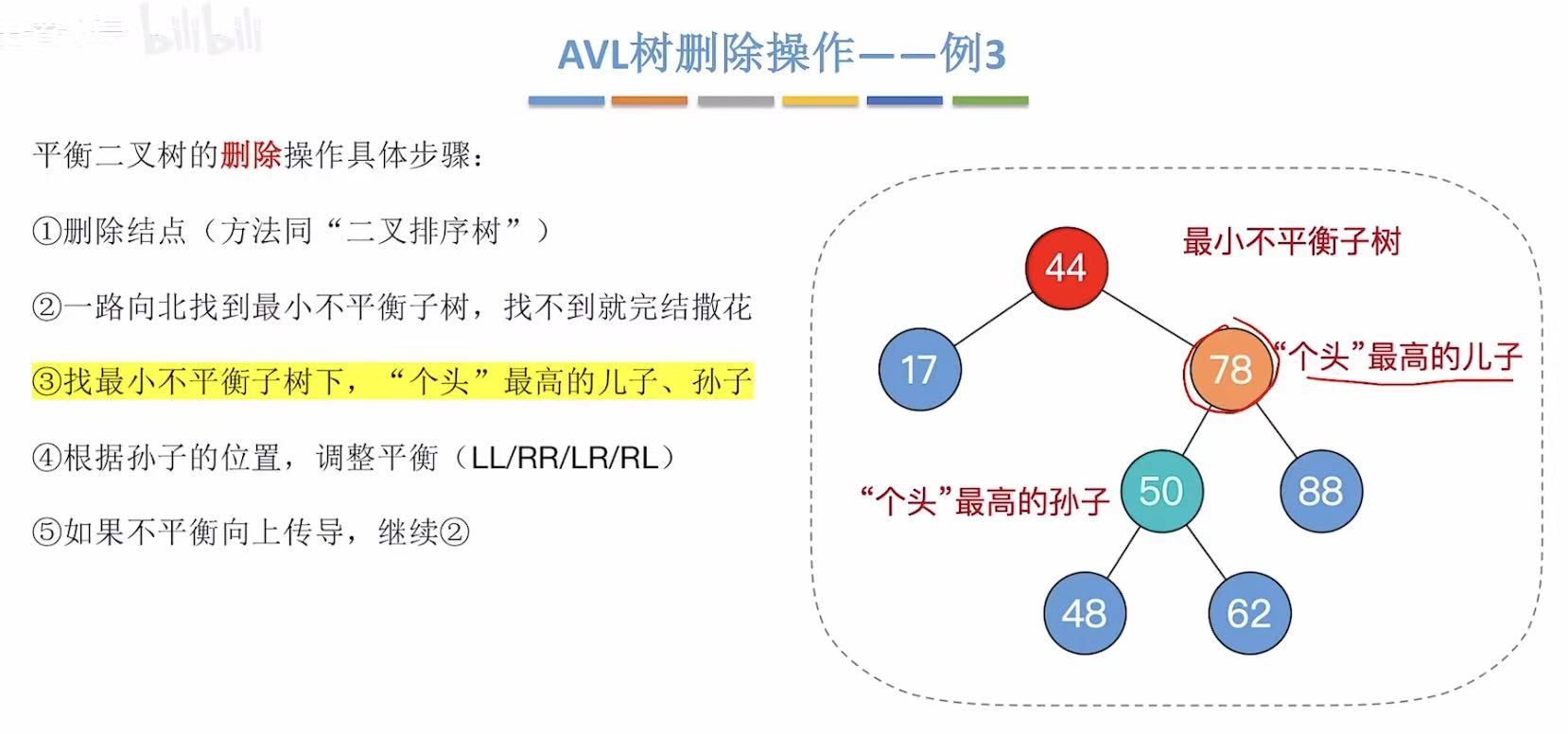
孙子是根节点的右孩子的左子树,即RL
所以需要先右旋再左旋:
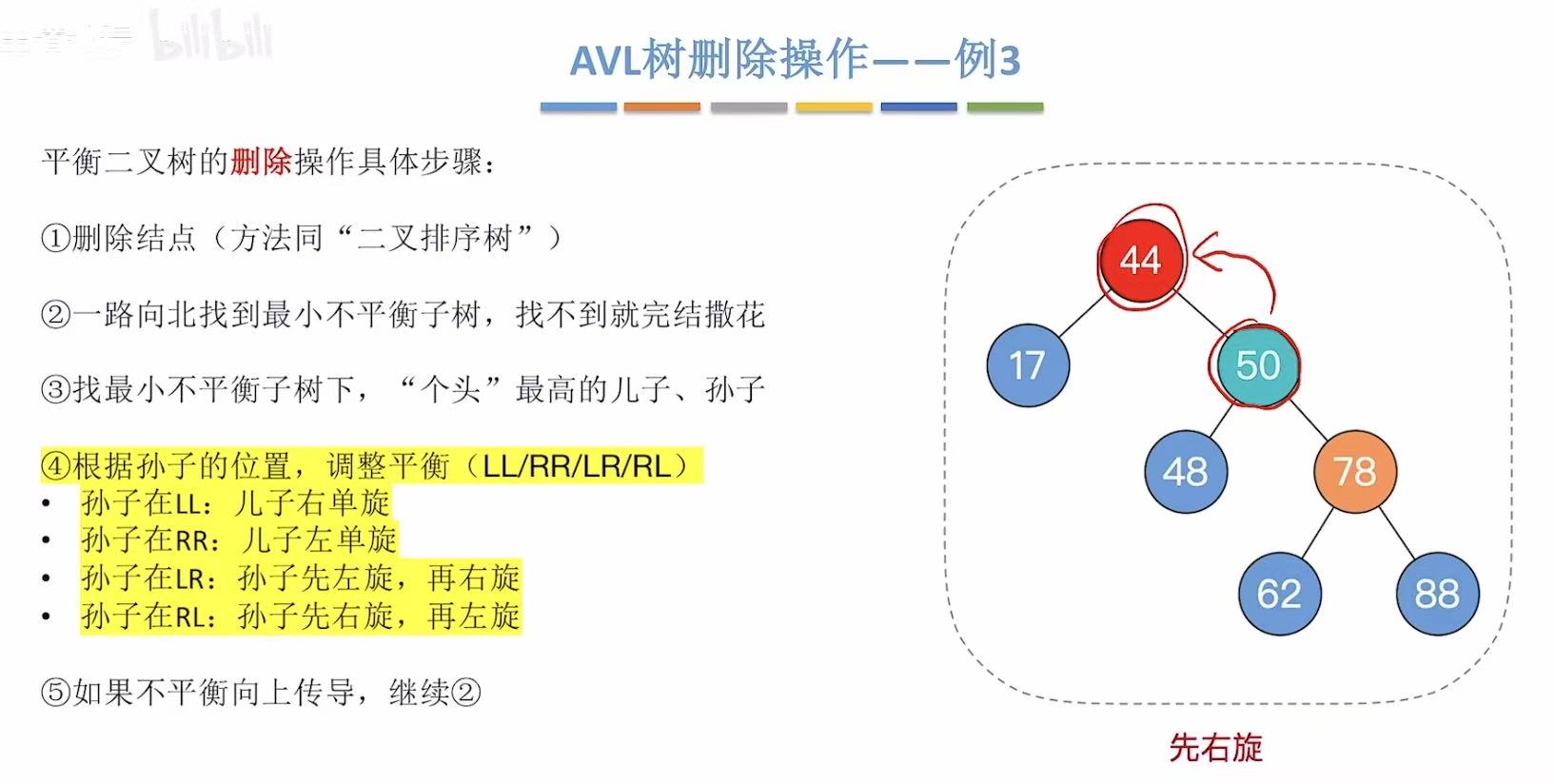
平衡后:
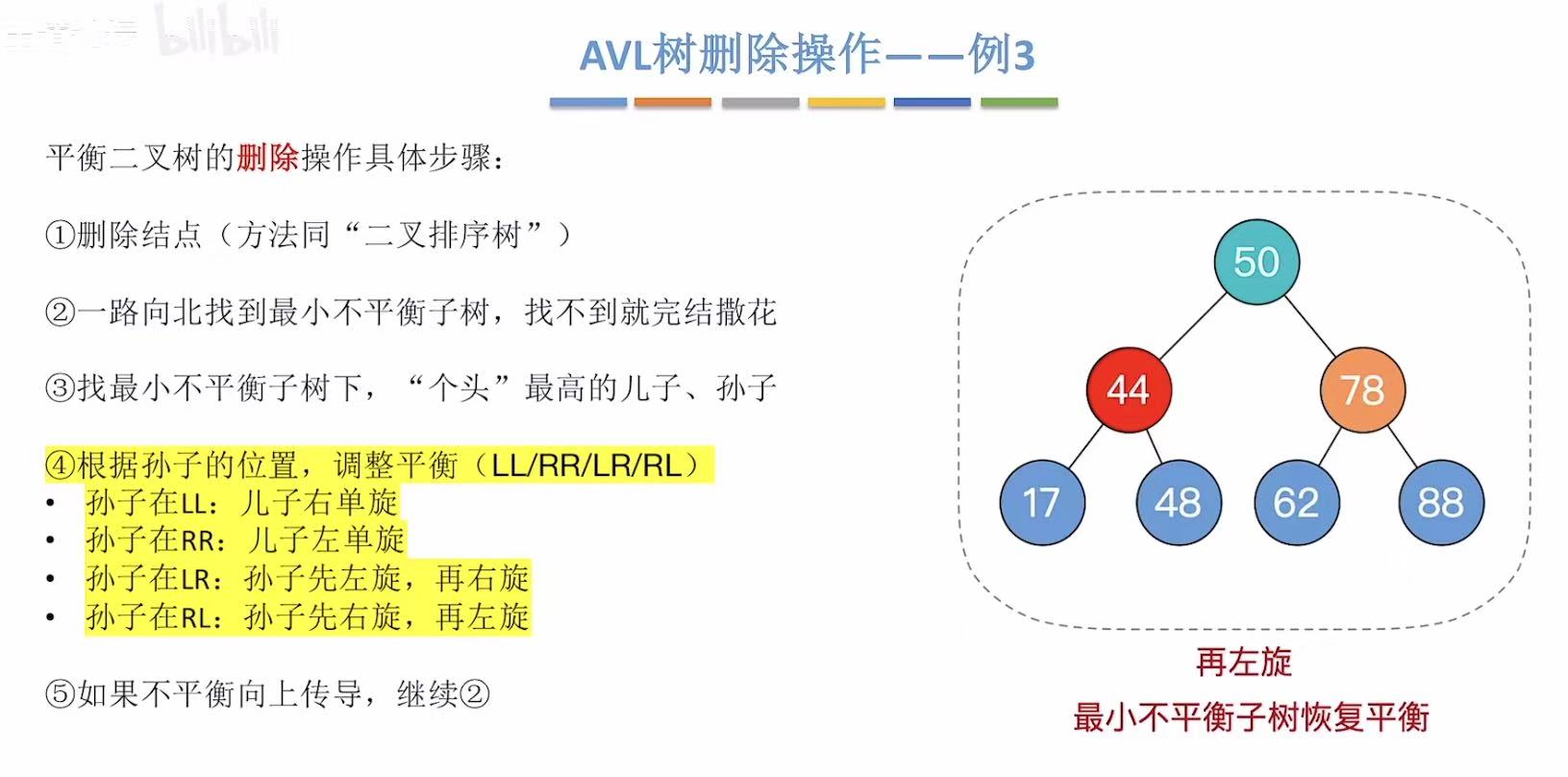
此时已经是平衡的了,所以第五条步骤直接跳过。
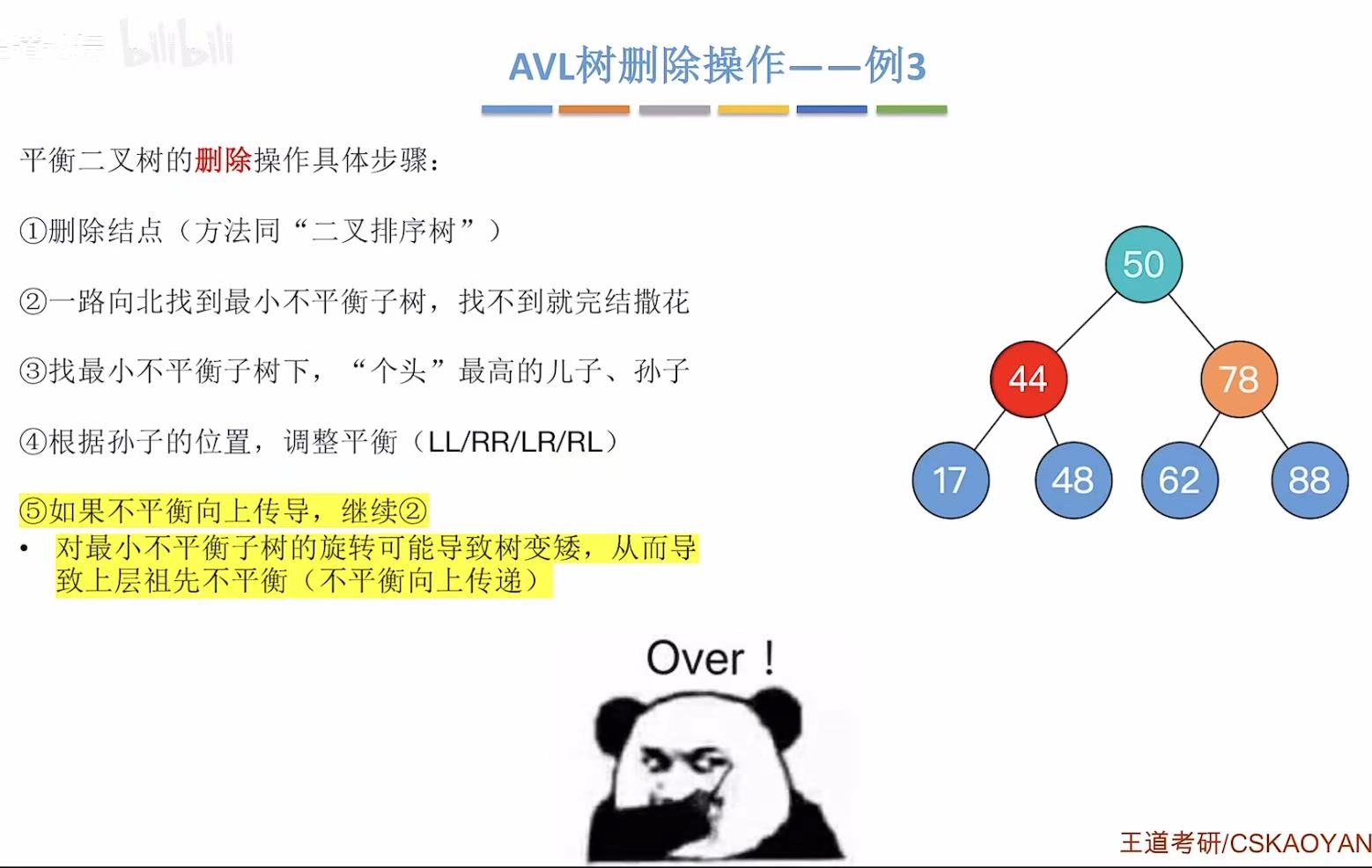
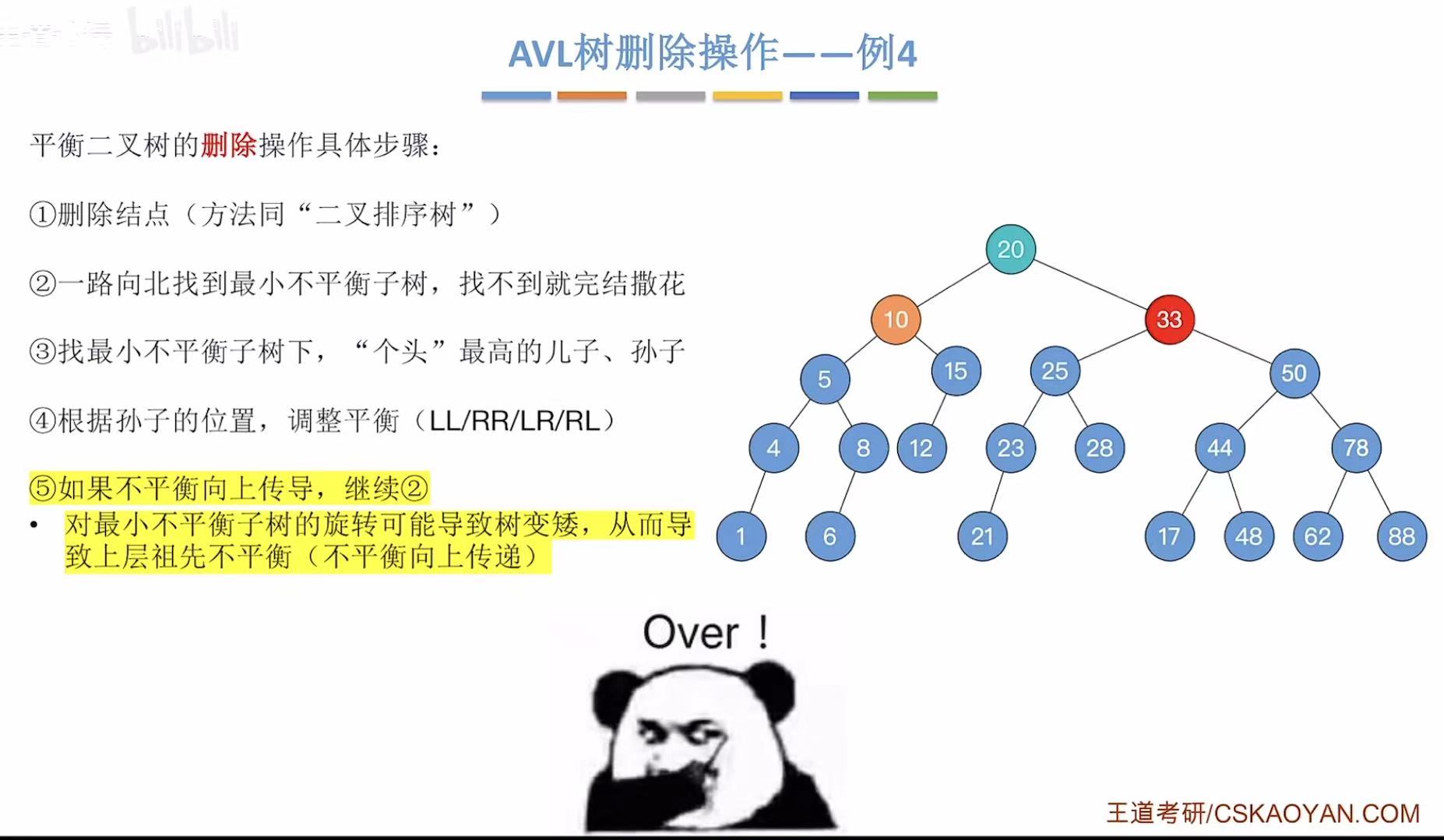
2.4 例4-删32
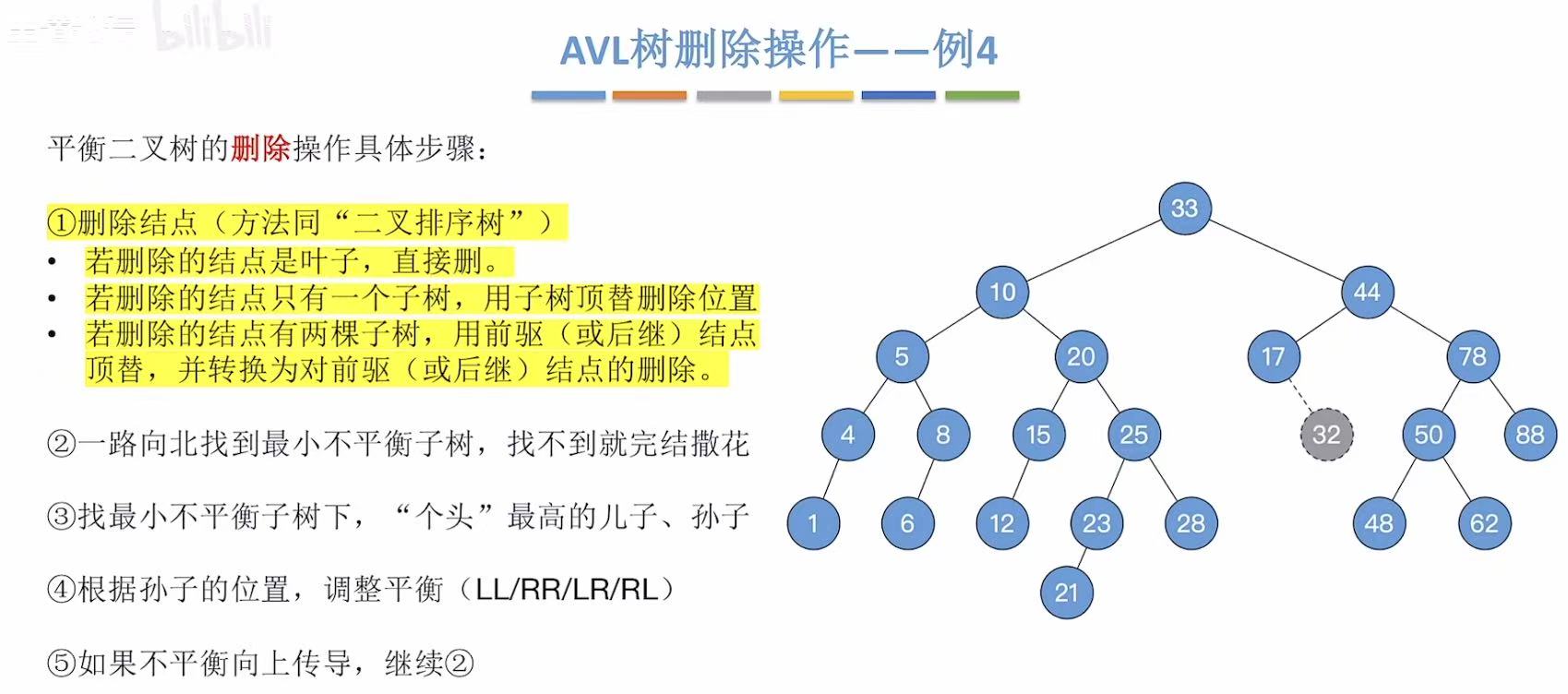
这里和例3删除过程完全相同。
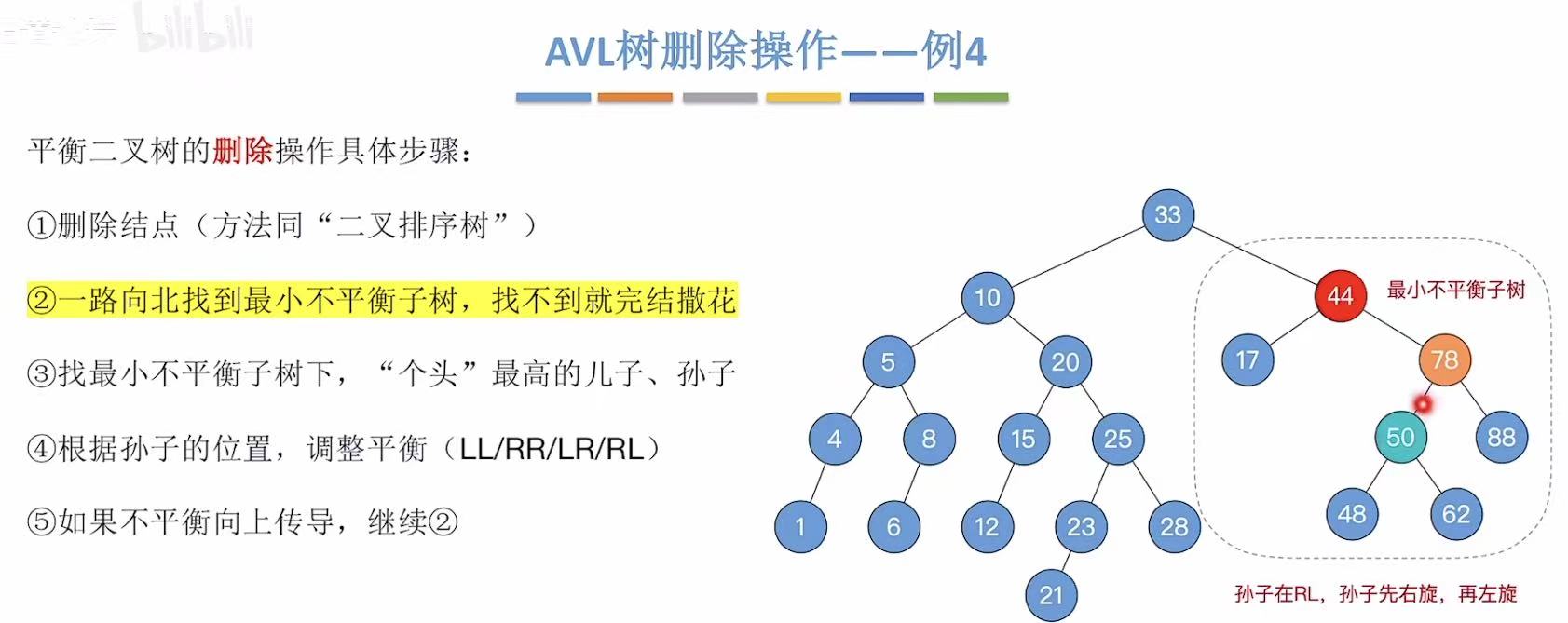
到达最后一步,我们不难看出此时的二叉树依旧是不平衡的。
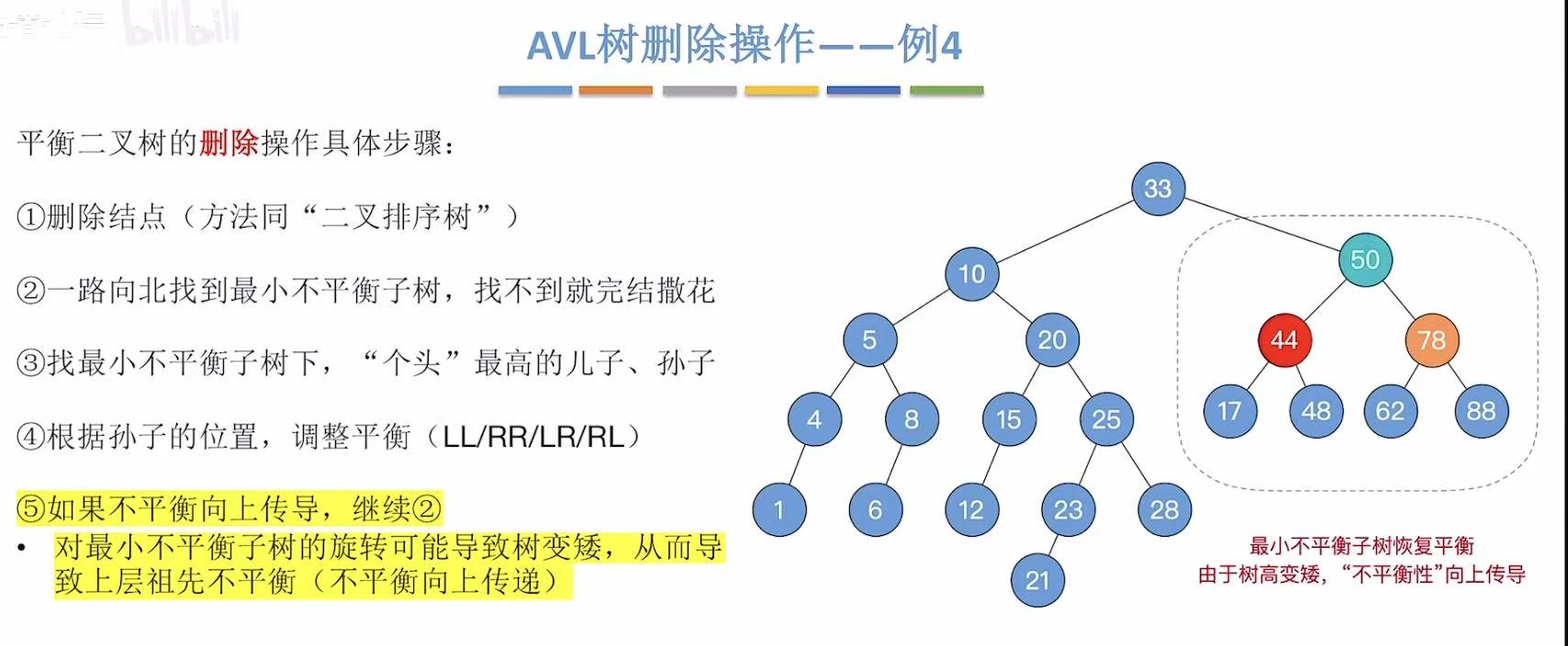
所以我们重新返回步骤二,找到最小不平衡子树。
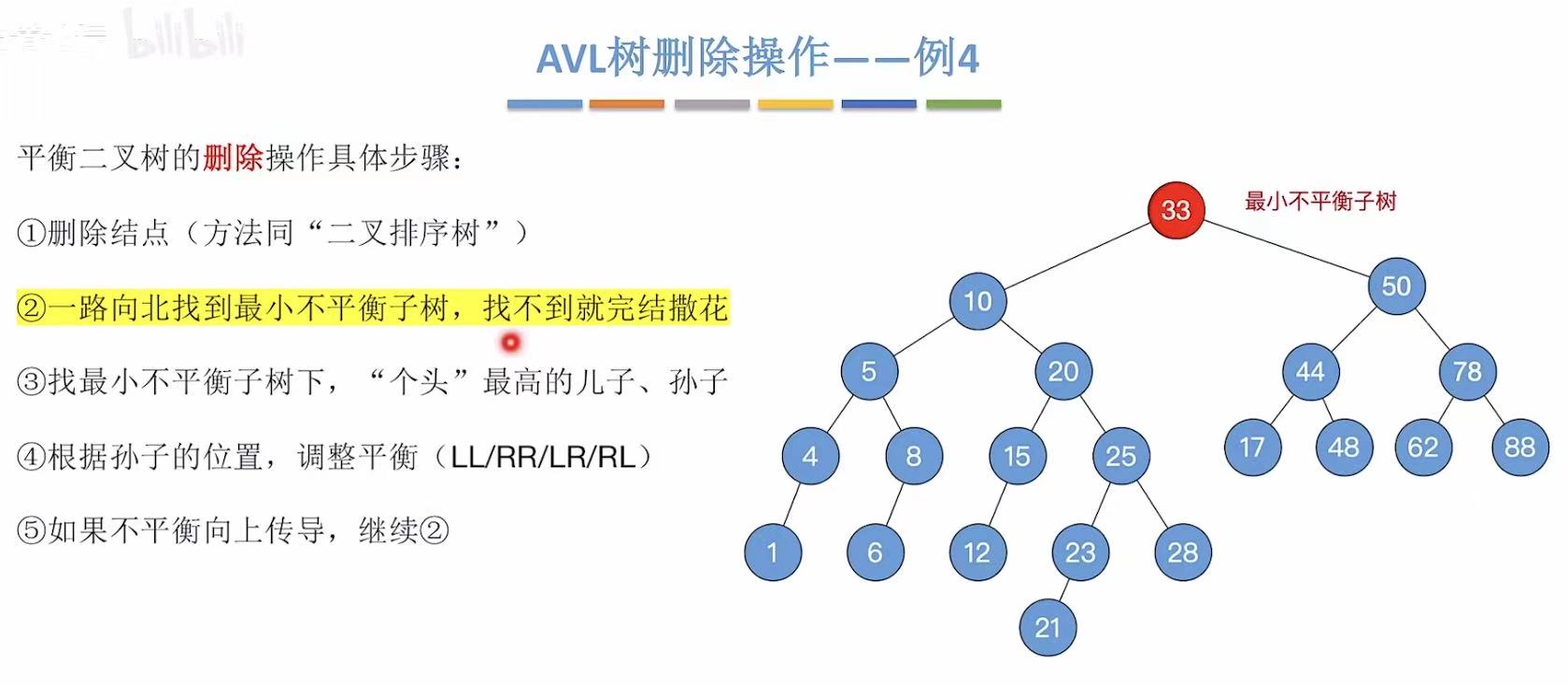
找到个头最高的儿子、孙子。
孙子在根节点的左孩子的右子树上,即LR
所以我们需要先左旋,后右旋。
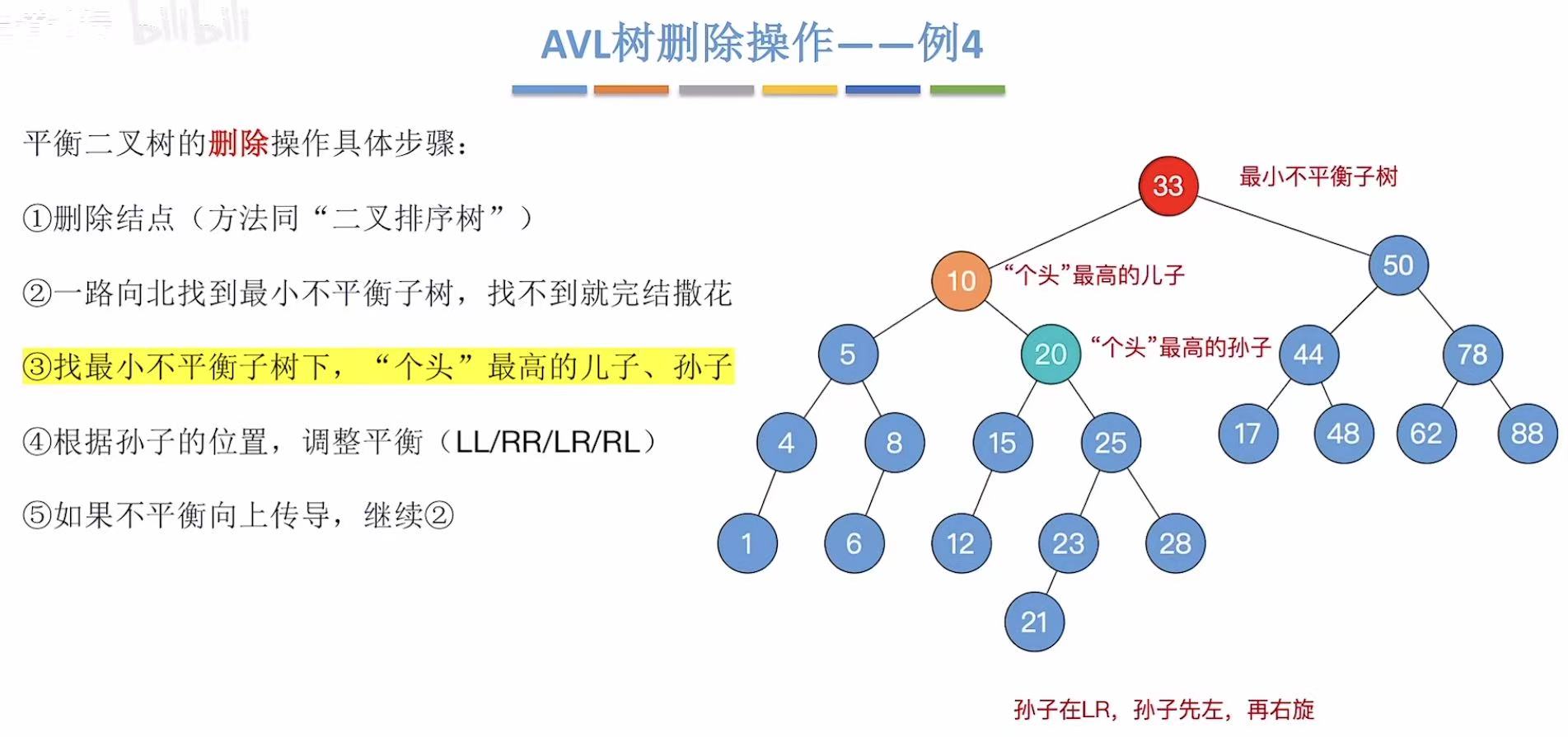
左旋后:
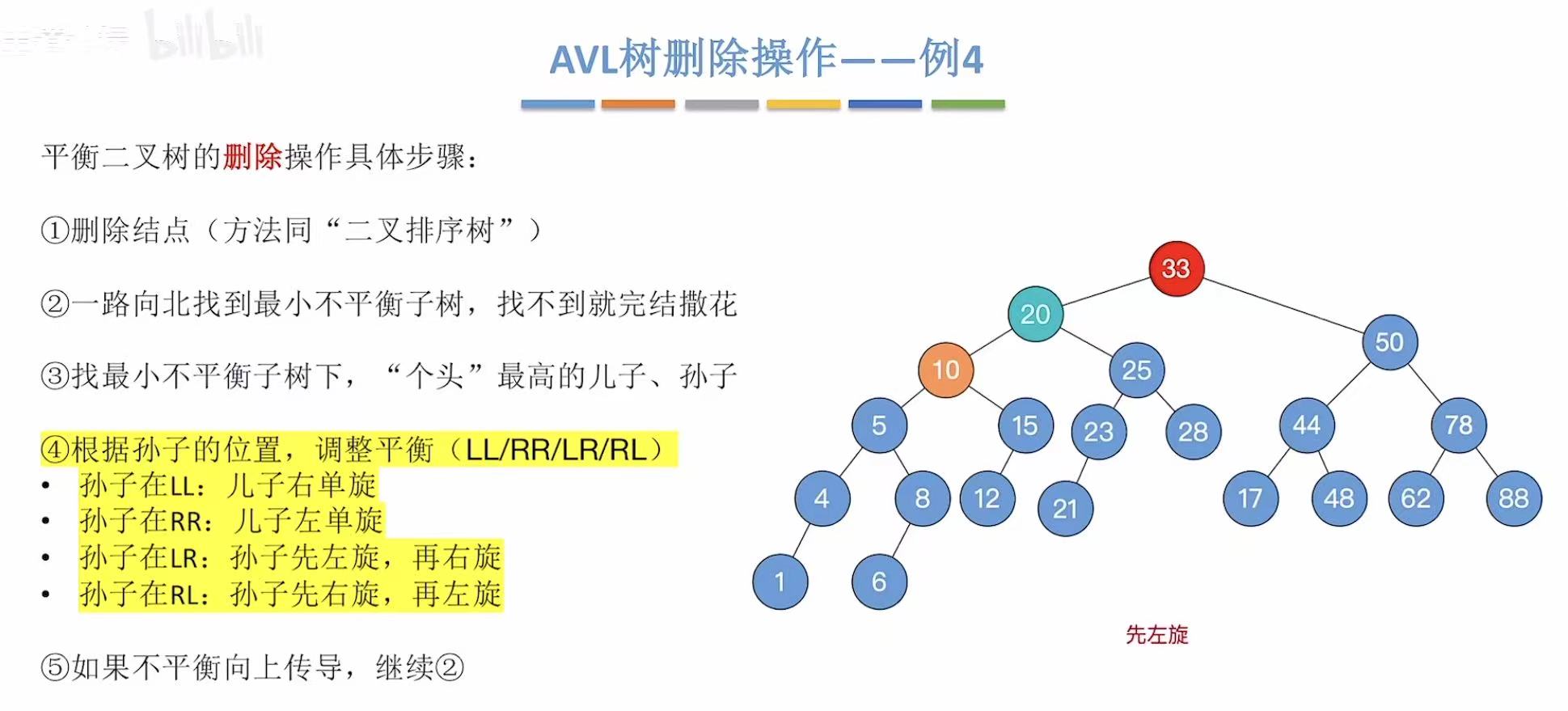
右旋后:
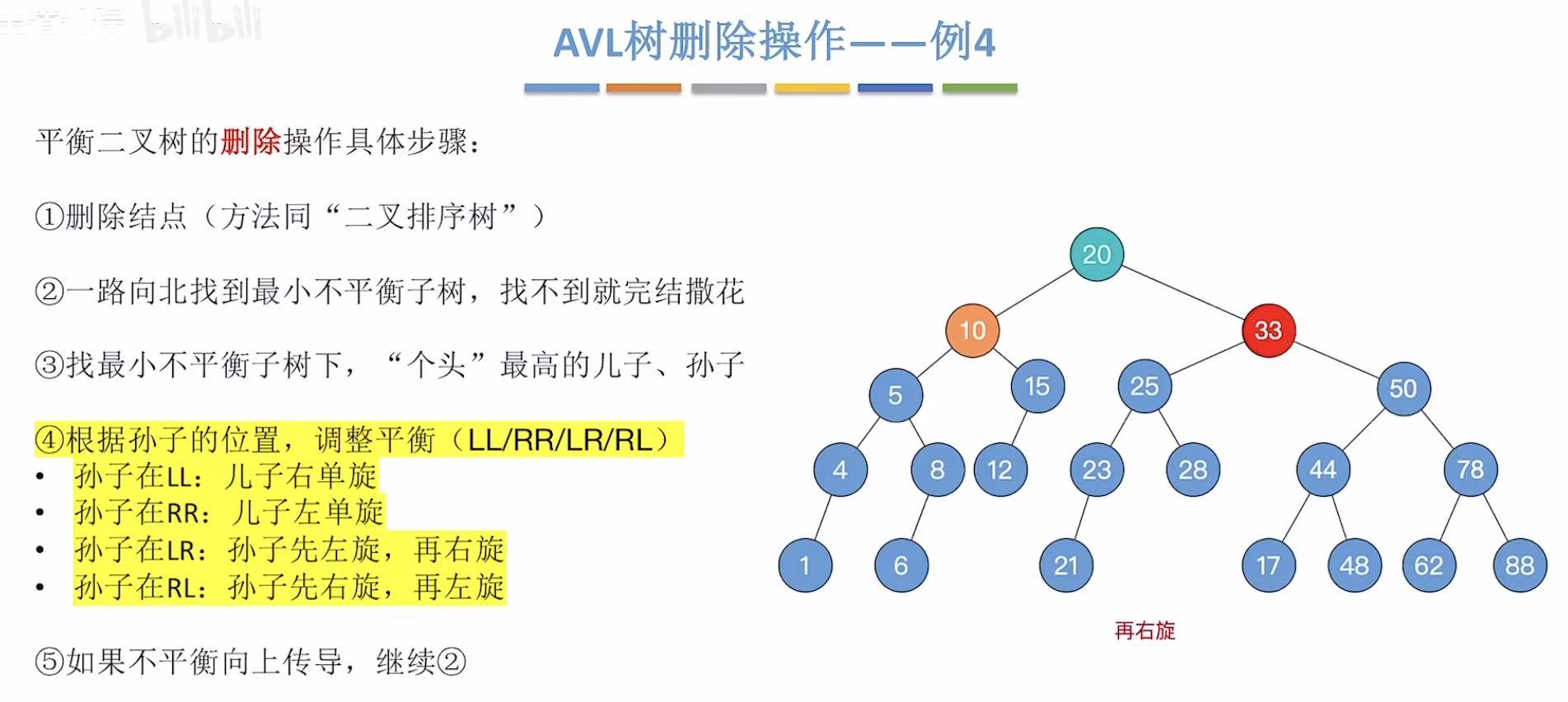
最后成功实现平衡。
2.5 例5-删75
这次删除的结点有两颗子树。
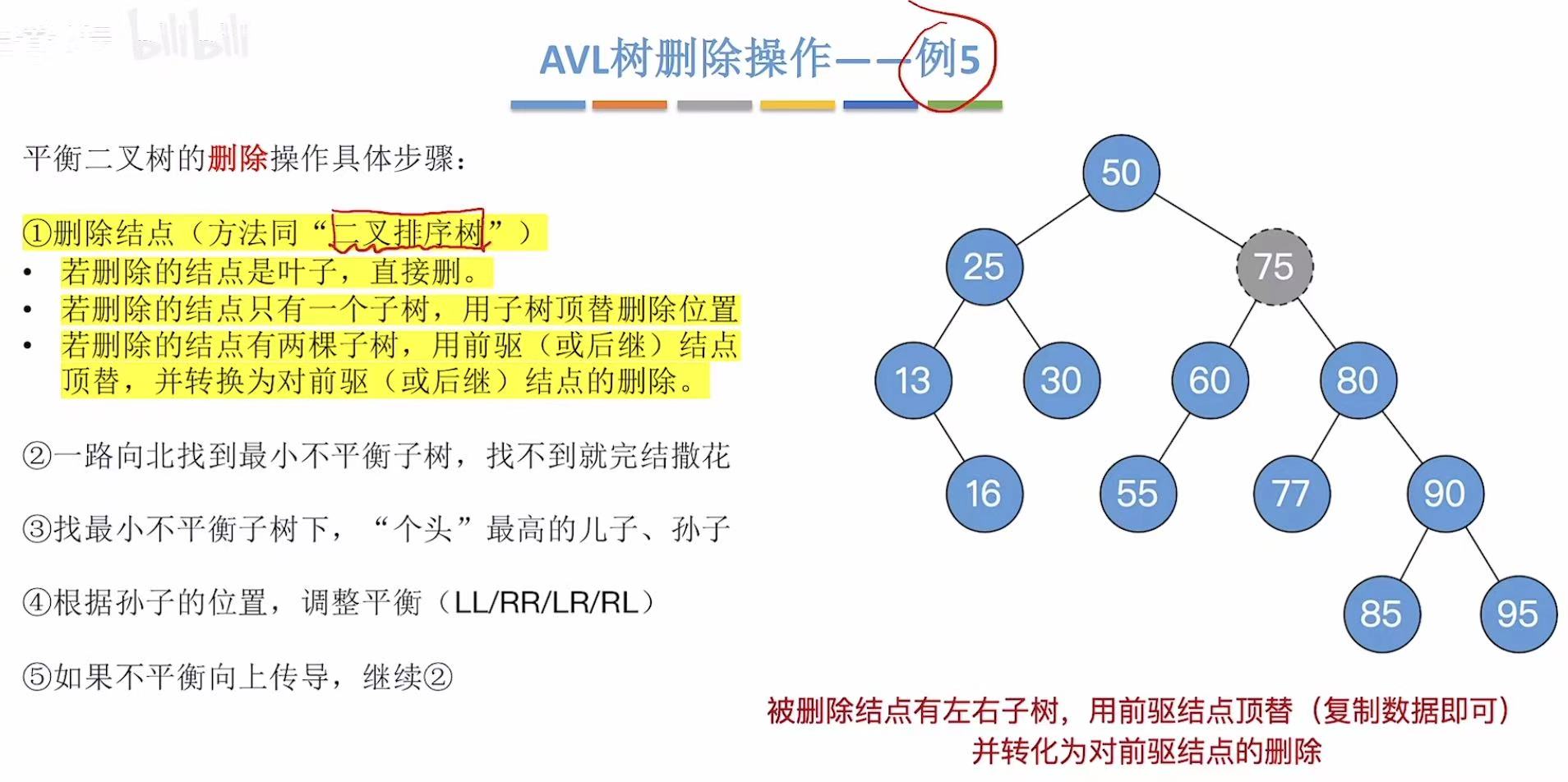
用前驱结点顶替被删除结点的位置。
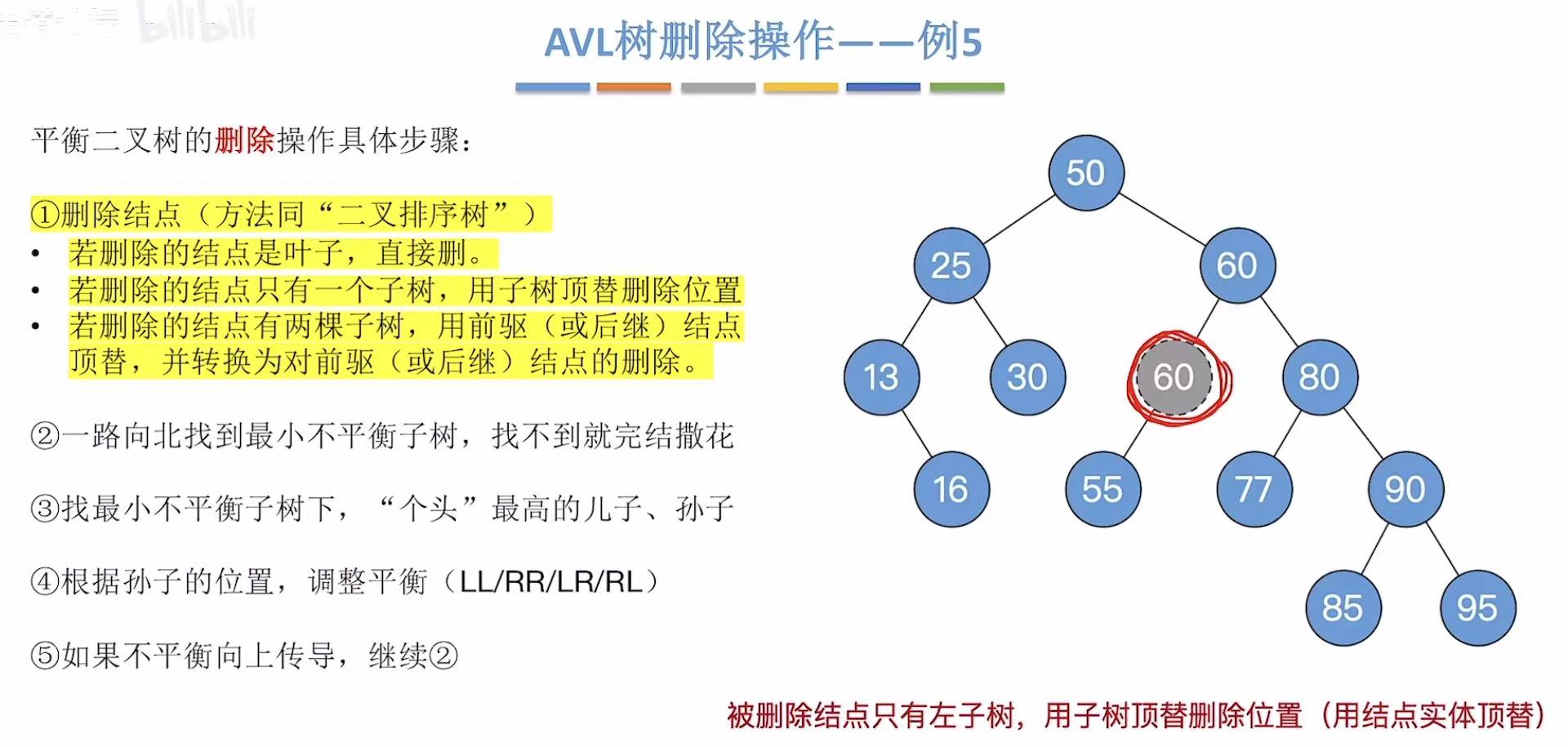
变成这样:
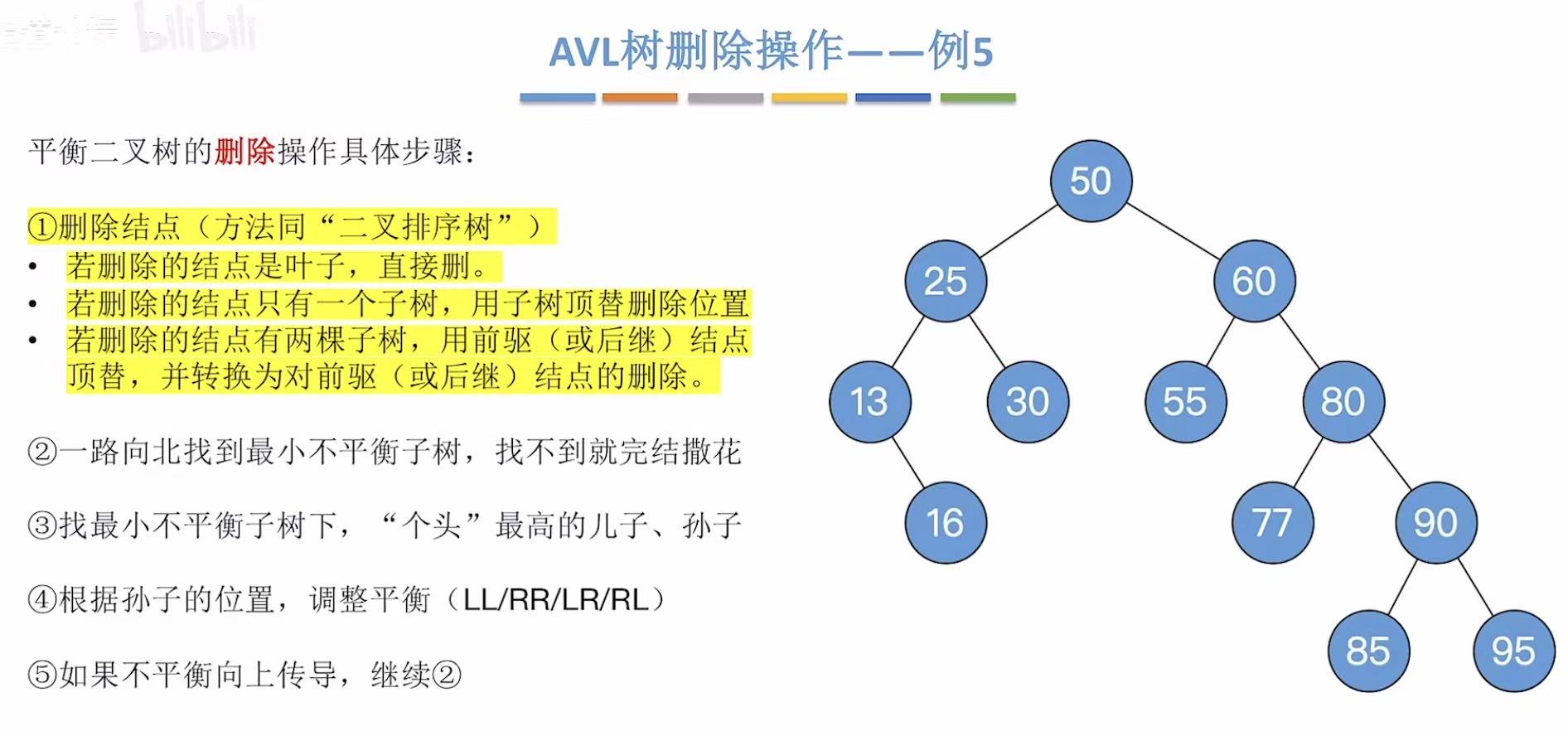
然后继续老顺序:
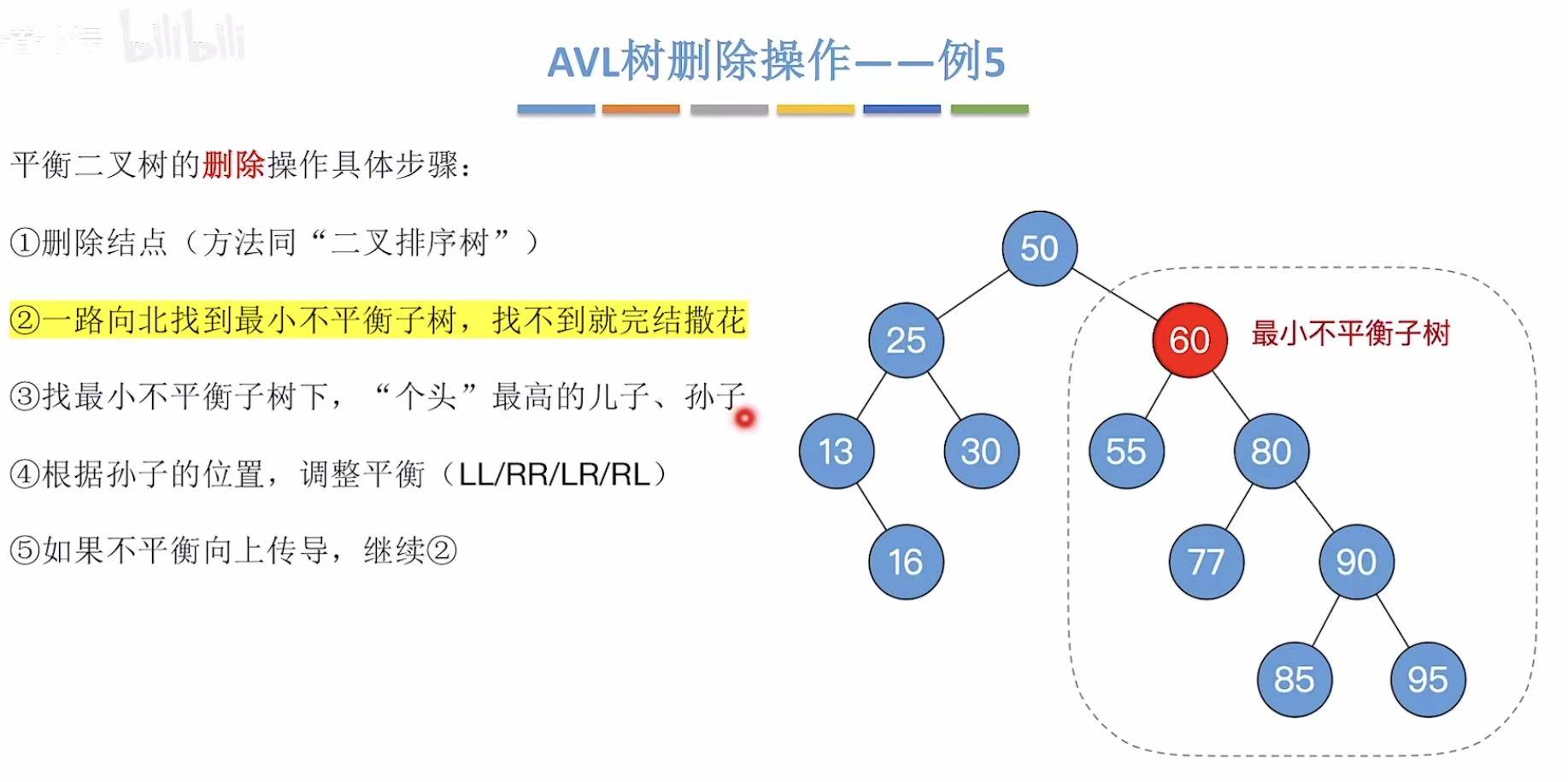
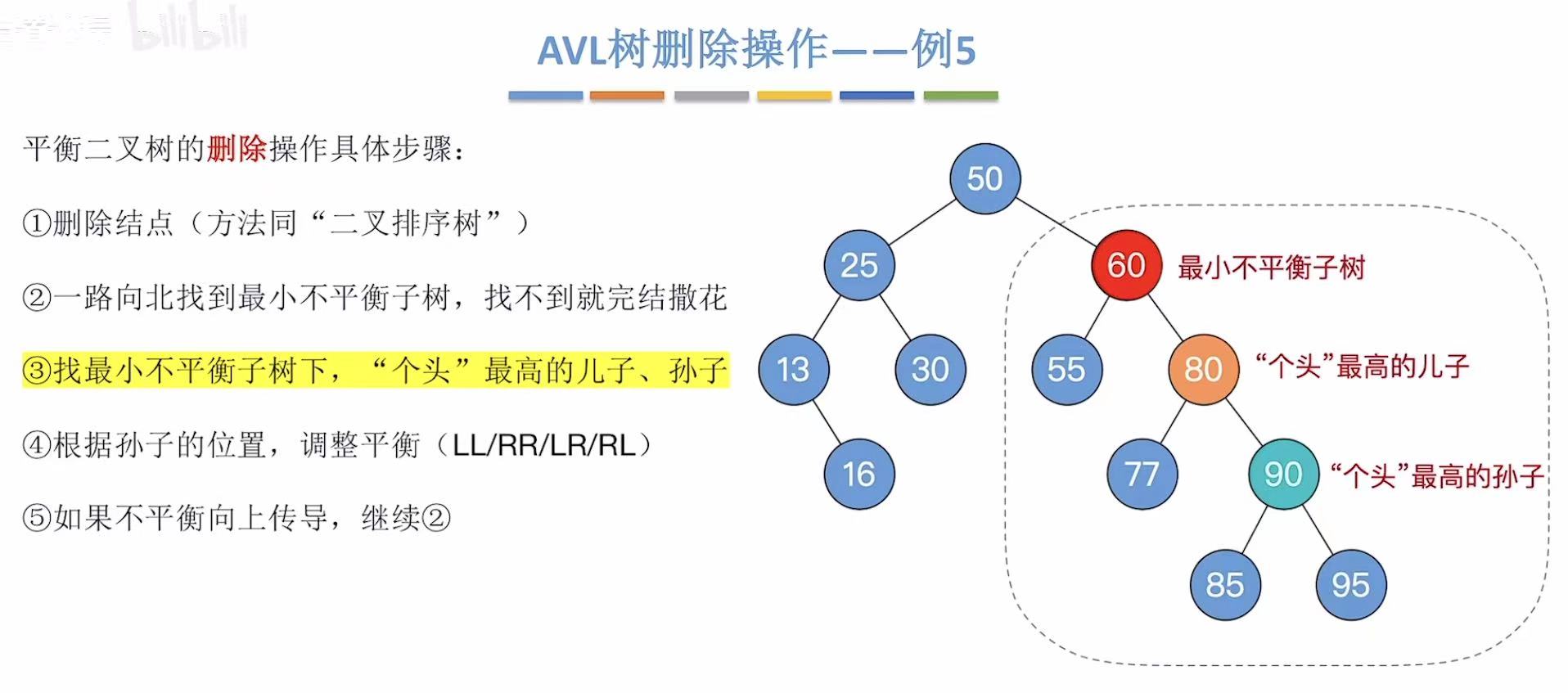
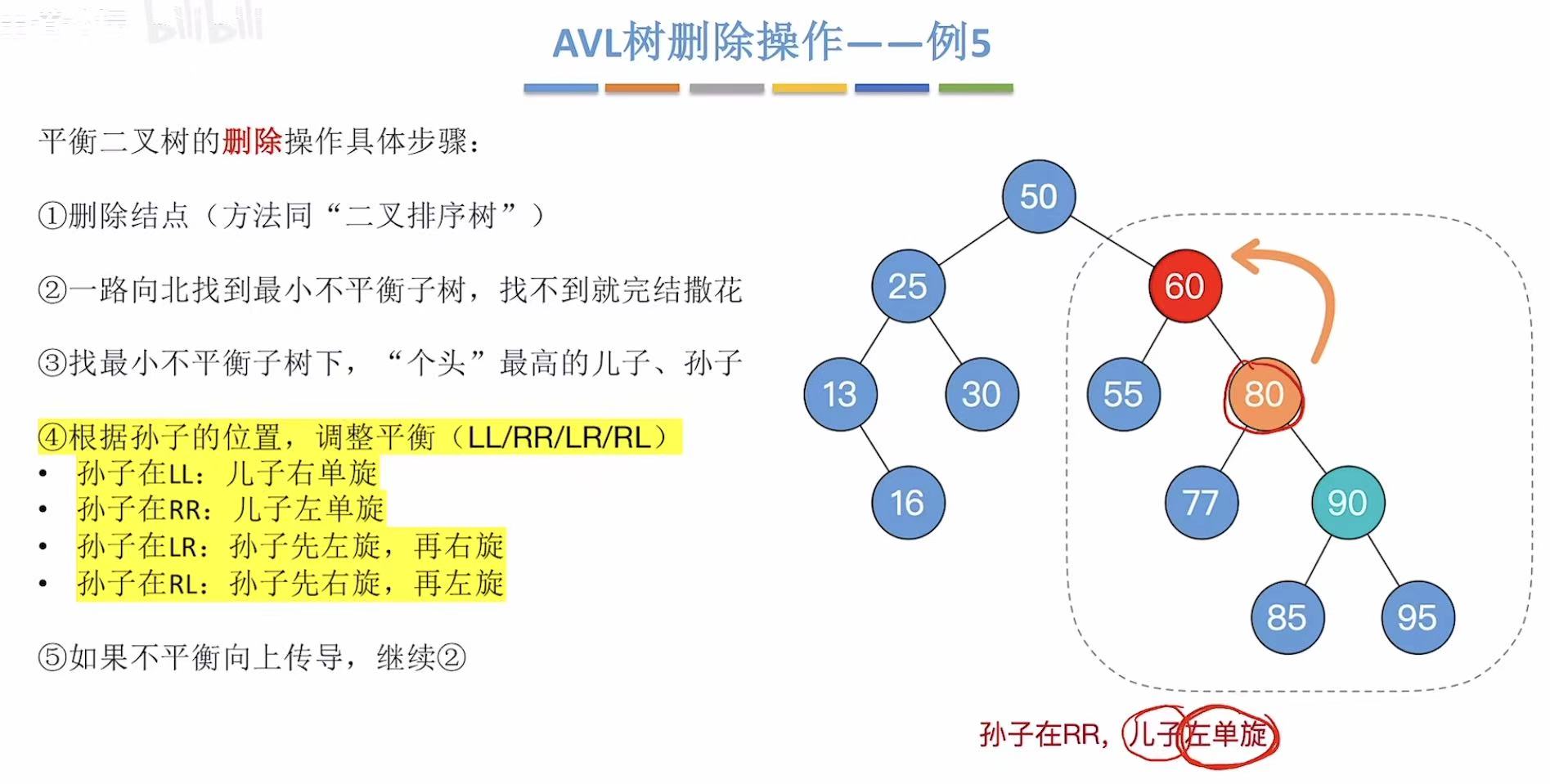
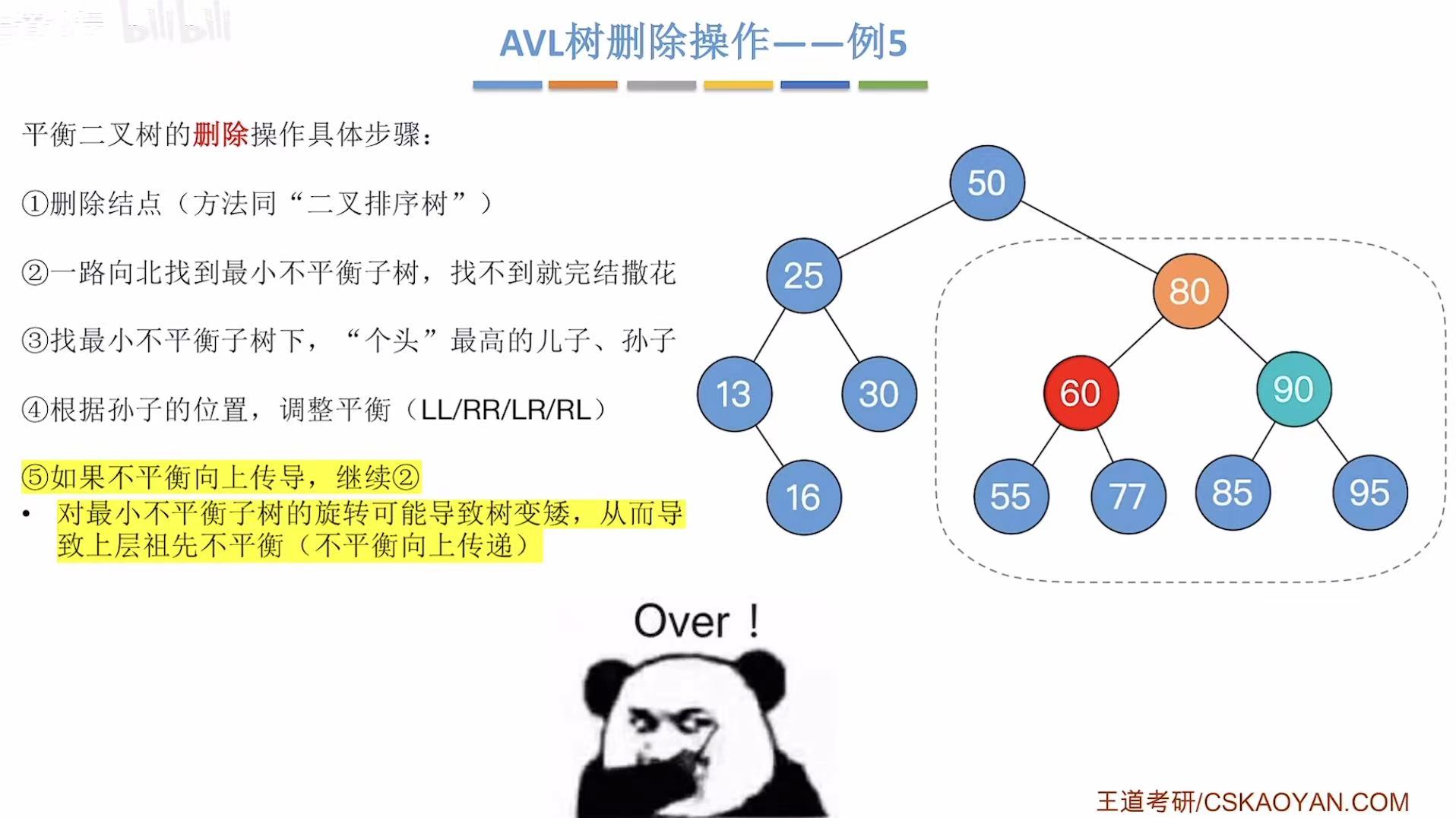
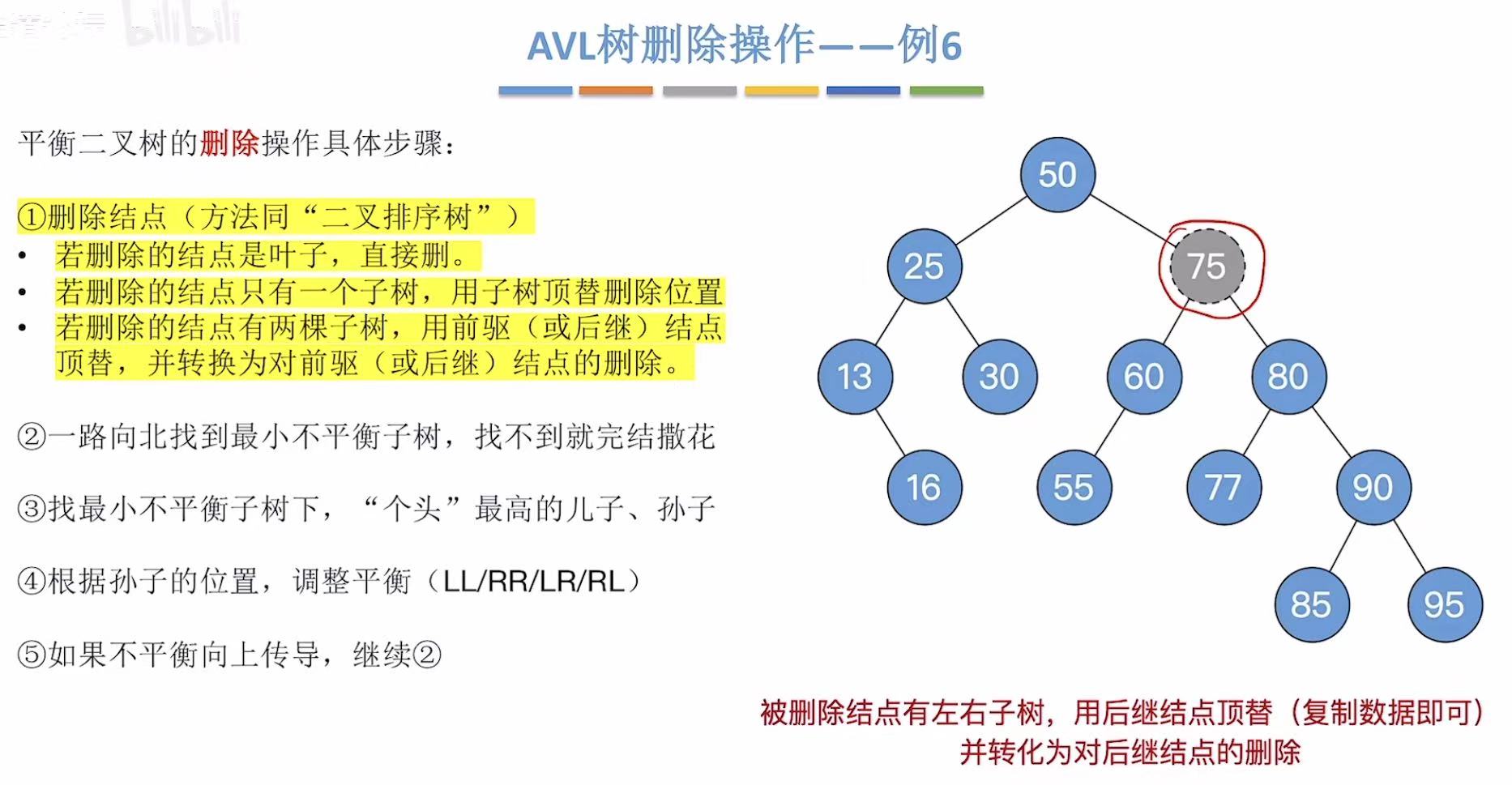
2.6 例6-删75
这次用后继结点来顶替被删除结点的位置:
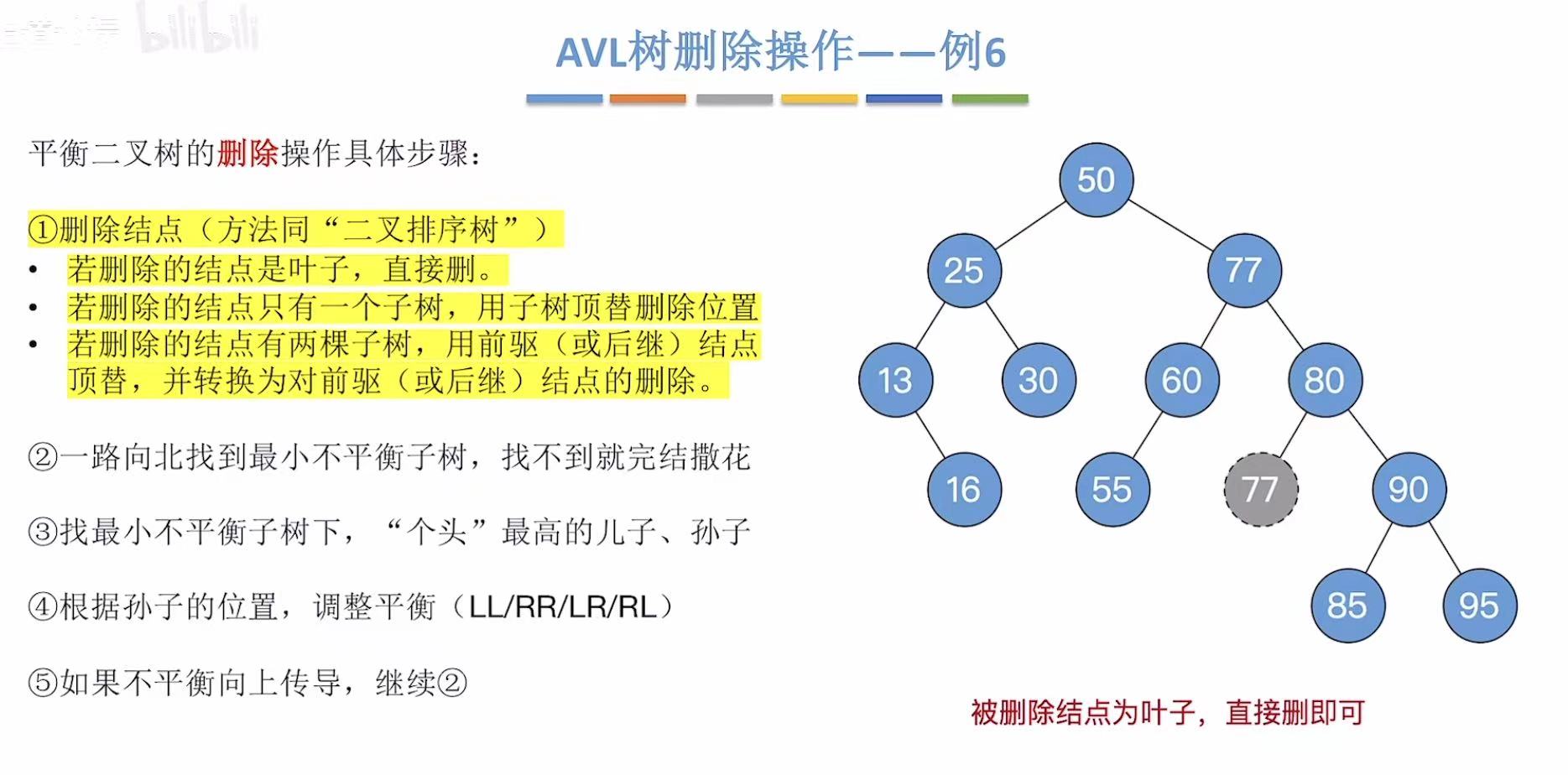
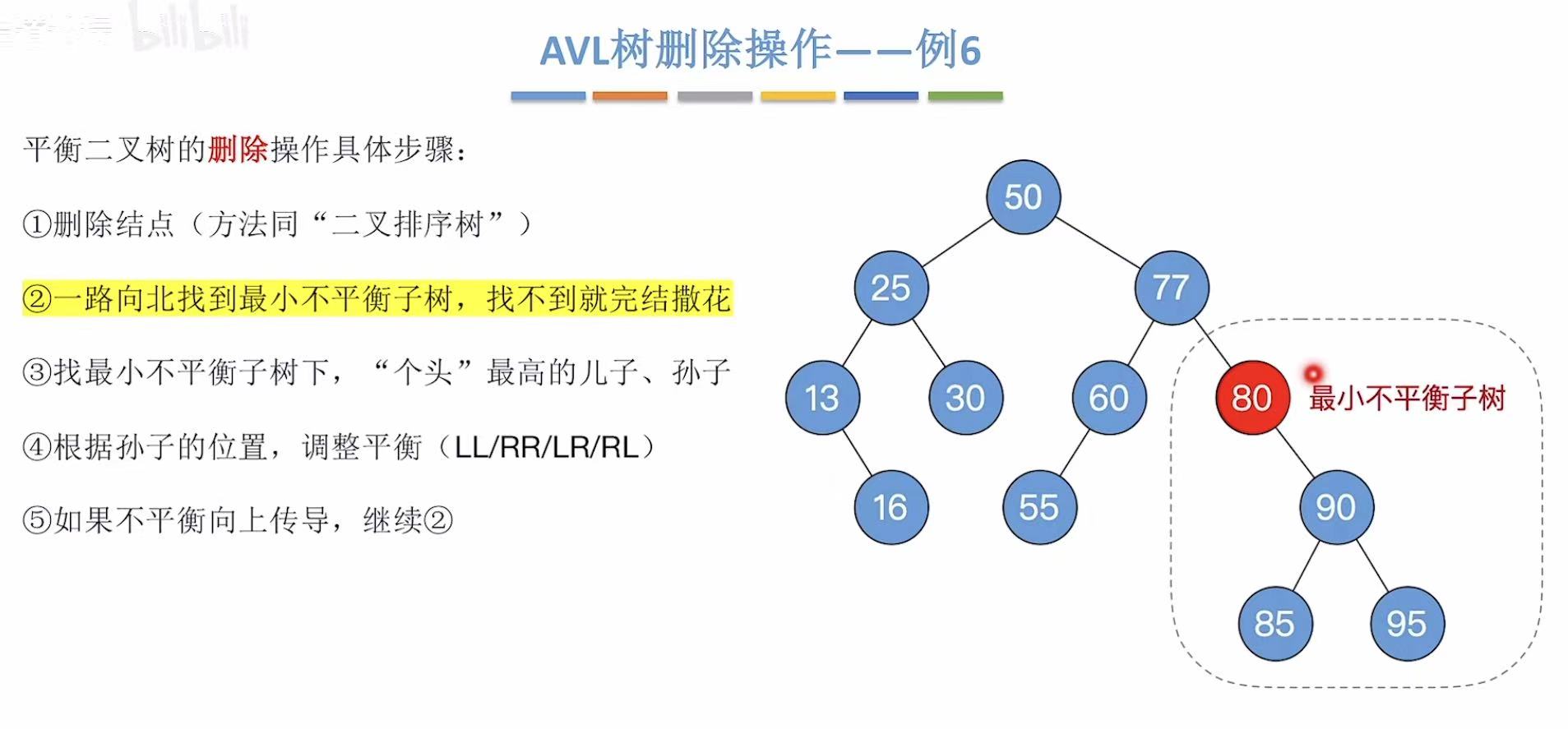
孙子用95:
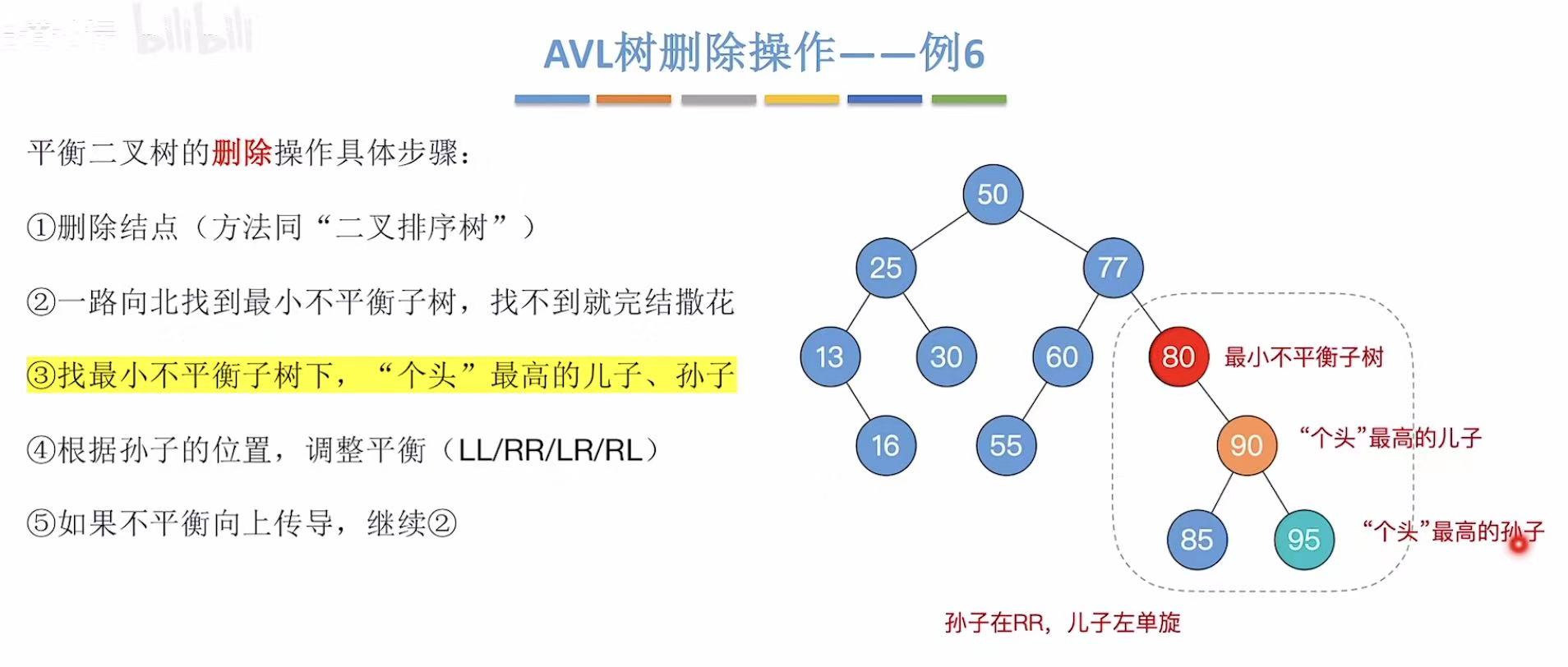
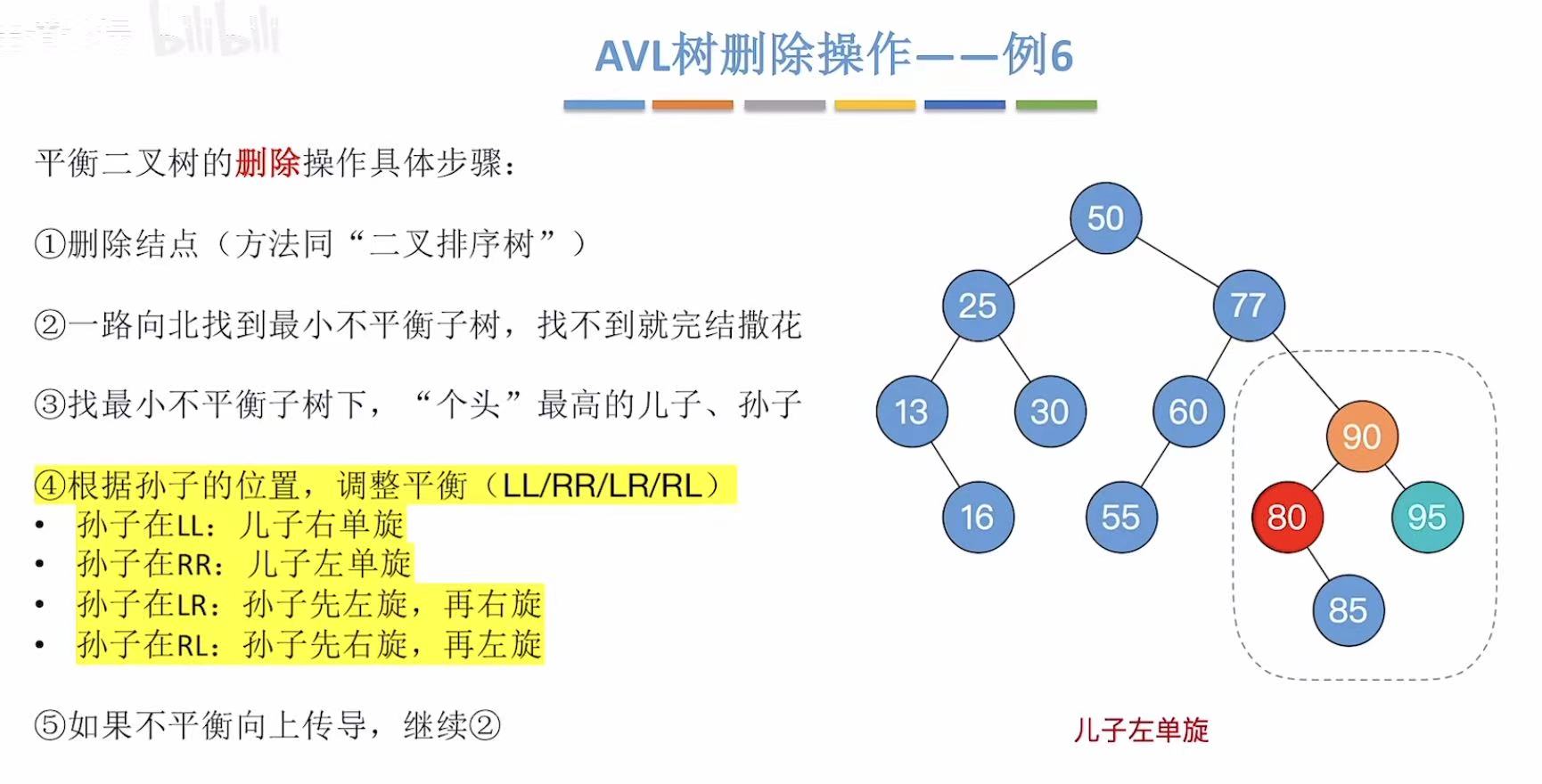
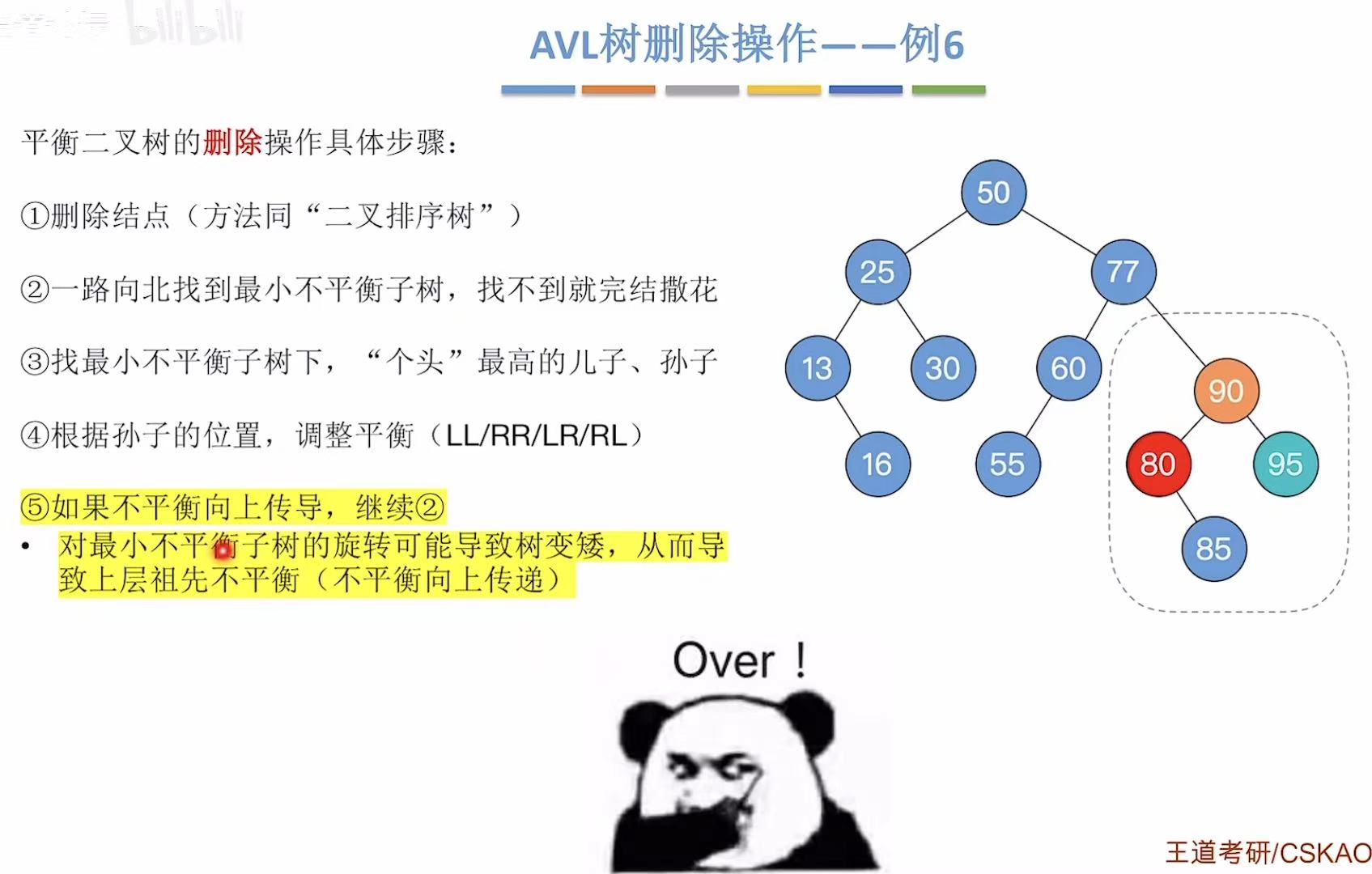
孙子用85:
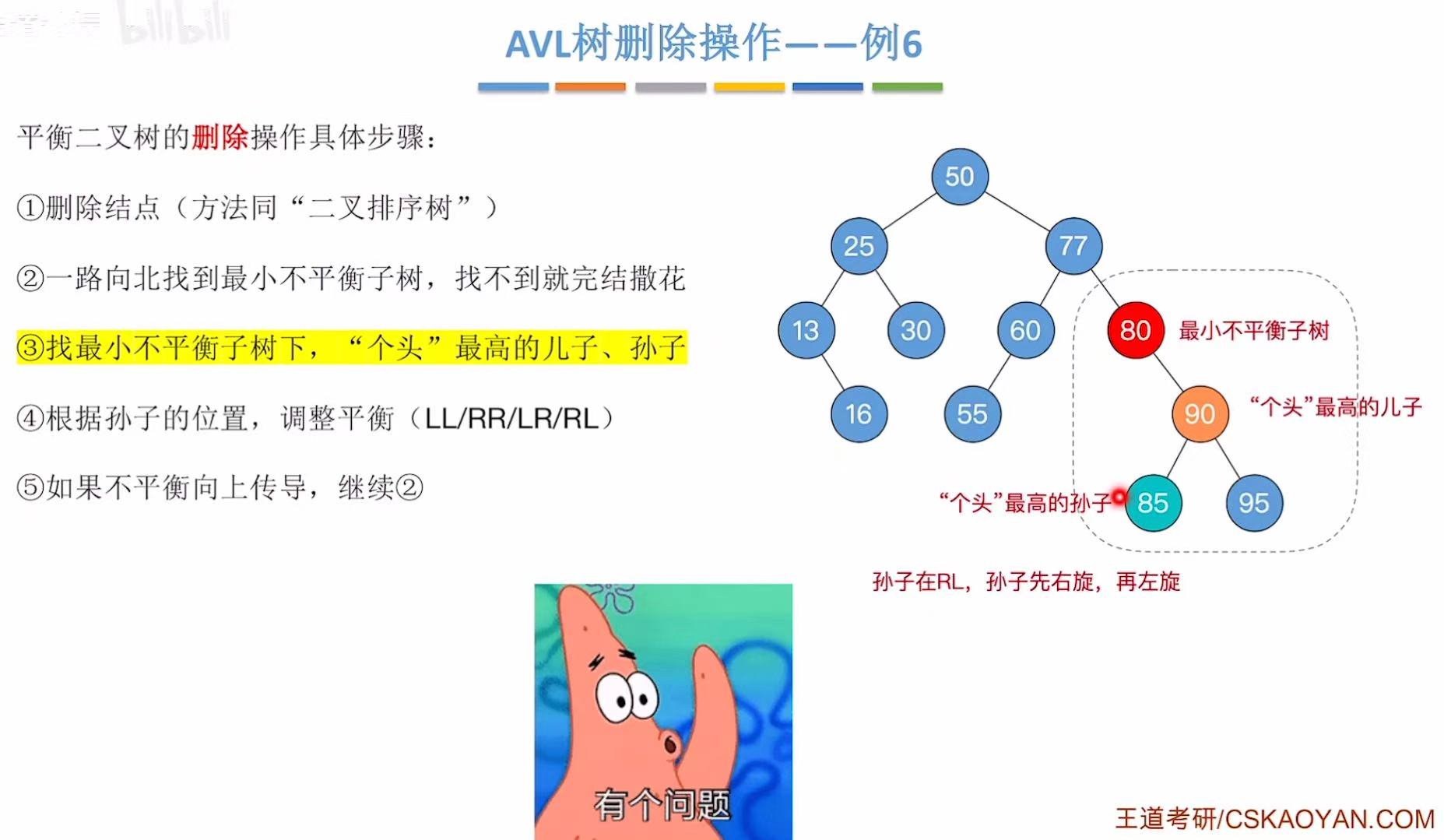
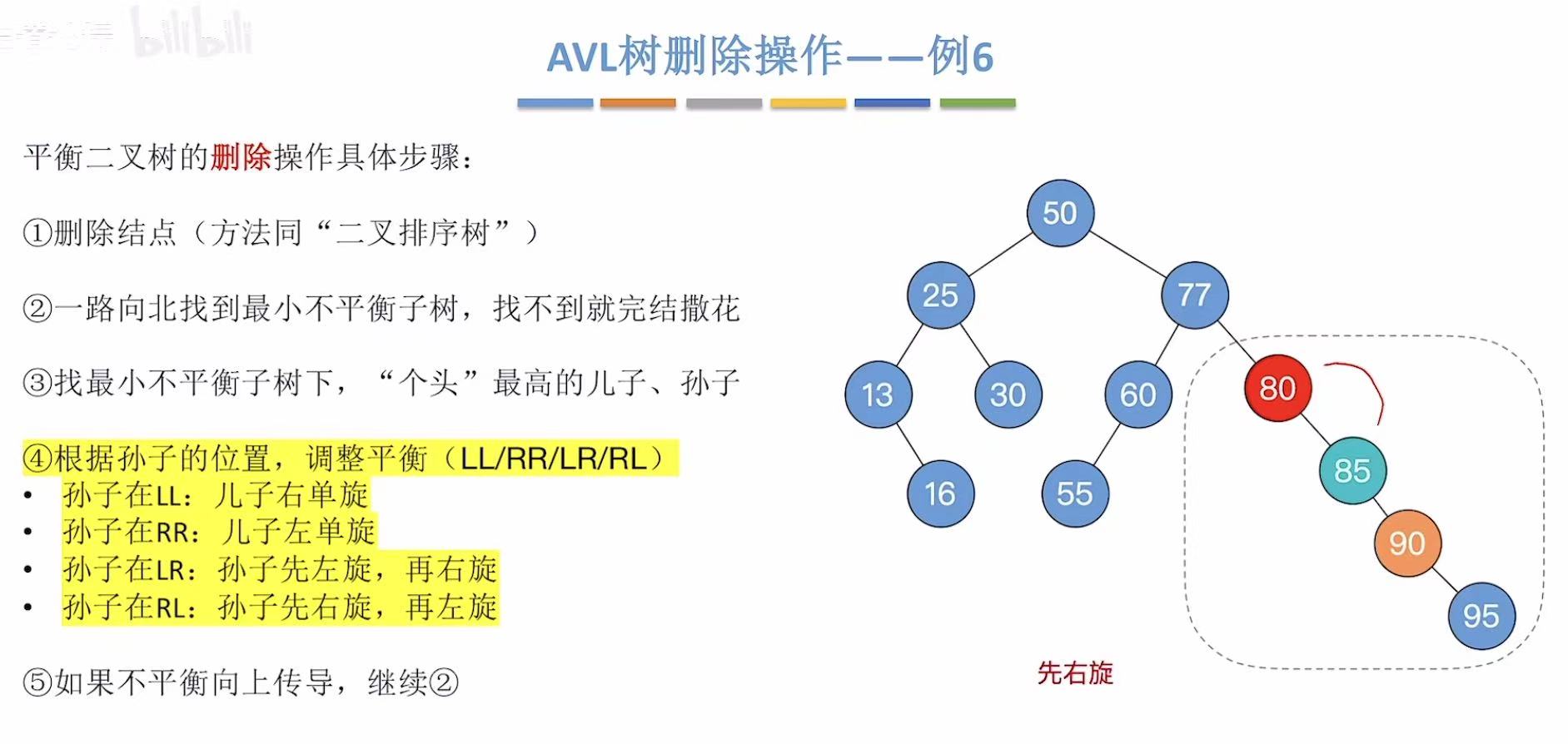
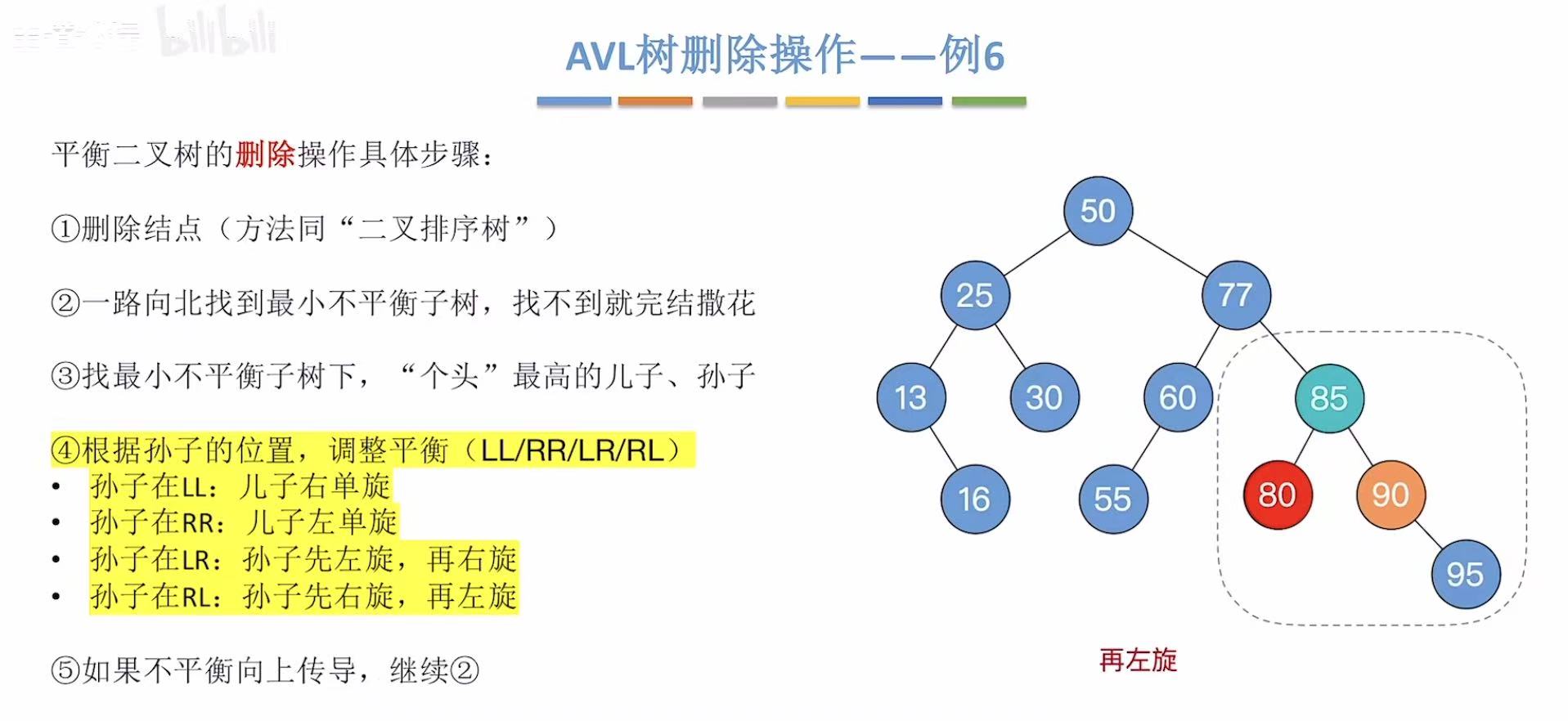
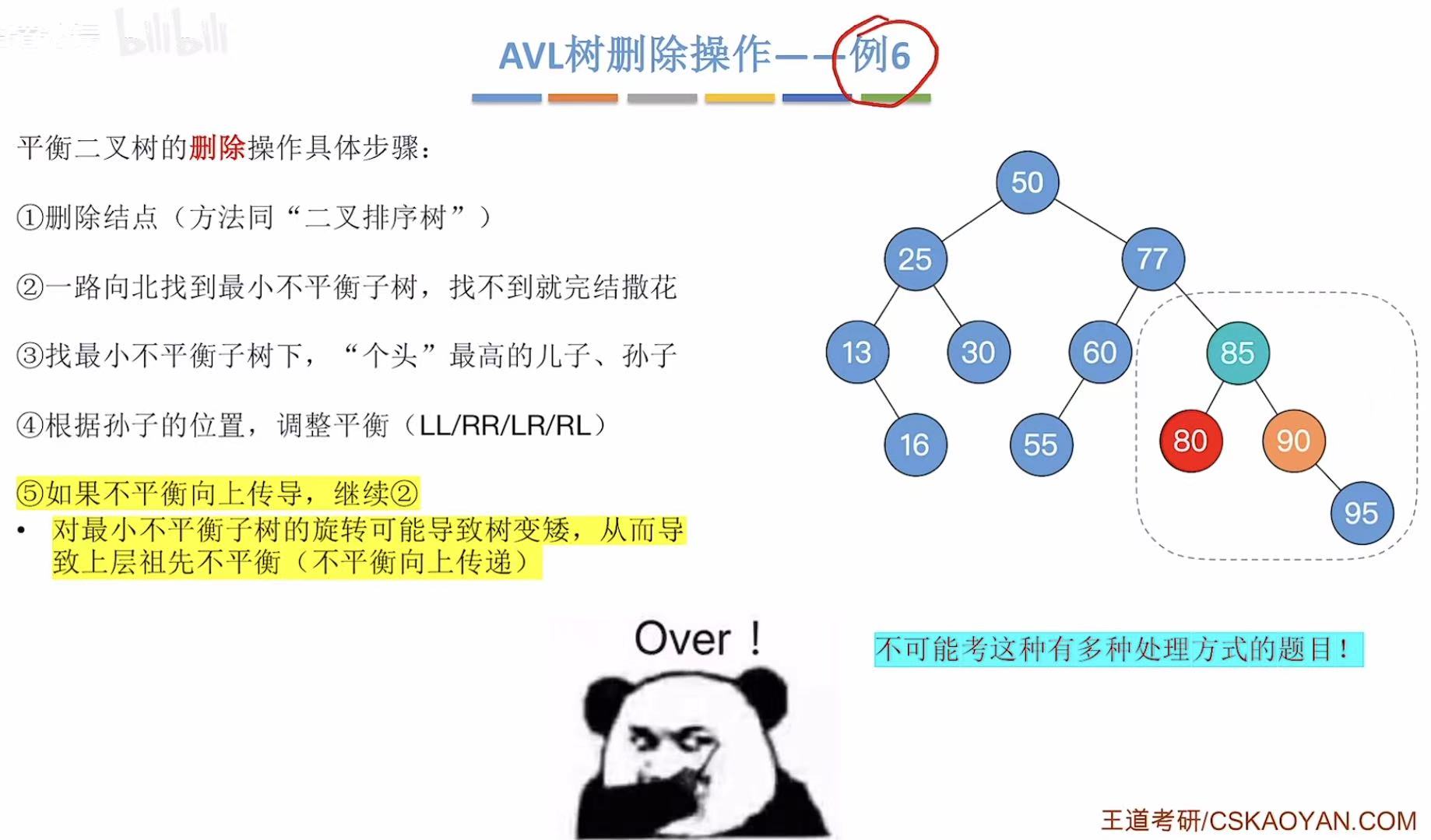
3. 小结

红黑树的定义和性质
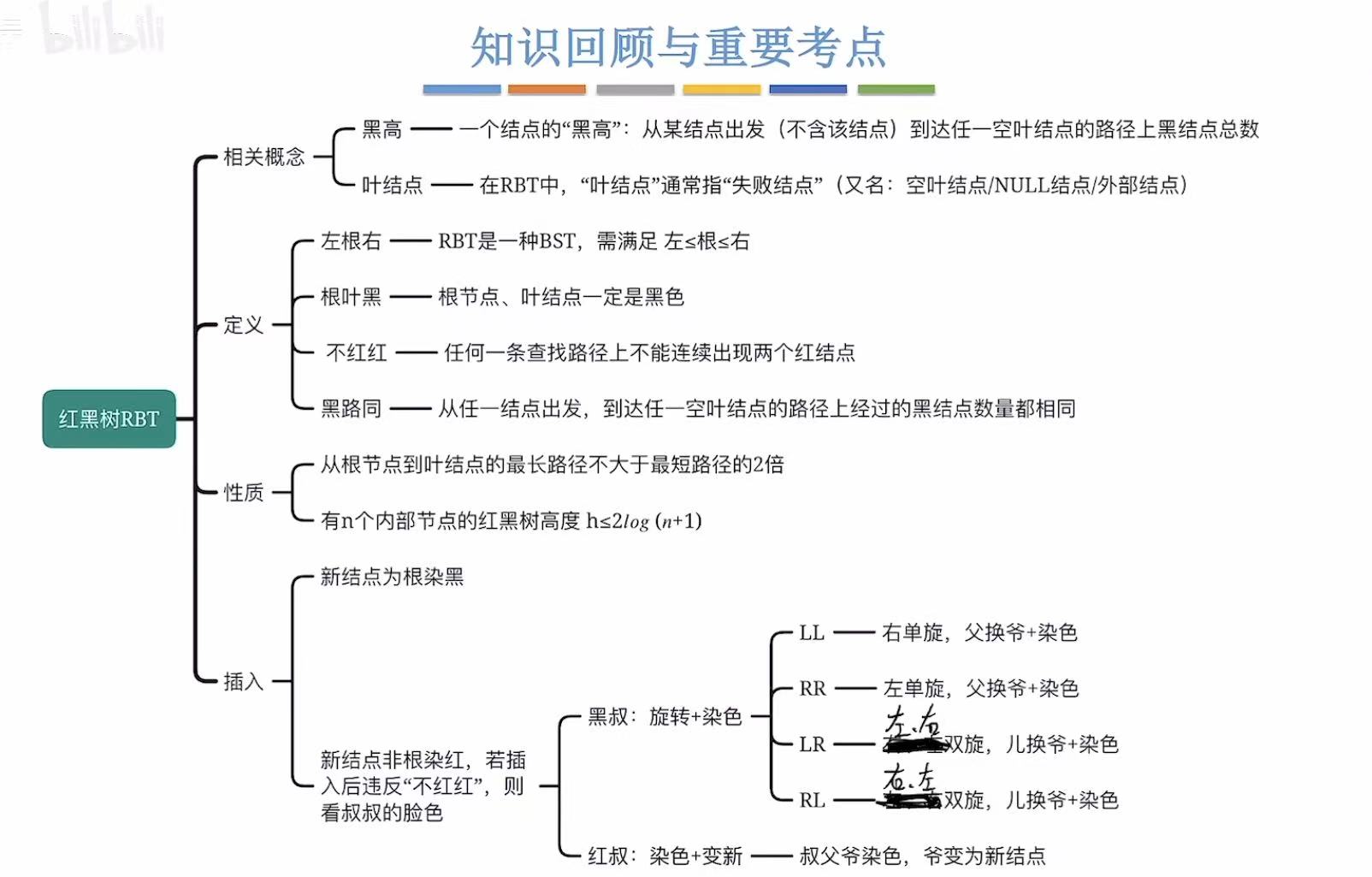
1. 定义
因为平衡二叉树插入删除都会影响平衡就需要调整树的形态,所以红黑树就出现了,因为红黑树在插入删除的时候不需要调整树的形态。
省流版 :平衡二叉树-->插入删除繁琐;红黑树-->插入删除简单。
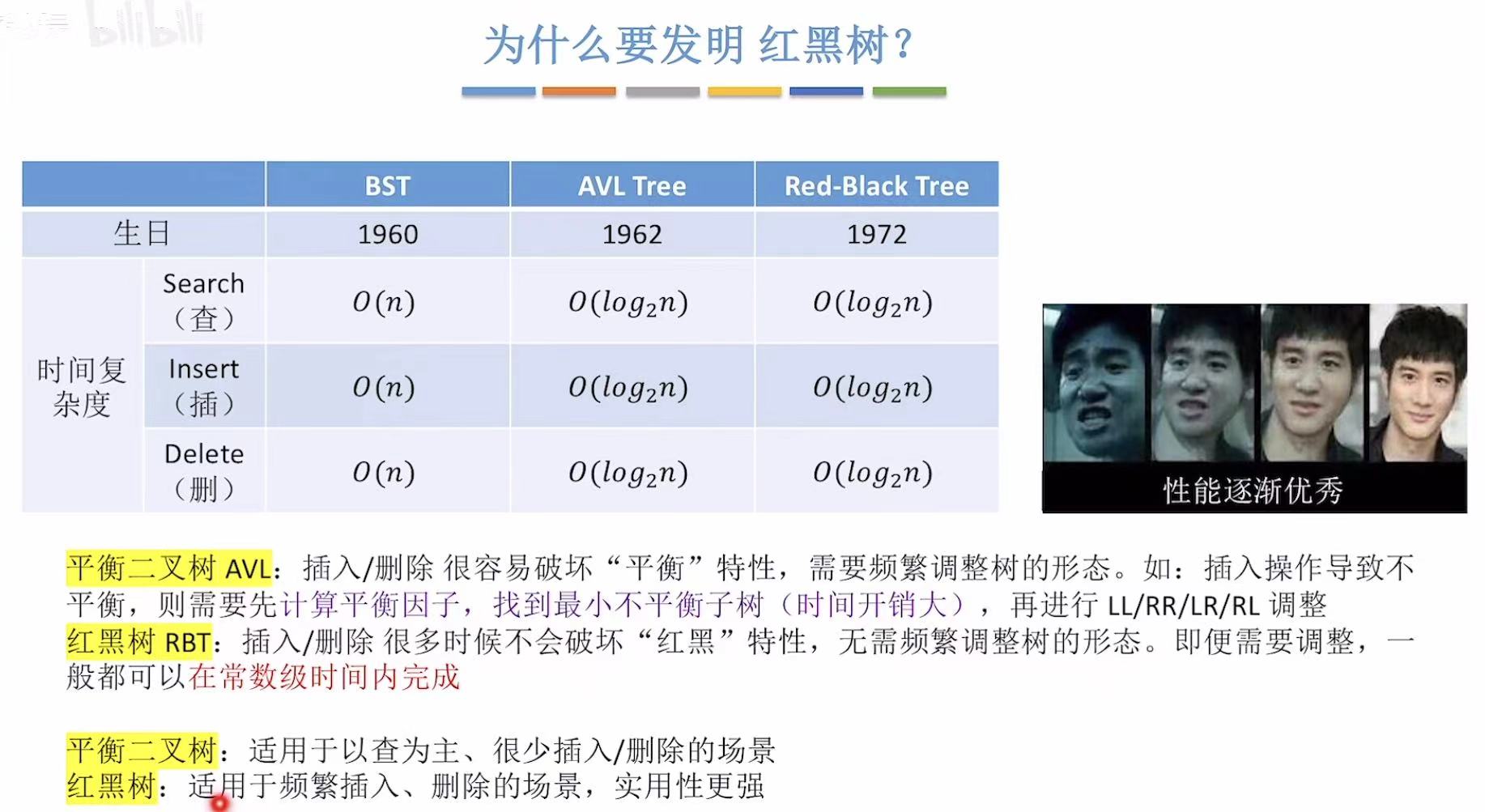

其实就是从根节点开始,一层红一层黑,依次往下。
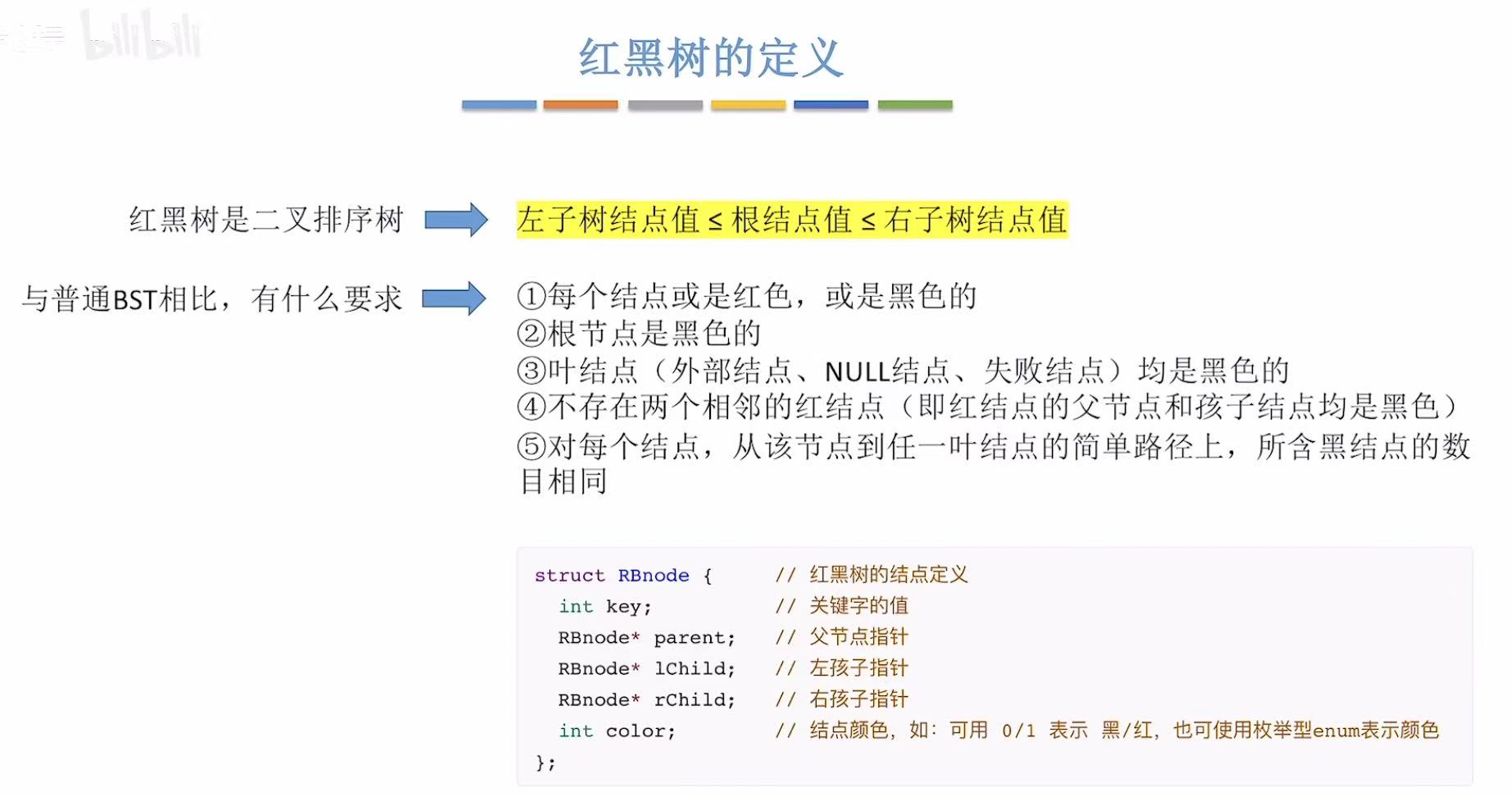
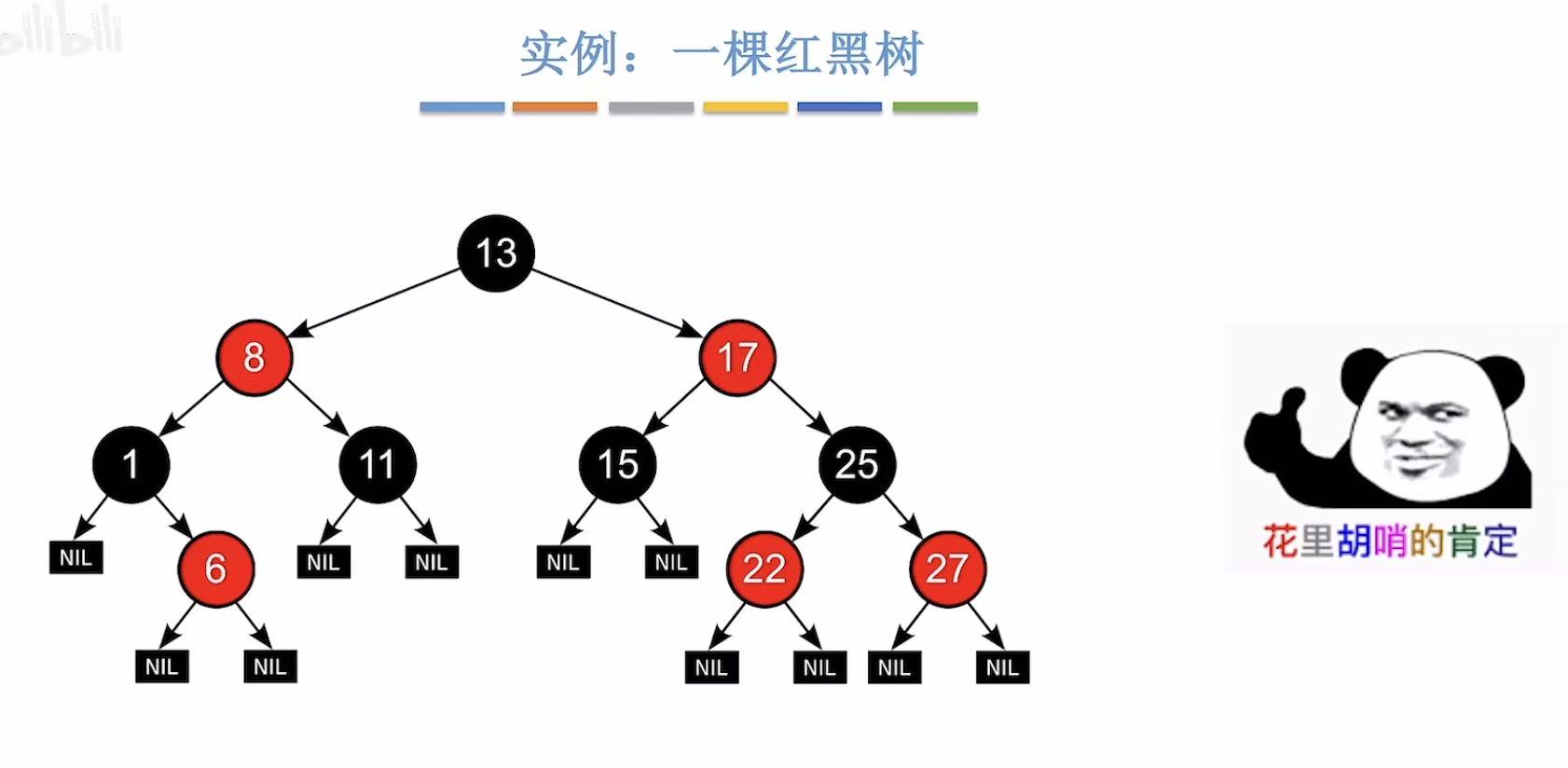
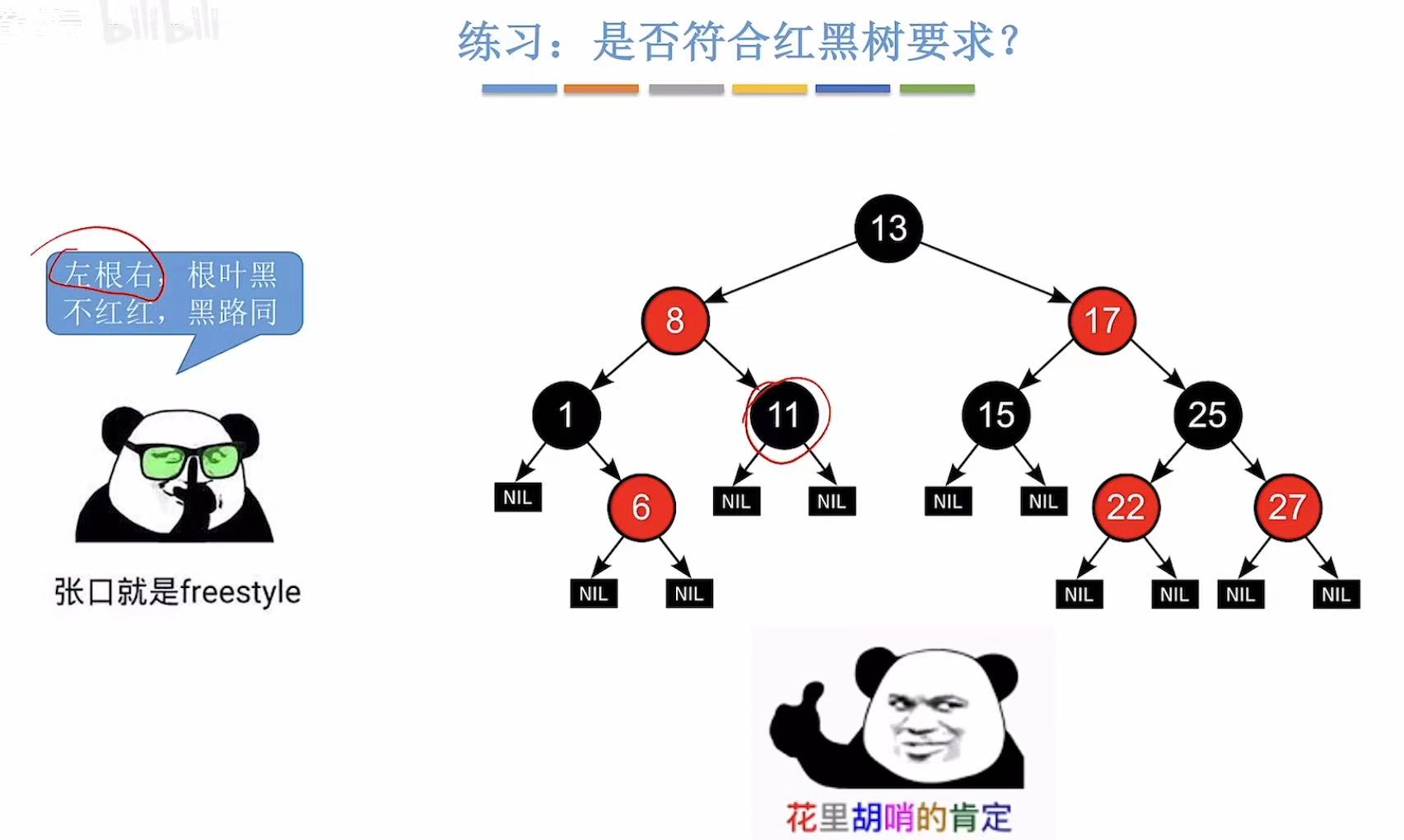
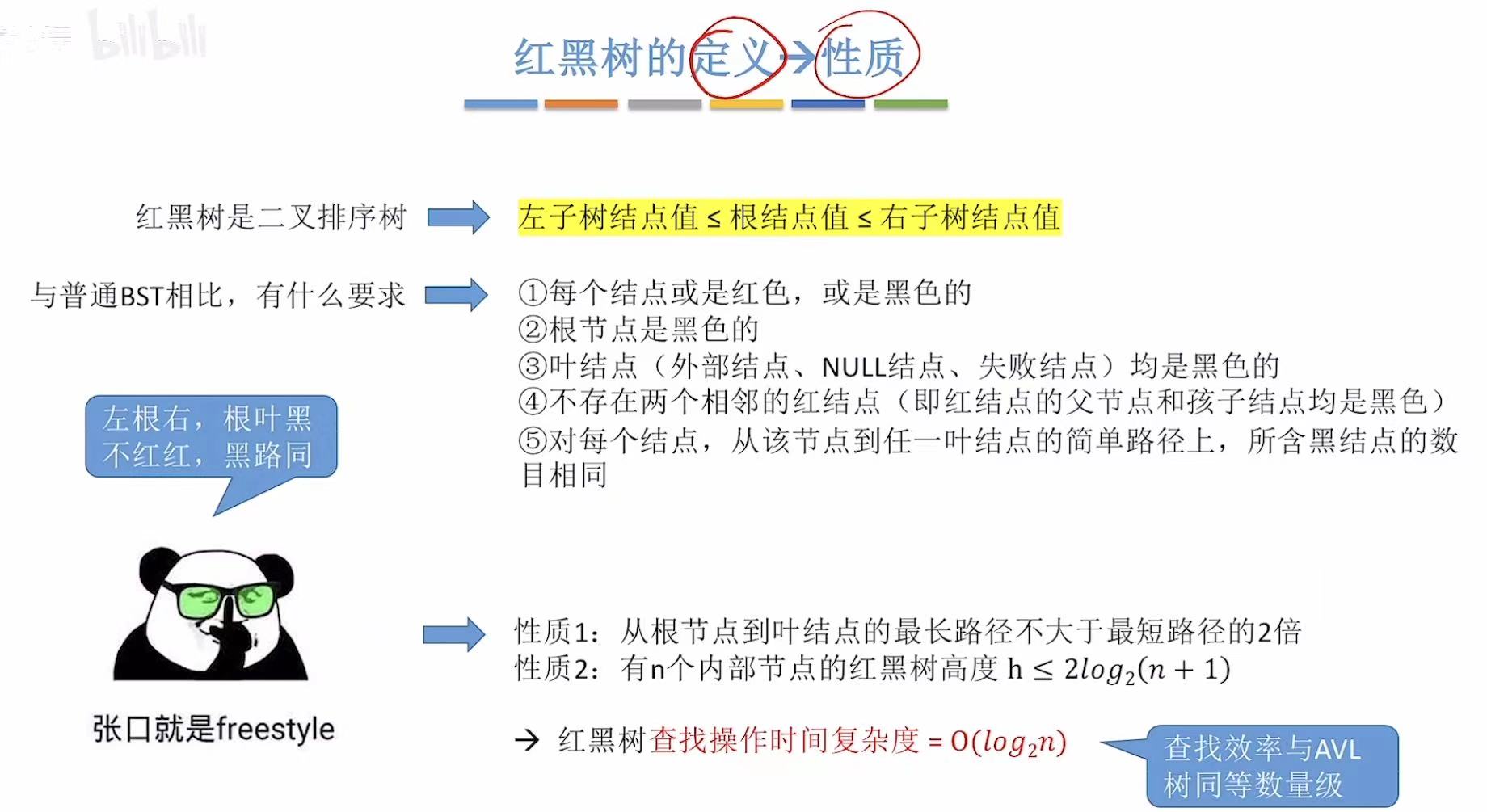
- 左根右:值从小往大
- 根叶黑:根节点和叶子节点是黑色的
- 不红红:红色不会和红色连在一起
- 黑路同 :到达一个结点,经过的黑色结点数量都是相同的。

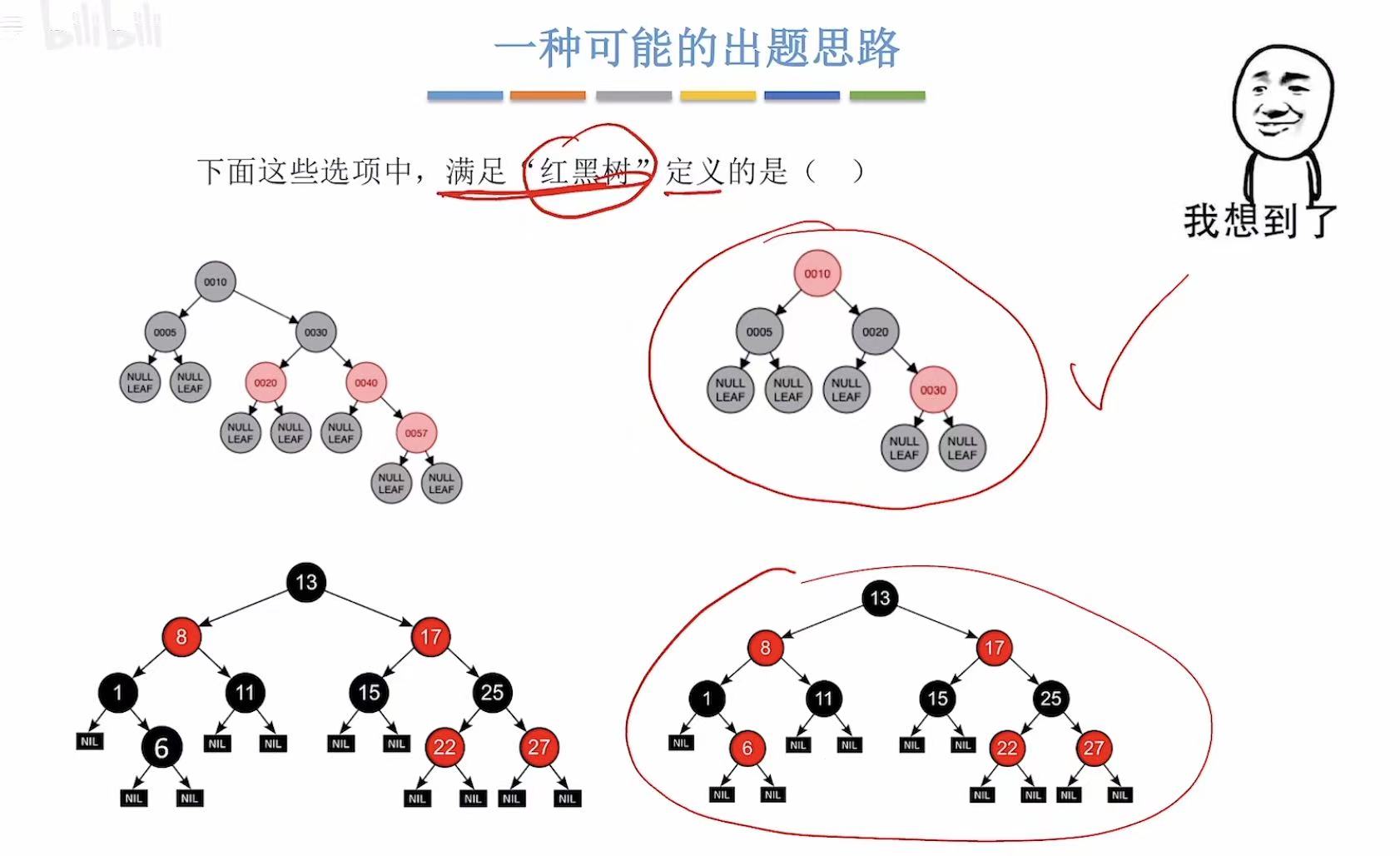
2. 练习:是否符合红黑树要求?
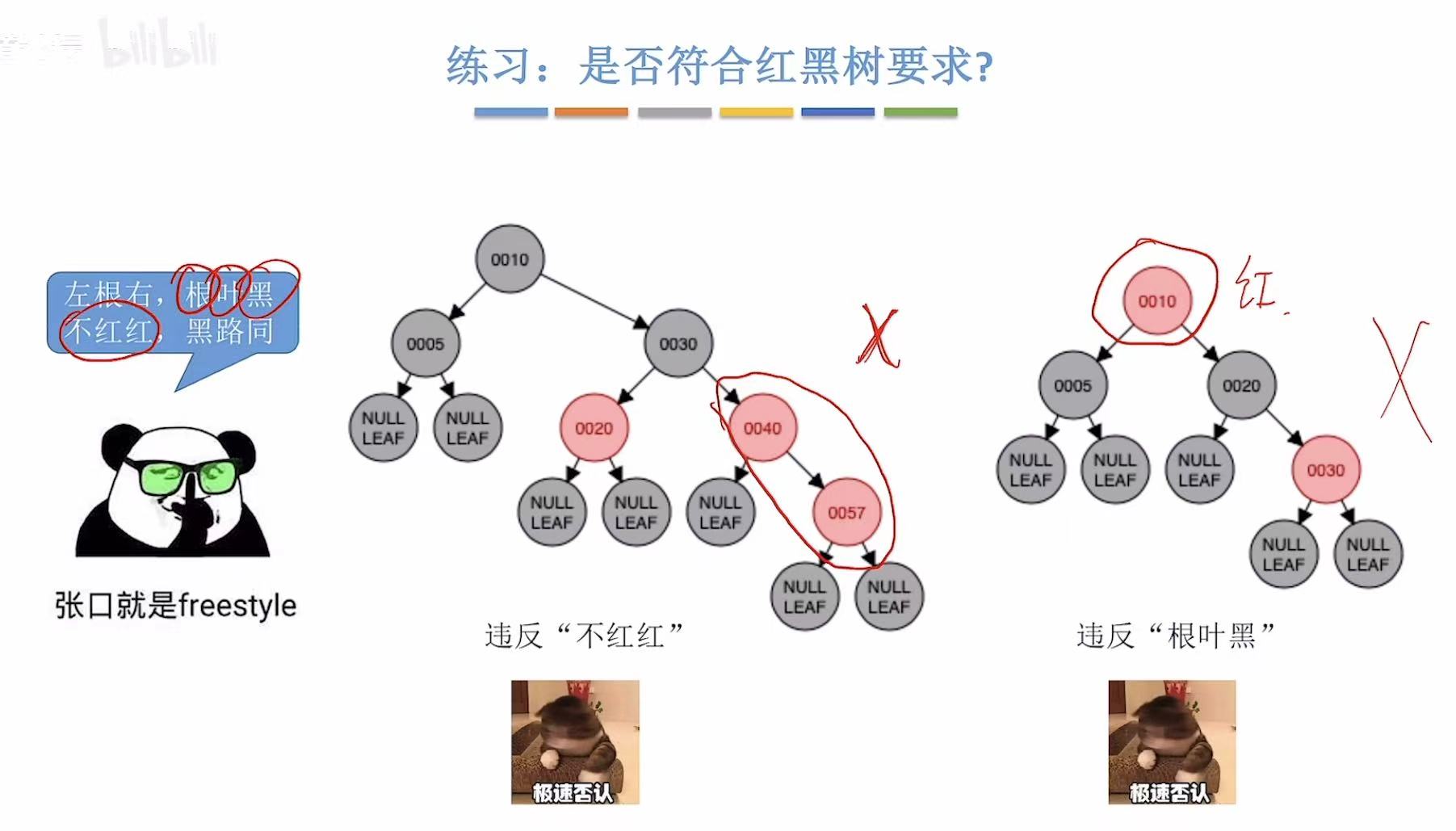
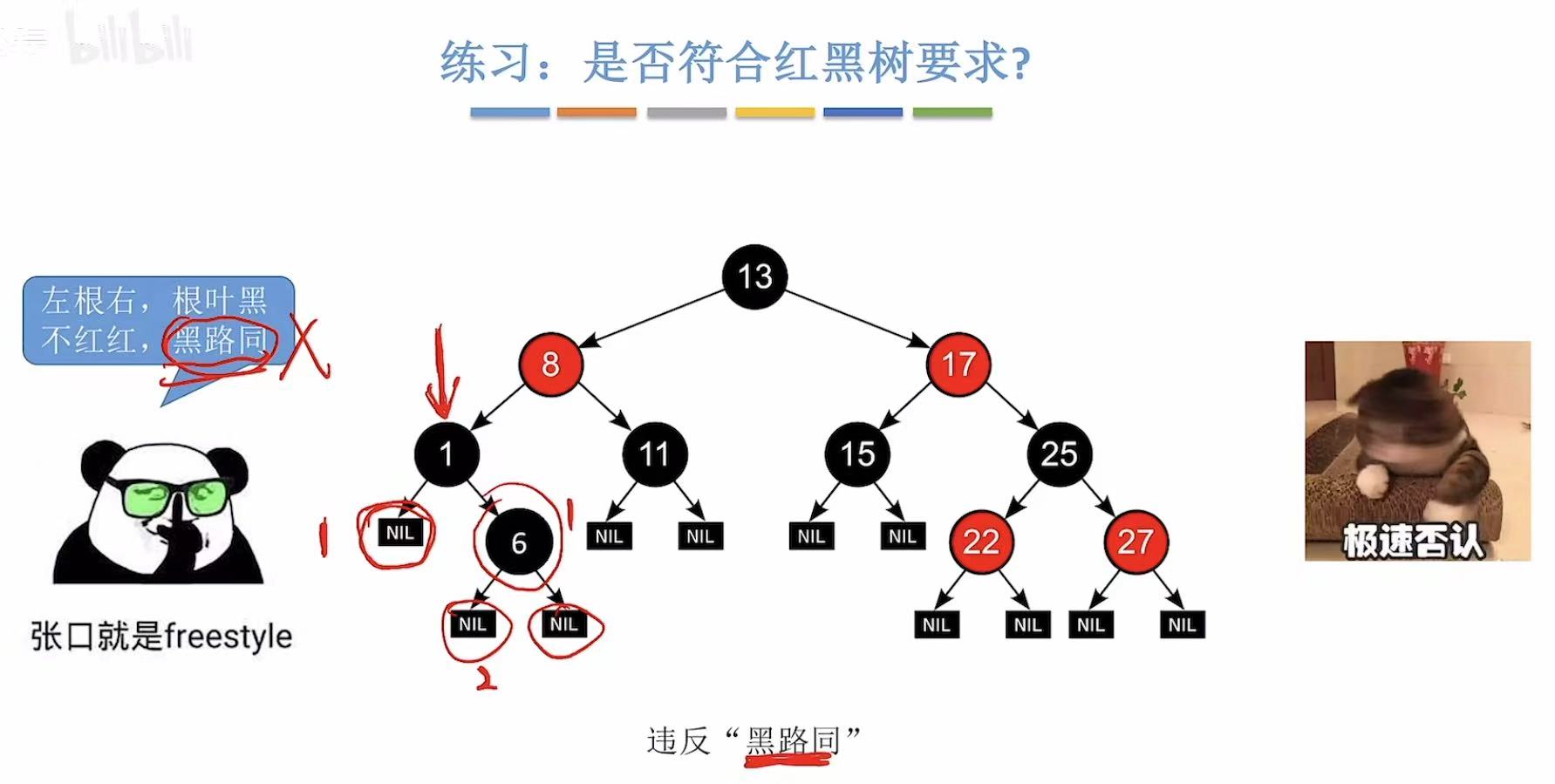
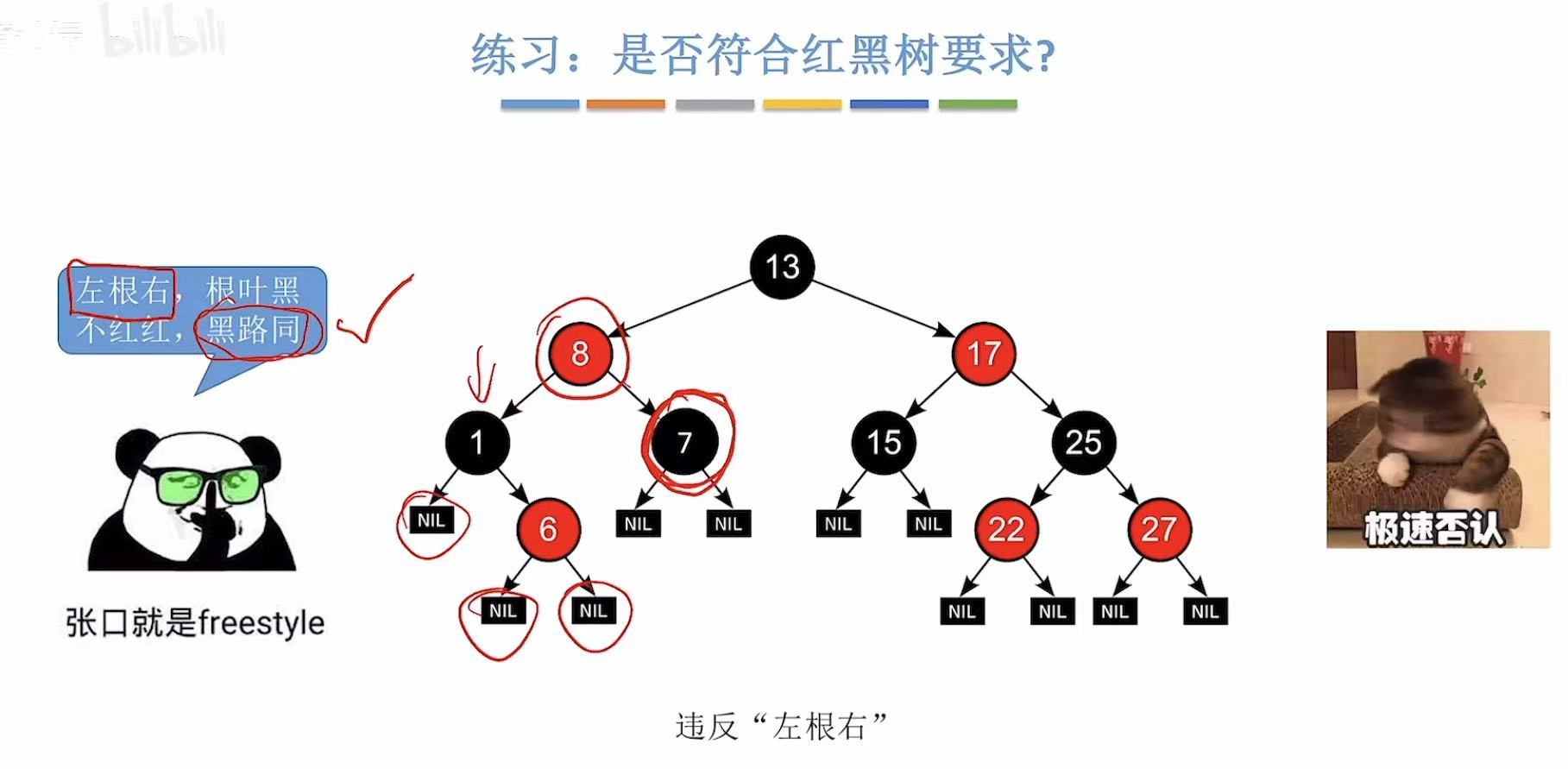
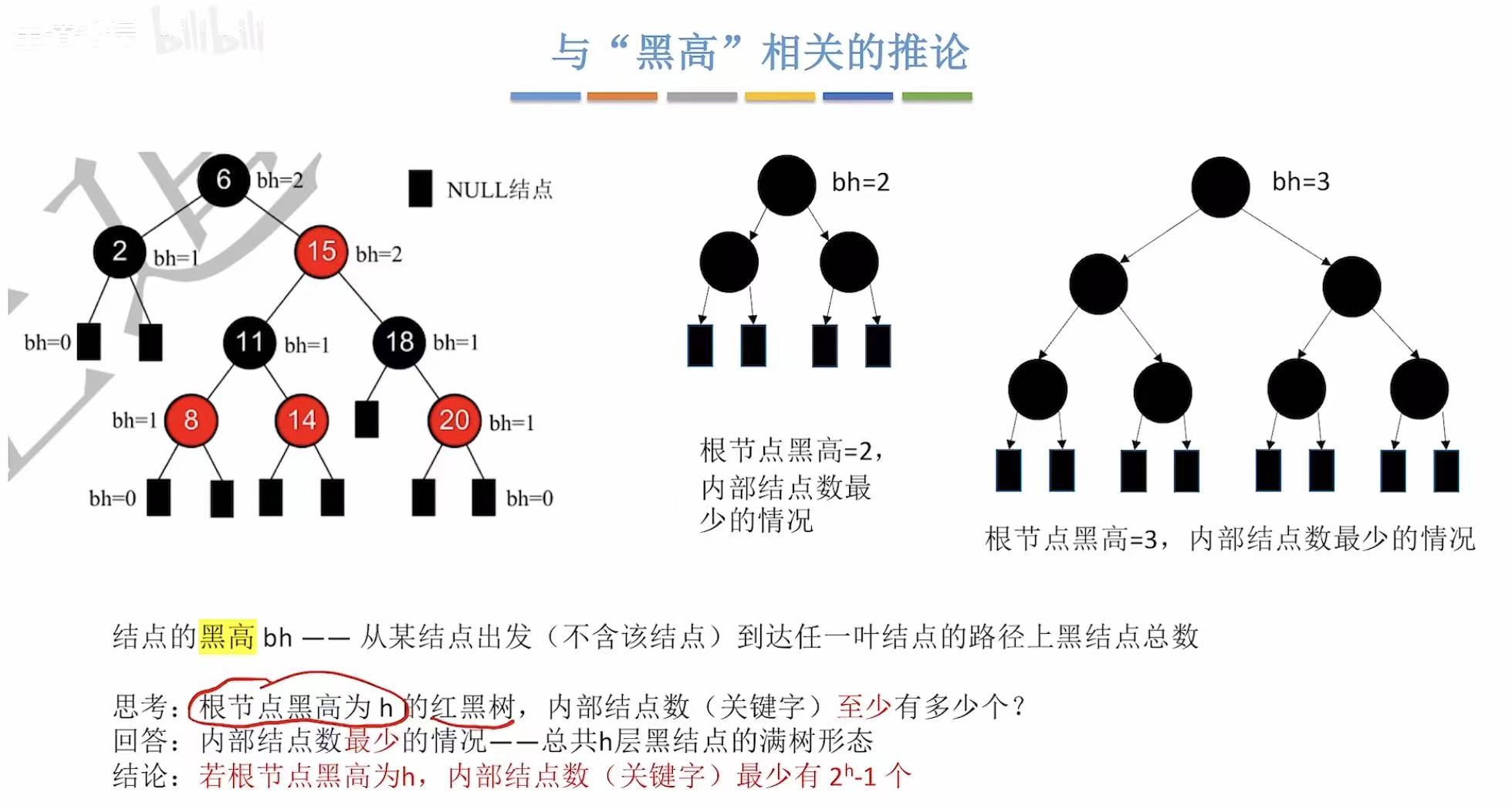
3. 黑高
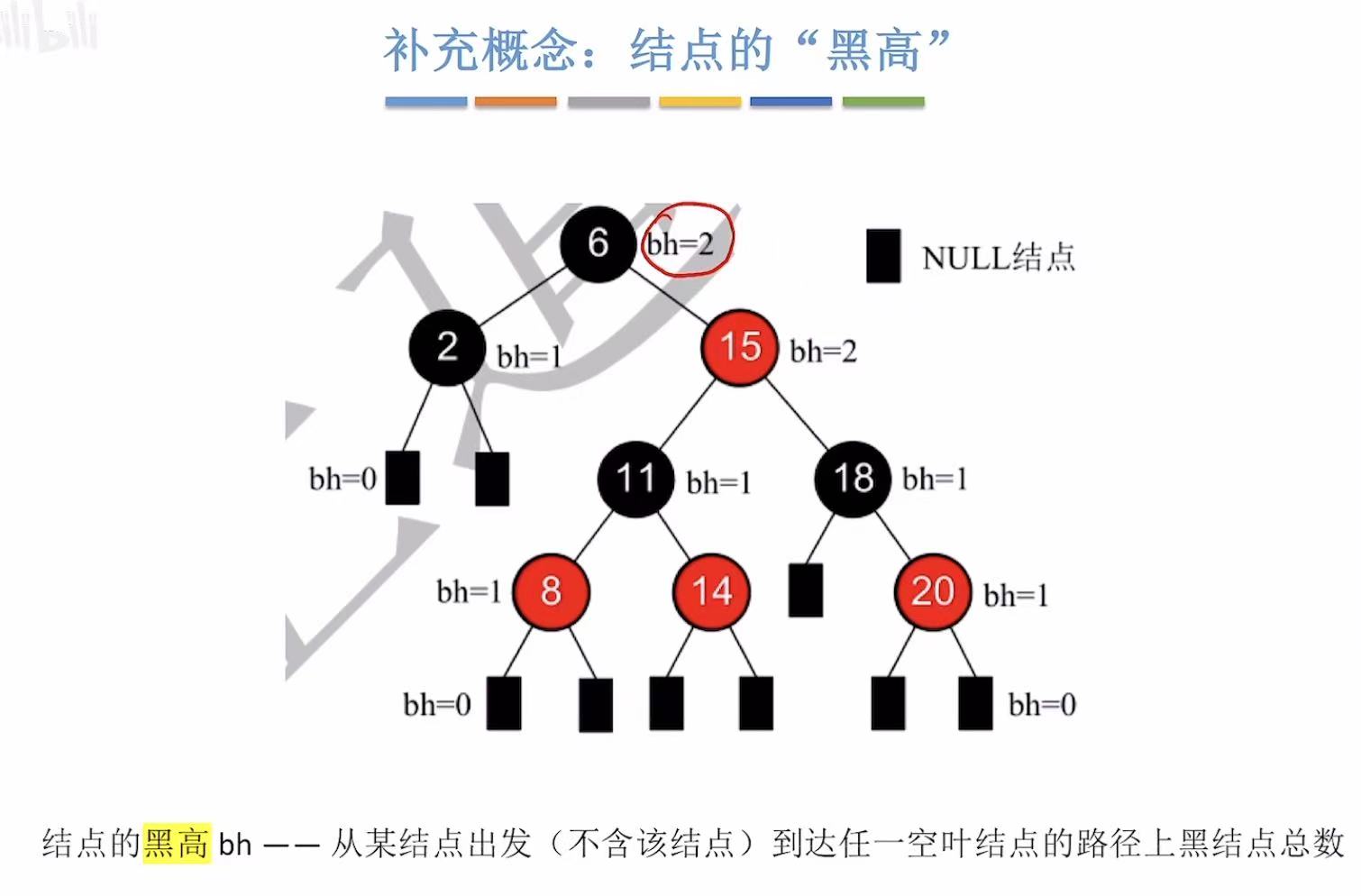
- 6~2下面的空叶子节点:经过6、2,所以bh=2
- 2~自己下面的空叶子节点:经过2.所以bh=1
- 2下面的空叶子结点~自己本身:没经过任何结点,所以bh=0
4. 性质
5. 查找
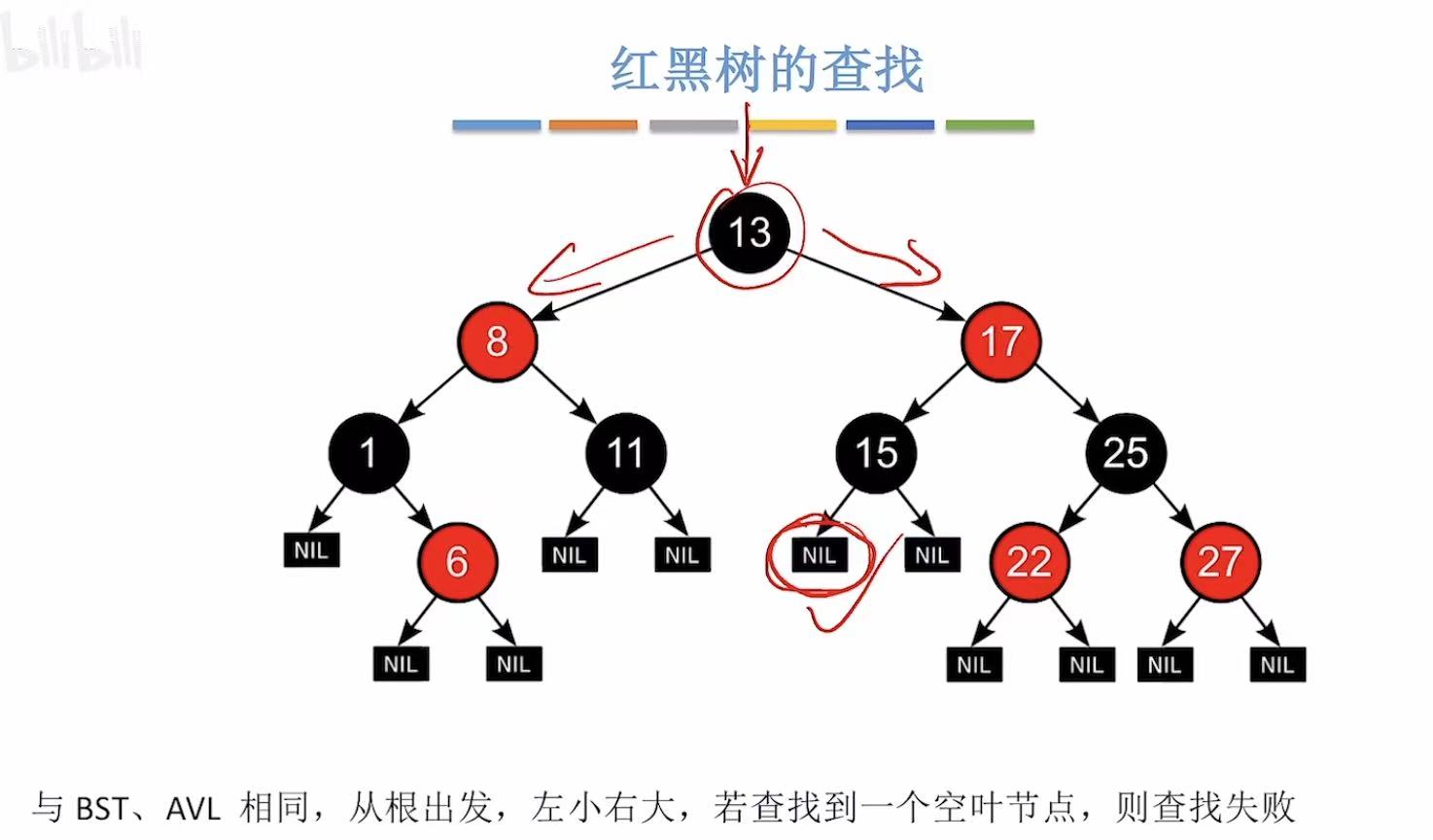
红黑树的插入
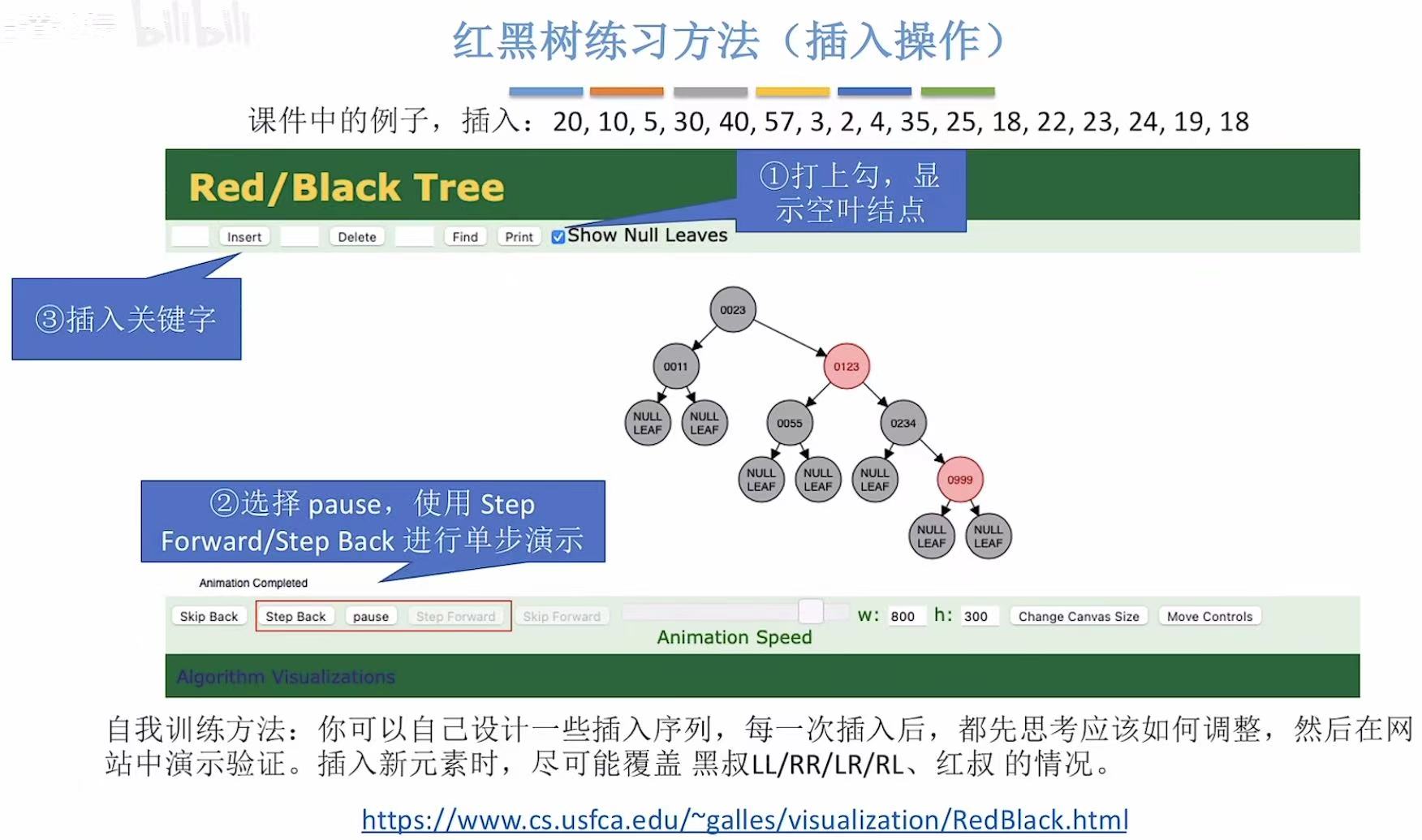
1. 概述
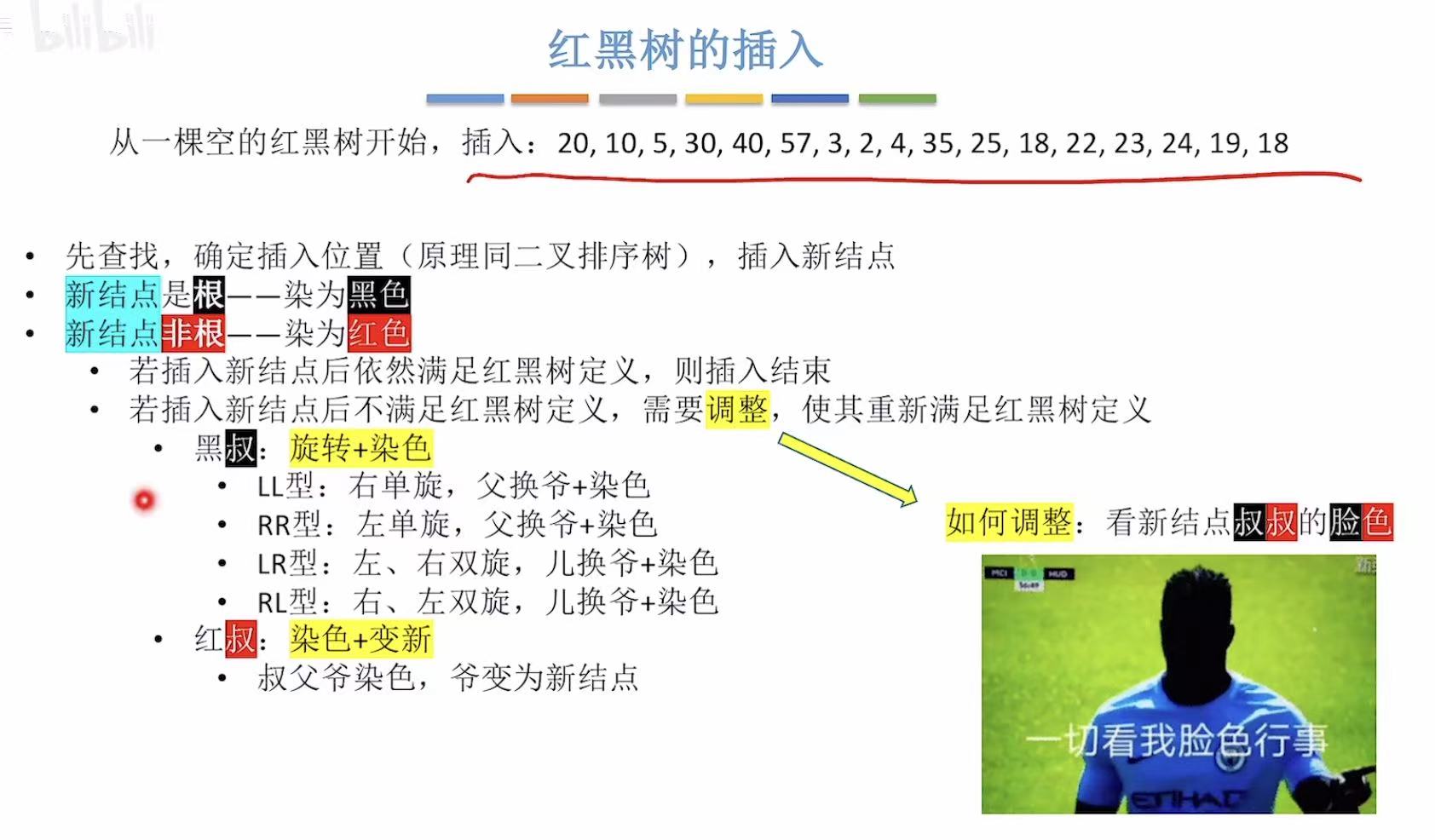
2. 练习
- 添加20:根节点,为黑色
- 添加10:非根,为红色
- 添加5:非根,为红色-->违反不红红-->黑叔-->LL型-->旋转+染色
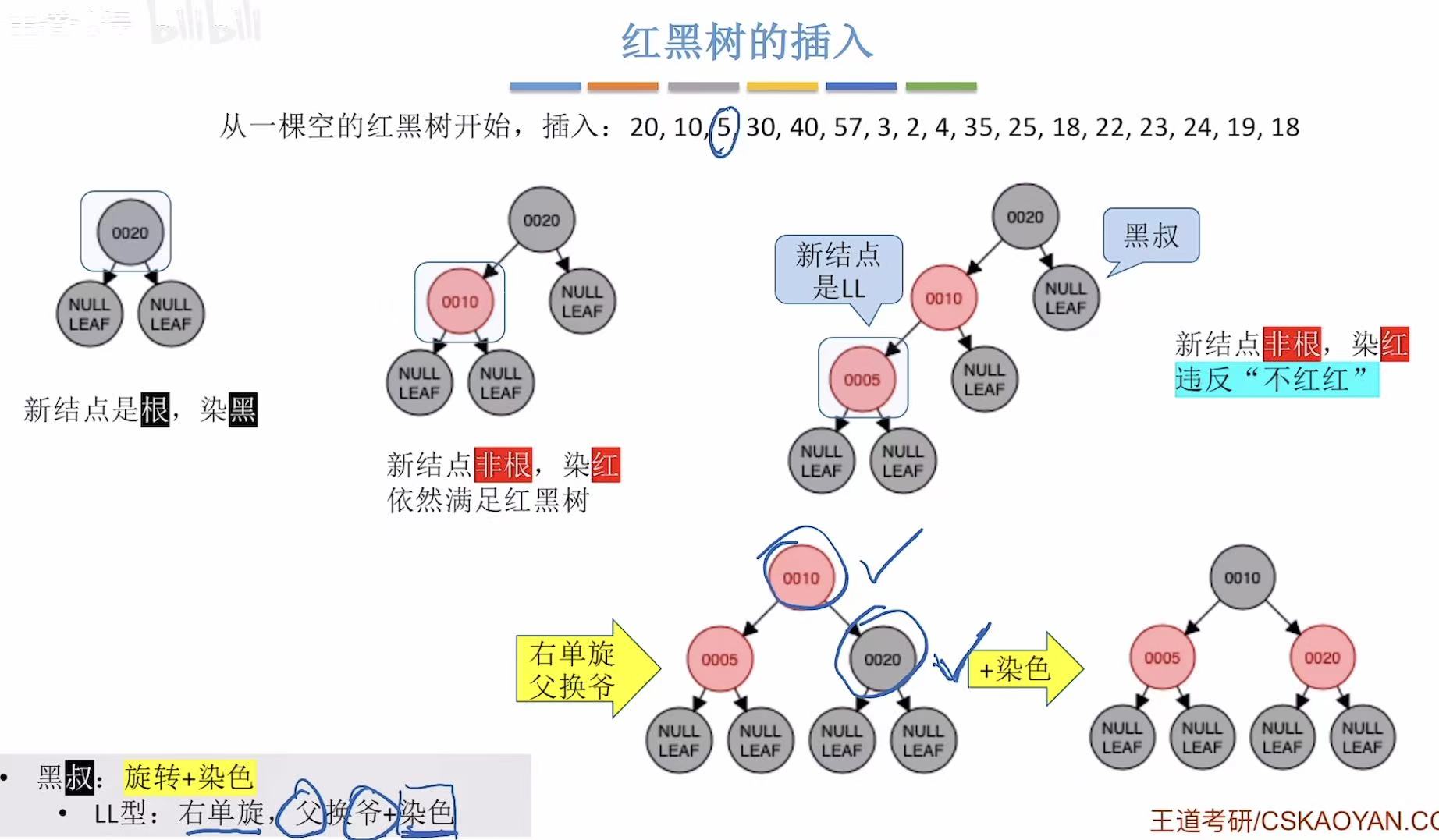
- 添加30:非根,为红色-->违反不红红-->红叔-->染色+变新
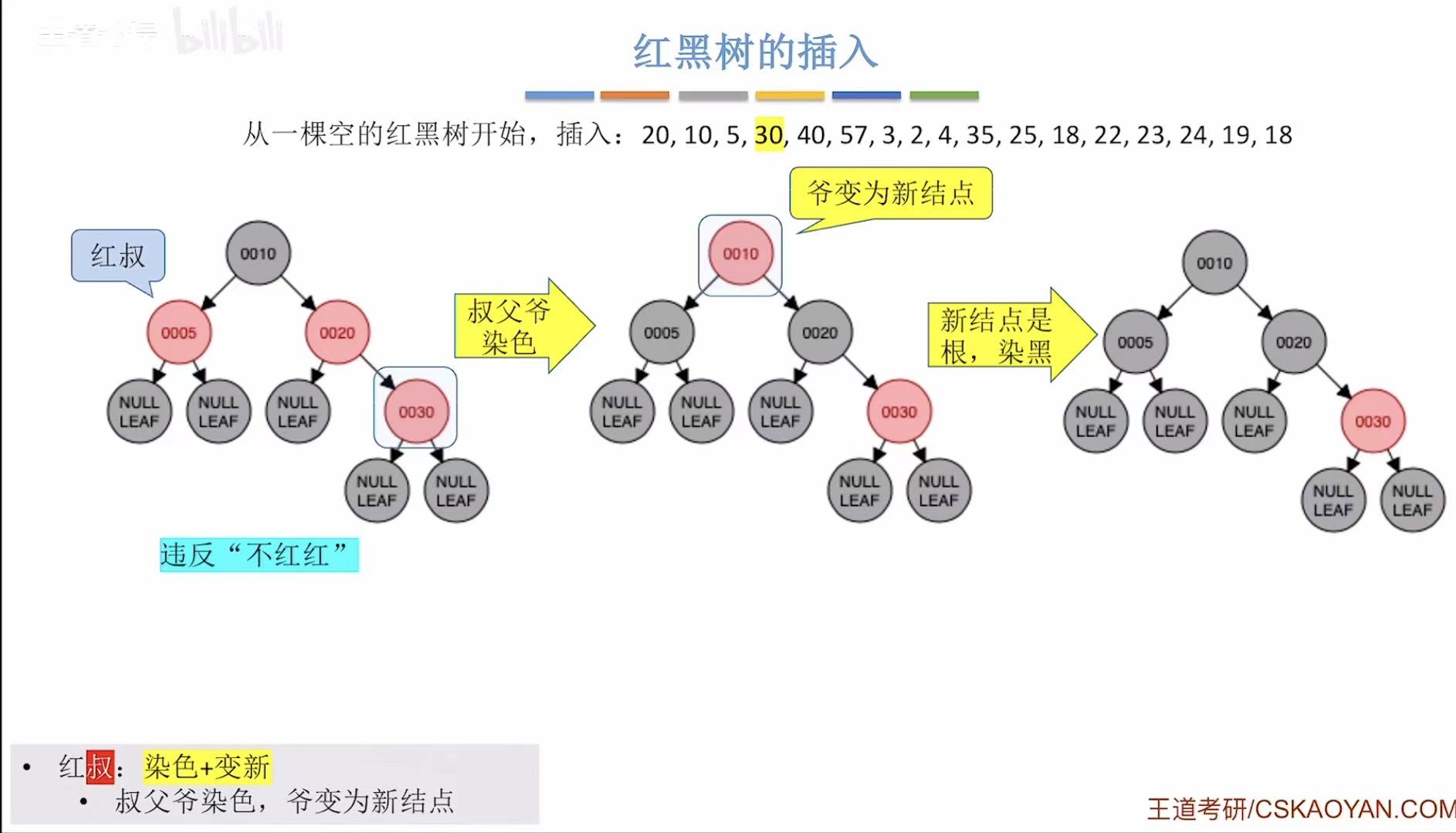
- 添加40:非根,为红色-->违反不红红-->黑叔-->RR型-->旋转+染色
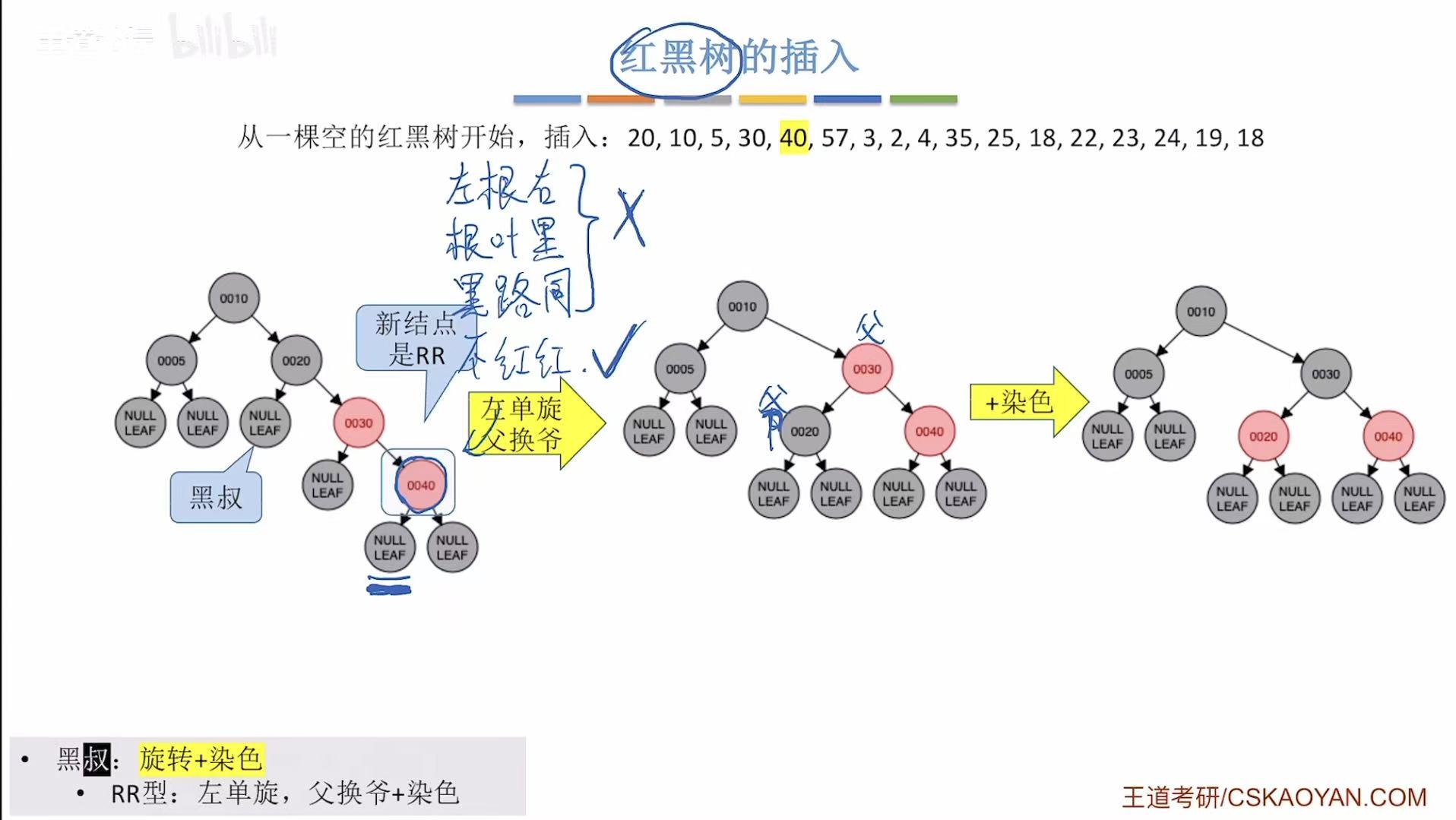
- 添加57:非根,为红色-->违反不红红-->红叔-->染色+变新
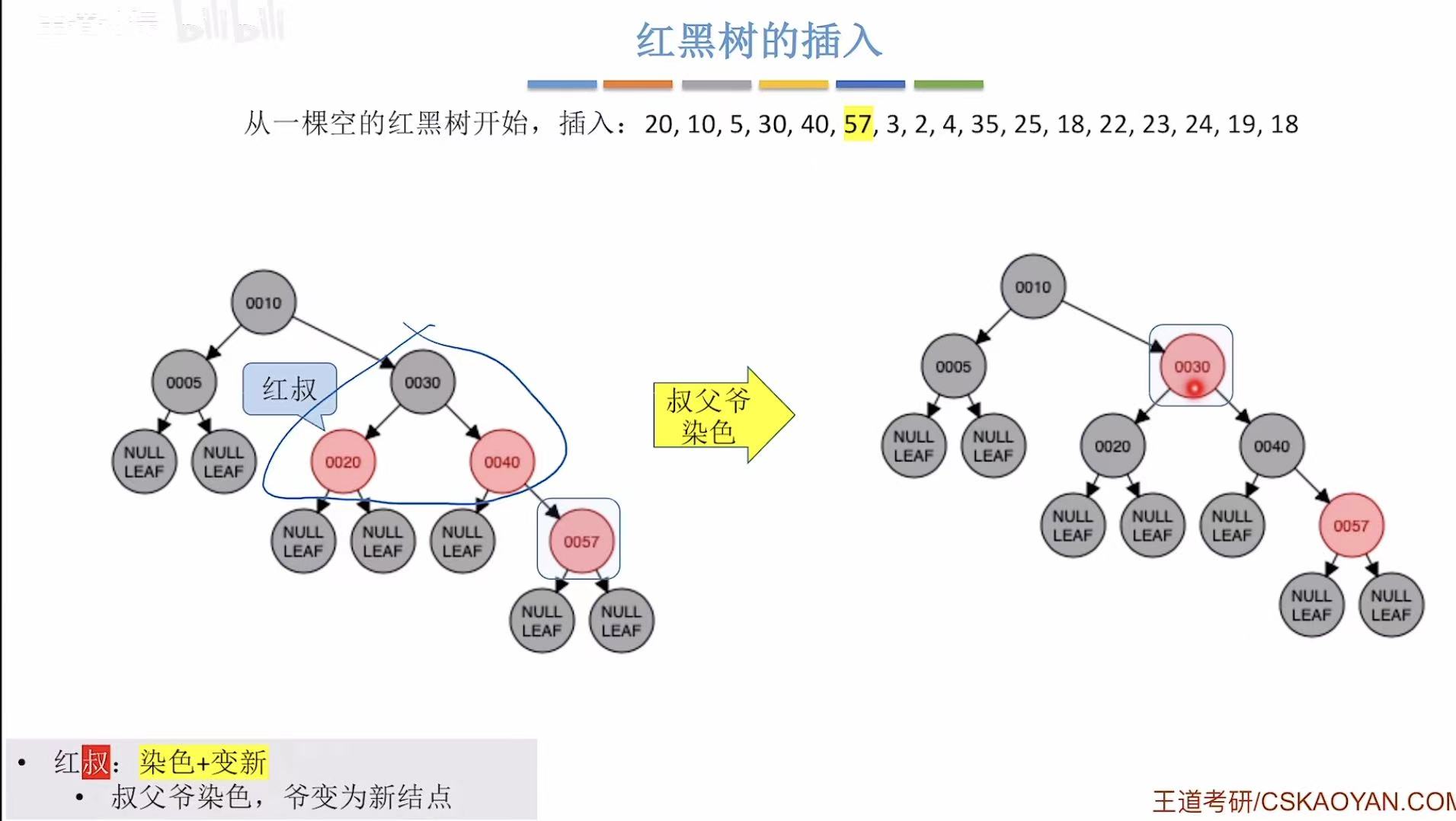
- 添加3:非根,为红色
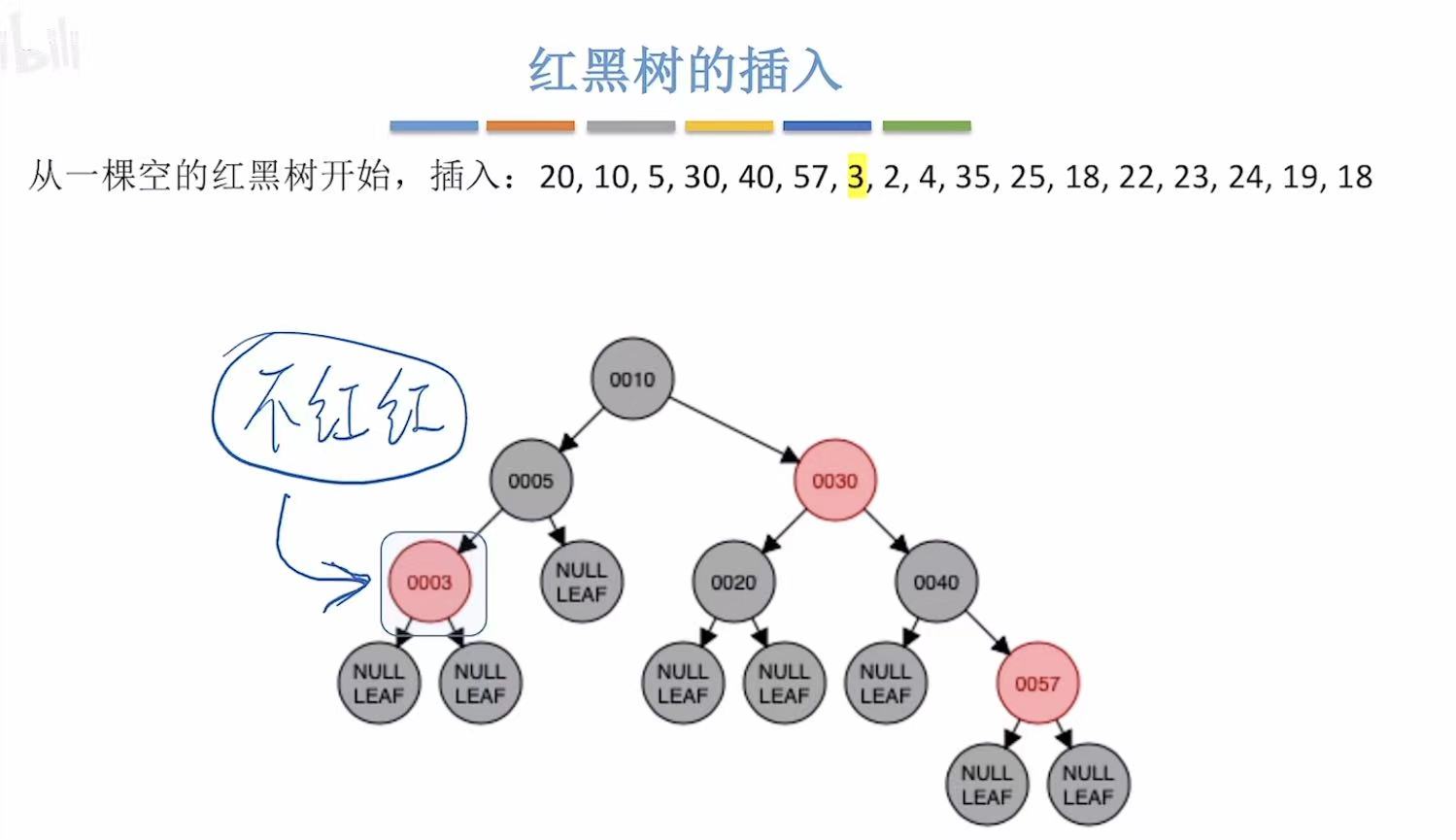
- 添加2:非根,为红色-->违反不红红-->黑叔-->LL型-->旋转+染色
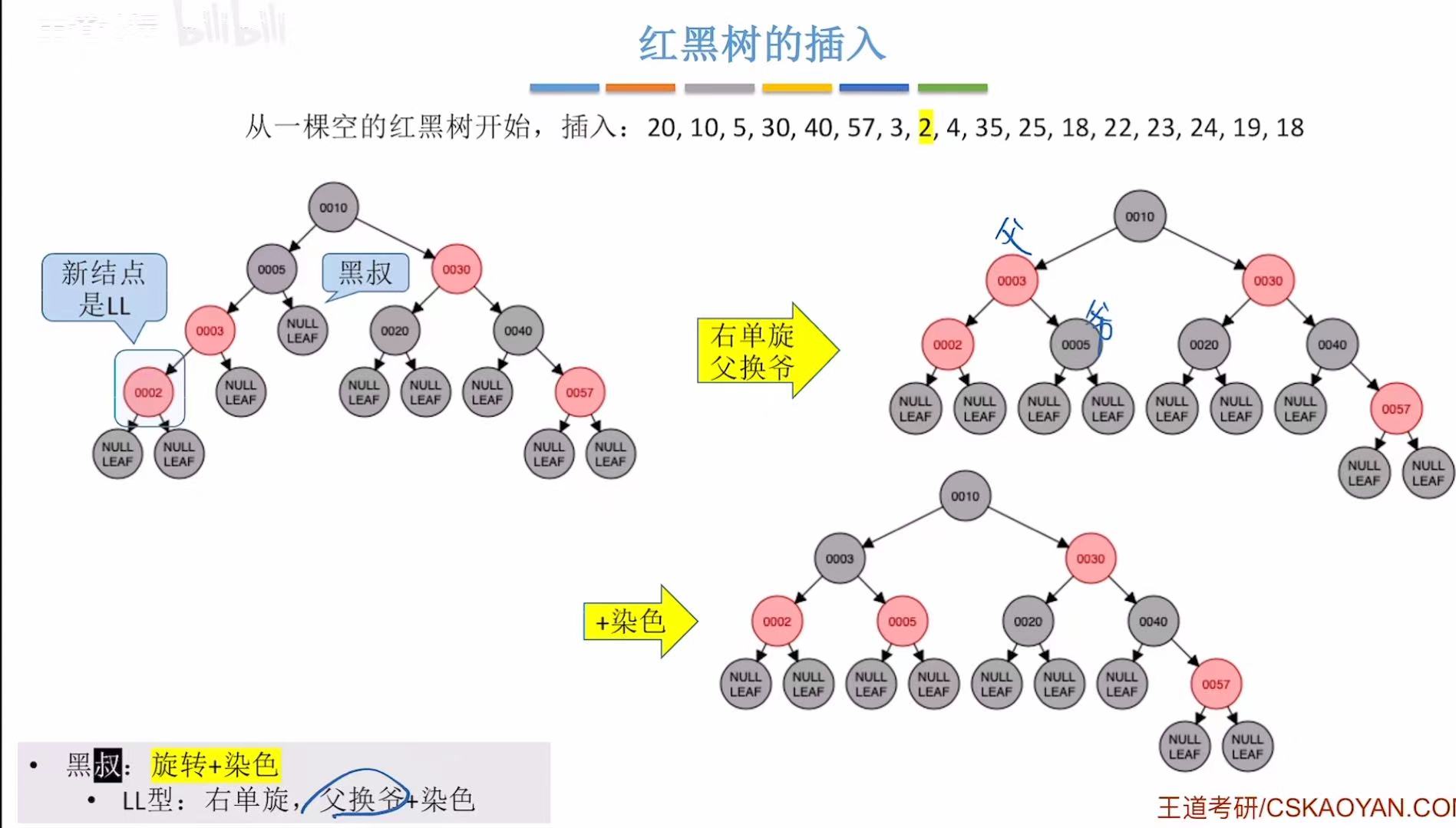
- 添加4:非根,为红色-->违反不红红-->红叔-->染色+变新
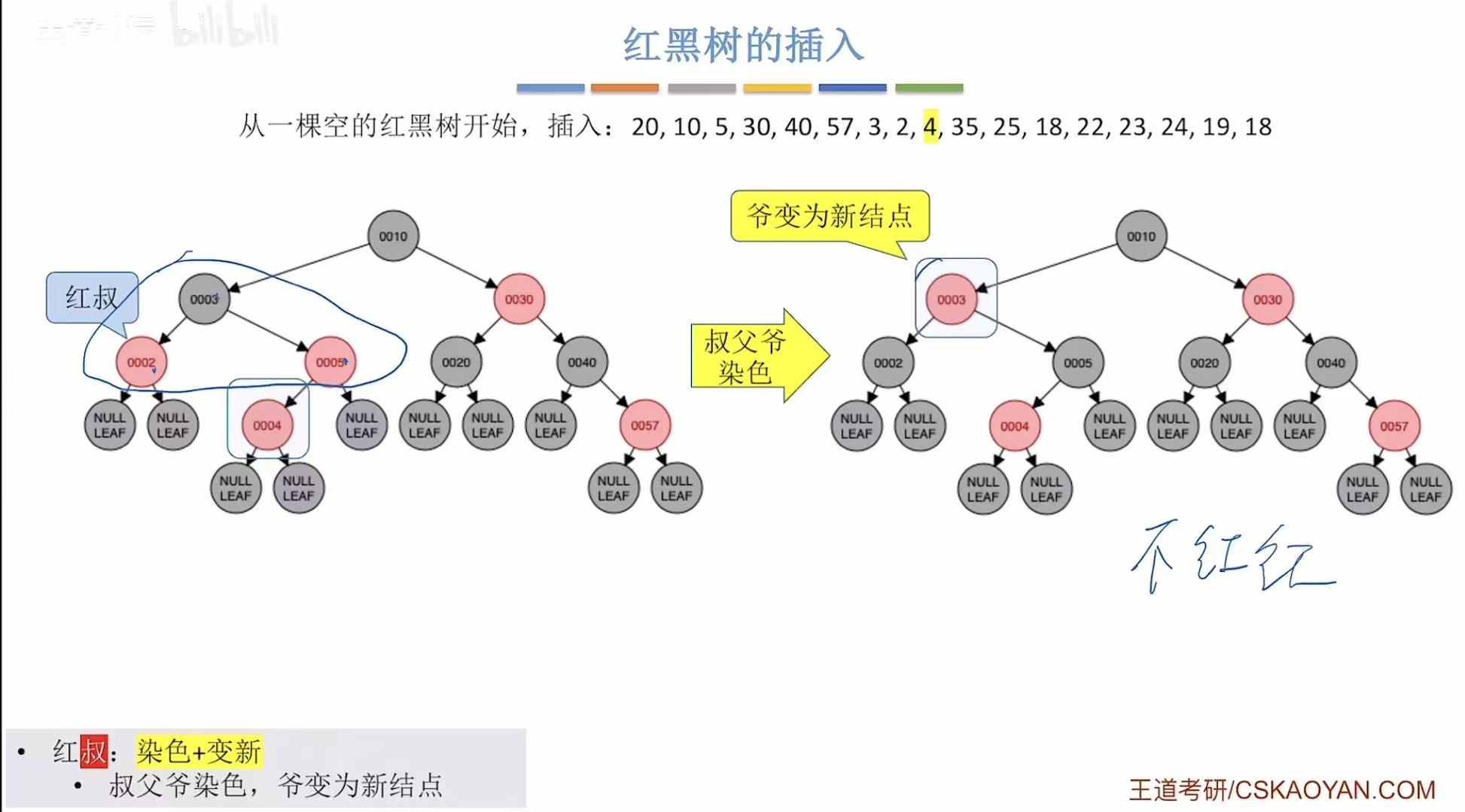
- 添加35:非根,为红色
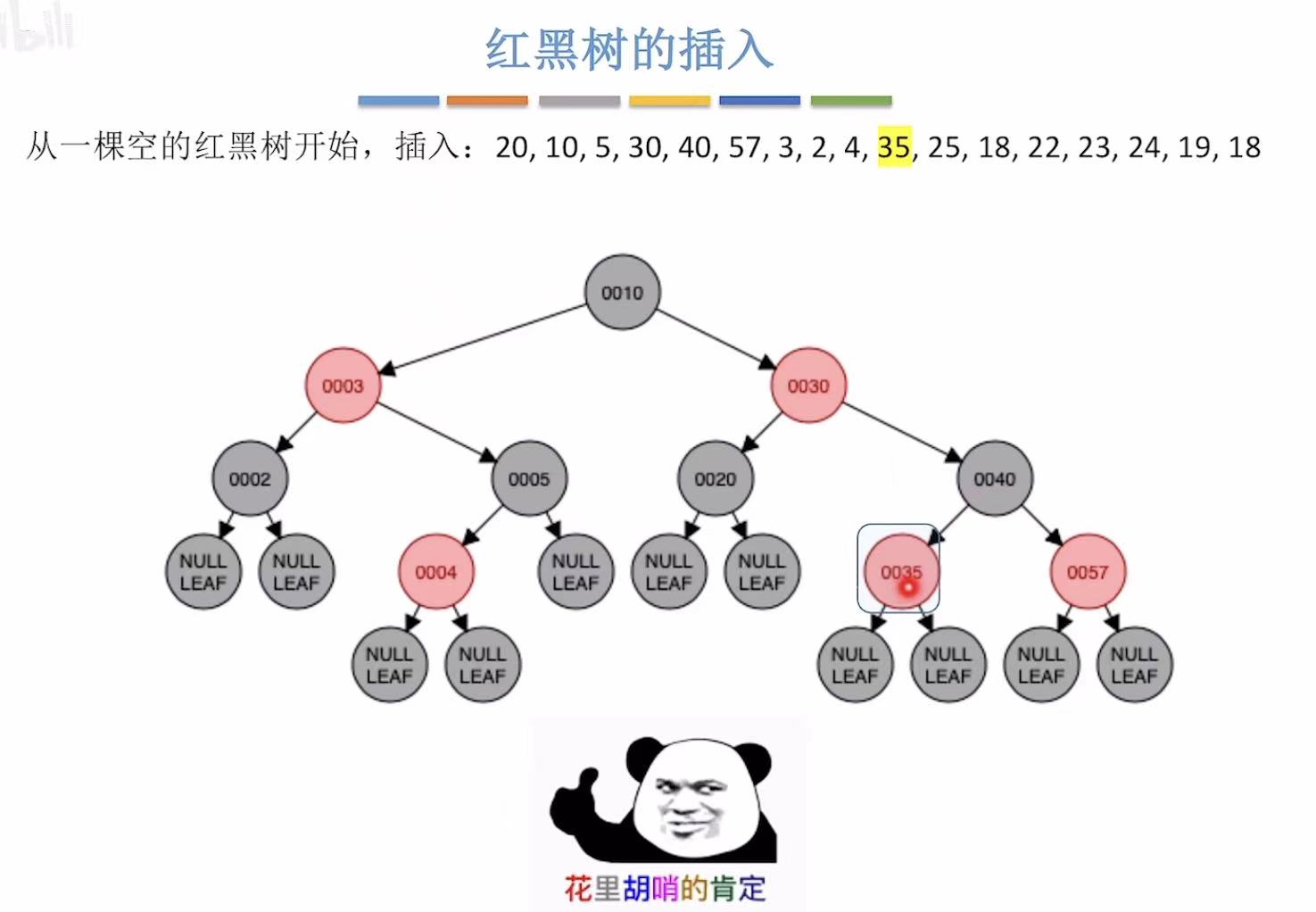
- 添加25:非根,为红色
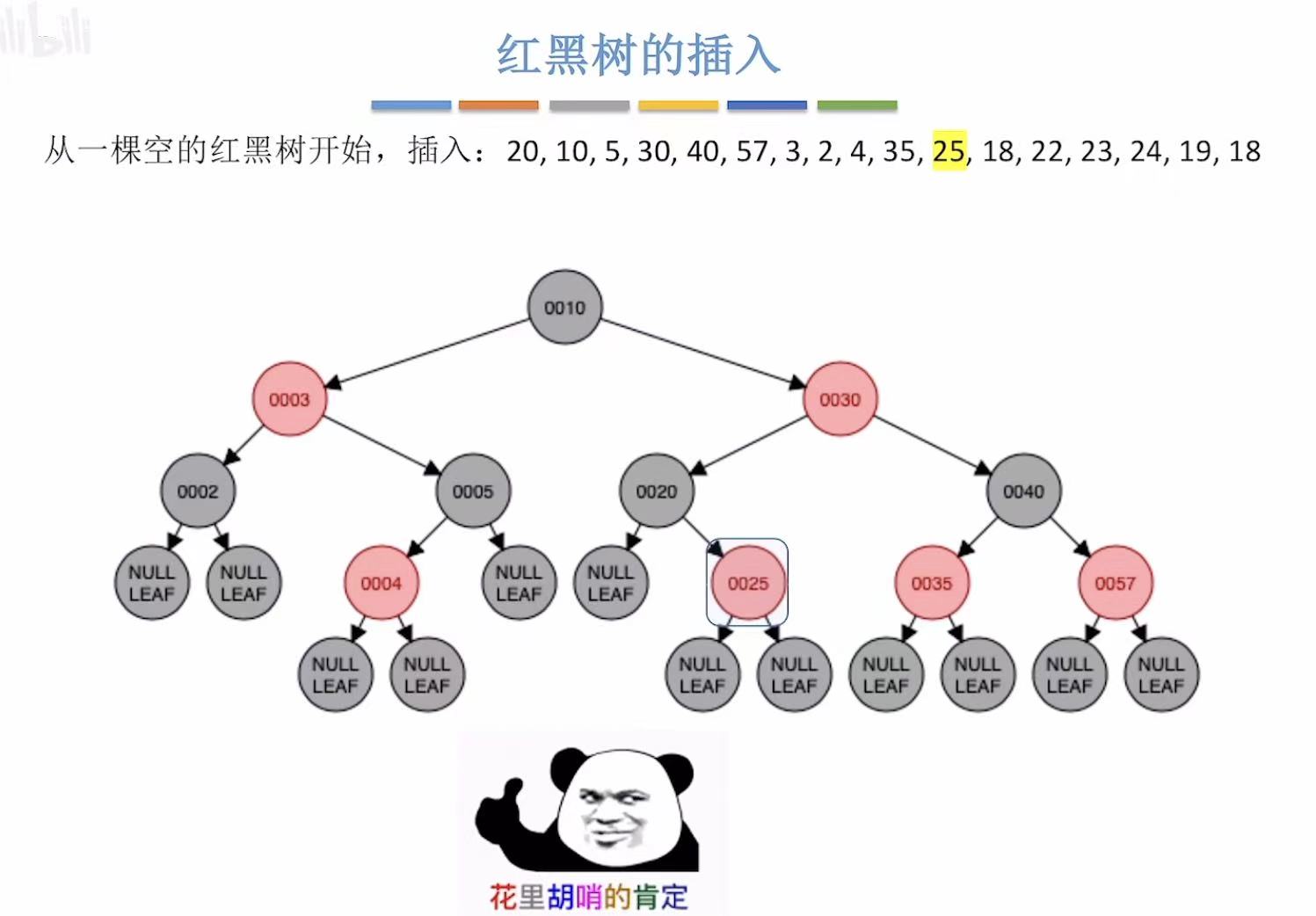
- 添加18:非根,为红色
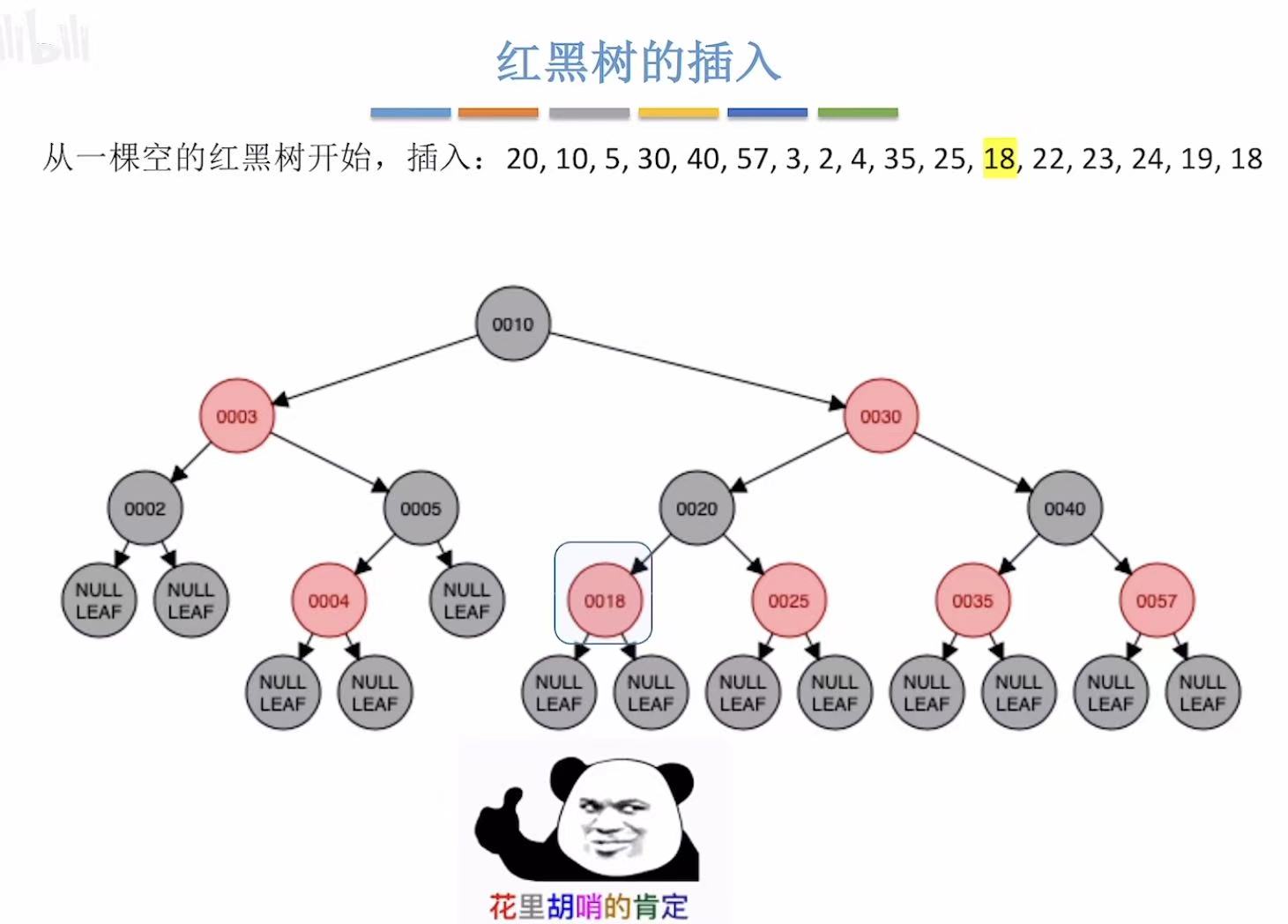
- 添加22:非根,为红色-->违反不红红-->红叔-->染色+变新
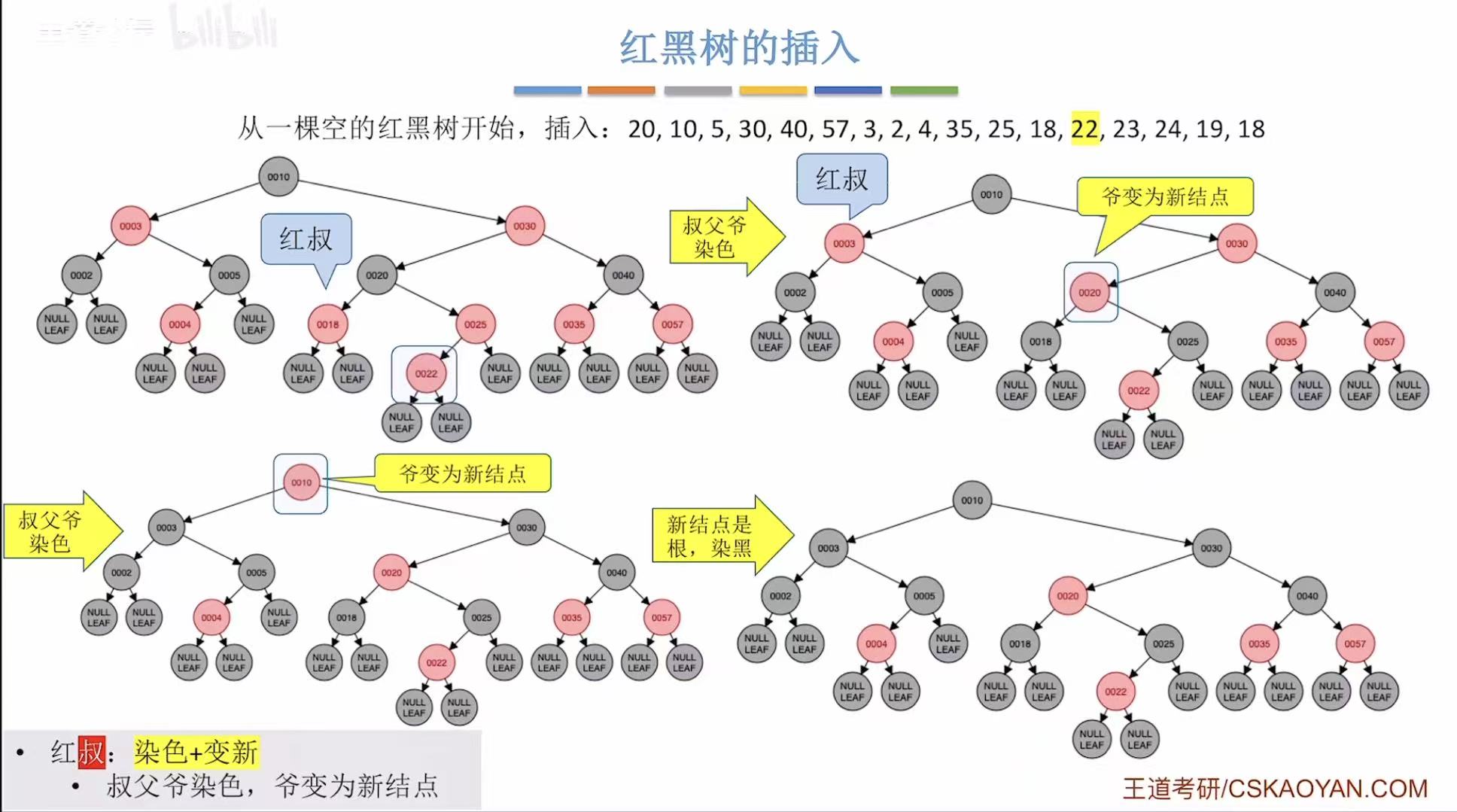
- 添加23:非根,为红色-->违反不红红-->黑叔-->LR型-->旋转+染色
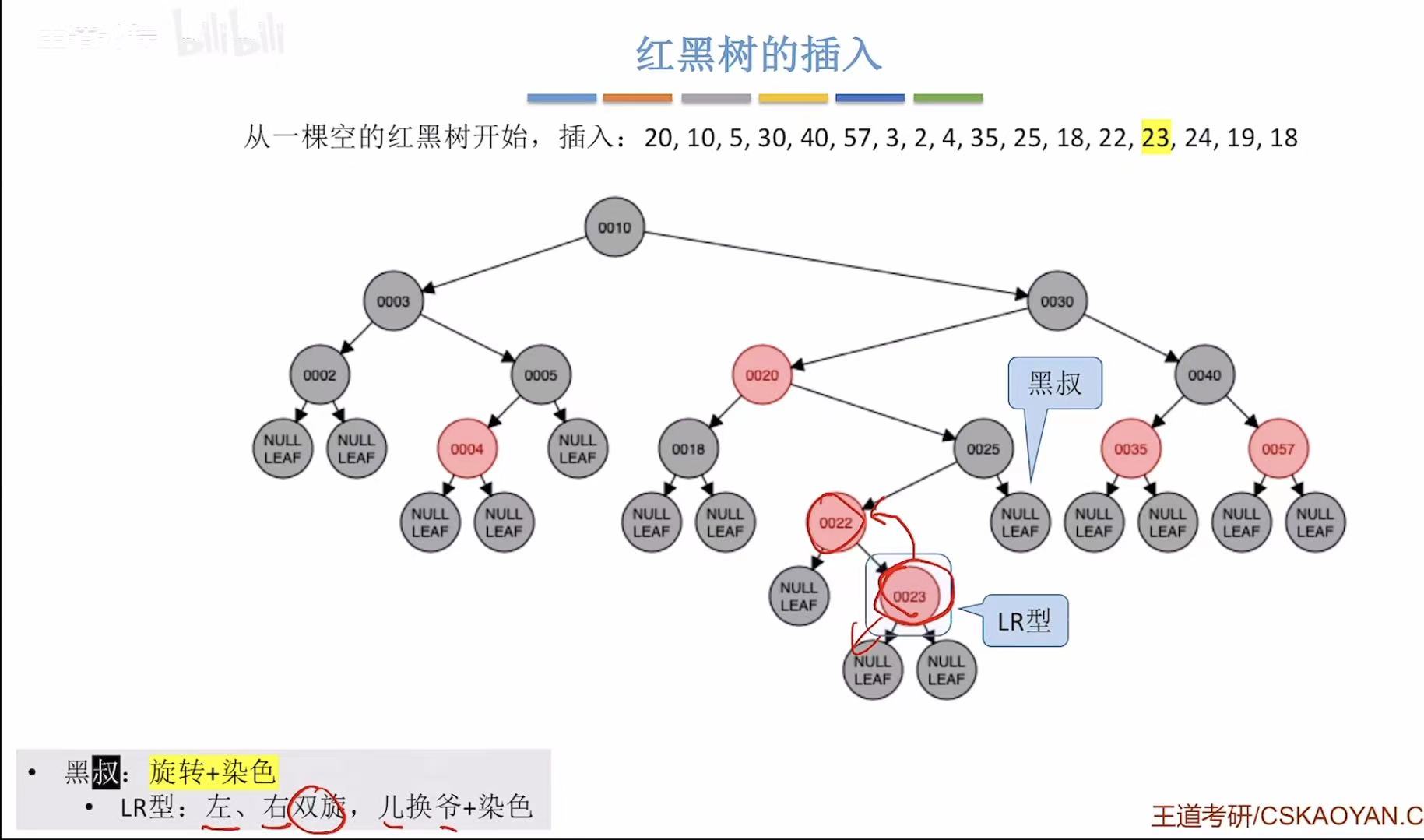
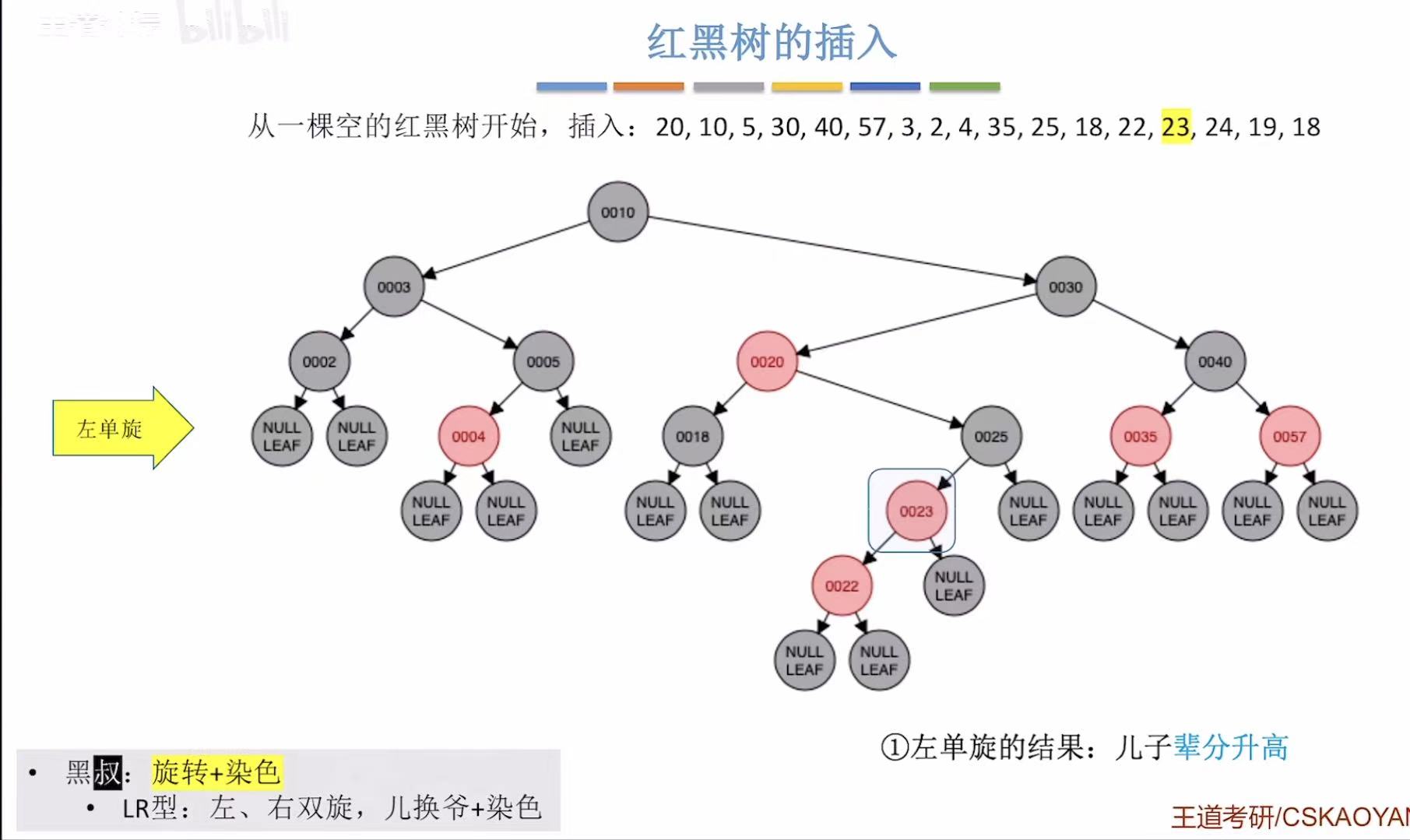
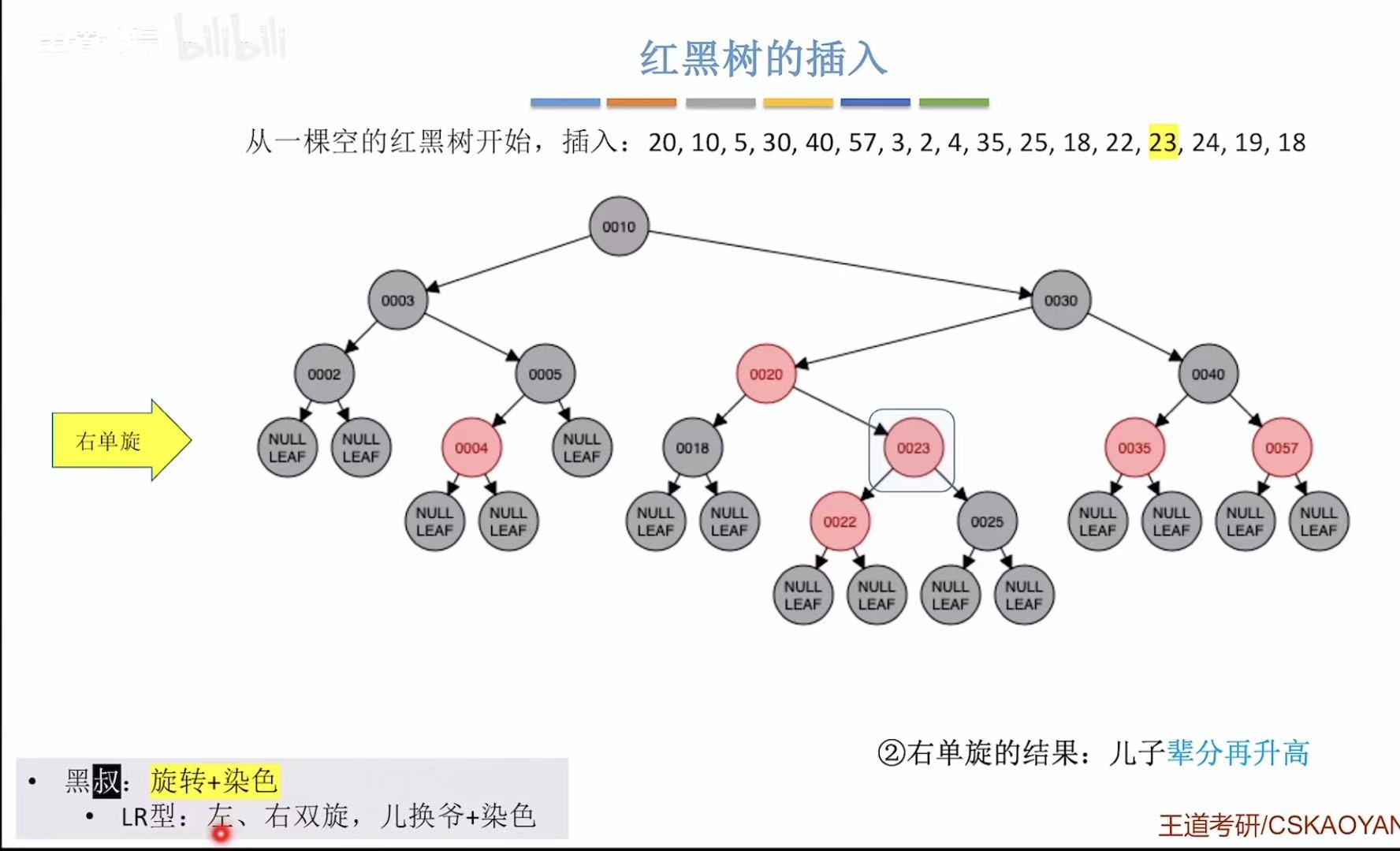
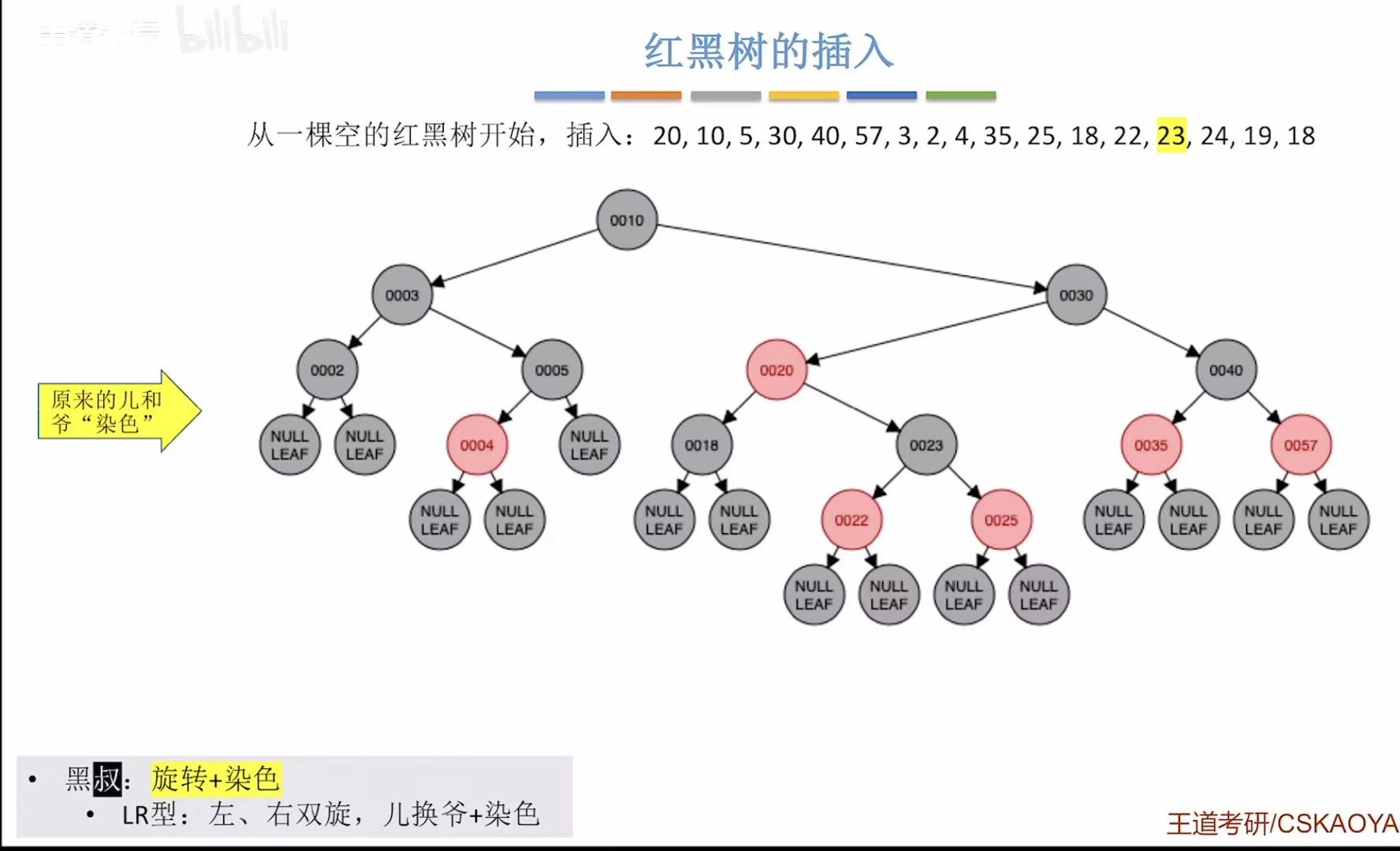
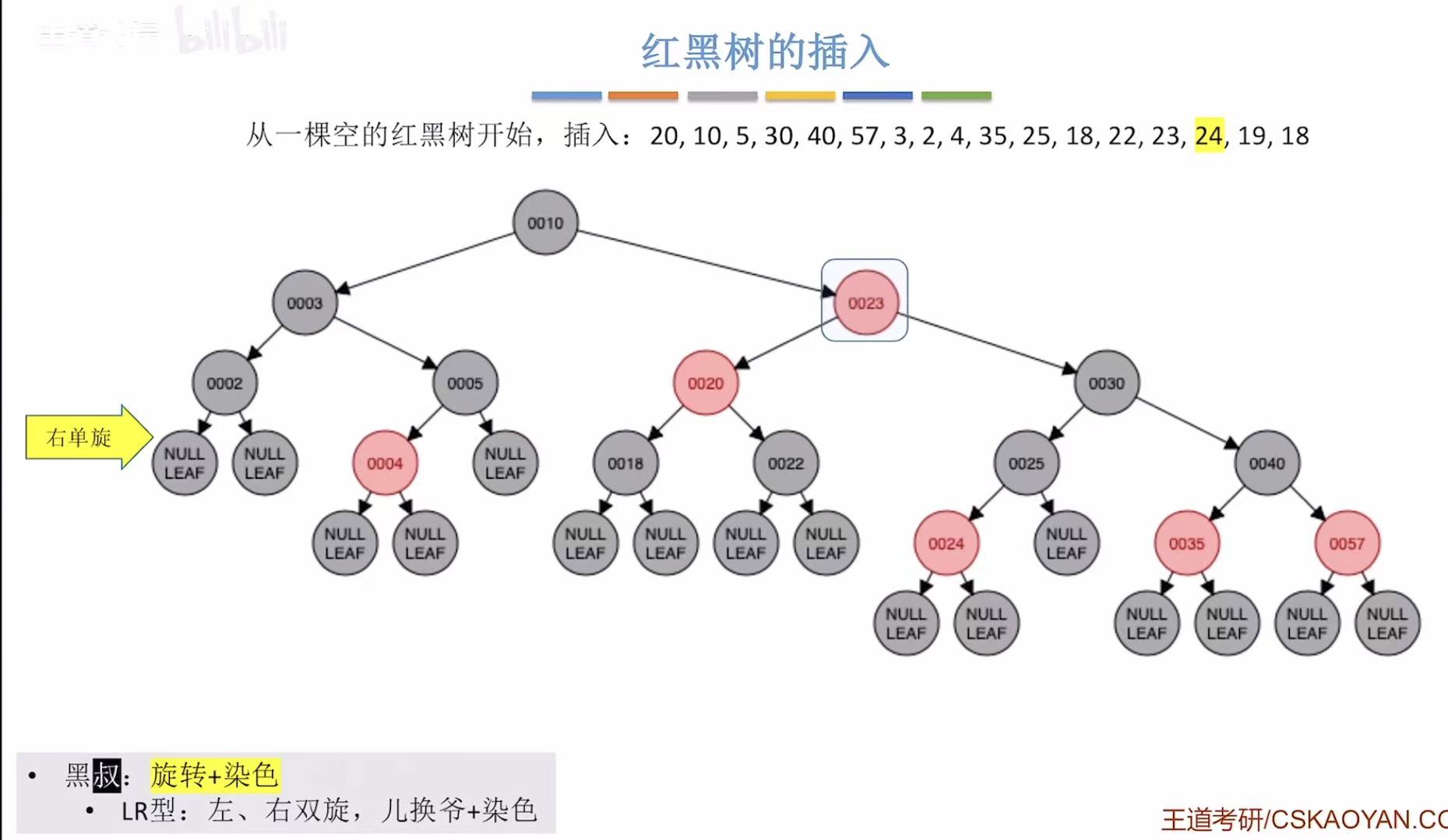
- 添加24:非根,为红色-->违反不红红-->红叔-->染色+变新
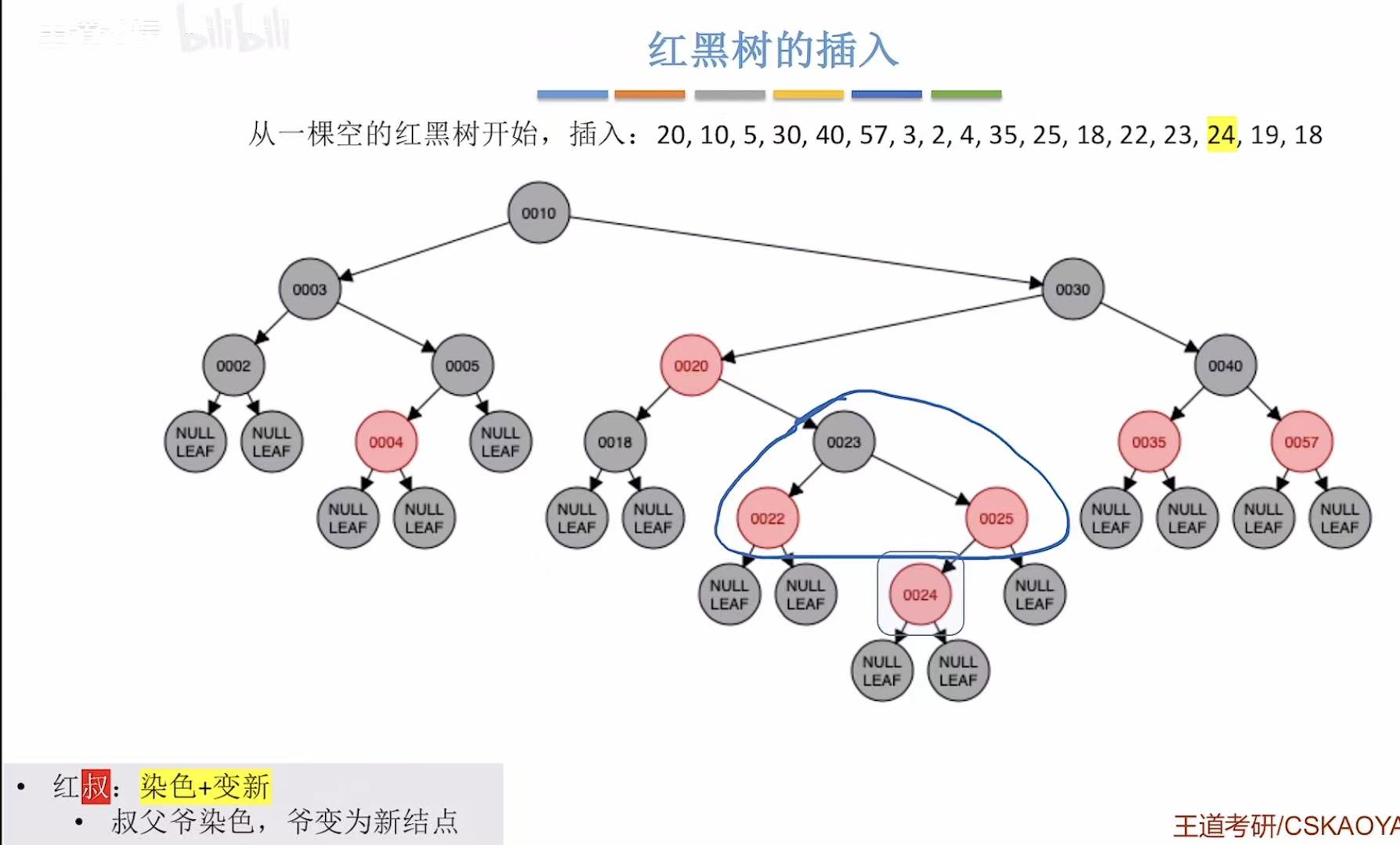
- 变新-->违反不红红-->黑叔-->LR型-->旋转+染色
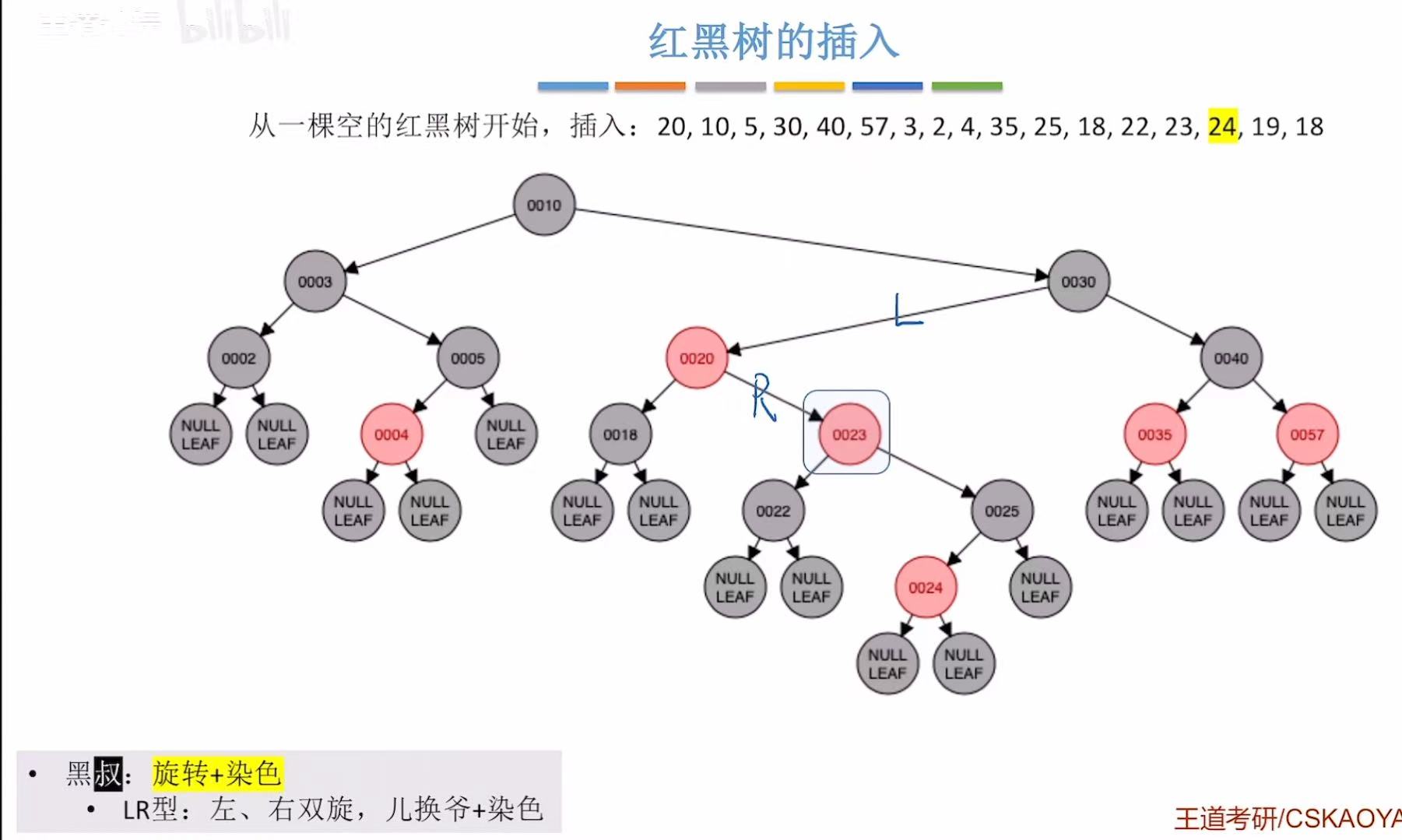
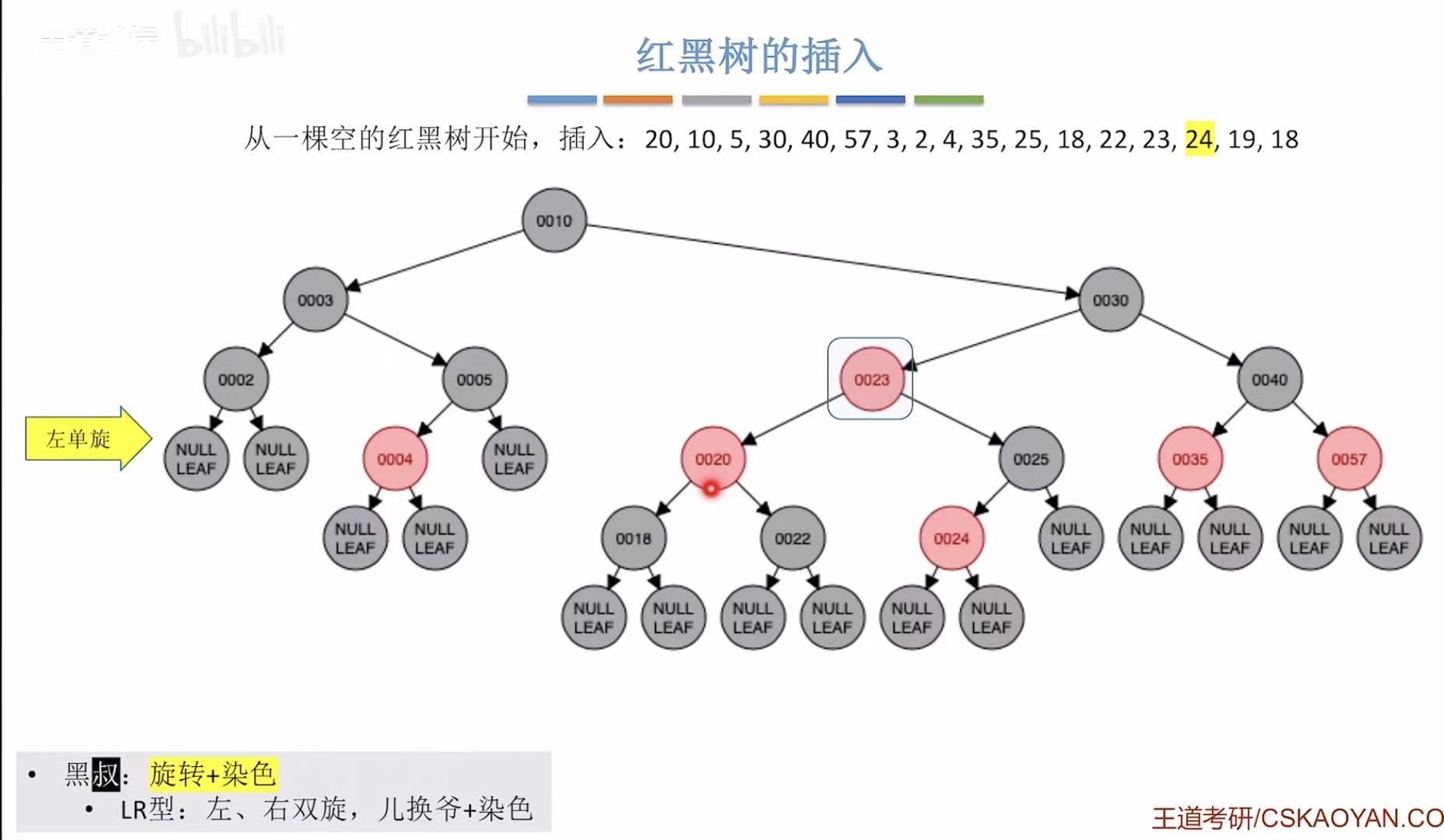
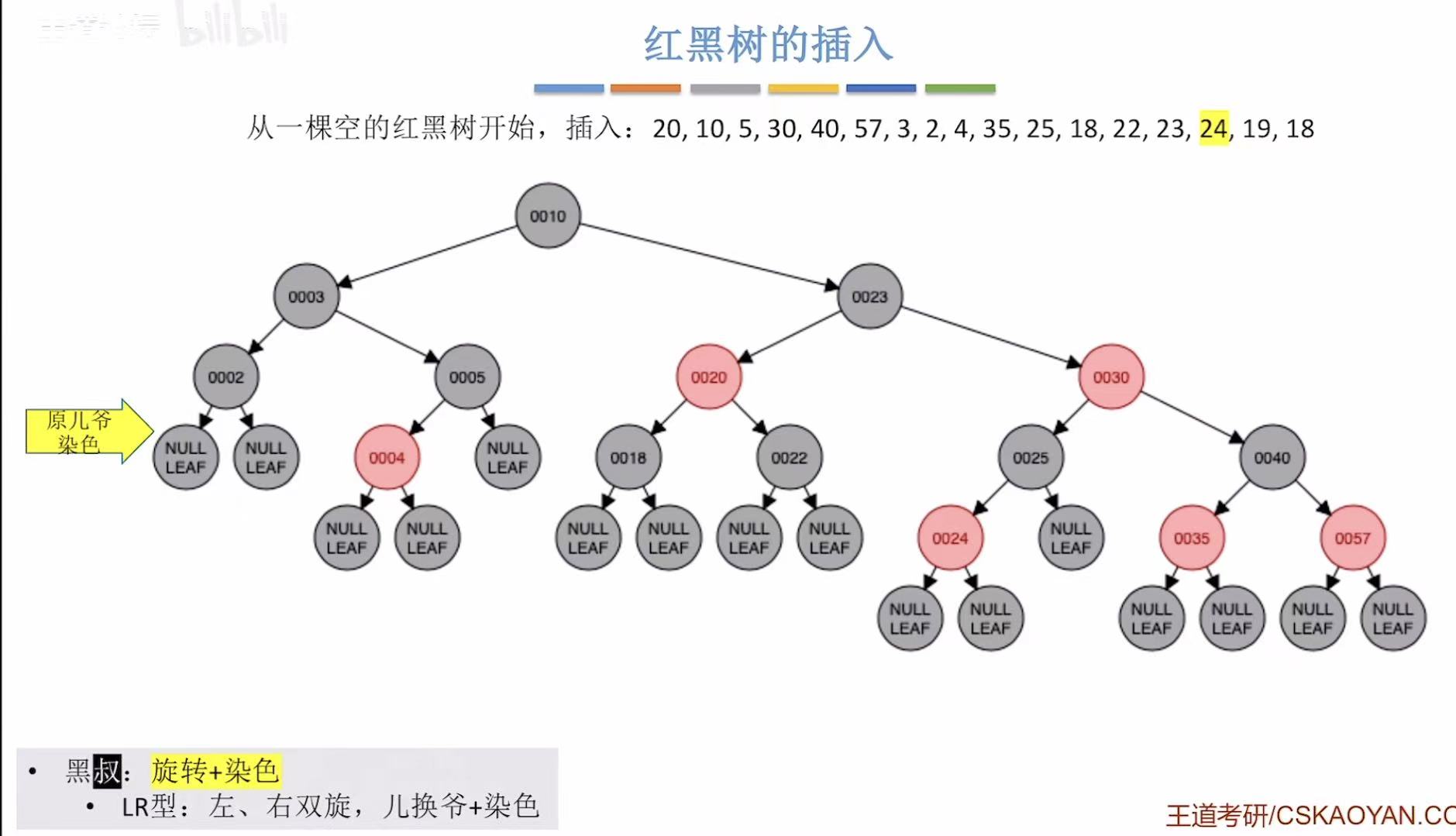
- 添加19:非根,为红色
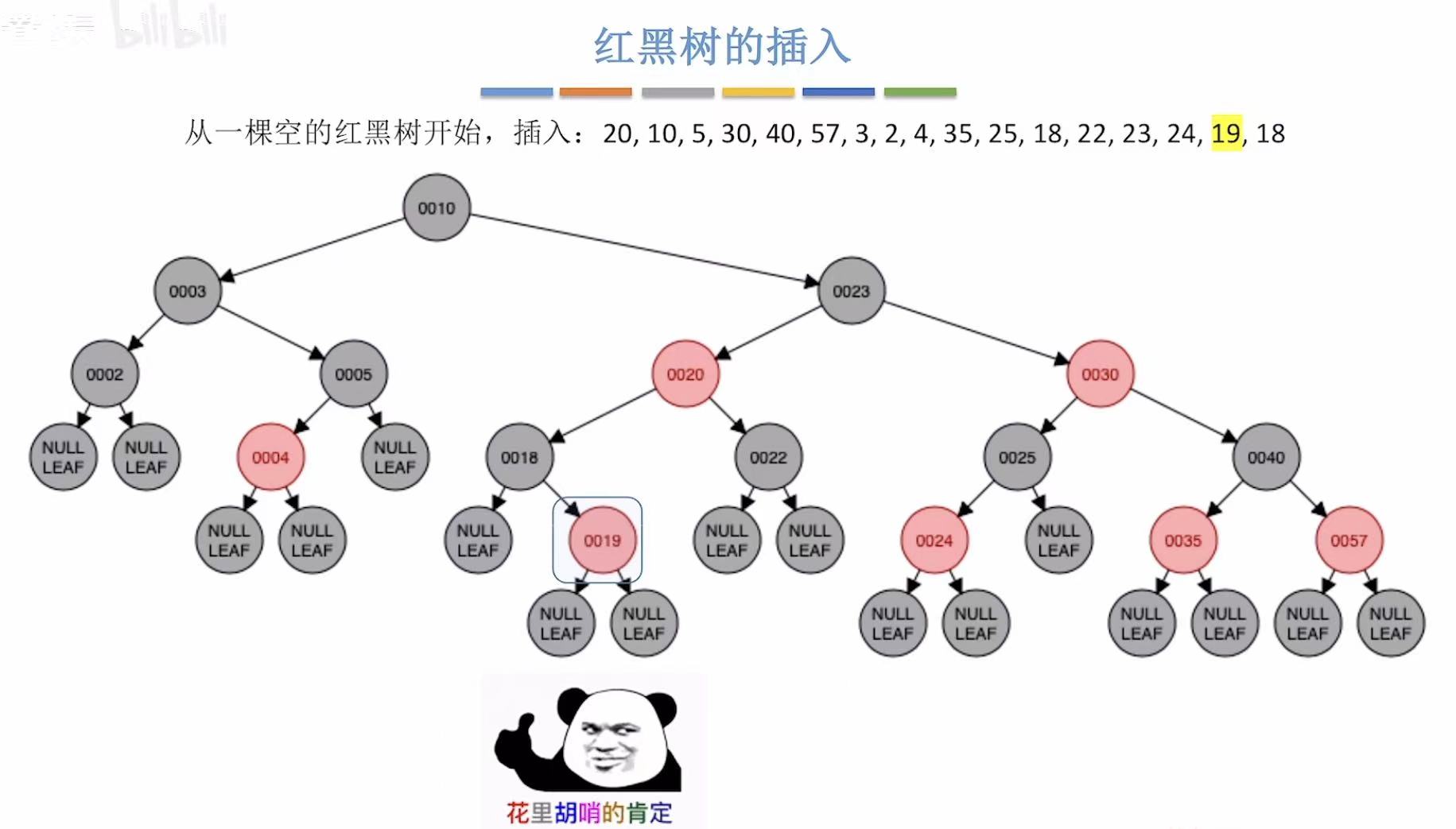
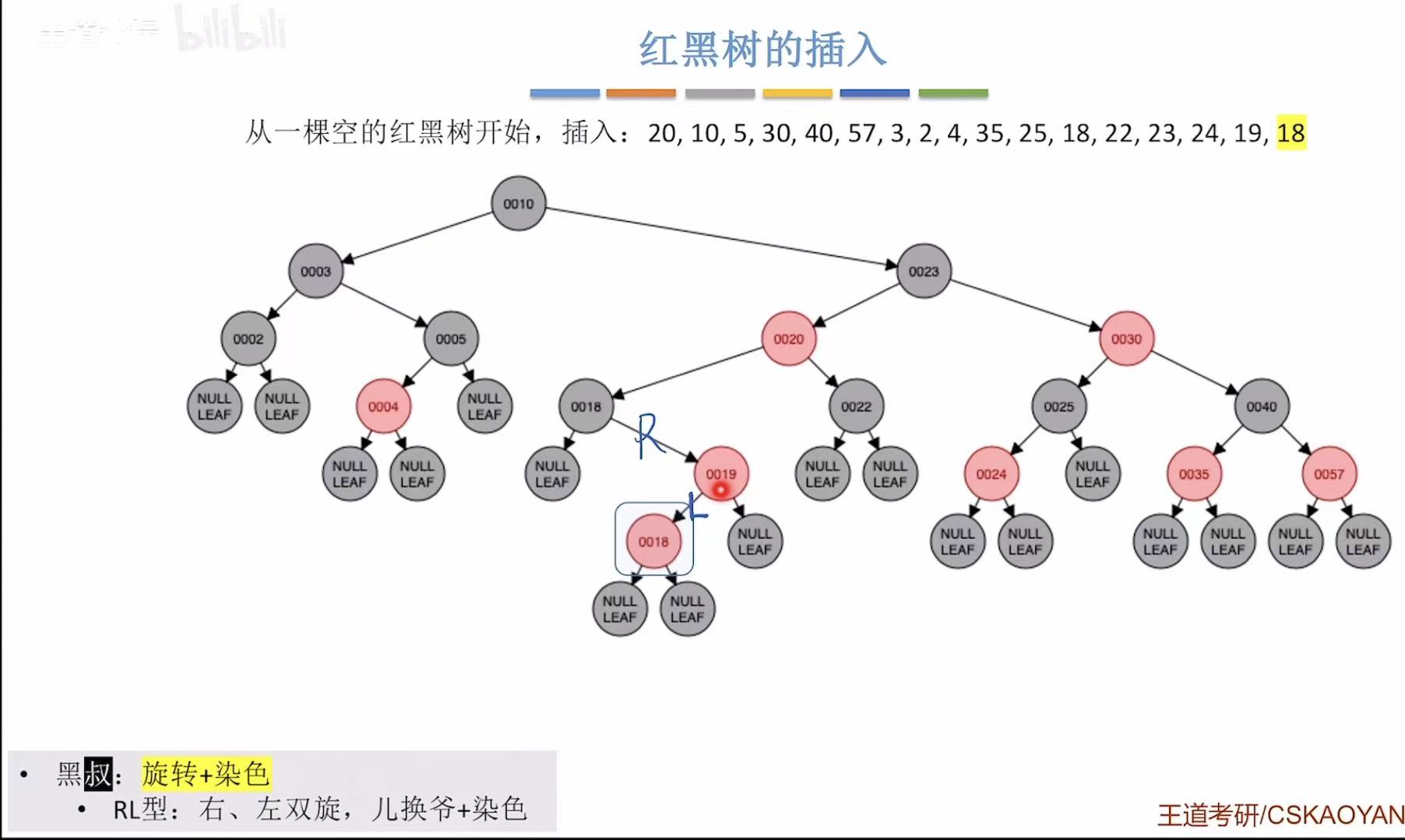
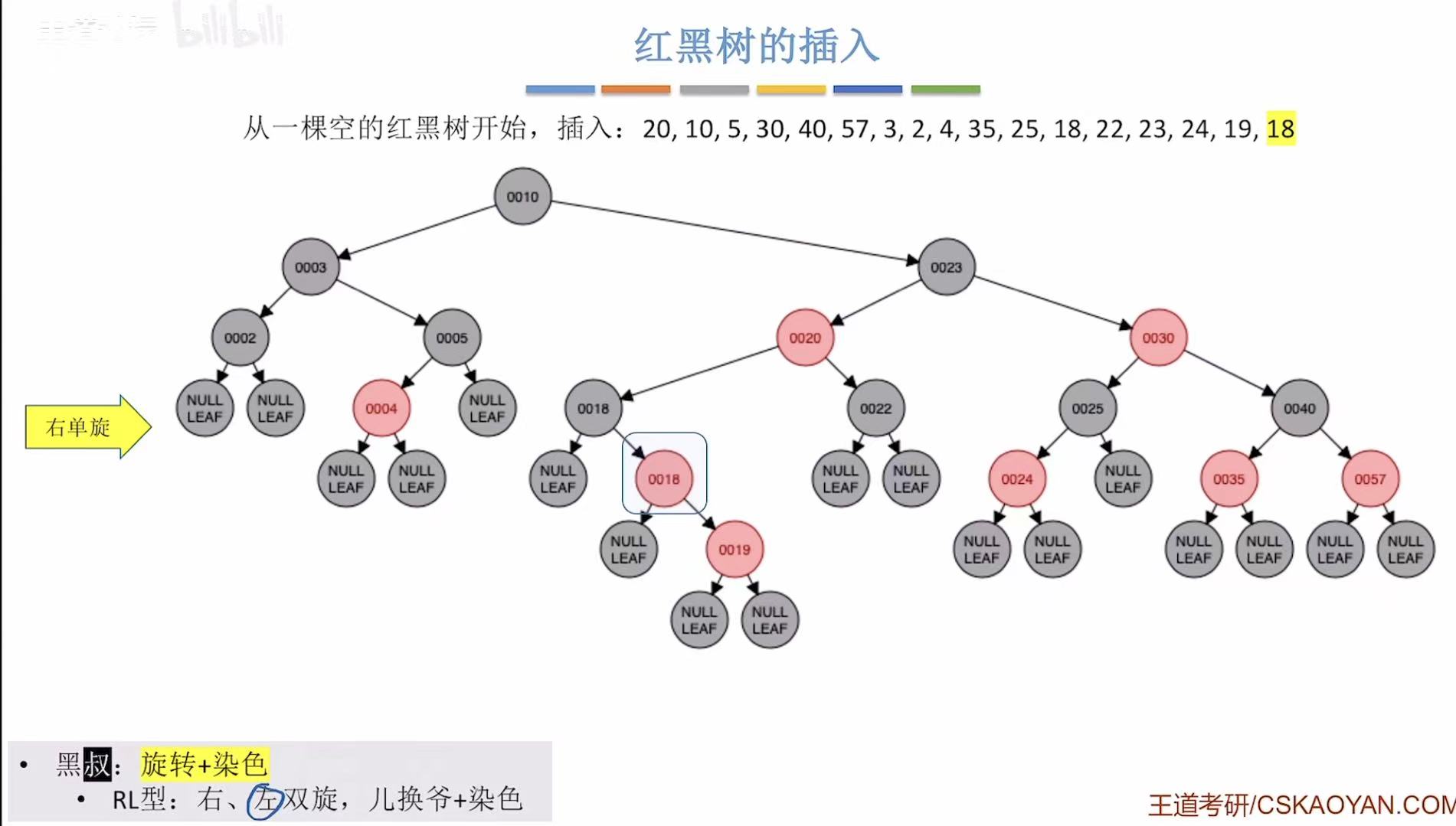
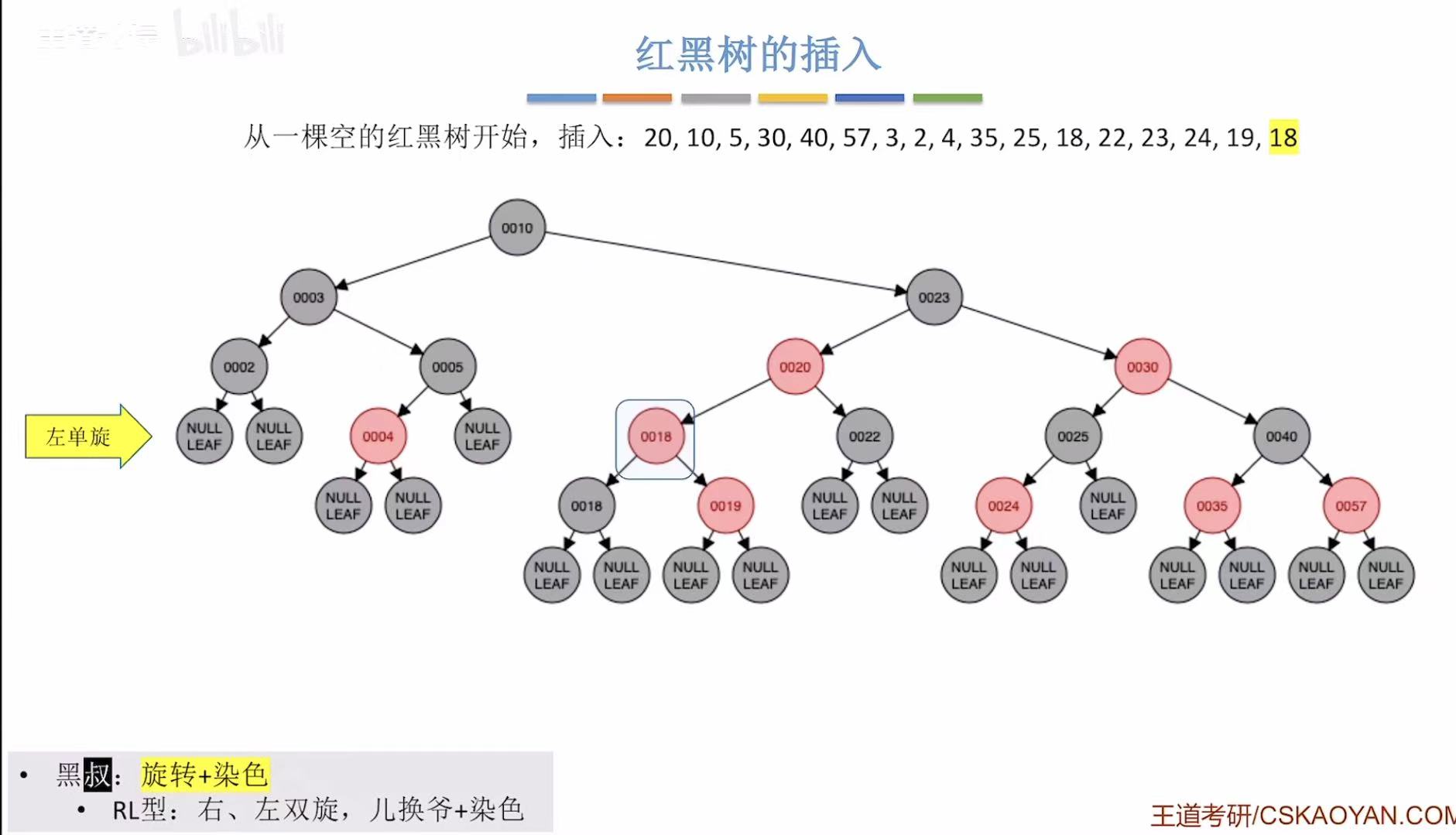
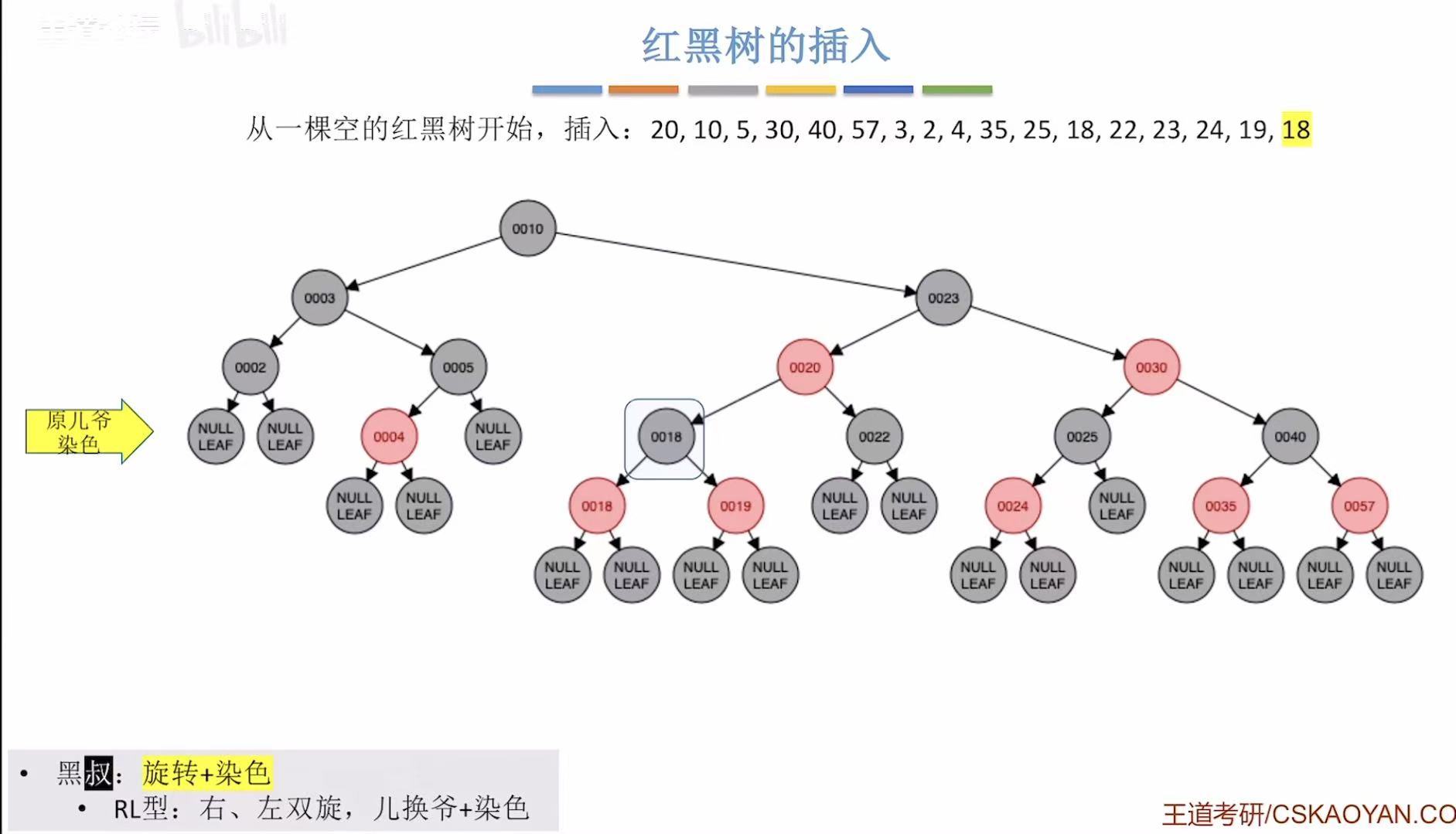
- 添加18:非根,为红色-->违反不红红-->黑叔-->RL型-->旋转+染色
3. 小结

红黑树的删除

