在人工智能和大模型(尤其是我们之前提到的 RAG 检索增强生成)中,把文字、图像变成一段段由数字组成的"向量"后,接下来最重要的一步就是计算这些向量之间的相似度。相似度越高,说明这两段文字或两张图片的意思越相近。
计算向量相似度主要有以下几种常见的方式,它们在几何意义和应用场景上各有侧重:
1. 余弦相似度 (Cosine Similarity) ------ 最常用于文本和 NLP
余弦相似度不关心向量的"长短"(绝对数值的大小),而是只看它们在空间中指向的"方向"是否一致。它通过计算两个向量夹角的余弦值来衡量相似度。
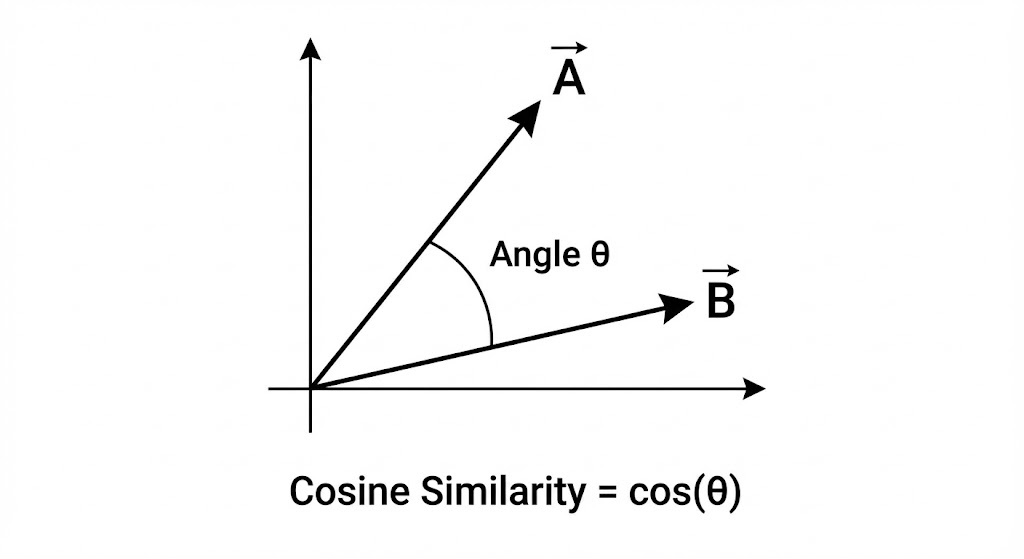
计算公式:
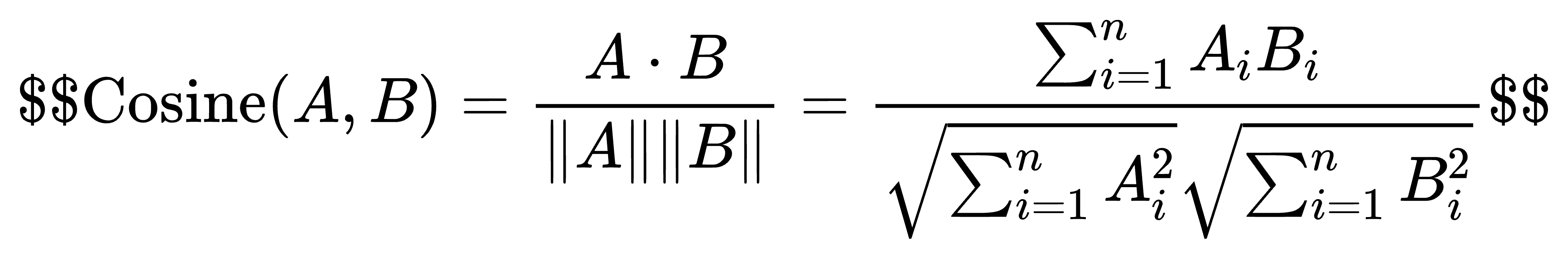
取值范围:\[-1, 1\]。1 表示方向完全相同(最相似),0 表示相互垂直(完全不相关),-1 表示方向完全相反。
应用场景:文本检索、语义搜索。比如两篇文章,一篇 100 字,一篇 10000 字,只要它们都在高频使用"大模型"、"人工智能"这些词(方向一致),即使文章长度(向量模长)差异巨大,余弦相似度也会认为它们高度相似。
2. 欧氏距离 (Euclidean Distance / L2 距离) ------ 关注绝对距离
欧氏距离就是我们在初中几何里学过的,空间中两点之间的直线距离。它既关心向量的方向,也关心向量的"长短"(模长)。
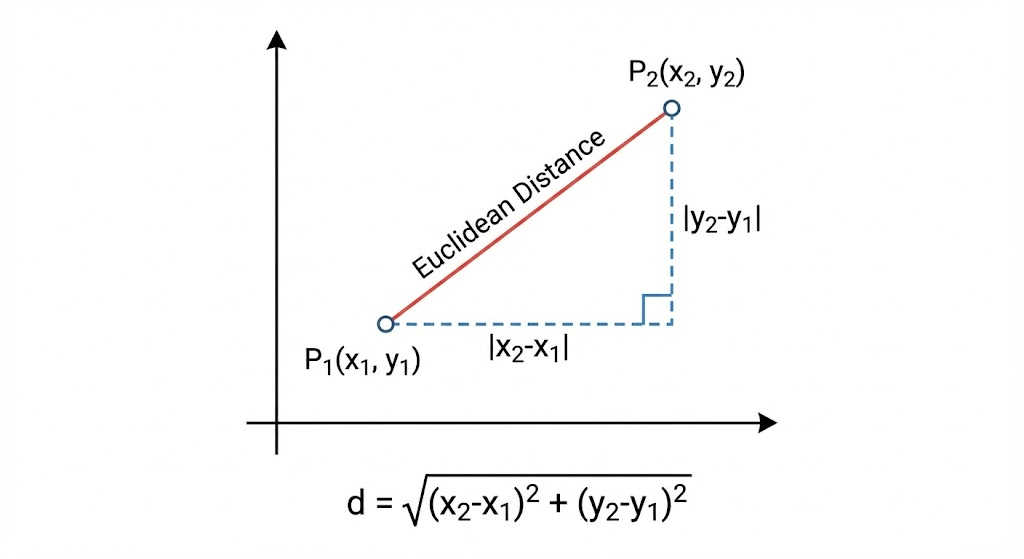 计算公式:
计算公式:
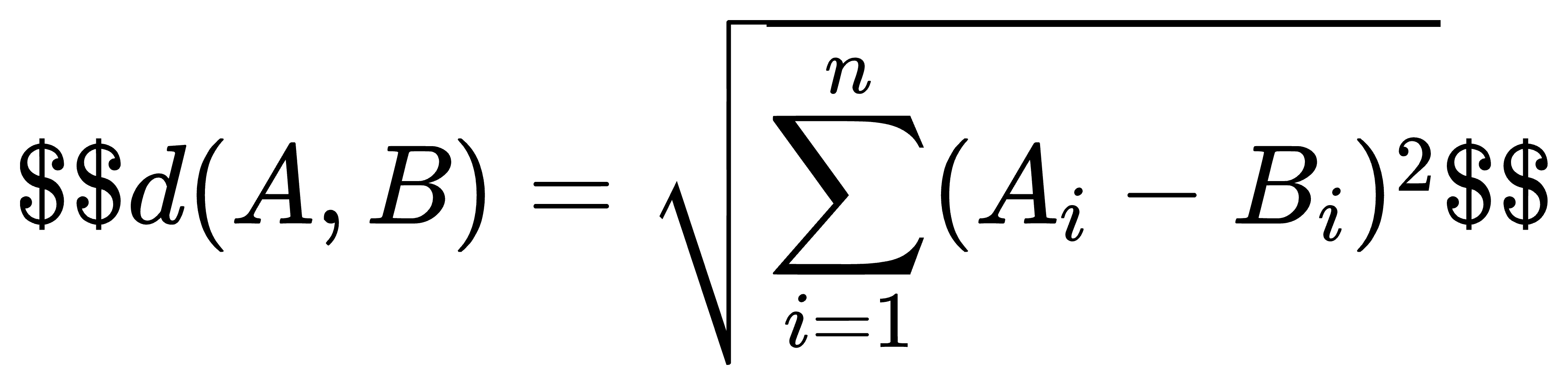
取值范围 :\[0, +\\infty)。注意: 距离越小,代表越相似;距离为 0 代表完全一样。
应用场景:图像识别、特征匹配、推荐系统中的用户画像对比。当你需要严格比较两个对象的各项指标的绝对数值差异时,用欧氏距离最合适。
3. 点积 / 内积 (Dot Product) ------ 兼顾方向与长度,计算极快
点积是将一个向量投影到另一个向量上,然后将它们的长度相乘。它不仅受向量夹角的影响,也受向量本身长度的影响。
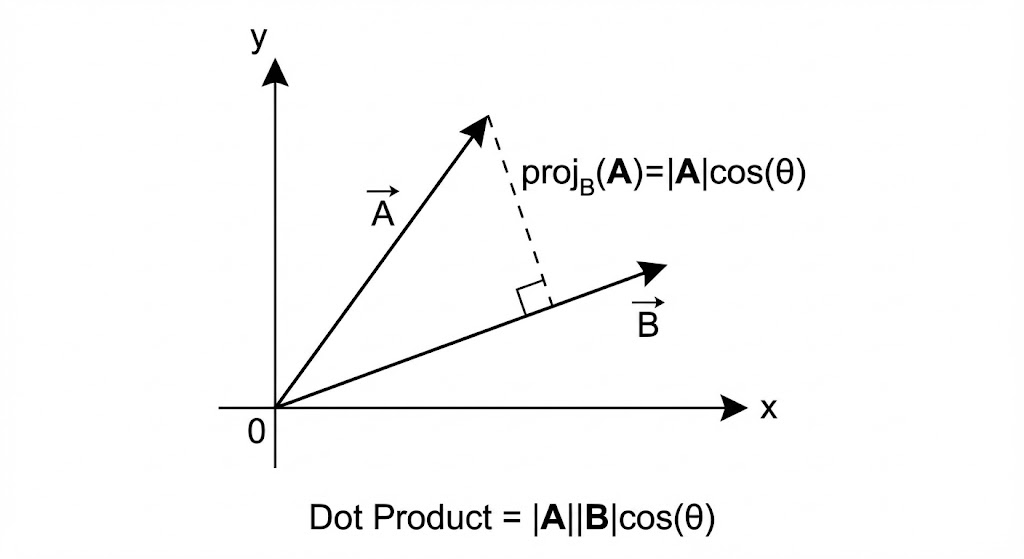
计算公式:
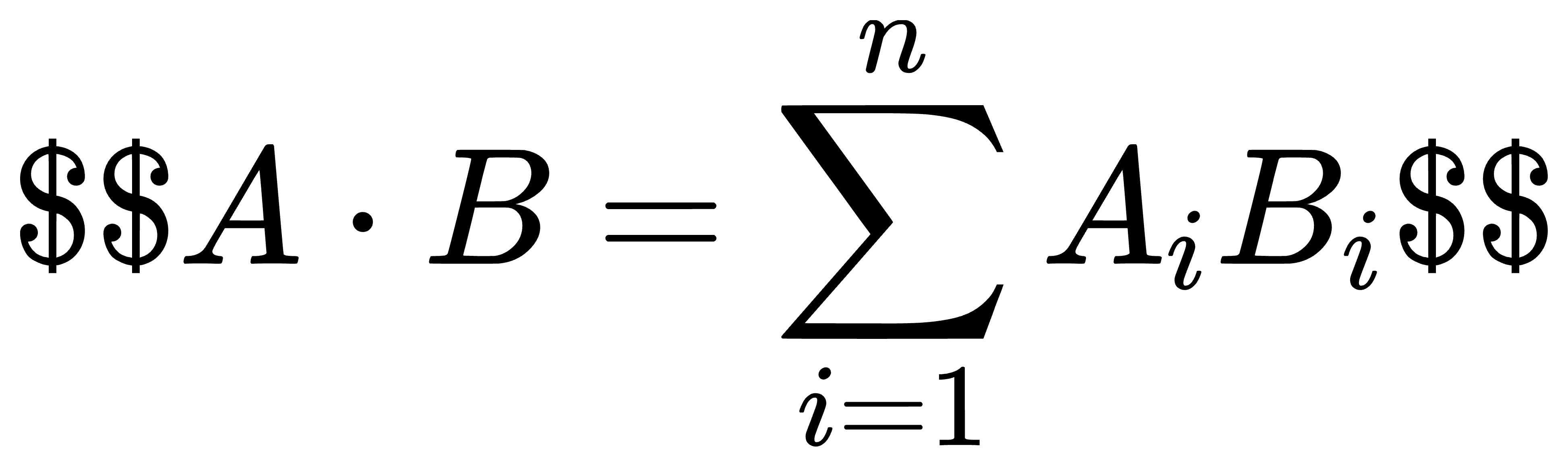
取值范围:(-\\infty, +\\infty)。值越大,越相似。
特殊情况:如果我们在计算前,把所有向量的长度都缩放为 1(这叫"归一化"),那么点积的计算结果将和余弦相似度完全一样。
应用场景:由于计算过程只有乘法和加法,没有开根号或除法,计算速度非常快。在很多大规模的工业级推荐系统或向量数据库中,通常会先将向量归一化,然后直接使用点积来代替余弦相似度,以换取极致的性能。
4. 曼哈顿距离 (Manhattan Distance / L1 距离) ------ 像在城市街区中穿梭
想象你在纽约的曼哈顿街区(棋盘状的街道),你不能穿墙走直线(欧氏距离),只能沿着街道横着走、竖着走。曼哈顿距离就是各个维度上的绝对差值之和。
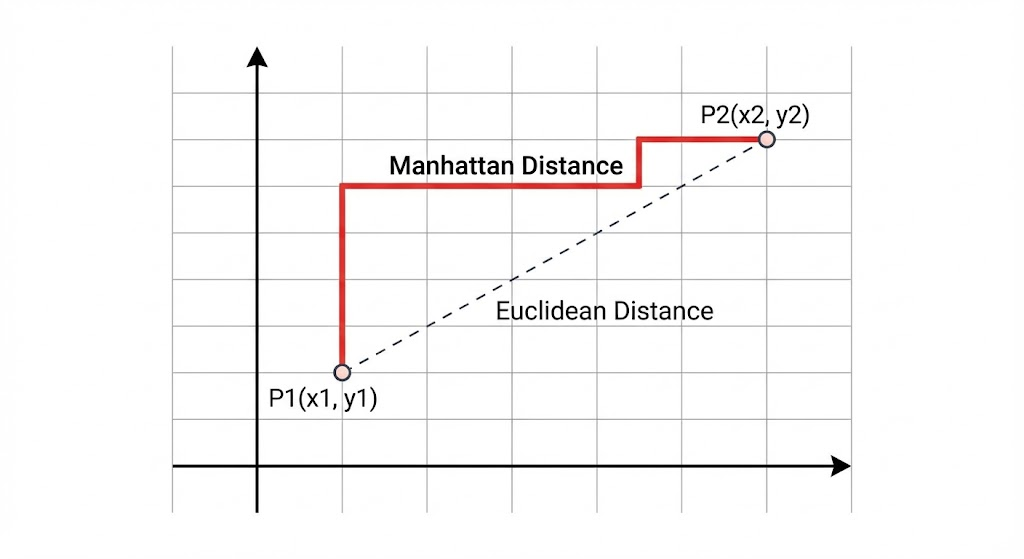 计算公式:
计算公式:
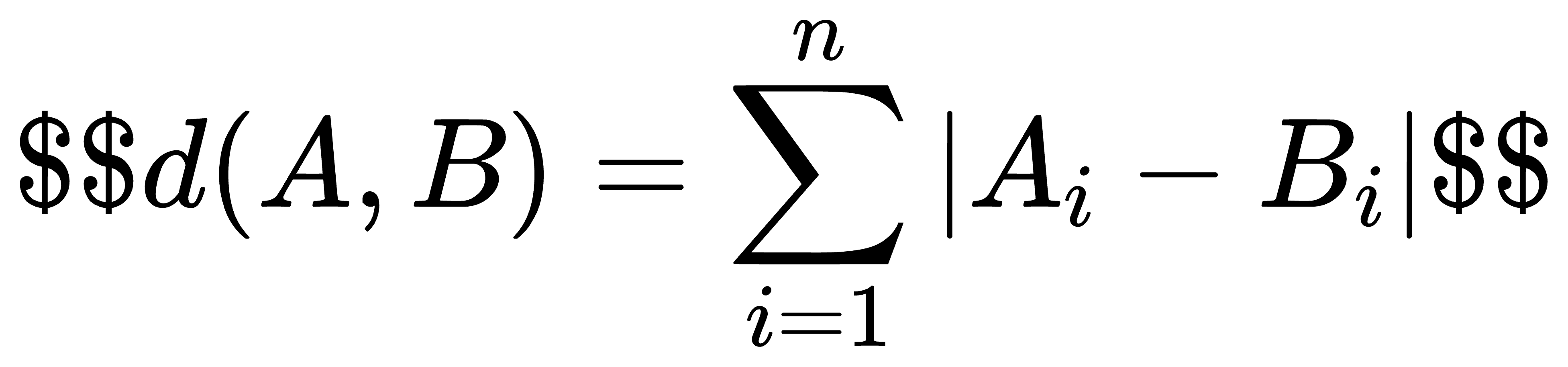
取值范围:\[0, +\\infty)。同样,距离越小越相似。
应用场景:当数据维度非常高,或者某些维度的数值存在异常大的波动(离群点)时,曼哈顿距离比欧氏距离更稳定,因为它不会像欧氏距离那样因为平方运算而过度放大误差。
总结:我该怎么选?
对于你在前面博客里提到的 RAG(检索增强生成)系统,在从"知识库"中检索最相关的文档时,目前业界绝大多数情况下使用的都是余弦相似度(或者归一化后的点积),因为我们更看重提问和文档在"语义方向"上的一致性。