【深度学习基础篇】线性回归代码解析

目录

• 一、库介绍
• 二、创建一组随机数据
• • 1.normal函数
  • 2.加噪声
• 三、生成模拟数据
• 四、定义批量数据加载器data_provider
• 五、定义核心函数（预测、损失、优化）
• • 1.预测
  • 2.损失
  • 3.优化
• 六、初始化训练参数
• 七、模型训练（核心循环）
• [八、打印结果 + 可视化](#八、打印结果 + 可视化)
• 九、总结

先看下完整的代码：

import torch
import matplotlib.pyplot as plt #  画图的

import random  #随机

def create_data(w, b, data_num):  #生成数据
    x = torch.normal(0, 1, (data_num, len(w)))
    y = torch.matmul(x, w) + b    #matmul表示矩阵相乘

    noise = torch.normal(0, 0.01, y.shape)  #噪声要加到y上
    y += noise

    return x, y

num = 500

true_w = torch.tensor([8.1,2,2,4])
true_b = torch.tensor(1.1)


X, Y = create_data(true_w, true_b, num)


plt.scatter(X[:, 3], Y, 1)
plt.show()


def data_provider(data, label, batchsize):       #每次访问这个函数， 就能提供一批数据
    length = len(label)
    indices = list(range(length))
    #我不能按顺序取  把数据打乱
    random.shuffle(indices)

    for each in range(0, length, batchsize):
        get_indices = indices[each: each+batchsize]
        get_data = data[get_indices]
        get_label = label[get_indices]

        yield get_data,get_label  #有存档点的return

batchsize = 16
# for batch_x, batch_y in data_provider(X, Y, batchsize):
#     print(batch_x, batch_y)
#     break


def fun(x, w, b):
    pred_y = torch.matmul(x, w) + b
    return pred_y

def maeLoss(pre_y, y):
    return torch.sum(abs(pre_y-y))/len(y)

def sgd(paras, lr):          #随机梯度下降，更新参数
    with torch.no_grad():  #属于这句代码的部分，不计算梯度
        for para in paras:
            para -= para.grad * lr      #不能写成   para = para - para.grad*lr
            para.grad.zero_()      #使用过的梯度，归0


lr = 0.03
w_0 = torch.normal(0, 0.01, true_w.shape, requires_grad=True)   #这个w需要计算梯度
b_0 = torch.tensor(0.01, requires_grad=True)
print(w_0, b_0)


epochs = 50

for epoch in range(epochs):
    data_loss = 0
    for batch_x, batch_y in data_provider(X, Y, batchsize):
        pred_y = fun(batch_x,w_0, b_0)
        loss = maeLoss(pred_y, batch_y)
        loss.backward()
        sgd([w_0, b_0], lr)
        data_loss += loss

    print("epoch %03d: loss: %.6f"%(epoch, data_loss))

print("真实的函数值是", true_w, true_b)
print("训练得到的参数值是", w_0, b_0)

idx = 3
plt.plot(X[:, idx].detach().numpy(), X[:, idx].detach().numpy()*w_0[idx].detach().numpy()+b_0.detach().numpy())
plt.scatter(X[:, idx], Y, 1)
plt.show()

今天的任务是初次体验一下深度学习，我们以一个最简单的线性回归为例

简单来说，就是我们先要创造一组随机的数据，之后用我们写的随机梯度下降程序来计算出预测的参数，最后画图来比较预测结果的好坏

一、库介绍

本次学习需要的库：

import torch

import matplotlib.pyplot as plt

import random

torch：PyTorch 核心库，用于张量运算、梯度计算（自动求导是深度学习的关键）；

matplotlib.pyplot：画图工具，最后用来展示数据分布和拟合结果；

random：用来打乱数据索引，避免按顺序训练导致模型过拟合。

二、创建一组随机数据

def create_data(w, b, data_num):  #生成数据
    x = torch.normal(0, 1, (data_num, len(w)))
    y = torch.matmul(x, w) + b    #matmul表示矩阵相乘
    noise = torch.normal(0, 0.01, y.shape)  #噪声要加到y上
    y += noise
    return x, y

1.normal函数

torch.normal(0, 1, (data_num, len(w)))：生成data_num个样本，每个样本有len(w)个特征（比如true_w是 4 维，每个样本就有 4 个特征）；

这里是一个标准的正太分布，放在一个有四个特征的样本上。比如：我们研究身高、颜值、金钱和文化对人的受欢迎程度的影响，这里就是四个特征，每个特征所占有的权重是不同的

我们可以暂时把他理解成：

受欢迎程度

2.加噪声

加噪声的目的：真实世界的数据不会完美符合线性关系，噪声模拟这种 "误差"。

三、生成模拟数据

num = 500  # 总样本数
# 真实权重（4维）和真实偏置（标量）------模型要拟合的目标值
true_w = torch.tensor([8.1,2,2,4])
true_b = torch.tensor(1.1)
#这里的两个参数里面的值是我随手打的，你也可以随手打出来

# 调用函数生成特征X和标签Y
X, Y = create_data(true_w, true_b, num)

# 可视化：只画第3个特征（索引3）和Y的关系（散点图）
plt.scatter(X[:, 3], Y, 1)  # X[:,3]：取所有样本的第3个特征；1是点的大小
plt.show()
# 这里可以把3换成其他的，0就代表第一列，3代表第四列，也就是第四个参数和Y之间的关系

plt.scatter(X[:, 3], Y, 1)

这里可以把3换成其他的，0就代表第一列，3代表第四列，也就是第四个参数和Y之间的关系

可以自己试试，因为我们设置的true_w = torch.tensor([8.1,2,2,4])，因此如果我们画出各个列对应Y的图，可以发现第一列对Y最像线性的，因为他的权重更大。

四、定义批量数据加载器data_provider

def data_provider(data, label, batchsize):       #每次访问这个函数， 就能提供一批数据
    length = len(label)  # 总样本数（标签数=样本数）
    indices = list(range(length))  # 生成样本索引列表：[0,1,2,...,499]
    random.shuffle(indices)  # 打乱索引------必须要！！！避免按顺序训练，否则会过拟合

    # 按批次切分索引：从0开始，步长batchsize
    for each in range(0, length, batchsize):
        get_indices = indices[each: each+batchsize]  # 当前批次的索引
        get_data = data[get_indices]  # 按索引取对应特征
        get_label = label[get_indices]  # 按索引取对应标签
        yield get_data,get_label  # 生成器返回批次数据（有存档点的return）

用了这个函数，就能够一段一段地加载数据，而不是一股脑全部加载进内存。
yield：生成器关键字，和return的区别是：return会直接结束函数，yield会 "暂停" 函数并返回数据，下次调用时从暂停处继续 ------省内存（不用一次性加载所有数据）；

示例：如果batchsize=16，第一次返回索引 0-15 的样本，第二次返回 16-31 的样本，直到所有样本取完

五、定义核心函数（预测、损失、优化）

经典三板斧，先生成一个预测的值，再计算loss，最后进行随机梯度下降

1.预测

def fun(x, w, b):
    pred_y = torch.matmul(x, w) + b  # 和生成数据的逻辑一致：y = x*w + b
    return pred_y

就是一个简单的计算预测的y值

2.损失

def maeLoss(pre_y, y):
    # MAE：平均绝对误差 = 所有|预测值-真实值|的和 / 样本数
    return torch.sum(abs(pre_y-y))/len(y)

拿这个预测的pred_y-y得到loss，记得还要取平均值

• 损失函数的作用：衡量模型预测值和真实值的差距，损失越小，模型越准。

3.优化

def sgd(paras, lr):          #随机梯度下降，更新参数
    with torch.no_grad():  #属于这句代码的部分，不计算梯度
        for para in paras:  # 遍历所有需要更新的参数（w和b）
            # 核心更新公式：参数 = 参数 - 学习率×梯度
            para -= para.grad * lr      #不能写成   para = para - para.grad*lr
            para.grad.zero_()      #使用过的梯度，归0

• para -= para.grad * lr：梯度下降的核心公式：

para.grad：参数的梯度（由loss.backward()计算得到，梯度表示 "参数往哪个方向变能让损失变小"）；

lr：学习率（步长），控制参数更新的幅度（0.03 是经验值，太大容易震荡，太小收敛慢）；

• 为什么不能写para = para - ...：para是带梯度的张量，直接赋值会丢失梯度信息，-=是 "原地更新"，保留张量属性；
• para.grad.zero_()：梯度清零 ------ 每批数据计算的梯度只用于当前更新，否则梯度会累加，导致更新错误。

六、初始化训练参数

lr = 0.03  # 学习率
# 初始化权重：和true_w形状一致，正态分布，需要计算梯度（requires_grad=True）
w_0 = torch.normal(0, 0.01, true_w.shape, requires_grad=True)   
# 初始化偏置：标量，需要计算梯度
b_0 = torch.tensor(0.01, requires_grad=True)
print(w_0, b_0)  # 打印初始值（随机的，和true_w/true_b差距大）

这里就是让w和b都取一个随机的初始值，再打印出来看看

七、模型训练（核心循环）

epochs = 50  # 训练轮数：把所有数据训练50遍

for epoch in range(epochs):  # 遍历每一轮
    data_loss = 0  # 累计本轮所有批次的损失
    # 遍历每一批数据
    for batch_x, batch_y in data_provider(X, Y, batchsize):
        pred_y = fun(batch_x,w_0, b_0)  # 用当前参数预测
        loss = maeLoss(pred_y, batch_y)  # 计算批次损失
        loss.backward()  # 反向传播：计算w_0和b_0的梯度
        sgd([w_0, b_0], lr)  # 调用SGD更新参数
        data_loss += loss  # 累加批次损失

    # 打印本轮的总损失（损失逐渐下降，说明模型在收敛）
    print("epoch %03d: loss: %.6f"%(epoch, data_loss))

• 核心逻辑

每一轮（epoch）都会把所有数据过一遍；

损失逐渐下降 → 模型的预测值越来越接近真实值 → 参数w_0/b_0越来越接近true_w/true_b。

八、打印结果 + 可视化

# 打印真实值和训练后的参数值（对比看拟合效果）
print("真实的函数值是", true_w, true_b)
print("训练得到的参数值是", w_0, b_0)

# 可视化：画第3个特征的拟合直线
idx = 3  # 对应true_w的第4个值（4）
# 拟合直线：y = x*w_0[idx] + b_0（转成numpy才能画图）
plt.plot(X[:, idx].detach().numpy(), X[:, idx].detach().numpy()*w_0[idx].detach().numpy()+b_0.detach().numpy())
plt.scatter(X[:, idx], Y, 1)  # 原始数据散点
plt.show()

看着很复杂，其实是因为PyTorch 张量不能直接给 matplotlib 画图，需要：

detach()：分离张量，脱离计算图（不再关联梯度）；

.numpy()：转换成 NumPy 数组；

原始代码是这样的：

print("真实的函数值是", true_w, true_b)
print("训练得到的参数值是", w_0, b_0)
idx = 3  
plt.plot(X[:, idx], X[:, idx]*w_0[idx]+b_0)
plt.scatter(X[:, idx], Y, 1)  # 原始数据散点
plt.show()

是不是清爽很多了？

当我们把idx改成0时，图是这样的：

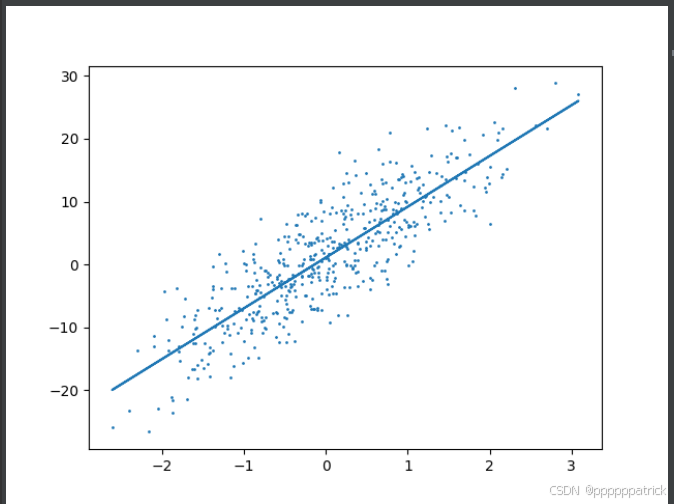
idx=1时：

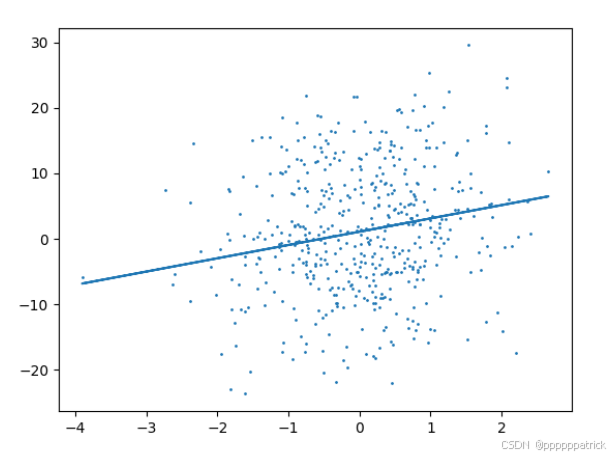
可以发现没有太线性，这是符合我们的预期结果的，因为我们的w_0初始赋值为：

true_w = torch.tensor([8.1,2,2,4])

因此第一个参数的权重最大，相关性是最大的

九、总结

• 线性回归的核心是拟合 y=x⋅w+b，通过最小化损失优化w和b；
• 自动求导（requires_grad=True + loss.backward()）是 PyTorch 的核心，不用手动算梯度；
• 批次训练 + 梯度下降是深度学习的基础：打乱数据→分批计算→更新参数→重复收敛；
• MAE 损失是回归任务的常用损失，SGD 是最基础的优化器。