本文涉及知识点
预备知识
费马引理
费马引理 :设函数f(x)在点 x 0 x_0 x0的某邻域 U ( x 0 ) U(x_0) U(x0)内有定义,并在 x 0 处 x_0处 x0处可导,如果对任意 x ∈ U ( x 0 ) x\in U(x_0) x∈U(x0),有
f ( x ) ≤ f ( x 0 ) ( 或 f ( x ) ≥ f ( x 0 ) f(x)\leq f(x_0)(或f(x) \geq f(x_0) f(x)≤f(x0)(或f(x)≥f(x0)
那么f'(x0)=0。
可以用反证法证明:
令 f − ′ = f + ′ = a f_{-}'=f_+'=a f−′=f+′=a,如果a>0,则 f ( x − Δ x ) < f ( x 0 ) f(x-\Delta x) <f(x_0) f(x−Δx)<f(x0);如果a<0,则 f ( x + Δ x ) < f ( x 0 ) f(x+\Delta x) <f(x_0) f(x+Δx)<f(x0)
通常称导数等于零的点为函数驻点(稳定点,临界点)。
罗尔定理
罗尔定理 :如果函数f(x)满足:
(1),在闭区间[a,b]上连续。
(2),在开区间(a,b)内可导。
(3),在区间端点处函数值相等,即f(a)=f(b)。
那么:在(a,b)内至少一点 ξ ( a < ξ < b ) ,使得 f ′ ( ξ ) = 0 \xi(a<\xi<b),使得f'(\xi)=0 ξ(a<ξ<b),使得f′(ξ)=0
证明:
如果 ∃ f ( x ) > f ( a ) ,则取 f ( x ) 的最大值 f ( x 1 ) \exist f(x)>f(a),则取f(x)的最大值f(x_1) ∃f(x)>f(a),则取f(x)的最大值f(x1),根据费马引理, f ′ ( x 1 ) = 0 f'(x_1)=0 f′(x1)=0。
否则,取f(x)的最小值 f ( x 2 ) , f ' ( x 2 ) = 0 f(x_2),f'(x_2)=0 f(x2),f'(x2)=0。
拉格朗日中值定理
如果函数f(x)满足:
(1),在闭区间[a,b]上连续。
(2),在开区间(a,b)内可导。
那么,至少存在一点 ξ , a < ξ < b ,使得等式 \xi,a<\xi<b,使得等式 ξ,a<ξ<b,使得等式
f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) f(b)-f(a)=f'(\xi)(b-a) f(b)−f(a)=f′(ξ)(b−a)
⟺ f ( b ) − f ( a ) b − a = f ′ ( ξ ) \iff \frac{f(b)-f(a)}{b-a}=f'(\xi) ⟺b−af(b)−f(a)=f′(ξ)
即直线AB的斜率等于 ( ξ , f ( ξ ) ) (\xi,f(\xi)) (ξ,f(ξ))切线的斜率,A(a,f(a)),B(b,f(b))。
不严格的证明:
以A为中心,旋转整个曲线至AB水平。便是罗尔定理。
定理 如果函数f(x)在区间I上连续,I内可导且导数恒为0,那么f(x)在区间I上是一个常数。
∀ x 1 , x 2 , x 1 < x 2 \forall x_1,x_2,x_1<x_2 ∀x1,x2,x1<x2根据拉格朗日中值定理: f ( x 2 ) − f ( x 1 ) x 2 − x 1 = f ′ ( ξ ) = 0 , 即 f ( x 2 ) ≡ f ( x 1 ) \frac{f(x2)-f(x1)}{x2-x1}=f'(\xi)=0,即f(x_2) \equiv f(x_1) x2−x1f(x2)−f(x1)=f′(ξ)=0,即f(x2)≡f(x1)
例题:证明当x>0时, x 1 + x < ln ( 1 + x ) < x \frac x {1+x}<\ln (1+x)<x 1+xx<ln(1+x)<x。令f(t)= ln ( 1 + t ) \ln (1+t) ln(1+t),则 f ′ ( t ) = 1 1 + t f'(t)=\frac 1 {1+t} f′(t)=1+t1,f(0)=0。
根据拉格朗日定理:
f ( x ) − f ( 0 ) = ( x − 0 ) f ′ ( ξ ) f(x)-f(0)=(x-0)f'(\xi) f(x)−f(0)=(x−0)f′(ξ)
⟺ f ( x ) = x f ′ ( ξ ) \iff f(x)=xf'(\xi) ⟺f(x)=xf′(ξ)
⟺ ln ( 1 + x ) = x 1 + ξ \iff \ln(1+x)=\frac x {1+\xi} ⟺ln(1+x)=1+ξx
即: f ( x ) ∈ [ x 1 + x , x ] f(x)\in[\frac x {1+x},x] f(x)∈[1+xx,x]
柯西中值定理
如果函数f(x)即F(x)满足:
(1),在闭区间[a,b]上连续。
(2),在开区间(a,b)内可导。
(3),对任意x ∈ ( a , b ) , F ′ ( x ) ≠ 0 , 那么在 ( a , b ) 内至少有一点 ξ , 使等式 \in(a,b),F'(x)\neq 0,那么在(a,b)内至少有一点\xi,使等式 ∈(a,b),F′(x)=0,那么在(a,b)内至少有一点ξ,使等式
f ( b ) − f ( a ) F ( b ) − F ( a ) = f ′ ( ξ ) F ′ ( ξ ) \frac{f(b)-f(a)}{F(b)-F(a)}=\frac {f'(\xi)}{F'(\xi)} F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)
成立。
根据罗尔定理证明拉格朗日中值定理过程如下:
设辅助函数 ϕ ( x ) = f ( x ) − f ( a ) − f ( b ) F ( a ) − F ( b ) F ( x ) \phi(x)=f(x)-\frac{f(a)-f(b)}{F(a)-F(b)}F(x) ϕ(x)=f(x)−F(a)−F(b)f(a)−f(b)F(x)
ϕ ( a ) = f ( a ) − f ( a ) − f ( b ) F ( a ) − F ( b ) F ( a ) = f ( a ) F ( a ) − f ( a ) F ( b ) − f ( a ) F ( a ) + F ( a ) f ( b ) F ( a ) − F ( b ) \phi(a)=f(a)-\frac{f(a)-f(b)}{F(a)-F(b)}{F(a)}=\frac{f(a)F(a)-f(a)F(b)-f(a)F(a)+F(a)f(b)}{F(a)-F(b)} ϕ(a)=f(a)−F(a)−F(b)f(a)−f(b)F(a)=F(a)−F(b)f(a)F(a)−f(a)F(b)−f(a)F(a)+F(a)f(b)
⟺ F ( a ) f ( b ) − f ( a ) F ( b ) F ( a ) − F ( b ) \iff \frac{F(a)f(b)-f(a)F(b)}{F(a)-F(b)} ⟺F(a)−F(b)F(a)f(b)−f(a)F(b)
ϕ ( b ) = f ( b ) − f ( a ) − f ( b ) F ( a ) − F ( b ) F ( b ) = f ( b ) F ( a ) − f ( b ) F ( b ) − f ( a ) F ( b ) + f ( b ) F ( b ) F ( a ) − F ( b ) \phi(b)=f(b)-\frac{f(a)-f(b)}{F(a)-F(b)}F(b)=\frac{f(b)F(a)-f(b)F(b)-f(a)F(b)+f(b)F(b)}{F(a)-F(b)} ϕ(b)=f(b)−F(a)−F(b)f(a)−f(b)F(b)=F(a)−F(b)f(b)F(a)−f(b)F(b)−f(a)F(b)+f(b)F(b)
⟺ F ( a ) f ( b ) − f ( a ) F ( b ) F ( a ) − F ( b ) \iff \frac{F(a)f(b)-f(a)F(b)}{F(a)-F(b)} ⟺F(a)−F(b)F(a)f(b)−f(a)F(b)
即 ϕ ( a ) = p h i ( b ) \phi(a)=phi(b) ϕ(a)=phi(b)
ϕ ( x ) = f ′ ( x ) − f ( a ) − f ( b ) F ( a ) − F ( b ) F ′ ( x ) \phi(x)=f'(x)-\frac{f(a)-f(b)}{F(a)-F(b)}F'(x) ϕ(x)=f′(x)−F(a)−F(b)f(a)−f(b)F′(x)
根据罗尔定理, ∃ ξ , ϕ ( ξ ) ′ = 0 \exist \xi,\phi(\xi)'=0 ∃ξ,ϕ(ξ)′=0
⟺ f ′ ( ξ ) ÷ F ′ ( ξ ) = f ( a ) − f ( b ) F ( a ) − F ( b ) \iff f'(\xi)\div F'(\xi)=\frac {f(a)-f(b)}{F(a)-F(b)} ⟺f′(ξ)÷F′(ξ)=F(a)−F(b)f(a)−f(b)
根据拉格朗日定理证明罗尔定理:
令F(x)=x,则F'(x)=1。代入拉格朗日定理:
f ′ ( ξ ) = f ( a ) − f ( b ) a − b f'(\xi)=\frac{f(a)-f(b)}{a-b} f′(ξ)=a−bf(a)−f(b)即罗尔定理。
洛必达法则
定理一 :a,当 x → a x \to a x→a时,函数f(x)及F(x)都趋于零。b,在点a的某去心邻域内,f'(x)及F'(x)都存在且F'(x) ≠ 0 \neq 0 =0;(3), lim x → a f ′ ( x ) F ′ ( x ) \lim\limits_{x \to a} \frac {f'(x)}{F'(x)} x→alimF′(x)f′(x)则:
lim x → a f ( x ) F ( x ) = lim x → a f ′ ( x ) F ′ ( x ) \lim\limits_{x \to a} \frac {f(x)}{F(x)}=\lim\limits_{x \to a} \frac {f'(x)}{F'(x)} x→alimF(x)f(x)=x→alimF′(x)f′(x)
定理二 :a,当 x → + ∞ x \to +\infty x→+∞时,f(x)及F(x)都趋于零。b,当|x|>N时,f'(x)和F'(x)都存在,且F'(x) ≠ 0 \neq 0 =0。c, lim x → + ∞ f ′ ( x ) F ′ ( x ) \lim\limits_{x \to +\infty}\frac{f'(x)}{F'(x)} x→+∞limF′(x)f′(x)存在或为无穷大。
则:
lim x → + ∞ f ( x ) F ( x ) = lim x → + ∞ f ′ ( x ) F ′ ( x ) \lim\limits_{x \to +\infty}\frac{f(x)}{F(x)}=\lim\limits_{x \to +\infty}\frac{f'(x)}{F'(x)} x→+∞limF(x)f(x)=x→+∞limF′(x)f′(x)
注意 :只要是未定式,就可以。
∞ ÷ ∞ = ( 1 ÷ ∞ ) ÷ ( 1 ÷ ∞ ) \infty \div \infty=(1\div \infty) \div (1 \div \infty) ∞÷∞=(1÷∞)÷(1÷∞)
0 × ∞ = 0 ÷ ( 1 ÷ ∞ ) 0 \times \infty=0 \div (1 \div \infty) 0×∞=0÷(1÷∞)
例:求 lim x → 0 + x x \lim\limits_{x \to 0+}x^x x→0+limxx
令 y= x y x^y xy, lim x → 0 + ln y = ln ( e ln x × x ) = ln x × x = 0 \lim\limits_{x \to 0+}\ln y =\ln (e^{\ln x \times x})=\ln x \times x =0 x→0+limlny=ln(elnx×x)=lnx×x=0
lim x → 0 x x = e ln x x = e 0 = 1 \lim\limits_{x \to 0}x^x=e{\ln x x}=e^0=1 x→0limxx=elnxx=e0=1
泰勒公式
泰勒中值定理一 :如果函数f(x)在 x 0 x_0 x0处具有n阶导数,那么存在 x 0 x_0 x0的一个邻域,对于改邻域的任意x,有
p n ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ f ( n ) ( x 0 ) n ! ( x − x 0 ) n p_n(x)=f(x_0)+f'(x_0)(x-x_0)+\frac {f''(x_0)}{2!}(x-x_0)^2+\cdots \frac {f^{(n)}(x_0)}{n!}(x-x_0)^n pn(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯n!f(n)(x0)(x−x0)n n次泰勒多项式
f ( x ) = p n ( x ) + R n ( x ) f(x)=p_n(x)+R_n(x) f(x)=pn(x)+Rn(x) 带有配亚诺余项的n次泰勒公式。
其中: R n ( x ) = o ( ( x − x 0 ) n ) R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n), R n ( x ) R_n(x) Rn(x)是配亚诺余项。
泰勒中值定理二 ,如果函数f(x)在 x 0 的某个邻域 U ( x 0 ) x_0的某个邻域U(x_0) x0的某个邻域U(x0)内具有n+1阶段导数,则:
f ( x ) = p n ( x ) + R n ( x ) f(x)=p_n(x)+R_n(x) f(x)=pn(x)+Rn(x)
其中 R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 , ξ 是 x 和 x 0 之间的值 R_n(x)=\frac {f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1},\xi是x和x_0之间的值 Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1,ξ是x和x0之间的值。此处的 R n R_n Rn是拉格朗日余项,方便估算误差。
如果n=0,带拉格朗日余项的泰勒公式就是拉格朗日中值定理。
如果 x 0 = = 0 x_0==0 x0==0,则:
带配亚诺的余项的泰勒公式就是带有配亚诺余项的麦克劳林(Maclaurin)公式:
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + f ′ ′ ′ ( 0 ) 3 ! x 3 ⋯ f ( n ) ( 0 ) n ! x n + o ( x n ) f(x)=f(0)+f'(0)x+\frac {f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3\cdots \frac{f^{(n)}(0)}{n!}x^n+o(x^n) f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′′(0)x3⋯n!f(n)(0)xn+o(xn)
带拉格朗日余项的泰勒公式就是带有拉格朗日的麦克林公式:
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + f ′ ′ ′ ( 0 ) 3 ! x 3 ⋯ f ( n ) ( 0 ) n ! x n + f ( n + 1 ) ( θ x ) ( n + 1 ) ! x n + 1 ( 0 < θ < 1 ) f(x)=f(0)+f'(0)x+\frac {f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3\cdots \frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1}(0<\theta<1) f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′′(0)x3⋯n!f(n)(0)xn+(n+1)!f(n+1)(θx)xn+1(0<θ<1)
函数的单调性与曲线的凸凹性
定理一 :设函数y=f(x)在[a,b]连续,在(a,b)内可导。
(1),如果在(a,b)内f'(x) ≥ 0 \ge 0 ≥0,且等号仅在有限多个点成立,那么函数y=f(x)在[a,b]上单调增加。
(2),如果在(a,b)内f'(x) ≤ 0 \le 0 ≤0,且等号仅在有限多个点处成立,那么函数y=f(x)在[a,b]上单调减少。
定义 :f(x)在区间I上连续,如果对I任意两点 x 1 , x 2 x_1,x_2 x1,x2
如果恒有: f ( x 1 + x 2 2 ) < f ( x 1 ) + f ( x 2 ) 2 f(\frac{x1+x2}{2})<\frac {f(x_1)+f(x_2)}{2} f(2x1+x2)<2f(x1)+f(x2)则称f(x)在I上的图像是凹的。
如果恒有 f ( x 1 + x 2 2 ) > f ( x 1 ) + f ( x 2 ) 2 f(\frac{x1+x2}{2})>\frac {f(x_1)+f(x_2)}{2} f(2x1+x2)>2f(x1)+f(x2)则称f(x)在I上的图像是凸的。
定理二 :设f(x)在[a,b]上连续,在(a,b)内有一阶和二阶导数,那么:
(1),若在(a,b)内,f''(x)>0,则f(x)在[a,b]上的图像是凹的。
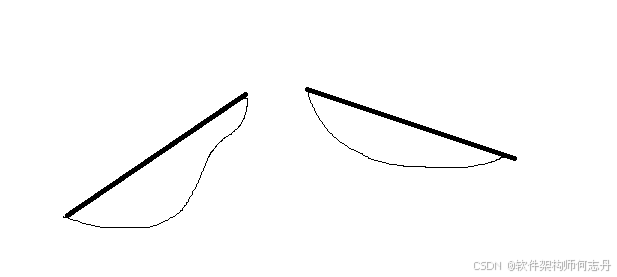
曲线的斜率都是变大。
(2),若在(a,b)内,f''(x)<0,则f(x)在[a,b]傻瓜的图像是凸的。
证明f''(x)>0,图像时凸的
令 x 1 , x 2 ∈ [ a , b ] , x 2 > x 1 , x 0 = ( x 1 + x 2 ) / 2 , h = ( x 2 − x 1 ) / 2 x1,x2 \in [a,b],x2>x1,x_0=(x_1+x_2)/2,h = (x2-x1)/2 x1,x2∈[a,b],x2>x1,x0=(x1+x2)/2,h=(x2−x1)/2,根据拉格朗日中值定理:
f ( x 0 + h ) − f ( x 0 ) = f ′ ( x 0 + h θ 1 ) h f(x0+h)-f(x0)=f'(x0+h\theta1)h f(x0+h)−f(x0)=f′(x0+hθ1)h
f ( x 0 ) − f ( x 0 − h ) = f ′ ( x 0 − h θ 2 ) h f(x0)-f(x0-h)=f'(x0-h\theta2)h f(x0)−f(x0−h)=f′(x0−hθ2)h
0 < θ 1 , θ 2 < 1 0 < \theta1,\theta2< 1 0<θ1,θ2<1
两者相减:
f ( x 0 + h ) + f ( x 0 − h ) − 2 f ( x 0 ) = f ′ ( x 0 + h θ 1 ) h − f ′ ( x 0 − h θ 2 ) h f(x0+h)+f(x0-h)-2f(x0)=f'(x0+h\theta1)h-f'(x0-h\theta2)h f(x0+h)+f(x0−h)−2f(x0)=f′(x0+hθ1)h−f′(x0−hθ2)h
对f'(x)在区间 [ x 0 − h θ 2 , x 0 + h θ 1 ] [x0-h\theta2,x0+h\theta1] [x0−hθ2,x0+hθ1]继续使用拉格朗日中值定理。
f ′ ( x 0 + h θ 1 ) − f ( x 0 − h θ 2 ) = f ′ ′ ( ξ ) ( h θ 1 + h θ 2 ) f'(x0+h\theta1)-f(x0-h\theta2)=f''(\xi)(h\theta1+h\theta2) f′(x0+hθ1)−f(x0−hθ2)=f′′(ξ)(hθ1+hθ2)
⟺ f ′ ( x 0 + h θ 1 ) − f ( x 0 − h θ 2 ) > 0 \iff {f'(x0+h\theta1)-f(x0-h\theta2)}>0 ⟺f′(x0+hθ1)−f(x0−hθ2)>0右式两个因子>0。
即 f ( x 0 + h ) + f ( x 0 − h ) > 2 f ( x 0 ) f(x0+h)+f(x0-h)>2f(x0) f(x0+h)+f(x0−h)>2f(x0)
即: f ( x 1 ) + f ( x 2 ) 2 > f ( x 1 + x 2 2 ) \frac {f(x1)+f(x2)}{2}>f(\frac {x1+x2}{2}) 2f(x1)+f(x2)>f(2x1+x2)
拐点
如果f''(x)在 x 0 x_0 x0的左右两侧临近异号,那么点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))就是曲线的一个拐点。如果 f ′ ′ ( x 0 ) f''(x_0) f′′(x0)存在则必定为0; f ′ ′ ( x 0 ) f''(x_0) f′′(x0)不存在,也可能是拐点。
函数的极值与最值
定义 :函数f(x)在点 x 0 x_0 x0的某邻域 U ( x 0 ) U(x_0) U(x0)内有定义,如果对于去心邻域 U ˚ ( x 0 ) \mathring U(x_0) U˚(x0)内的任意x,有:
f(x)<f( x 0 ) x_0) x0),那么就称f( x 0 x_0 x0)是函数f(x)的一个极大值。极小值类似。使函数取得极值的点称为极值点。
定理一(必要条件) :函数f(x)在f( x 0 x_0 x0)处可导,且在 x 0 x_0 x0处取得极值。
不是充分条件的理由,f(x)= x 3 , f ′ = 3 x 2 x^3,f'=3x^2 x3,f′=3x2,f'(0)=0,但(0,0)不是极值点。
定理二(第一充分条件) :设函数f(x)在 x 0 x_0 x0处连续,且在 x 0 x_0 x0的某去心邻域 U ˚ ( x 0 , δ ) \mathring U(x_0,\delta) U˚(x0,δ)内可导。
a,若 x ∈ ( x 0 − δ , x 0 ) x\in(x_0-\delta,x_0) x∈(x0−δ,x0)时,f'(x)>0;而 x ∈ ( x 0 , x 0 + δ ) 时 , f ′ ( x ) < 0 。则 f ( x ) 在 x 0 处取最大值。 x\in(x_0,x_0+\delta)时,f'(x)<0。则f(x)在x_0处取最大值。 x∈(x0,x0+δ)时,f′(x)<0。则f(x)在x0处取最大值。
b,若 x ∈ ( x 0 − δ , x 0 ) x\in(x_0-\delta,x_0) x∈(x0−δ,x0)时,f'(x)<0;而 x ∈ ( x 0 , x 0 + δ ) 时 , f ′ ( x ) > 0 。则 f ( x ) 在 x 0 处取最小值。 x\in(x_0,x_0+\delta)时,f'(x)>0。则f(x)在x_0处取最小值。 x∈(x0,x0+δ)时,f′(x)>0。则f(x)在x0处取最小值。
c,若 x ∈ U ˚ ( x 0 , δ ) 时 f ′ ( x ) 符号不变,则 f ( x ) 在 x 0 处没有极值。 x\in \mathring U(x_0,\delta)时f'(x)符号不变,则f(x)在x_0处没有极值。 x∈U˚(x0,δ)时f′(x)符号不变,则f(x)在x0处没有极值。
定理三(第二充分条件) :设函数f(x)在 x 0 x_0 x0处具有二阶导数且f'(x0)=0,f''(x_0) ≠ 0 \neq 0 =0,则:
a,当f''( x 0 ) < 0 x_0)<0 x0)<0时,函数f(x)在 x 0 x_0 x0处取得最大值。
b,当f''( x 0 ) > 0 x_0)>0 x0)>0时,函数f(x)在 x 0 x_0 x0处取得最大值。
下面证明情况a:
f(x)存在二阶导数,说明f'(x_0)的左右导数相等。
f ′ ′ ( x 0 ) = lim x → x 0 + f ′ ( x ) − f ′ ( x 0 ) x − x 0 < 0 即 x > x 0 , f ′ ( x ) < 0 。 f''(x_0)=\lim\limits_{x \to x_0^+} \frac{f'(x)-f'(x_0)}{x-x_0}<0即x>x_0,f'(x)<0。 f′′(x0)=x→x0+limx−x0f′(x)−f′(x0)<0即x>x0,f′(x)<0。
f ′ ′ ( x 0 ) = lim x → x 0 − f ′ ( x ) − f ′ ( x 0 ) x − x 0 < 0 即 x < x 0 , f ′ ( x ) > 0 。 f''(x_0)=\lim\limits_{x \to x_0^-} \frac{f'(x)-f'(x_0)}{x-x_0}<0即x<x_0,f'(x)>0。 f′′(x0)=x→x0−limx−x0f′(x)−f′(x0)<0即x<x0,f′(x)>0。
即符合定理二。
函数图形的绘制
第一步:确定函数y=f(x)的定义域及函数所具有的某些特性(如奇偶性、周期性等),并求出函数的一阶导数和二阶导数。
第二步:求出f'(x)和f''(x)在定义域的全部零点,并求出函数f(x)的间断点及f'(x)和f''(x)不存在点,用这些点把函数的定义域划分成几个区间。
第三步:确定在这些区间内f'(x)和f''(x)的符号,并由此确定此函数图形的升降、凹凸和拐点。
第四步:确定函数图形的水平、铅直渐进性及其它变化趋势。
第五步:算出f'(x)和f''(x)的零点以及不存在的点所对应的函数值,定出图形上相应的点;为了把图形描绘得准确些,有时还需要补充一些点,然后结合第三、第四步中得到得结果,连接这些点画出函数y=f(x)得图形。
曲率
弧微分
设函数f(x)在区间(a,b)内具有连续导数,在曲线y=f(x)上取固定点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)作为度量弧长的基点,并规定依x增大的方向为正方向。对曲线任意一点M(x,y),规定有向弧 M 0 M ⌢ \overset{\frown}{M_0M} M0M⌢的值s为这段弧的长度。
( Δ s Δ x ) 2 = ( M M ′ ⌢ Δ x ) 2 (\frac {\Delta s}{\Delta x})^2=(\frac{\overset{\frown}{MM'}}{\Delta x})^2 (ΔxΔs)2=(ΔxMM′⌢)2
= ( M M ′ ⌢ ∣ M M ′ ∣ ) 2 ( ∣ M M ′ ∣ Δ x ) 2 =(\frac{\overset{\frown}{MM'}}{|MM'|})^2(\frac{|MM'|}{\Delta x})^2 =(∣MM′∣MM′⌢)2(Δx∣MM′∣)2
= ( M M ′ ⌢ ∣ M M ′ ∣ ) 2 Δ 2 x + Δ 2 y Δ 2 x =(\frac{\overset{\frown}{MM'}}{|MM'|})^2 \frac{\Delta^2x + \Delta^2 y}{\Delta^2 x} =(∣MM′∣MM′⌢)2Δ2xΔ2x+Δ2y
= ( M M ′ ⌢ ∣ M M ′ ∣ ) 2 ( 1 + ( Δ y Δ x ) 2 ) =(\frac{\overset{\frown}{MM'}}{|MM'|})^2 (1+(\frac {\Delta y}{\Delta x})^2) =(∣MM′∣MM′⌢)2(1+(ΔxΔy)2)
= ( 1 + ( Δ y Δ x ) 2 ) 因为 Δ x → 0 , 弧线和切线相等 = (1+(\frac {\Delta y}{\Delta x})^2) 因为 \Delta x\to 0,弧线和切线相等 =(1+(ΔxΔy)2)因为Δx→0,弧线和切线相等
故 Δ s Δ x = ± 1 + y ′ 2 \frac {\Delta s}{\Delta x}=\pm \sqrt{1+y'^2} ΔxΔs=±1+y′2
d s = 1 + y ′ 2 d x ds=\sqrt{1+y'^2}dx ds=1+y′2 dx弧微分公式
曲率及其计算公式
α \alpha α表示切线转过的角度。我们用比值 Δ α Δ s \frac{\Delta \alpha}{\Delta s} ΔsΔα来表达 M M ′ ⌢ \overset{\frown}{MM'} MM′⌢平均弯曲程度,即平均曲率。记作 K ‾ = ∣ Δ α Δ s ∣ \overline{K}=|\frac{\Delta \alpha}{\Delta s}| K=∣ΔsΔα∣
上述平均曲率的极限叫做曲线C的M处的曲率,即:
K = lim Δ s → 0 ∣ Δ α Δ s ∣ K=\lim\limits_{\Delta s \to 0}|\frac{\Delta \alpha}{\Delta s}| K=Δs→0lim∣ΔsΔα∣
直线的曲率为0。
求圆的曲率:令 ∠ M O M ′ = Δ α , M M ′ ⌢ = Δ α × r \angle MOM'=\Delta \alpha,\overset{\frown}{MM'}=\Delta\alpha \times r ∠MOM′=Δα,MM′⌢=Δα×r,r是圆的半径。
曲率= Δ α r Δ α = 1 r \frac{\Delta \alpha}{r \Delta \alpha}=\frac 1 r rΔαΔα=r1,同一个圆各处曲率相等,曲率和半场成反比。
曲线的曲率
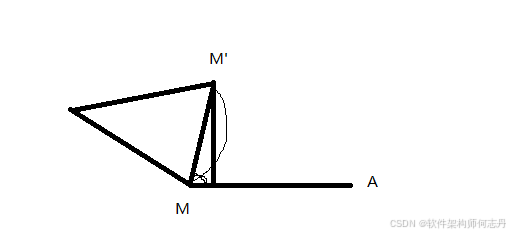
M M ′ ⌢ 的切线和水平线组成的夹角为 ∠ M ′ M A = α \overset{\frown}{MM'}的切线和水平线组成的夹角为\angle {M'MA}=\alpha MM′⌢的切线和水平线组成的夹角为∠M′MA=α。故:
f ′ = d y d x = tan α f'=\frac {dy}{dx}= \tan \alpha f′=dxdy=tanα
根据复合函数的求导法则 f ′ ′ = sec 2 α d a d x f''=\sec^2 \alpha \frac {da}{dx} f′′=sec2αdxda
即: d a d x = f ′ ′ cos 2 α = f ′ ′ cos 2 α sin 2 α + cos 2 α = f ′ ′ 1 tan 2 α + 1 = y ′ ′ 1 + y ′ 2 \frac {da}{dx}=f''\cos^2 \alpha=f'' \frac {\cos^2 \alpha}{\sin^2\alpha+\cos^2 \alpha}=f''\frac 1 {\tan^2\alpha +1}=\frac {y''}{1+y'^2} dxda=f′′cos2α=f′′sin2α+cos2αcos2α=f′′tan2α+11=1+y′2y′′
d α d s = d a ÷ d x d s ÷ d x = ( y ′ ′ ÷ ( 1 + y ′ 2 ) ) ÷ 1 + y ′ 2 = y ′ ′ ( 1 + y ′ 2 ) 3 2 \frac {d\alpha}{ds}=\frac{da \div dx}{ds \div dx}=(y'' \div (1+y'^2))\div \sqrt{1+y'^2}=\frac {y''}{(1+y'^2)^\frac 3 2} dsdα=ds÷dxda÷dx=(y′′÷(1+y′2))÷1+y′2 =(1+y′2)23y′′
曲率= ∣ d a d s ∣ |\frac{da}{ds}| ∣dsda∣
下面用直线和园来验证。
直线的二阶导数为0,故曲率为0。
以圆心旋转圆,图形没有发生变化,故各处曲率相等。圆心在原点的园公式: x 2 + y 2 − r 2 = 0 x^2+y^2-r^2=0 x2+y2−r2=0对隐式函数在(0,r)求导:
2 x + 2 y y ′ = 0 ⟺ y ′ = − x ÷ y , f ′ ( 0 ) = 0 2x+2yy'=0 \iff y'=-x \div y ,f'(0)=0 2x+2yy′=0⟺y′=−x÷y,f′(0)=0
f ′ ′ ( x ) = y + x y ′ y 2 f''(x)=\frac{y+xy'}{y^2} f′′(x)=y2y+xy′ 代入(0,r) f''(0)= 1 r \frac 1 r r1
曲率为: 1 ÷ r ( 1 + 0 ) 3 2 = 1 r \frac{ 1 \div r}{(1+0)^{\frac 3 2}}=\frac 1 r (1+0)231÷r=r1
曲率圆和曲率半径
设曲线y=f(x)在点M(x,y)处的曲率为K( K ≠ 0 K \neq 0 K=0)。在点M处的曲线法线上,在凹的一侧取一点D,使得|DM|= 1 K \frac 1 K K1。以D为圆心, 1 K \frac 1 K K1为半径做圆。这个圆叫做曲线在点M处的曲率圆,D叫曲率中心, 1 K \frac 1 K K1叫曲率半径。
曲线上点M(x,y)的曲率中心D( α , β \alpha, \beta α,β)坐标公式:
{ α = x − y ′ ( 1 + y ′ 2 ) y ′ ′ β = y + 1 + y ′ 2 y ′ ′ \begin{cases} \alpha=x-\frac{y'(1+y'^2)}{y''}\\ \beta=y+\frac{1+y'^2}{y''} \end{cases} {α=x−y′′y′(1+y′2)β=y+y′′1+y′2
当点(x,f(x))沿曲线C移动时,相应的曲率中心D的轨迹曲线G称为曲线C的渐屈线,而曲线C称为曲线G的渐伸线。
光滑
C n C^n Cn表示n阶导数连续。数学中的光滑,往往指的是: C ∞ C^{\infty} C∞;图形学和CAD中的光滑往往指的是 C 1 或 C 2 C^1或C^2 C1或C2
方程的近似根
二分法对程序员很容易理解,不赘述。
切线法
牛顿法,牛顿迭代法,牛顿-拉弗森方法。
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
设函数f(x)在[a,b]上具有二阶导数,f(a).f(b)<0 且f'(x)及f''(x)在[a,b]上保持定号。
f '(x) 定号 ⇒ 函数单调 ⇒ 区间内只有一个根 ξ \xi ξ,称[a,b]为根的一个隔离区间。
如果f(a)和f''(x)同号,则 x 0 = a x_0=a x0=a;否则 x 0 = b x_0=b x0=b。以 x 0 x_0 x0为初始值,必定收敛
割线法
x n + 1 = x n − x n − x n − 1 f ( x n ) − f ( x n − 1 ) . f ( x n ) x_{n+1}=x_n-\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}.f(x_n) xn+1=xn−f(xn)−f(xn−1)xn−xn−1.f(xn),用 x n , x n + 1 x_n,x_{n+1} xn,xn+1的切线代替f'(x)。
割线法本身没有简单的初值选取规则保证全局收敛。
其它
f'(x0)=0,驻点;
扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。