树形DP
在树这种数据结构做DP很常见:给定一棵树,要求以最少代价(或最大收益)完成给定操作。在树上做DP显得很自然,因为树本身有"子结构"性质,具有递归性,符合"记忆化递归"的思路。
最优苹果树
问题描述
有一棵苹果树,这棵树共有n个节点,编号1~n,树根编号为1,用一根树枝两端连接的节点编号描述一根树枝的位置。一棵树的枝条太多需要剪枝。但是一些树枝上长有苹果,最好别剪。给定保留树枝的数量,求最多能保留多少个苹果。
输入:第一行输入两个整数n,q,n表示节点数,q表示要保留的树枝数量。接下来n-1行描述树枝信息。每输入3个整数表示连接的节点编号和苹果数量。
输出:能保留的最多苹果数。
思路分析
定义dp[u][j]表示节点u为根的子树留j条边时保留最多的苹果数。dp[1][q]就是答案。
根据树的性质,考虑u的子树,如果子树son留k条边(加上与根节点u的边),其他子树就最多留j-k条边(加上与根节点u的边),将k在[0,j]内遍历不同的分割取最优值。
二叉树状态转移代码
cpp
int dfs(int u,int j){
if(dp[u][j]>=0) return dp[u][j];
for(int k=0;k<j;k++){
dp[u][j]=max(dp[u][j],dfs(u.lson,k)+dfs(u.rson,j-k)); //左右节点结合起来
}
}多叉树状态转移代码
cpp
for(int j=sum[u];j>=0;j--){
for(int k=0;k<=j-1;k++){
dp[u][j]=max(dp[u][j],dp[u][j-k-1]+dp[v][k]+w); //状态转移方程
}
}代码
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=200;
struct node{
int v,w; //v是子节点,w是边[u,v]的值
node(int v=0,int w=0):v(v),w(w){} //括号中的变量为参数值,不用担心二义性问题,可指定默认值
};
vector<node>edge[N];
int dp[N][N]={0},sum[N]={0}; //sum[i]记录以i为根的子树的总边数
int n,q;
void dfs(int u,int f){ //f表示u的父节点,避免回溯访问到父节点造成死循环
for(int i=0;i<edge[u].size();i++){ //遍历u的所有子节点
int v=edge[u][v].v,w=edeg[u][i].w;
if(v==f) continue; //不回头搜索父节点
dfs(v,u); //后续遍历,访问完所有子节点,再来处理该节点
sum[u]+=sum[v]+1; //记录子树(左半边或右半边)上总边数
for(int j=min(q,sum[u]);j>=0;j--){ //子树超出q的部分不用算,节省时间。
for(int k=0;k<=min(sum[v],j-1);k++){ //遍历k进行分割
dp[u][j]=max(dp[u][j],dp[u][j-k-1]+dp[v][k]+w);
}
}
}
}
main(){
scanf("%d %d",&n,&q);
for(int i=1;i<n;i++){
int u,v,w; scanf("%d %d %d",&u,&v,&w); //存无向边
edge[u].push_back(node(v,w));
edge[v].push_back(node(u,w));
}
dfs(1,0);
printf("%d",dp[1][q]);
}代码中 dp[v][k]表示在v留k条边。
dp[u][j-k-1]表示除v上的k条边,以及[u,v]边的u的其他子树上的j-k-1条边。刚开始遍历第一个子树时,dp[u][j-k-1]=0;
关键点:dfs函数中j的循环方向是从sum[u]开始递减的 ,例如,先计算j=5;dp[u][5]用到了dp[u][4],dp[u][3]等,他们都是正确的原值(不含v子树),下一步计算j=4时,新的dp[u][4]用到dp[u][3],dp[u][2]等,新的dp[u][4]会被覆盖,但dp[u][5]已先算好,不会影响,
若j递增循环,先计算dp[u][4]再计算dp[u][5]时,dp[u][4] 已经不是正确的原值了(包含有v子树)。
移除边之后的边权最大和
问题描述
存在一棵具有 n 个节点的无向 树,节点编号为 0 到 n - 1。给你一个长度为 n - 1 的二维整数数组 edges,其中 edges[i] = [ui, vi, wi] 表示在树中节点 ui 和 vi 之间有一条权重为 wi 的边。
你的任务是移除零条或多条边,使得:
- 每个节点与至多
k个其他节点有边直接相连,其中k是给定的输入。 - 剩余边的权重之和 最大化 。
返回在进行必要的移除后,剩余边的权重的 最大 可能和。
思路分析
首先考虑直接的贪心法,保留每个节点权值最大的k条边的方法是否行得通?
对于如下树:
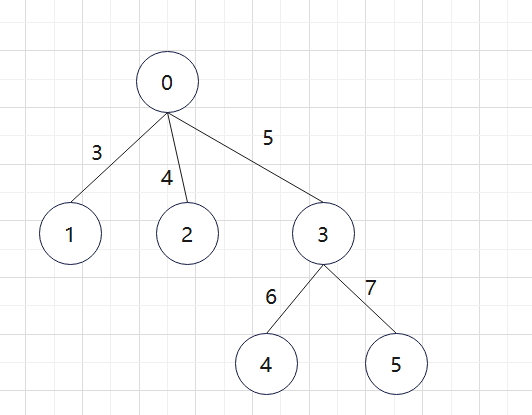
可以发现,按照上述暴力法,删除0号的权值为3的边,删除3号节点的权值为5的边后,权重和为(4+6+7)=17
而上述实例的正确答案为删除权值为5的边后的权重和,即(3+4+6+7)=20
所以这题用简单的贪心遍历是行不通的,应该考虑每个子状态的最优解,应该考虑动态规划。
树形 DP + 贪心
本题是树,考虑节点 x 和它的儿子 y 的这条边(x-y)选或不选:
- 不选 :那么在节点 y 与其儿子的边中,至多选 k 条边。
- 选:那么节点y与其儿子的边中,至多选k-1条边。
对于每个子树root
- 计算并记录
root子树选根节点与其父节点的边 (在与root子树的边中选至多k-1条)的最大权值和c, - 计算并记录
root子树不选根节点与其父节点的边 (在与root子树的边中选至多k条)的最大权值和nc
在与子节点的边中选k条或k-1条边,又该如何选呢?
首先都不选,此时的权重和为所有子树的nci(子树 i 的nc记为nci)之和not_choose,
记录如果选择root根节点与子树 i 的边(权值为wt)带来的权重和增量d[i]=wt+ci-nci
此时选择最大的k-1个增量d添加进not_choose,此时root的c即为该not_choose
再选择第k大的增量d添加进not_choose,此时root的nc即为该not_choose
最后的答案即为题给树的根节点的nc,由于在计算子树root的(c,nc)之前要把root的所有子树的(c,nc)都算出来,所以应采用自底而上的dfs后序遍历。
该算法通过计算每个子树的(c,nc),为上层节点提供了最优的子状态数据,保证了最终结果的正确性。
代码
cpp
long long maximizeSumOfWeights(vector<vector<int>>& edges, int k) {
vector<vector<pair<int, int>>> g(edges.size() + 1);
long long sum_wt = 0; //所有边的权值
for (auto& e : edges) {
int x = e[0], y = e[1], wt = e[2];
g[x].emplace_back(y, wt); //记录邻接边终点及权值
g[y].emplace_back(x, wt);
sum_wt += wt;
}
// 优化
bool simple = true;
for (auto& to : g) {
if (to.size() > k) {
simple = false;
break;
}
}
if (simple) { //所有节点相连边数都小于等于k
return sum_wt;
}
auto dfs = [&](auto& dfs, int x, int fa) -> pair<long long, long long> {
long long not_choose = 0;
vector<long long> inc;
for (auto& [y, wt] : g[x]) {
if (y == fa) { //邻接边终点为父节点直接退出当前循环
continue;
}
auto [nc, c] = dfs(dfs, y, x); //
not_choose += nc; // 先都不选
long long d = c + wt - nc;
if (d > 0) {
inc.push_back(d);
}
}
// 再选增量最大的 k 个或者 k-1 个
ranges::sort(inc, greater()); // 从大到小排序
for (int i = 0; i < min((int) inc.size(), k - 1); i++) {
not_choose += inc[i];
}
long long choose = not_choose;
if (inc.size() >= k) {
not_choose += inc[k - 1];
}
return {not_choose, choose};
};
return dfs(dfs, 0, -1).first; // not_choose >= choose
}
//作者:灵茶山艾府左孩子右兄弟
蓝桥杯2021年省赛题
问题描述
对于一棵多叉树,可以通过"左孩子右兄弟"表示法,将其转化为一棵二叉树。如果我们认为每个节点的子节点是无序的,那么得到的二叉树可能不唯一。
换句话说,每个节点可以选任意子节点作为左孩子,并按任意顺序连接右兄弟。给定包含N个节点的多叉树,节点编号1到N,其中1号节点是根节点,每个节点的父节点编号比自己编号小。请计算通过"左孩子右兄弟"表示法转化成的二叉树,高度最高是多少?
注:根节点的深度为0.
输入
第一行输入一个N,后面N-1行,每行输入一个整数,依次表示2~N节点的父节点编号
思路分析
回顾一下"左孩子右兄弟"表示法,对于根节点x,首先选择节点x的一个孩子lson作为左孩子,其他孩子(即lson的兄弟节点)加线连接到lson作为lson的右子树。在转化产生的二叉树中,左分支上的各节点在原树中是父子关系,右分支上的各节点在原树上是兄弟关系。
题目要求产生的树的高度最高,而树的高度由叶子的最大深度决定。
我们可以让根节点的所有子树转化为二叉树后高度(设其高度为h)最高的那棵 作为右分支的底端 ,这样便能最大化叶子深度,此时的答案就是max{h}+size(size表示子树数量)。
图例附上
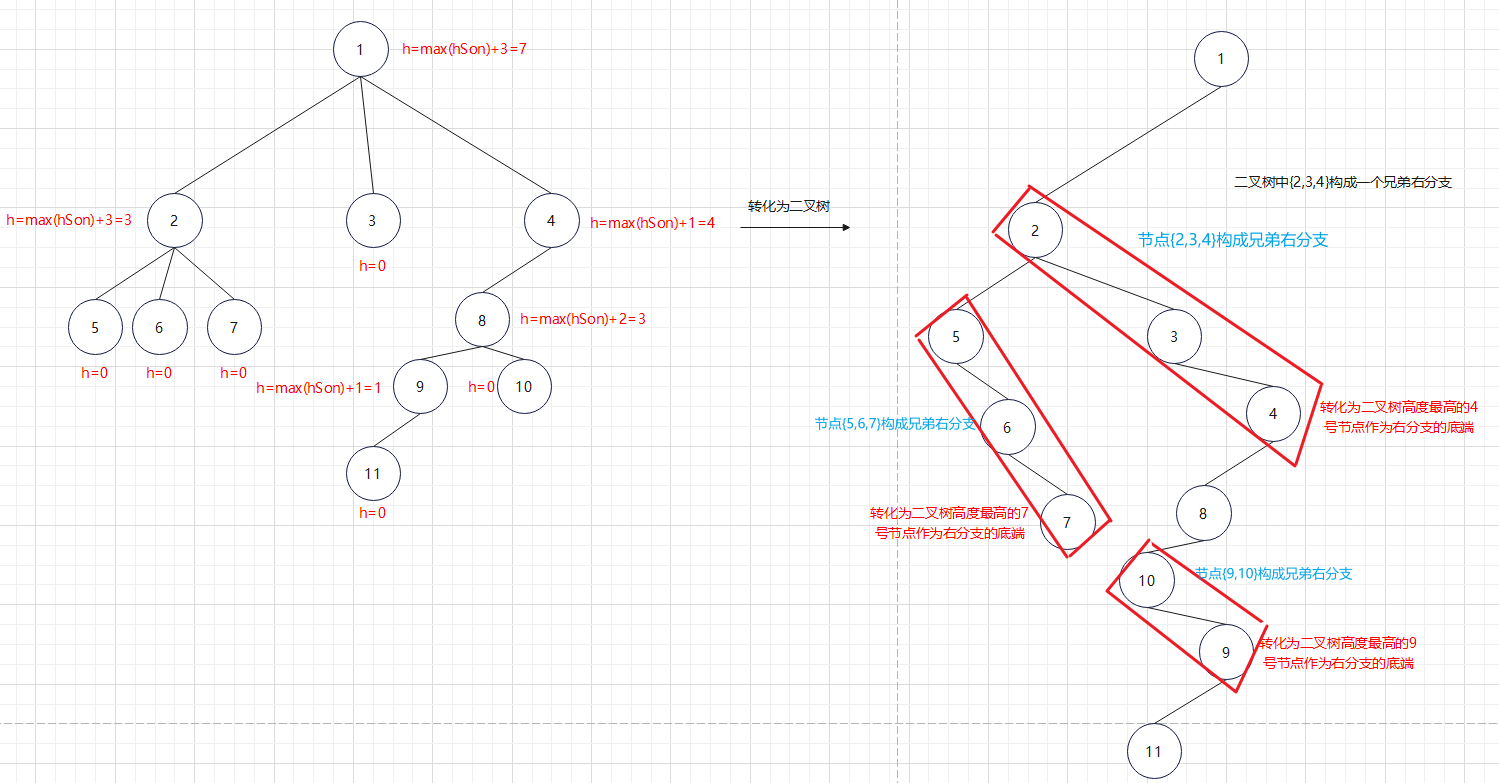
而求子树转化为二叉树后最高高度又是一个规模更小的子问题,用树形dp就是最佳解决方案。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>>son;
int dfs(int root){ //以root节点为根节点的最大高度
int s=0;
for(int i=0;i<son[root].size();i++){
s=max(s,dfs(son[root][i]));
}
return s+son[root].size();
}
int main()
{
int n; cin>>n;
son.resize(n+1); //son[i]记录节点i的孩子
for(int i=2;i<=n;i++){
int t; cin>>t;
son[t].push_back(i);
}
cout<<dfs(1);
return 0;
}