【数据结构】排序

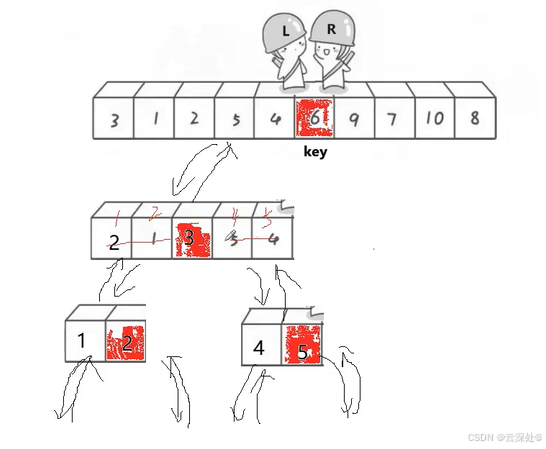
常见排序算法有插入排序（直接插入排序，希尔排序），选择排序（选择排序，堆排序），交换排序（冒泡排序，快速排序），归并排序

插入排序

直接插入排序

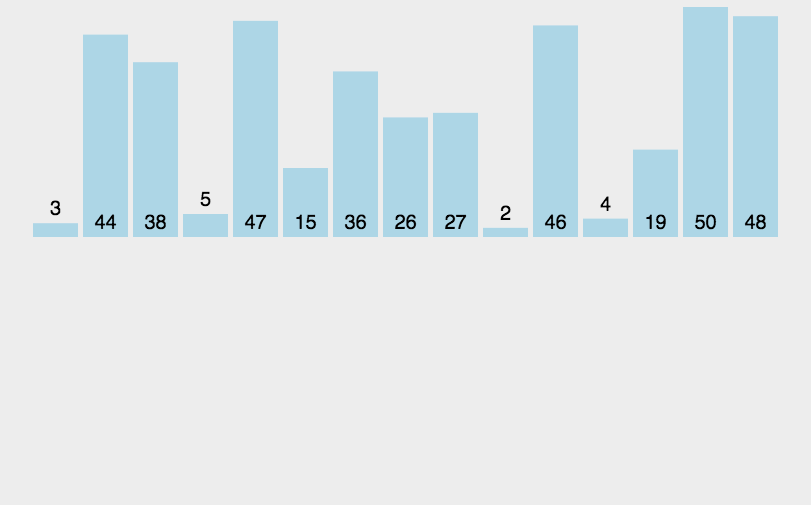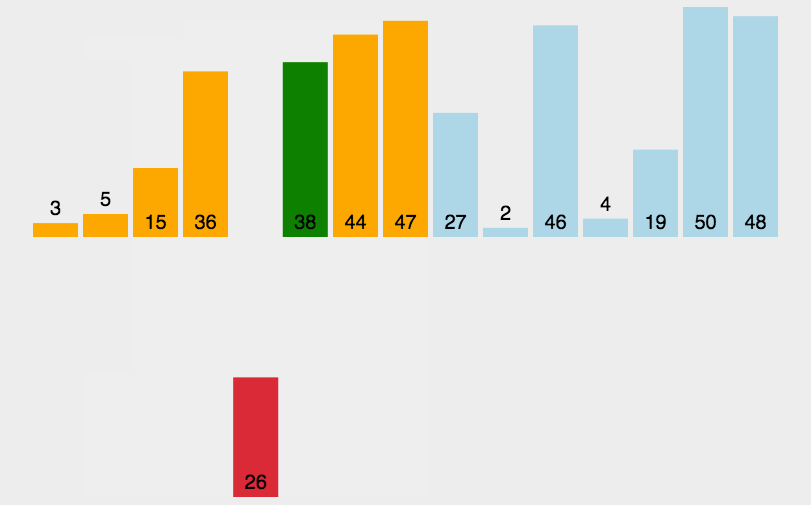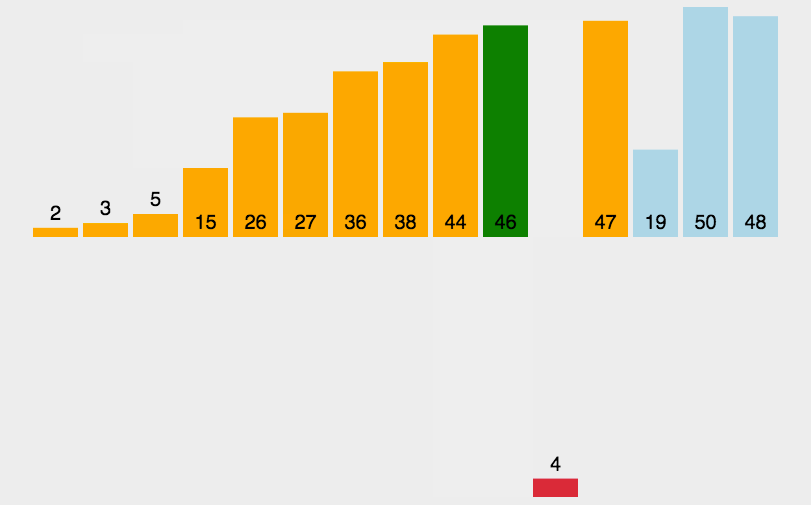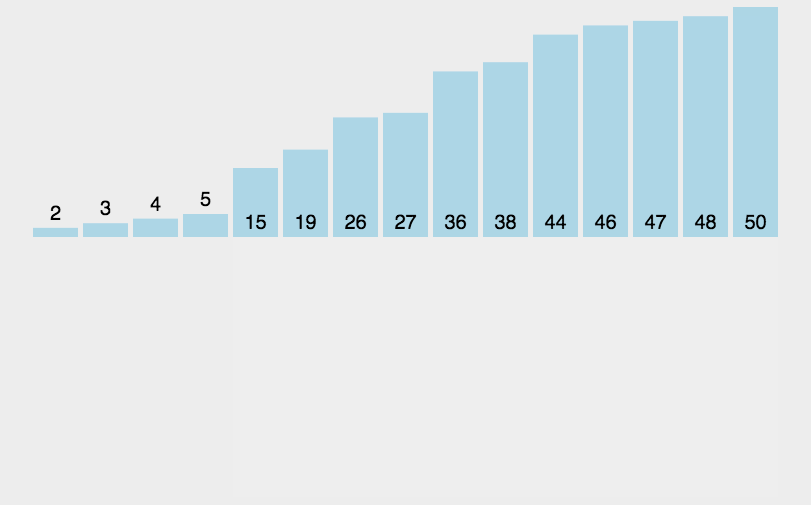
把待排序的记录按关键码值大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列

• 可以看到end的位置一直变化（需要for循环，end的位置从0到n-1），tmp一直在end的后面，且需要先保存下来
• 使用while循环，从end位置到0一次遍历，当end位置的值大于tmp时，end位置的值和下一个位置的值交换，接着end--，直到end小于0

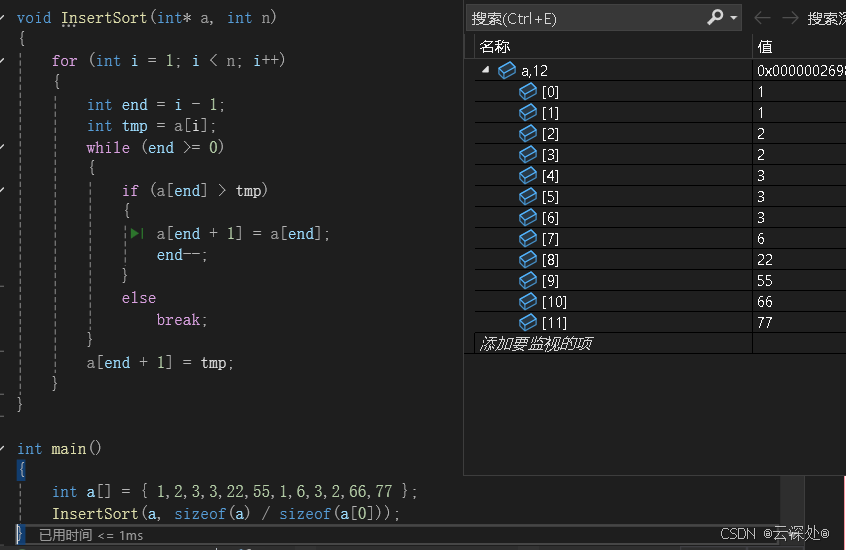
void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
				break;
		}
		a[end + 1] = tmp;
	}
}

总结：插入排序的时间复杂度最坏达到O（N^2），最好达到O（N），有序情况下。空间复杂度O（1），是一种有序的算法

希尔排序（最小增量排序）

• 预排序，定义每gap为一组，对每组数据排序，在直接插入排序的基础上加上了gap
• 一组排完排另一组，或者按照位置排，走到哪里排哪里（多组并排）
• 使用变化的gap可以提高排序效率，gap越大每组的间隔越大，跳的越快，越不接近有序 。gap越小 ，跳的越慢，越接近有序

时间复杂度：约O(n^1.3)

• 再直接插入排序的基础上优化

---

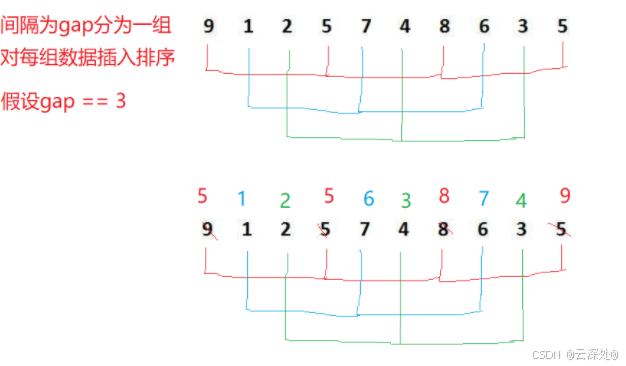
当gap==3时

---

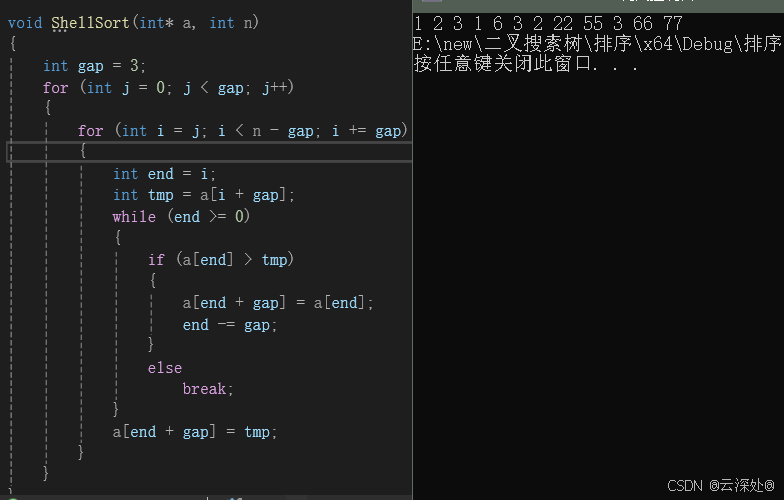
• 变化的gap是完成希尔排序的核心，当gap==1时，降为直接插入排序

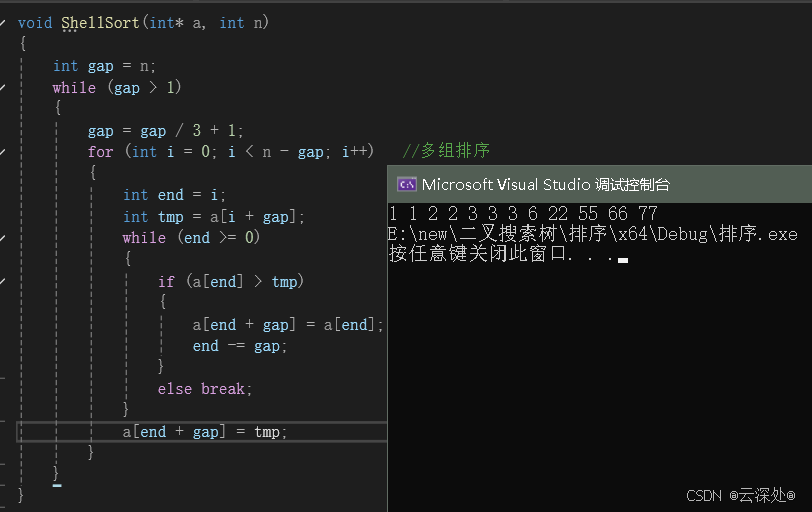
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;	//保证gap最低数1
		for (int i = 0; i < n - gap; i++)	//多组排序
		{
			int end = i;
			int tmp = a[i + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else break;
			}
			a[end + gap] = tmp;
		}
	}
}

选择排序

直接选择排序

• 在数组中依次遍历，选择最大和最小的元素，（交换）分别放在数组的索引最大位置和最低位置
• 在进一步缩小数组范围，选择最大和最小元素放置在数组两端

时间复杂度：O（N^2），空间复杂度O（1），是一种稳定的排序算法

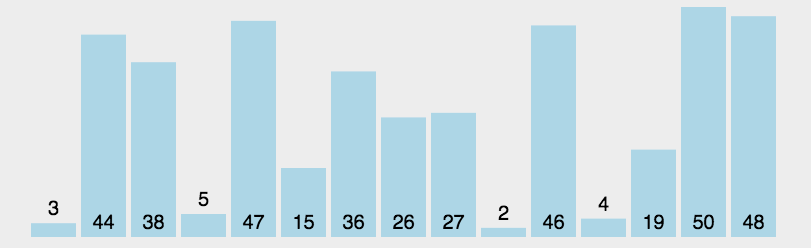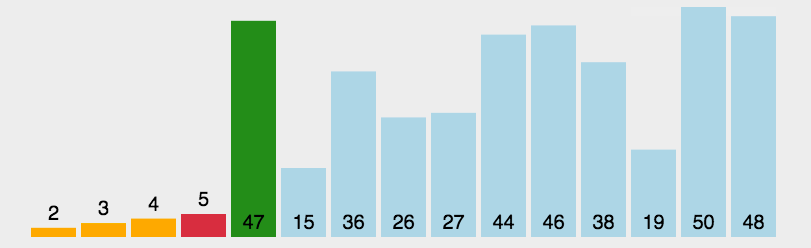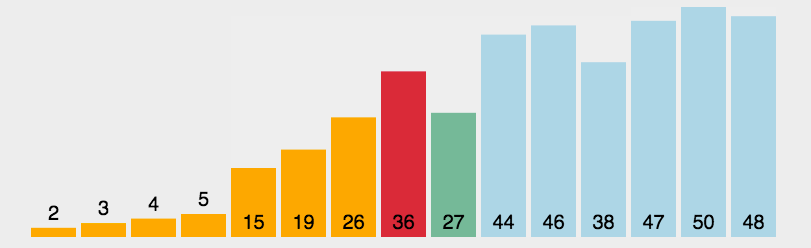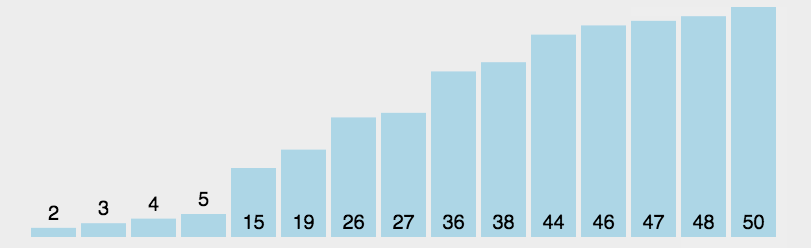
实现：

在下面场景交换会出问题，max的下标为3，min的下标为5，交换后max的下标仍然为3，但是值已经变成3，所以需要修正。在left==max的索引时，交换后修正

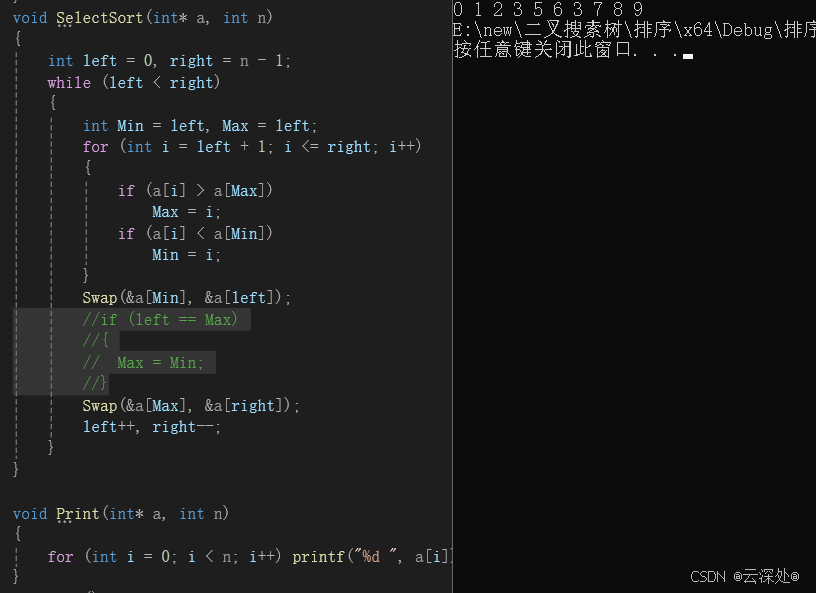
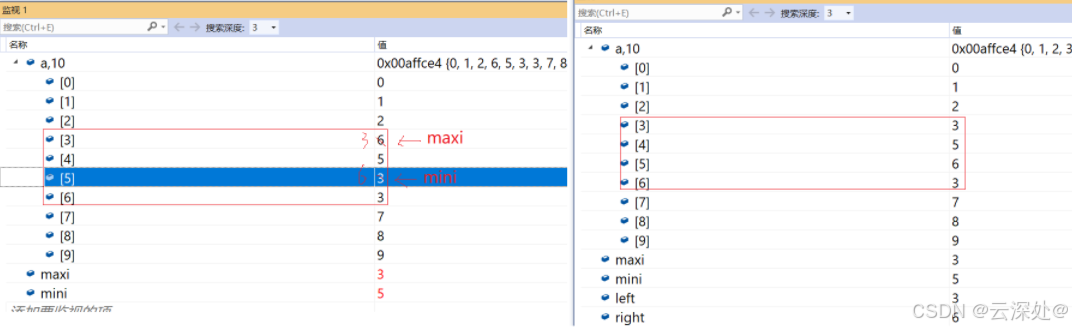
修正：

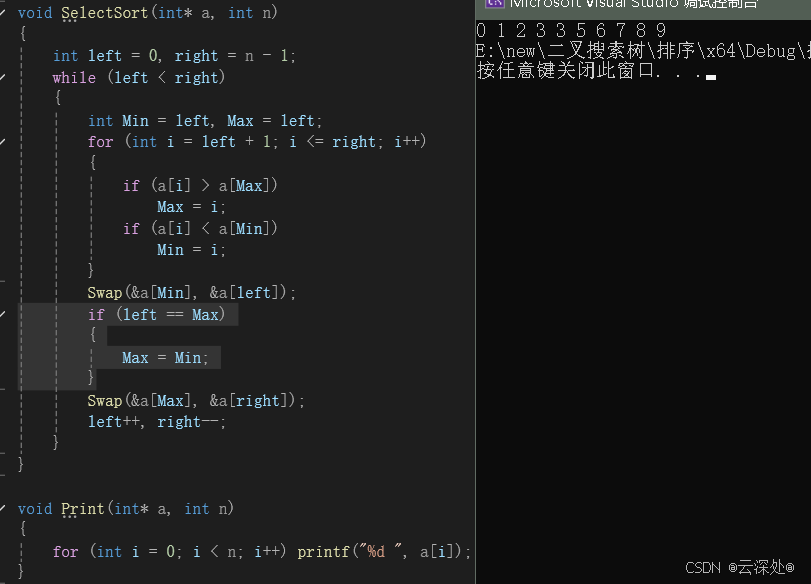
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void SelectSort(int* a, int n)
{
	int left = 0, right = n - 1;
	while (left < right)
	{
		int Min = left, Max = left;
		for (int i = left + 1; i <= right; i++)
		{
			if (a[i] > a[Max])
				Max = i;
			if (a[i] < a[Min])
				Min = i;
		}
		Swap(&a[Min], &a[left]);
		//如果left和max重叠，修正
		if (left == Max)
		{
			Max = Min;
		}
		Swap(&a[Max], &a[right]);
		left++, right--;
	}
}

堆排序

https://blog.csdn.net/2401_88972077/article/details/151254829

交换排序

冒泡排序

• 两两交换位置，当排好一个后，需要排的个数以此减少

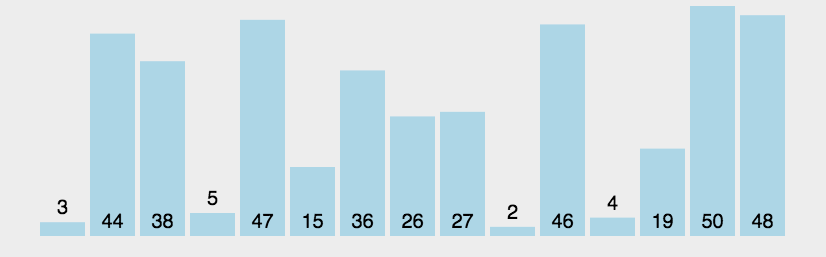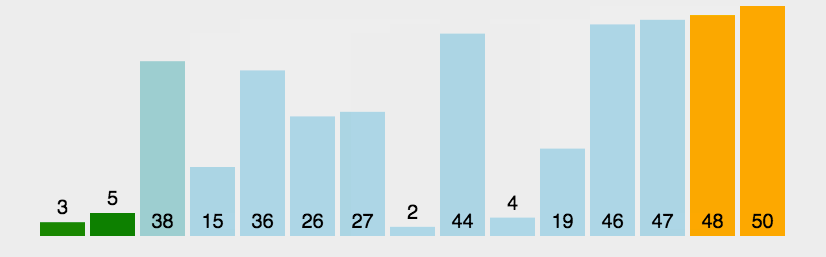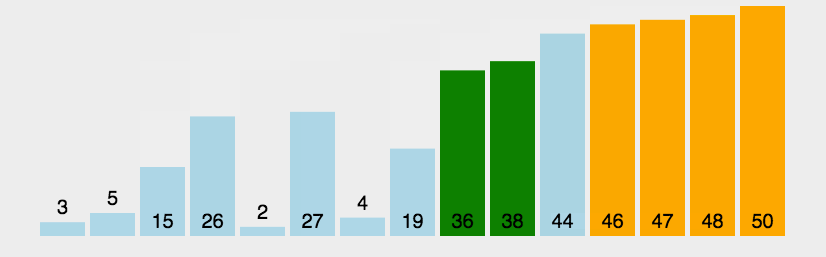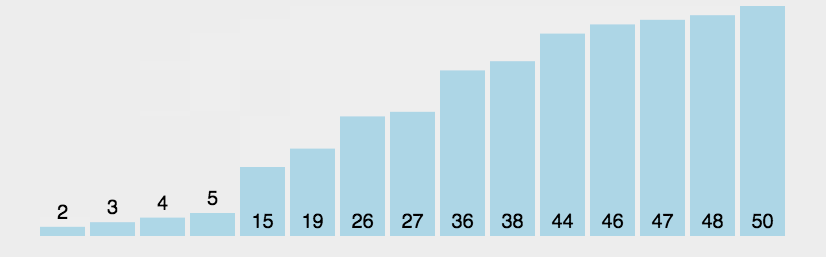
void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		bool exchange = false;
		for (int j = 1; j < n - i; j++)
		{
			if (a[j - 1] > a[j])
			{
				Swap(&a[j], &a[j - 1]);
				exchange = true;
			}
		}
		if (exchange == false) break;
	}
}

选择排序

• 任取待排序列中的某元素作为基准值，按照排序码将待排序集合分割成两子序列
• 左子序列所有元素均小于基准值，右子序列基准值均大于基准值
• 递归调用，直到一个元素
• 有序时，时间复杂度会变大

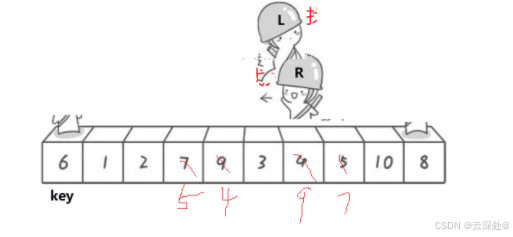
hoare版本：

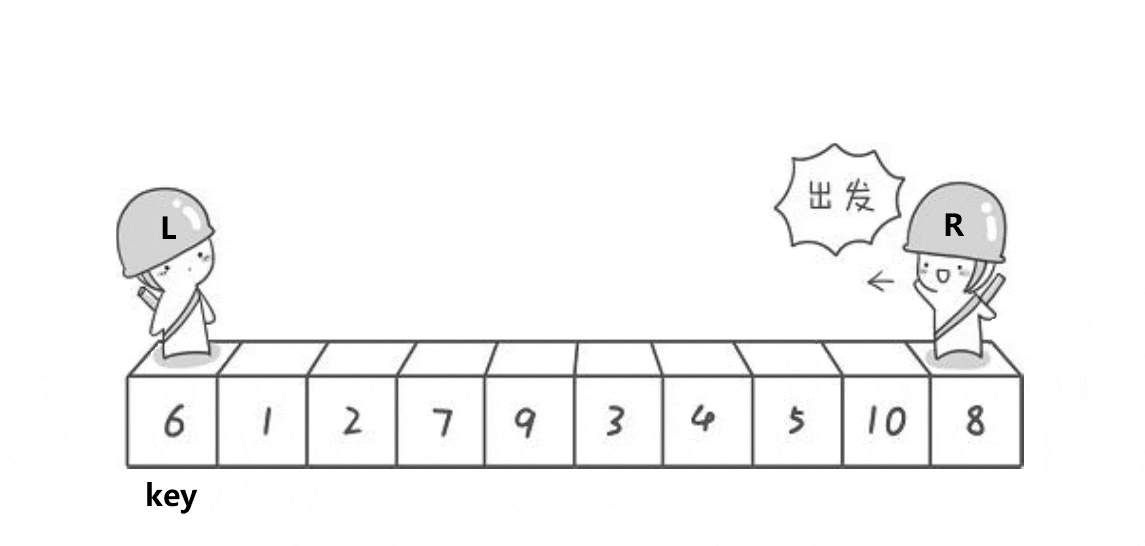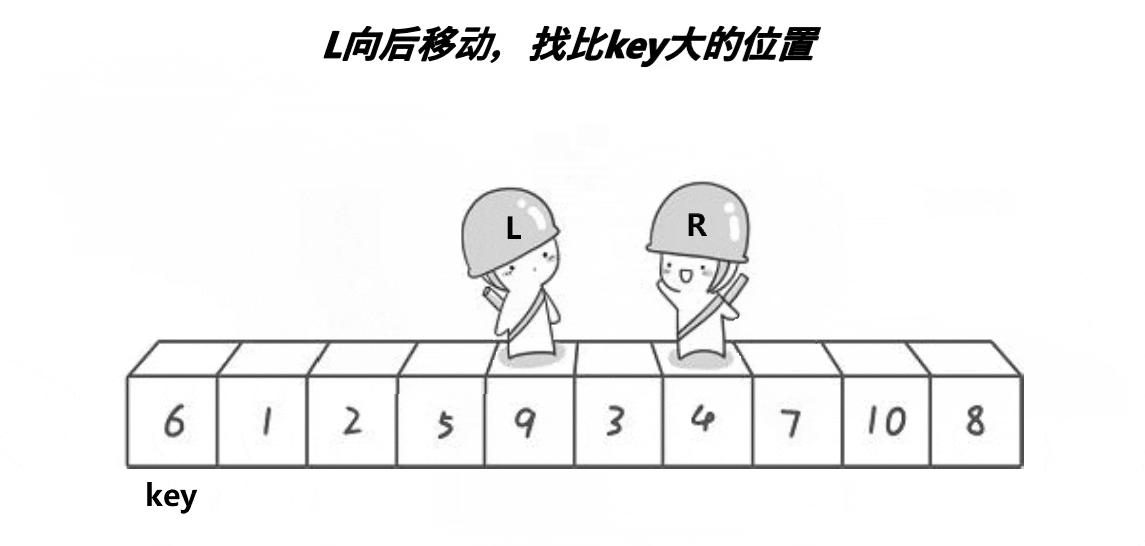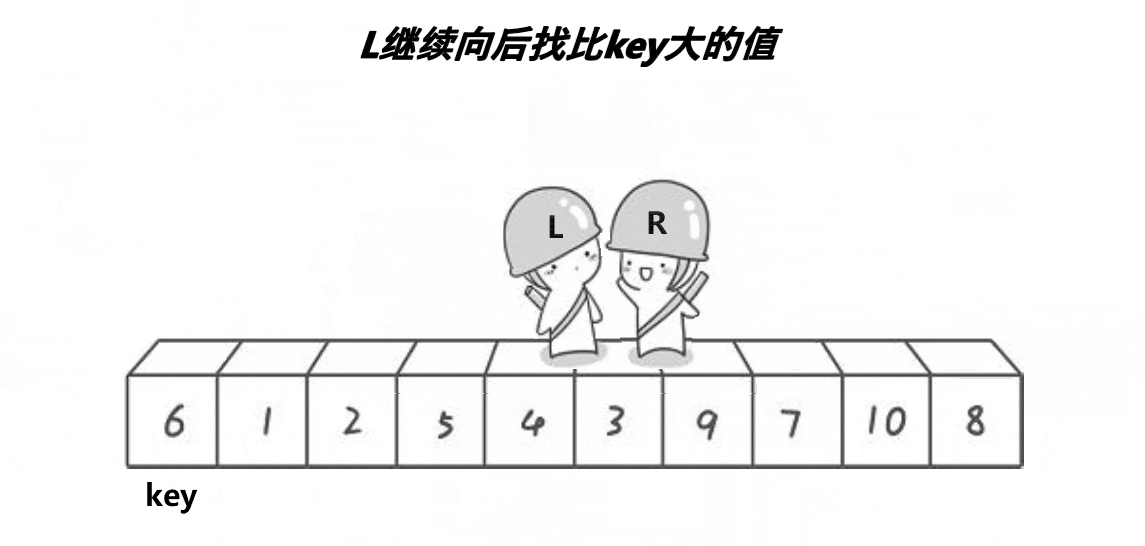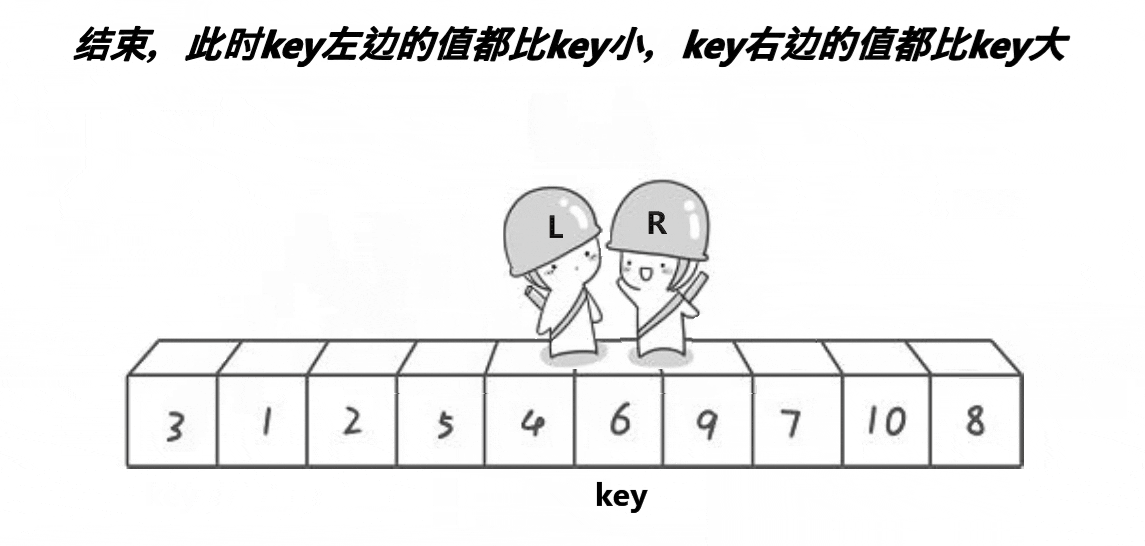
类似二叉树先序遍历：根，左子树，右子树

• 右指针找比key小的元素，找到后停止
• 之后左指针找比key大的元素，找到后与右指针的值交换
• 直到左右指针相遇，将将相遇位置的值与key交换，此时key的左边为小于key的，key的右边为大于key的
• 在key分割的左右两个子区间中再次寻找key值（递归）

• ++左边做key，右边先走，保证相遇位置比key小。或者就是key的位置++
  • ++相遇：右边找到小，左边没有找到大，左遇到右++。++右找小，没有找到，遇到左边得到比key小的++
• ++同理：右边做key，左边先走，相遇位置比key大或就是key的位置++

三数取中优化：

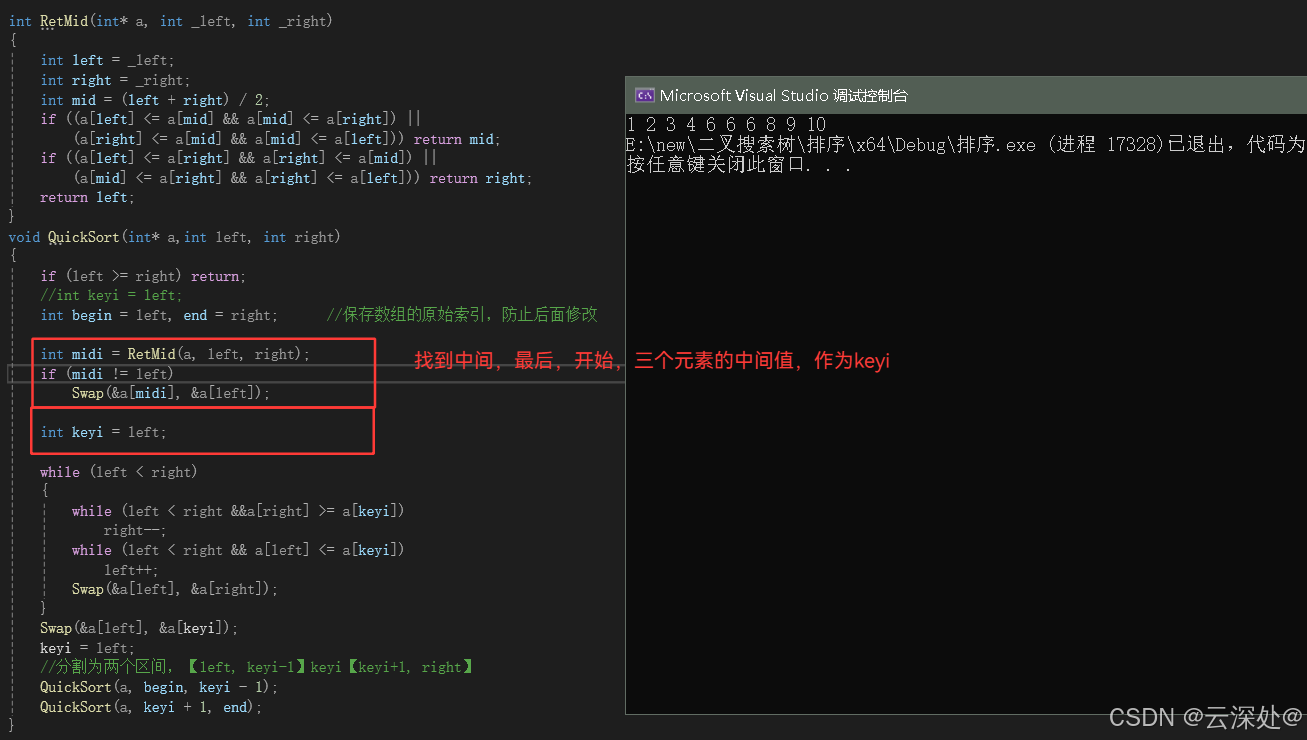
int RetMid(int* a, int _left, int _right)
{
	int left = _left;
	int right = _right;
	int mid = (left + right) / 2;
	if ((a[left] <= a[mid] && a[mid] <= a[right]) ||
		(a[right] <= a[mid] && a[mid] <= a[left])) return mid;
	if ((a[left] <= a[right] && a[right] <= a[mid]) ||
		(a[mid] <= a[right] && a[right] <= a[left])) return right;
	return left;
}
void QuickSort(int* a,int left, int right)
{
	if (left >= right) return;
	//int keyi = left;
	int begin = left, end = right;		//保存数组的原始索引，防止后面修改
	
	int midi = RetMid(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	//int randi = left + (rand() % (right - left));	//随机数选keyi值
	//Swap(&a[left], &a[randi]);

	int keyi = left;

	while (left < right)	//找到比keyi大的和比keyi小的
	{
		while (left < right &&a[right] >= a[keyi])
			right--;
		while (left < right && a[left] <= a[keyi])
			left++;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);	//当left等于right，交换keyi和left的值
	keyi = left;				//将keyi更新为中间值
	//分割为两个区间，【left, keyi-1】keyi【keyi+1, right】
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

挖坑法：

定义坑位，用第三方交换数值

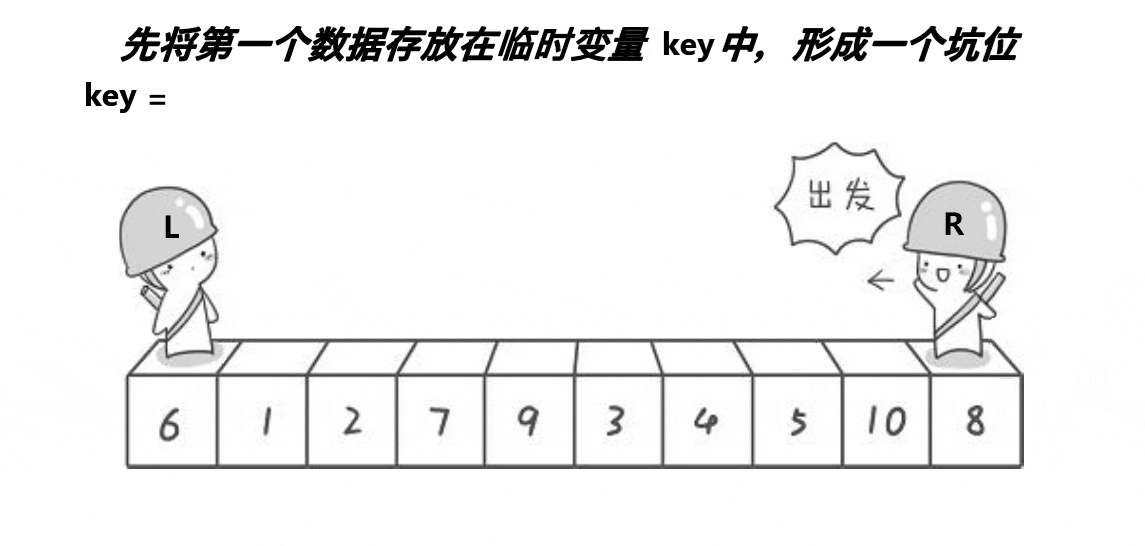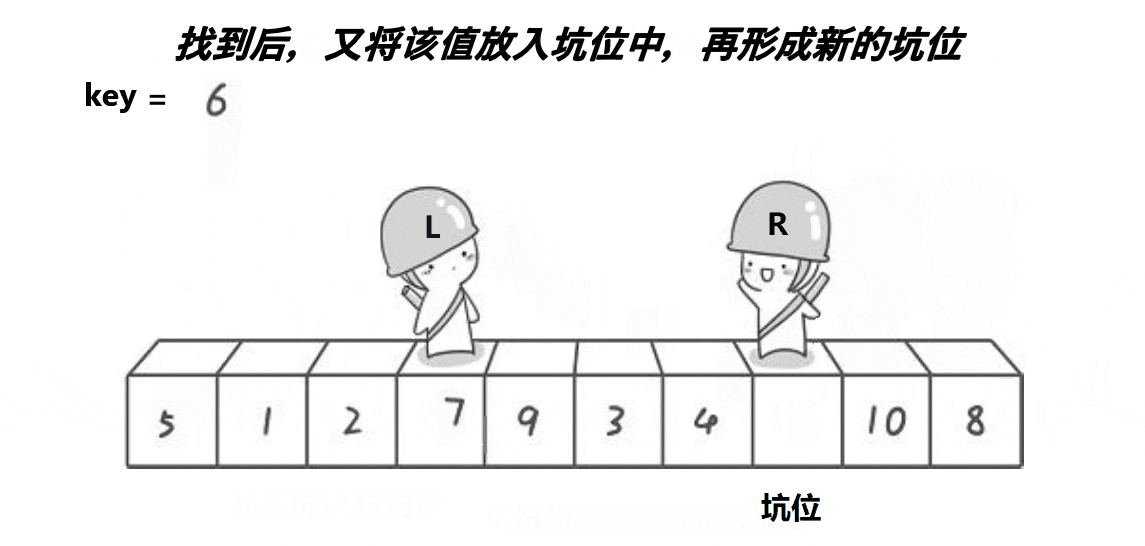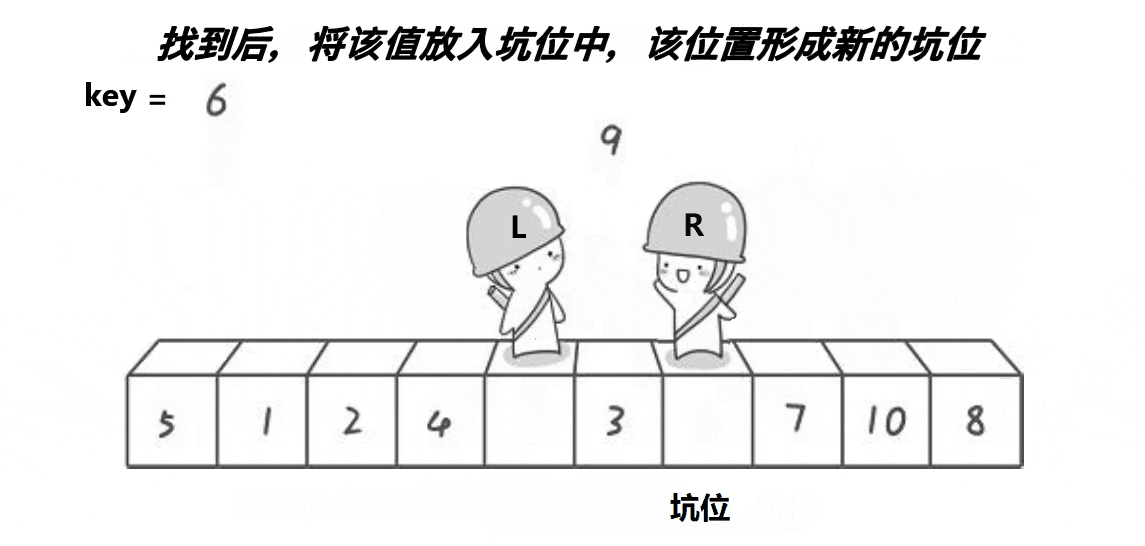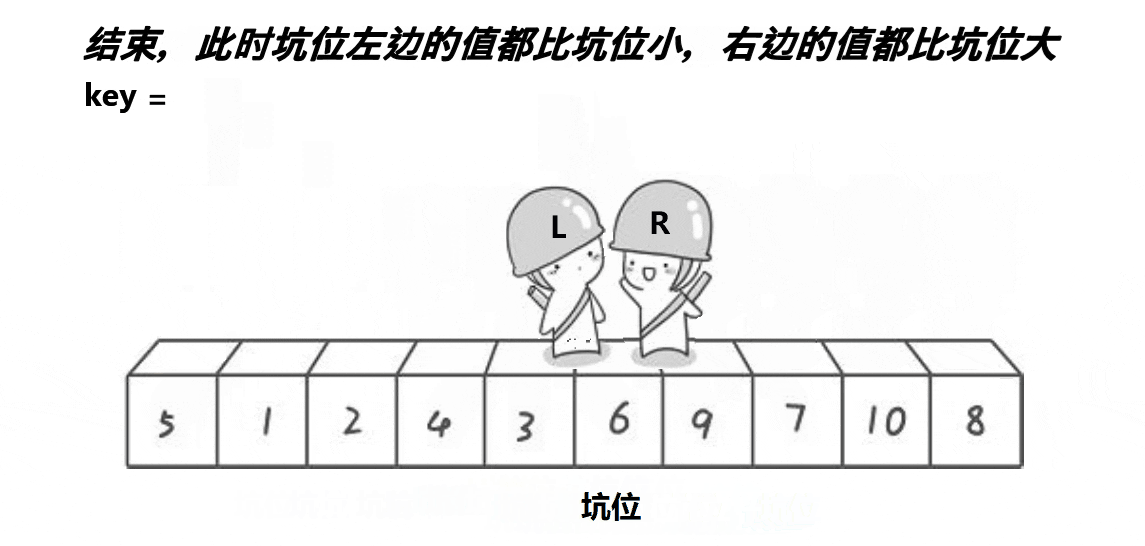
void QuickSort(int* a, int left, int right)		//挖坑法
{
	if (left >= right) return;
	//int keyi = left;
	int begin = left, end = right;		//保存数组的原始索引，防止后面修改

	int midi = RetMid(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	//int randi = left + (rand() % (right - left));	//随机数选keyi值
	//Swap(&a[left], &a[randi]);

	int key = a[left];
	int hole = left;
	while (left < right)	//找到比keyi大的和比keyi小的
	{
		while (left < right && a[right] >= key)
			right--;
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
			left++;
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;

	//分割为两个区间，【left, hole-1】hole【hole+1, right】
	QuickSort(a, begin, hole - 1);
	QuickSort(a, hole + 1, end);
}

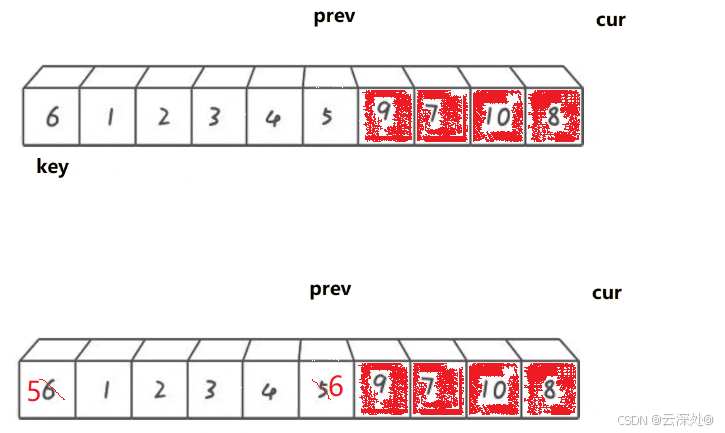
前后指针

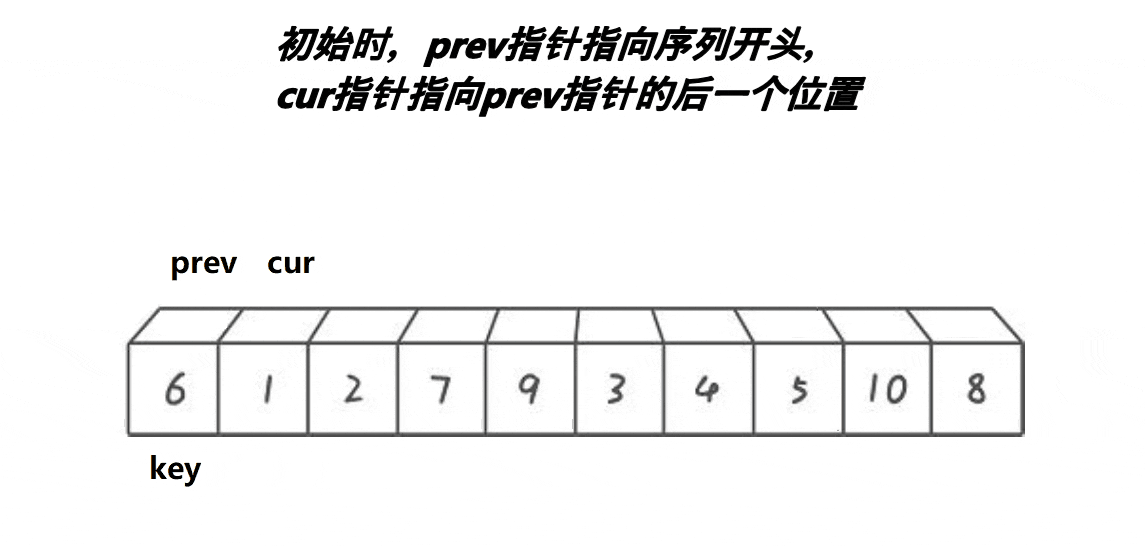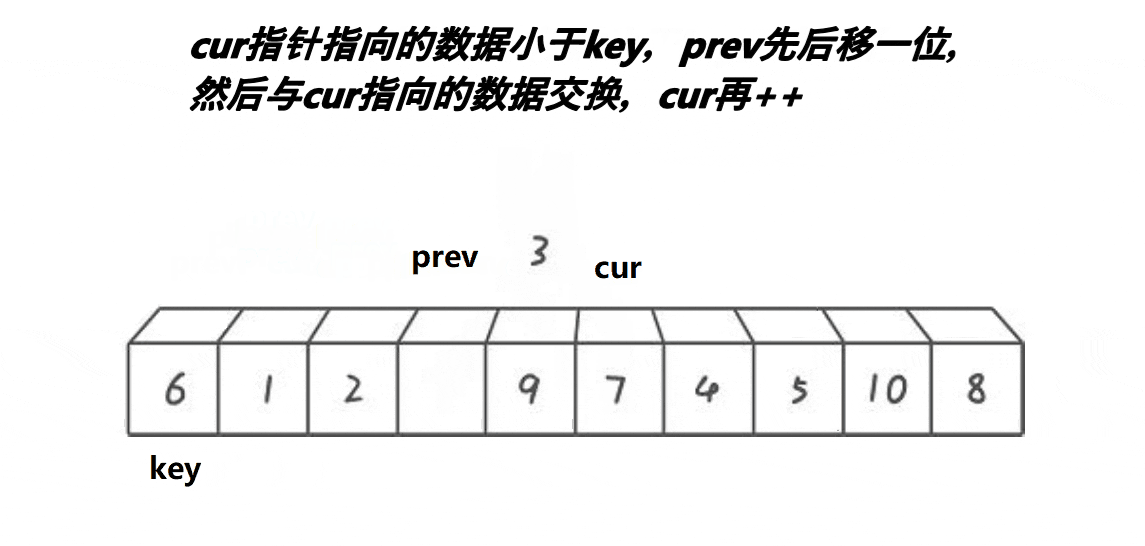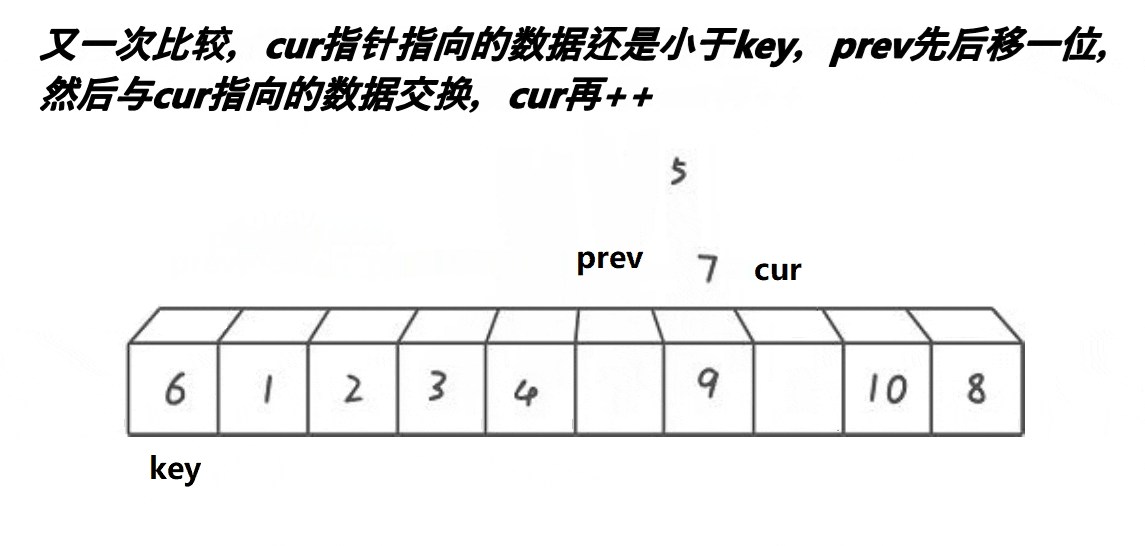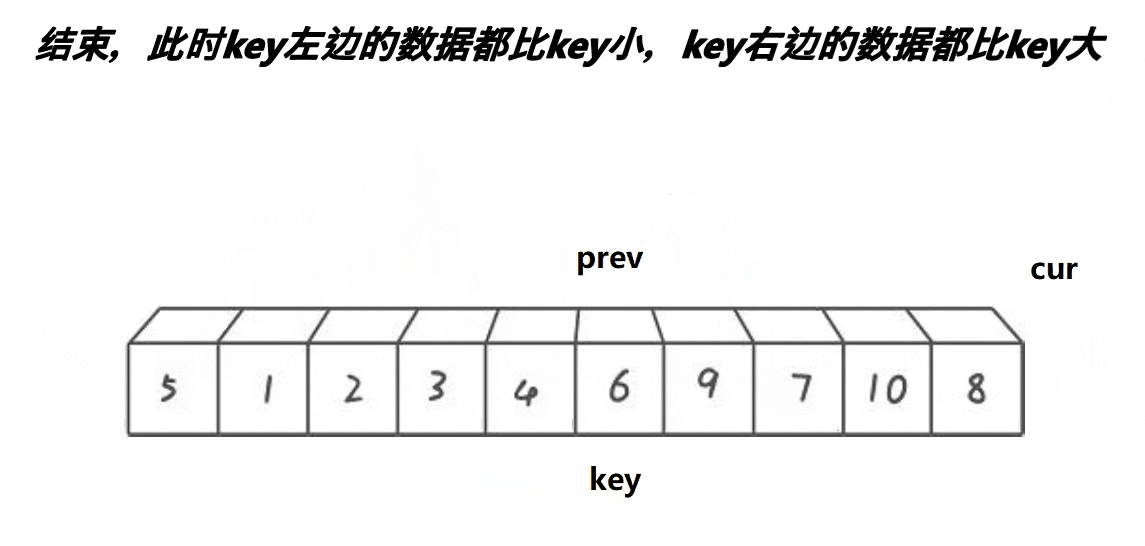
• cur找到比key小的，++prev，交换cur和prev指向的内容，++cur
• cur找到比key大的，++cur
• 其中prev紧跟cur或者间隔比key大的一段区间

整体上把比key大的值搬到右边，比key小的搬到左边，最后keyi = prev

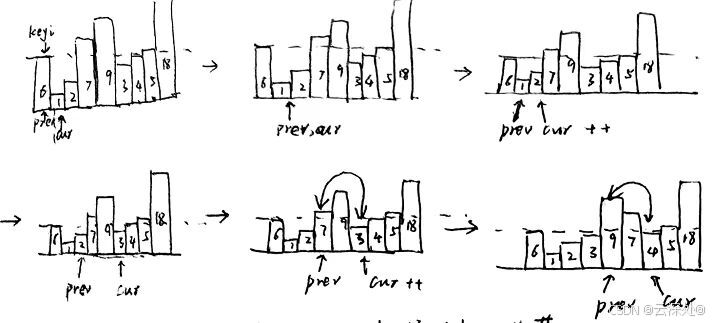
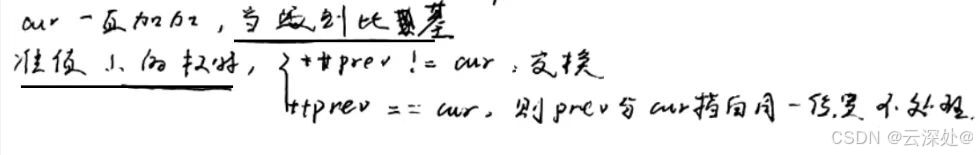
• 这里cur <= right由于排序时是左闭右闭

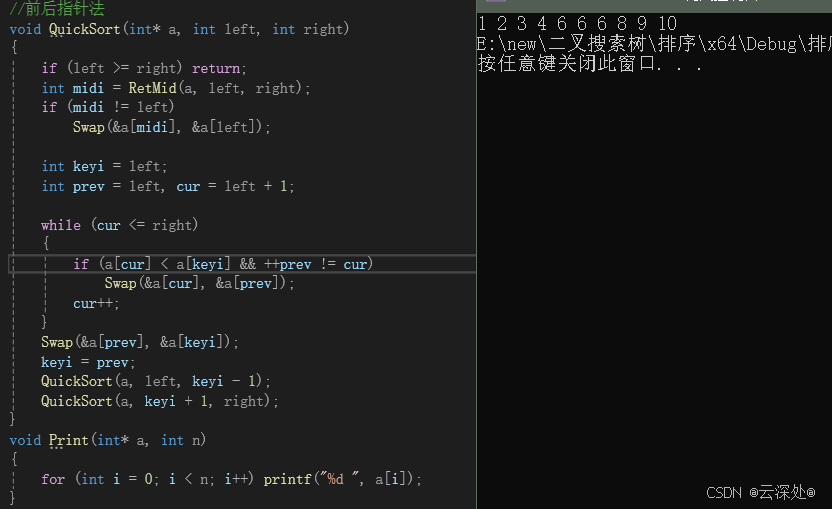
//前后指针法
void QuickSort(int* a, int left, int right)	
{
	if (left >= right) return;
	int midi = RetMid(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	int keyi = left;
	int prev = left, cur = left + 1;

	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[cur], &a[prev]);
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}