考研408--数据结构--day14--B树&B+树&散列表

（以下内容全部出自上述课程）

目录

• B树
• • [1. 引入](#1. 引入)
  • • [1.1 m叉查找树](#1.1 m叉查找树)
    • [1.2 如何查找](#1.2 如何查找)
    • [1.3 如何保证查找效率](#1.3 如何保证查找效率)
  • [2. 定义](#2. 定义)
  • • [2.1 B树](#2.1 B树)
    • [2.2 B树的高度](#2.2 B树的高度)
    • [2.3 小结](#2.3 小结)
  • [3. 基本操作](#3. 基本操作)
  • • [3.1 B树的插入](#3.1 B树的插入)
    • • [3.1.1 第一次溢出](#3.1.1 第一次溢出)
      • [3.1.2 第二次溢出](#3.1.2 第二次溢出)
      • [3.1.3 第三次溢出](#3.1.3 第三次溢出)
      • [3.1.4 第四次溢出](#3.1.4 第四次溢出)
      • [3.1.5 第五次溢出](#3.1.5 第五次溢出)
      • [3.1.6 第六次溢出](#3.1.6 第六次溢出)
    • [3.2 B树的删除](#3.2 B树的删除)
    • • [3.2.1 终端结点](#3.2.1 终端结点)
      • [3.2.2 非终端结点](#3.2.2 非终端结点)
      • [3.2.3 兄弟够借](#3.2.3 兄弟够借)
      • [3.2.4 兄弟不够借](#3.2.4 兄弟不够借)
    • [3.3 小结](#3.3 小结)
• B+树
• • [1. B+树](#1. B+树)
  • [2. B+树的查找](#2. B+树的查找)
  • [3. B+树 vs B树](#3. B+树 vs B树)
  • [4. 小结](#4. 小结)
• 散列表
• • [1. 介绍](#1. 介绍)
  • • [1.1 基本术语](#1.1 基本术语)
    • [1.2 如何处理冲突？（了解）](#1.2 如何处理冲突？（了解）)
    • [1.3 小结](#1.3 小结)
  • [2. 散列函数的构造](#2. 散列函数的构造)
  • • [2.1 设计散列函数时应该注意什么？](#2.1 设计散列函数时应该注意什么？)
    • [2.2 除留余数法](#2.2 除留余数法)
    • [2.3 直接定址法](#2.3 直接定址法)
    • [2.4 数字分析法](#2.4 数字分析法)
    • [2.5 平方取中法](#2.5 平方取中法)
    • [2.6 小结](#2.6 小结)
  • [3. 处理冲突的方法](#3. 处理冲突的方法)
  • • [3.1 拉链法](#3.1 拉链法)
    • • [3.1.1 插入操作](#3.1.1 插入操作)
      • [3.1.2 查找操作](#3.1.2 查找操作)
      • [3.1.3 删除操作](#3.1.3 删除操作)
      • [3.1.4 小结及拓展](#3.1.4 小结及拓展)
    • [3.2 开放定址法](#3.2 开放定址法)
    • • [3.2.1 基本原理](#3.2.1 基本原理)
      • [3.2.2 插入、查找操作](#3.2.2 插入、查找操作)
      • [3.2.3 删除操作](#3.2.3 删除操作)
      • [3.2.4 小结及拓展](#3.2.4 小结及拓展)
  • [4. 散列查找的性能分析](#4. 散列查找的性能分析)
  • • [4.1 性能分析](#4.1 性能分析)
    • [4.2 装填因子](#4.2 装填因子)
    • [4.3 聚集现象](#4.3 聚集现象)
    • [4.4 回顾](#4.4 回顾)

B树

1. 引入

1.1 m叉查找树

回顾二叉查找树，我们就会出现一个疑问：二叉查找树查找那么方便，变成m叉查找树 岂不更方便？

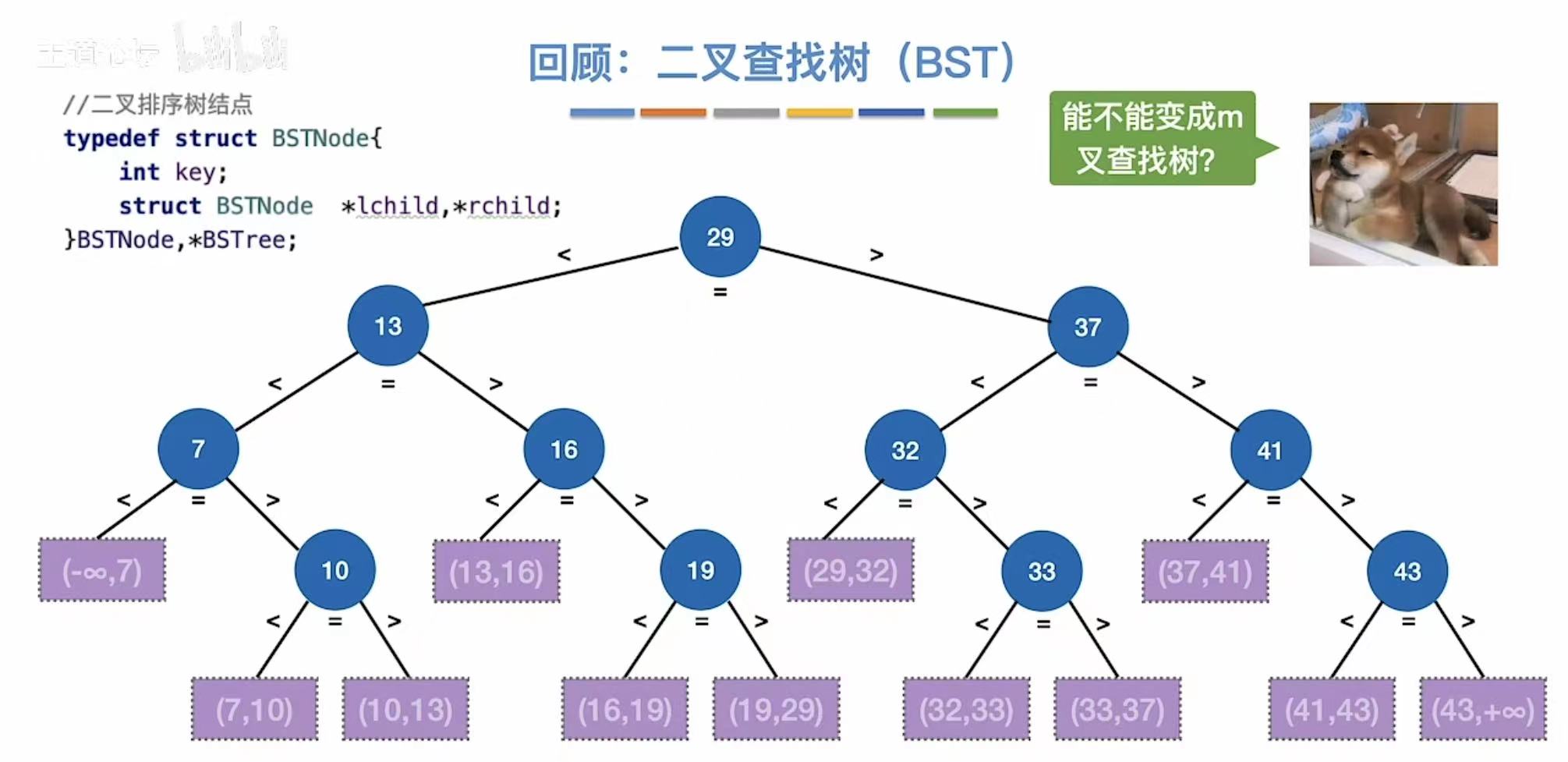
根据上面的想法，我们可以实现出一个5叉查找树，如图所示：

• 一个结点最多可以有4个关键字，也就是5个分叉
• 一个结点最少可以有1个关键字，也就是2个分叉
  

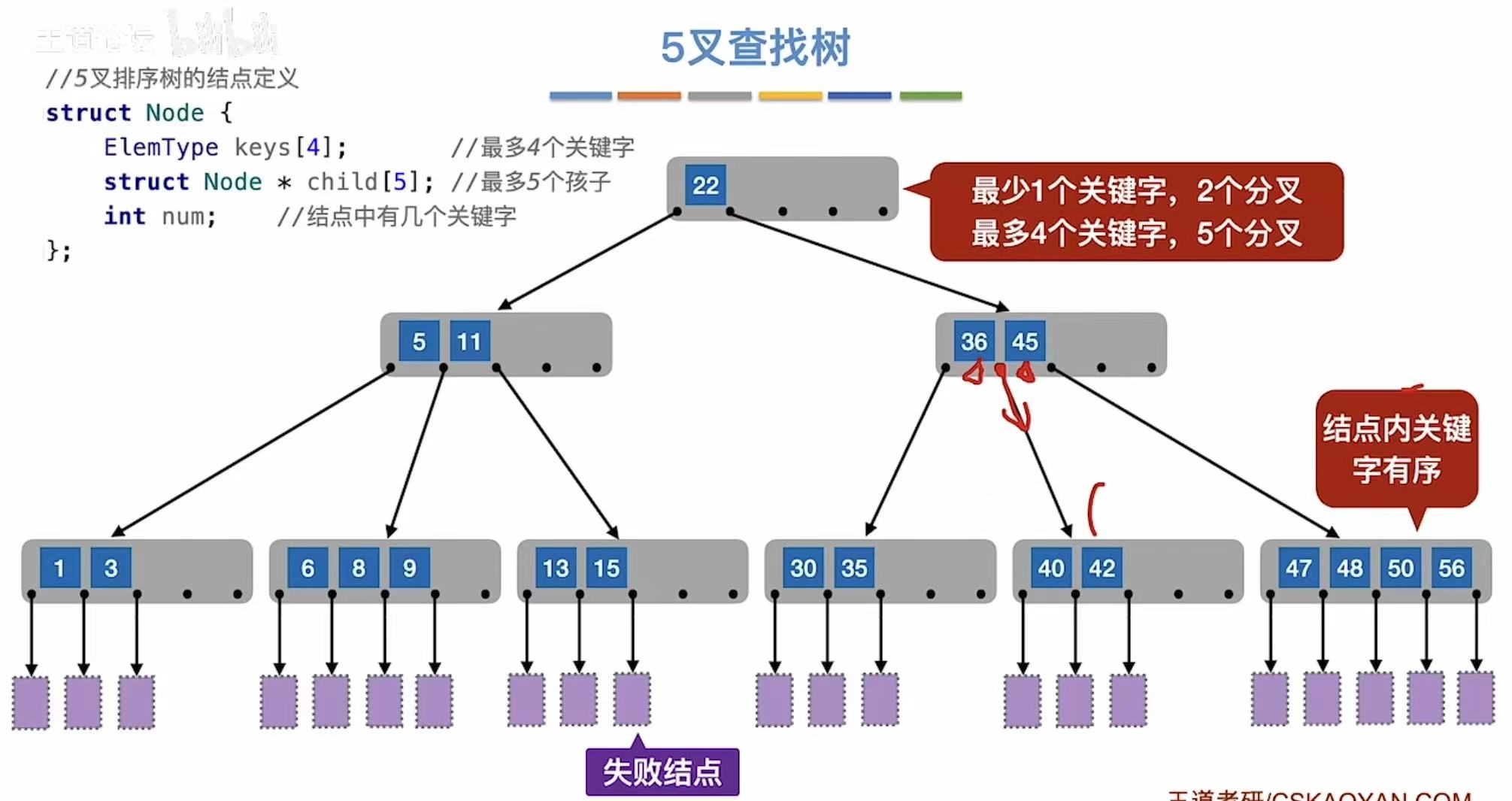
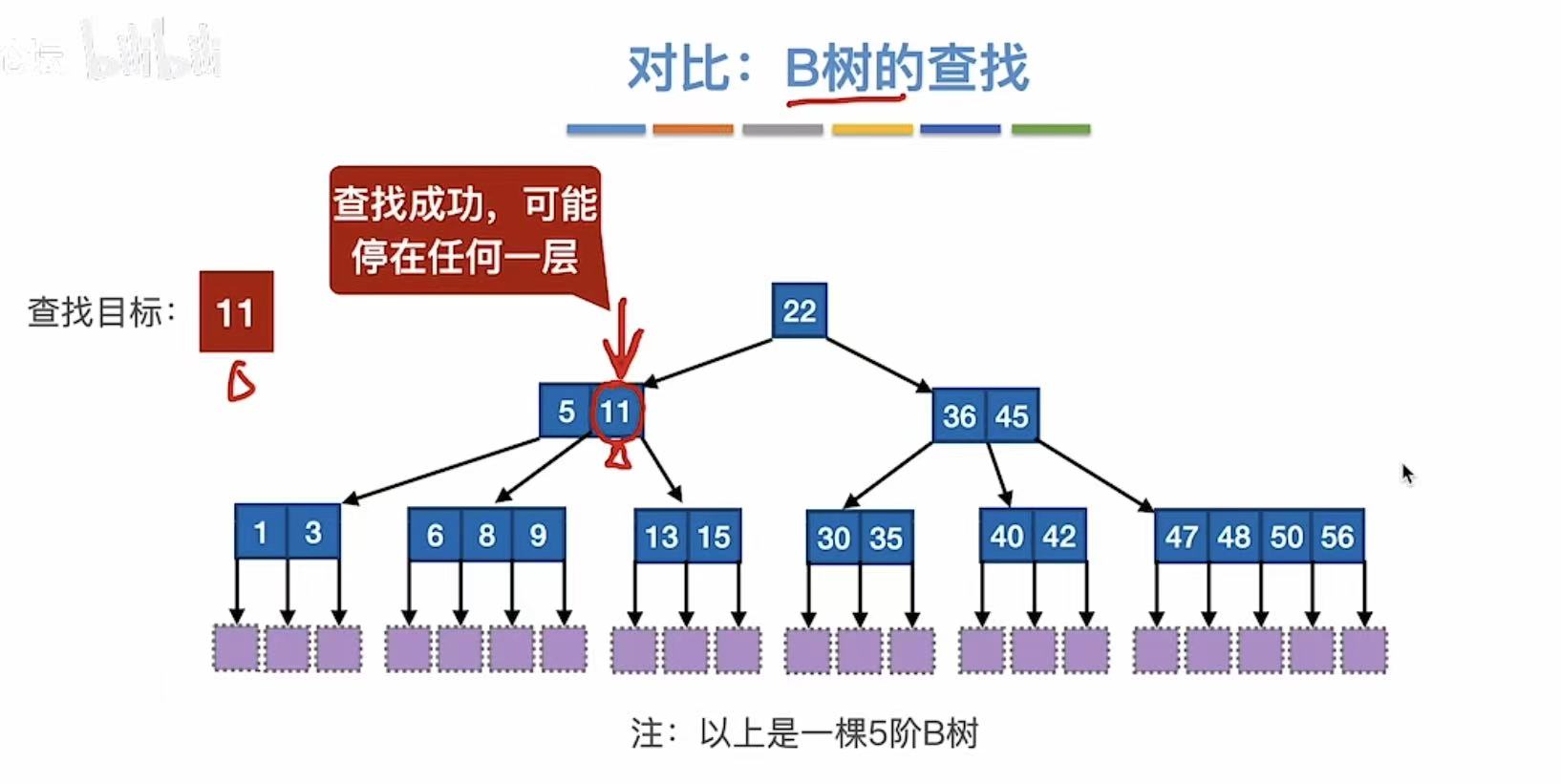
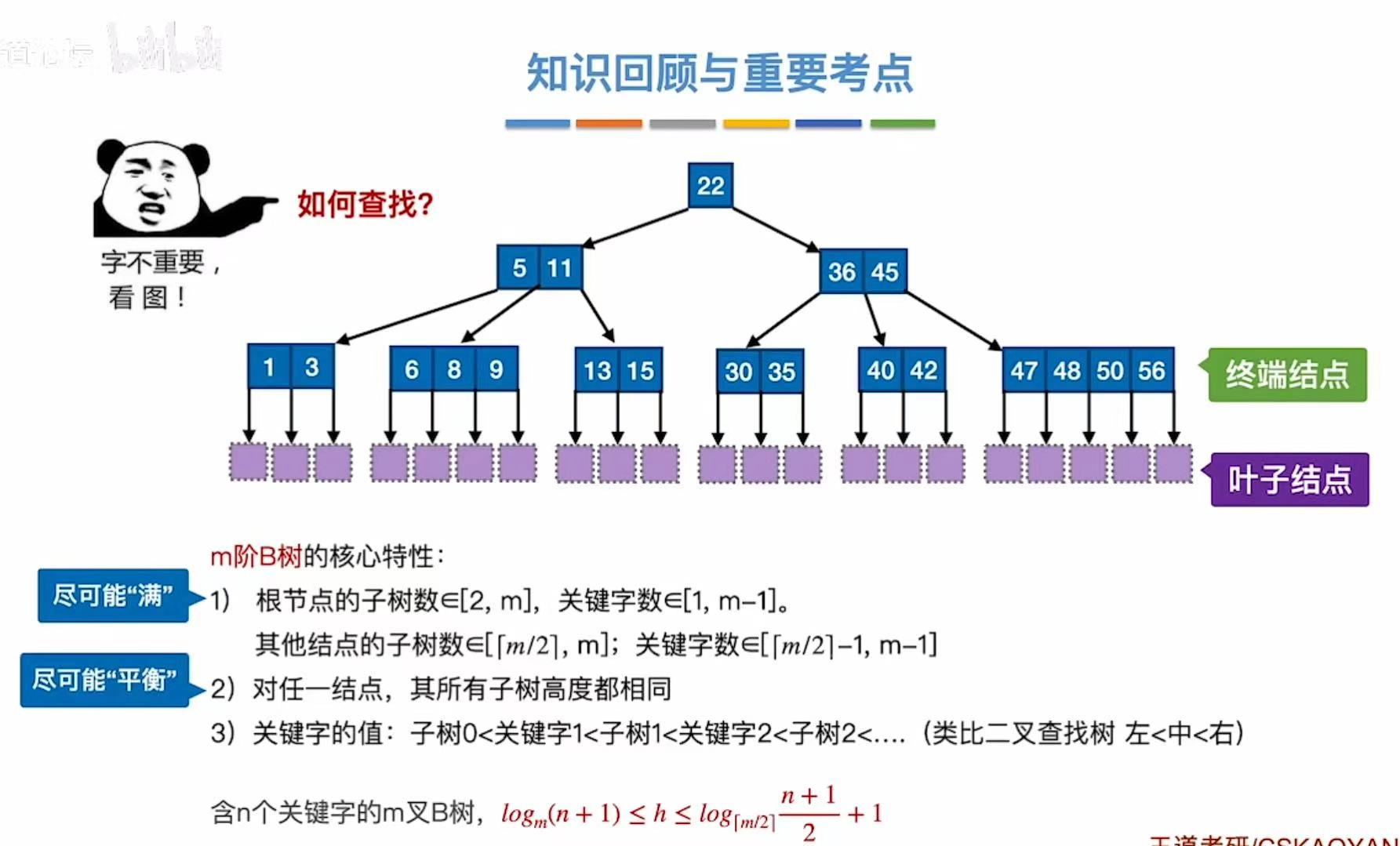
1.2 如何查找

和二叉查找树的模式一模一样，和结点中的数字比大小然后确认继续去那个组进行查找。

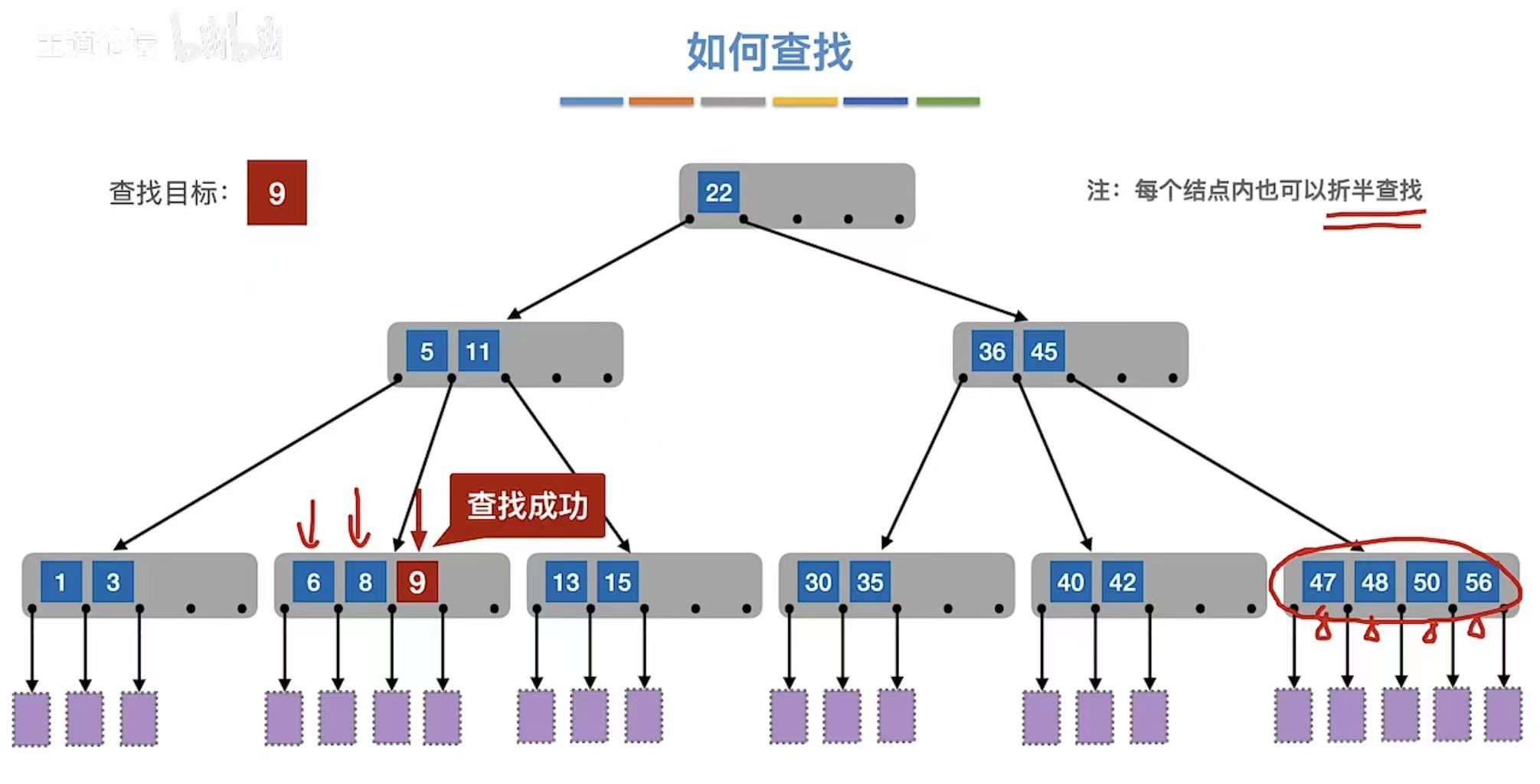
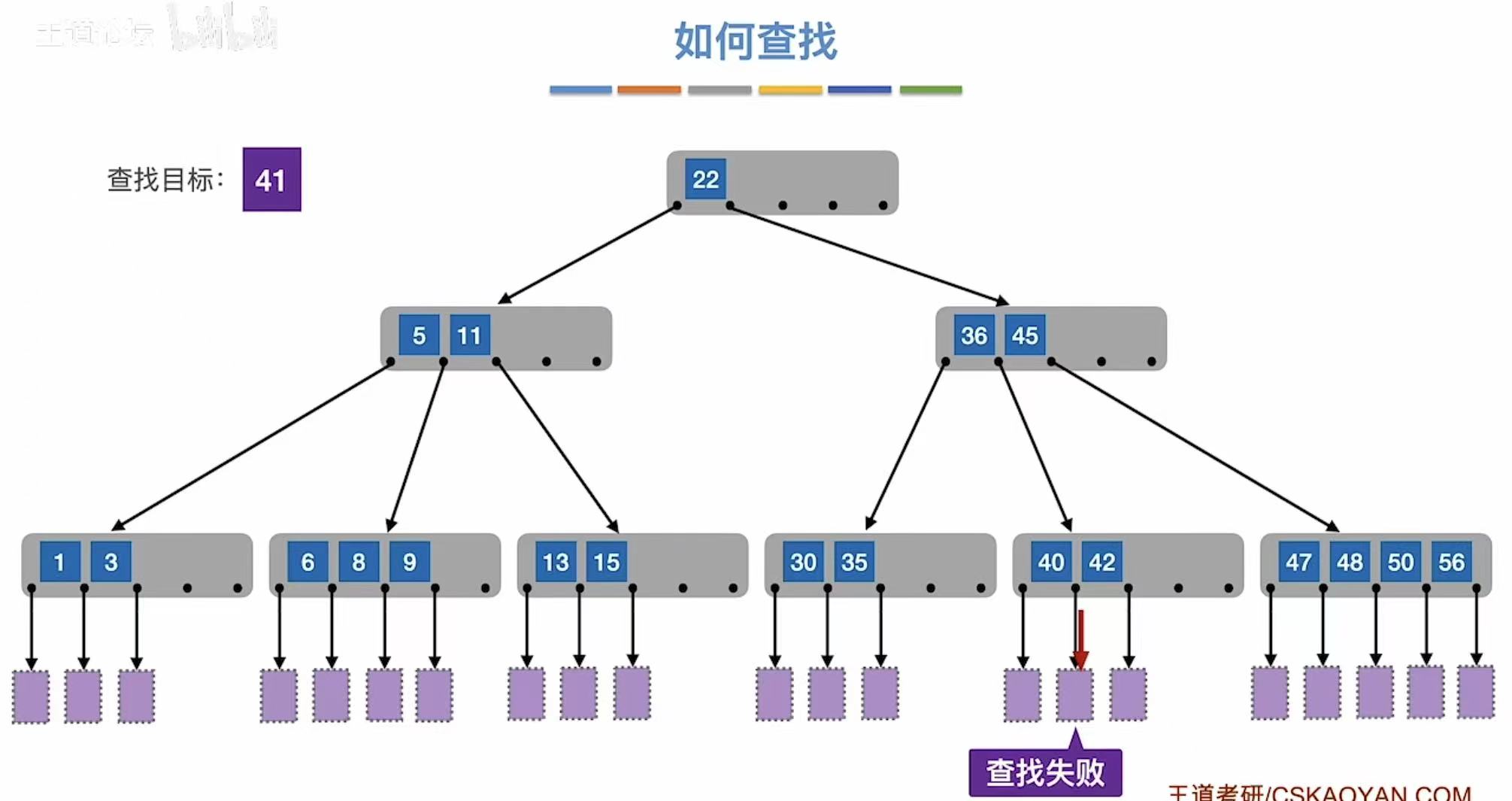
1.3 如何保证查找效率

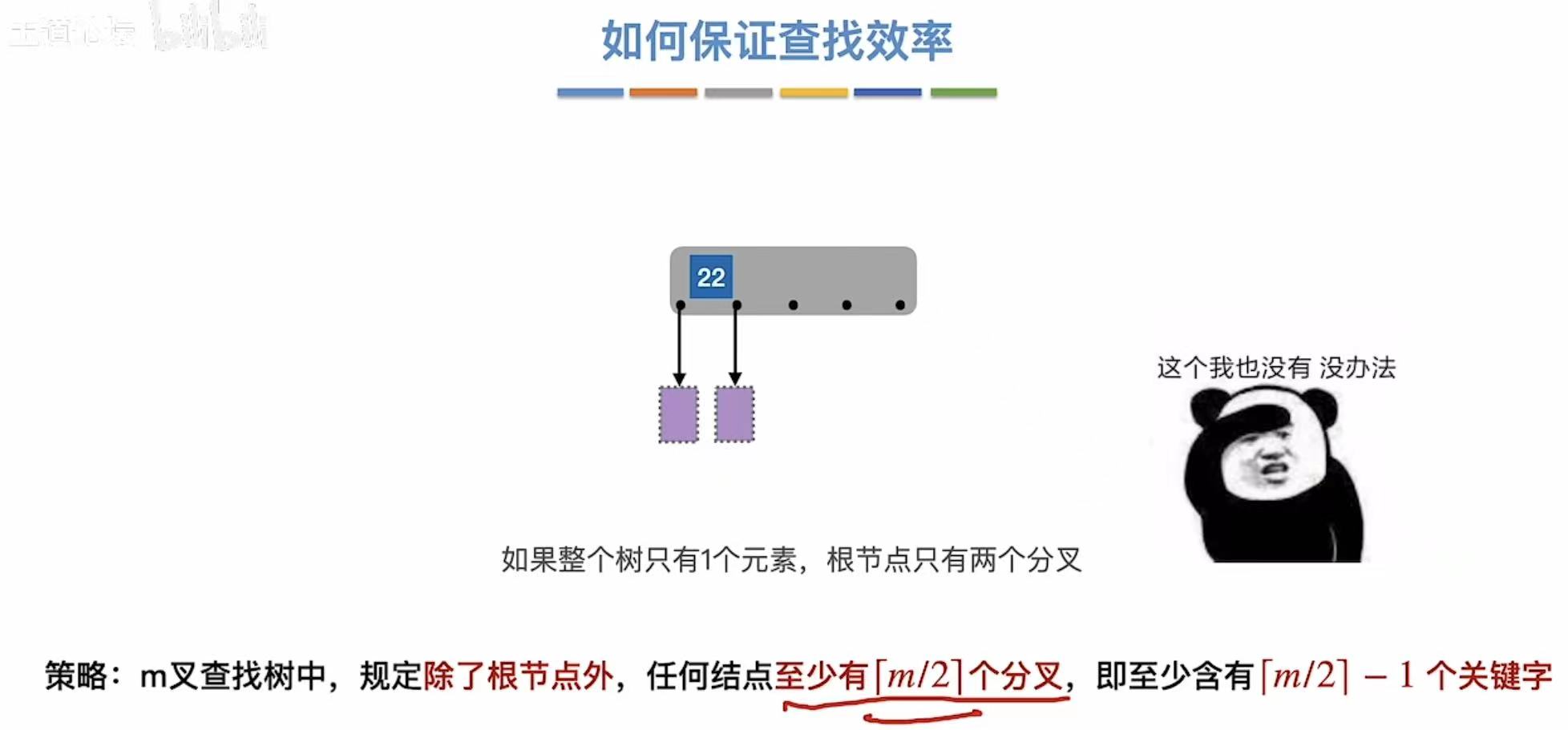
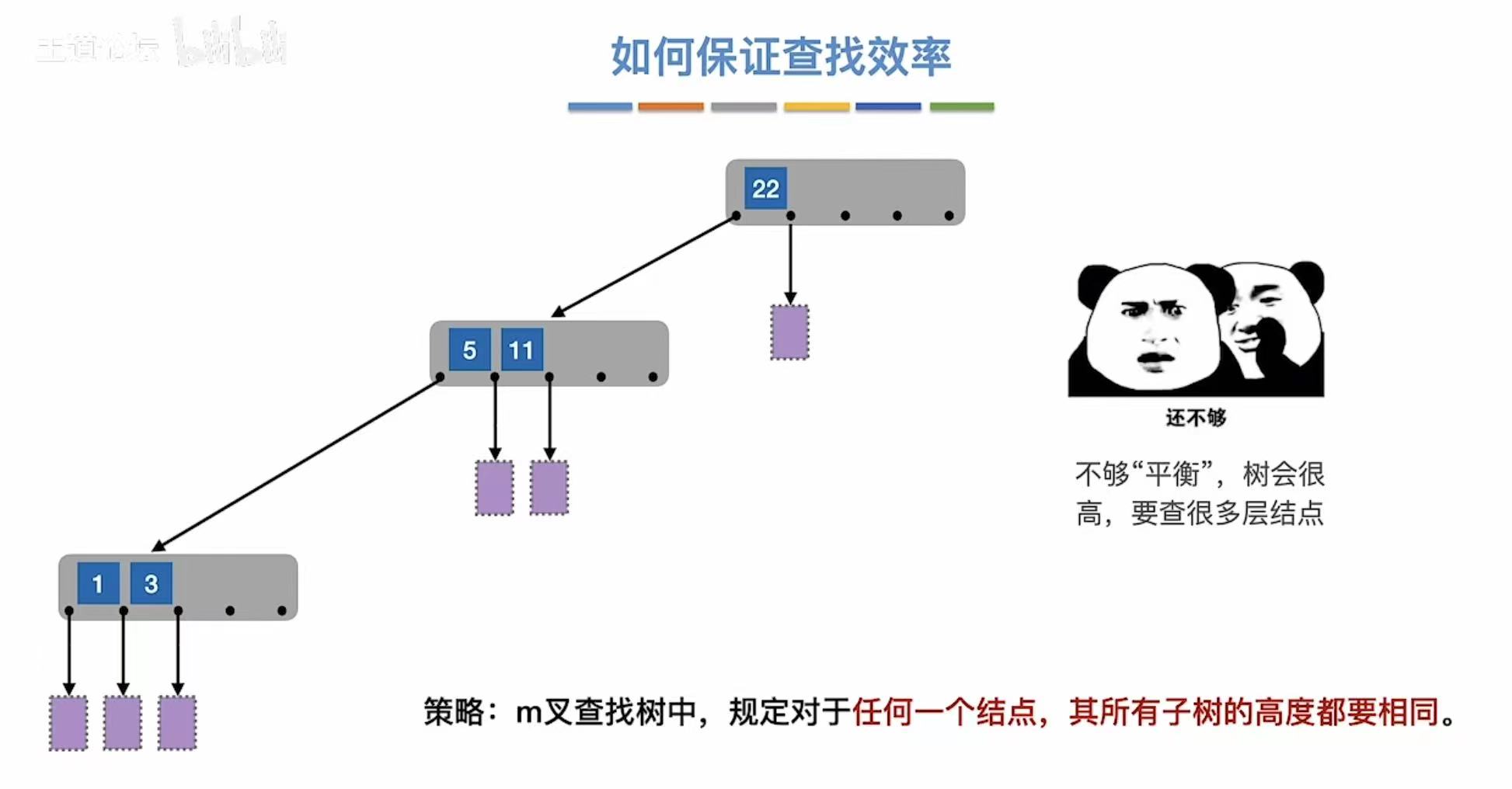
最好的状态 ：结点关键字多，树矮且平衡，效率高。
策略 ：5叉查找树中，除了根节点外，任何结点至少有2个分叉，即至少含有1个关键字。

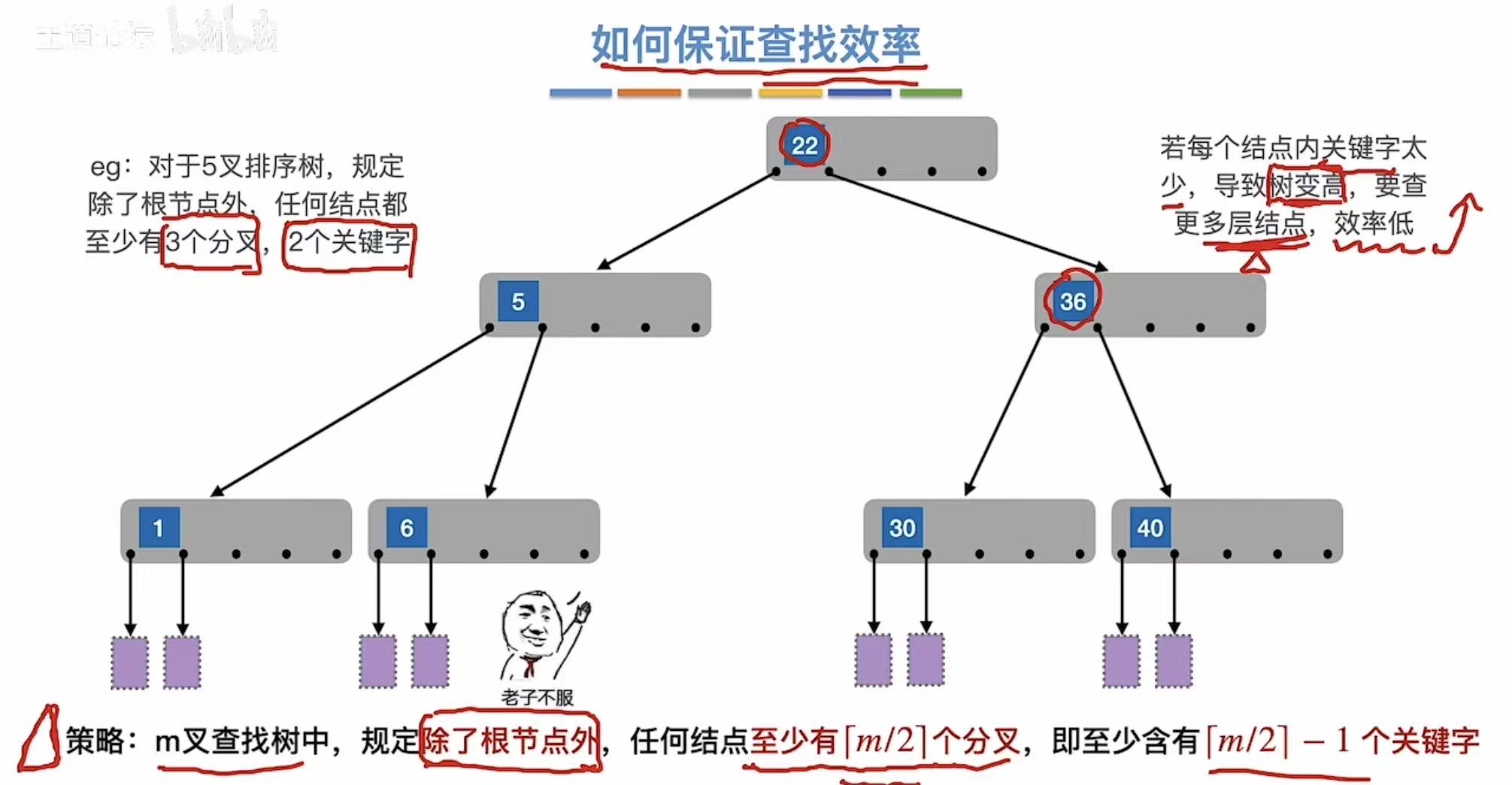
这里根节点只有一个元素，且是终端结点，那就只有两个分叉。

2. 定义

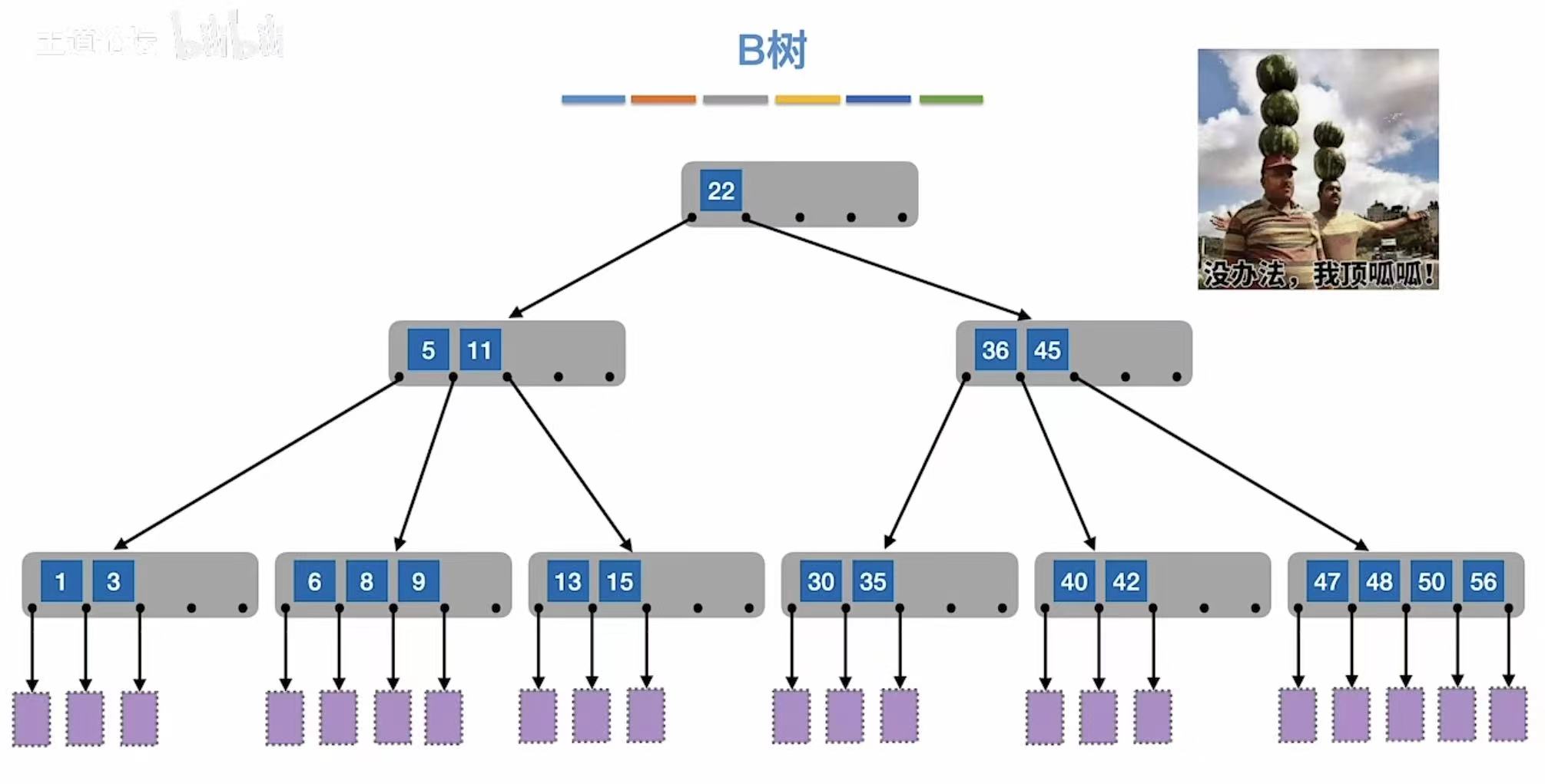
2.1 B树

满足上面要求的树，也就是m叉查找树，就是B树。

m阶B树：

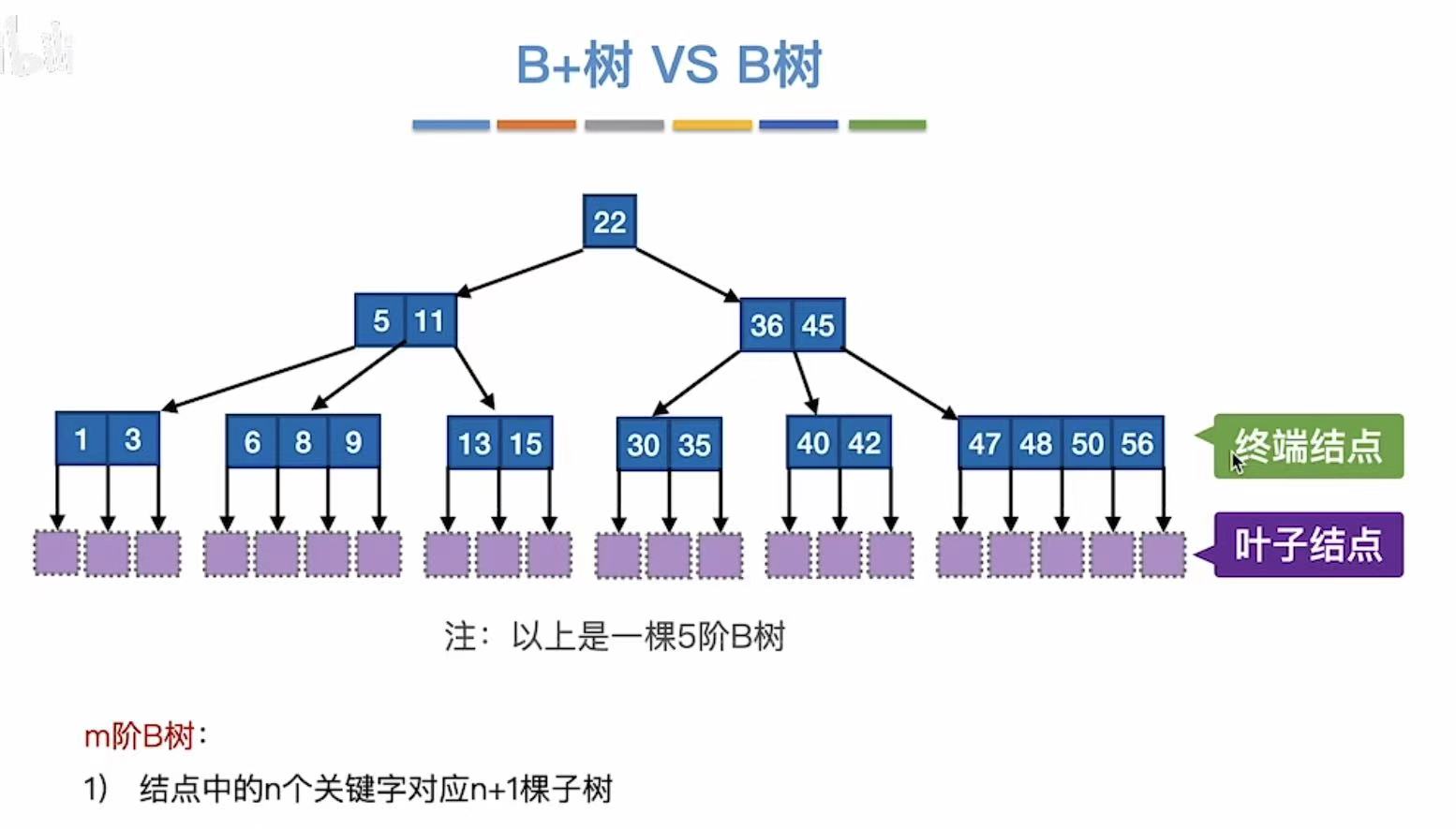
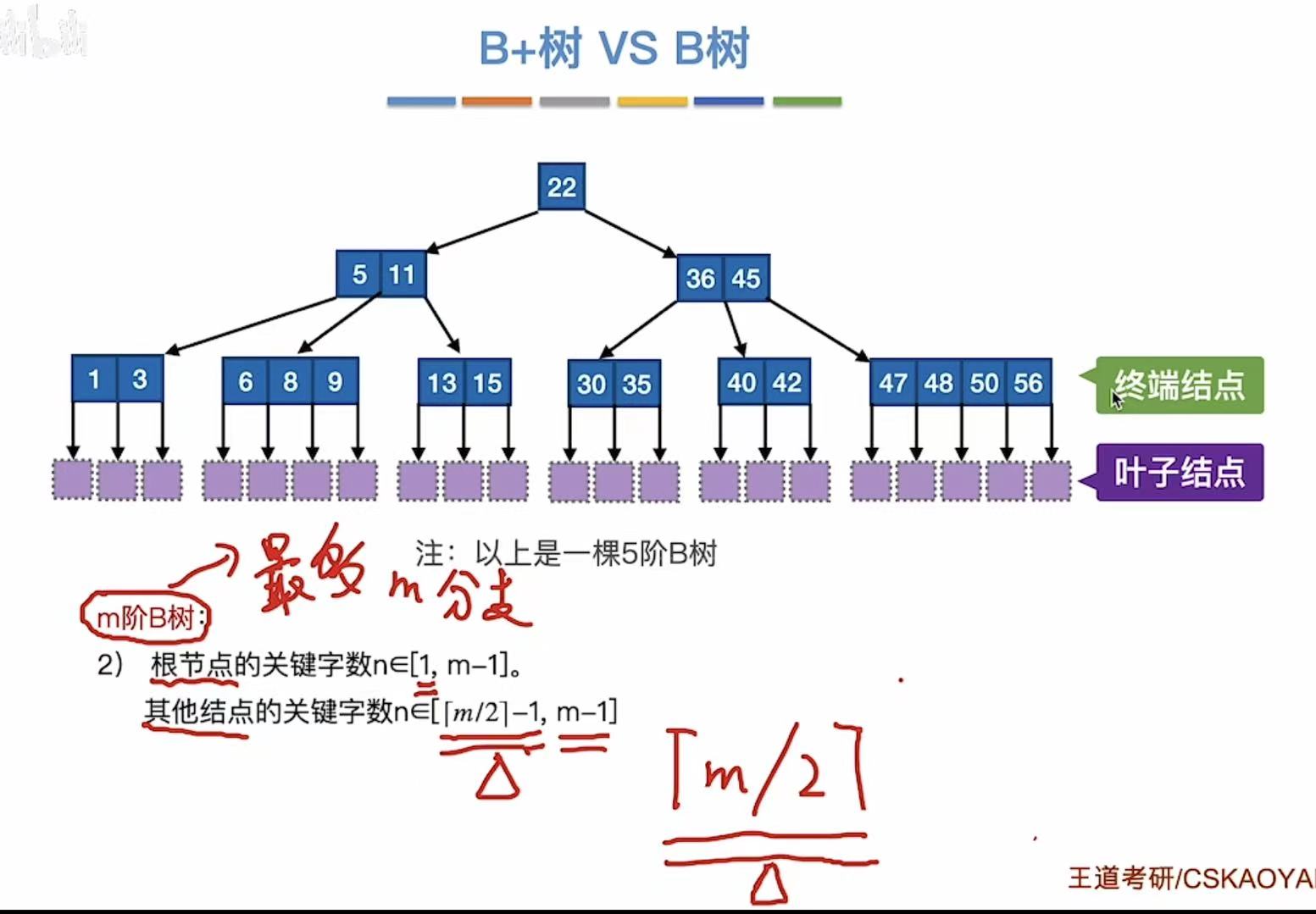
• 每个结点至多有m棵子树，即至多含m-1个关键字
• 如果根节点不是终端结点，则至少有两棵子树
• 除根节点外的所有非叶子结点至少有m/2个子树，即至多含m/2-1个关键字
• 所有叶子节点都出现在同一个层次上，并且不带信息
  
  
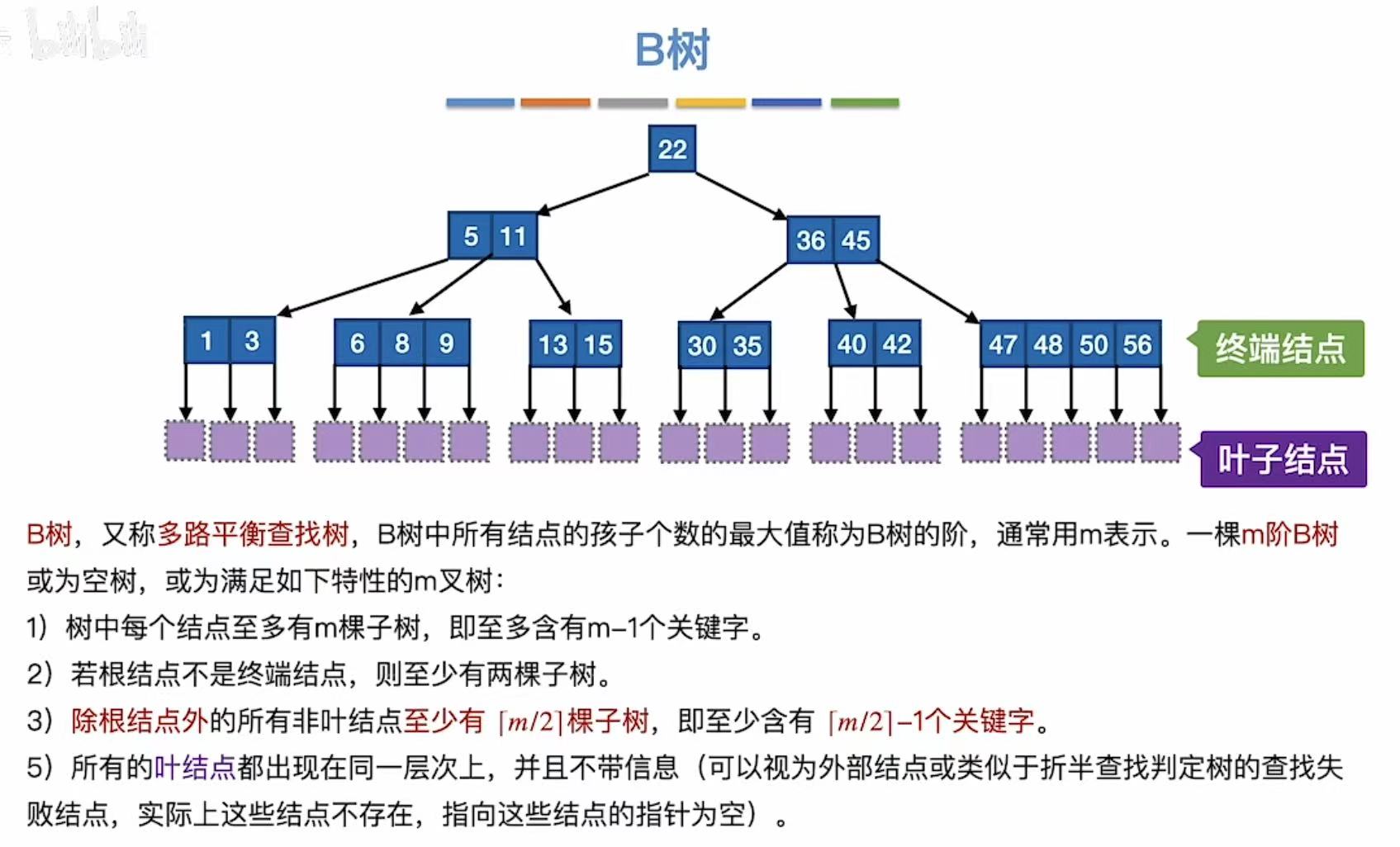
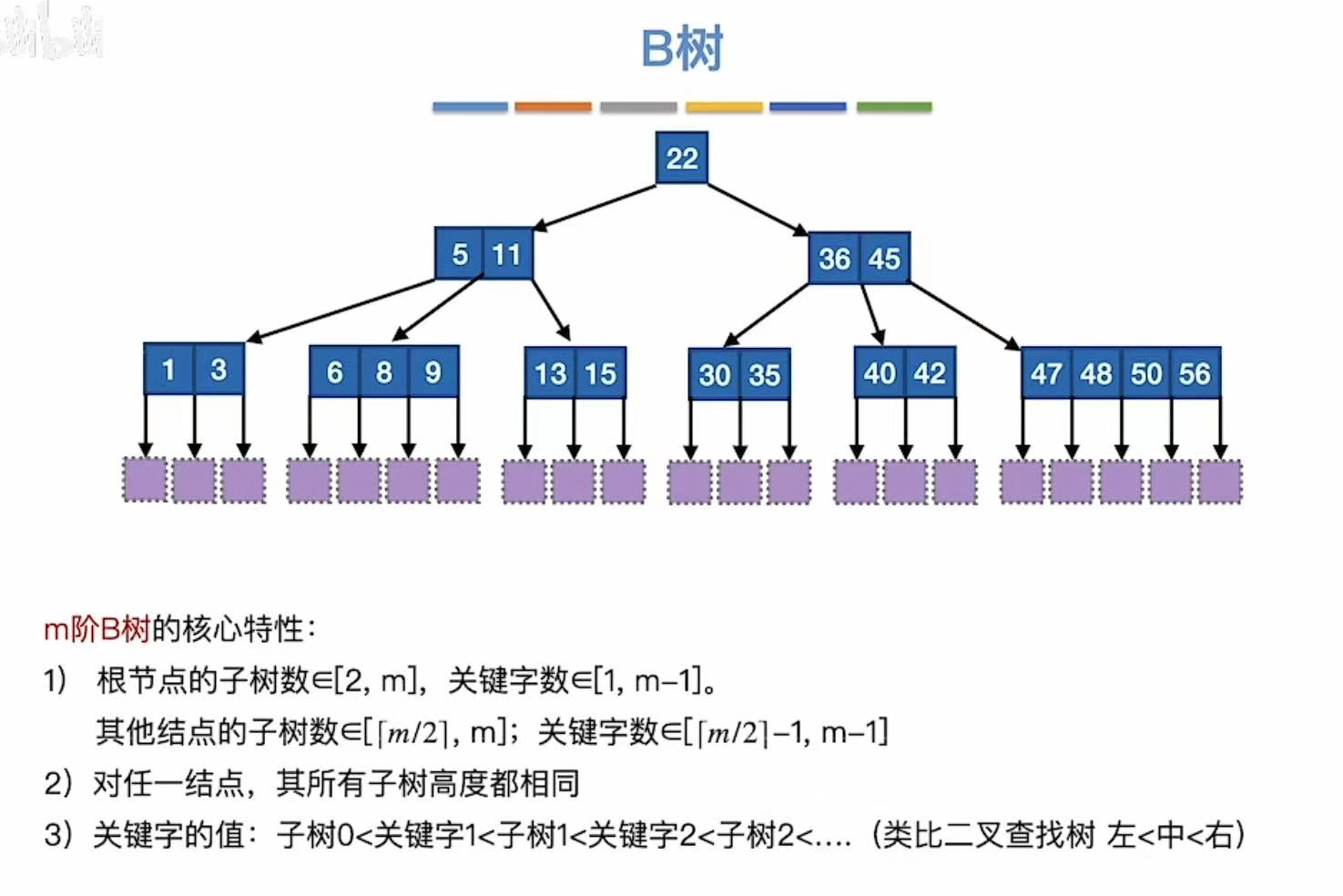
• 关键字从小到大排序；
• 对于每个关键字 Ki：
• 左边的子树（由 P_{i-1} 指向）中所有值都 < Ki
• 右边的子树（由 P_i 指向）中所有值都 > Ki

例如：[5,11] 结点：

• P₀ 指向 [1,3] → 所有值 < 5
• P₁ 指向 [6,8,9] → 所有值 ∈ (5,11)
• P₂ 指向 [13,15] → 所有值 > 11
  

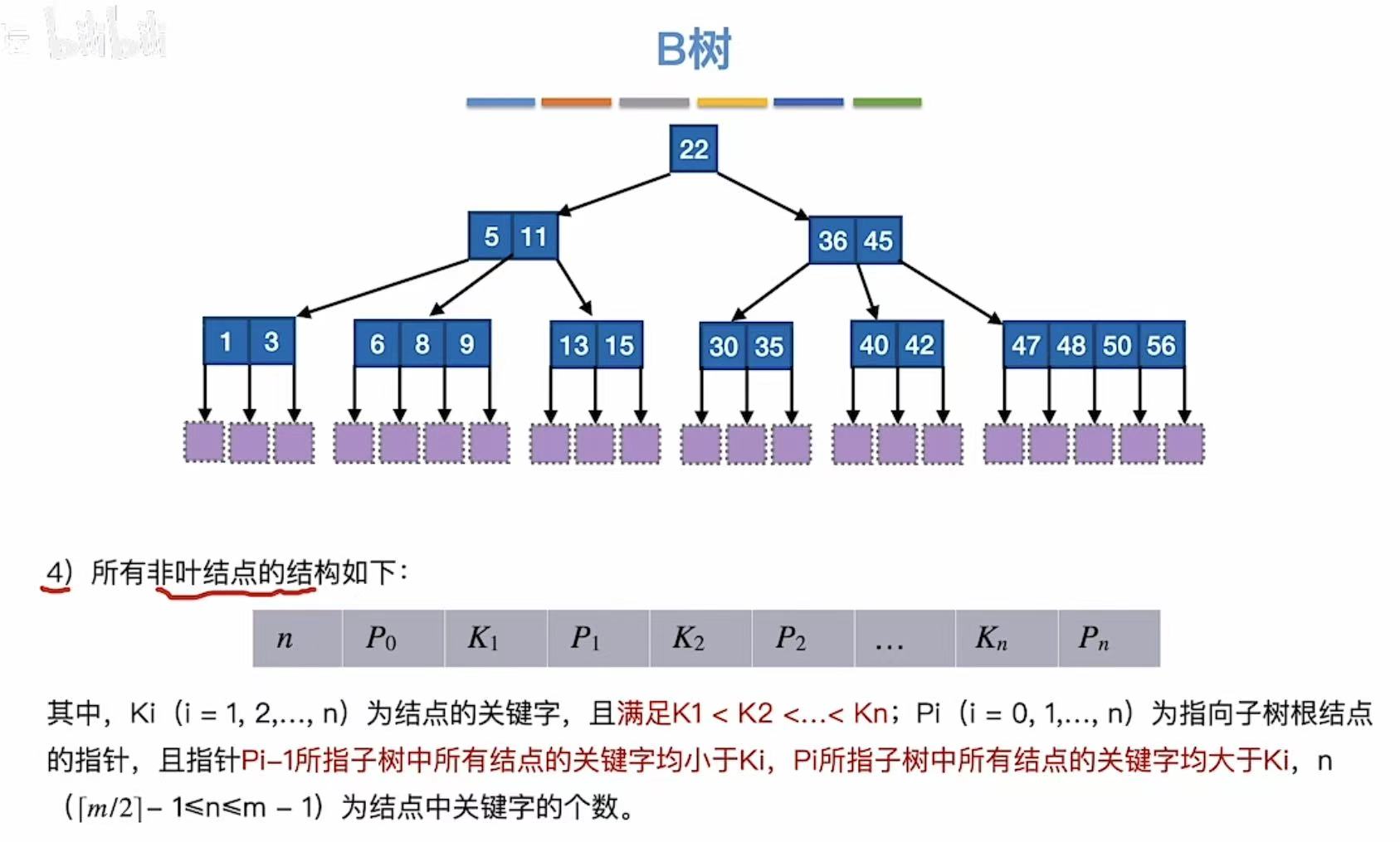
2.2 B树的高度

最小高度（满）：

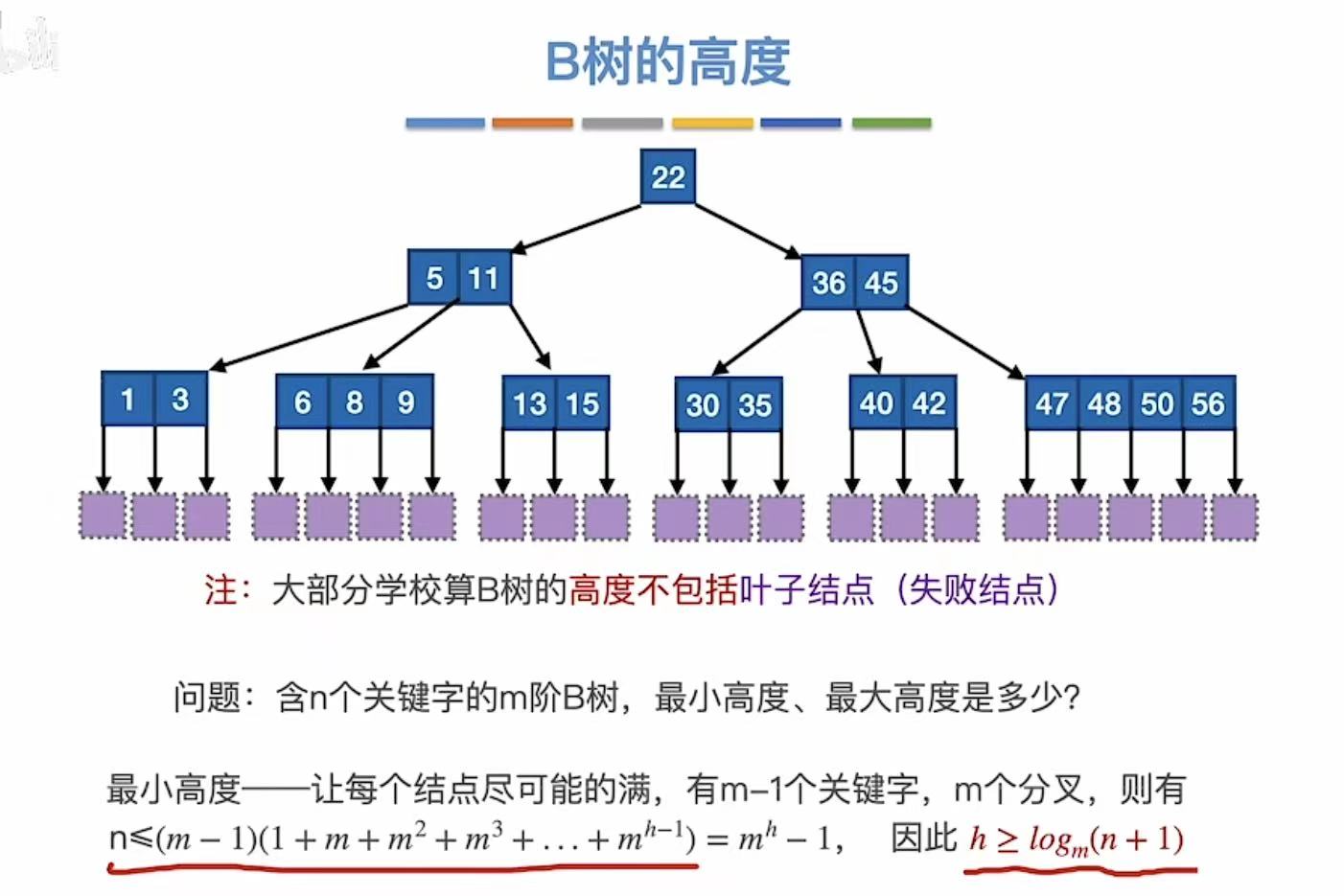
最大高度（空）：

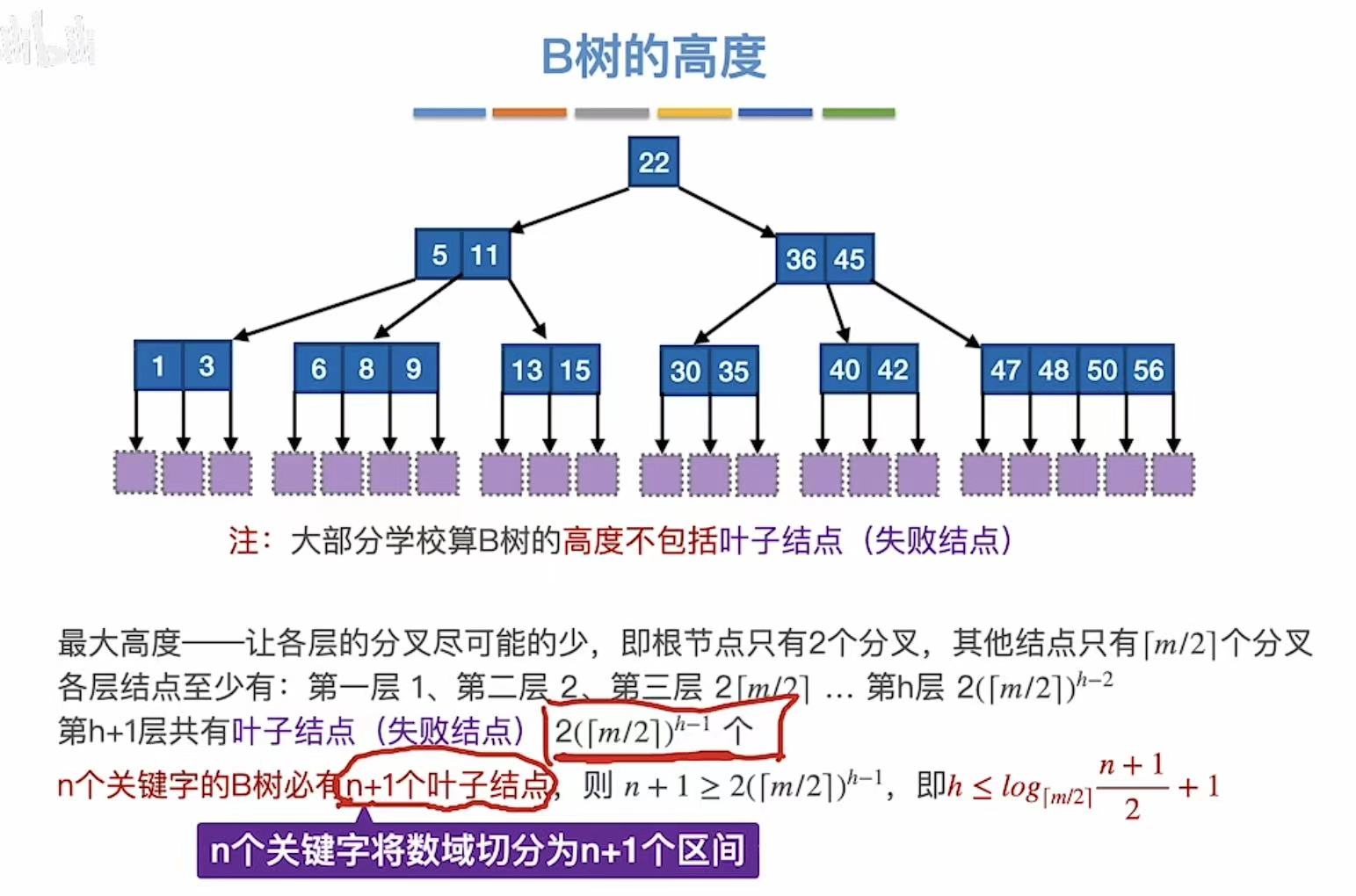
2.3 小结

3. 基本操作

3.1 B树的插入

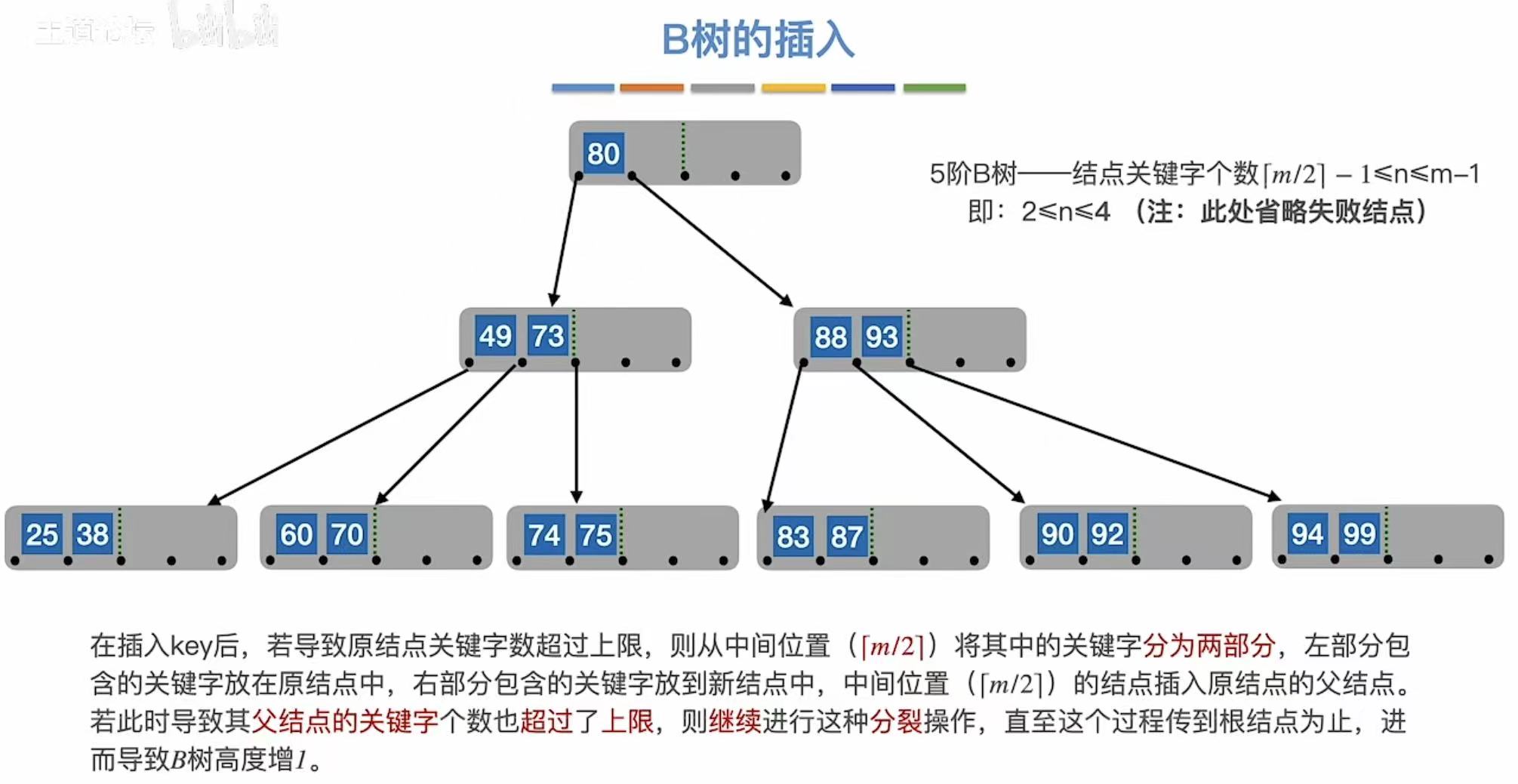
如图，一个结点最多有m-1个关键字，如果再塞进来一个就会溢出：

3.1.1 第一次溢出

一旦溢出，我们就可以取中间的位置，把所有的关键字分成左右两部分：

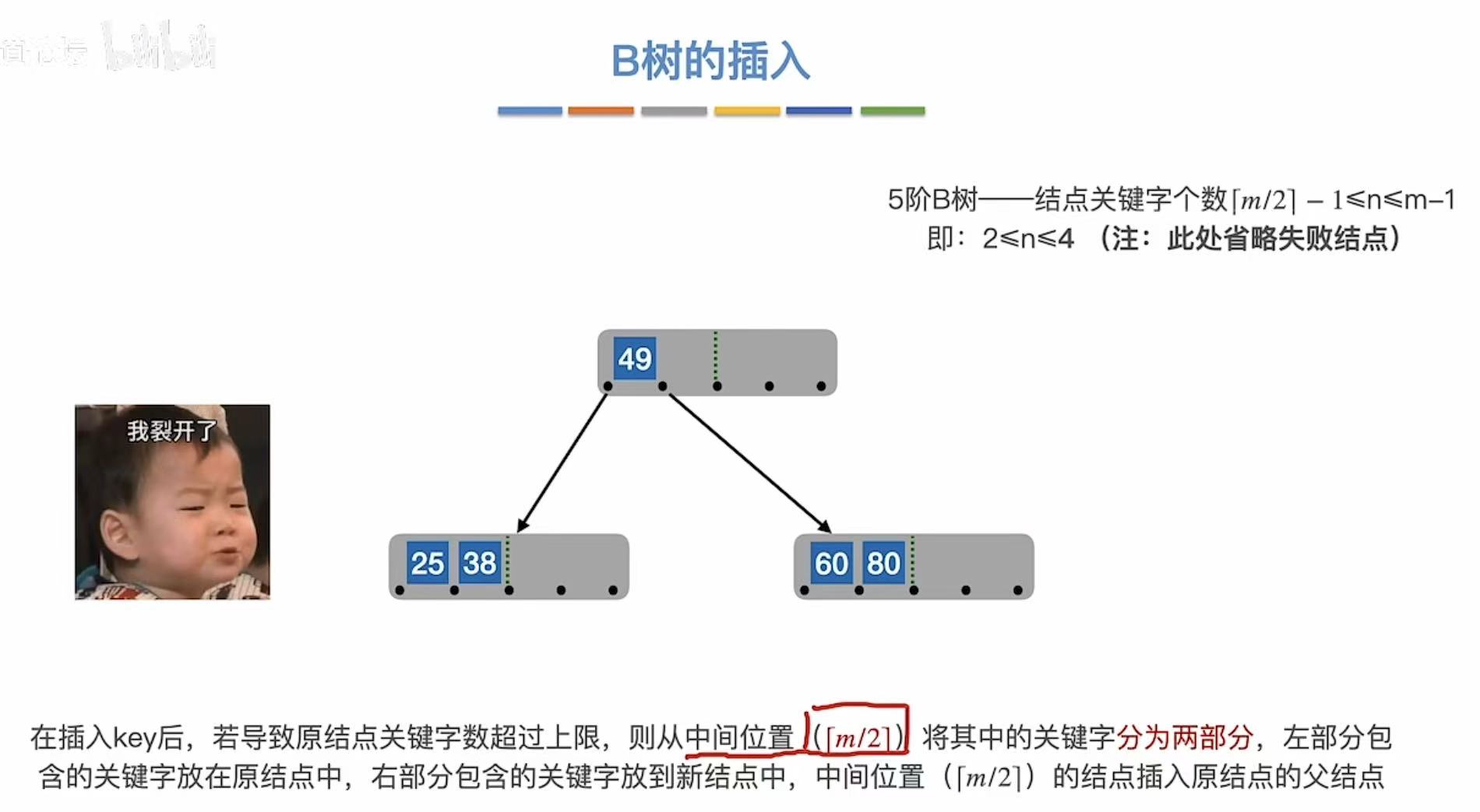
再插入新元素，就往终端结点上插入：

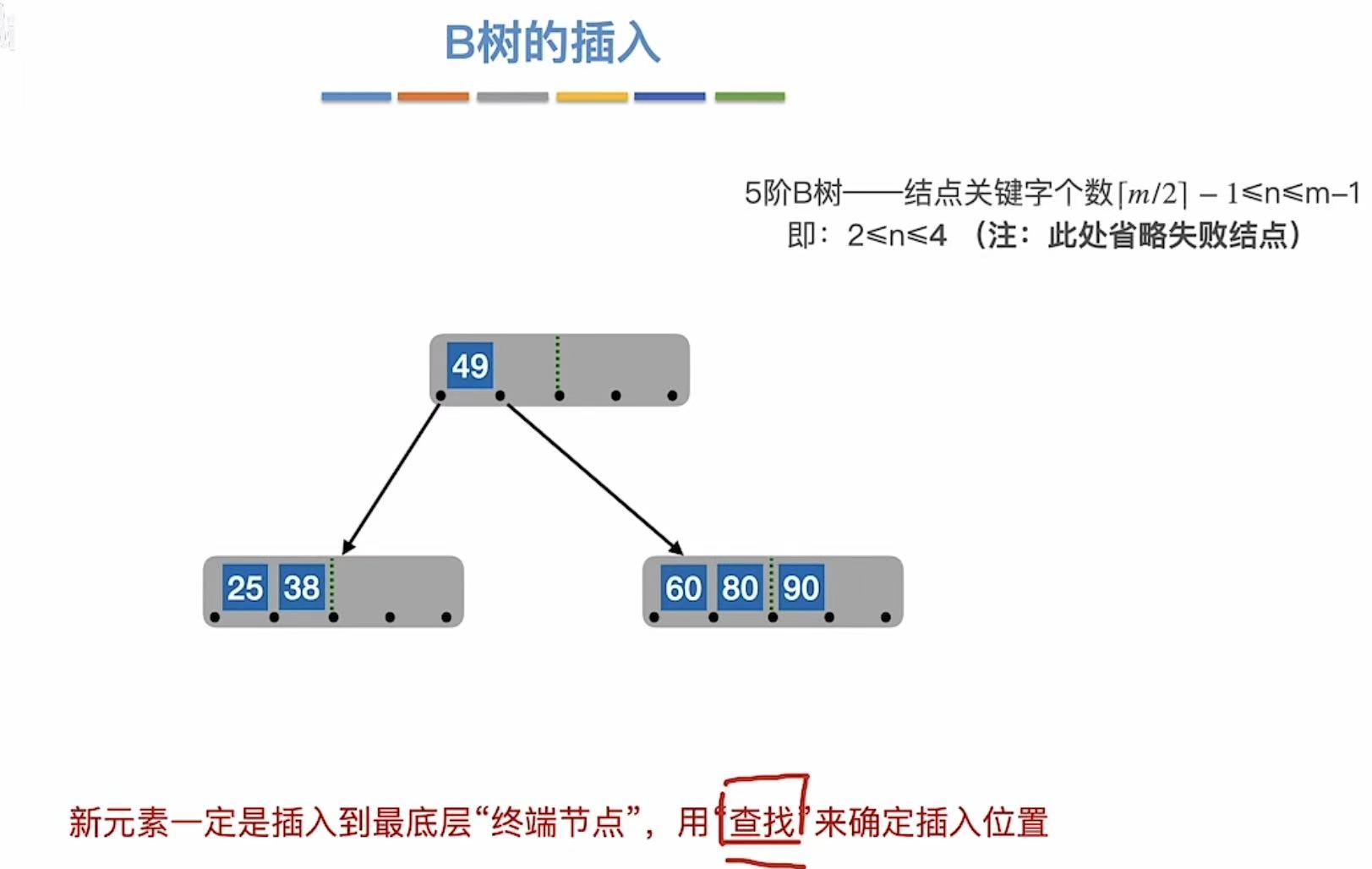
错误示范：不可以插在根节点上。

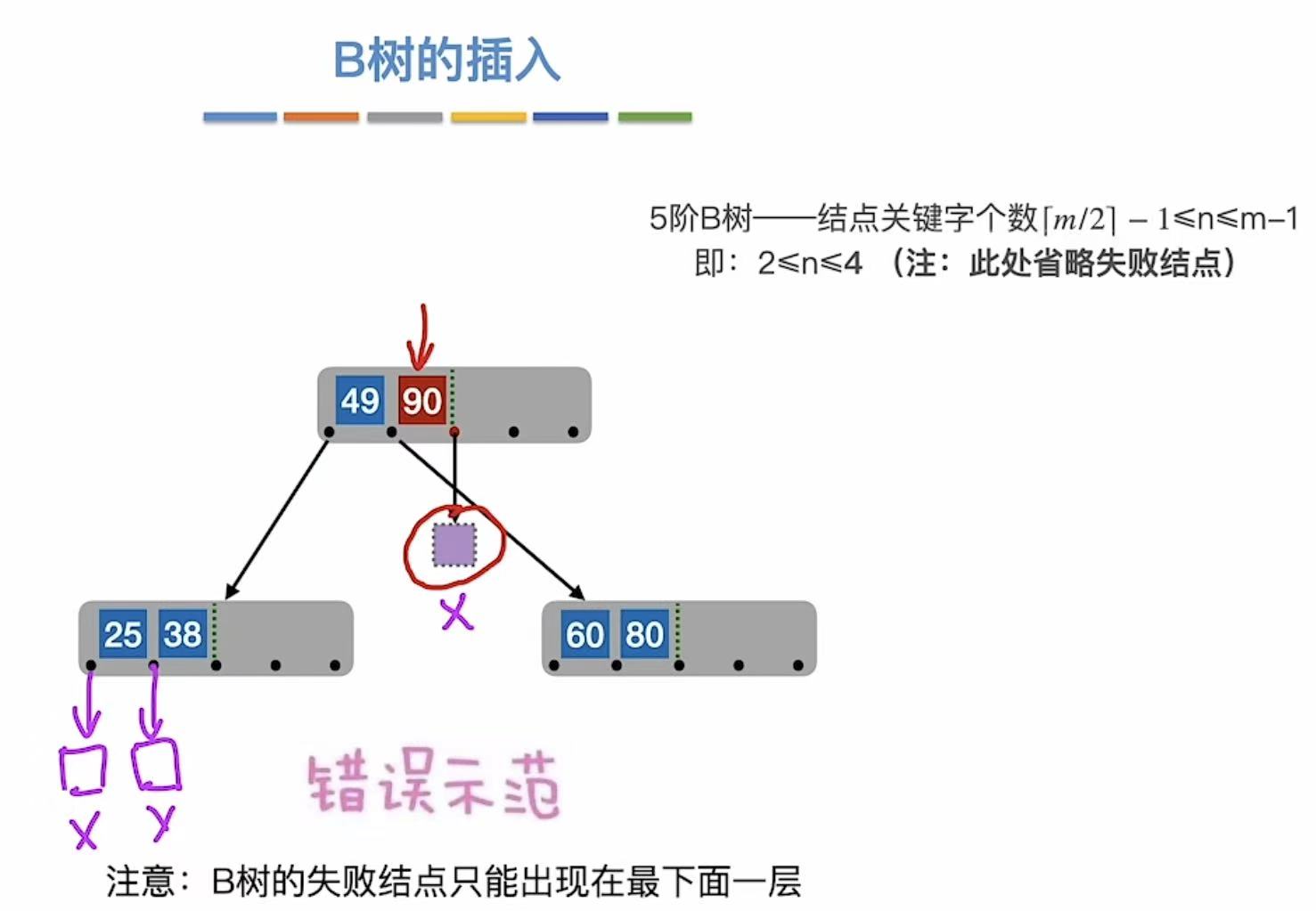
3.1.2 第二次溢出

那如果终端结点溢出了，该怎么办呢？

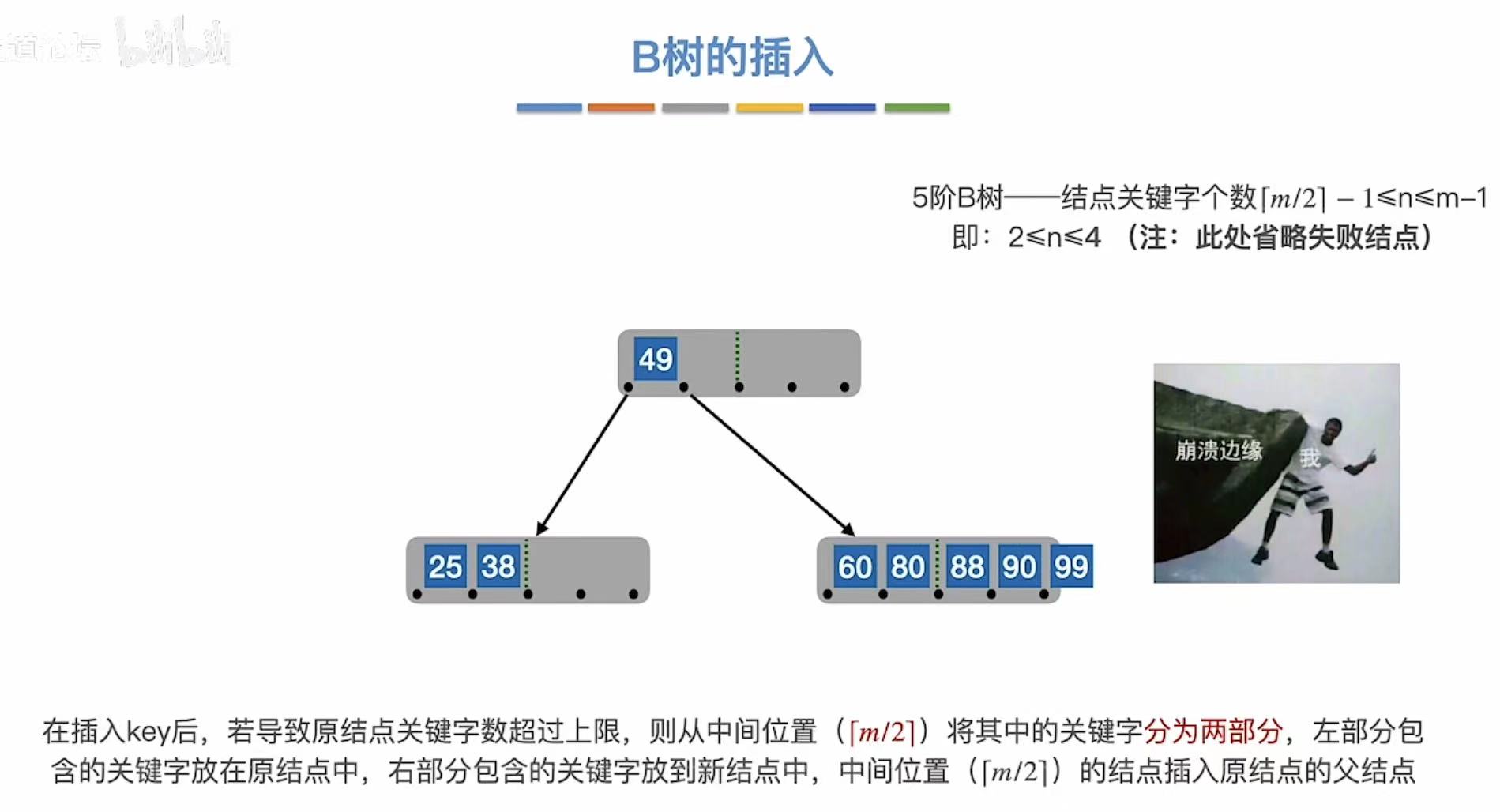
老样子从中间切开，把中间的标准提拔到根节点那里。

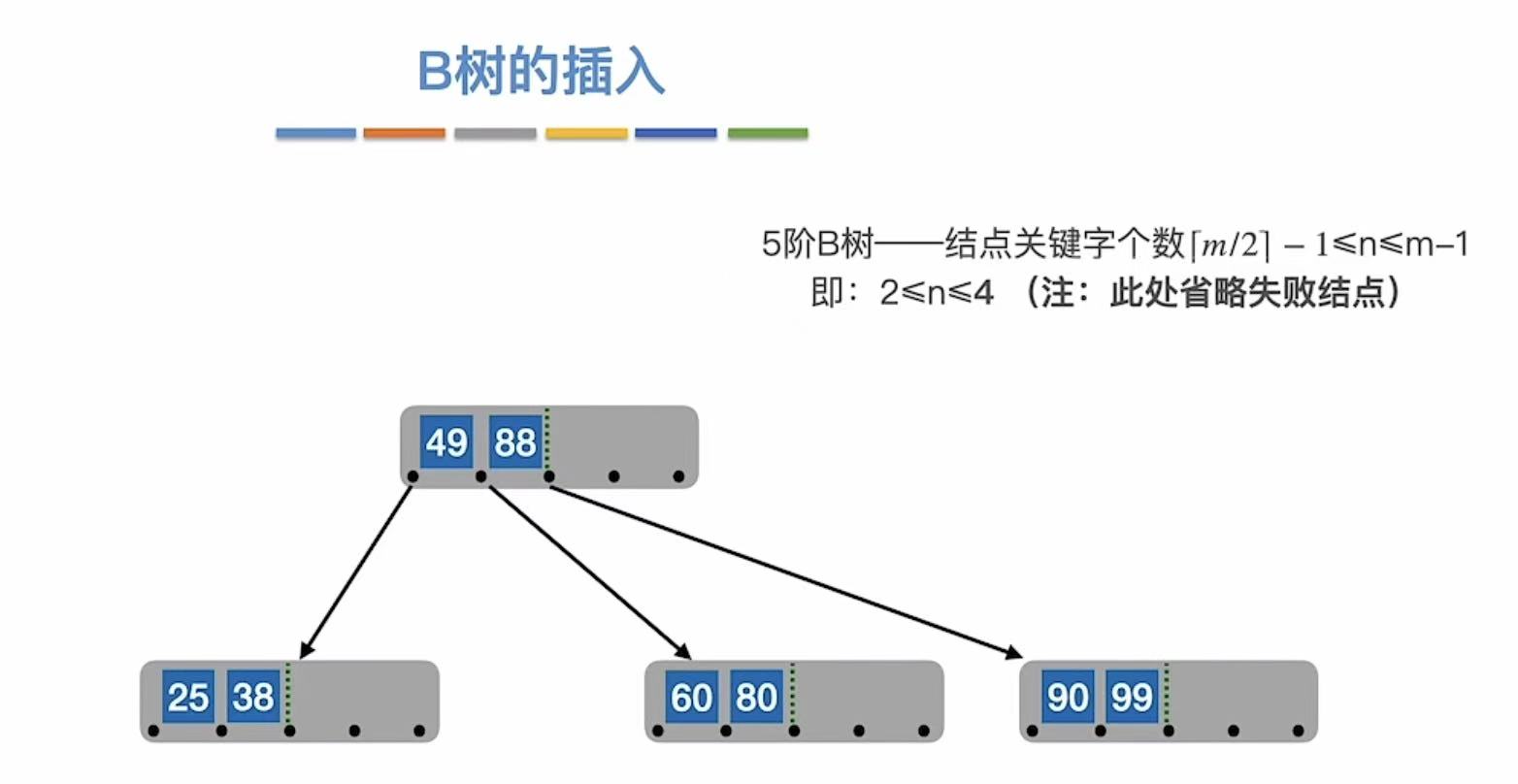
3.1.3 第三次溢出

和上一次相同，从中间切开，把标准提到根节点上。

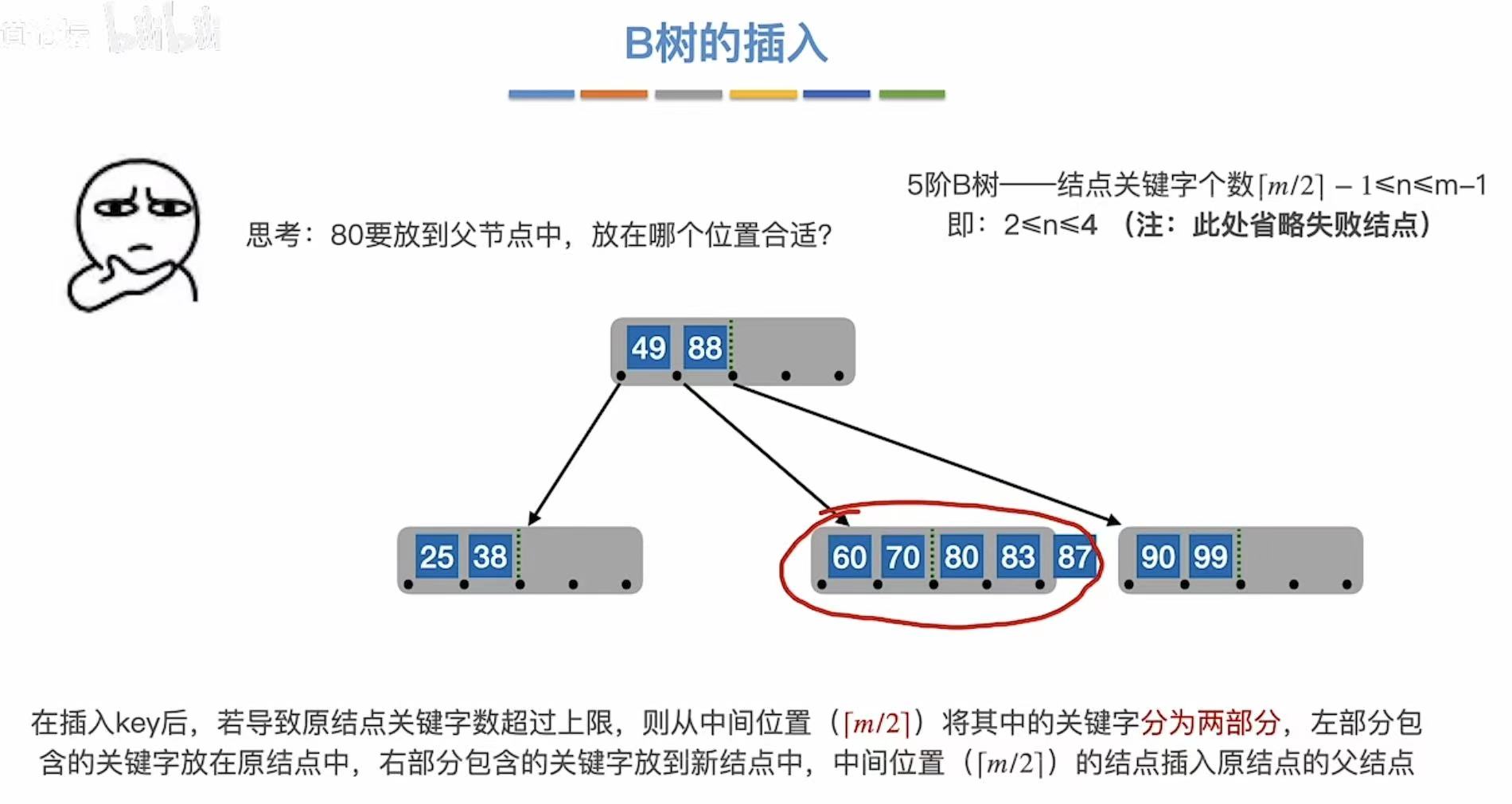
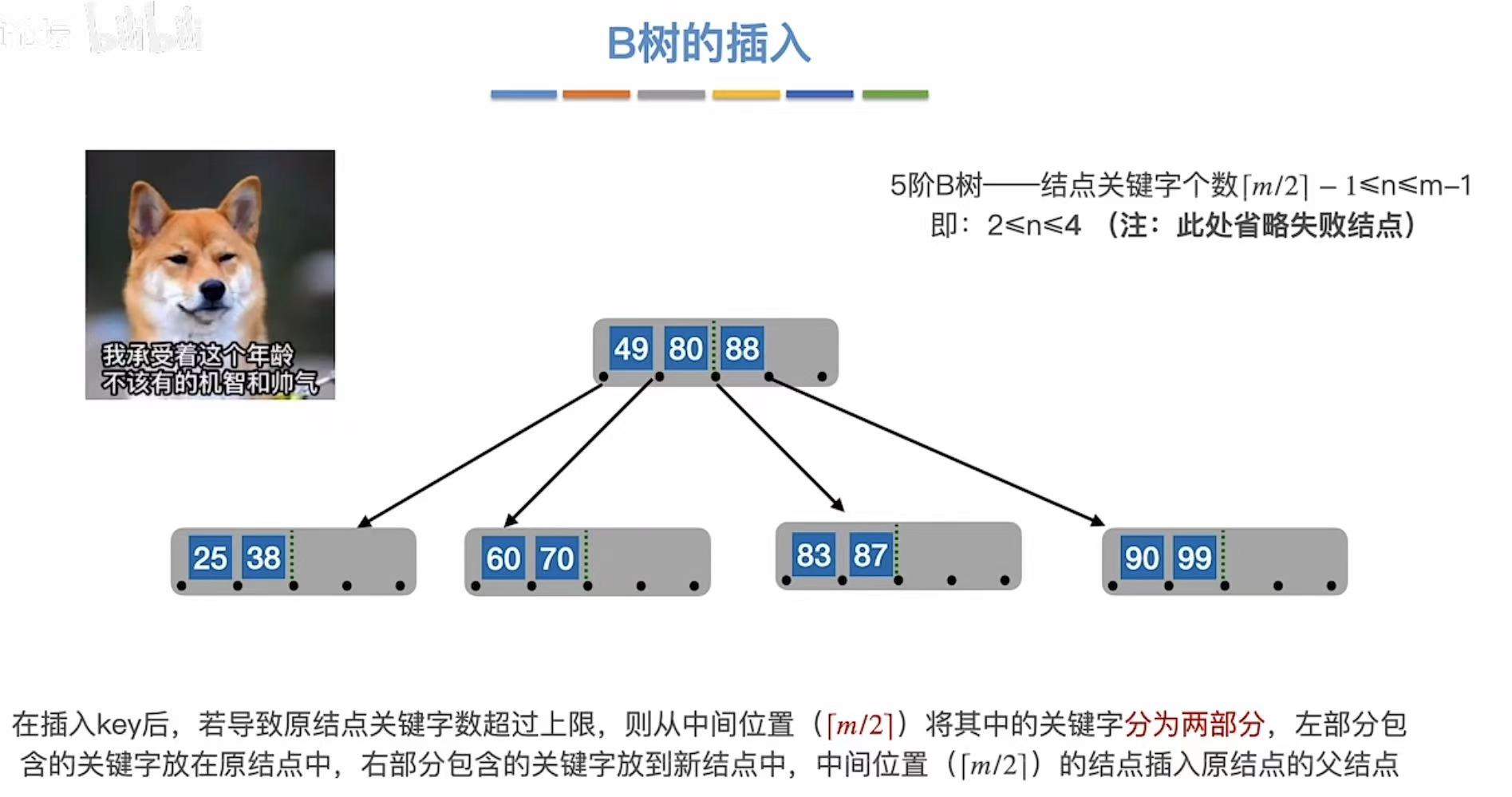
3.1.4 第四次溢出

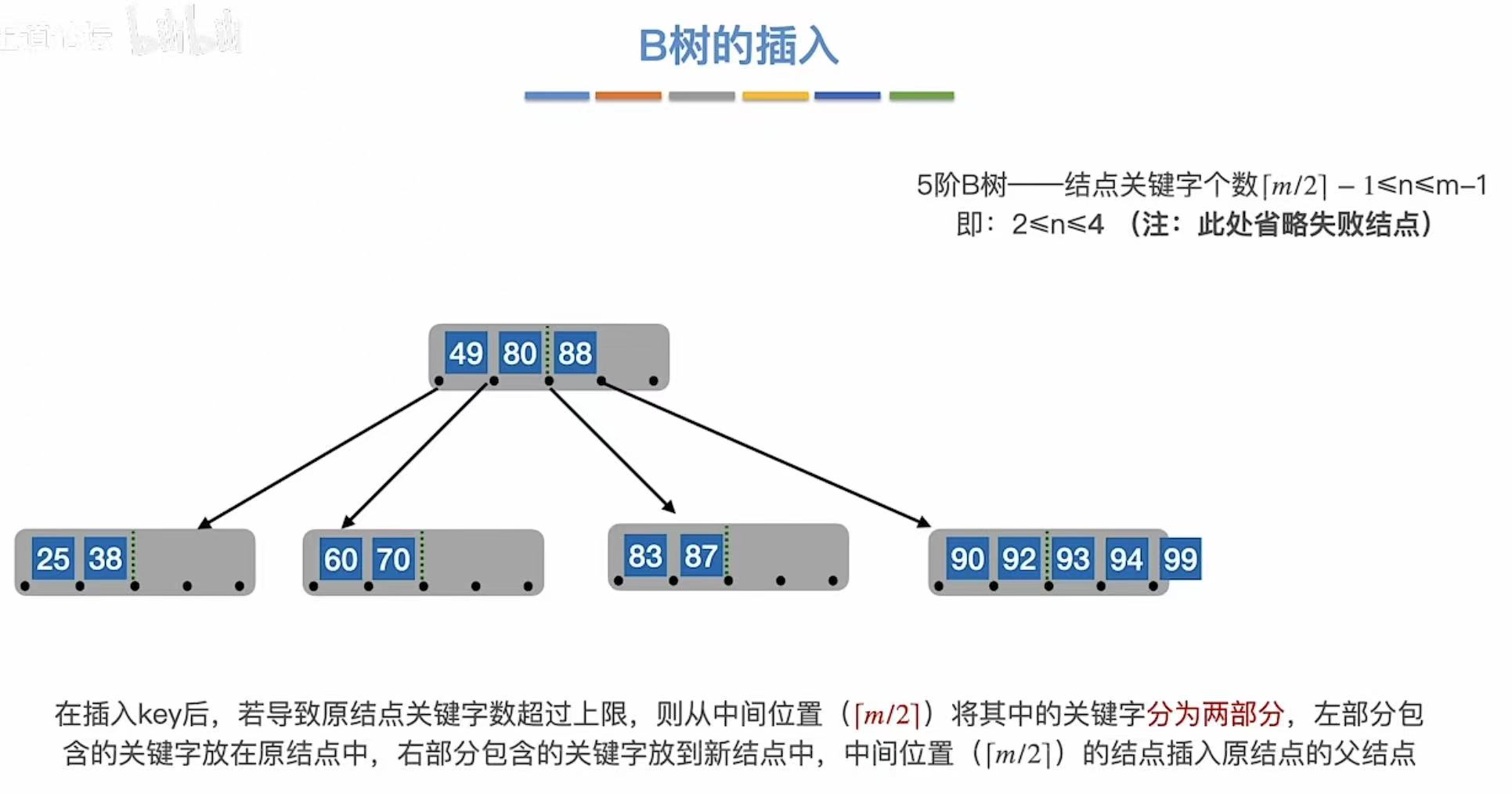
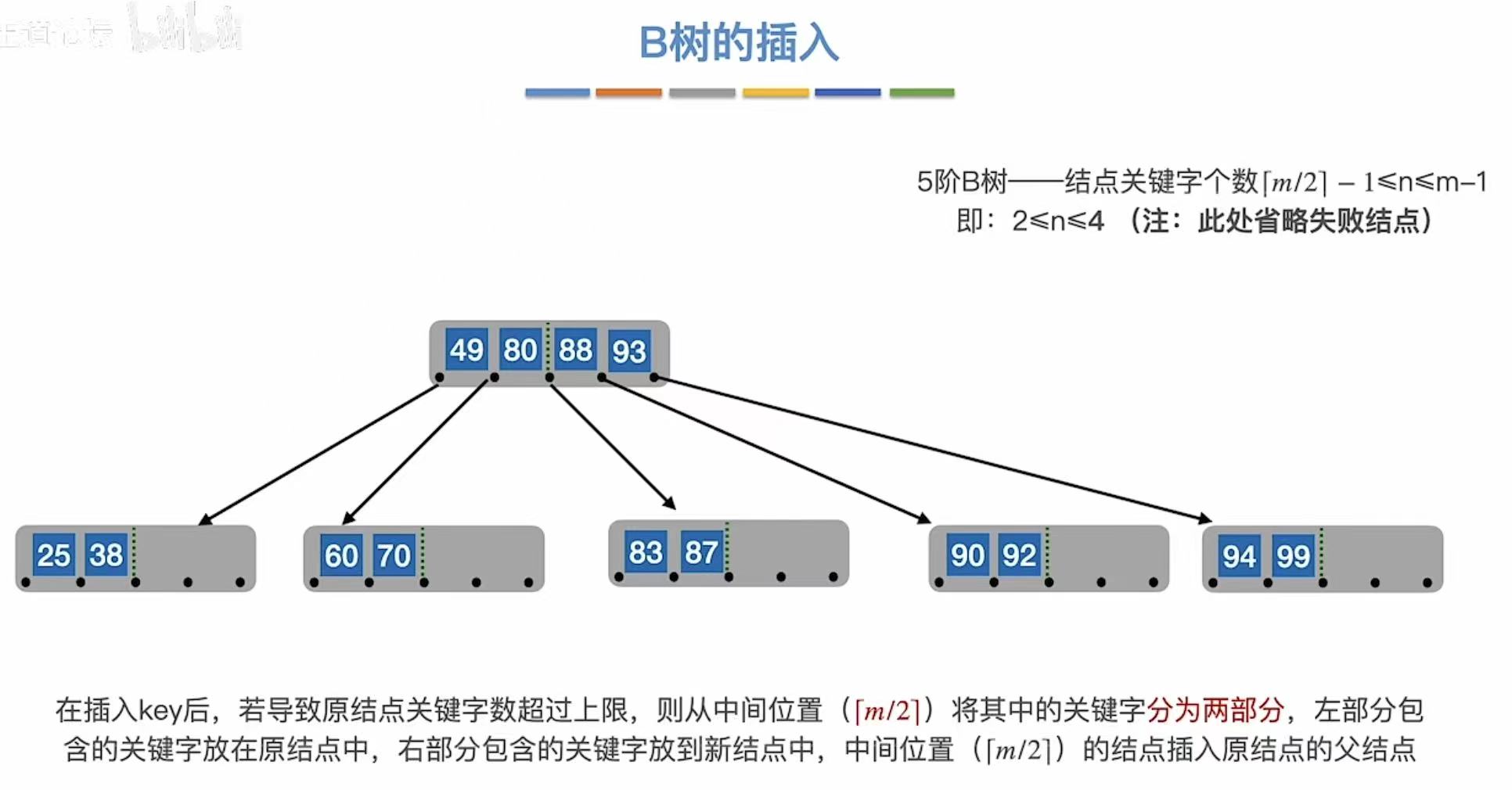
3.1.5 第五次溢出

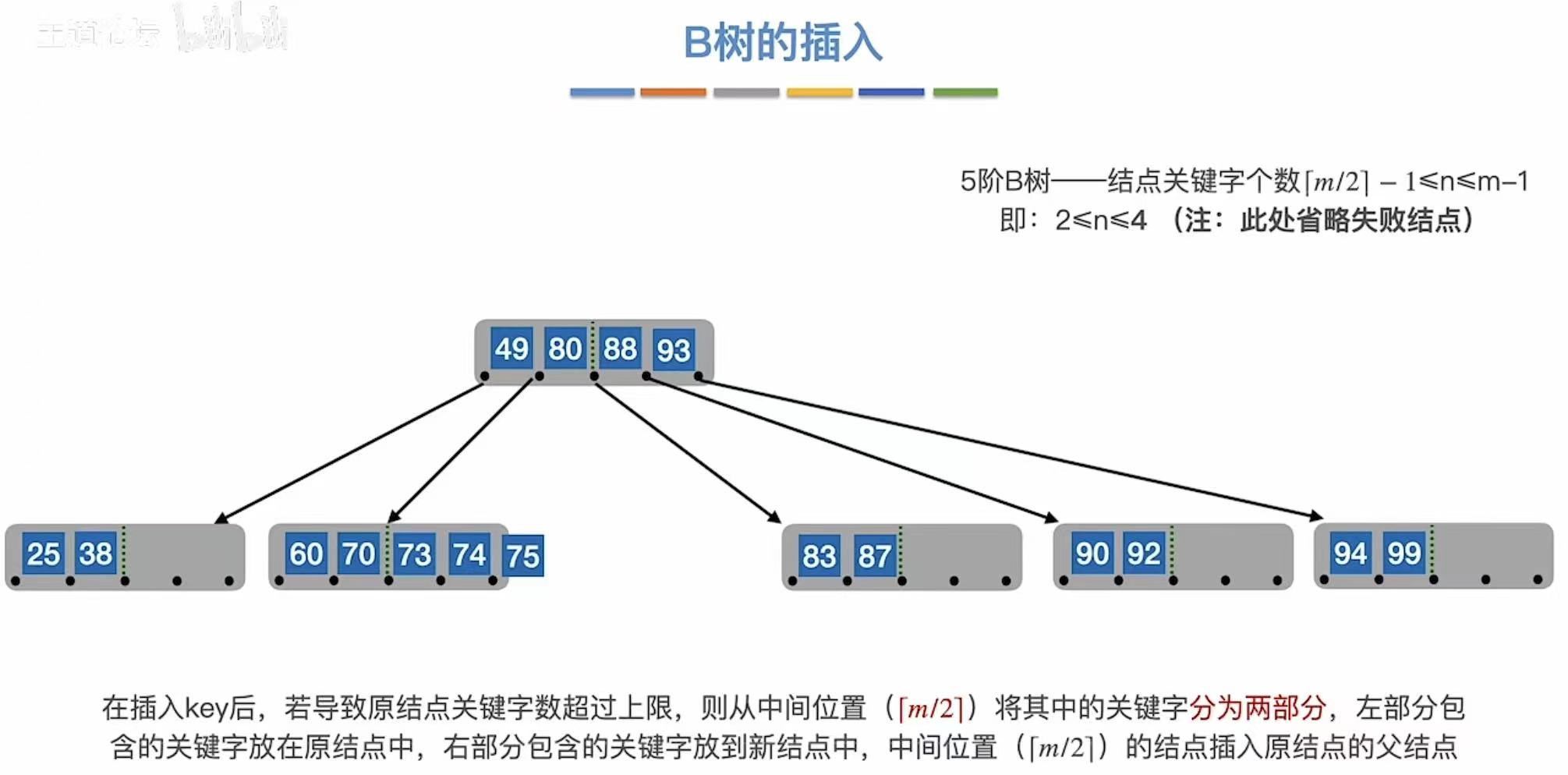
3.1.6 第六次溢出

一层满了，就继续向上分化。

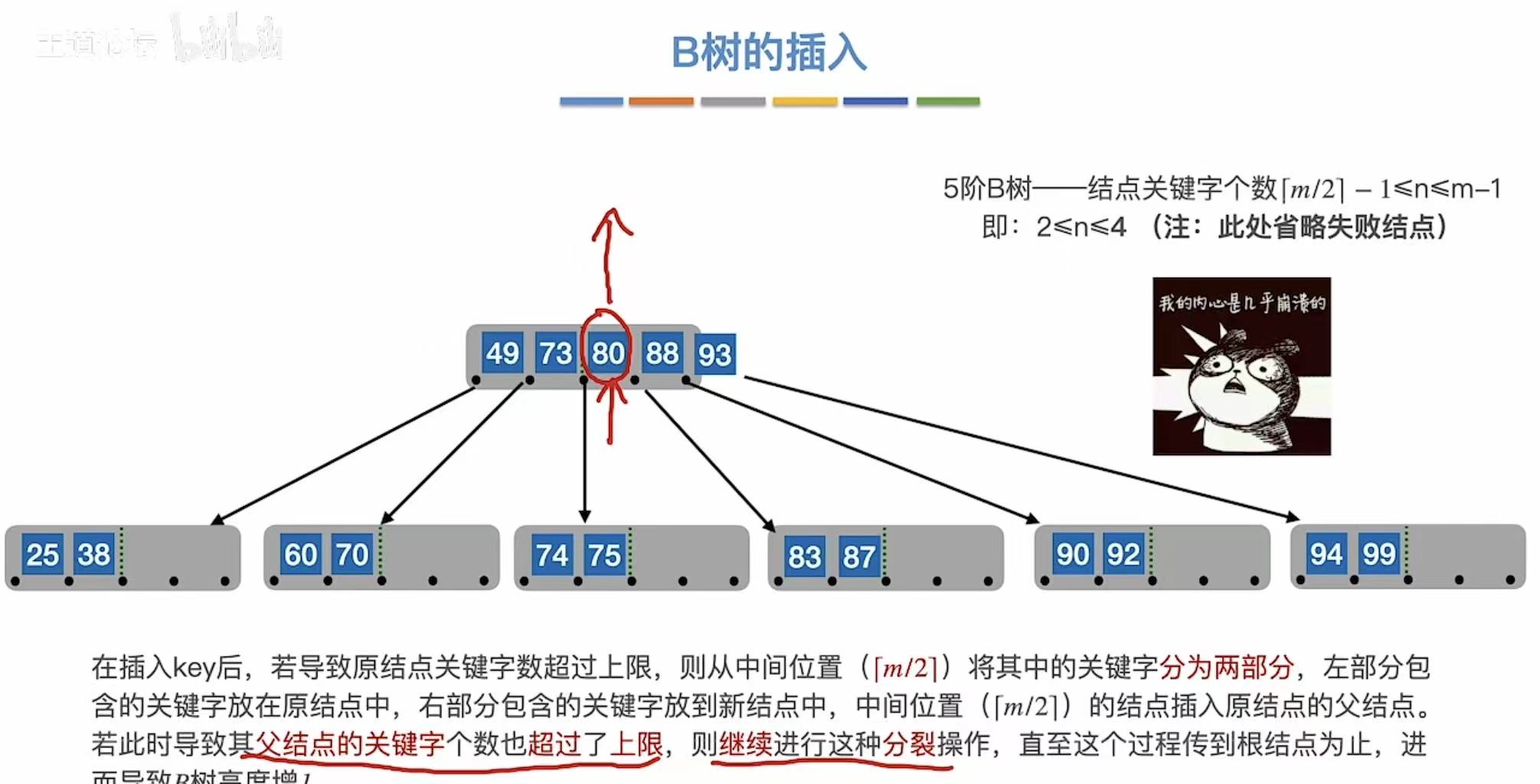
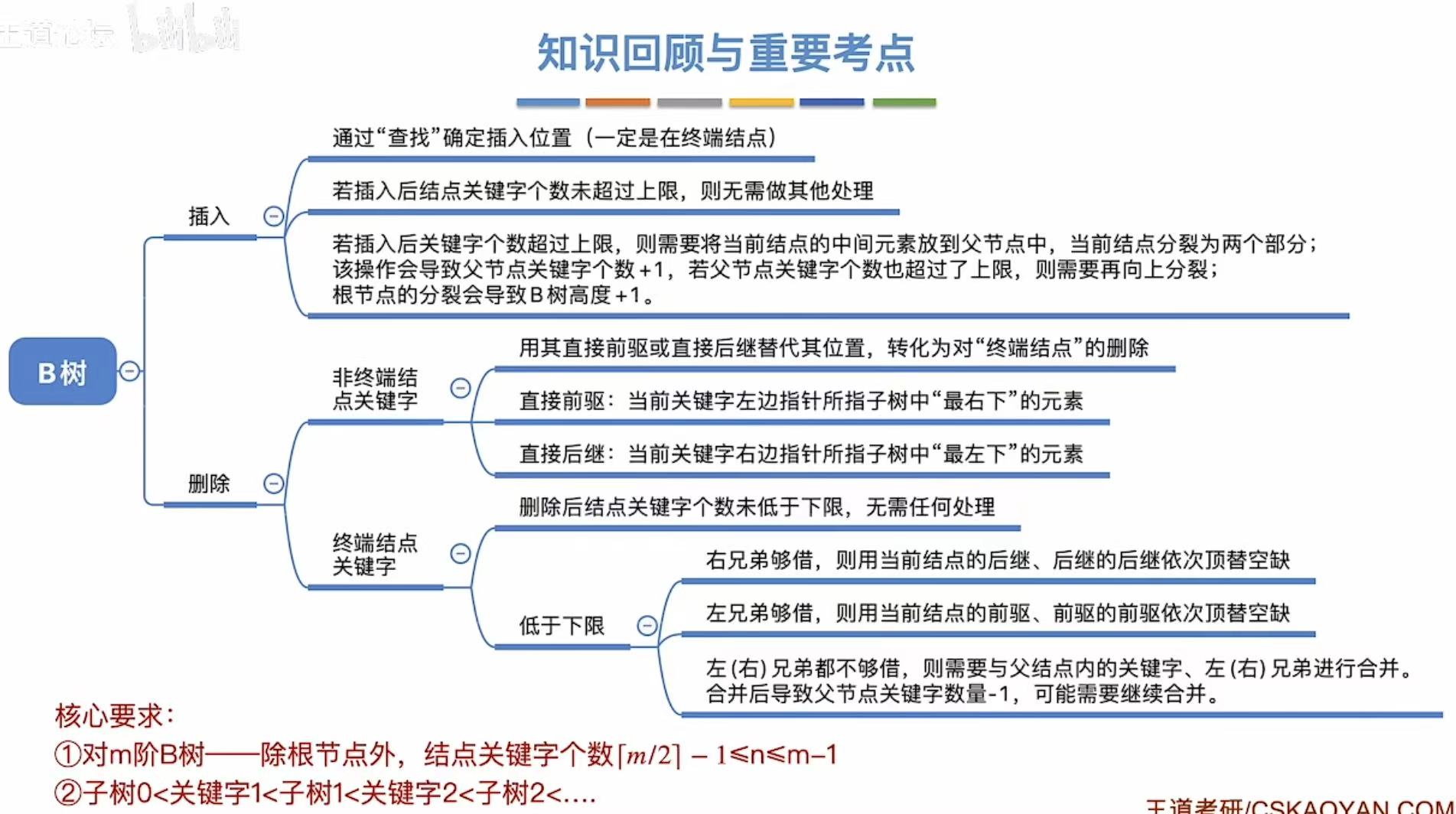
3.2 B树的删除

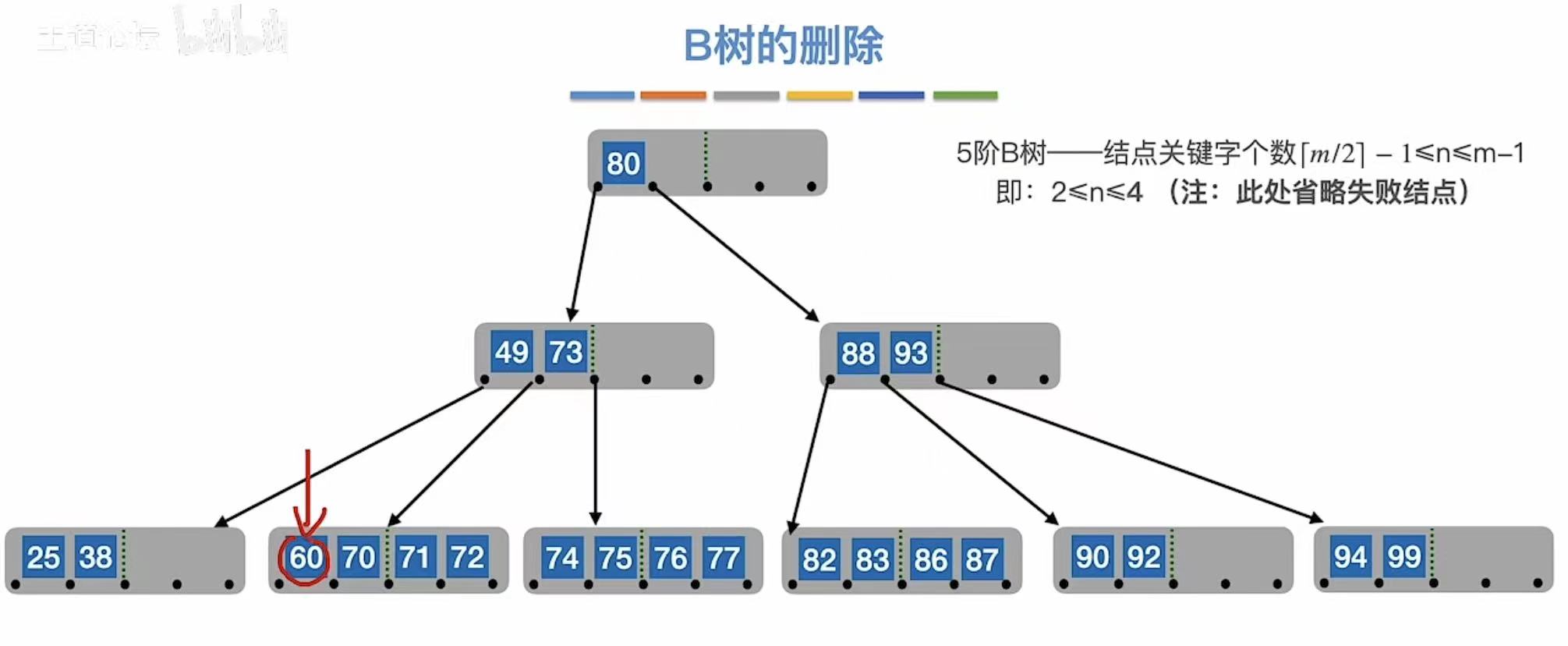
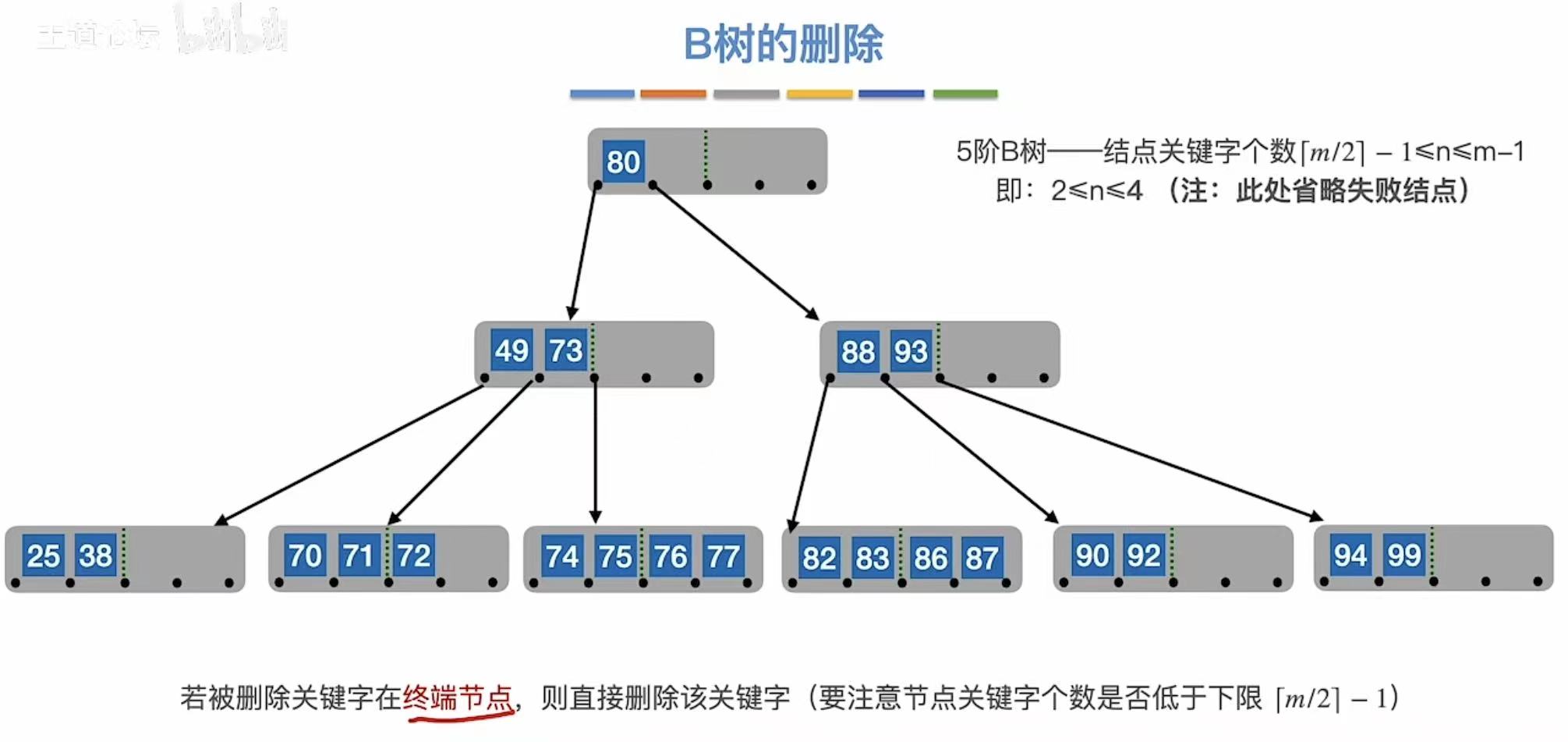
3.2.1 终端结点

终端结点：直接删掉

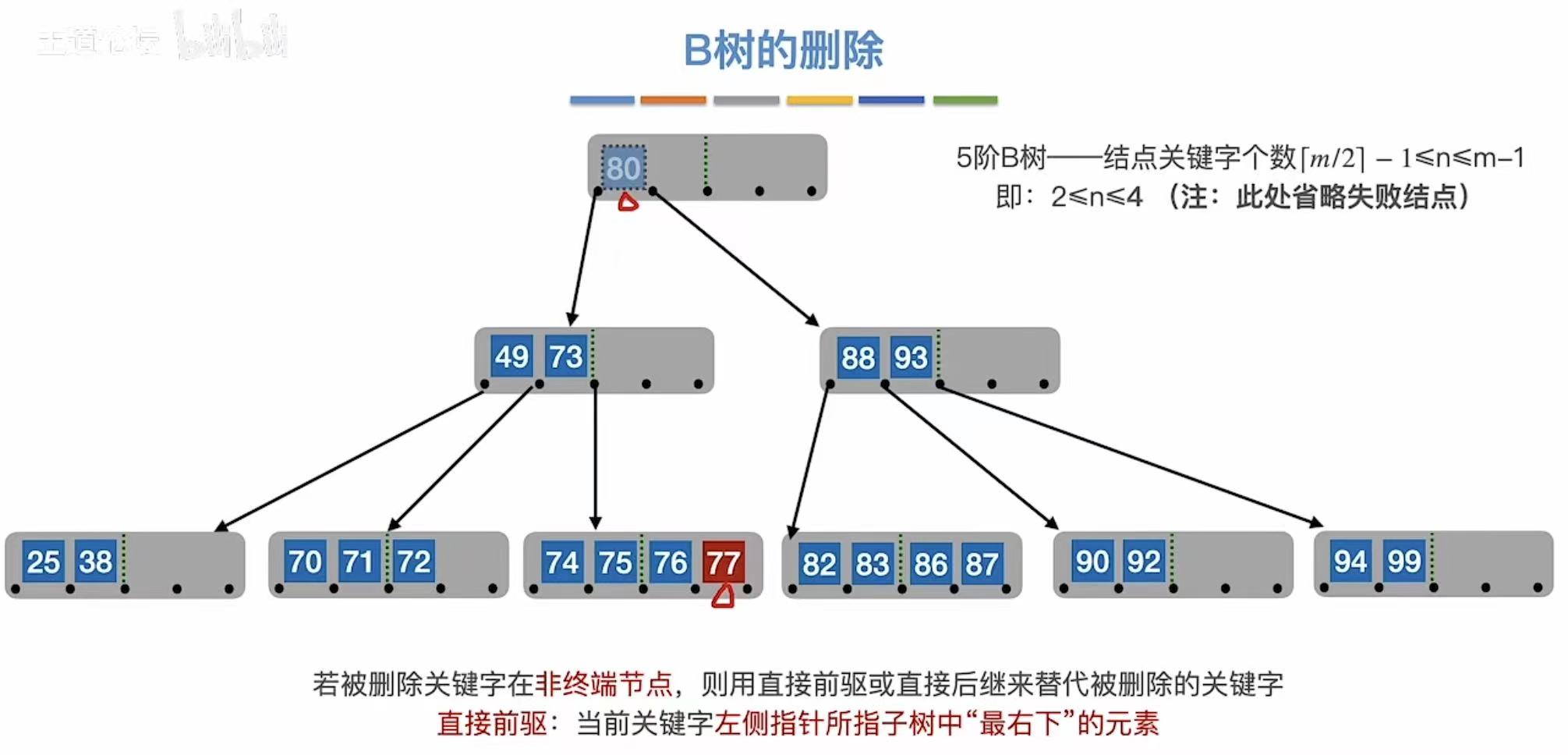
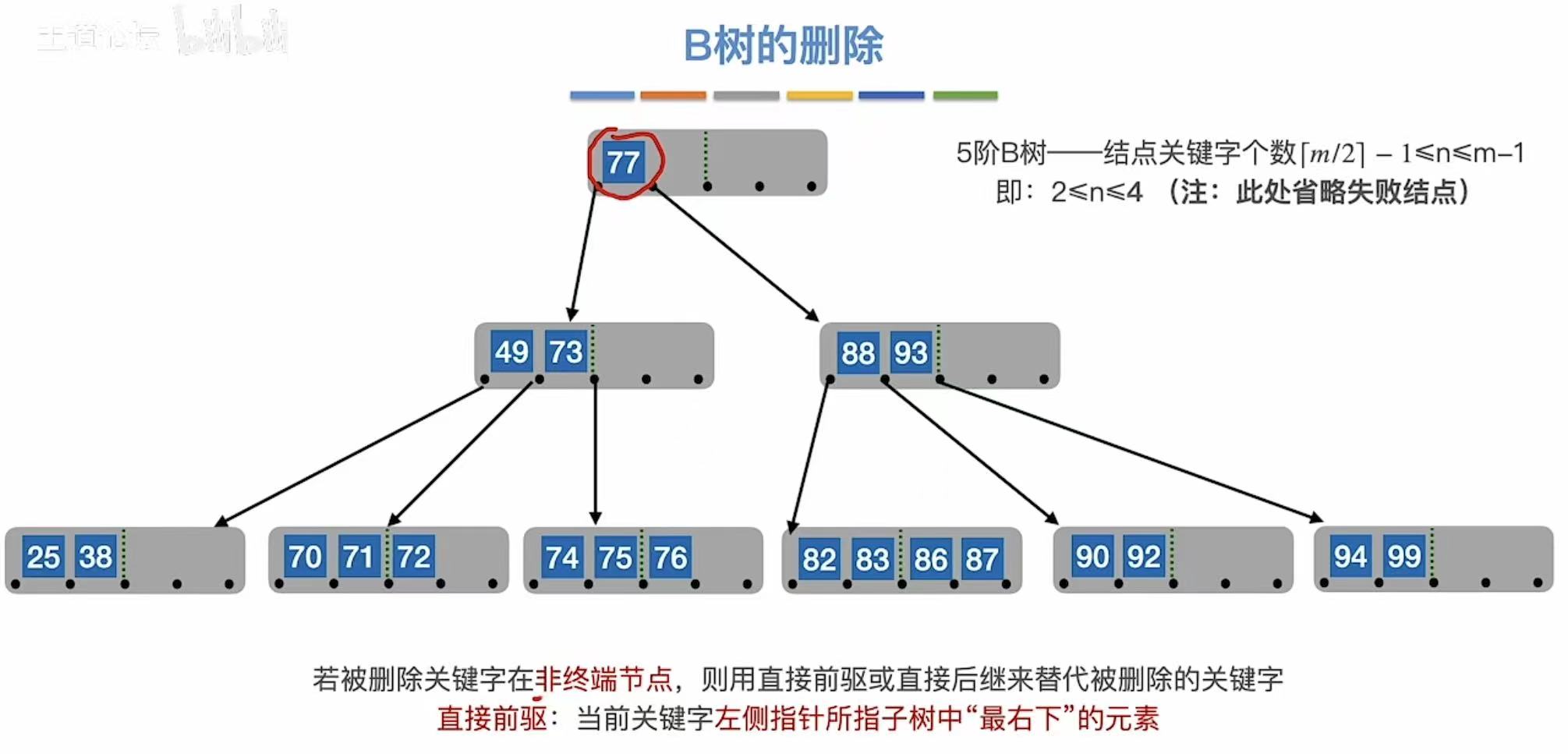
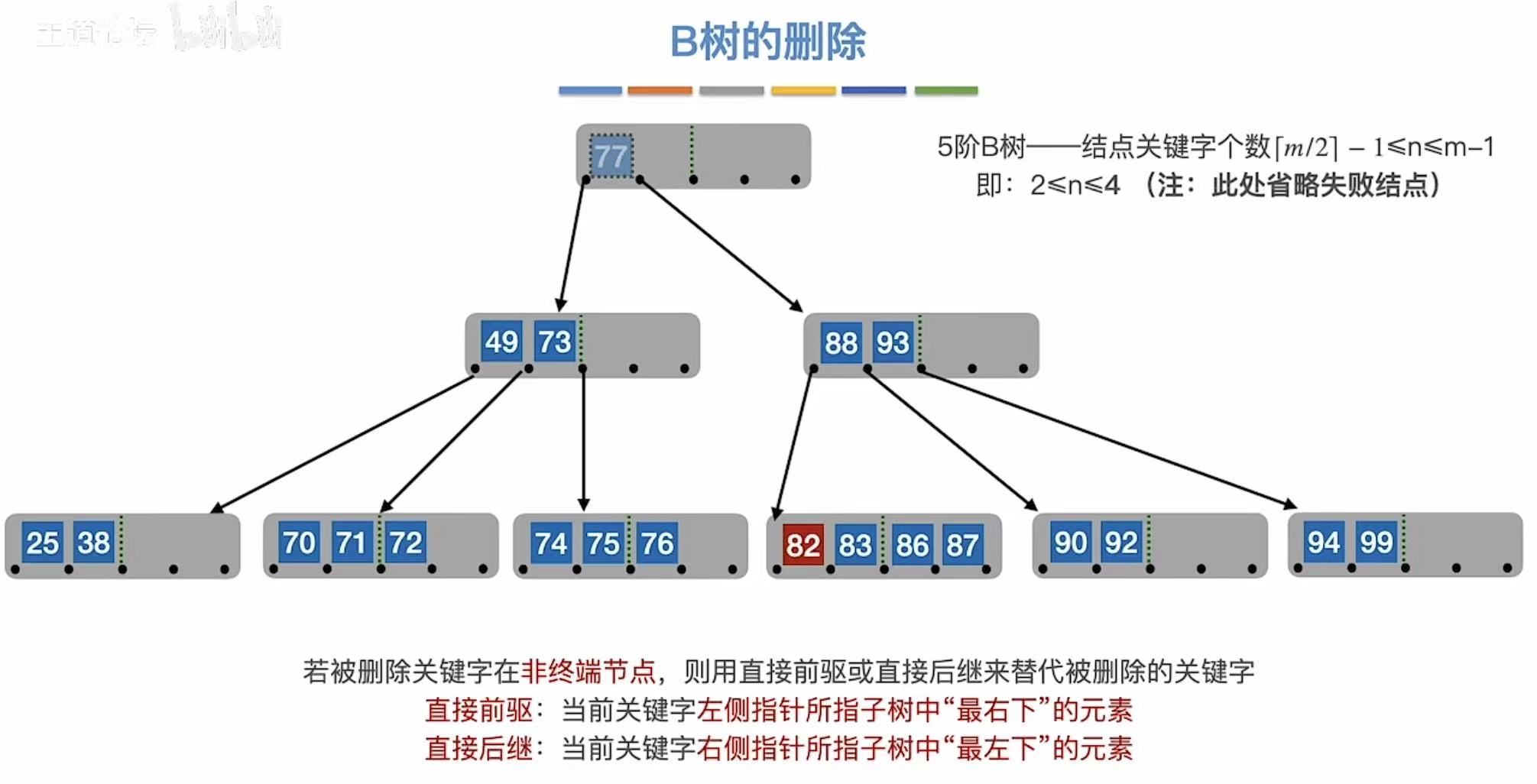
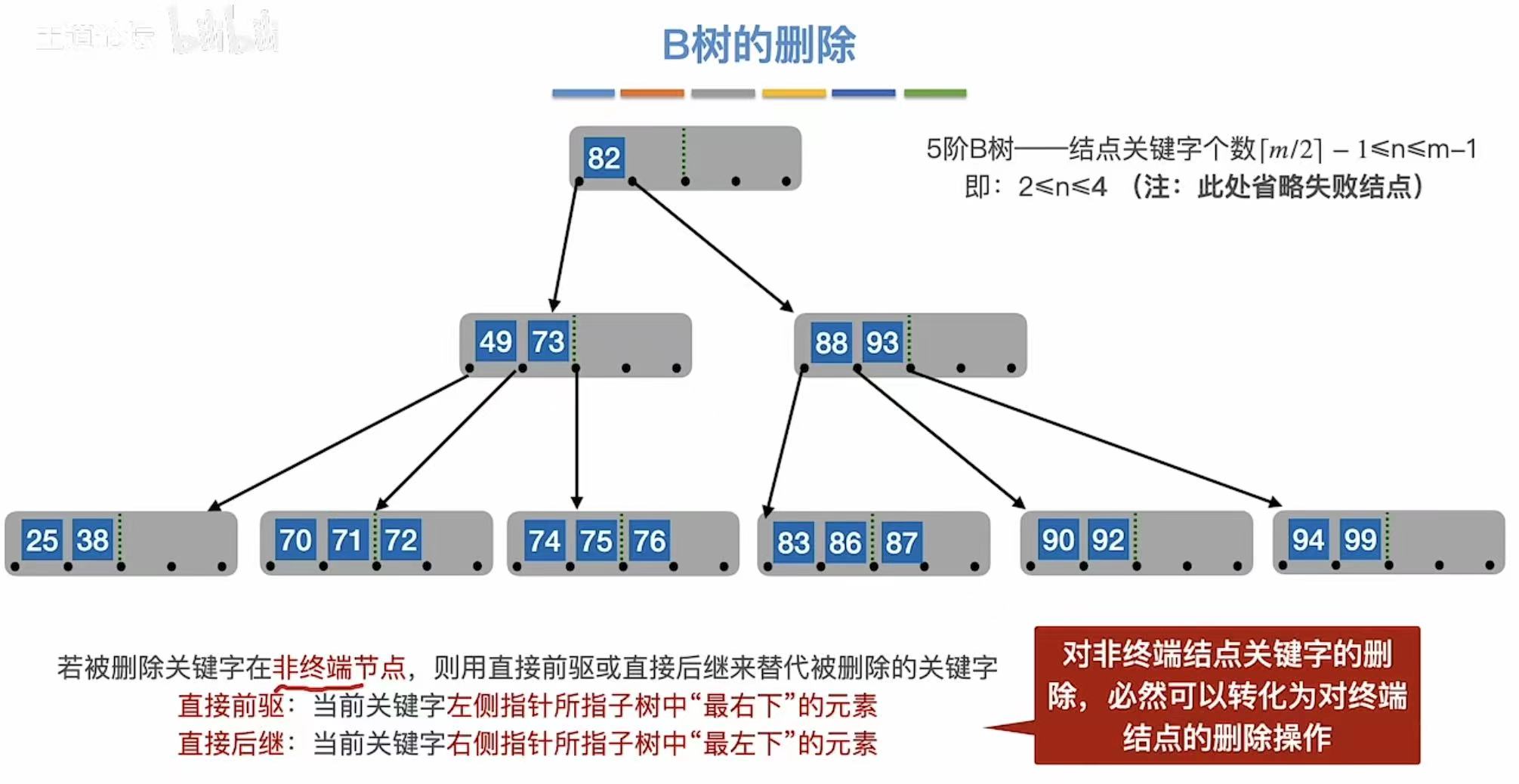
3.2.2 非终端结点

非终端结点：直接前驱/后继来代替。

3.2.3 兄弟够借

兄弟够借：自己不满足最低条件了，旁边有人满足，就可以借一个关键字。

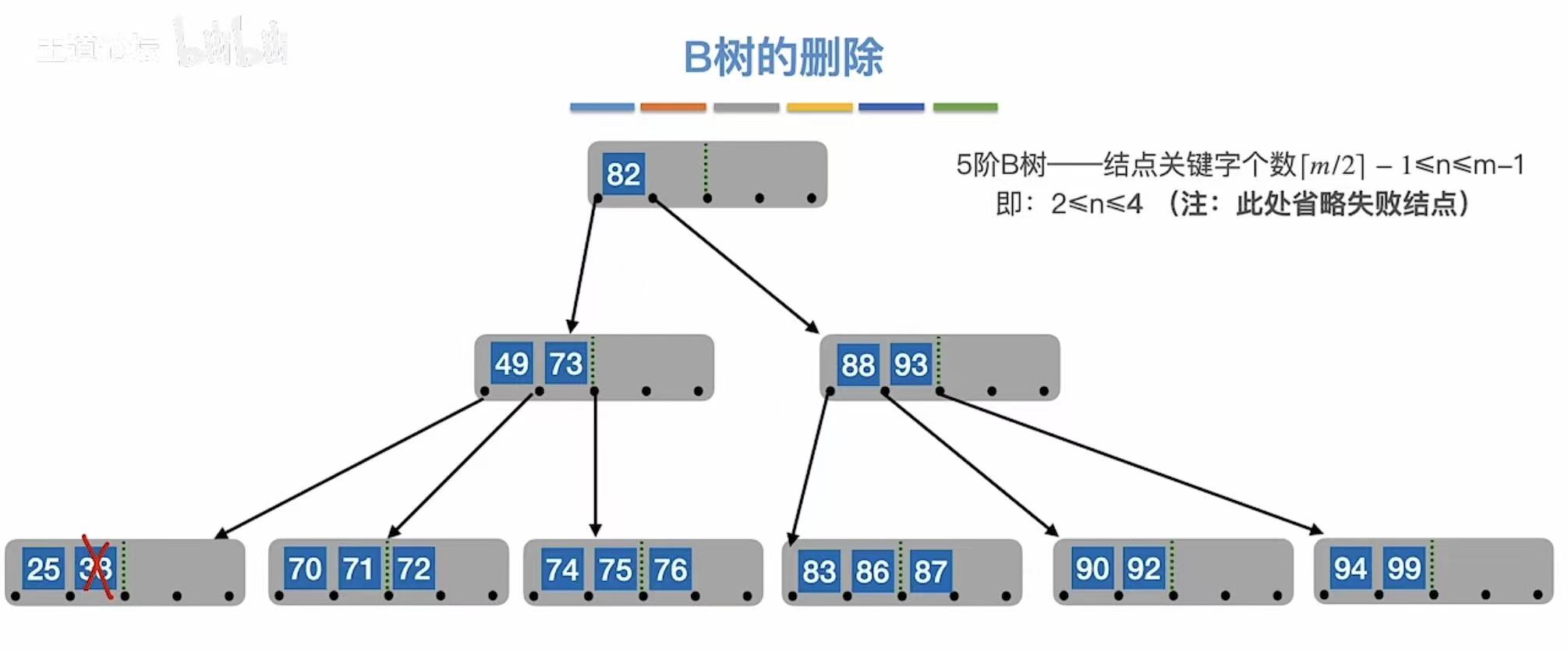
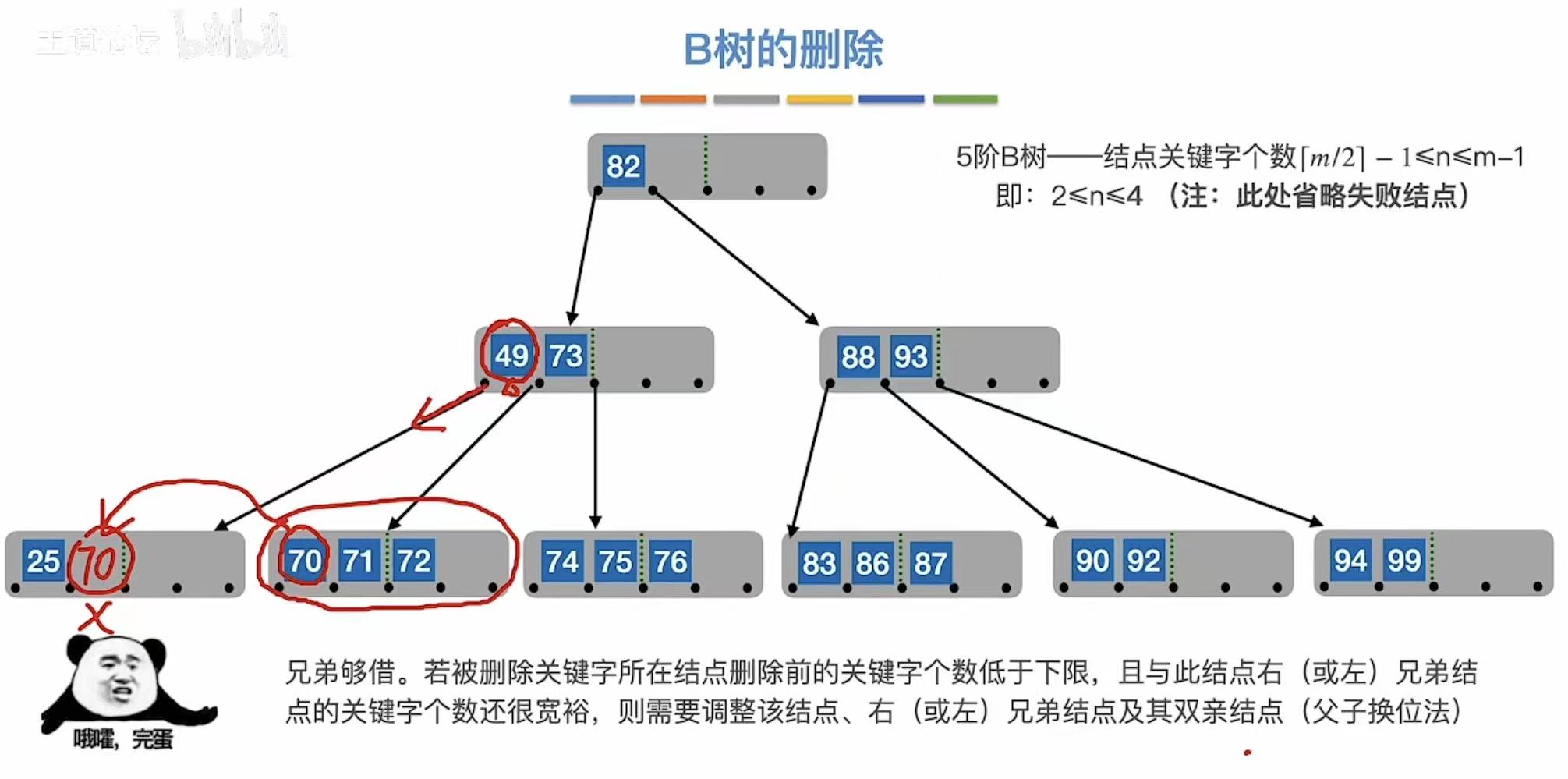
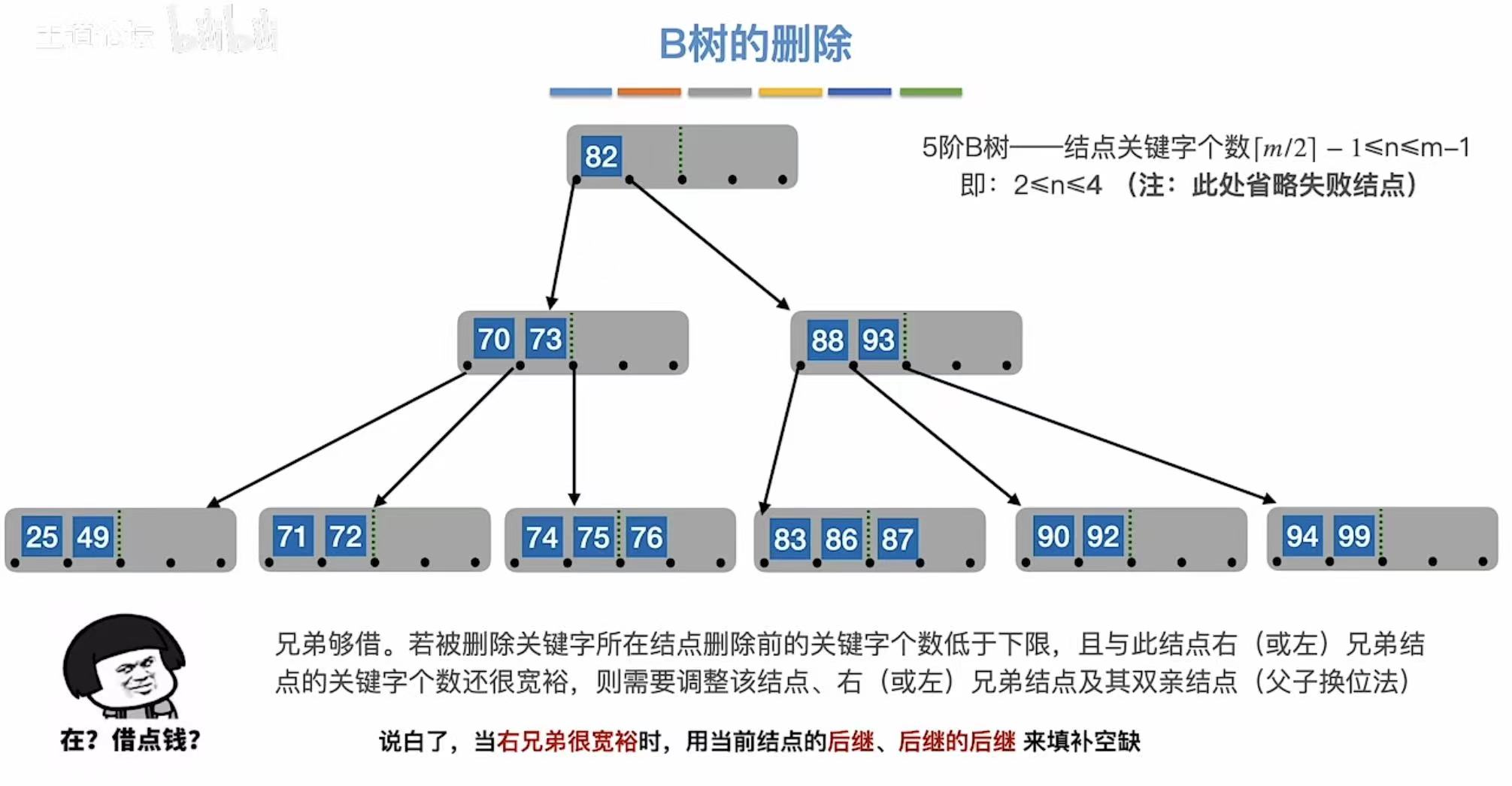
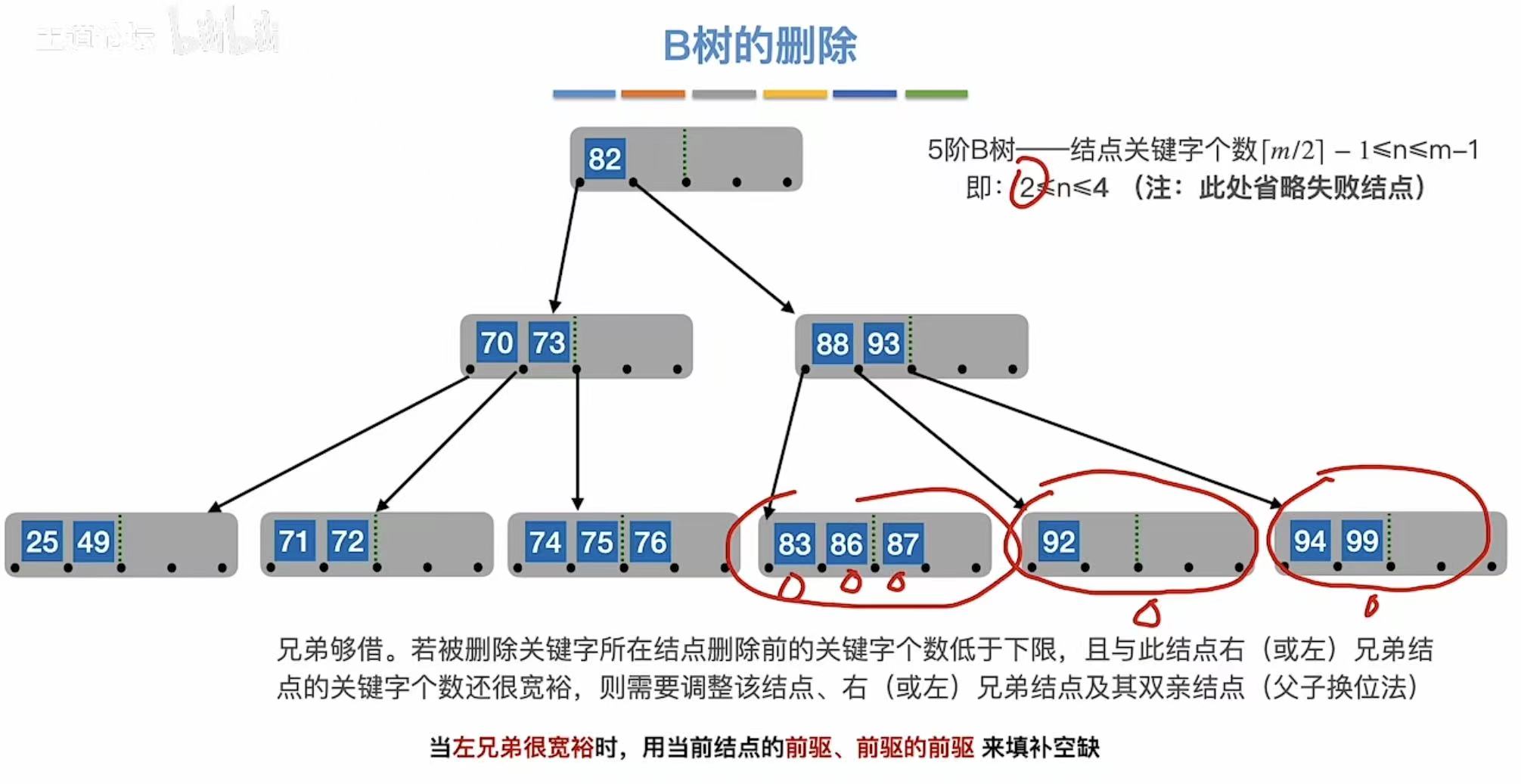
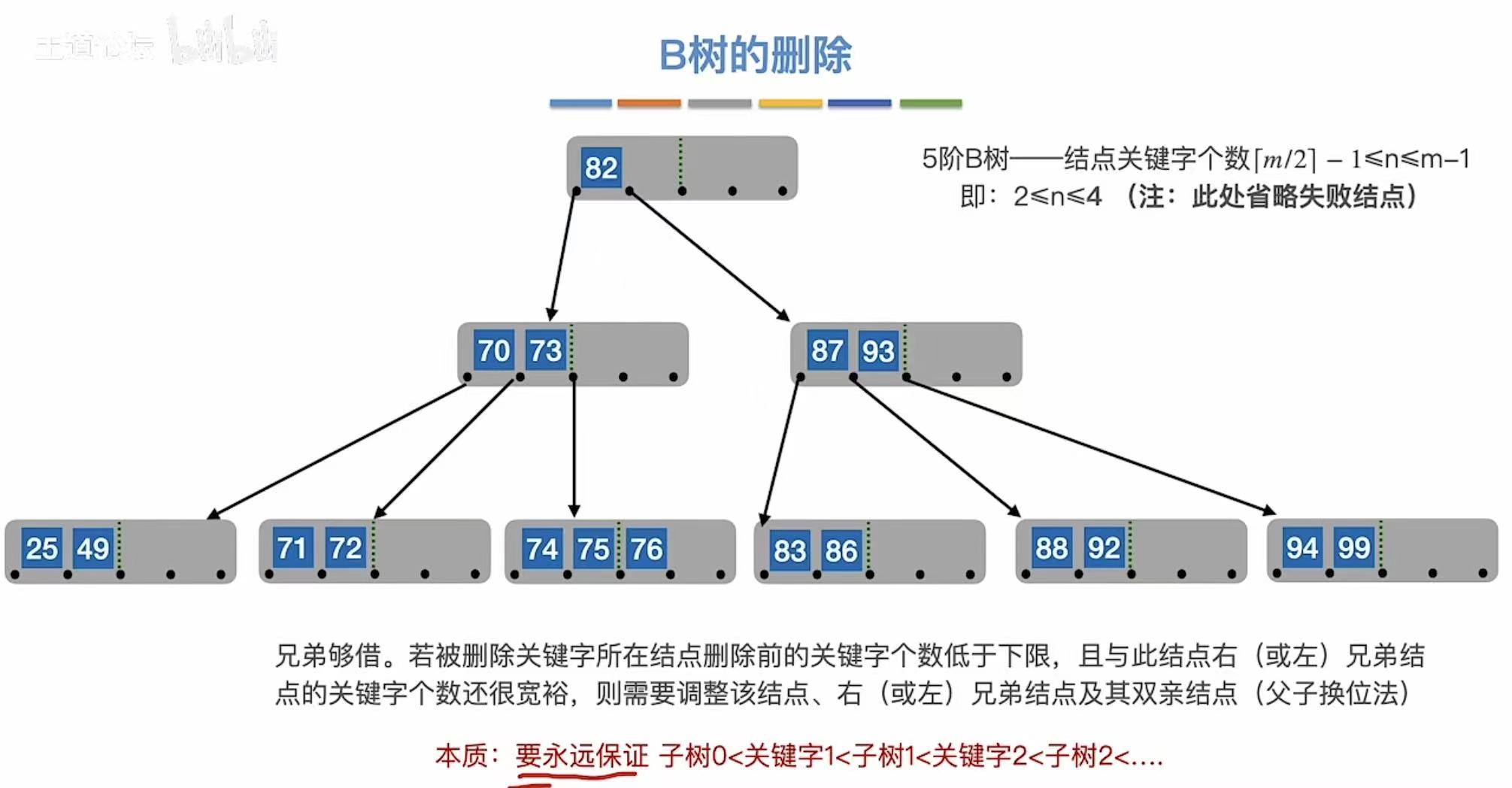
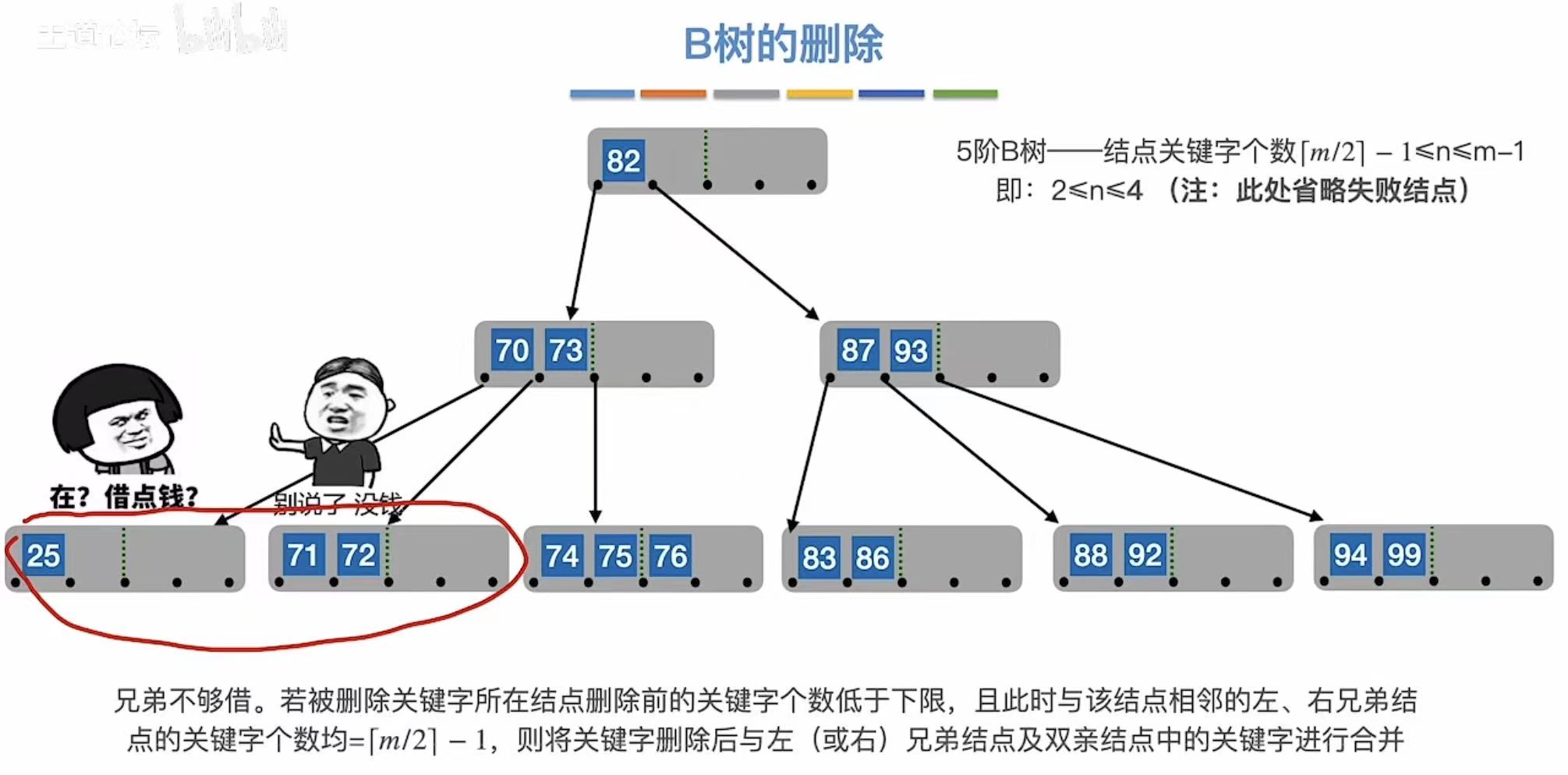
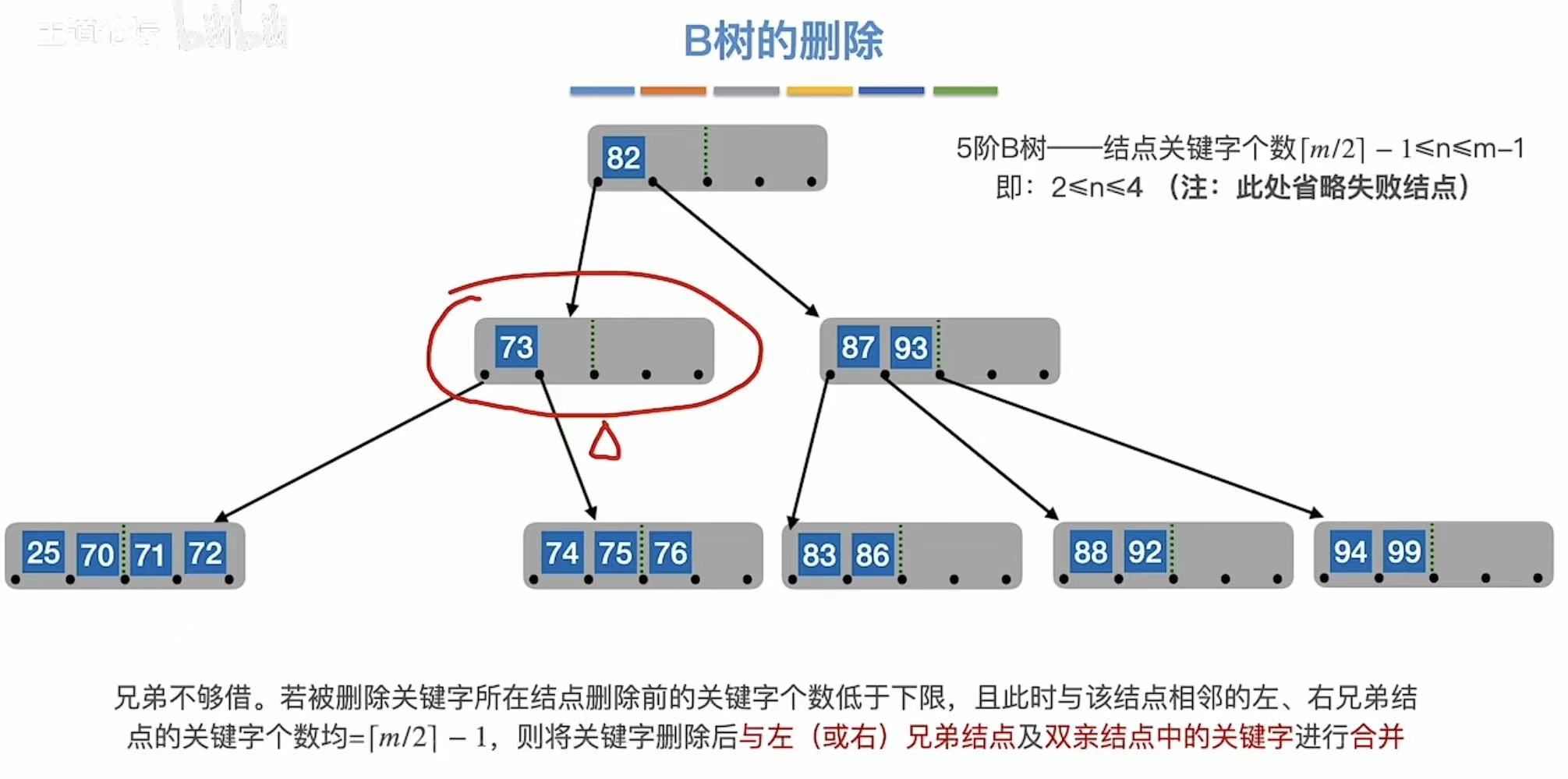
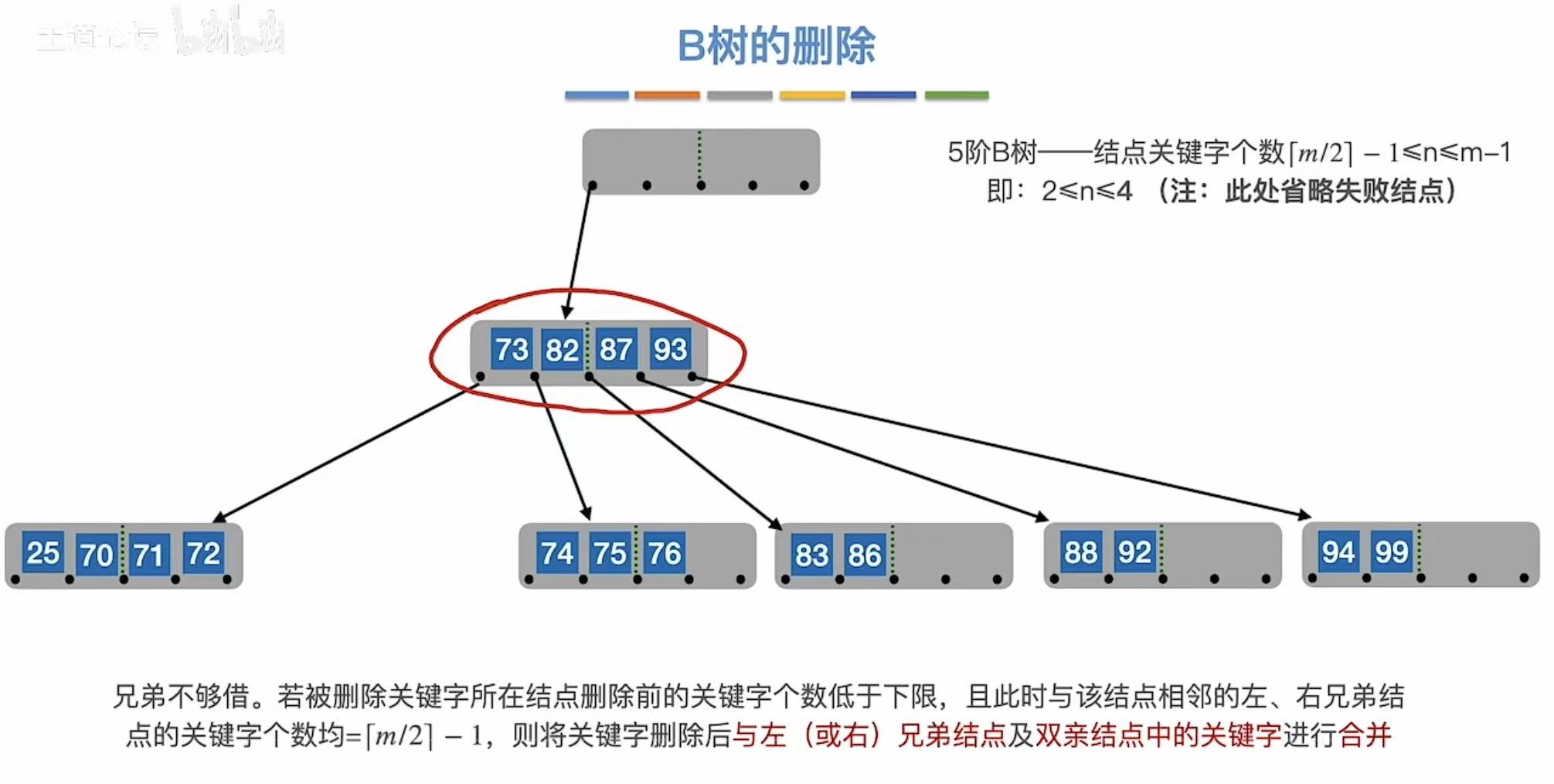
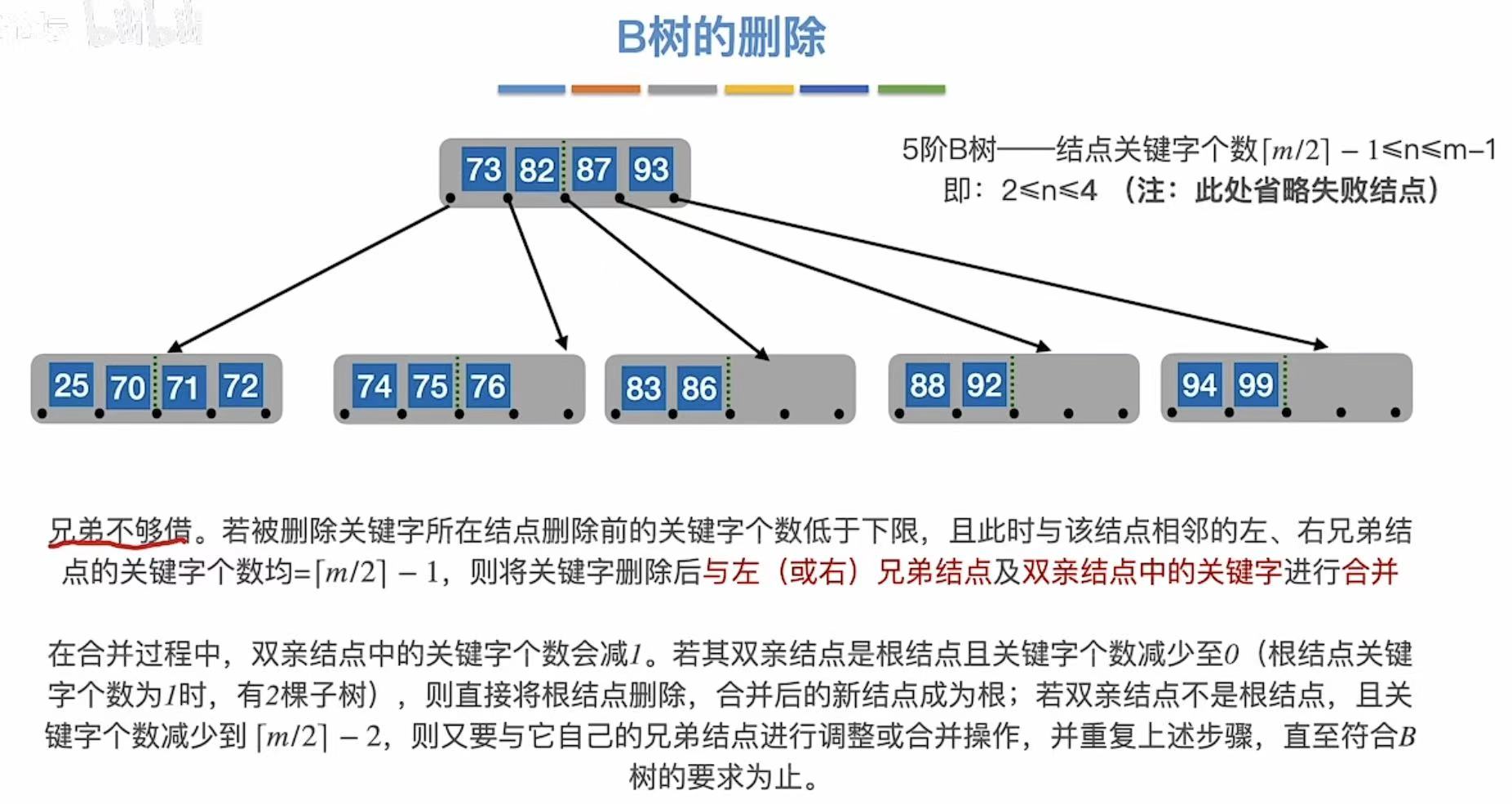
3.2.4 兄弟不够借

兄弟不够借：旁边儿也自身难保，那就穷穷结合。

3.3 小结

B+树

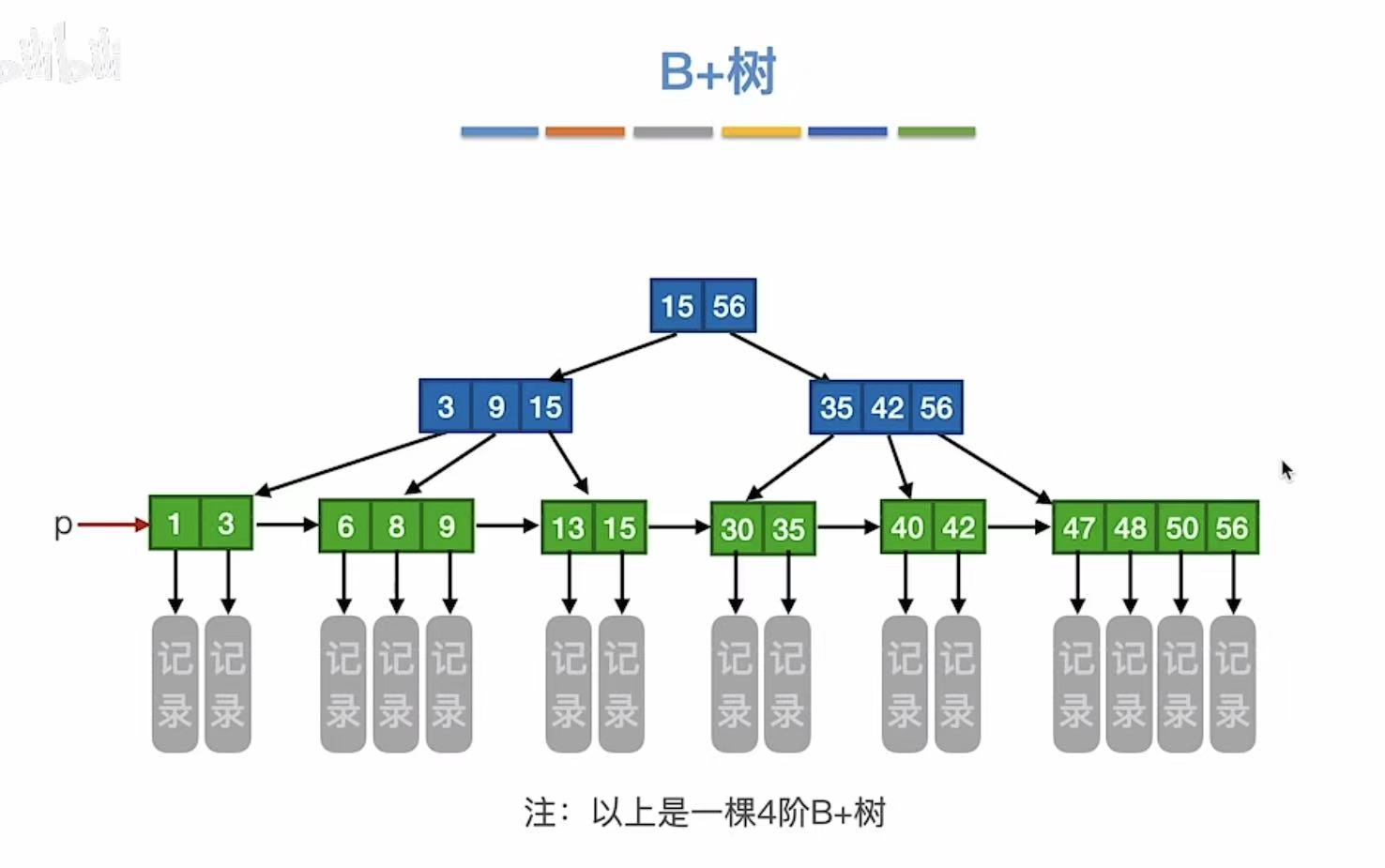
1. B+树

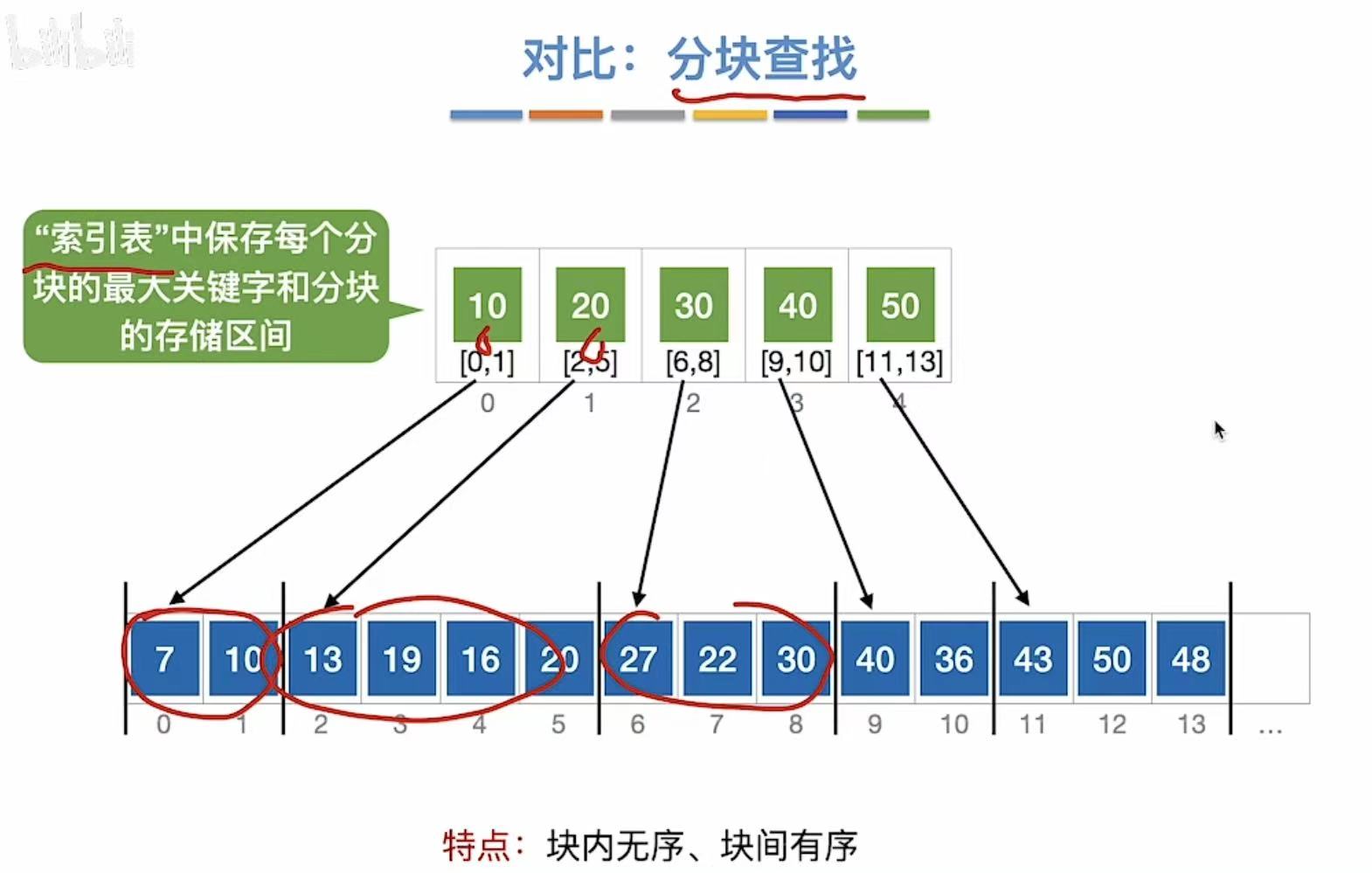
B+树可以和分块查找对比学习，简单说就是都用到了索引 这个东西。

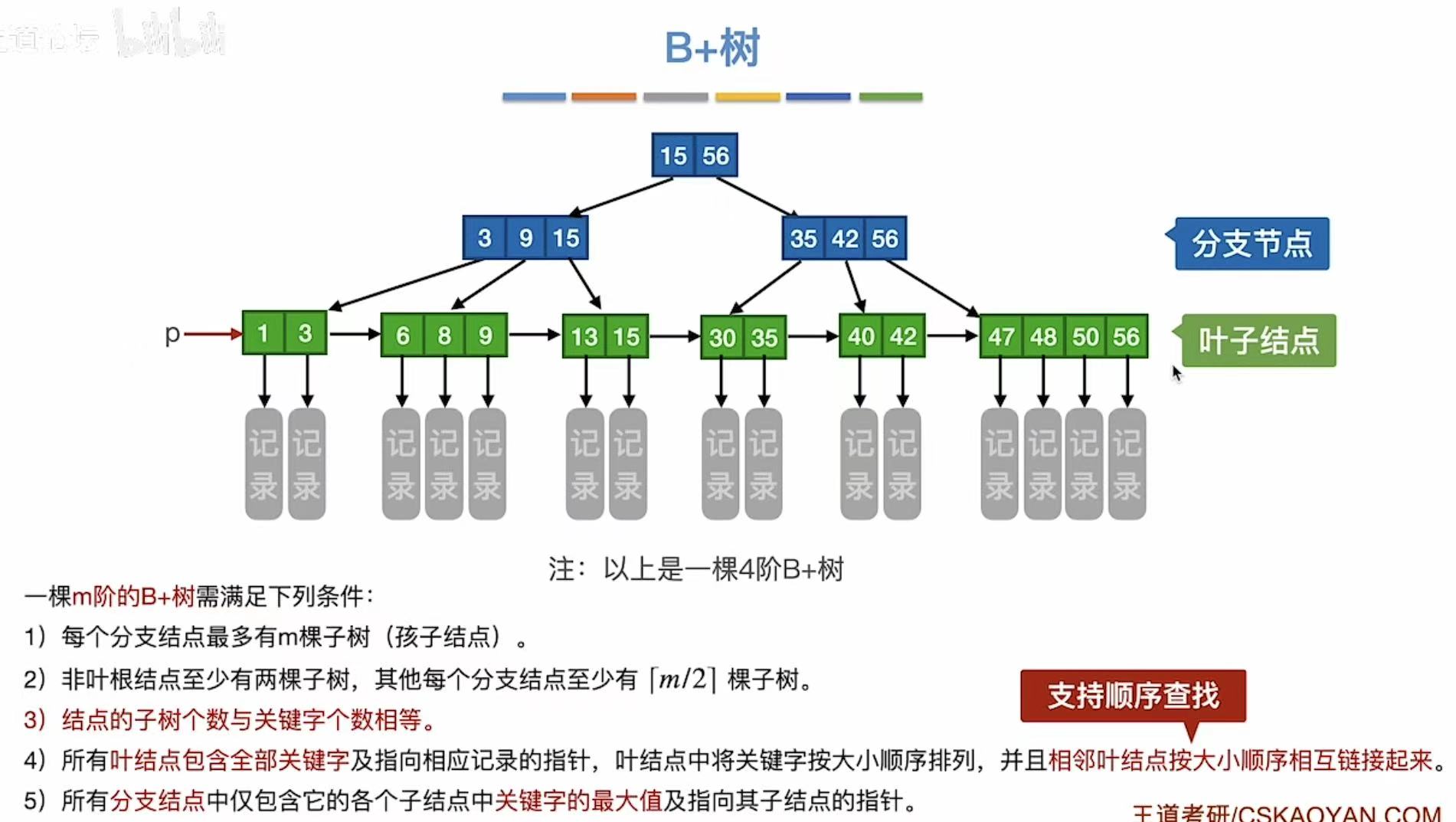
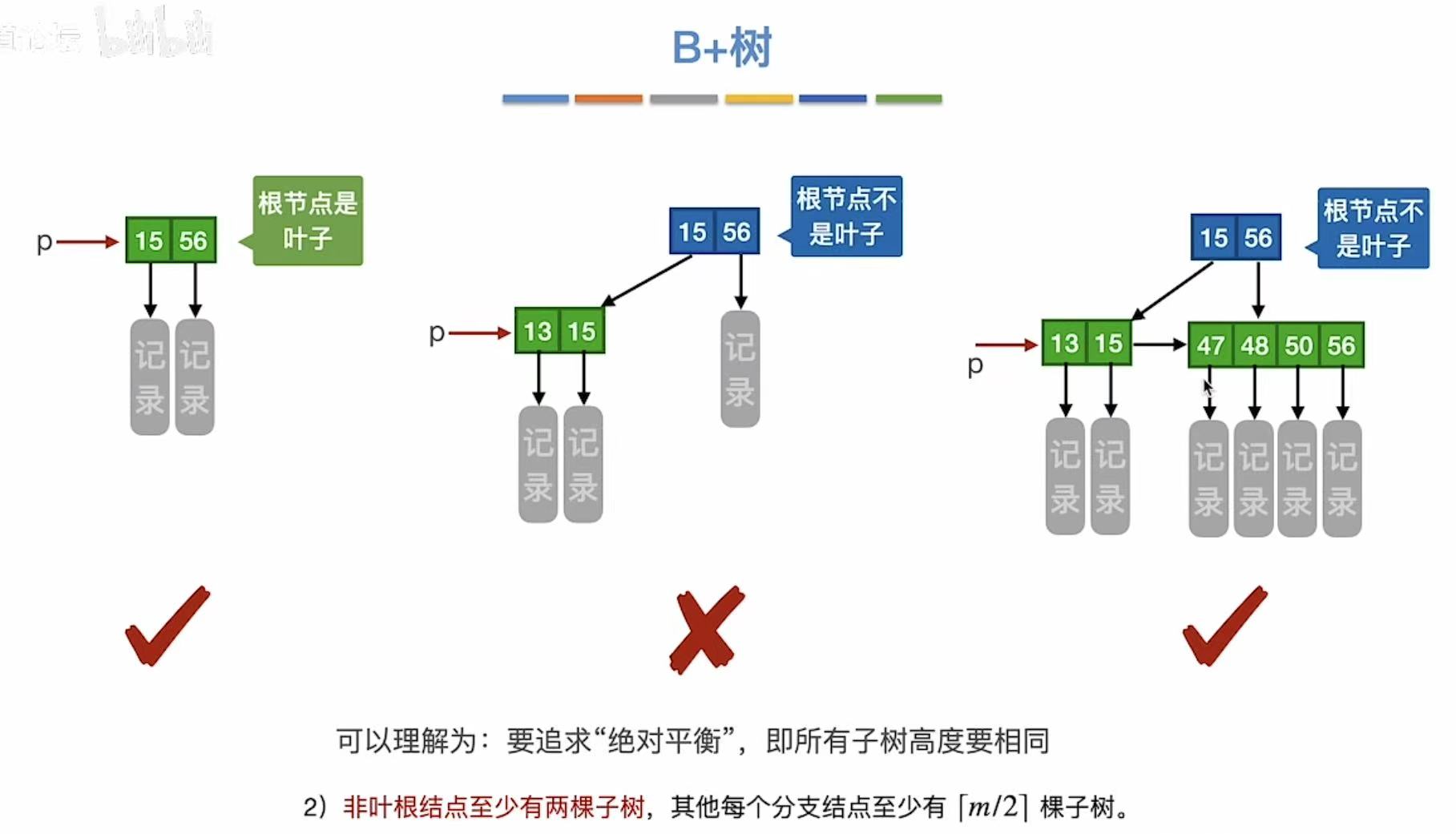
m阶B+树：

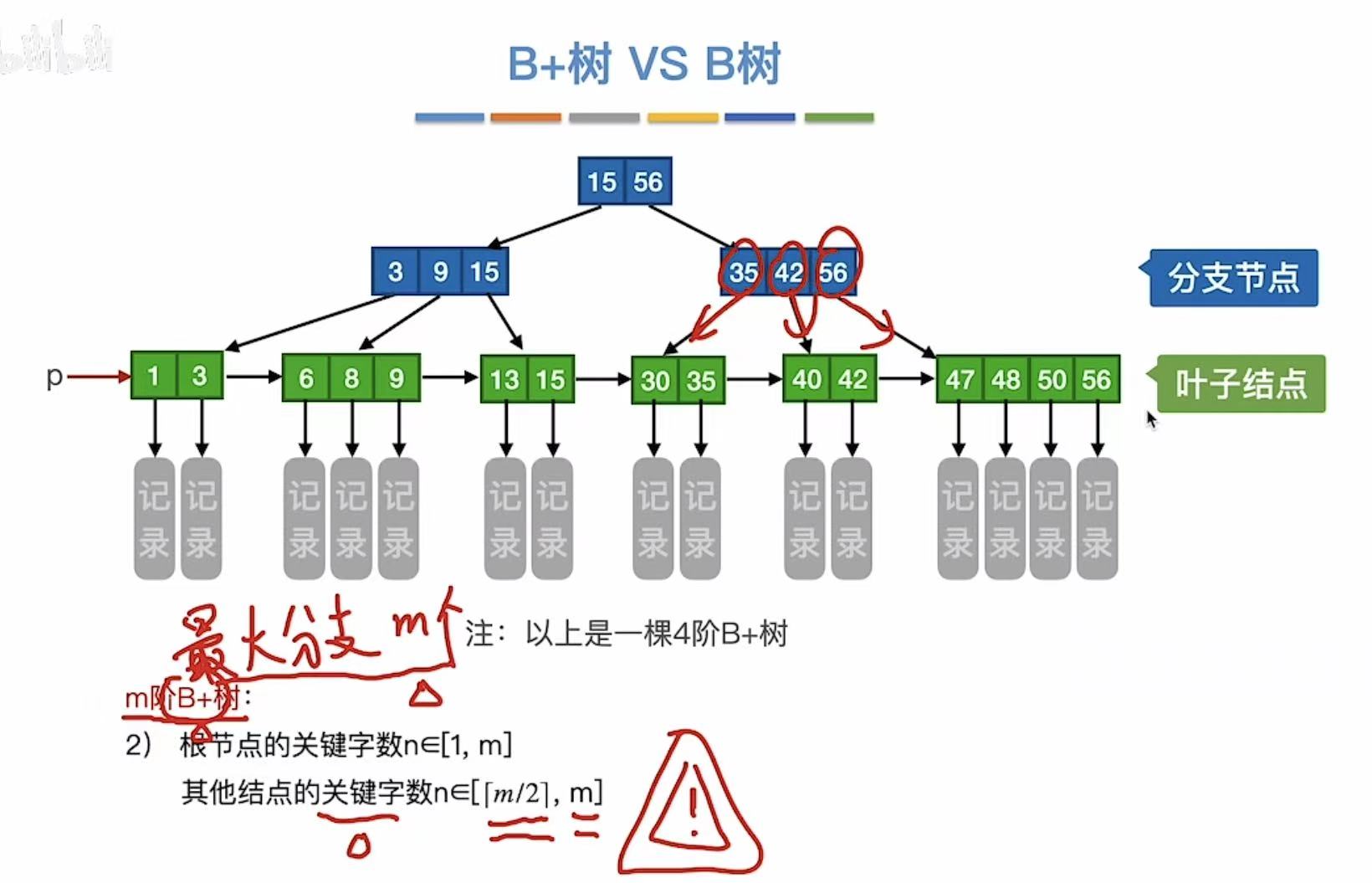
• 每个分支结点最多有m棵子树
• 非根结点至少有两棵子树，其他每个分支结点至少有m/2棵子树
• 结点的子树 个数与关键字个数相同
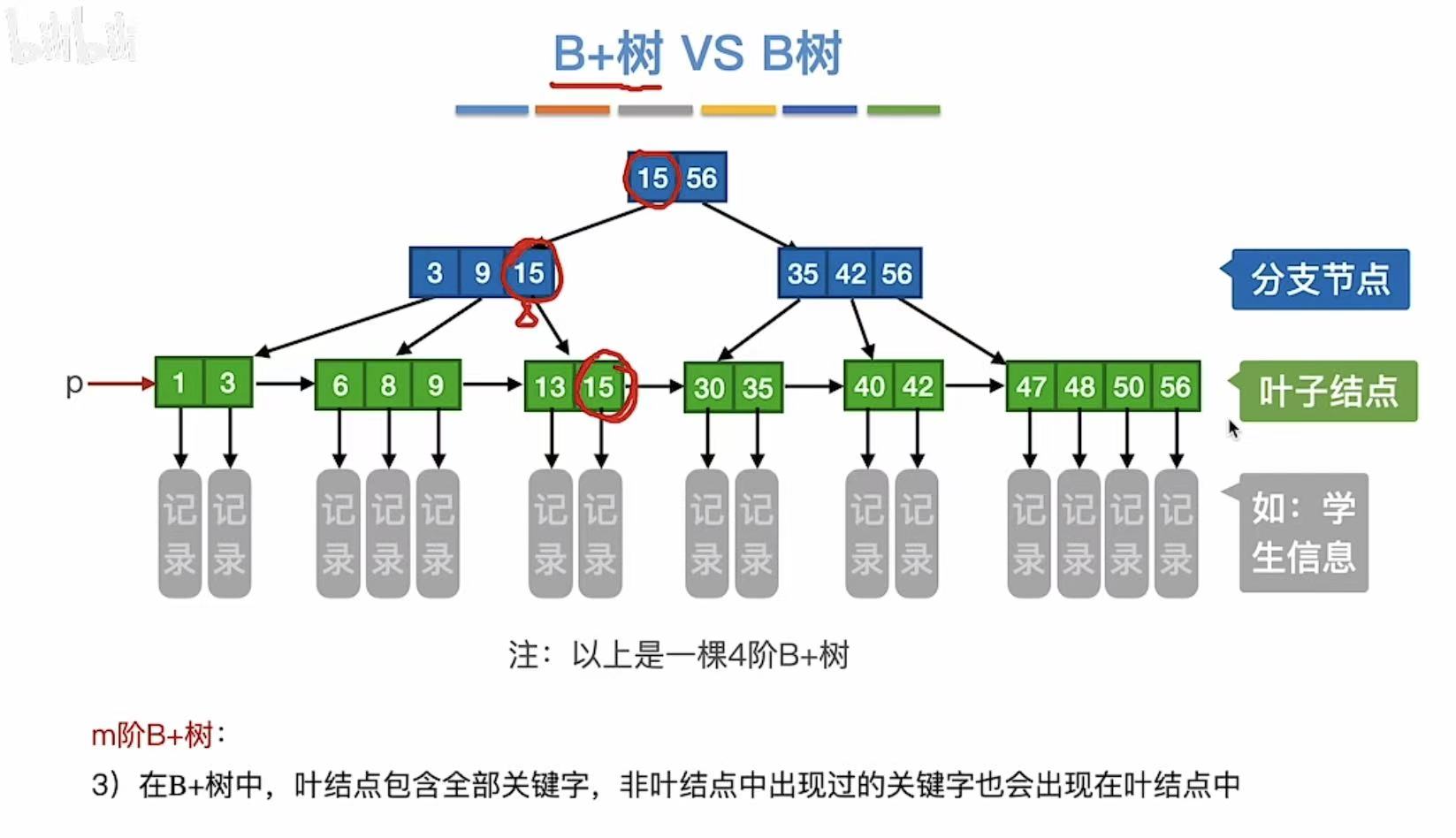
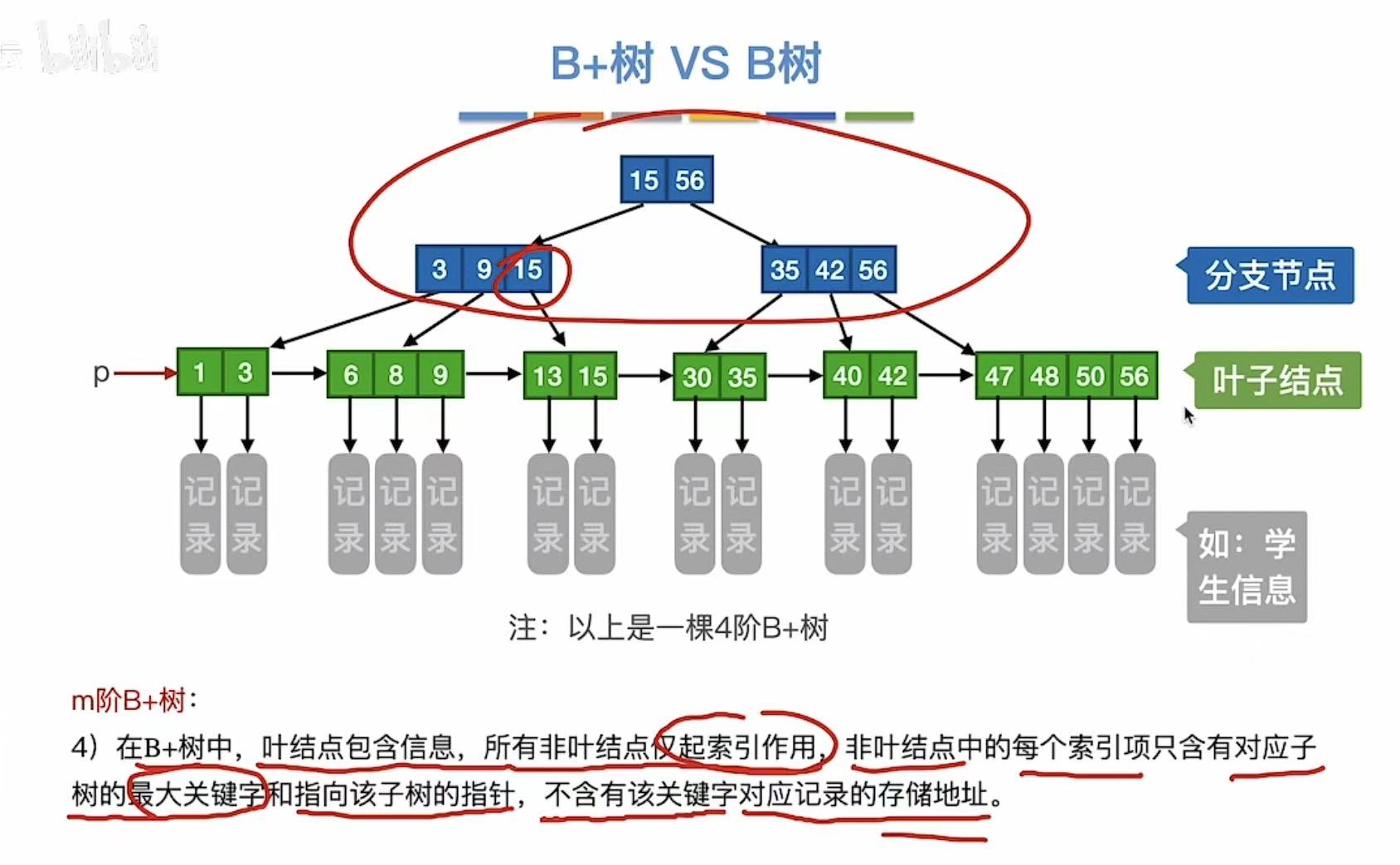
• 叶节点包含全部关键字 及记录，按大小顺序排列
• 分支结点包含关键字的最大值 和指针
  
  

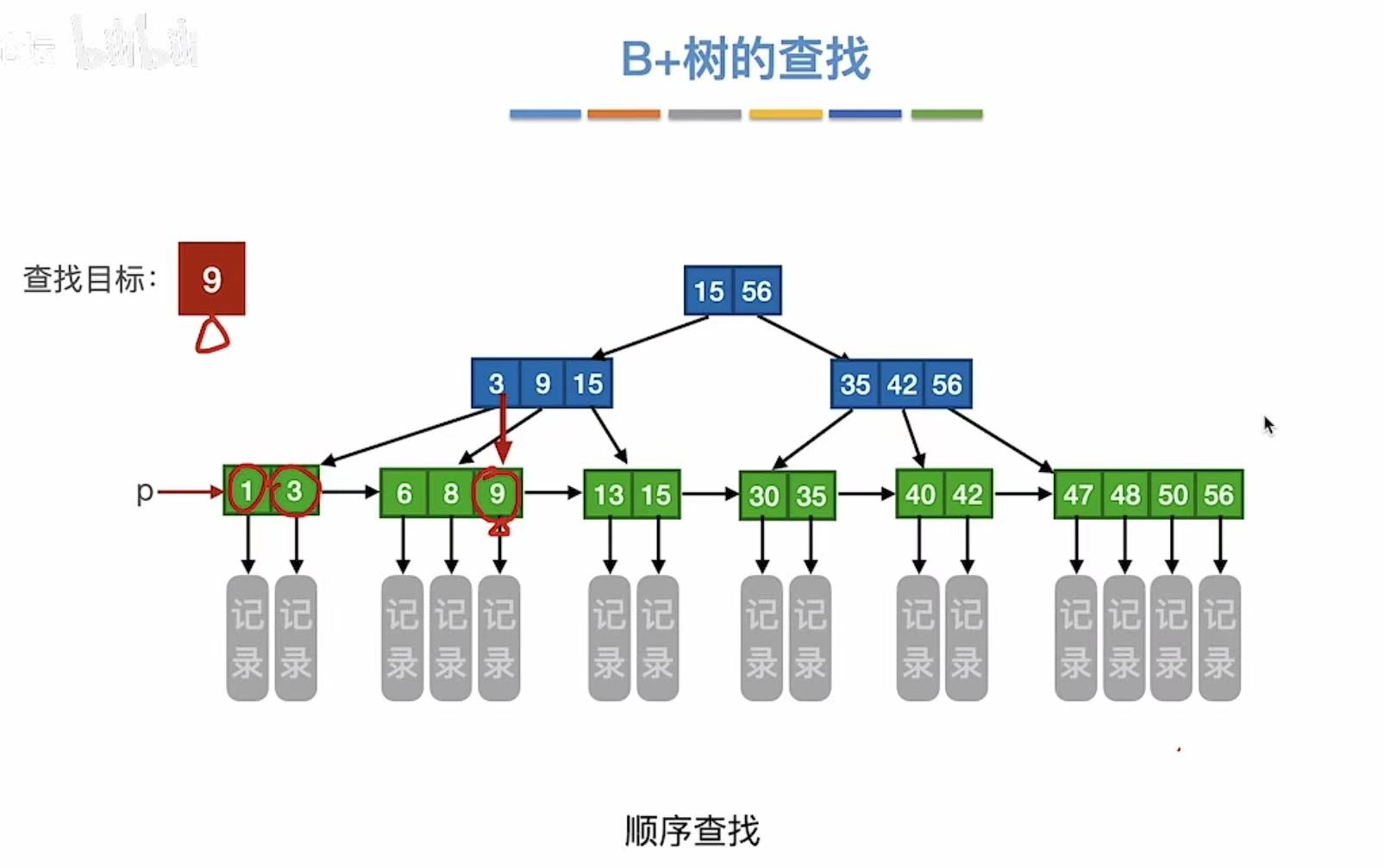
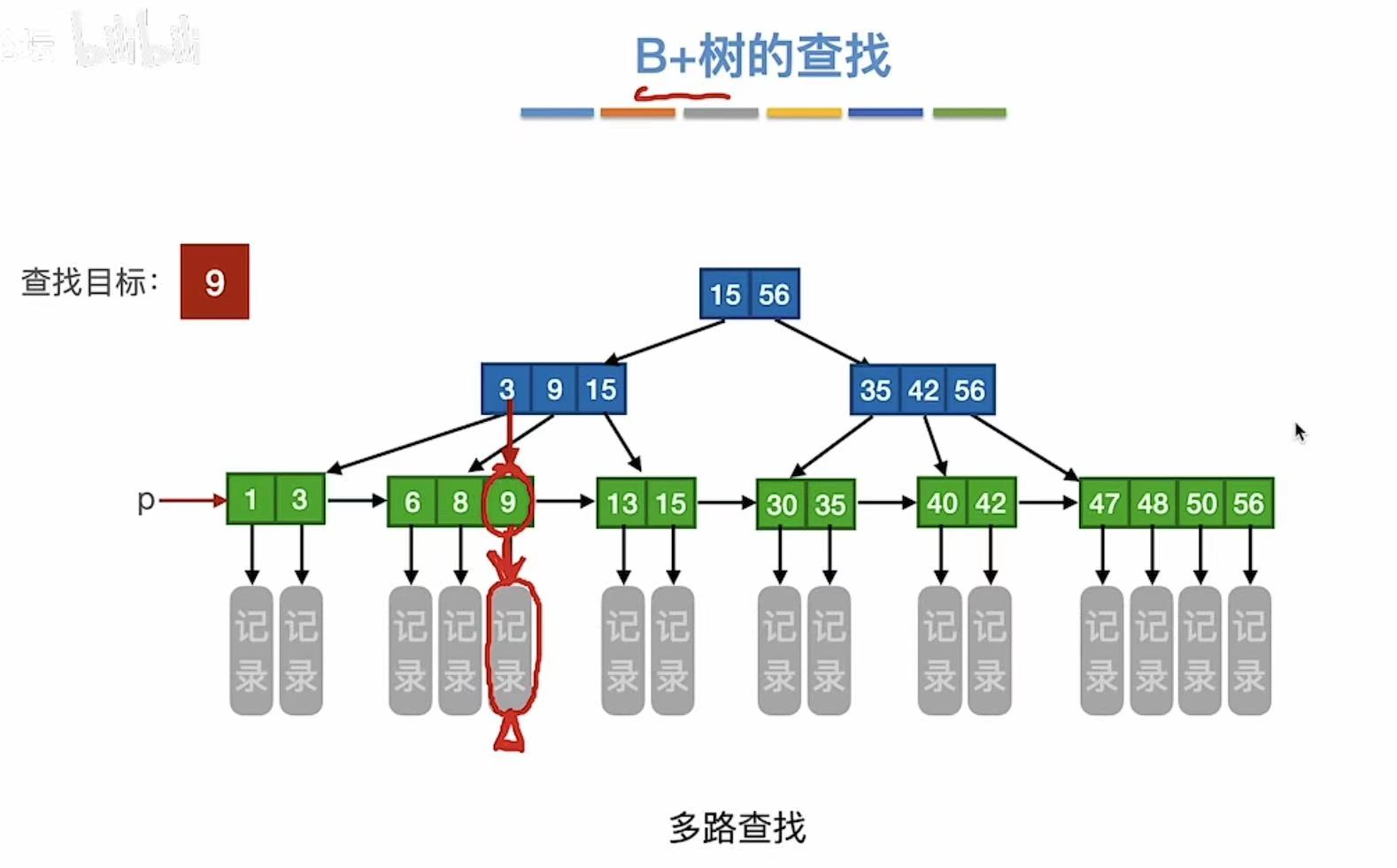
2. B+树的查找

查找9：

• 可以从根节点往下查找
• 也可以p指针从左往右查找
  
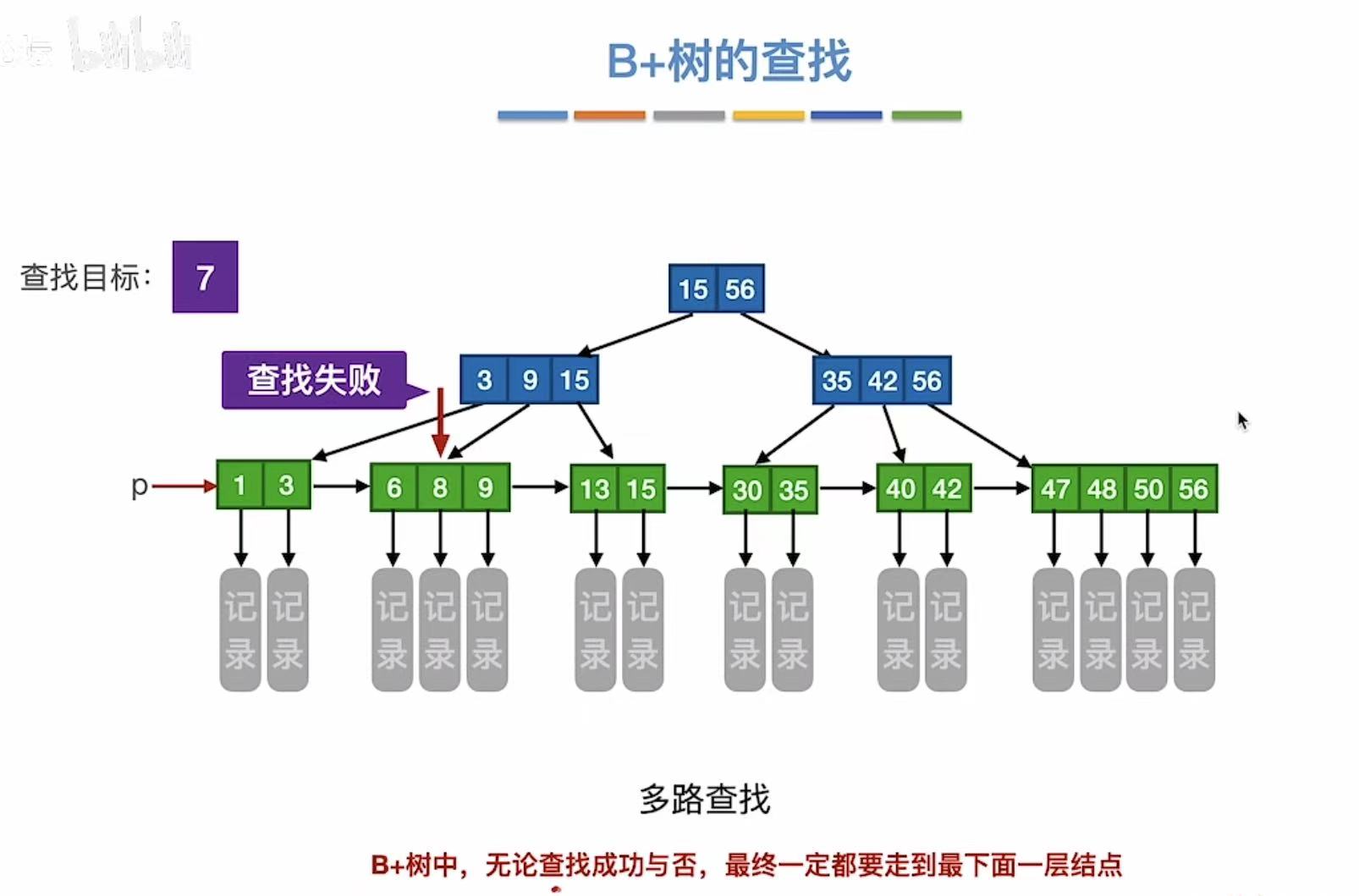
  查找7：
• 可以从根节点往下查找
• 也可以p指针从左往右查找
• 不管成功还是失败，总会走到最下一层的结点
  

对比：

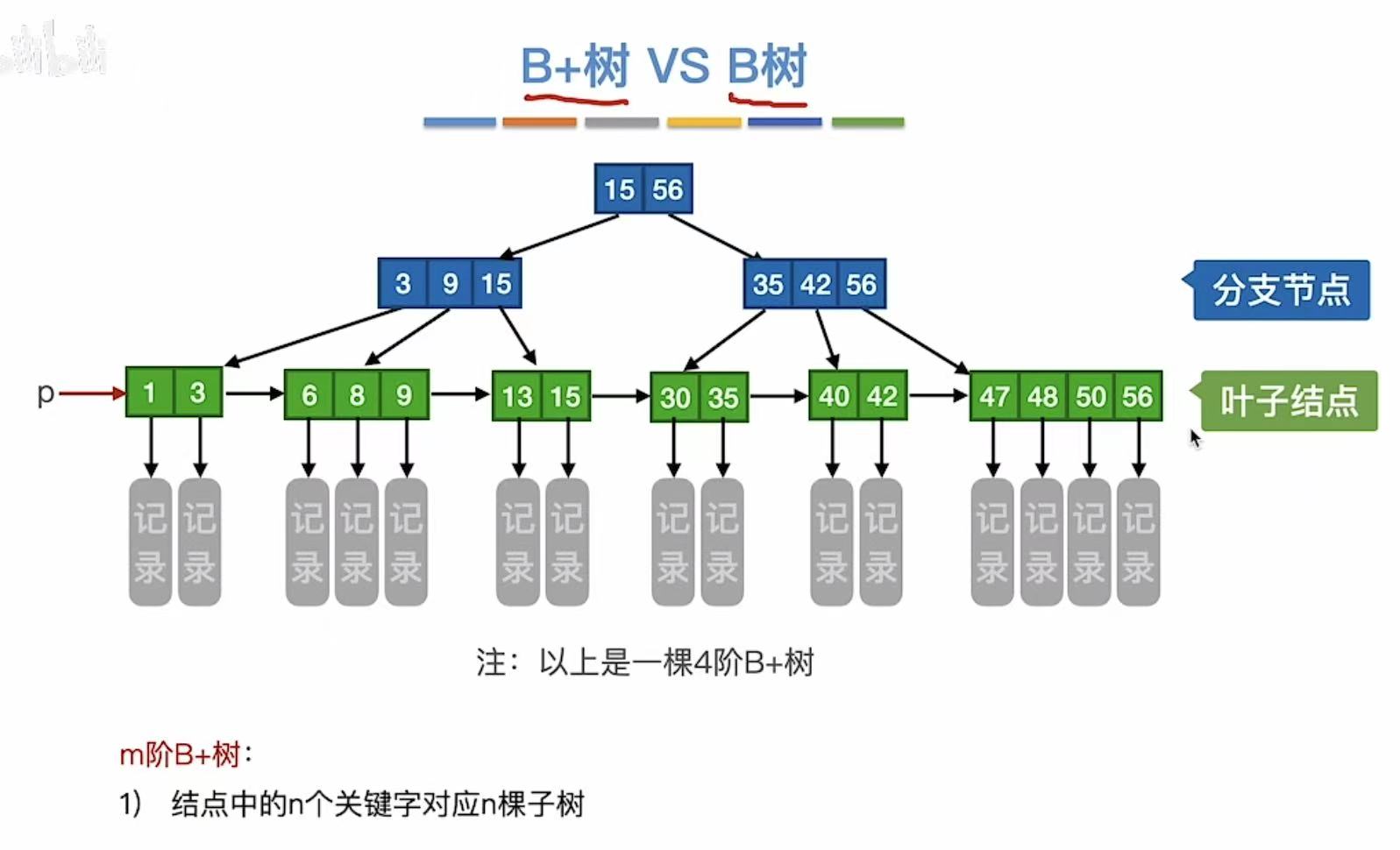
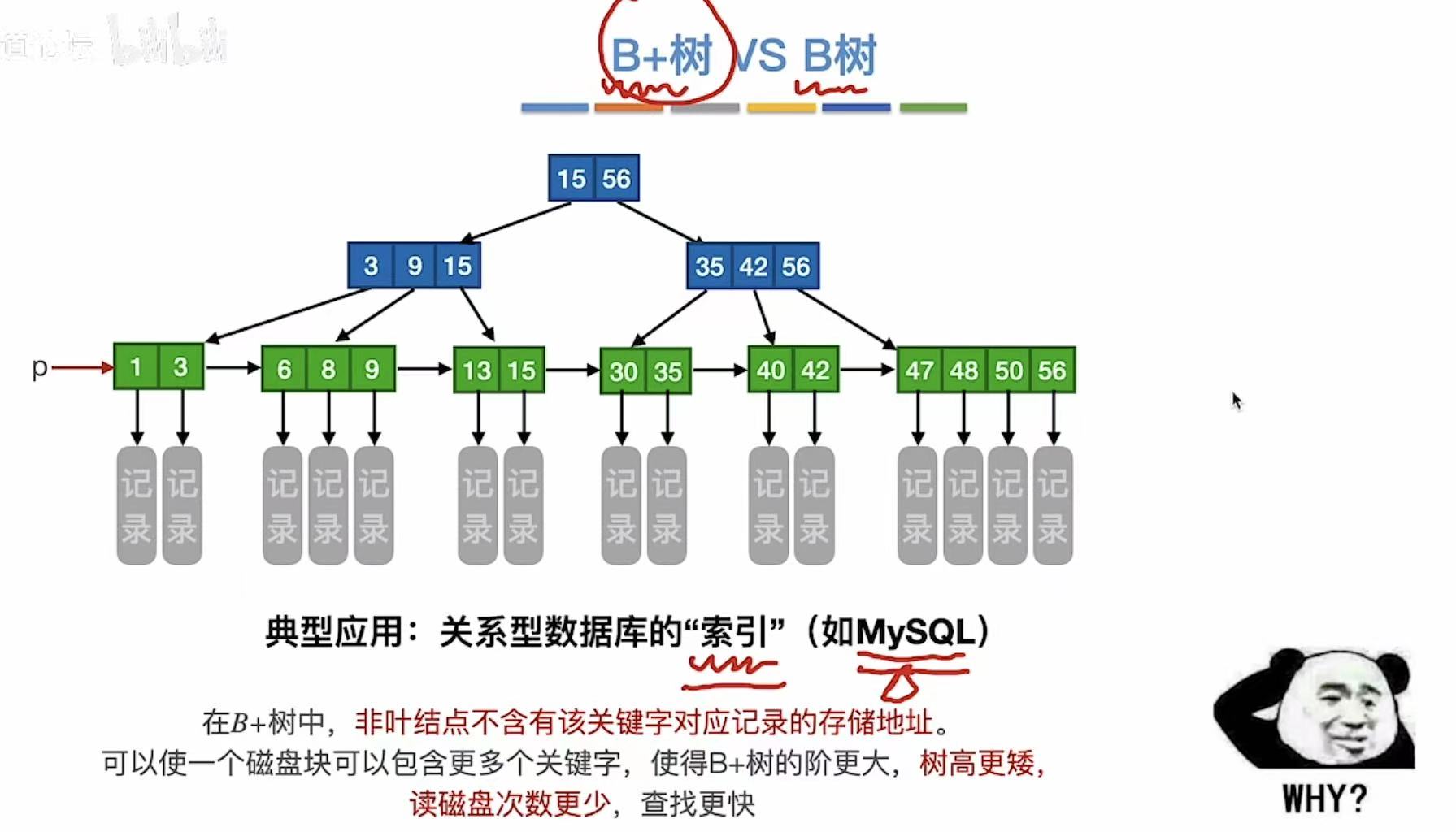
3. B+树 vs B树

第一组：

B+树：关键字是索引，是谁就指到谁

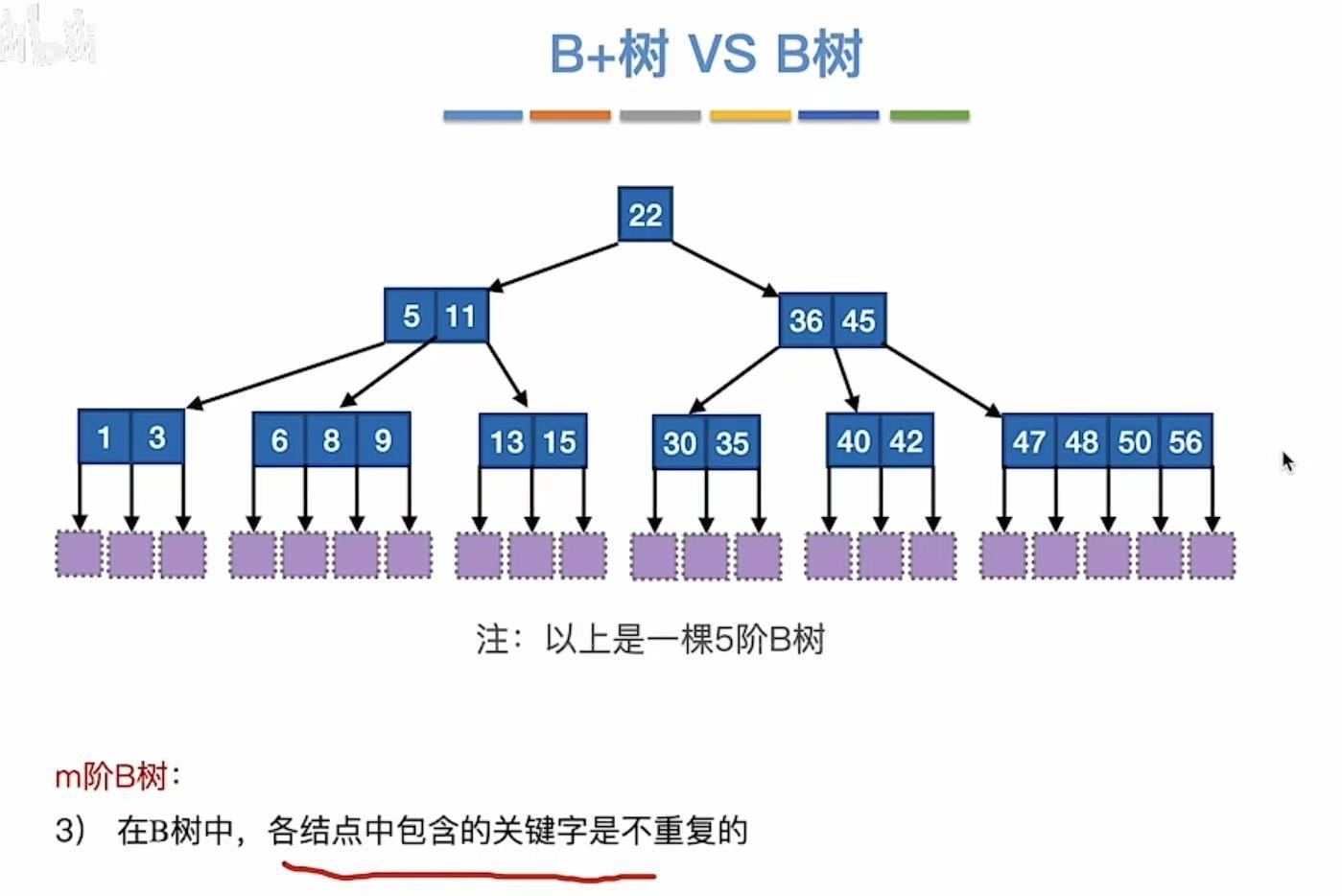
B树：关键字是分割线，分隔两个范围

第二组：

B+树：因为索引直接指向，所以没有-1（一个关键字就是一个关键字）

B树：因为是分隔，所以需要-1（一个关键字可以分两个分叉）
第三组：

B+树：索引，索引的书页对应书上的具体页码，所以自然而然会有重复

B树：因为是分隔，且关键字本身也是具体页码，所以没有重复
第四组：

B+树：只有最后一层才记录了有效数据（记录），因为前面的都是索引

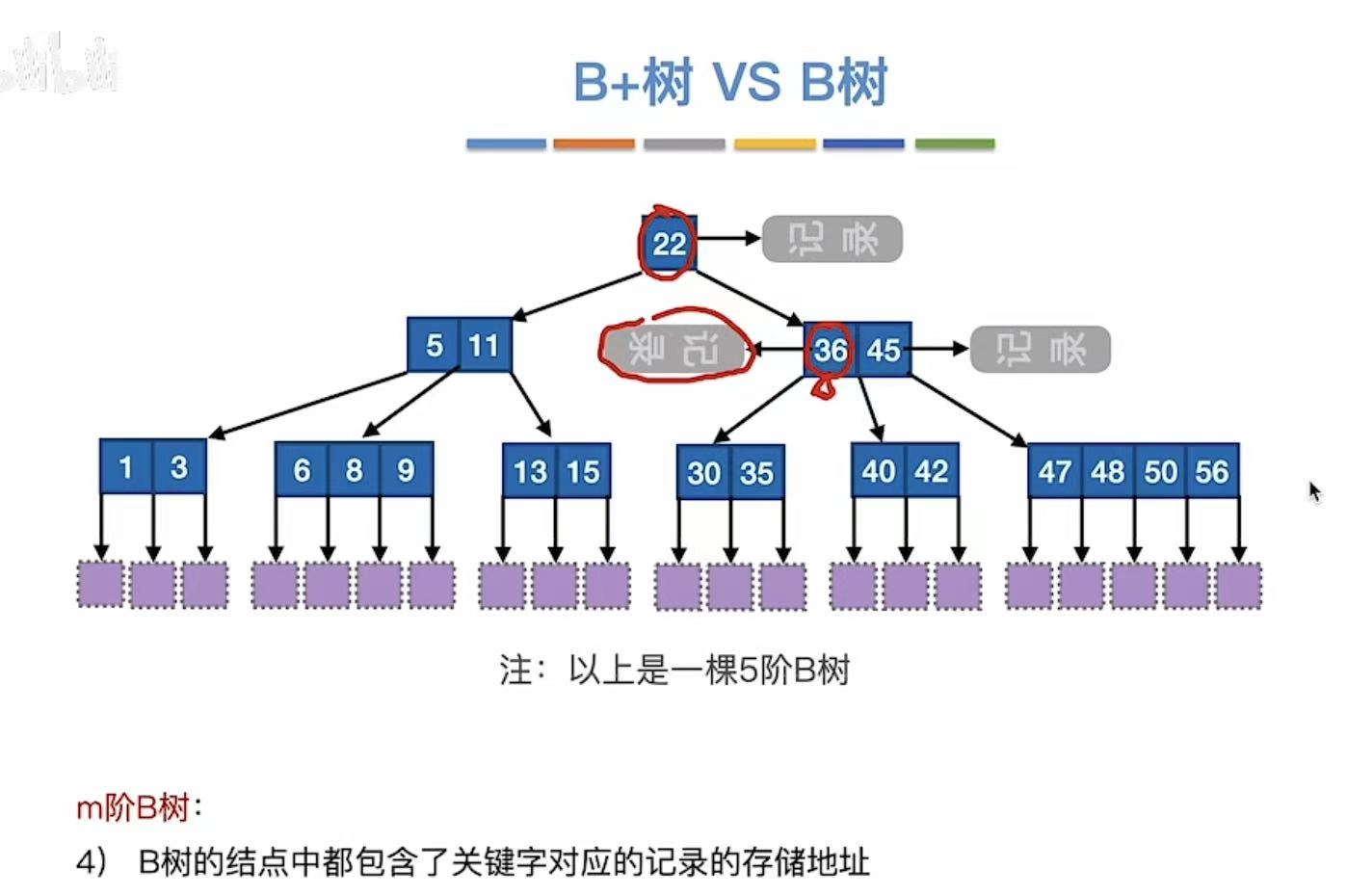
B树：每个关键字都有记录，无索引概念，就相当于夹了书签的书

4. 小结

散列表

1. 介绍

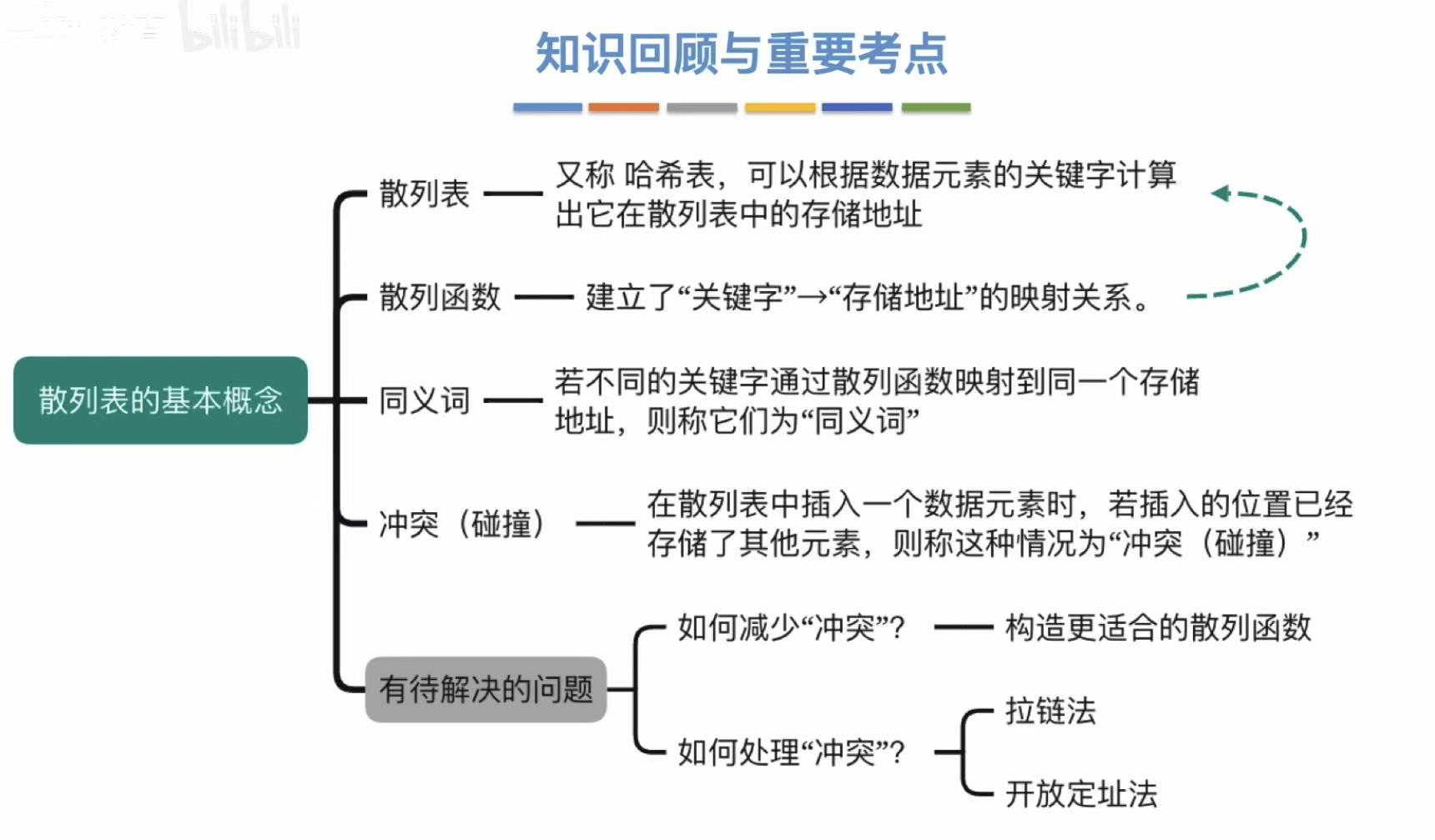
1.1 基本术语

• 散列表：一种数据结构。（就是一个表）
• 散列函数 ：决定了关键字，通过什么方式，被添加进这个散列表。
  
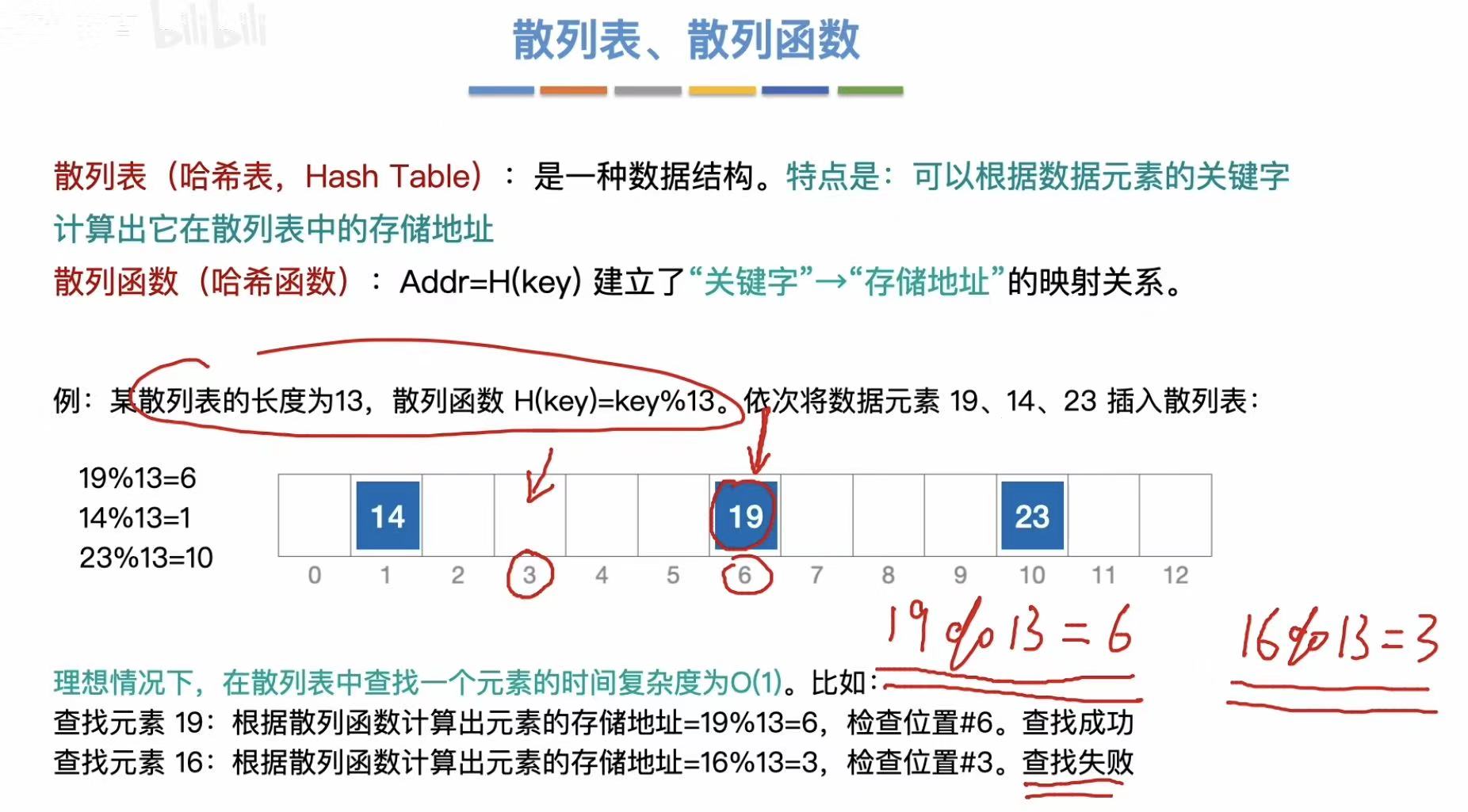
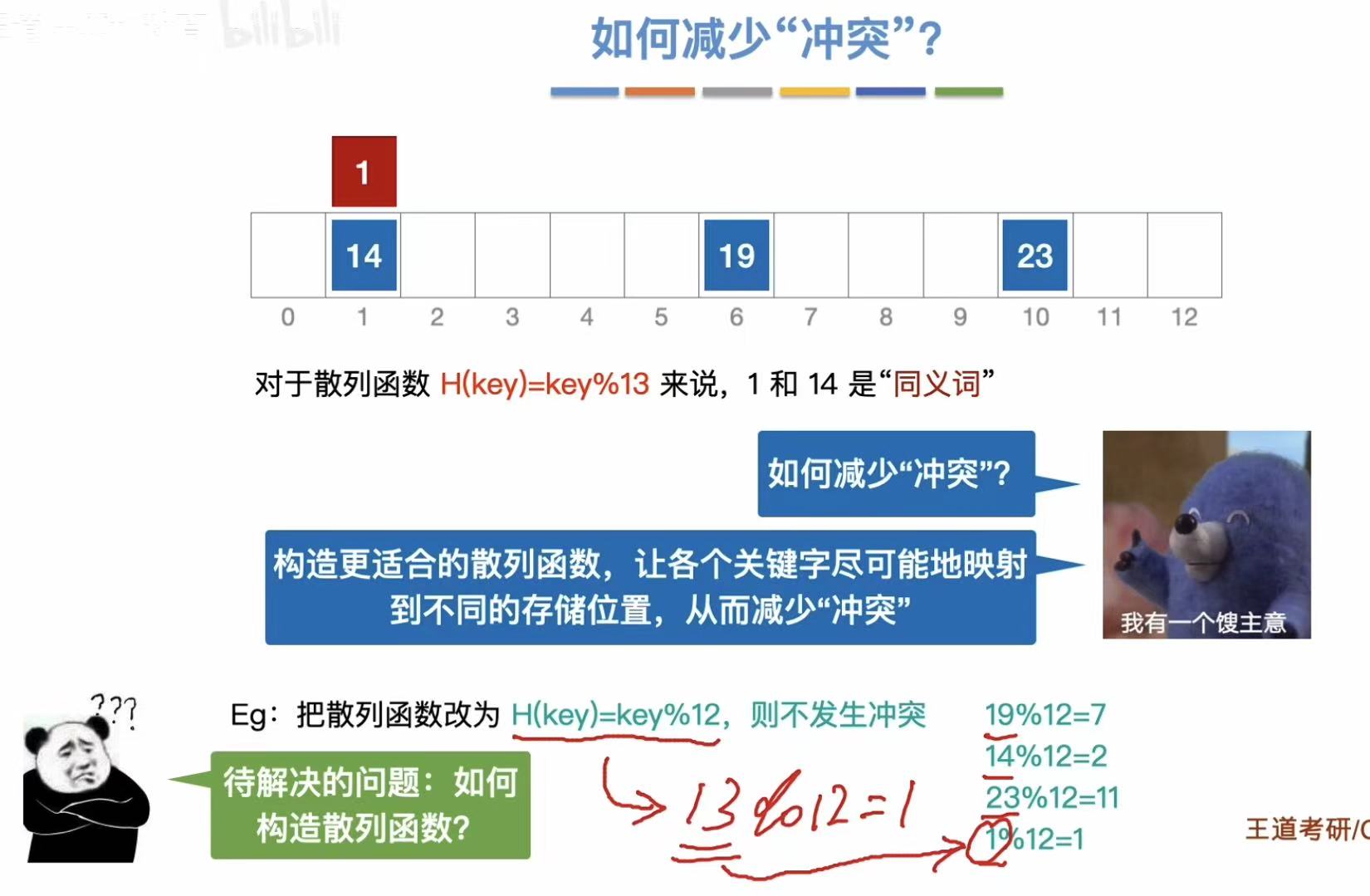
• 冲突：通过同一种方式添加进散列表的时候，有两个数关键字可以添加进同一个表格。
• 同义词 ：会发生冲突的两个关键字。
  

1.2 如何处理冲突？（了解）

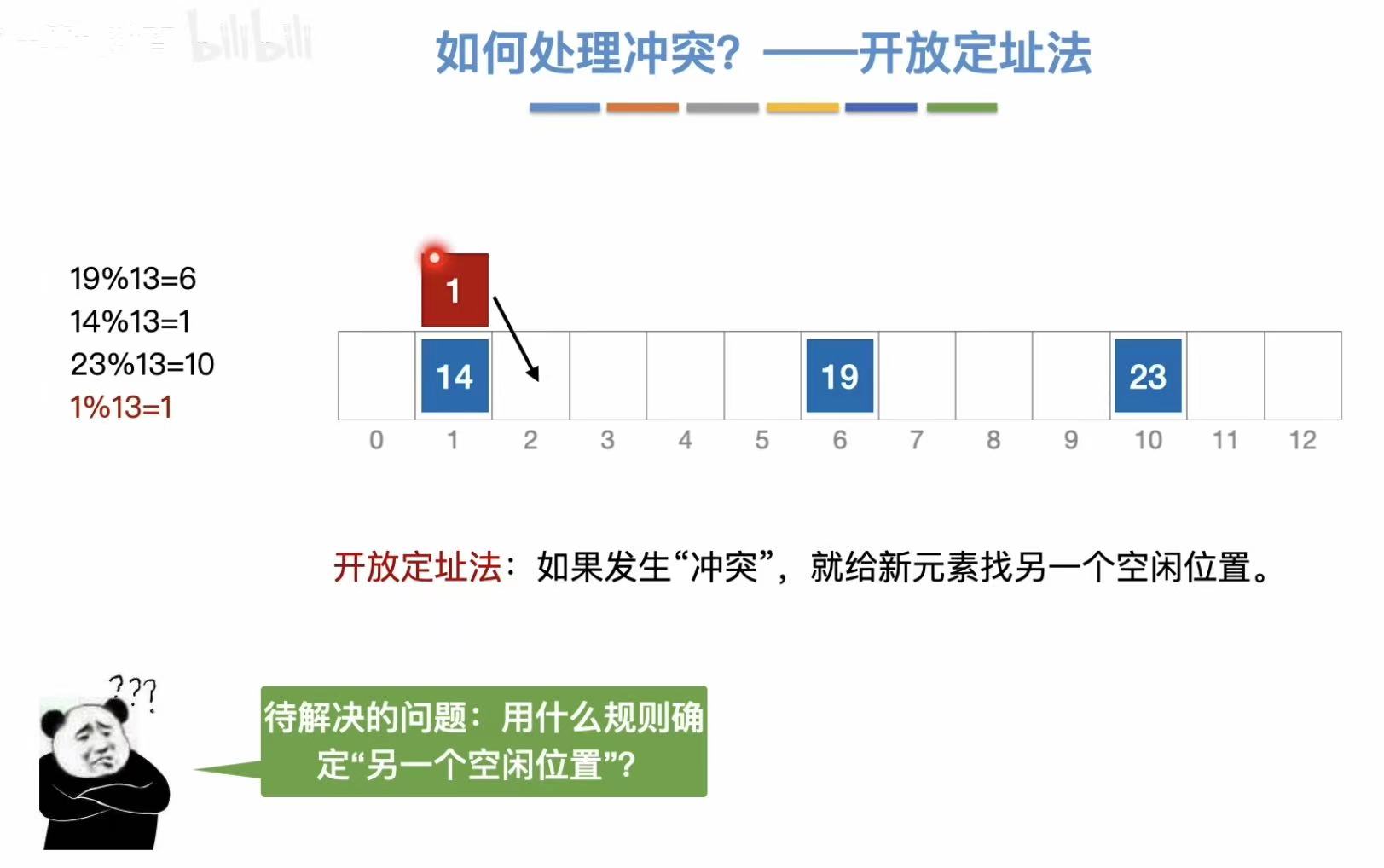
1.3 小结

2. 散列函数的构造

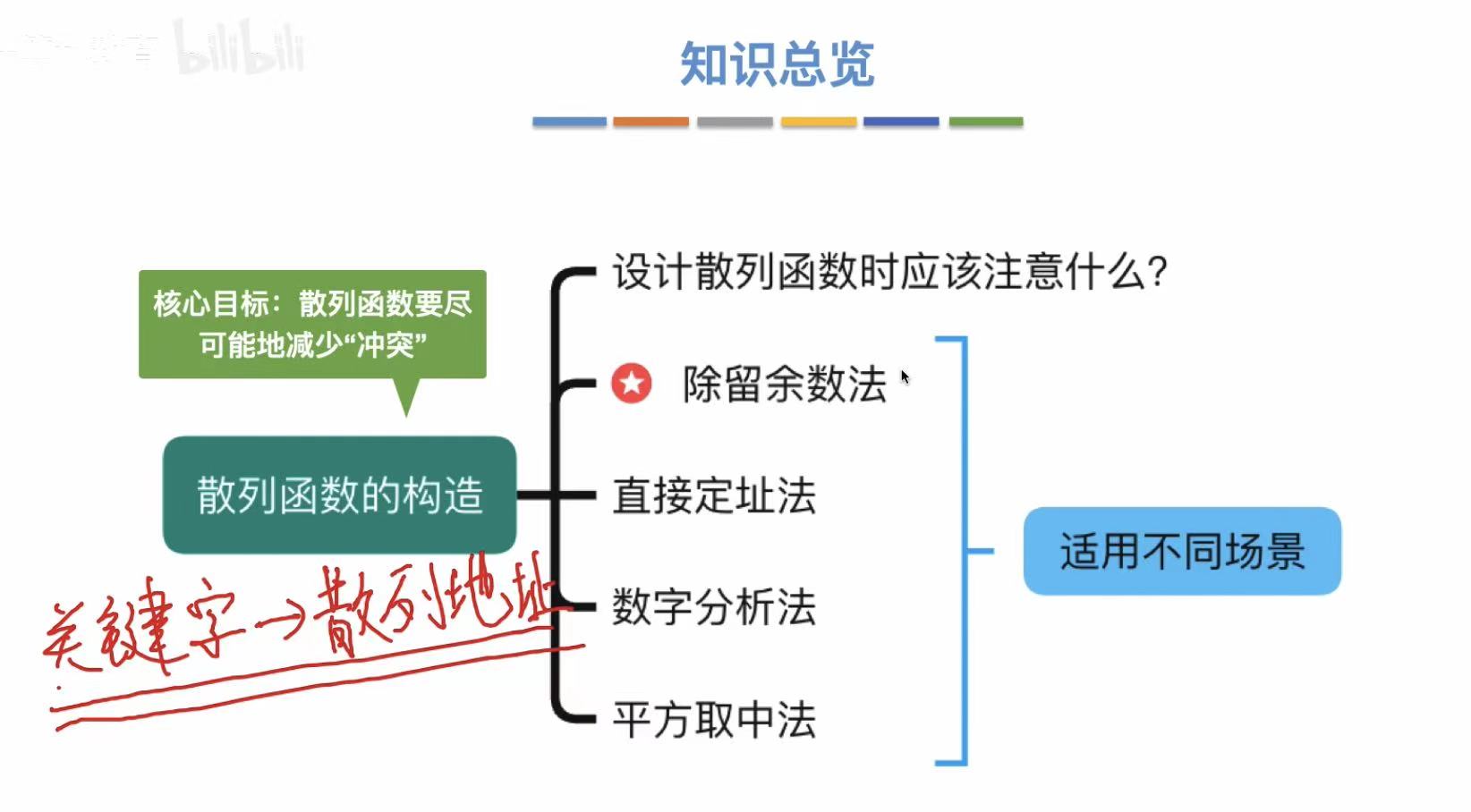
2.1 设计散列函数时应该注意什么？

注意点：

• 涵盖所有关键字
• 不能超出散列表的地址范围
• 尽可能减少冲突
• 尽可能简单
  

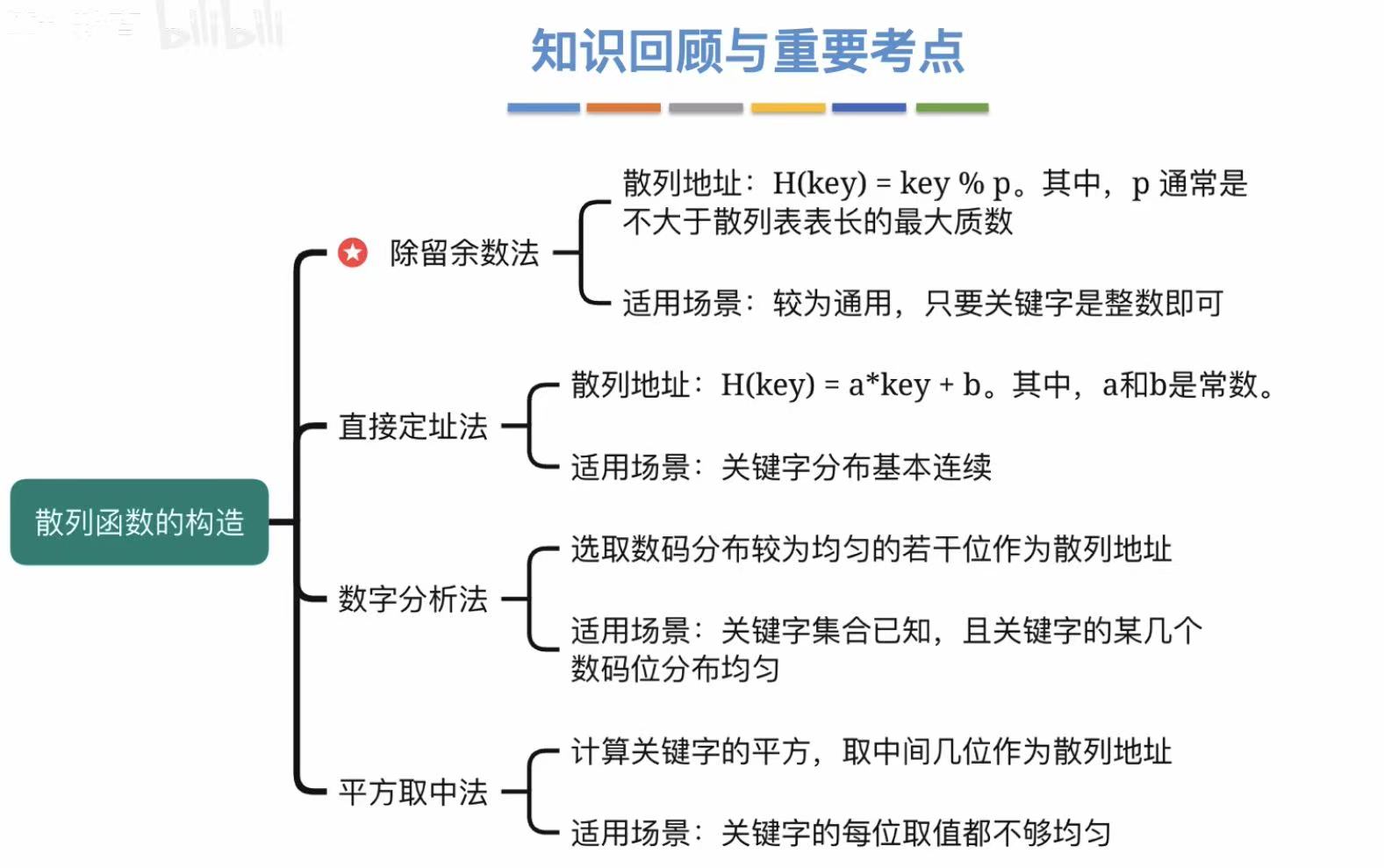
2.2 除留余数法

存入数/质数=存入地址

质数通常选择不大于表长，但最接近表长的质数。

• 如果大了：就可能把要存入的数存到表长之外的位置
• 如果太小了：浪费表格空间

适用场景 ：通用

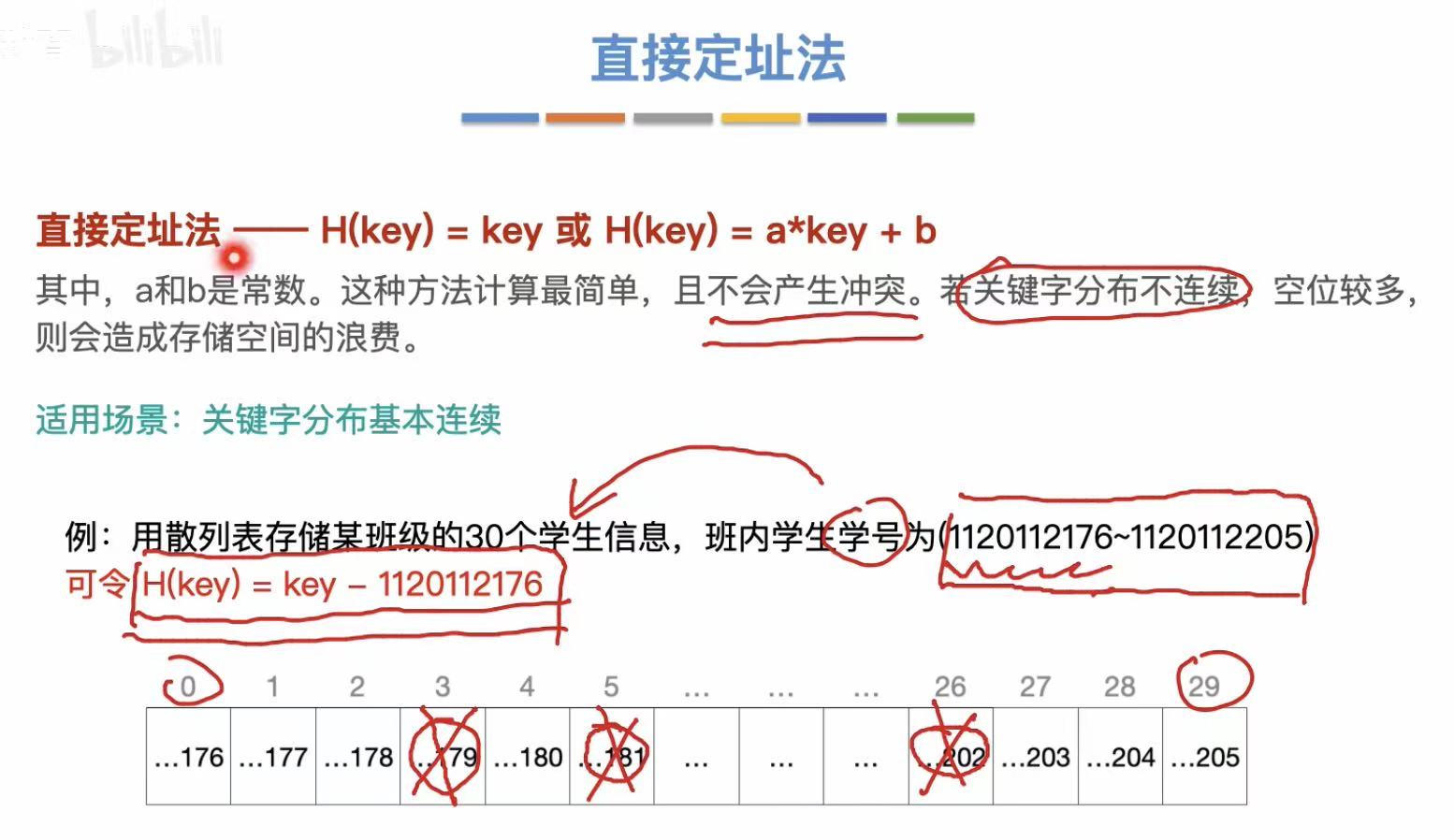
2.3 直接定址法

直接存入。
适用场景 ：关键字分布基本连续

2.4 数字分析法

选分布均匀的部分作为散列地址。
适用场景 ：关键字集合已知，且关键字的某几个数码位分布均匀。

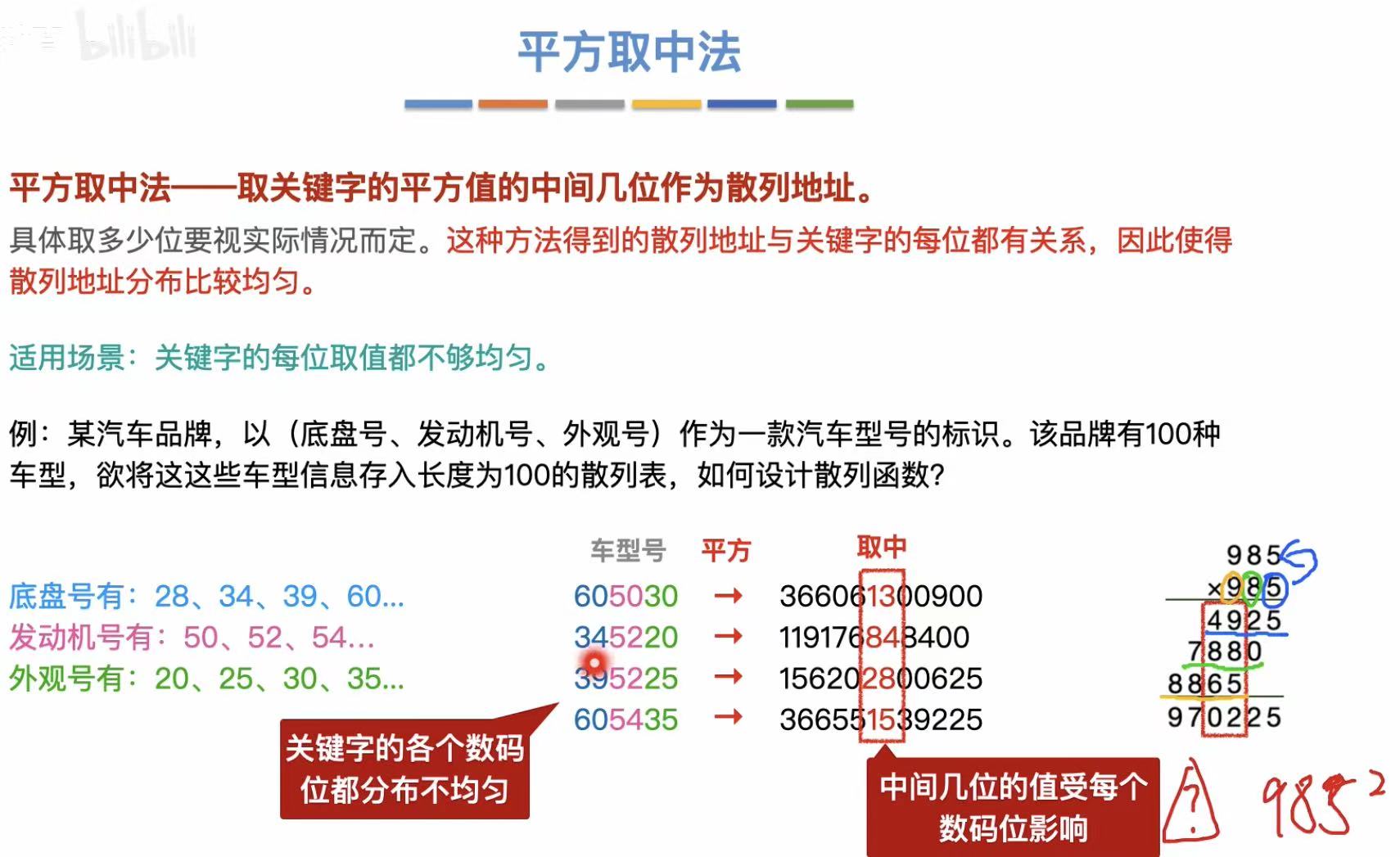
2.5 平方取中法

取需要存入的数的平方值的中间几位作为散列地址。
适用场景 ：关键字的每位取值都不够均匀。

2.6 小结

3. 处理冲突的方法

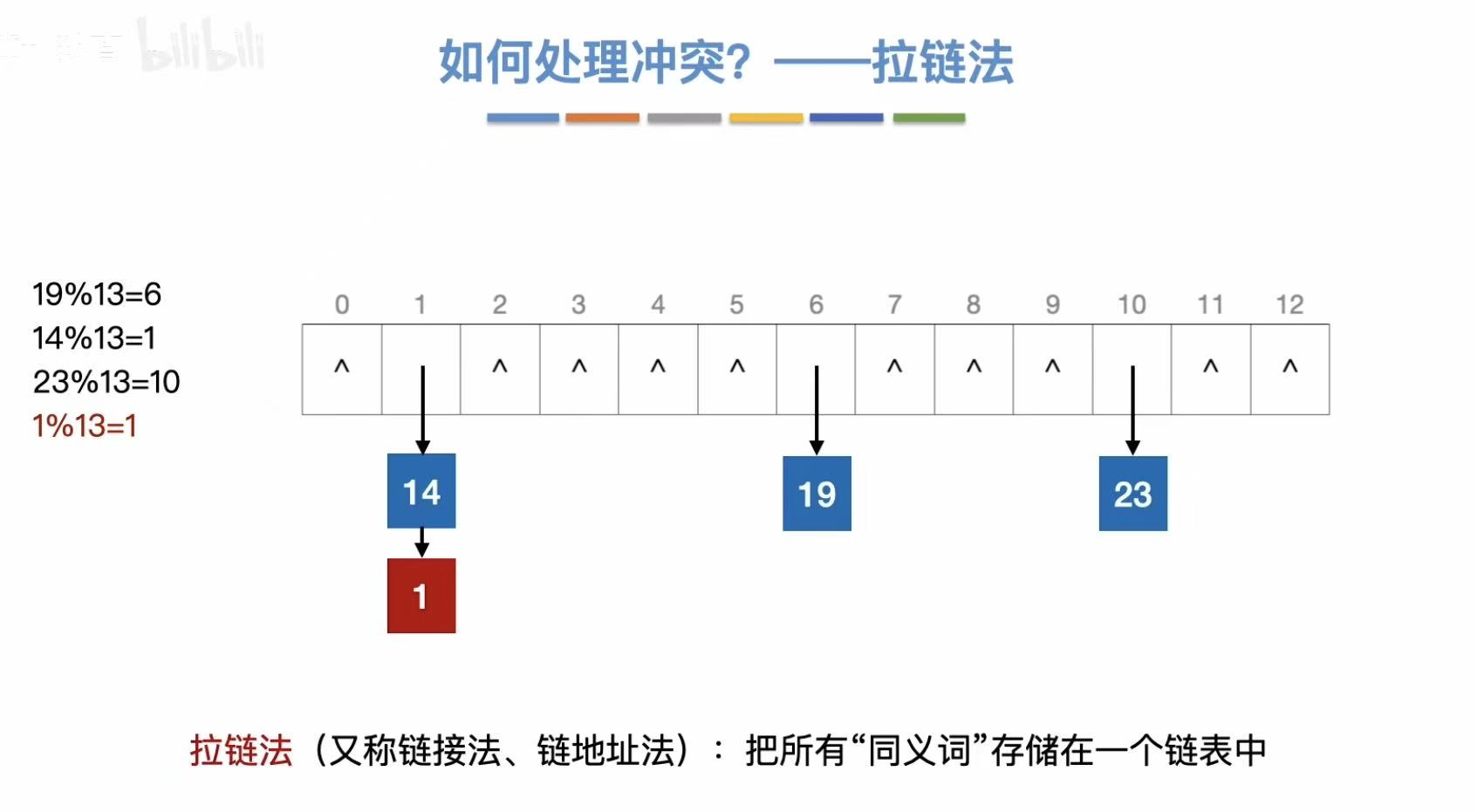
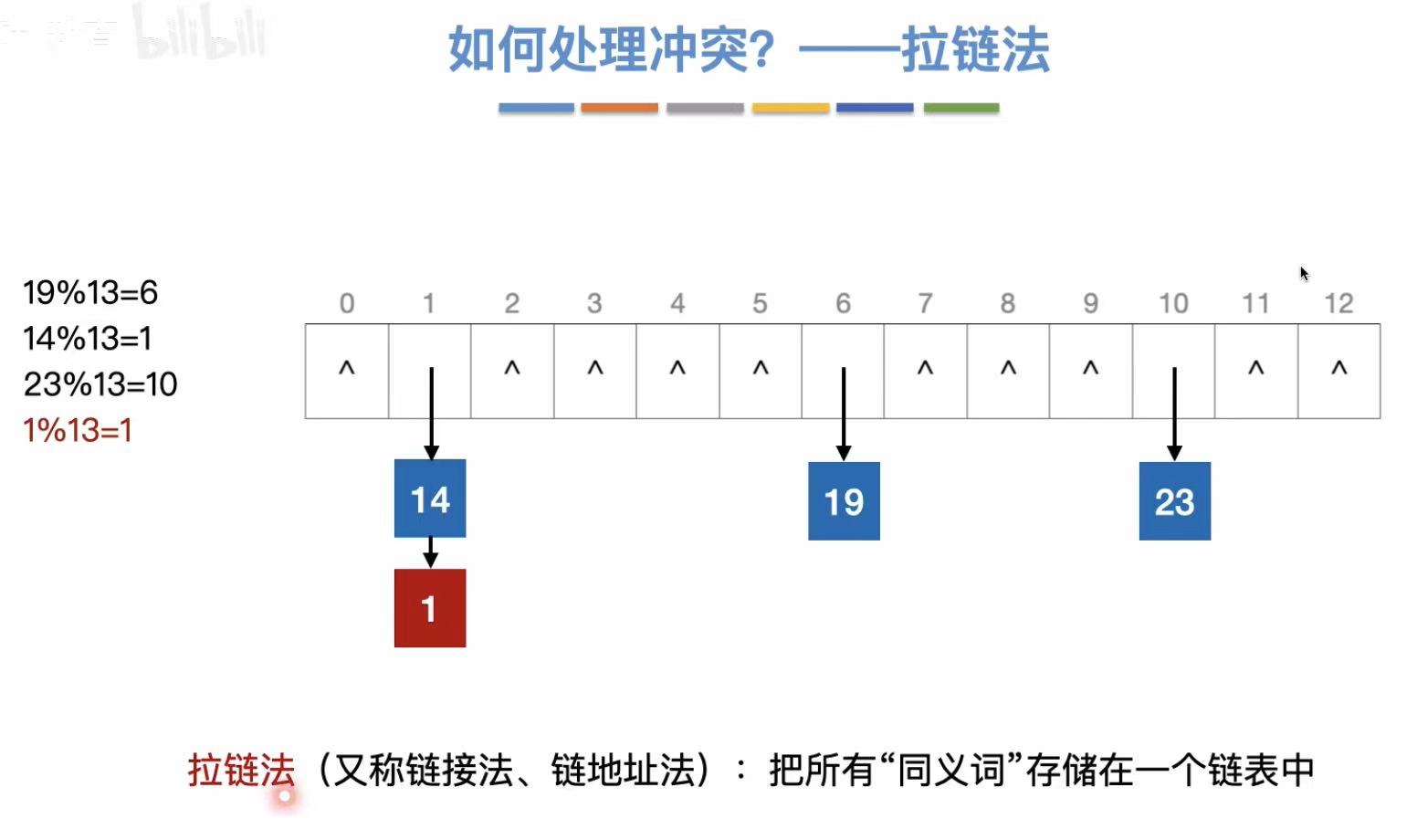
3.1 拉链法

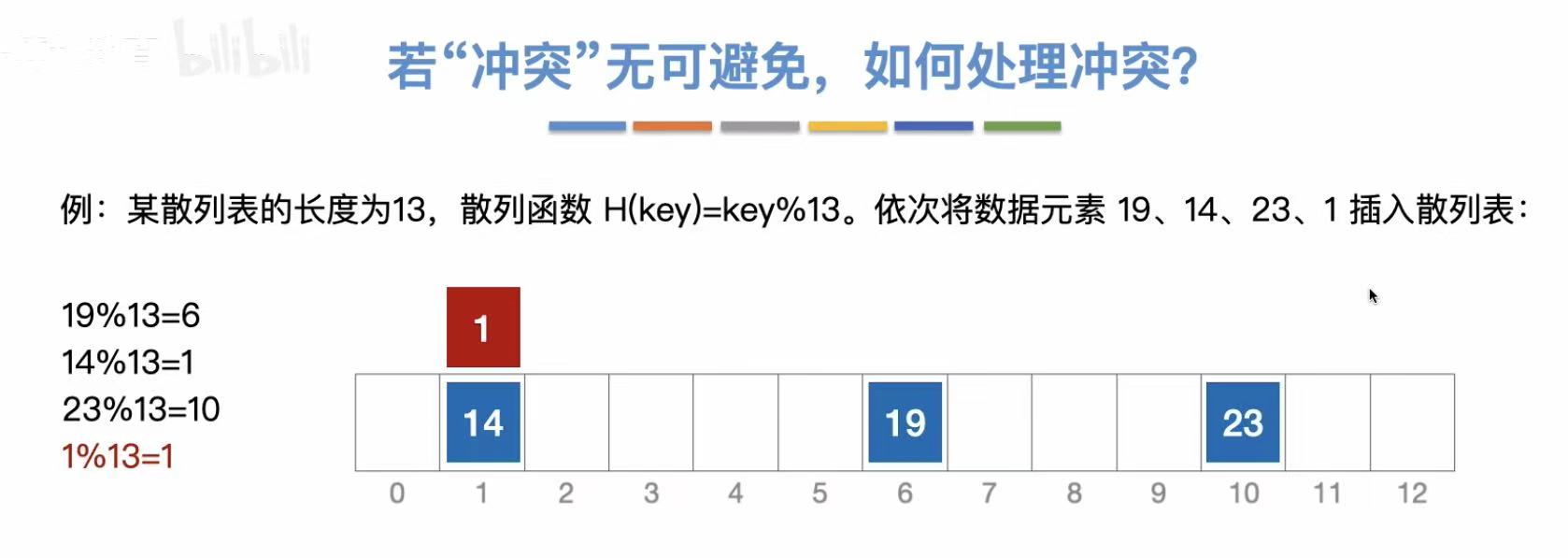
发生冲突，可以把第二个关键字挂载在已经存入的数字下方/上方。

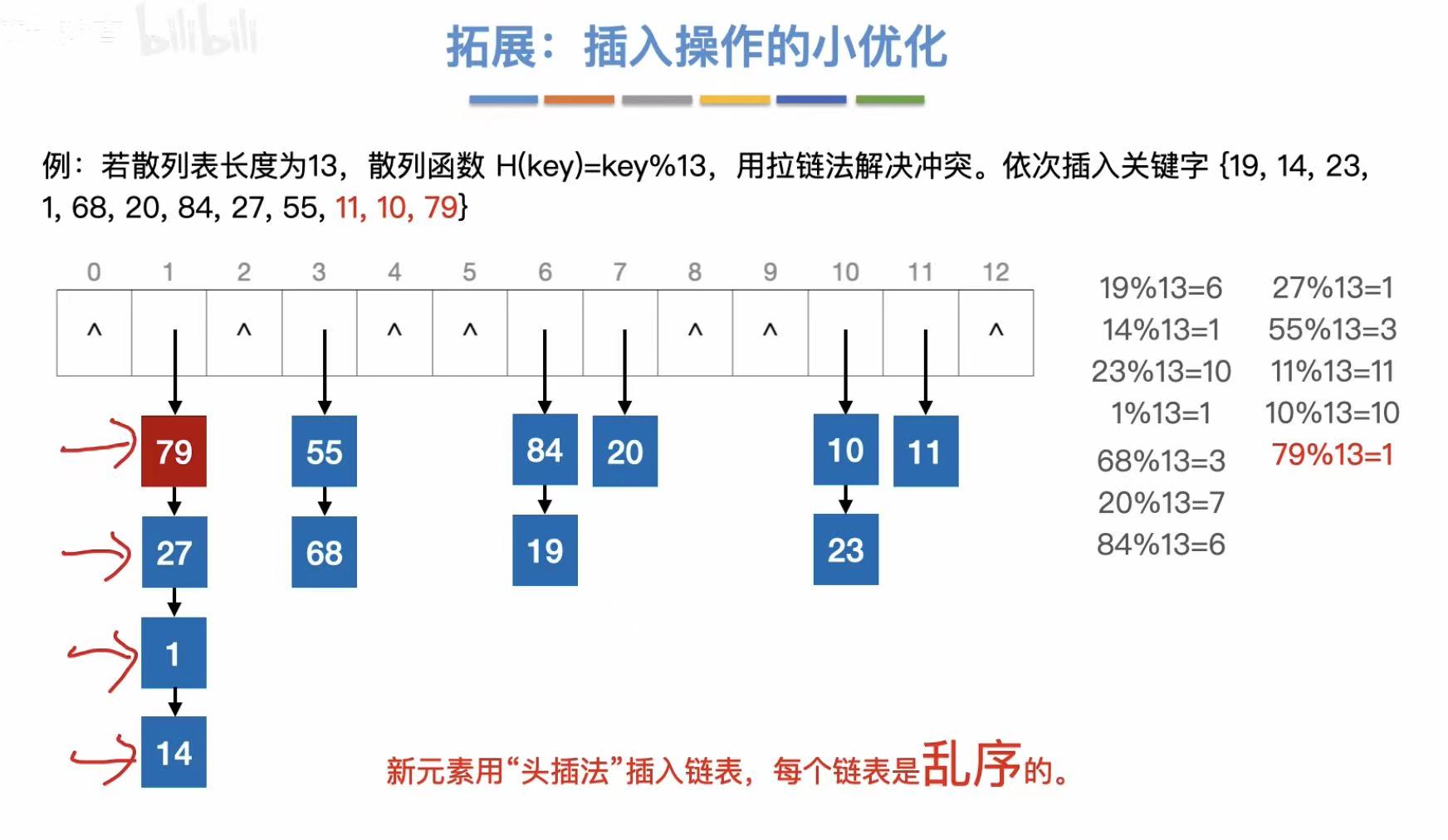
3.1.1 插入操作

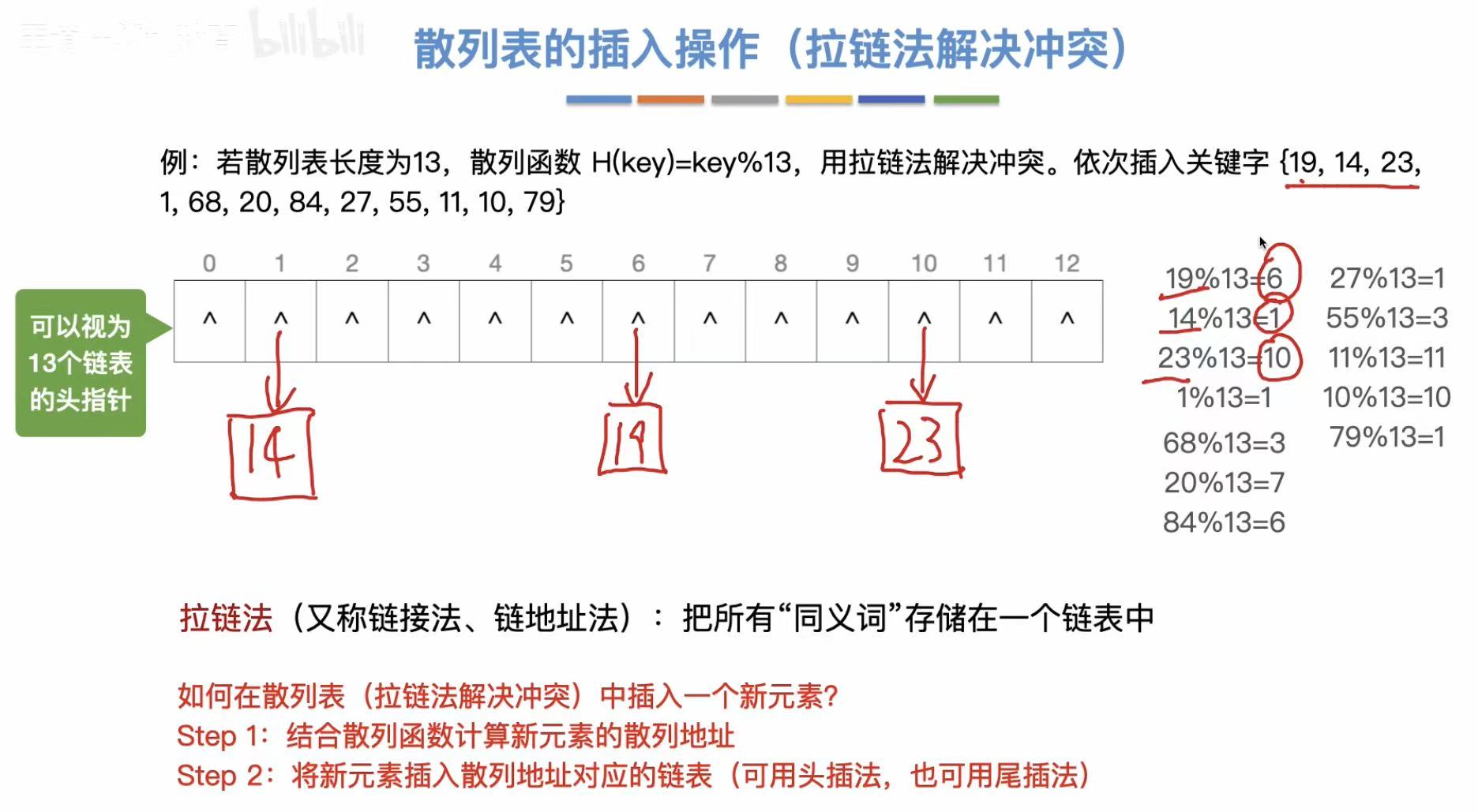
头插法：从上往下插入。

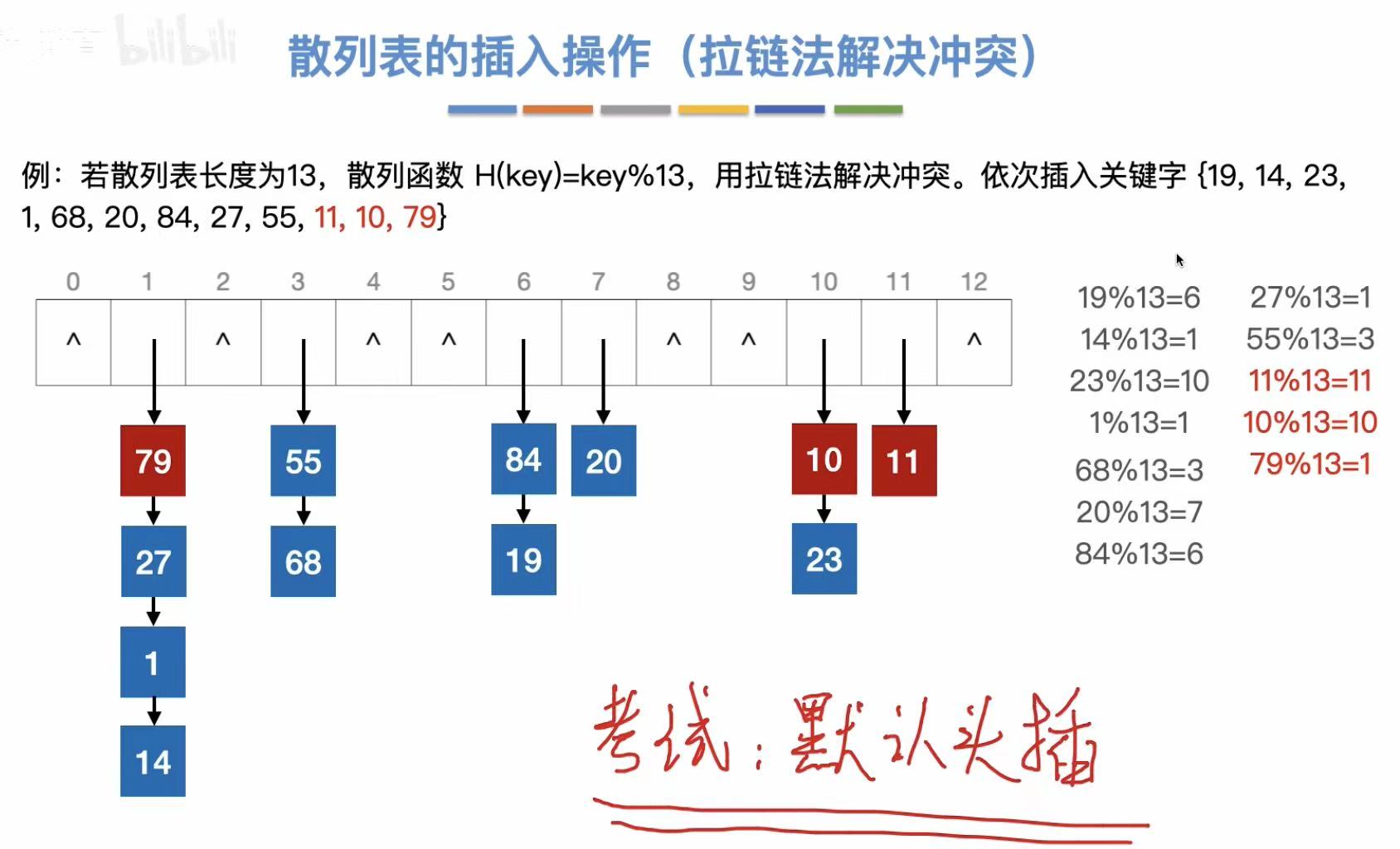
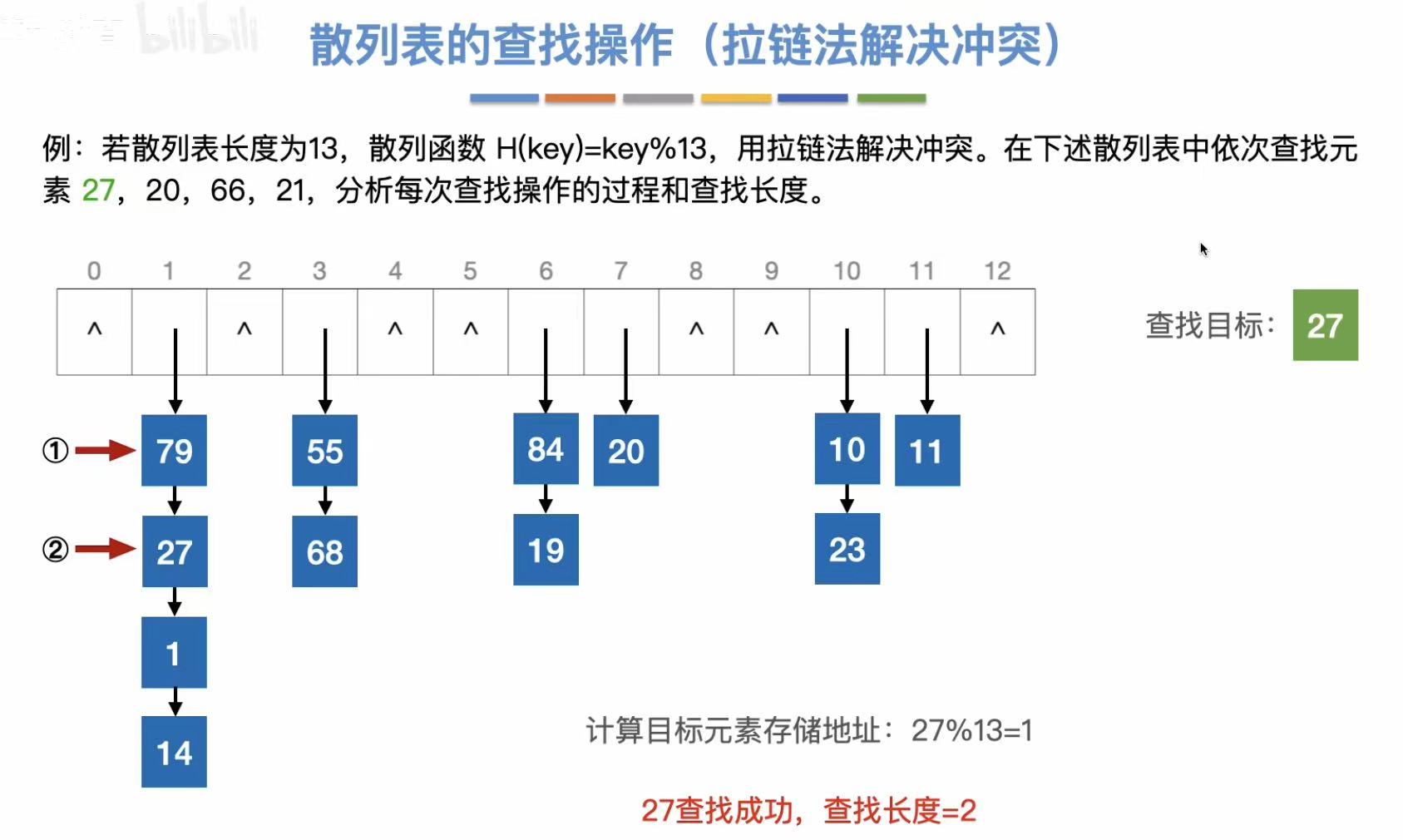
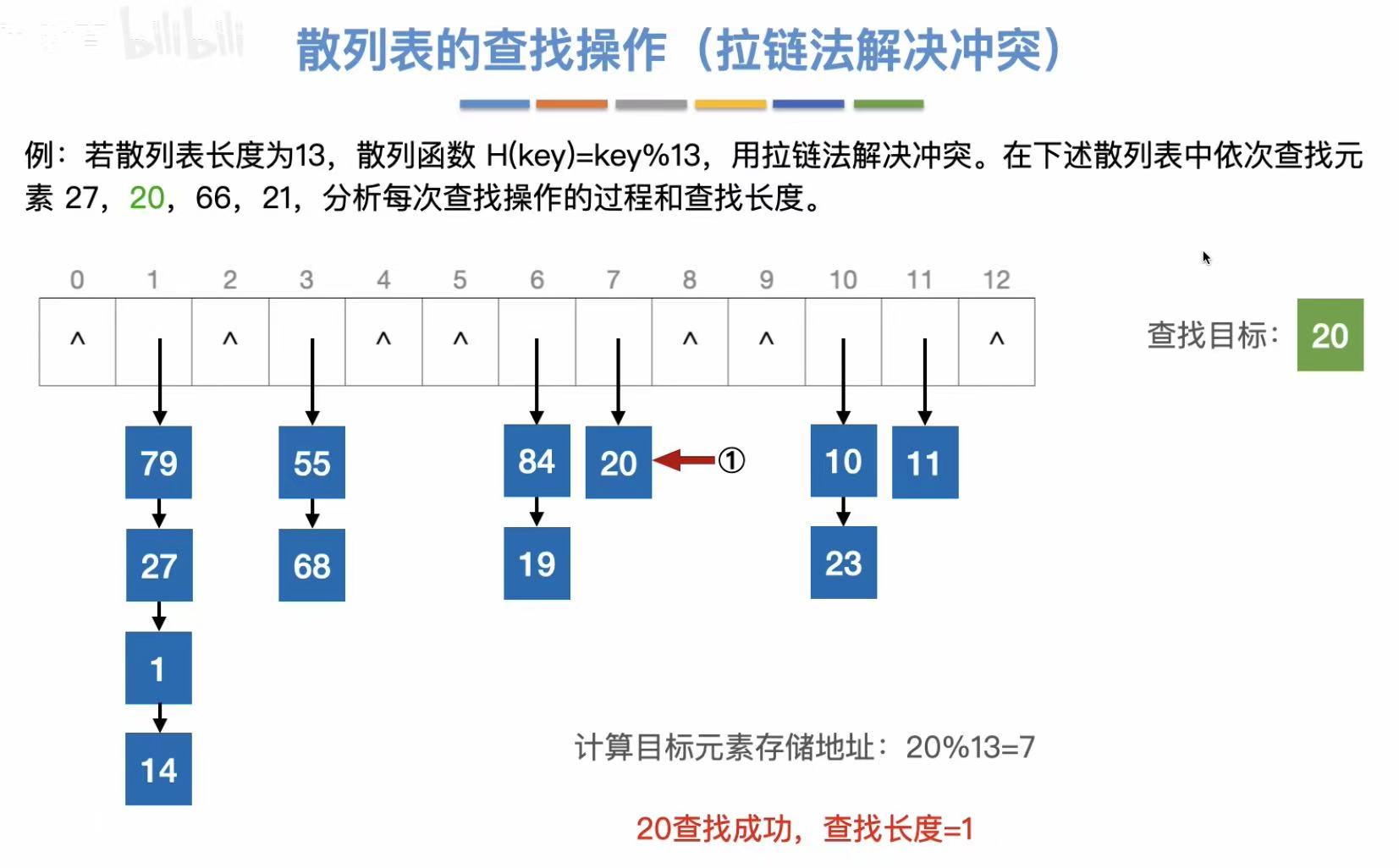
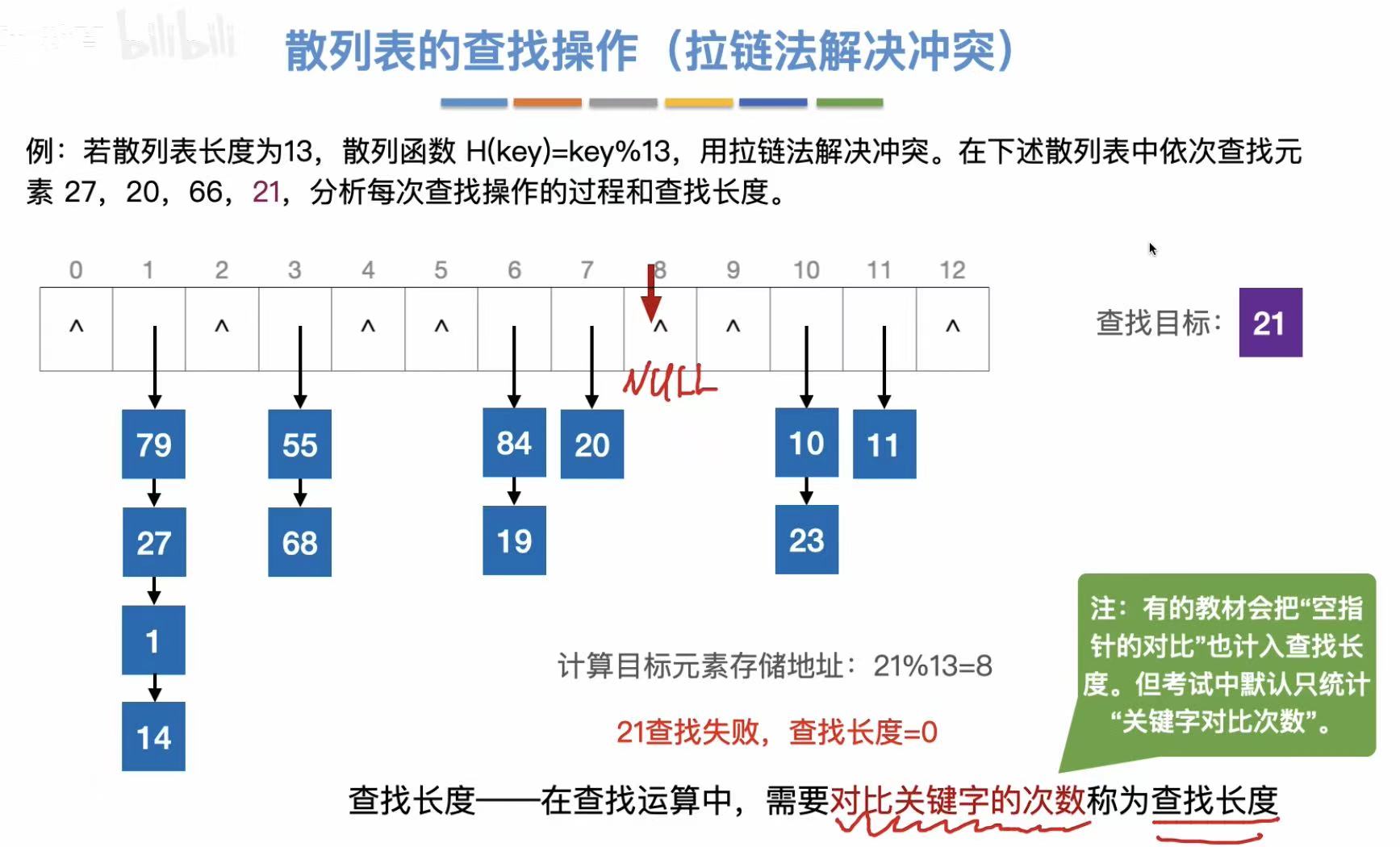
3.1.2 查找操作

按照散列函数的逻辑，将需要查找的数字处理后得到地址，去这个地址里找有没有这个数。

查找长度：与关键字对比的次数。

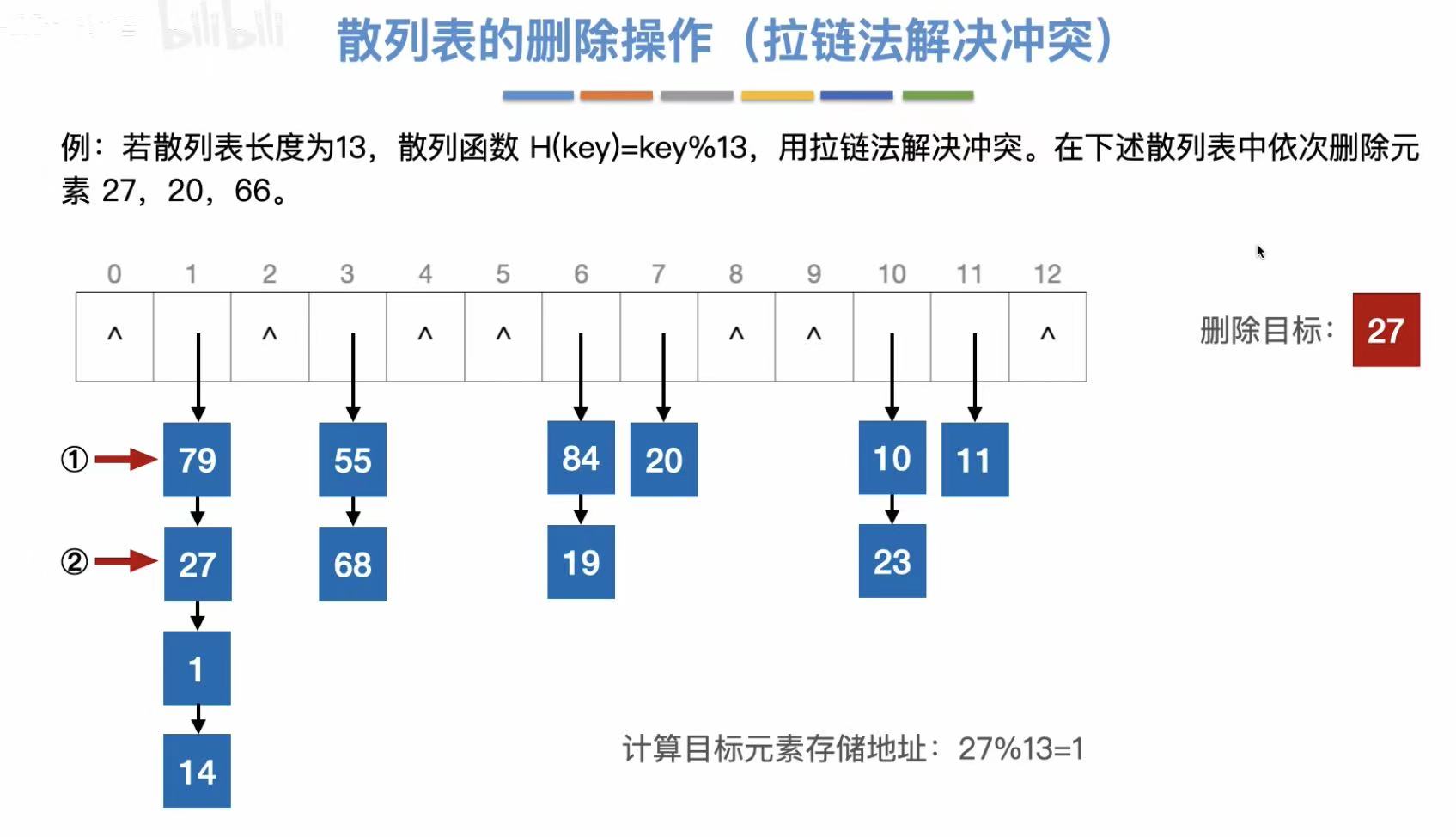
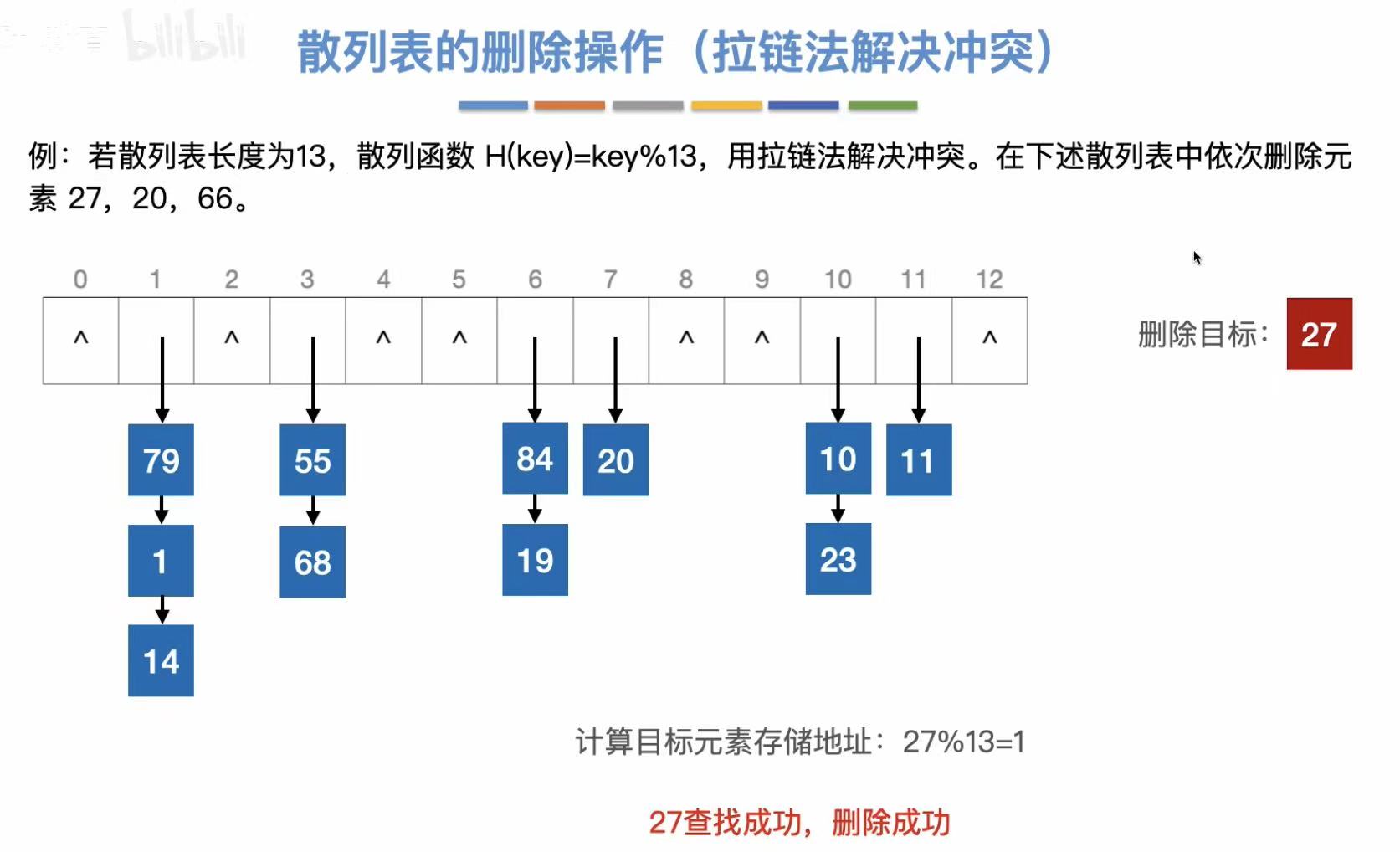
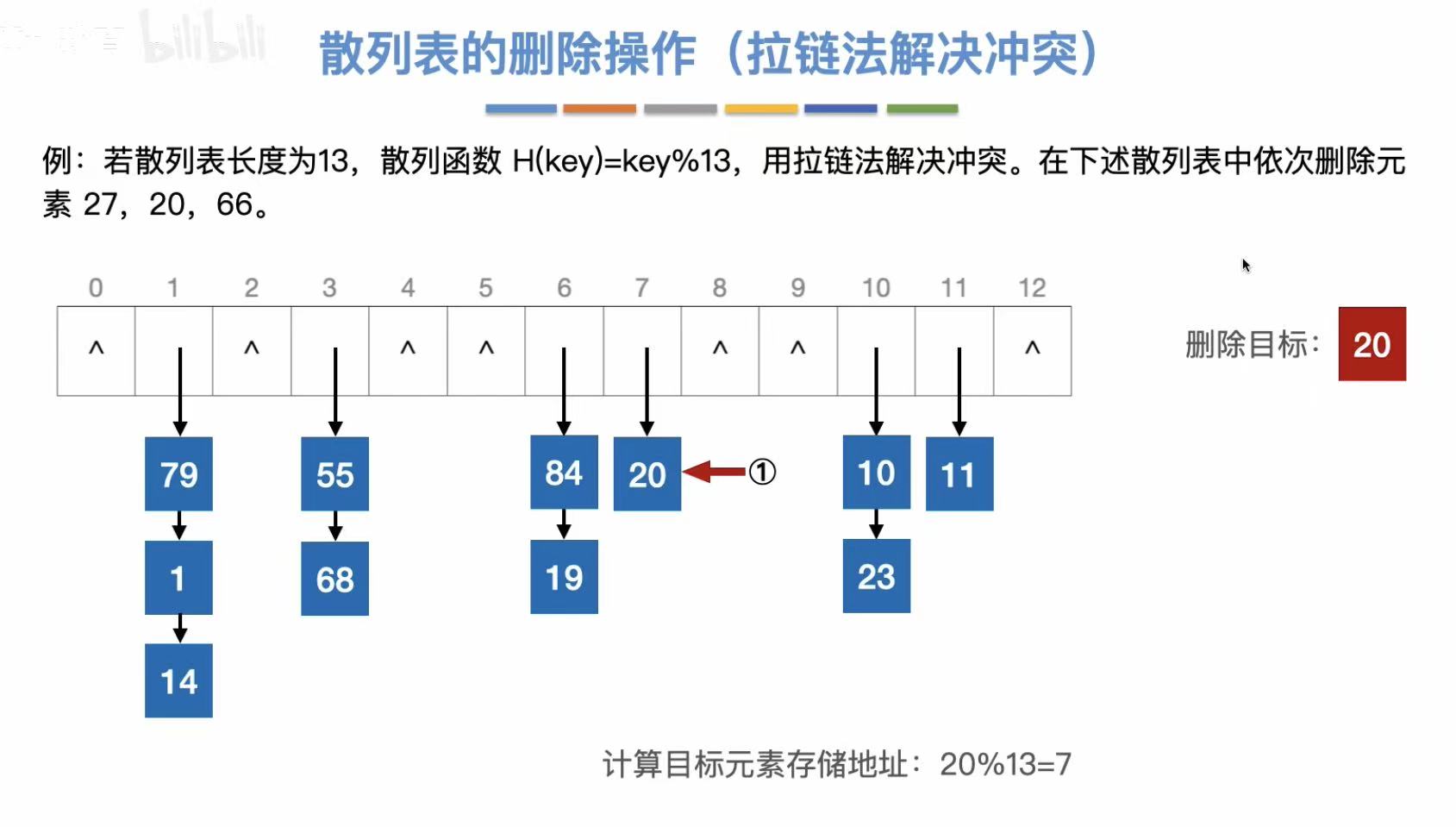
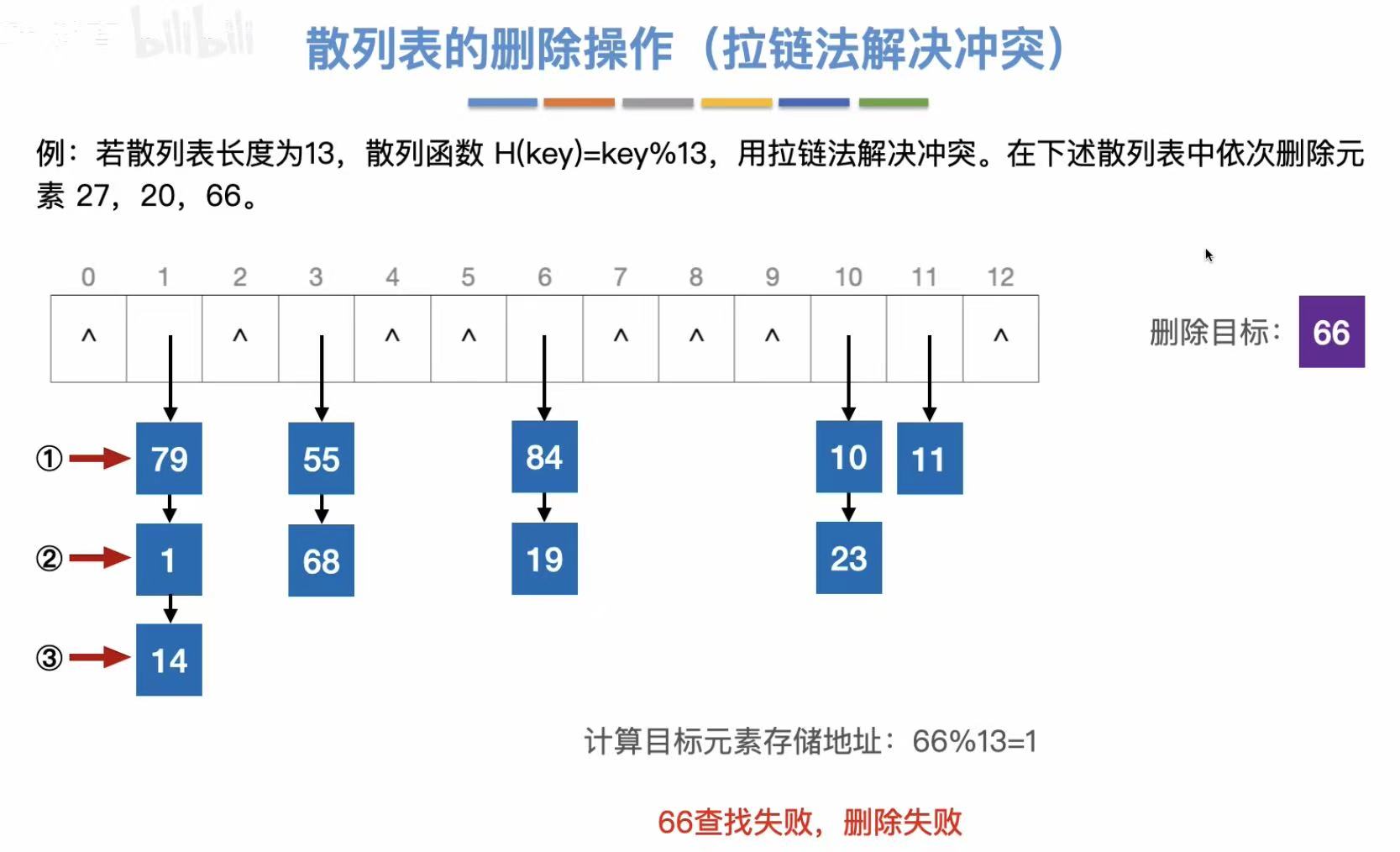
3.1.3 删除操作

和查找一样，必须先找到这个关键字，确定有这个关键字，才能删除它。

3.1.4 小结及拓展

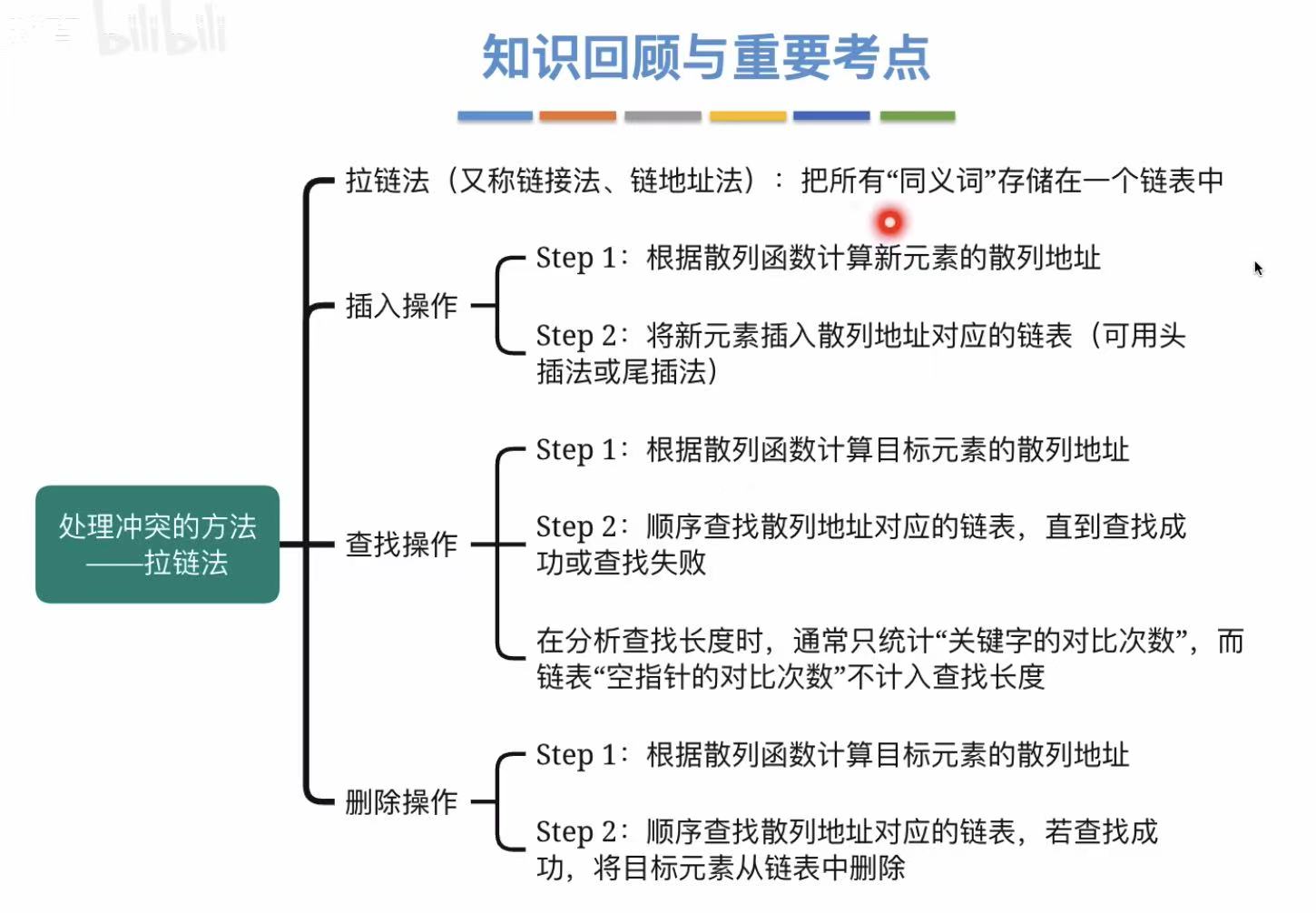
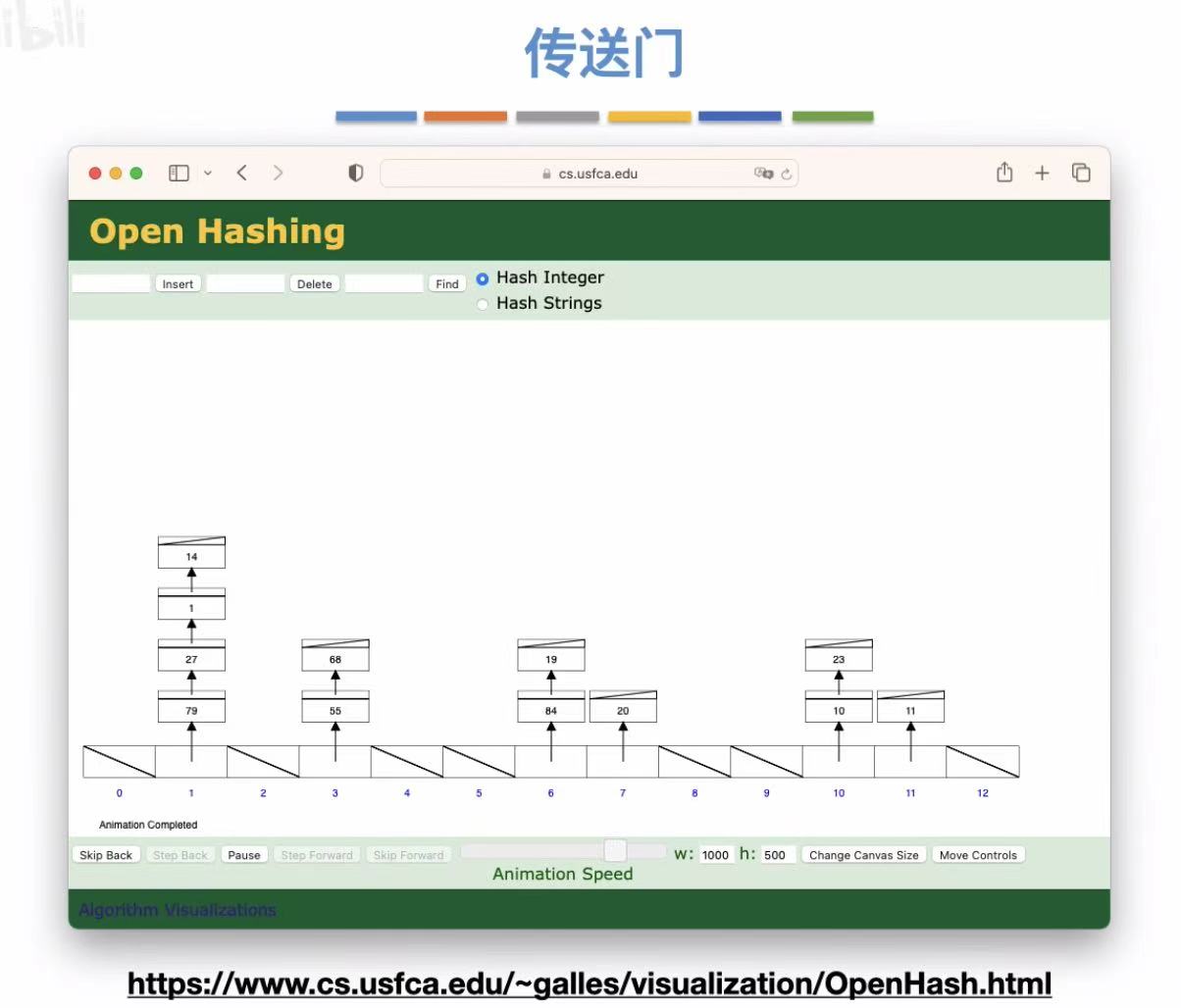
因为我们头插法插入的数字最后是乱序的，那么就可以在插入结束后按照大小顺序重新排列，提高查找效率。

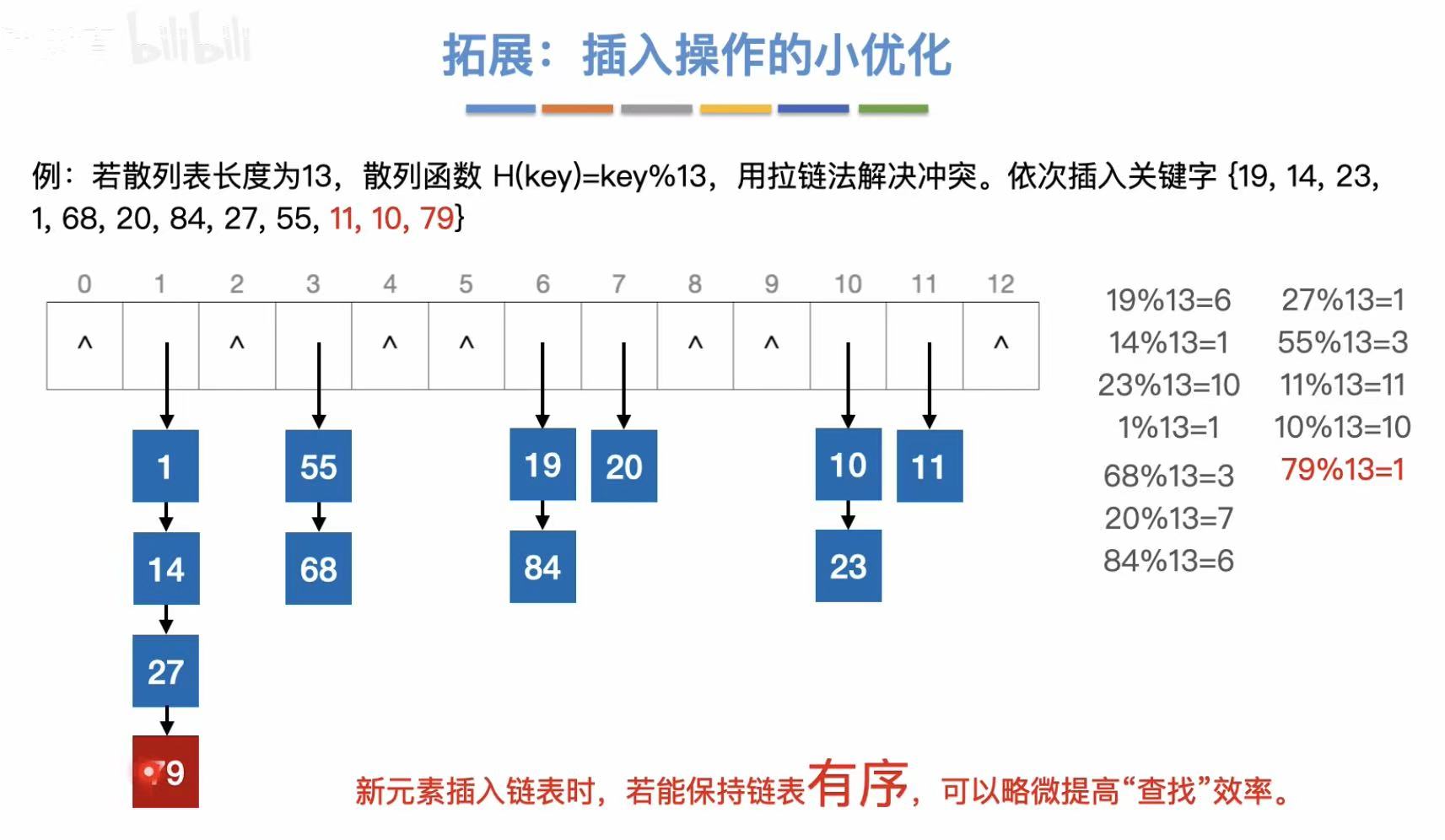
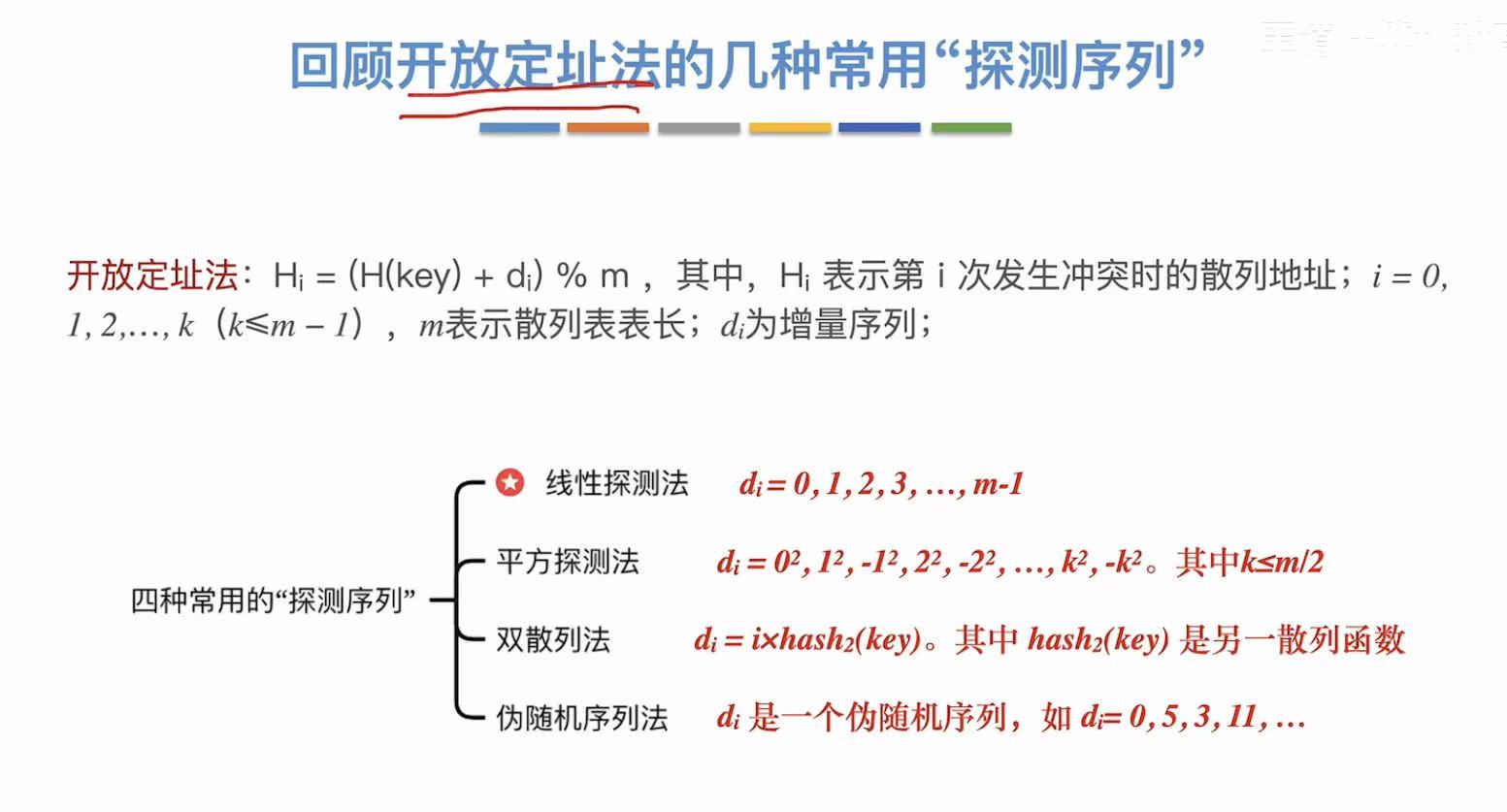
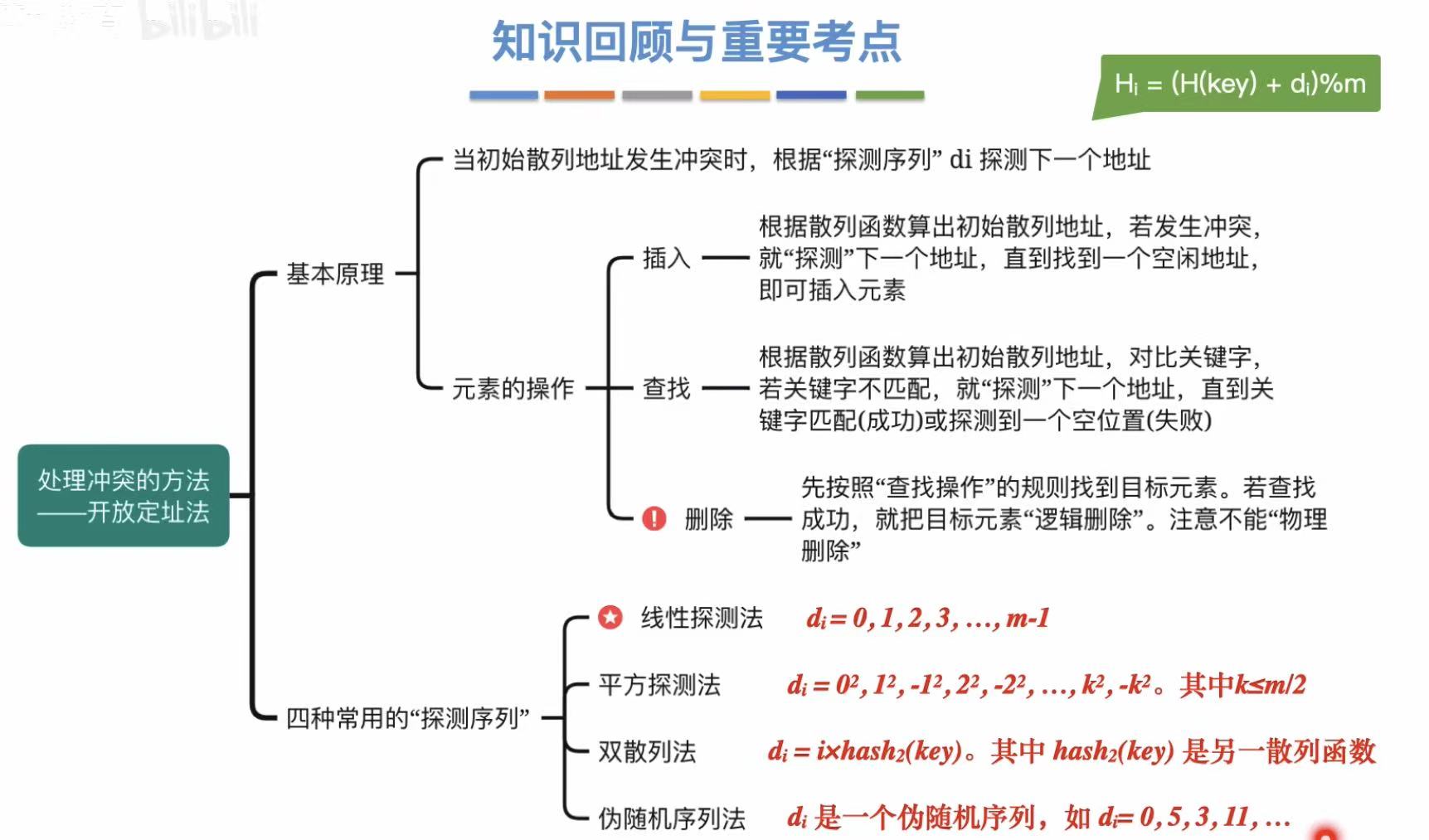
3.2 开放定址法

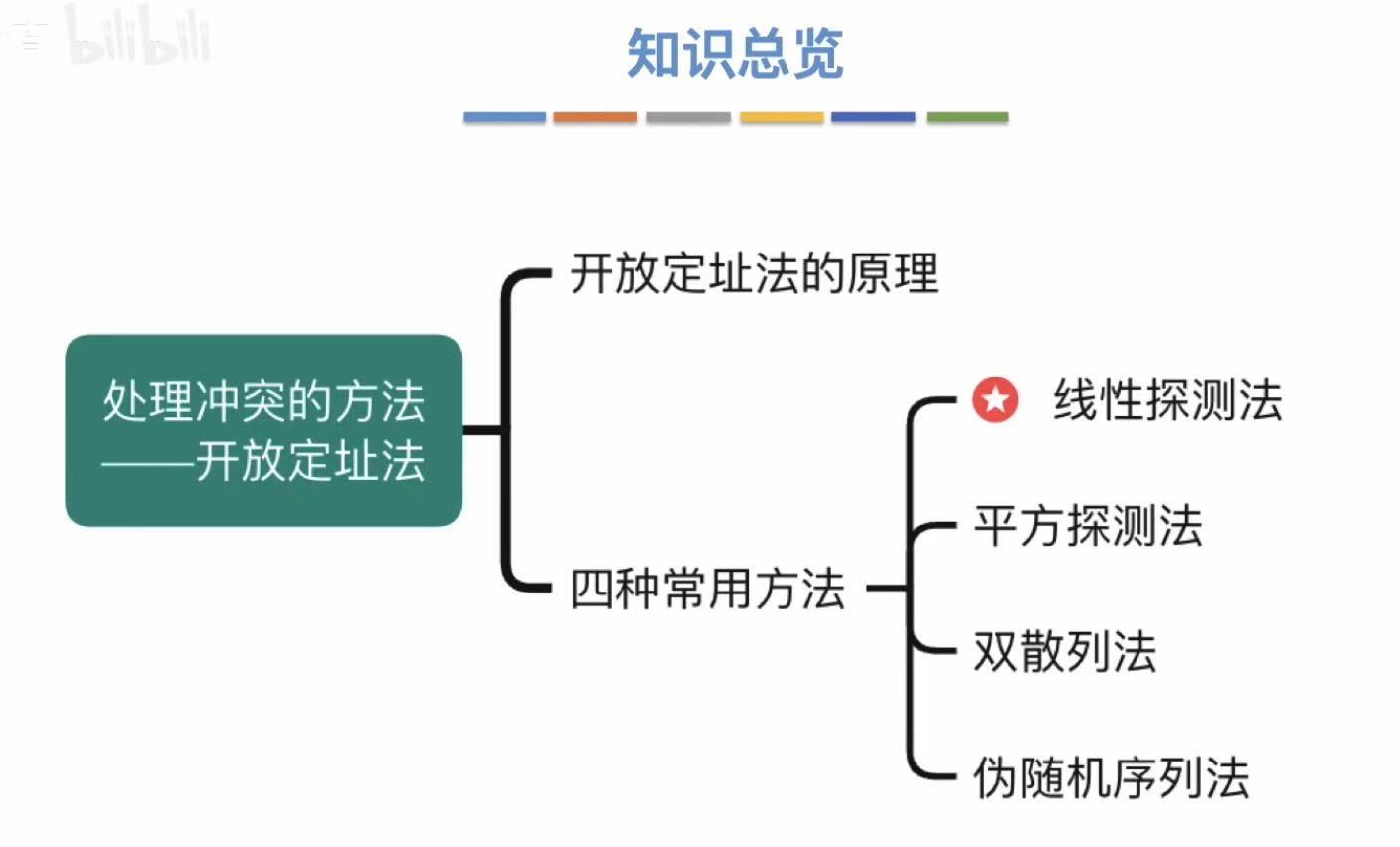
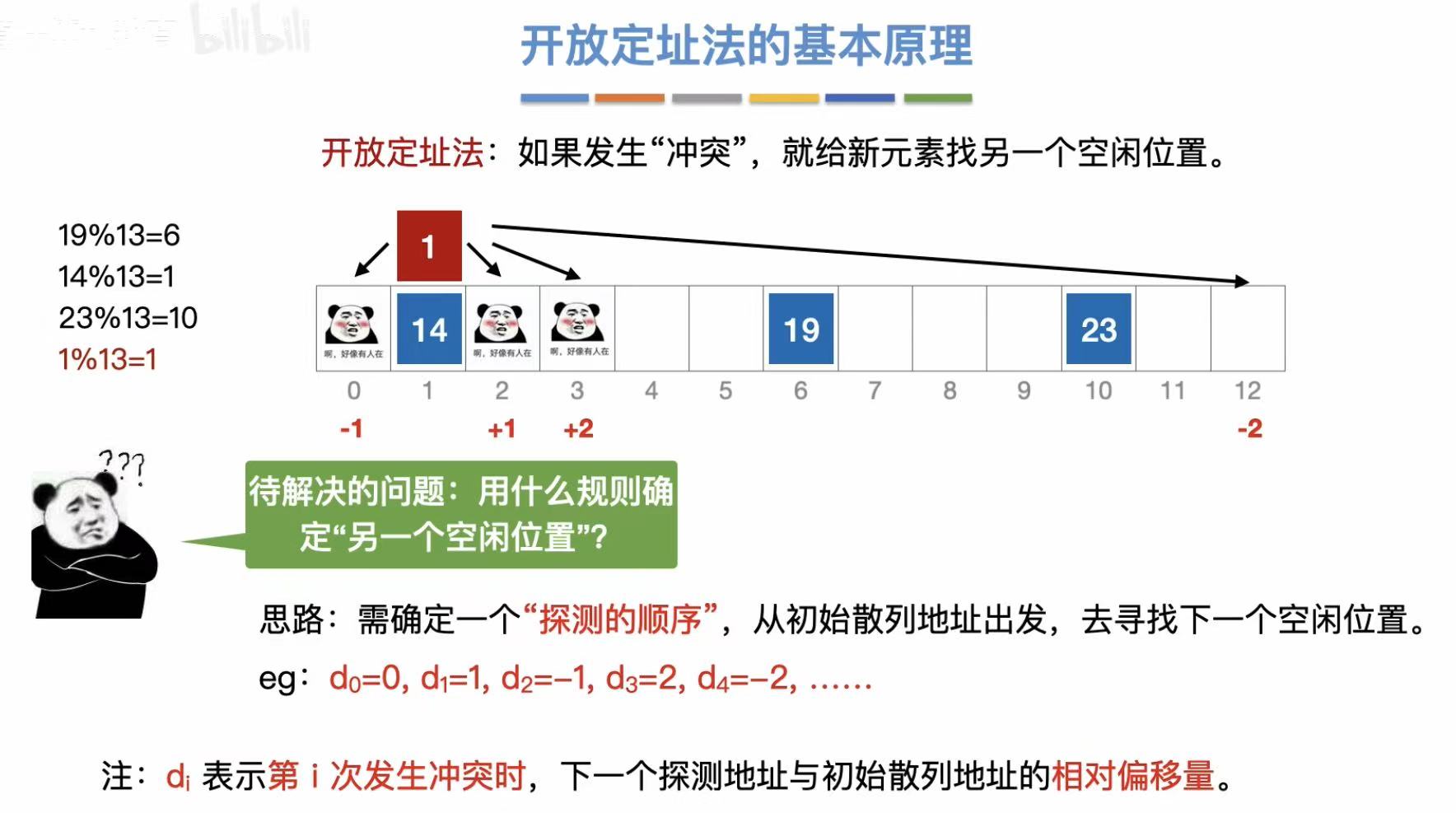
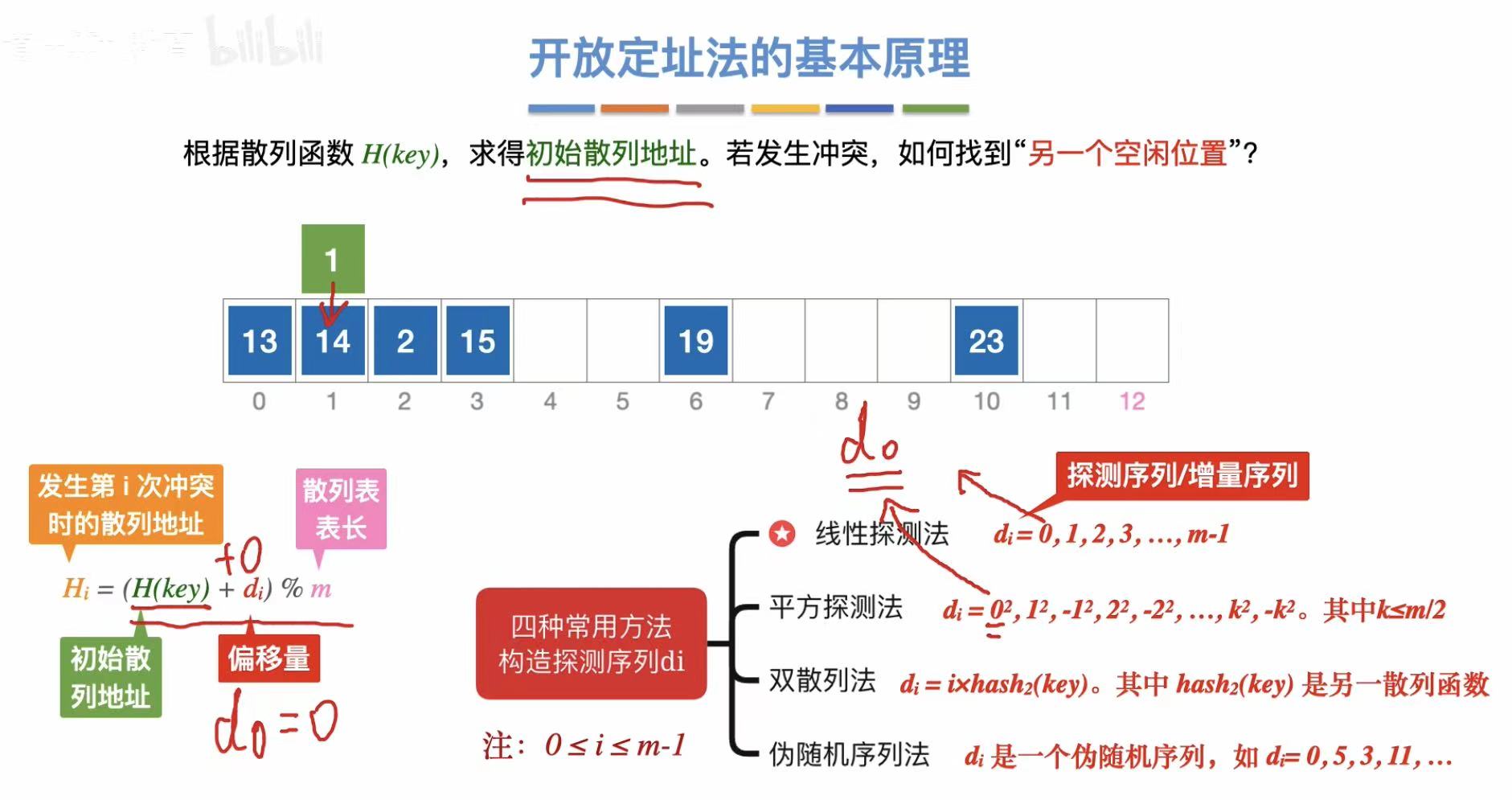
3.2.1 基本原理

开放定址 ：通过不同的方法，找到一个空位把这个新元素放进去。

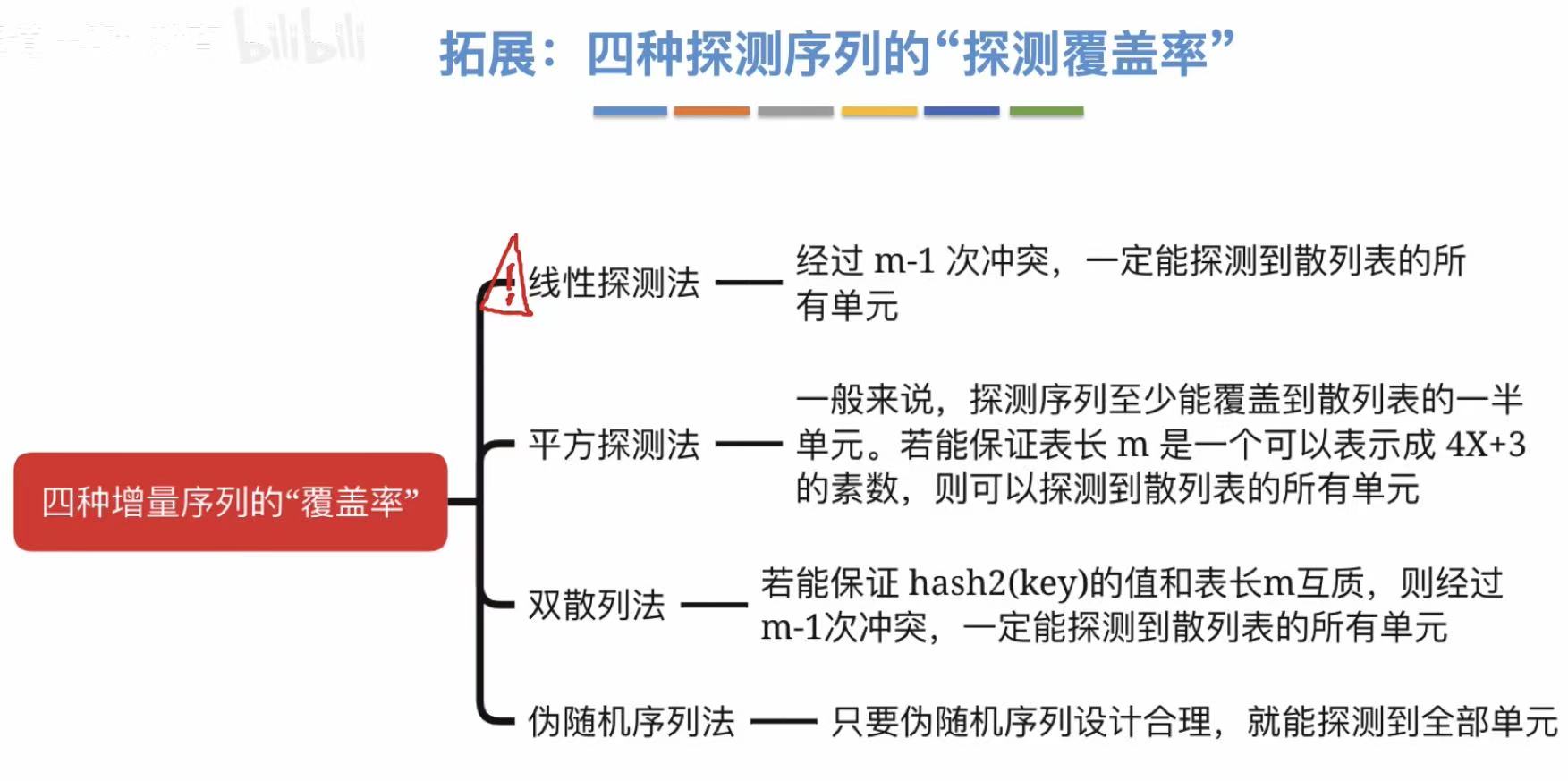
• 线性探测法：顺着往后找
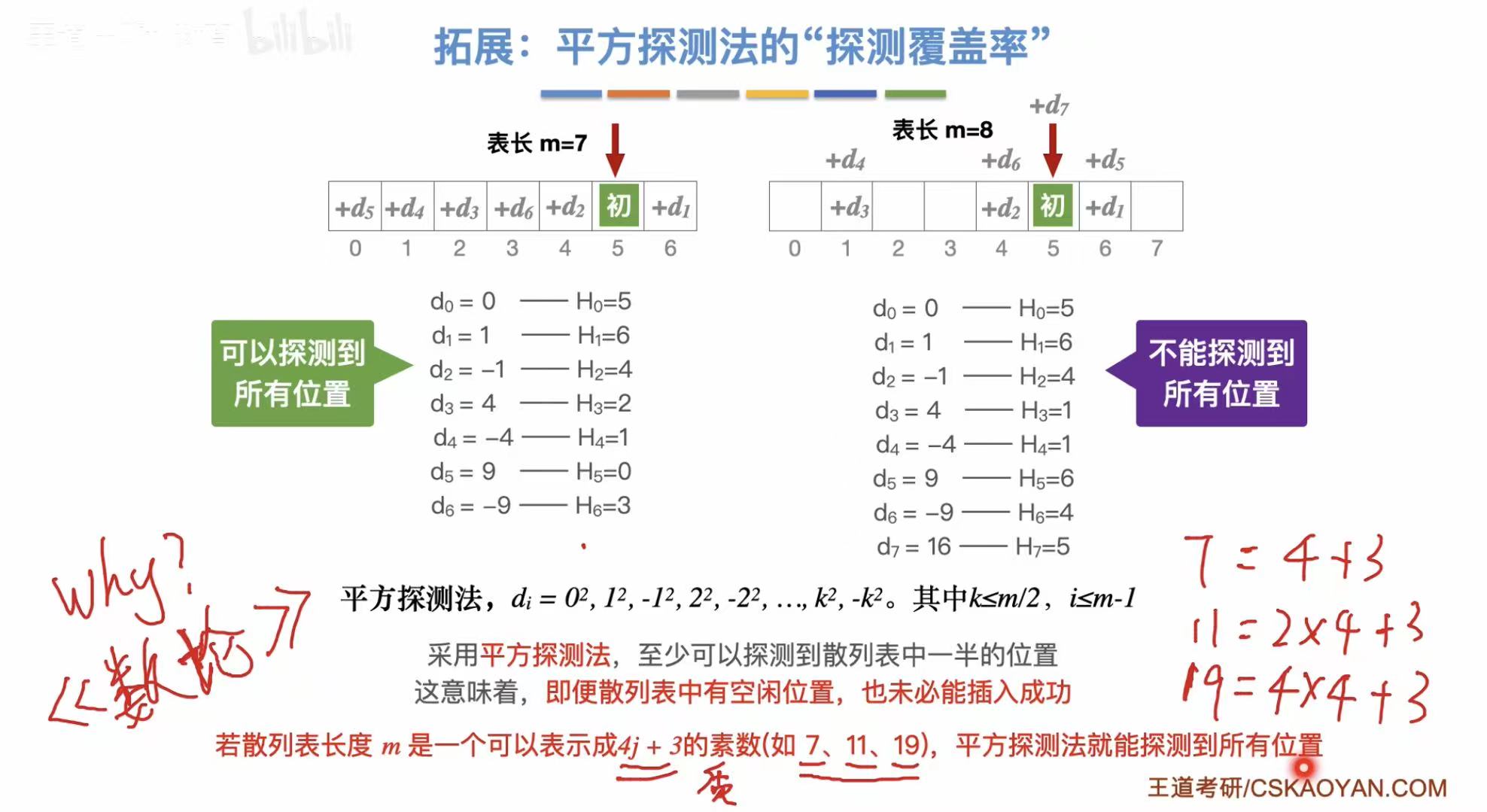
• 平方探测法：依次正负平方往后找
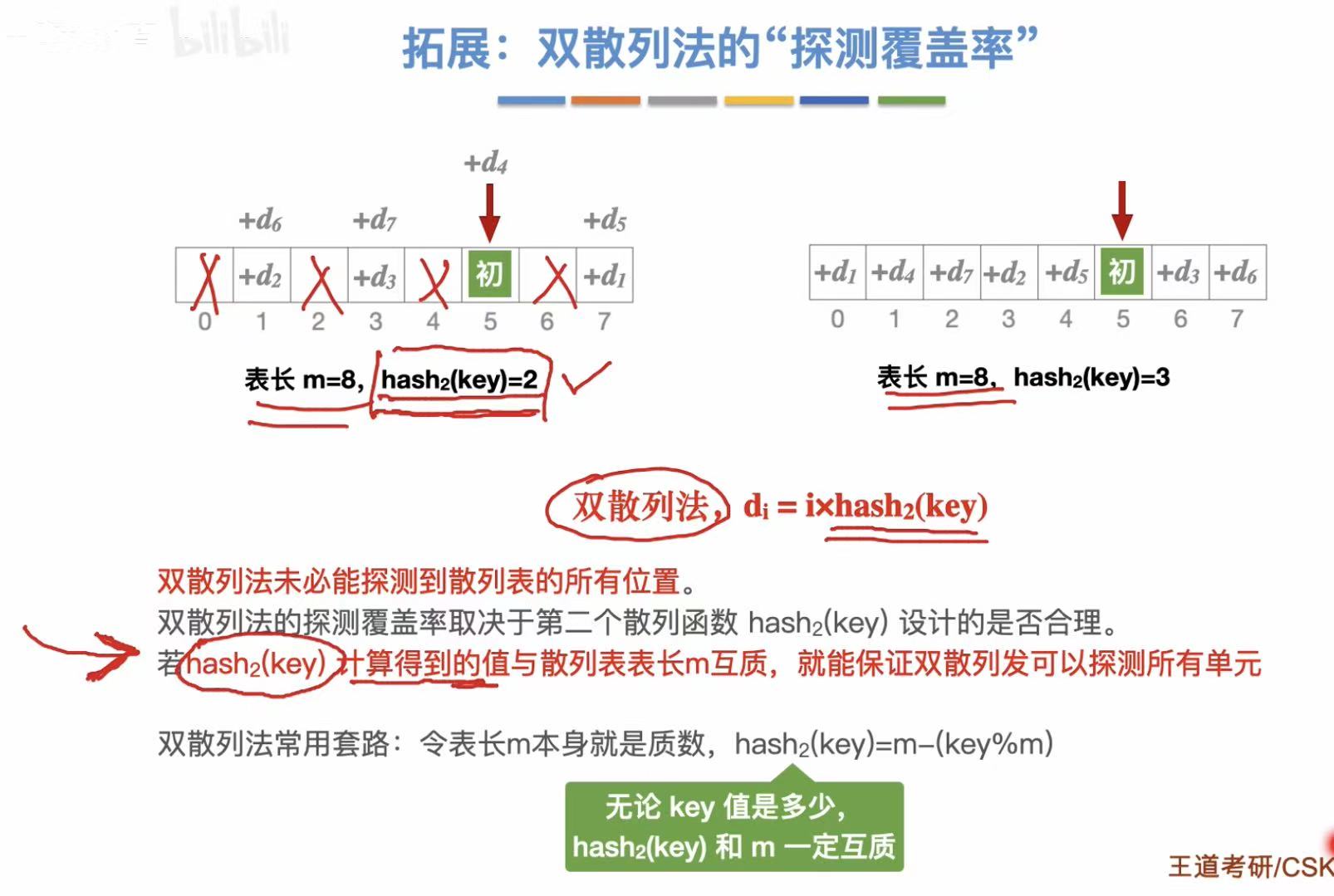
• 双散列法：再加一个散列函数来限制查找空格
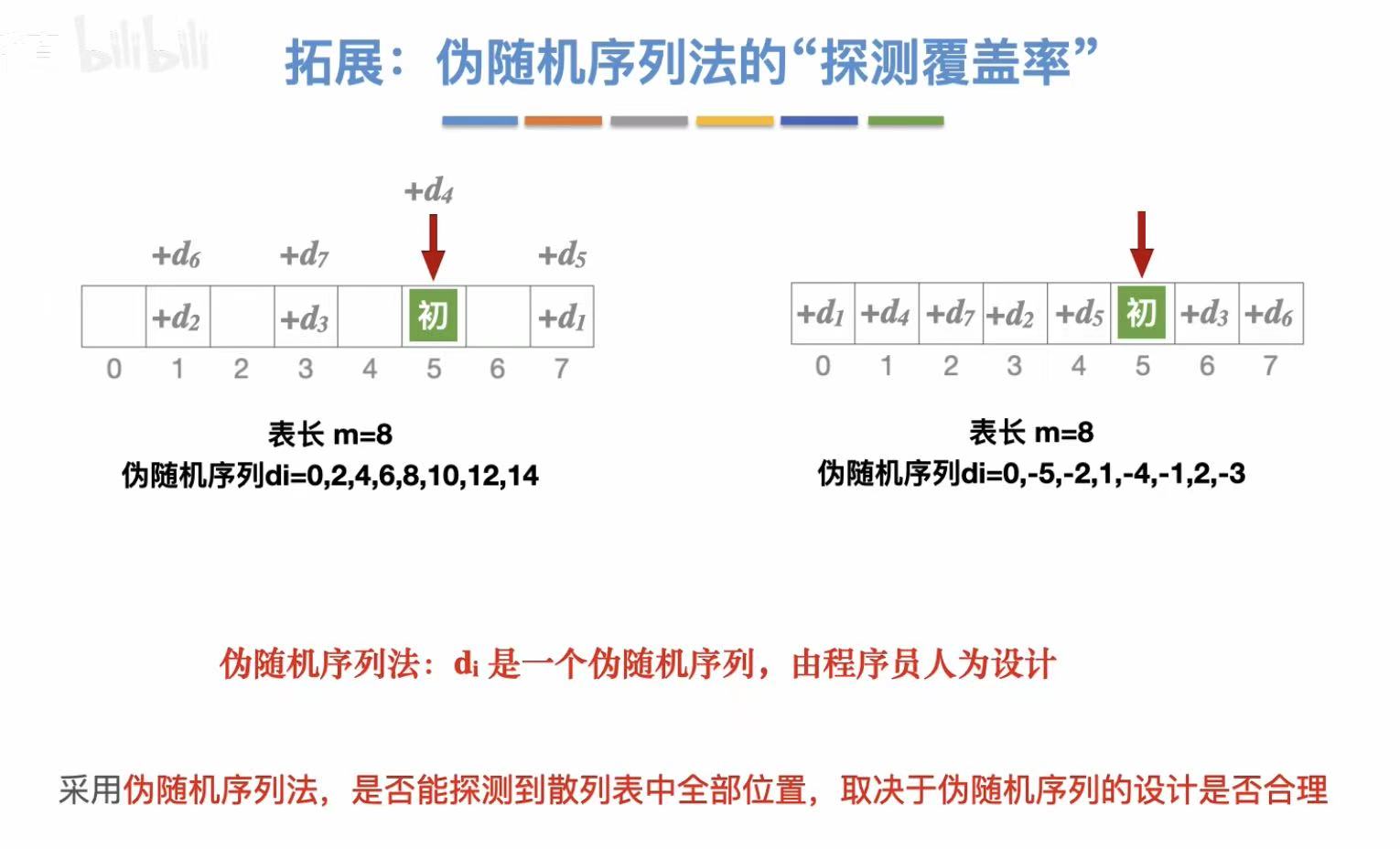
• 伪随机序列 ：自己设定好的按什么顺序找空格
  

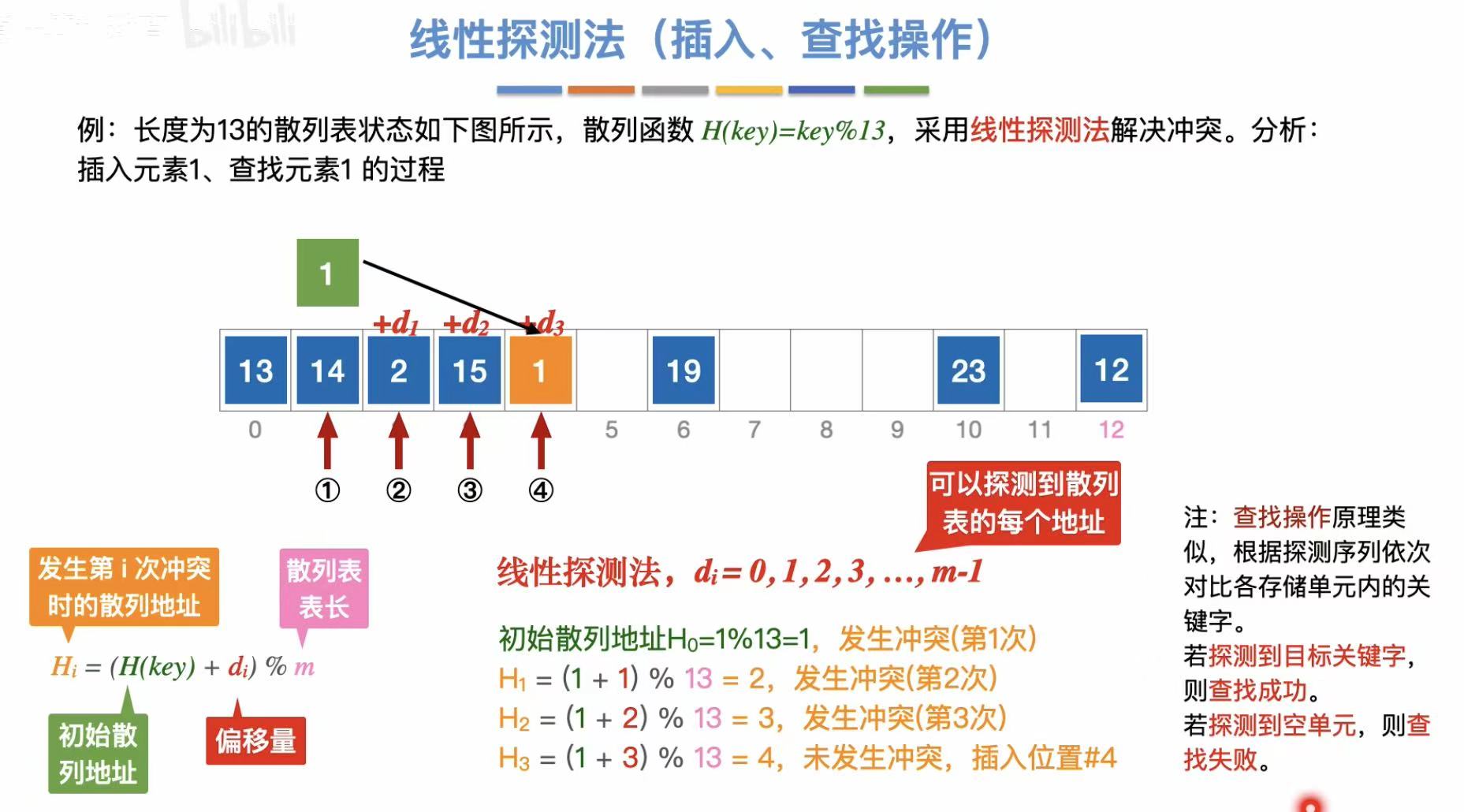
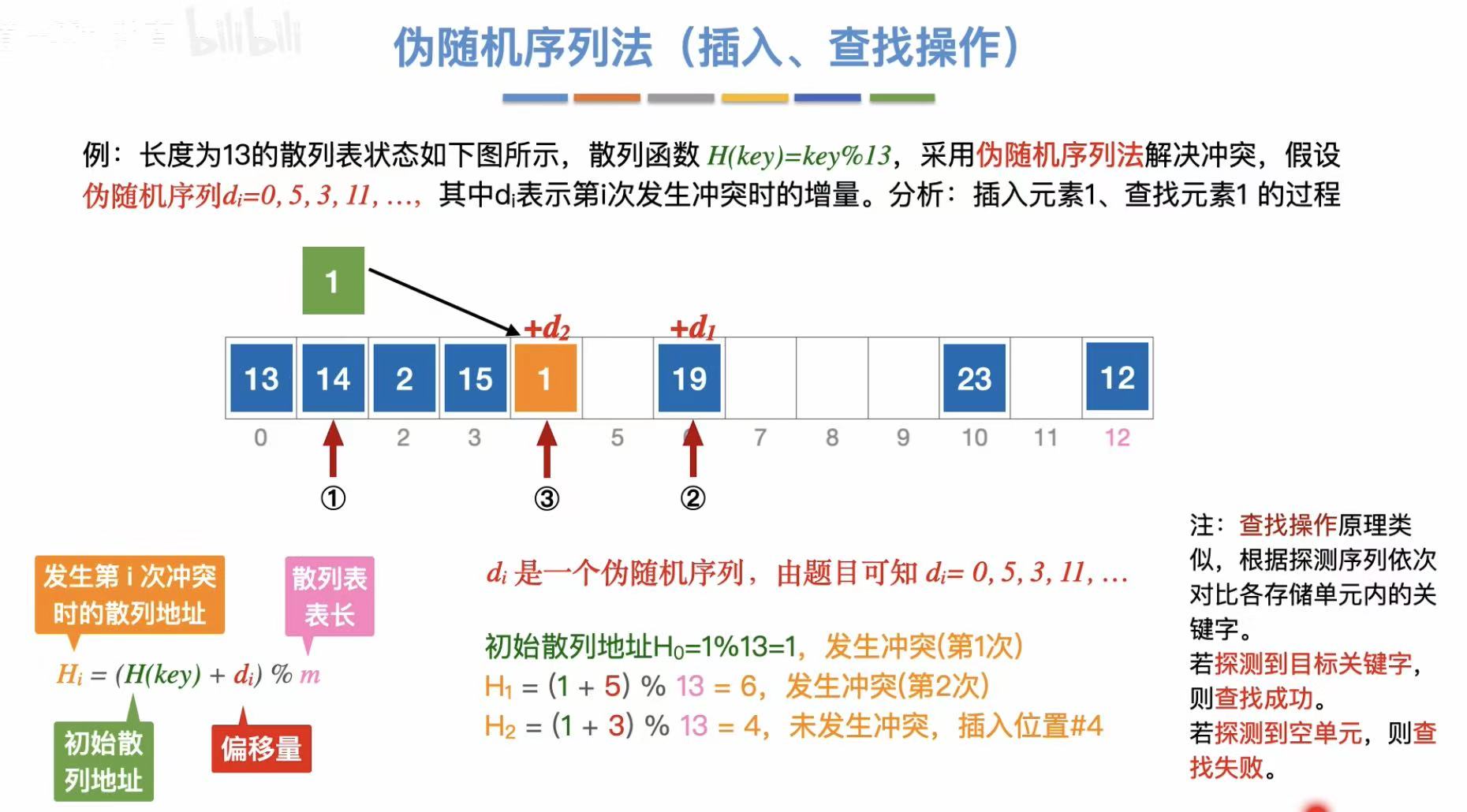
3.2.2 插入、查找操作

线性探测法：

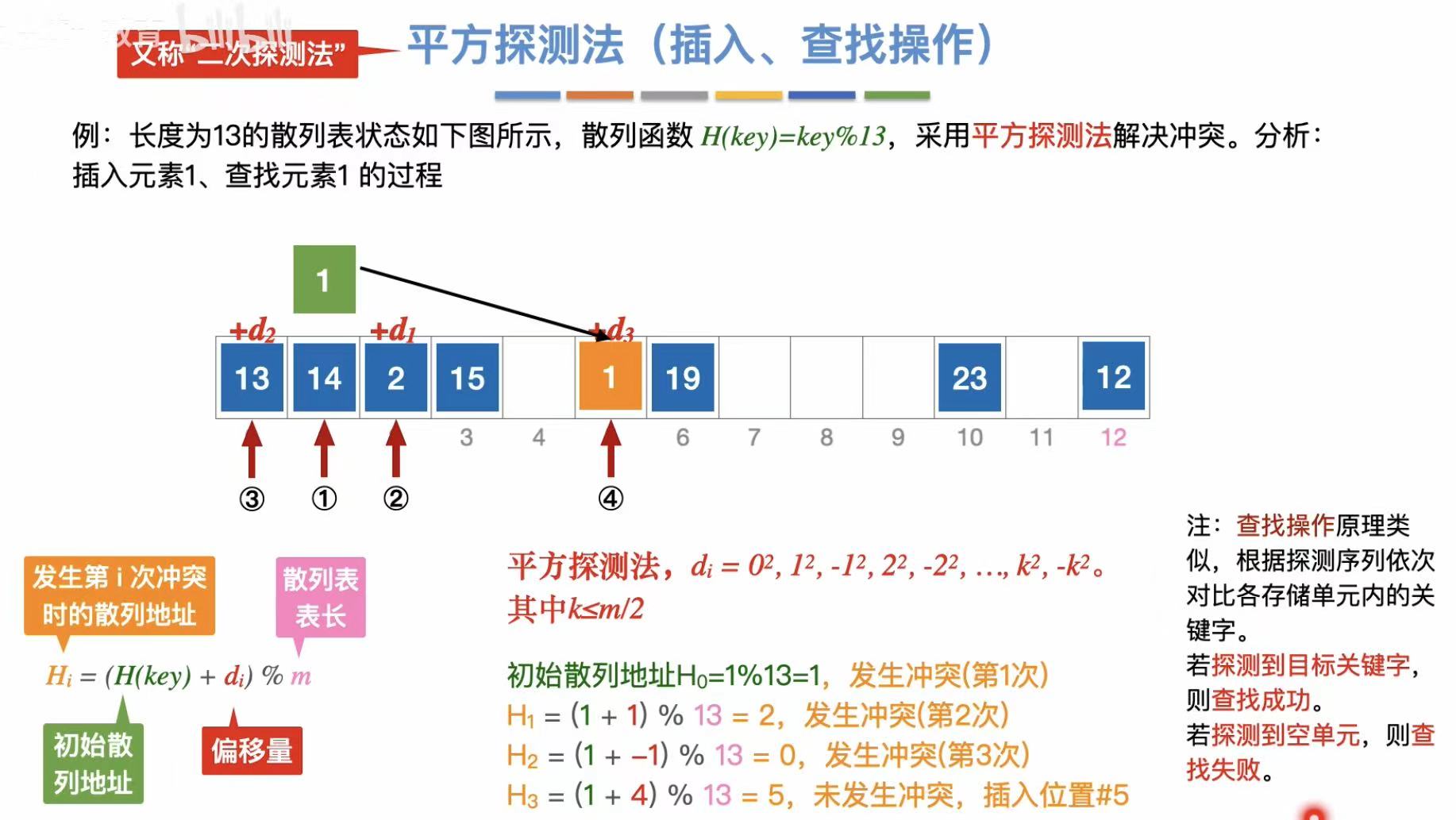
平方探测法：

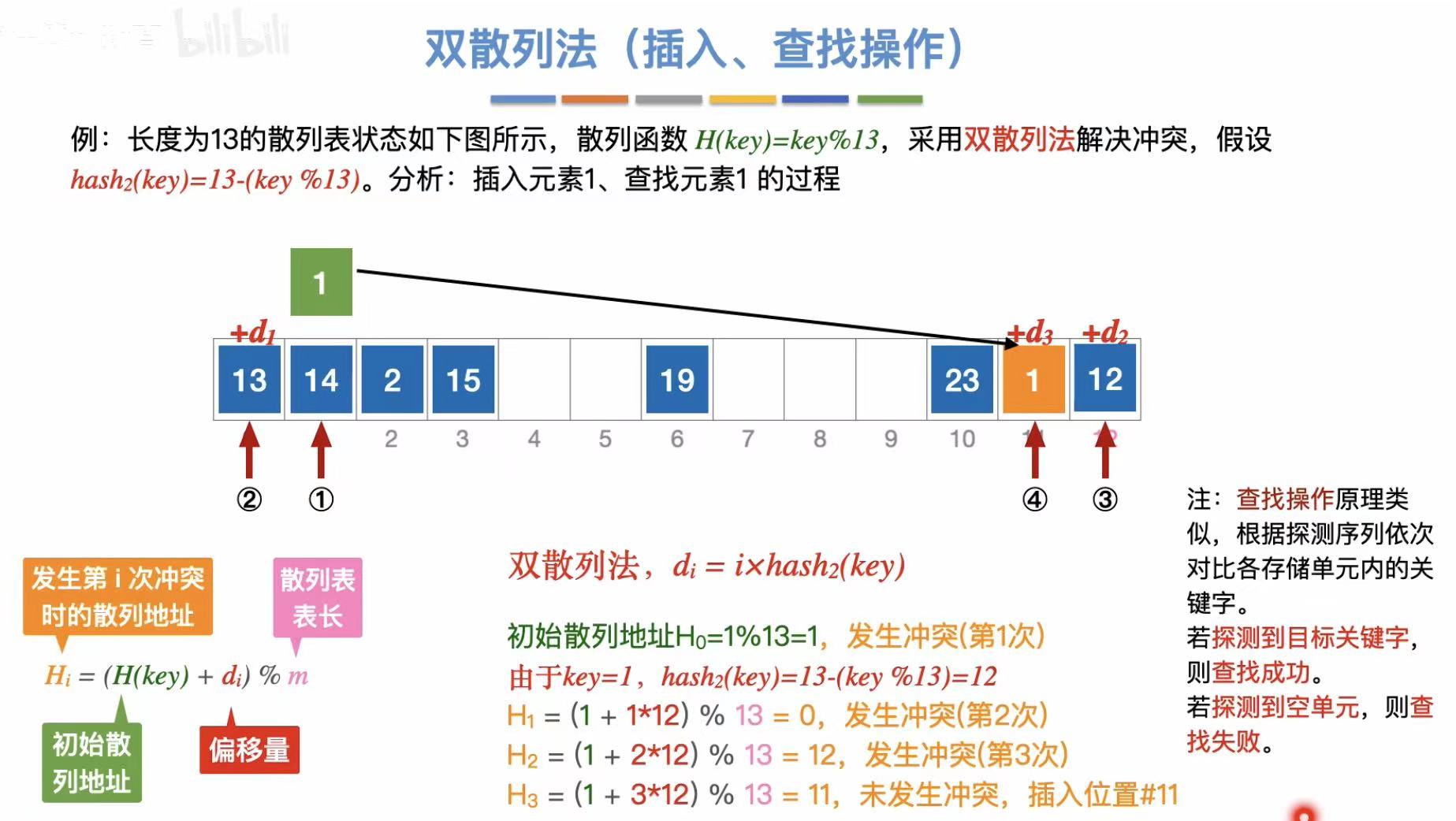
双散列法：

伪随机序列法：

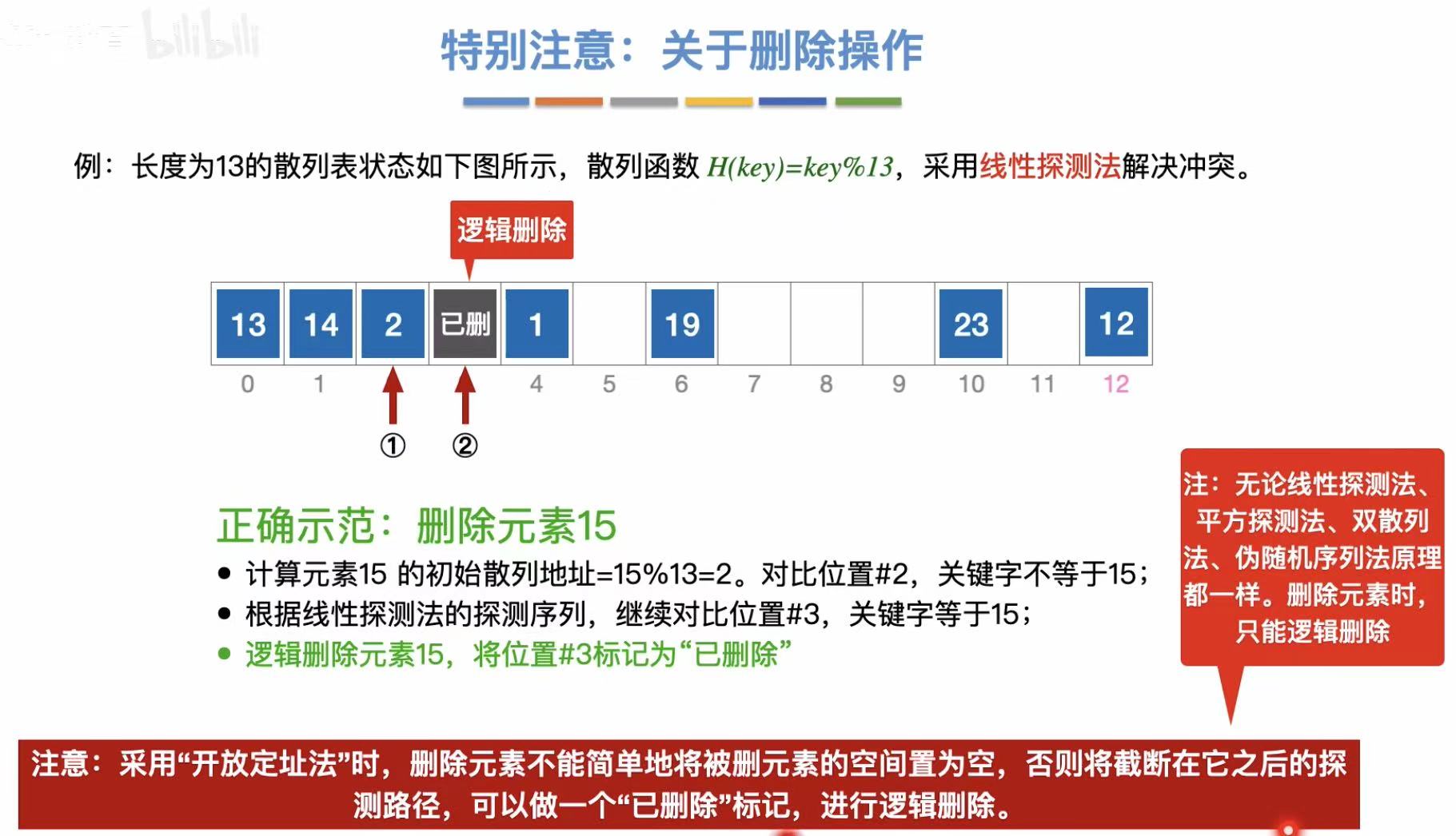
3.2.3 删除操作

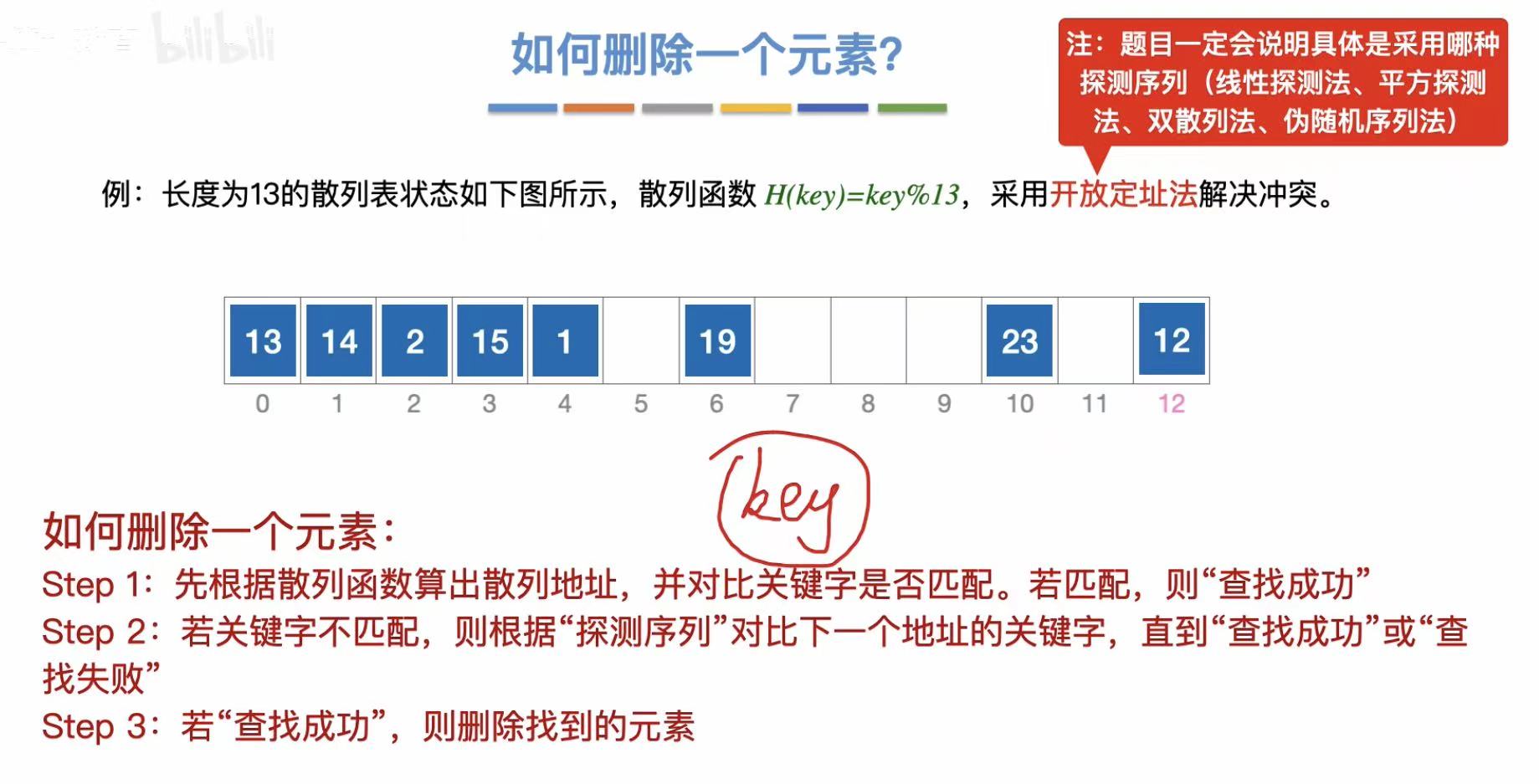
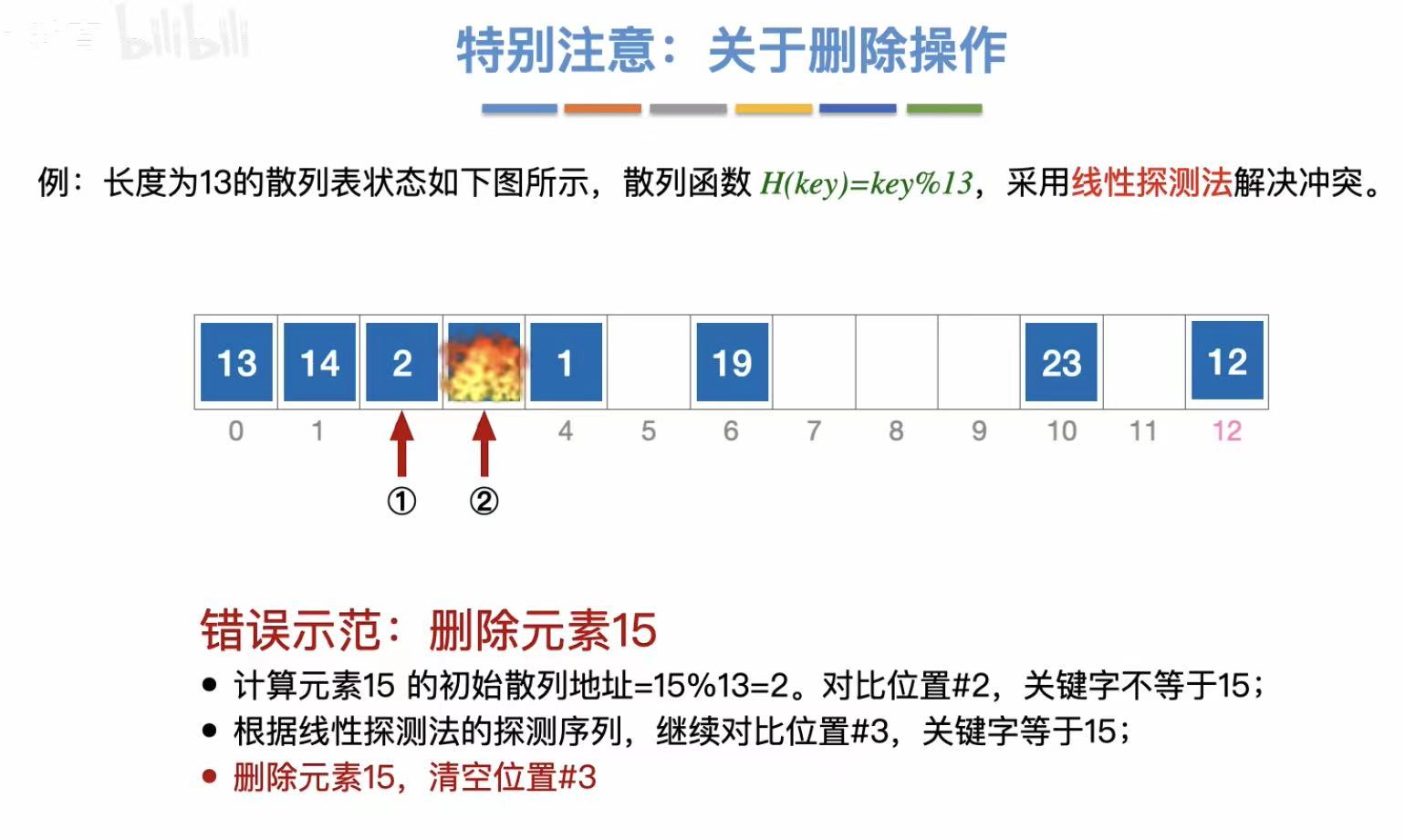
删除15：

• 先根据散列函数找到散列地址
• 没找到就再用探测序列找
• 查找成功即可删除
• 这里直接清空位置3，其实是错误的（往下看）
  
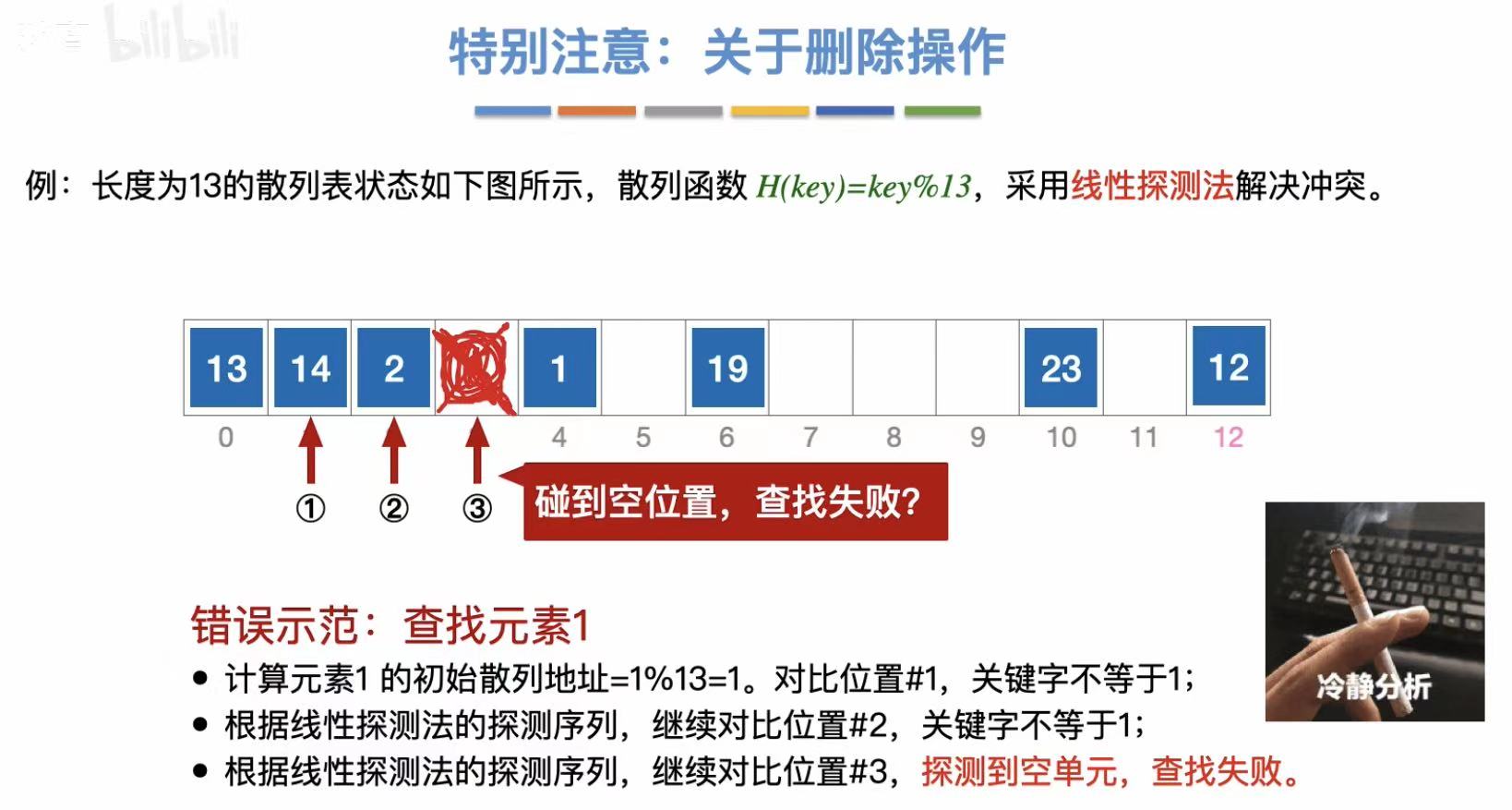
  删除1：
• 按照之前的步骤
• 当查找到位置3的时候发现是空的，就直接判定失败
• 但其实1就在位置4
• 所以上一步删除15时直接清空数据是不对的
  
  所以当我们删除数据的时候，我们应该将这个位置标为已删除，就是从逻辑上删除了，实际上还有，防止它变为空，截断查找。
  
  这样重新查找数据，就可以很顺利地找到了。
  
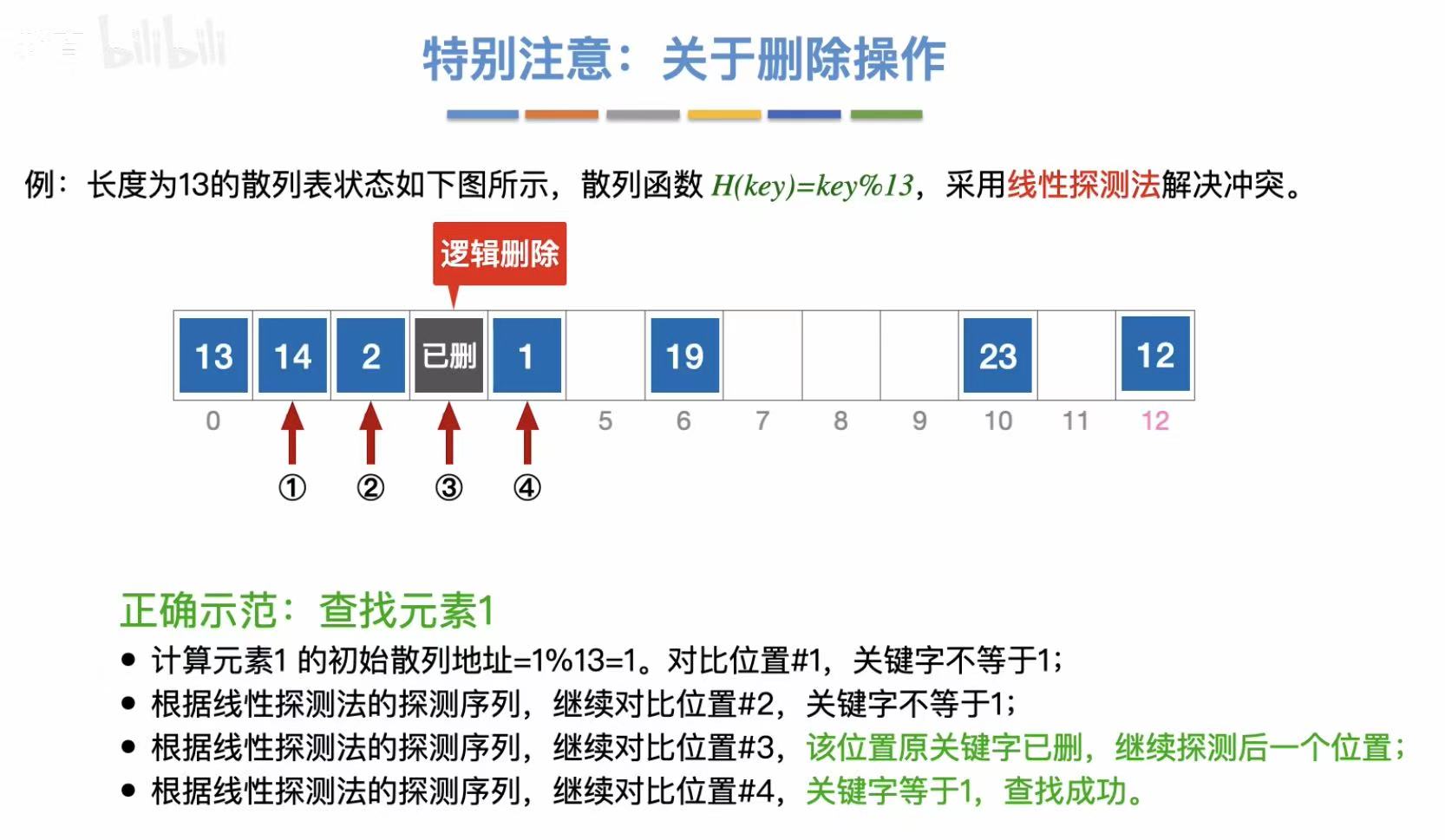
  当然，如果有太多标为已删除的数据，有的时候还会拉慢我们的查找速率，所以我们需要不定时地清理数据。
  

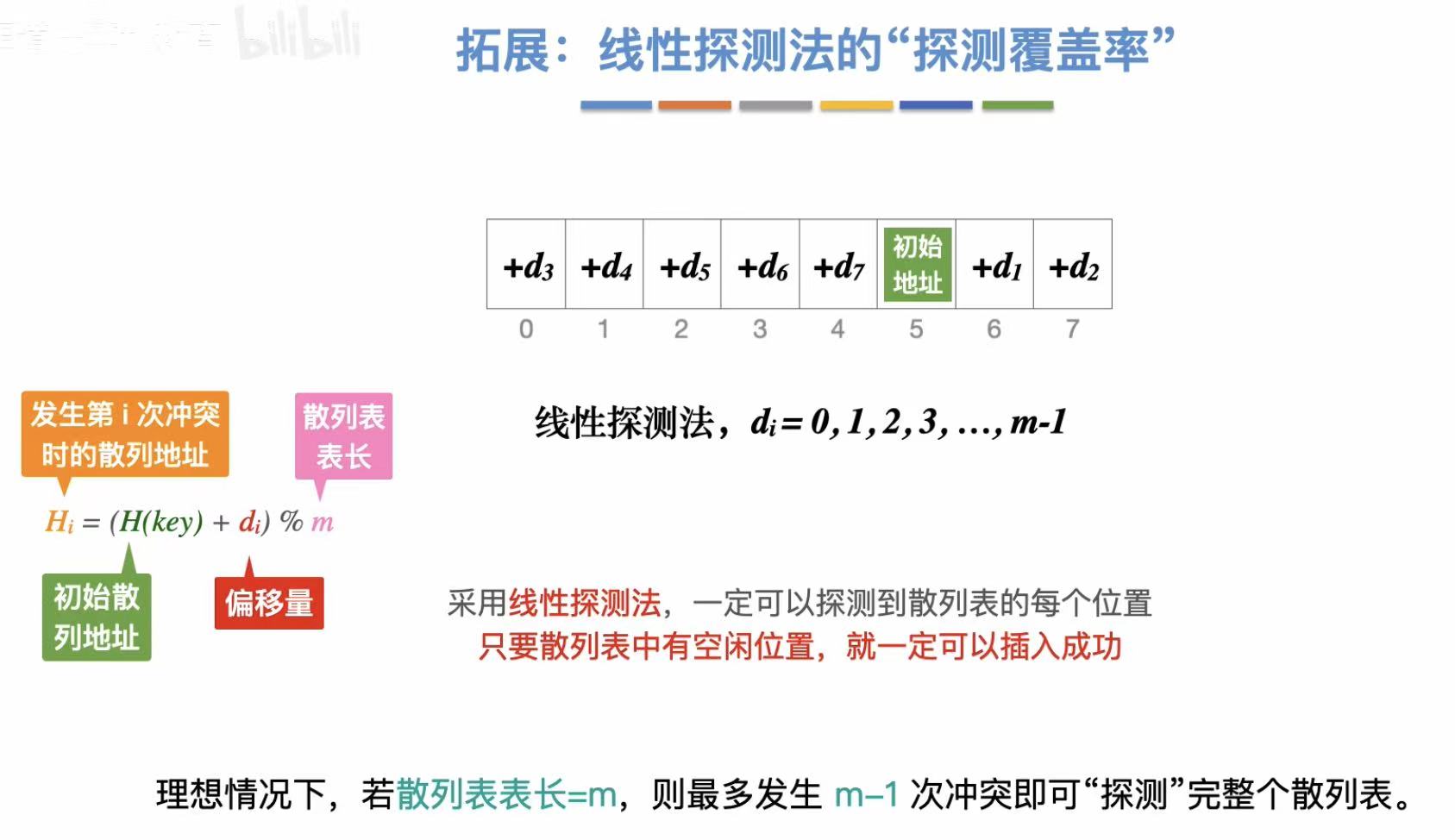
3.2.4 小结及拓展

4. 散列查找的性能分析

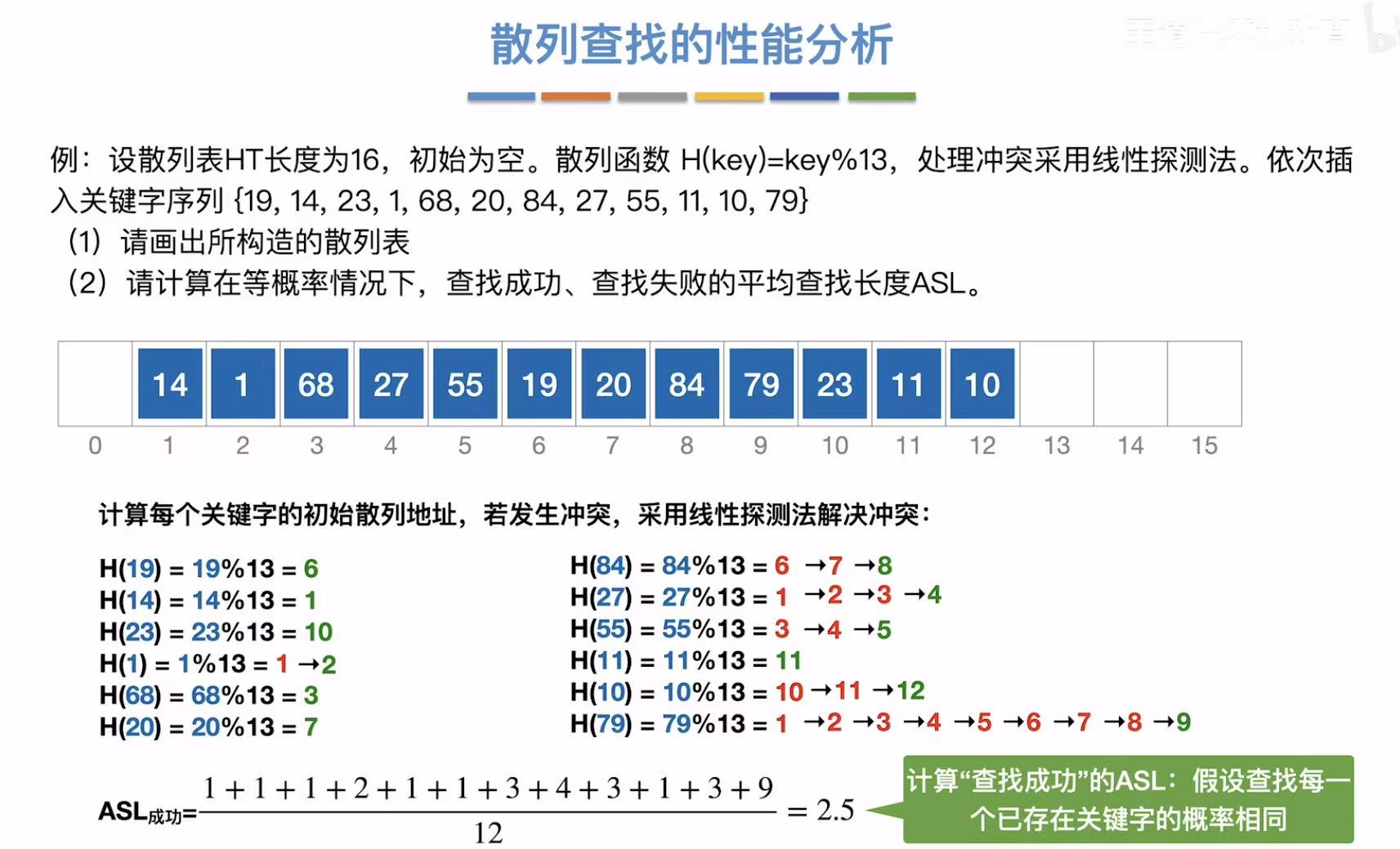
4.1 性能分析

成功ASL：

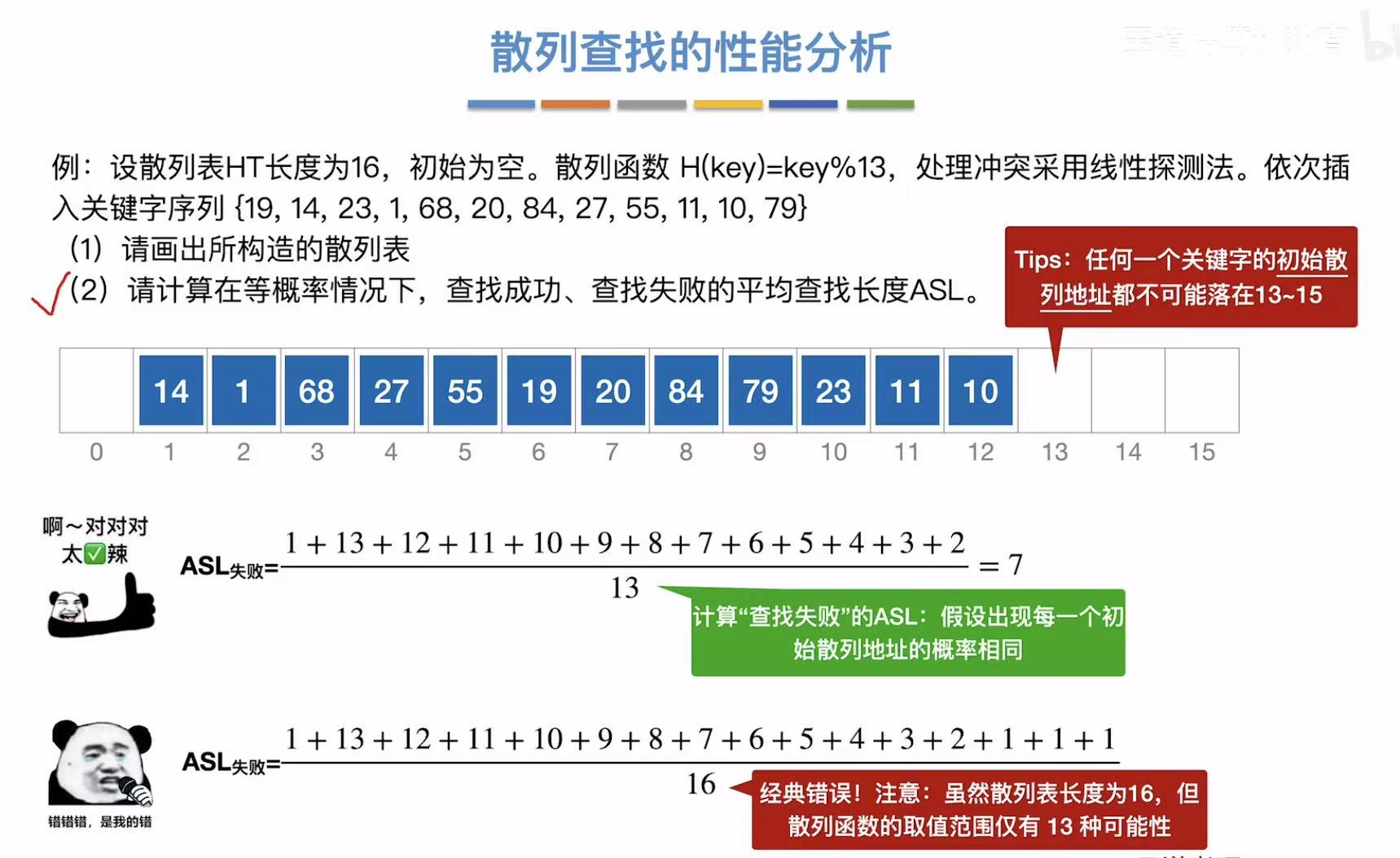
失败ASL：

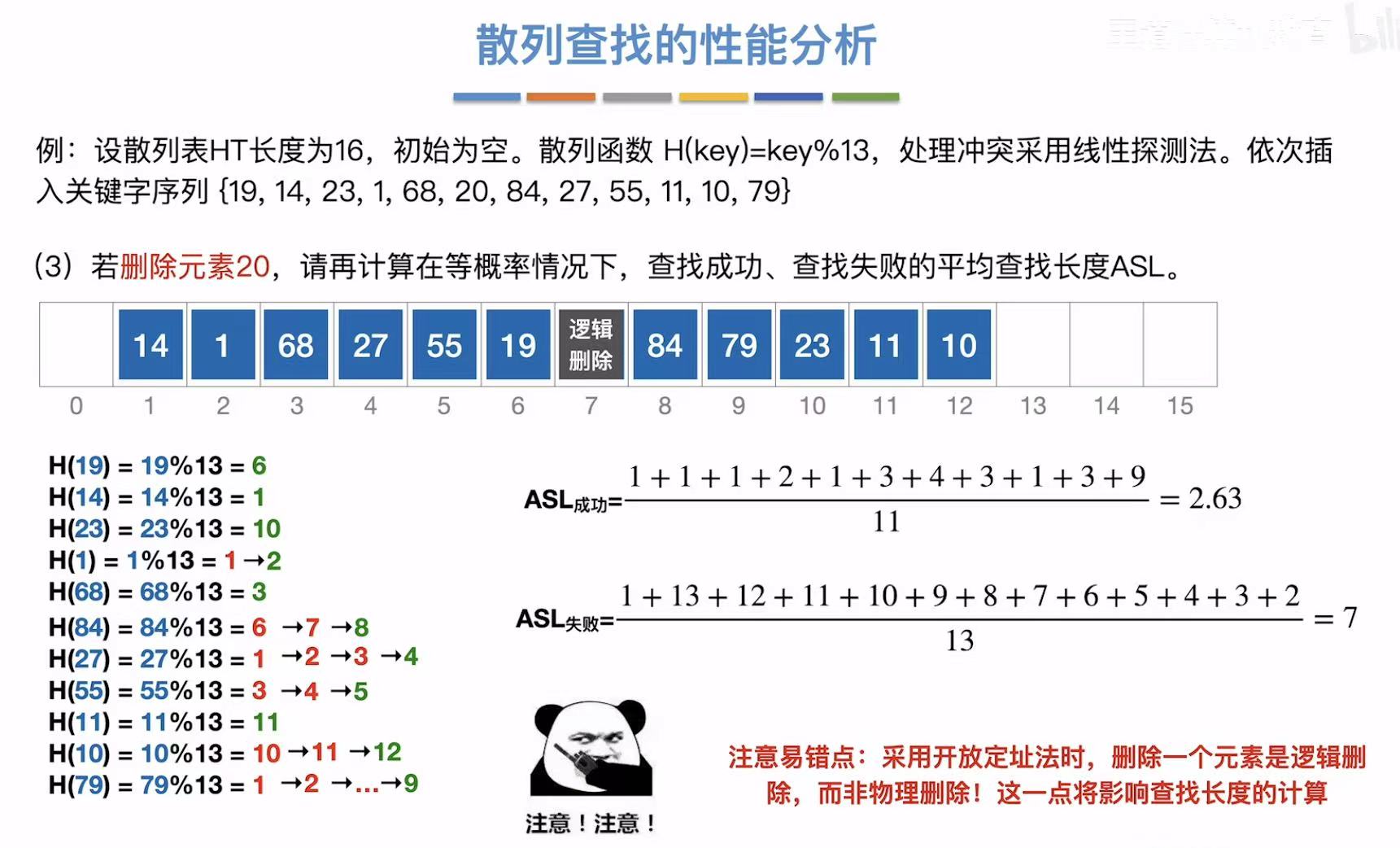
4.2 装填因子

4.3 聚集现象

4.4 回顾