一、题目解析

评分标准分为三个阶段:
阶段一(1~2赛季):排名法
评委的排名 + 粉丝的排名 = 选手最终的 排名,而选手最终的排名越高,意味着表现越差,越应该被淘汰;
阶段二(3~27赛季):百分比法
评委评分的百分比 + 粉丝评分的百分比 = 选手最终得分百分比 ,选手得分百分比越低,说明选手表现越差,越应该被淘汰;
阶段三(28~34赛季):回归排名法+评委裁决制度
先按照阶段一的方法确定出排名最低的两位选手,然后评委裁决谁被淘汰。
二、第一问思路总结以及公式推导
往常的预测类问题都是已知一堆的和
,然后根据
去预测未知的
。但是,这道题是我们已知评委打分和淘汰结果,需要去估计粉丝的票数。相当于是已知一部分的
和所有的
,让我们预测另一部分
,而这种问题在数学上是"约束逆问题"。
"约束逆问题"的解的特征是:具有非唯一性,存在多组粉丝票数均满足约束
那么,我们可以利用淘汰约束缩小可行解的空间,同时引入正则化约束,最终通过Bayes方法量化确定性。(由于从一个点解预测为一个区域解,是唯一解,而Bayes方法能够量化区域解(最小的可行解空间))
将逆问题视为优化问题,求解可行解空间。
1.百分比法------对应的数据是连续数据
设定选手i的裁判得分百分比为,观众得分百分比为
,合并得分百分比为
,那么,我们可以得到
其中,,
那么,
可以看出,合并得分百分比是一个零和博弈的结构(可以理解为1号选手得分比例上升了,那么其他所有选手的得分百分比就下降了)
(1)我们构造一下约束条件:
1)淘汰约束:本周分数最低的选手淘汰出局
即,即
2)所有选手投票比例和为1:
3)非负性:
4)正则化边界:
令,取
根据正则化以及上述条件可知,V的可行域为 (n - 1)维的多面体
接下来,我们来构造目标函数:
(2)构造目标函数,主要依据启发性原则。
1)温和性原则:粉丝投票不能过于极端,要相对均匀,采用最大熵的原理,也就是说选择不确定性最大、最平坦的分布。
为了量化,可以找一个比较均匀的分布作为惩罚项。
2)相关性原理:认为粉丝投票与评委投票正相关,利用此原则作为软引导,优化目标函数
3)多样性原则:允许粉丝的偏好与评委不同,引入差异化项
最终,我们设计出的目标函数为:
即
其中,越大,解就越趋向于粉丝票数与评委成正相关;
越大,就越趋向于差异化。
根据可以看出,最终的问题是一个凸二次优化问题。
2.排名法------对应的数据是离散数据
设定第i名选手的最终排名为,评委打分排名为
,观众打分排名为
,那么有
同理,我们定义淘汰约束:
由于排名是离散的,其可行解是一个排序,而且粉丝排名数可能是
当以后显然使用穷举法不再合适。那么,我们采用如下策略:
1)当n < 8时,采用穷举法
2)当n  8时,采用蒙特卡洛模拟求解
8时,采用蒙特卡洛模拟求解
3.最终,结合两种方法,使用Bayes模型进行量化不确定性
(1)问题形式化
我们有一个参数向量,代表
个选手的"真实实力"或"内在质量"。观测数据
包括:
-
粉丝投票结果
-
专家评分或其他约束条件
(2)贝叶斯框架建立
1)Likelihood
假设观测数据 在给定参数
下的分布为:
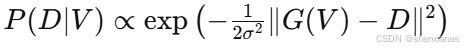
其中 是预测函数。在你提出的模型中,如果我们认为目标函数
反映数据拟合程度,可以将其负指数作为似然:
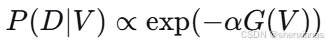
这里 控制数据拟合的精度。
2)后验分布
根据贝叶斯定理: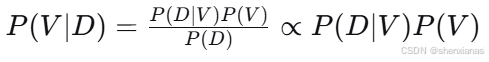
将似然和先验代入: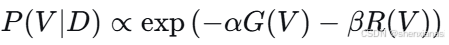
其中 控制先验强度。
(3)具体模型推导
1)完整目标函数形式
我们可以将其重新组织为:
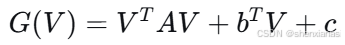
其中:
-
(
) 是方差项的矩阵形式)
-
-
为常数项
2)先验分布选择
-
非负约束 :
⇒ 使用截断正态或 Gamma 先验
-
正则化边界 :
⇒ 使用 Dirichlet 先验的变形
-
独立性假设 :
相互独立 ⇒ 先验可分解
使用: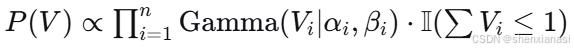
其中 是指示函数。
3)后验分布计算
后验分布为: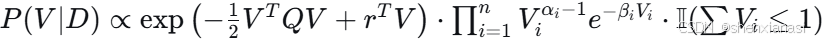
其中:
-
-
(
是先验参数向量)
这是一个带有线性约束的指数族分布。
(4)不确定性量化方法
1)后验均值和协方差(解析近似)
如果忽略截断约束,后验近似为多元正态分布:
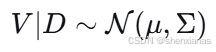
其中:
95%置信椭圆 :
对于参数,边际分布为
,其
% 置信区间为:
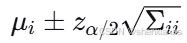
其中对应 95% 置信水平。
2)考虑约束的采样方法(MCMC)
当约束重要时,使用马尔可夫链蒙特卡洛:
a) Metropolis-Hastings 算法
-
初始化
-
对于
:
-
从提议分布
抽取候选点
-
计算接受概率:
-
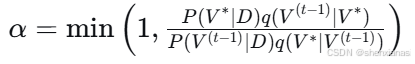
以概率 接受
,否则
b)Gibbs 采样(如果条件分布可求)
对于每个 ,从其全条件分布采样:
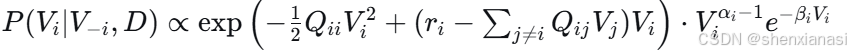
(5)不确定性度量
1)后验汇总统计量
从后验样本 计算:
-
点估计:
-
后验均值:
-
后验中位数:各分量中位数
-
MAP估计:
-
-
不确定性度量:
-
标准差:
-
95%可信区间:
(后验分位数)
-
后验相关系数矩阵:
-
2)排名不确定性
由于应用涉及排名,可以计算:
-
排名概率矩阵
:
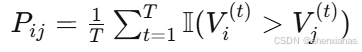
表示选手
强于选手
的后验概率。
-
预期排名分布 :
对于每个选手
,计算其排名
在所有样本中的分布。
-
排名熵:
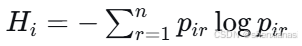
其中
是选手
排名为
的概率。