BISHI69 [HNOI2008]越狱

独自破碎E2026-02-22 8:48

这个问题可以通过计算"总方案数"减去"不越狱方案数"来得出结果。

总分配方案数 ：

每个房间有 M M M 种宗教选择，共有 N N N 个房间。

总数 = M × M × ⋯ × M = M N M \times M \times \dots \times M = M^N M×M×⋯×M=MN。

不越狱方案数 :

第 1 个房间有 M M M 种选择；

第 2 个房间为了不与第 1 个重复，有 M − 1 M-1 M−1 种选择；

第 3 个房间为了不与第 2 个重复，有 M − 1 M-1 M−1 种选择；

以此类推，剩下的 N − 1 N-1 N−1 个房间每个都有 M − 1 M-1 M−1 种选择。

不越狱总数 = M × ( M − 1 ) N − 1 M \times (M-1)^{N-1} M×(M−1)N−1。

可能发生越狱的方案数 ：

越狱方案 = 总方案数 - 不越狱方案数
结果 = M N − M × ( M − 1 ) N − 1 M^N - M \times (M-1)^{N-1} MN−M×(M−1)N−1

流程图

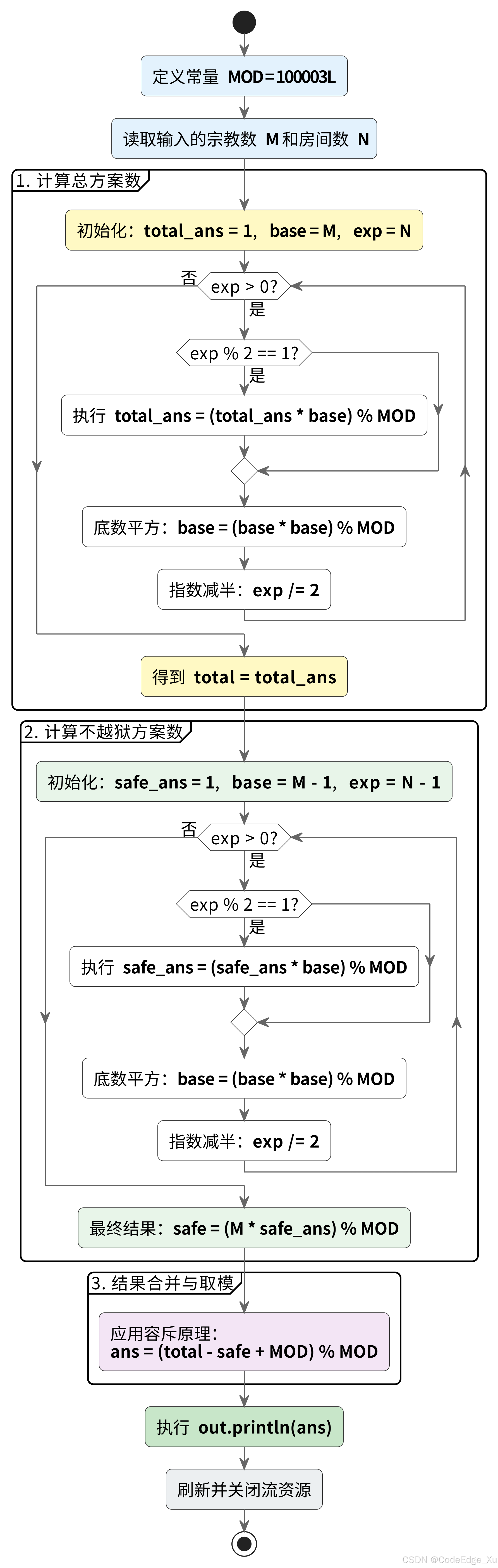
代码实现

java 复制代码

 private static final long MOD = 100003L;

    public static void main(String[] args) throws IOException {
        // 使用BufferedReader读取输入，PrintWriter输出结果
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] str = br.readLine().split("\\s+");
        long M = Long.parseLong(str[0]);
        long N = Long.parseLong(str[1]);
        long total = mypower(M, N, MOD);
        long safe = M * mypower(M - 1, N - 1, MOD)%MOD;
        long ans = (total-safe+MOD)%MOD;

        out.println(ans);

        out.flush();
        out.close();
        br.close();
    }

    private static long mypower(long base, long exp, long mod) {

        long ans = 1 % mod;
        while (exp > 0) {

            if (exp % 2 == 1) {
                ans = (ans * base) % mod;
            }

            base = (base * base) % mod;
            exp /= 2;
        }

        return ans;
    }