线性 dp--数字三角形模型
数字三角形 Number Triangles
题目链接:
P1216 [IOI 1994 / USACO1.5] 数字三角形 Number Triangles - 洛谷
思路:
把这个三角抽象为二维数组。
动态规划,我们设 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示从 ( 1 , 1 ) (1,1) (1,1) 到 ( i , j ) (i,j) (i,j) 的所有方案的集合的最大值。这个点可以由 ( i − 1 , j ) (i-1,j) (i−1,j) 或者 ( i − 1 , j − 1 ) (i-1,j-1) (i−1,j−1) 走过来。
所以状态转移方程为 d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − 1 ] ) + a [ i ] [ j ] dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j] dp[i][j]=max(dp[i−1][j],dp[i−1][j−1])+a[i][j]。
答案就是最下面一层的最大值。
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
const int N=1050;
int a[N][N];
int dp[N][N];
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
}
}
int ans=-1e18;
for(int i=1;i<=n;i++)ans=max(ans,dp[n][i]);
cout<<ans<<endl;
}
signed main(){
IOS
int t=1;
while(t--)
{
solve();
}
}U280643 摘花生
题目链接:
U280643 摘花生 - 洛谷
思路:
数字三角形模型,我们可以开一个二维数组 dp[i][j] 来表示从 ( 1 , 1 ) (1,1) (1,1) 走到 ( i , j ) (i,j) (i,j) 的所有路线所能采摘到花生数量的最大值,最后答案为 d p [ R ] [ C ] dp[R][C] dp[R][C]。
推导状态转移方程,由于题目限制, ( i , j ) (i,j) (i,j) 点只能从 ( i − 1 , j ) (i-1,j) (i−1,j) 或 ( i , j − 1 ) (i,j-1) (i,j−1) 到达,所以最终方程为 d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) + w [ i ] [ j ] dp[i][j]=max(dp[i-1][j],dp[i][j-1])+w[i][j] dp[i][j]=max(dp[i−1][j],dp[i][j−1])+w[i][j]。
还可以进行优化,由于第 i 层只依赖于第 i 层和第 i-1 层,所以可以优化为一维数组。在当前层可以由上一层的该列到达或者由当前层的前列到达。
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
const int N=150;
int w[N][N];
int dp[N][N];
void solve()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>w[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+w[i][j];
}
}
cout<<dp[n][m]<<endl;
}
/*一维数组优化空间
//用dp[m]来表示当前计算行第m列的最大值,当计算结束后直接输出dp[m]即可
//记得及时清理数组
void solve()
{
int n,m;
cin>>n>>m;
int w;
memset(dp,0,sizeof dp);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>w;
dp[j]=max(dp[j-1],dp[j])+w;
}
}
cout<<dp[m]<<endl;
}
*/
signed main(){
IOS
int t;
cin>>t;
while(t--)
{
solve();
}
}最低通行费
题目链接:
T118735 [ybt1287]最低通行费 - 洛谷
思路:
题目限制了不能超过 2 n − 1 2n-1 2n−1 这其实就是不能往回走。所以我们的状态表示 d p [ i ] [ j ] dp[i][j] dp[i][j] 仍然是从 ( 1 , 1 ) (1,1) (1,1) 走到 ( i , j ) (i,j) (i,j) 的所有方案的集合的最小值。
( i , j ) (i,j) (i,j) 点只能从 ( i − 1 , j ) (i-1,j) (i−1,j) 或 ( i , j − 1 ) (i,j-1) (i,j−1) 到达,所以最终方程为 d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) + w [ i ] [ j ] dp[i][j]=min(dp[i-1][j],dp[i][j-1])+w[i][j] dp[i][j]=min(dp[i−1][j],dp[i][j−1])+w[i][j]。
求最小值,那么初始化为最大值。
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
const int N=1050;
int w[N][N];
int dp[N][N];
void solve()
{
int n;
cin>>n;
memset(dp,0x3f,sizeof dp);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>w[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==1&&j==1)dp[1][1]=w[1][1];
else dp[i][j]=min(dp[i-1][j],dp[i][j-1])+w[i][j];
}
}
cout<<dp[n][n];
}
signed main(){
IOS
int t=1;
while(t--)
{
solve();
}
}方格取数
题目链接:
P1004 [NOIP 2000 提高组] 方格取数 - 洛谷
思路:
如果只走一次使用 d p [ i ] [ j ] dp[i][j] dp[i][j] 来表示从 ( 1 , 1 ) (1,1) (1,1) 走到 ( i , j ) (i,j) (i,j) 所有路径集合的最大值。状态转移公式为 d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) + w [ i ] [ j ] dp[i][j]=max(dp[i-1][j],dp[i][j-1])+w[i][j] dp[i][j]=max(dp[i−1][j],dp[i][j−1])+w[i][j]。
不同的是这个题目要求走两次,那么以 d p [ i 1 ] [ j 1 ] [ i 2 ] [ j 2 ] dp[i1][j1][i2][j2] dp[i1][j1][i2][j2] 来表示分别走到 ( i 1 , j 1 ) (i1,j1) (i1,j1) 、 ( i 2 , j 2 ) (i2,j2) (i2,j2) 的路径最大值。四维不太好做,可以发现只有当 i 1 + j 1 = i 2 + j 2 = k i1+j1=i2+j2=k i1+j1=i2+j2=k 时才可能踩到重复的格子。
这样我们就可以用三维数组 d p [ k ] [ i 1 ] [ i 2 ] dp[k][i1][i2] dp[k][i1][i2] 来表示分别走到 ( i 1 , k − i 1 ) (i1,k-i1) (i1,k−i1) 、 ( i 2 , k − i 2 ) (i2,k-i2) (i2,k−i2) 的路径最大值。
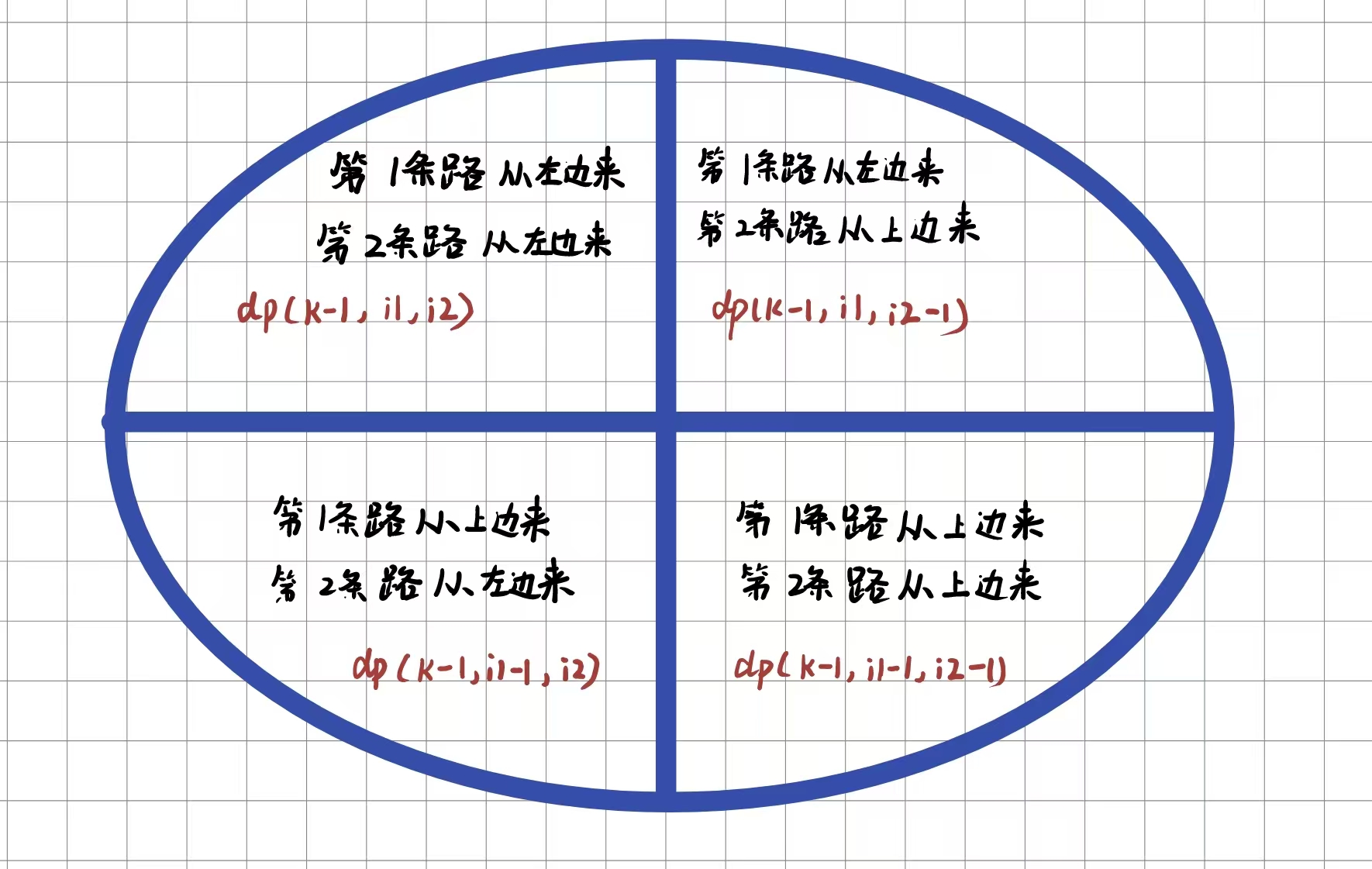
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
const int N=15;
int w[N][N];
int dp[2*N][N][N];
void solve()
{
int n;
cin>>n;
int a,b,c;
while(cin>>a>>b>>c){
w[a][b]=c;
}
for(int k=2;k<=n*2;k++){
for(int i1=1;i1<=n;i1++)
{
for(int i2=1;i2<=n;i2++)
{
int j1=k-i1,j2=k-i2;
if(j1>0&&j2>0&&j1<=n&&j2<=n){
int m=w[i1][j1];
if(i1!=i2)m+=w[i2][j2];
int &x=dp[k][i1][i2];
x=max(x,dp[k-1][i1-1][i2-1]+m);
x=max(x,dp[k-1][i1-1][i2]+m);
x=max(x,dp[k-1][i1][i2-1]+m);
x=max(x,dp[k-1][i1][i2]+m);
}
}
}
}
cout<<dp[2*n][n][n];
}
signed main(){
IOS
int t=1;
while(t--)
{
solve();
}
}传纸条
题目链接:
P1006 [NOIP 2008 提高组] 传纸条 - 洛谷
思路:
这个题目同上面方格取数的思路,这里的好感度可以看作是格子里的数字,每个数字只能用一次。
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define endl '\n'
const int N=55;
int w[N][N];
int dp[2*N][N][N];
void solve()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>w[i][j];
}
}
for(int k=2;k<=n+m;k++){
for(int i1=1;i1<=n;i1++)
{
for(int i2=1;i2<=n;i2++)
{
int j1=k-i1,j2=k-i2;
if(j1>0&&j2>0&&j1<=m&&j2<=m){
int t=w[i1][j1];
if(i1!=i2)t+=w[i2][j2];
int &x=dp[k][i1][i2];
x=max(x,dp[k-1][i1-1][i2-1]+t);
x=max(x,dp[k-1][i1-1][i2]+t);
x=max(x,dp[k-1][i1][i2-1]+t);
x=max(x,dp[k-1][i1][i2]+t);
}
}
}
}
cout<<dp[m+n][n][n];
}
signed main(){
IOS
int t=1;
while(t--)
{
solve();
}
}