
论文链接:https://arxiv.org/abs/2602.12275
发布时间:2026.02.12
机构:微软研究院
我猜每个经常用大模型的朋友,都有过这样的日常:
为了让模型做好数学推理,你精心准备了高质量的few-shot示例,贴在prompt开头,它的准确率一下涨了十几个点。
甚至你让模型自己复盘了几十道题的解题经验,总结成通用方法论,贴进去之后,它做题又稳又准。
但麻烦也跟着来了:这些好用的内容,每次开新对话都要重新贴一遍,不仅占着宝贵的上下文窗口,还会增加推理耗时、拉高算力成本,甚至有时候上下文太长,模型还会把关键信息给"忘了"。
这时候你肯定会想:能不能让模型把这些放在上下文里的临时知识,直接学进自己的参数里?以后不用每次都贴,它天生就会这些本事。
这就是上下文蒸馏这个技术的核心目标。
微软这篇最新的论文,提出了On-Policy Context Distillation(简称OPCD)方案,将上下文蒸馏与当前比较流行的在策略蒸馏融合。
先搞懂:之前的上下文蒸馏,到底拉胯在哪?
首先补个最基础的概念:什么是上下文蒸馏?
说白了,就是我们有一个"老师模型",给它喂上上下文(比如系统提示、解题经验),它就能输出很好的效果。我们想训练一个"学生模型",让它不用带这个上下文,也能复刻老师的输出效果,相当于把上下文里的知识,压缩进学生的参数里。
这个想法特别美好,但之前的方法,全有两个致命的硬伤:
第一,曝光偏差 。
之前的方法全是off-policy(离策略)的,训练的时候,学生学的全是老师生成的标准答案。但推理的时候,学生得自己一步步生成内容,训练和推理的场景完全不匹配。
第二,越学越乱,还容易瞎编 。
之前的方法用的是前向KL散度,逼着学生去拟合老师的所有输出,包括那些概率极低的长尾内容。如果学生模型的能力不够,根本学不来老师这么复杂的分布,最后就会变成"雨露均沾",输出特别散,甚至出现幻觉,瞎编内容。
那有没有办法解决这两个问题?这篇论文的OPCD,就是冲着这两个痛点来的。
OPCD到底是什么?一句话讲透核心逻辑
OPCD,全称是On-Policy Context Distillation,中文叫在策略上下文蒸馏。
它的核心逻辑,我用一句话来解释就是:让学生模型自己先跑一遍生成流程,然后拿着自己生成的完整轨迹,去跟带上下文的老师模型对标,让老师在学生走过的每一步都给指导,用反向KL散度优化,让学生在自己踩过的坑里,学会正确的做法。
我给大家拆解一下它的完整流程:
- 先给一个输入prompt,学生模型完全不带要内化的上下文c,自己独立生成完整的回复轨迹y;
- 把同样的输入prompt,加上上下文c,喂给老师模型,让老师沿着学生生成的这条轨迹,在每一个token的位置,都输出对应的概率分布;
- 计算学生和老师在这条轨迹上,每一个token位置的反向KL散度,把所有位置的散度取平均,作为损失函数;
- 用这个损失函数更新学生模型的参数,反复迭代,直到学生不用带上下文c,也能输出和带c的老师几乎一样的效果。
这里有两个最核心的创新点,也是它能解决之前所有问题的关键:on-policy采样 ,还有反向KL散度。
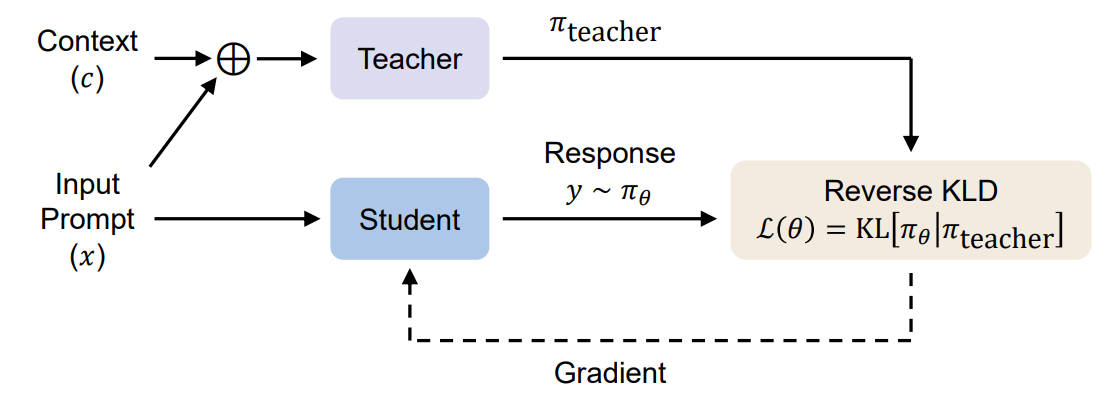
核心公式大白话解读
先给大家放论文里的核心损失函数:
L(θ)=E(x,c)∼D,y∼πθ(⋅∣x)[1∣y∣∑t=1∣y∣DKL(πθ(⋅∣x,y<t)∥πteacher(⋅∣c,x,y<t))]\mathcal{L}(\theta)=\mathbb{E}{(x, c) \sim \mathcal{D}, y \sim \pi{\theta}(\cdot | x)}\left[\frac{1}{|y|} \sum_{t=1}^{|y|} D_{KL}\left(\pi_{\theta}\left(\cdot | x, y_{<t}\right) \| \pi_{teacher }\left(\cdot | c, x, y_{<t}\right)\right)\right]L(θ)=E(x,c)∼D,y∼πθ(⋅∣x) ∣y∣1t=1∑∣y∣DKL(πθ(⋅∣x,y<t)∥πteacher(⋅∣c,x,y<t))
- L(θ)\mathcal{L}(\theta)L(θ):我们要最小化的损失,θ\thetaθ就是学生模型的参数;
- 外面的期望:就是我们从数据集里采样输入x和要内化的上下文c,然后让学生自己生成回复y,所有的学习都基于学生自己生成的这条轨迹;
- 里面的求和:就是把完整的回复拆成一个个token,算每一步的反向KL散度,再取平均,保证每一步都能学到老师的能力;
- 最核心的DKL(学生∣∣老师)D_{KL}(学生||老师)DKL(学生∣∣老师):这是反向KL散度 ,和之前方法的前向KL(DKL(老师∣∣学生)D_{KL}(老师||学生)DKL(老师∣∣学生))完全反过来了。
然后是token级的反向KL计算:
DKL(πθ(⋅∣x,y<t)∣πteacher(⋅∣c,x,y<t))=∑yt′∈Vπθ(yt′∣x,y<t)(logπθ(yt′∣x,y<t)−logπteacher(yt′∣c,x,y<t))\begin{aligned} & D_{KL}\left(\pi_{\theta}\left(\cdot | x, y_{<t}\right) | \pi_{teacher }\left(\cdot | c, x, y_{<t}\right)\right) \\ = & \sum_{y_{t}' \in \mathcal{V}} \pi_{\theta}\left(y_{t}' | x, y_{<t}\right)\left(log \pi_{\theta}\left(y_{t}' | x, y_{<t}\right)-log \pi_{teacher }\left(y_{t}' | c, x, y_{<t}\right)\right) \end{aligned}=DKL(πθ(⋅∣x,y<t)∣πteacher(⋅∣c,x,y<t))yt′∈V∑πθ(yt′∣x,y<t)(logπθ(yt′∣x,y<t)−logπteacher(yt′∣c,x,y<t))
这里还有个工程上的小技巧:论文里不是对全词表计算,而是只取学生预测的top-k个token来算,大大降低了算力开销,普通人也能复现。
这两个创新,到底好在哪?
第一,on-policy采样,完美解决曝光偏差。
学生训练的时候走的路,就是推理的时候会走的路。它不是在学老师给的标准答案,而是在自己生成的每一步里,学习老师的正确决策。
第二,反向KL散度,解决幻觉和输出散乱的问题。
反向KL是模式寻找,不是模式覆盖。它只会逼着学生去聚焦老师觉得高概率的token,老师觉得概率低的内容,学生直接忽略就行。
举个例子,老师说"今天天气很好"这句话里,"很"后面接"好"的概率是99%,接"差"的概率是1%。反向KL只会让学生学好"好"这个高概率的token,不会逼着学生去学那个1%的"差"。
而之前的前向KL,会逼着学生把这两个都学了,学生学不好就会乱输出,一会儿好一会儿差,自然就有幻觉了。
OPCD到底有多牛?看实验结果说话
论文里做了两大方向的实验,全是我们平时能用得上的场景,效果直接拉满,我一个个给大家说。
场景一:经验知识蒸馏------让大模型把自己的解题经验,刻进参数里
这个场景让大模型自己做题,从做过的题里提炼通用经验,然后把这些经验直接内化到自己的参数里,越做越强,以后不用带超长的经验笔记,也能用上这些技巧。
论文里把这个过程分成了三步:
- 经验提取:给模型一堆题,让它自己生成解题轨迹,然后让它自己从轨迹里提炼出通用的、可迁移的经验,比如数学里的"模运算可以找周期性,简化大数计算";
- 经验积累:把不同题目里提炼的经验拼起来,形成一个完整的经验上下文c;
- 经验固化:用OPCD把这个经验上下文c,内化到学生模型的参数里。
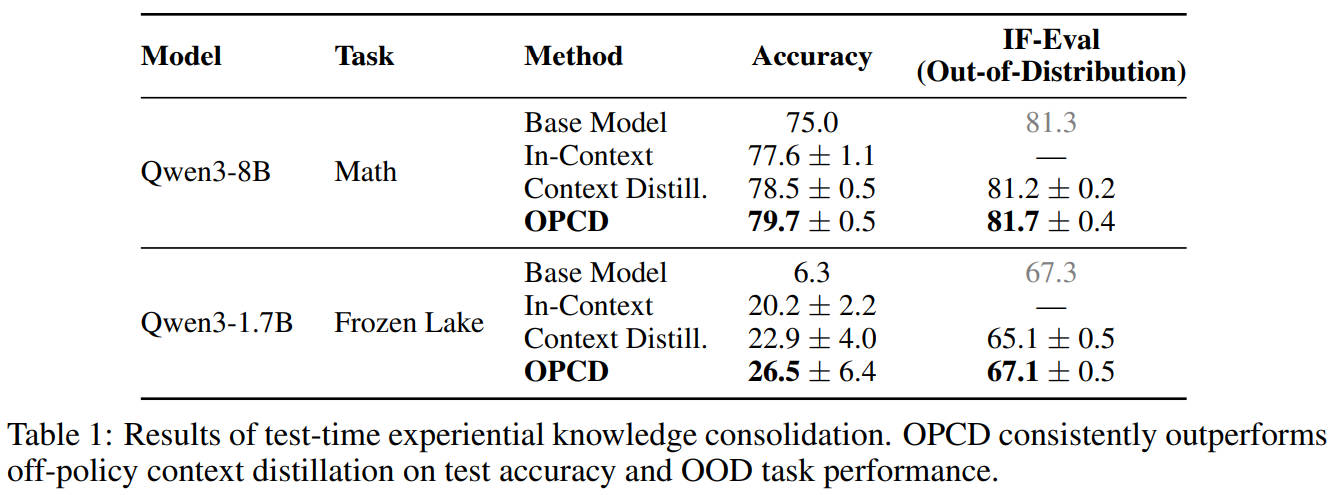
在Qwen3-8B的数学题任务里,基础模型准确率只有75.0;把经验放上下文里,准确率涨到77.6;用传统的上下文蒸馏,涨到78.5;而OPCD直接干到了79.7!
更能体现 OPCD 优势的是分布外(OOD)通用能力的保留:在 Frozen Lake 文本游戏任务上,传统蒸馏把模型本来的 OOD 能力从 67.3 掉到了 65.1,而 OPCD 还保持在 67.1,几乎和基础模型一模一样,完全没忘掉原来的指令遵循能力。
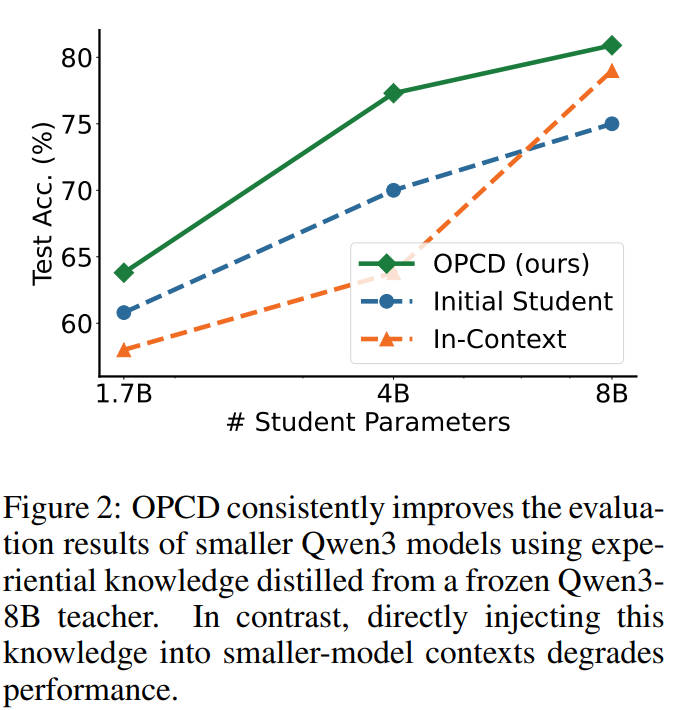
还有一个颠覆认知的结果,就是跨模型大小的蒸馏。
论文里用Qwen3-8B当老师,攒了经验,然后分别给1.7B、4B、8B的学生模型做蒸馏。
结果发现:直接把老师的经验上下文塞给1.7B和4B的小模型,它们的准确率反而掉了,完全水土不服。
但是用OPCD蒸馏之后,1.7B、4B、8B的模型,准确率全涨了!
这就说明,OPCD能让小模型完美继承大模型的经验,不会出现"大模型的笔记,小模型看不懂"的情况,以后小模型也能轻松用上大模型攒的经验了。
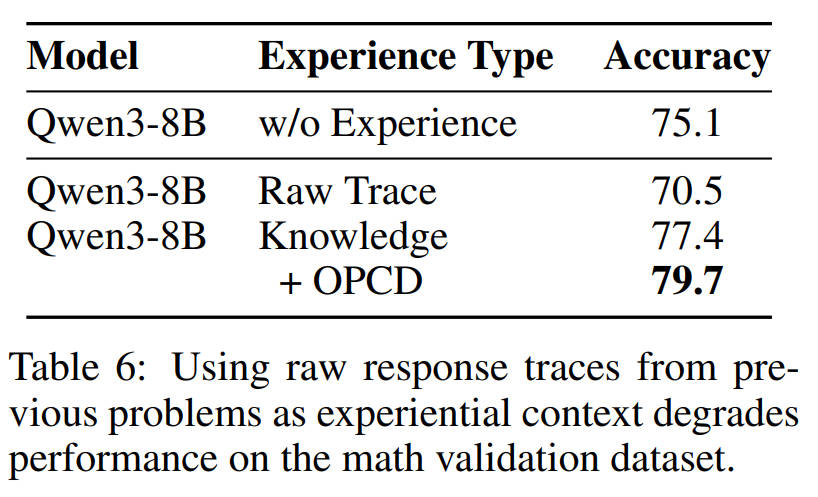
还有个很重要结论:随便堆解题轨迹无法有效提升效果。
直接把原始的解题轨迹当上下文,模型准确率从75.1掉到70.5,反而变差了;但是把轨迹提炼成通用的经验知识点之后,准确率涨到77.4;再用OPCD固化,直接干到79.7。
这说明,先提炼通用经验,再用OPCD固化,才是让大模型持续进化的正确路径。
场景二:系统提示蒸馏------把系统提示焊进模型里,彻底告别提示词依赖
这个场景大家天天都在用:比如给大模型写个安全审核的系统提示,让它精准识别违规内容。但每次推理都要带这个系统提示,长了不仅占窗口,还费钱费时间。
用OPCD,直接把这个系统提示的能力,内化到模型的参数里,以后推理不用带任何系统提示,也能有一模一样的效果。
我们直接看实验结果:
Llama-3.1-8B-Instruct,基础模型准确率68.4;带系统提示72.2;传统蒸馏75.2;OPCD直接干到76.7,全面领先。
最夸张的是Llama-3.2-3B这个小模型,基础模型准确率只有59.4;带系统提示66.4;传统蒸馏71.0;OPCD直接干到76.3,比基础模型涨了快17个点,直接把小模型的能力拉上了一个大台阶。
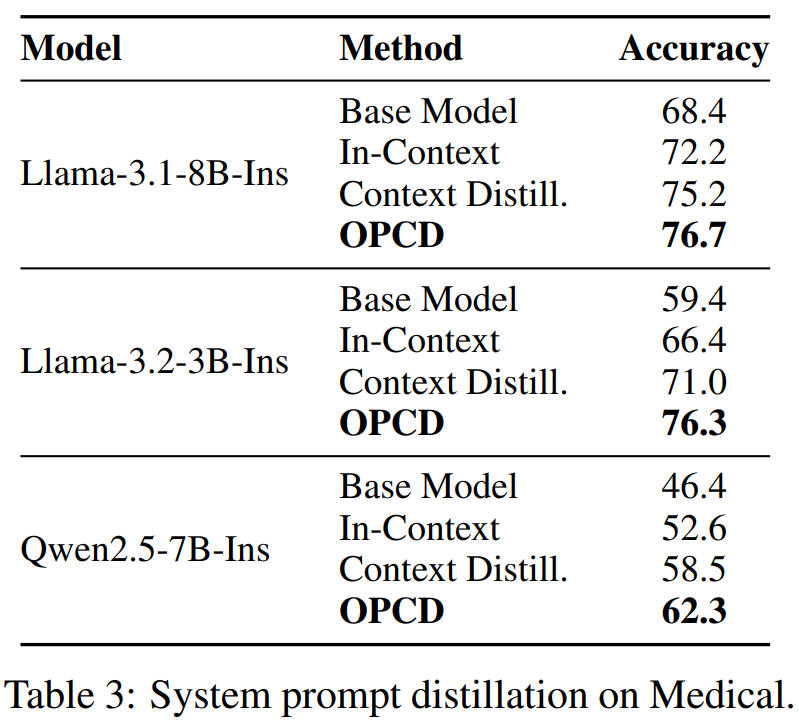
再看安全任务上的效果:
Llama-3.1-8B,基础模型70.7;带系统提示75.3;传统蒸馏77.2;OPCD直接79.6,又是全面碾压。
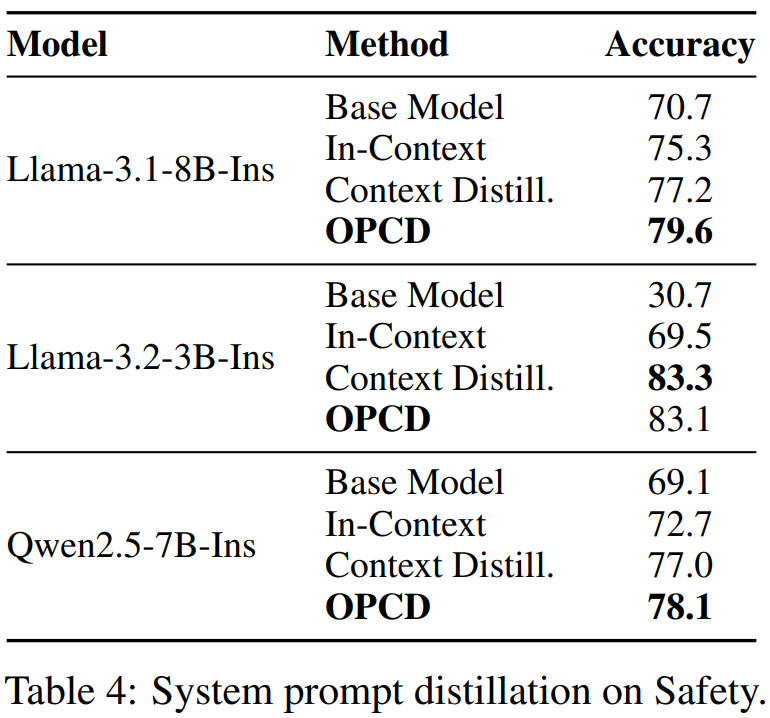
OPCD的王炸能力:缓解灾难性遗忘
大家都知道,模型微调之后,很容易出现"学了新的,忘了旧的",也就是灾难性遗忘,尤其是分布外的任务,能力掉的特别厉害。
那OPCD在这方面表现怎么样?
论文里做了个实验:用安全系统提示做蒸馏,下图左边是安全任务(分布内)的准确率,OPCD比传统蒸馏涨的更多;下图右边是医疗任务(分布外)的准确率,传统蒸馏直接掉了一大截,而OPCD几乎和初始模型持平,比传统蒸馏高了4个点左右。
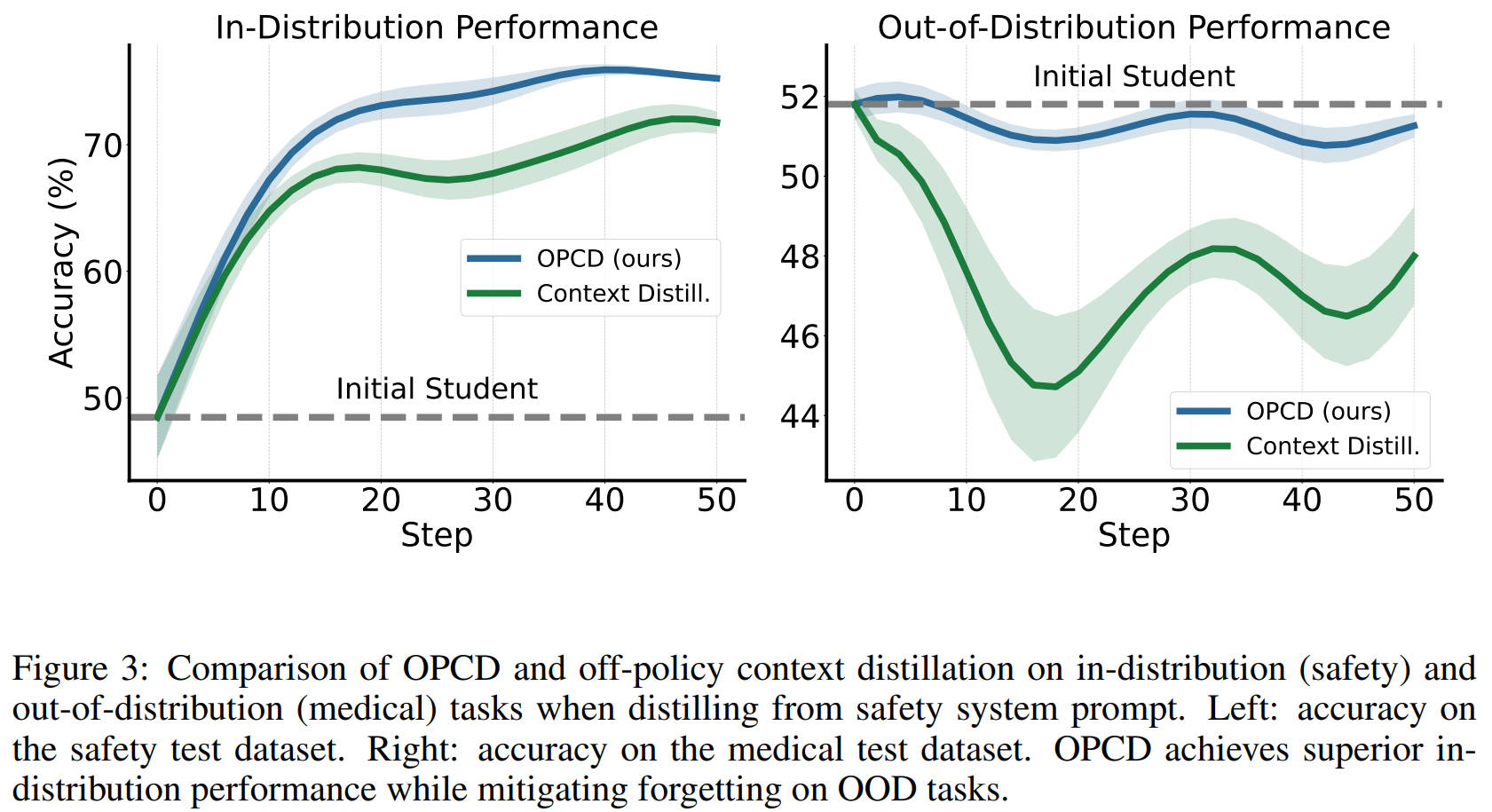
这就意味着,用OPCD给模型加新能力的时候,几乎不会影响它本来的能力,不会出现"学了安全审核,就不会答医学题了"的情况,这在实际落地里,简直是刚需。
还有,论文里还对比了师生蒸馏和自蒸馏。
师生蒸馏就是老师模型冻住,只更新学生;自蒸馏就是老师和学生是同一个模型,同时更新。
结果发现,师生蒸馏的效果比自蒸馏好太多:Sokoban任务里,自蒸馏只有18.8的准确率,师生蒸馏直接53.9;医疗任务里,自蒸馏50.0,师生蒸馏56.8。而且师生蒸馏训练更稳定,自蒸馏很容易训崩。
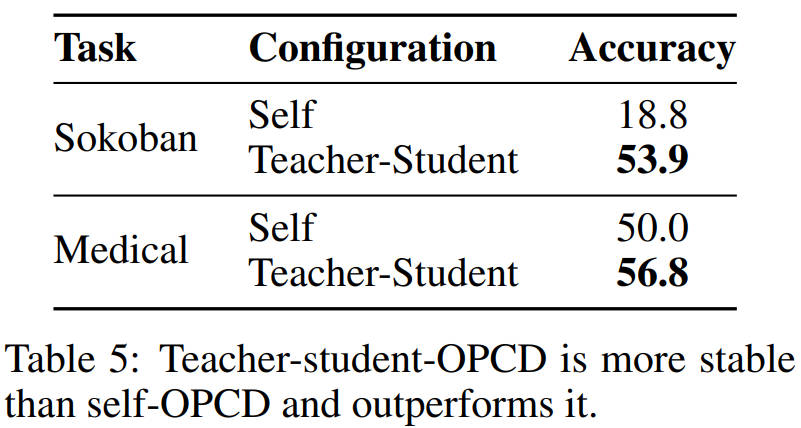
最后总结:OPCD到底带来了什么?
这篇论文不是搞了个花里胡哨的新架构,而是精准命中了上下文蒸馏的核心痛点,把on-policy蒸馏和上下文蒸馏完美结合,真正实现了让大模型把临时的上下文知识,变成永久的模型能力。
最后我想说,这篇论文最让我觉得有用的,是它打开了大模型持续进化的新路径:以后大模型不用每次都靠海量的标注数据微调,也不用靠超长的上下文提示词,它可以自己在使用中积累经验,把经验固化到参数里,越用越强,真正像人一样,在实践中持续学习、持续成长。