第十章-数论初步

除法表达式问题

给定一个除法表达式

x1x2/x3/.../xnx2/x3/.../xnx1

也就是

x1/x2/x3/.../xnx1/x2/x3/.../xn

（这里的除法是数学除法，不是整除）

你可以加任意括号来改变运算顺序，问最终能否使表达式的结果为整数。

解：

理解括号的作用

不加括号时，计算顺序从左到右：

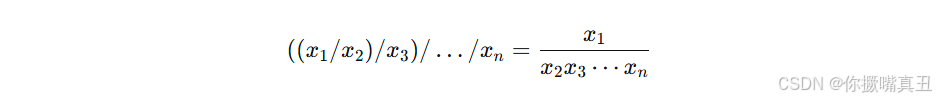
加上括号可以改变哪些数在分子、哪些数在分母。

例如：

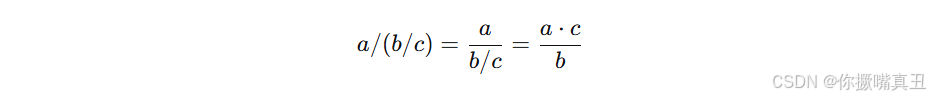
这样 c 从分母移到了分子。

一般规律

经过分析，在任意加括号的情况下：

x1x1 永远在分子
x2x2 永远在分母
x3,x4,...,xnx3,x4,...,xn 中的每一个都可以自由选择留在分母或移到分子

所以最终表达式一定形如：

变成整除条件

要使结果为整数，分母必须能整除分子。

为了让分子尽可能大（从而更容易整除），我们应该把所有 x3,...,xnx3,...,xn 都移到分子。

这时：

因此整数条件简化为：

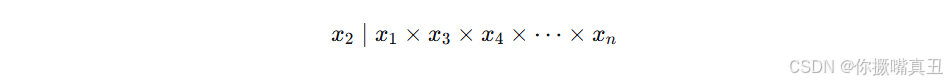
结论

最终判定条件：

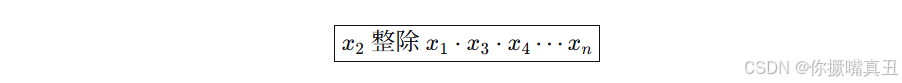
即 x2 的所有质因子都出现在 x1,x3,...,xn 的乘积中。

如果成立，就可以通过加括号得到整数结果；如果不成立，则无论怎样加括号，结果都不可能是整数。

例子

8/4/28/4/2

检查 4∣8×24∣8×2？ 4 整除 16 --- 可以整数（例：8/(4/2)=48/(4/2)=4）

3/2/53/2/5

检查 2∣3×52∣3×5？ 2 不整除 15 --- 无法整数

6/4/36/4/3

检查 4∣6×34∣6×3？ 4 不整除 18 --- 无法整数

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

// 计算最大公约数
long long gcd(long long a, long long b) {
    while (b) {
        long long temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

// 判断除法表达式能否通过加括号得到整数
bool canBeInteger(const vector<long long>& nums) {
    int n = nums.size();
    if (n == 1) return true;  // 只有一个数，本身就是整数
    if (n == 2) return (nums[0] % nums[1] == 0);  // x1/x2
    
    // 取 x2
    long long denominator = nums[1];
    
    // 计算 x1 * x3 * x4 * ... * xn
    long long numerator_product = nums[0];
    for (int i = 2; i < n; i++) {
        numerator_product *= nums[i];
    }
    
    // 检查 denominator 是否能整除 numerator_product
    // 为了避免大数溢出，用 gcd 逐步约分
    long long g = gcd(denominator, numerator_product);
    denominator /= g;
    
    return denominator == 1;
}

int main() {
    int n;
    cout << "请输入数字个数: ";
    cin >> n;
    
    vector<long long> nums(n);
    cout << "请输入 " << n << " 个整数: ";
    for (int i = 0; i < n; i++) {
        cin >> nums[i];
    }
    
    if (canBeInteger(nums)) {
        cout << "可以通垬加括号得到整数" << endl;
    } else {
        cout << "无法通过加括号得到整数" << endl;
    }
    
    return 0;
}

例题--10-3 UVA10375 "Choose and Divide

计算：

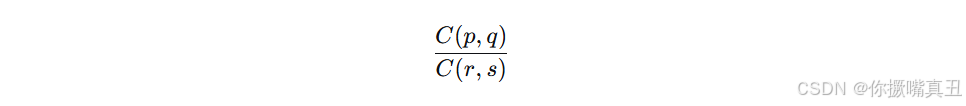
其中组合数定义为：

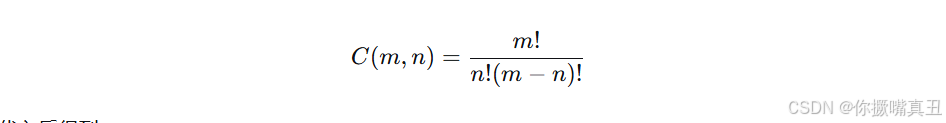
边乘边除:

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int p, q, r, s;
    while (cin >> p >> q >> r >> s) {
        // 优化：取较小的n值，减少计算量
        q = min(q, p - q);
        s = min(s, r - s);
        
        double ans = 1.0;
        for (int i = 1; i <= q || i <= s; i++) {
            if (i <= q) ans = ans * (p - q + i) / i;      // 乘分子项
            if (i <= s) ans = ans / (r - s + i) * i;      // 除分母项
        }
        
        printf("%.5lf\n", ans);
    }
    return 0;
}