直接法 读书笔记 06 第6章 LU分解

第6章 LU分解

在本文介绍的三种分解方法（Cholesky、QR和LU）中，LU分解是最古老的。作为一种分解方法，它将矩阵 分解为乘积，其中 是下三角矩阵， 是上三角矩阵。历史上用于稠密矩阵的方法是right-looking方法（高斯消元法）；本文同时介绍这种方法与left-looking方法。后者在CSparse中使用，因为它导致稀疏情况下的实现要简单得多。

6.1 填充的上界

描述Cholesky因子填充图的理论4.1，如果假设A是方阵且不发生主元选择，也适用于 的有向图。然而，更有用的分析考虑的是带有行交换的partial pivoting，这基于矩阵LU分解与QR分解之间的一个重要关系。考虑 和 ，其中P由partial pivoting决定。

理论6.1 (George and Ng [97], Gilbert [101], and Gilbert and Ng [106]) 。如果矩阵 是strong Hall 矩阵，则 是 的非零模式的上界。更精确地说， 非零当且仅当 。

这个上界在逐一的意义上是紧的；对于任何，都存在一个对 模式中条目的数值赋值，使得 。证明的概要可以通过比较高斯消元法和Householder反射看出。两者都消去对角线以下的条目。对于Householder反射，受变换影响的所有行的非零模式呈现出这些行的并集的非零模式（理论5.2）。通过partial pivoting和行交换，这些行是候选主元行（所有满足 或 的行）。其中只有一个被选为主元行。每一个其他候选主元行都通过向其加上主元行的缩放副本来修改。主元行模式的上界是所有候选主元行的并集。这个证明也建立了 的上界，即 的非零模式。

理论6.2 (Gilbert [101] and Gilbert and Ng [106]) 。如果矩阵 是strong Hall矩阵，并且假设对所有， ，则Householder矩阵 是通过partial pivoting获得的 的非零模式的上界。更精确地说，非零当且仅当 。

利用这种关系，符号QR排序和分析成为为LU分解对矩阵进行排序的一种可行方法。也可以静态地为 和 预分配空间。然而，这个上界可能是宽松的。特别是，如果矩阵是对角占优的，则不需要主元选择来保持数值精度。如果它还具有对称的非零模式（或者如果 模式中的所有条目都被认为是"非零"），则 和 的非零模式分别与具有与 相同非零模式的对称正定矩阵的 Cholesky 因子 和 的模式相同。在这种情况下，对 进行对称填充减少排序是合适的。或者，可以选择置换矩阵 以减少任何 下 的最坏情况填充，然后可以仅基于partial pivoting来选择置换 ，而不考虑稀疏性。因此，cs_sqr函数提供了四种基本策略来寻找减少填充的置换。

• order=0 : 不使用列置换；。如果已知A已经具有良好的列排序，这很有用。

• order=1 : 列置换 是从 的减少填充排序中找到的。在分解过程中，试图确保（优先选择 的对角线条目作为主元）。这种策略非常适合实践中出现的许多非对称矩阵，这些矩阵具有大致对称的非零结构和合理大的对角线条目。

• order=2 : 是从 的减少填充排序中获得的，其中 ，但移除了 中"稠密"行的所有条目。 中条目数超过启发式阈值的行被认为是稠密的。通过partial pivoting，（乐观地）希望这些行直到分解非常晚的时候才被选为主元行。

• order=3 : 是从 的排序中获得的，不丢弃稠密行。在这种情况下，排序试图减少理论6.1和6.2中给出的 和 的 上界。

如果cs_sqr的qr参数为真，则为置换矩阵 找到QR 上界（这里， 是列置换，而不是正交因子 ）。在这种情况下，LU分解可以使用静态分配的内存空间进行。然而，这个上界可能相当高（比较上界与实际 和 留作练习）。有时最好是猜测最终的 和，或者猜测不需要partial pivoting并使用符号Cholesky分析来确定对 和 的猜测（这留作练习）。有时可以从同一应用中相似矩阵的LU分解中获得一个好的猜测。如果 q r为假，cs_sqr会做出一个乐观的猜测，即 。这个猜测适用于某些矩阵，但对其他矩阵来说太低。调用cs_sqr后，可以轻松地根据需要修改猜测 S->lnz 和 S->unz 。做出错误猜测的唯一惩罚是，如果猜测太低，则必须重新分配 或 的内存空间，或者如果猜测太高，内存可能会耗尽。

6.2 Left-looking LU

Left-looking LU分解算法一次计算 和 的一列。在第 步，它访问L的第 1 到 列和 的第 列。如果忽略partial pivoting，它可以从下面的 3x3 块矩阵表达式中推导出来，这与left-looking Cholesky分解算法的(4.6)非常相似。假设 具有单位对角线。

(6.1)

每个矩阵的中间行和列分别是 、 和 的第 行和列。如果已知 和 的前 列，可以使用三个方程推导 和 的第 列： 是一个三角系统，可以求解 （ 的第 列）； 可以求解主元条目 ；然后 可以求解（ 的第 列）。然而，这三个方程可以重新排列，使得几乎所有方程都通过求解单个三角系统给出：

(6.2)

该系统的解给出 ，，以及 。该算法在 MATLAB 函数 lu_left中表达，除了添加了带行交换的partial pivoting。它返回L、U和P，使得 L*U = P*A 。它不利用稀疏性。

function [L,U,P] = lu_left (A)
n = size (A,1) ;
P = eye (n) ;
L = zeros (n) ;
U = zeros (n) ;
for k = 1:n
    x = [ L(:,1:k-1) [ zeros(k-1,n-k+1) ; eye(n-k+1) ]] \ (P * A (:,k)) ;
    U (1:k-1,k) = x (1:k-1) ;                       % the column of U
    [a i] = max (abs (x (k:n))) ;                   % find the pivot row i
    i = i + k - 1 ;
    L ([i k],:) = L ([k i], :) ;
    P ([i k],:) = P ([k i], :) ;
    x ([i k]) = x ([k i]) ;
    U (k,k) = x (k) ;
    L (k,k) = 1 ;
    L (k+1:n,k) = x (k+1:n) / x (k) ;               % divide the pivot column by U(k,k)
end

不包含关于partial pivoting如何在left-looking算法中工作的推导。下一节将在right-looking上下文中给出将行置换应用 于 L 的行的正确性证明。

直接实现lu_left的稀疏版本会很困难，因为它在第k步交换L的行i和k。访问L的行并不简单。cs_lu函数不是交换L的行，而是将L中的行索引保留在其原始顺序中。也就是说，L中的行索引i对应于原始未置换矩阵A中的同一行。每一步都使用稀疏三角求解cs_spsolve来求解(6.2)。它使用逆行置换pinv来执行置换的三角求解（L的列处于最终顺序，但L的行未被置换）。然后，当分解完成时，可以更新L的所有行索引以反映最终的行置换。

给定一个减少填充的列排序q，cs_lu计算L、U和pinv，使得L*U = A(p,q)（其中p是pinv的逆）。(6.2)中的单位矩阵被隐式地维护。对于一个非主元行索引i，jnew=pinv[i] = -1，当执行稀疏三角求解时，跳过该列jnew。

csn *cs_lu (const cs *A, const css *S, double tol)
{
    cs *L, *U ;
    csn *N ;
    double pivot, *Lx, *Ux, *x, a, t ;
    int *Lp, *Li, *Up, *Ui, *pinv, *xi, *q, n, ipiv, k, top, p, i, col, lnz,unz;
    if (!CS_CSC (A) || !S) return (NULL) ;                      /* check inputs */
    n = A->n ;
    q = S->q ; lnz = S->lnz ; unz = S->unz ;
    x = cs_malloc (n, sizeof (double)) ;                        /* get double workspace */
    xi = cs_malloc (2*n, sizeof (int)) ;                        /* get int workspace */
    N = cs_calloc (1, sizeof (csn)) ;                           /* allocate result */
    if (!x || !xi || !N) return (cs_ndone (N, NULL, xi, x, 0)) ;
    N->L = L = cs_spalloc (n, n, lnz, 1, 0) ;                   /* allocate result L */
    N->U = U = cs_spalloc (n, n, unz, 1, 0) ;                   /* allocate result U */
    N->pinv = pinv = cs_malloc (n, sizeof (int)) ;              /* allocate result pinv */
    if (!L || !U || !pinv) return (cs_ndone (N, NULL, xi, x, 0)) ;
    Lp = L->p ; Up = U->p ;
    for (i = 0 ; i < n ; i++) x [i] = 0 ;                       /* clear workspace */
    for (i = 0 ; i < n ; i++) pinv [i] = -1 ;                   /* no rows pivotal yet */
    for (k = 0 ; k <= n ; k++) Lp [k] = 0 ;                     /* no cols of L yet */
    for (k = 0 ; k <= n ; k++) Up [k] = 0 ;                     /* no cols of U yet */
    lnz = unz = 0 ;
    for (k = 0 ; k < n ; k++)
    {
        /* --- Triangular solve --------------------------------------------- */
        Lp [k] = lnz ;                                          /* L(:,k) starts here */
        Up [k] = unz ;                                          /* U(:,k) starts here */
        if ((lnz + n > L->nzmax && !cs_sprealloc (L, 2*L->nzmax + n)) ||
            (unz + n > U->nzmax && !cs_sprealloc (U, 2*U->nzmax + n)))
        {
            return (cs_ndone (N, NULL, xi, x, 0)) ;
        }
        Li = L->i ; Lx = L->x ; Ui = U->i ; Ux = U->x ;
        col = q ? (q [k]) : k ;
        top = cs_spsolve (L, A, col, xi, x, pinv, 1) ;          /* x = L\A(:,col) */
        /* --- Find pivot --------------------------------------------------- */
        ipiv = -1 ;
        a = -1 ;
        for (p = top ; p < n ; p++)
        {
            i = xi [p] ;                                        /* x(i) is nonzero */
            if (pinv [i] < 0)                                   /* row i is not yet pivotal */
            {
                if ((t = fabs (x [i])) > a)
                {
                    a = t ;                                     /* largest pivot candidate so far */
                    ipiv = i ;
                }
            }
            else                                                /* x(i) is the entry U(pinv[i],k) */
            {
                Ui [unz] = pinv [i] ;
                Ux [unz++] = x [i] ;
            }
        }
        /* ipiv is the kth pivot row */
        if (ipiv == -1 || a <= 0) return (cs_ndone (N, NULL, xi, x, 0)) ;
        if (pinv [col] < 0 && fabs (x [col]) >= a*tol) ipiv = col ;
        /* --- Divide by pivot ---------------------------------------------- */
        pivot = x [ipiv] ;                                      /* the chosen pivot */
        Ui [unz] = k ;                                          /* last entry in U(:,k) is U(k,k) */
        Ux [unz++] = pivot ;
        pinv [ipiv] = k ;                                       /* ipiv is pivotal */
        Li [lnz] = ipiv ;                                       /* first entry in L(:,k) is L(k,k) = 1 */
        Lx [lnz++] = 1 ;
        for (p = top ; p < n ; p++)                             /* L(k+1:n,k) = x / pivot */
        {
            i = xi [p] ;
            if (pinv [i] < 0)                                   /* x(i) is an entry in L(:,k) */
            {
                Li [lnz] = i ;                                  /* save unpermuted row in L */
                Lx [lnz++] = x [i] / pivot ;                    /* scale pivot column */
            }
            x [i] = 0 ;                                         /* x [0..n-1] = 0 for next k */
        }
    }
    /* --- Finalize L and U ------------------------------------------------ */
    Lp [n] = lnz ;
    Up [n] = unz ;
    Li = L->i ;                                                 /* fix row indices of L for final pinv */
    for (p = 0 ; p < lnz ; p++) Li [p] = pinv [Li [p]] ;
    cs_sprealloc (L, 0) ;                                       /* remove extra space from L and U */
    cs_sprealloc (U, 0) ;
    return (cs_ndone (N, NULL, xi, x, 1)) ;                     /* success */
}

cs_lu函数的第一部分分配工作空间并从符号排序和分析中获取信息。L和U中非零元的数量未知；S->lnz和S->unz要么是从符号QR分解计算出的上界，要么只是一个猜测。

三角求解：for k循环的第k次迭代首先记录L和U的第k列的开始，然后如果空间可能不足，则重新分配这两个矩阵。接下来，求解三角系统(6.2)得到x。U不需要后置换，因为pinv [i]是明确定义的。

寻找主元 ：在主元列中找到最大的非主元条目。对应于已经是主元的行i的条目x[i]被直接复制到U中。如果没有找到非主元行索引i（ipiv为-1），则矩阵在结构上是秩亏损的。如果非主元行中的最大条目数值为零（a为零），则矩阵在数值上是秩亏损的。如果对角线条目（x[col]，其中col是的第k列， 是减少填充的列排序）与partial pivoting选择（x[ipiv]）相比足够大，则选择它。

除以主元：主元条目保存为U(k,k)，即U(:,k)中的最后一个条目，这是cs_usolve所要求的。单位对角线条目存储为L(:,k)中的第一个条目，这是cs_lsolve所要求的。注意，ipiv对应于A的行索引，而不是PA。

完成L和U：记录L和U的最后列指针，修复L的行索引以引用它们的置换顺序，并从L和U中移除任何额外空间。

该算法耗时 ，其中 是执行的浮点运算次数。这基本上是 ，除非（例如）A是对角矩阵。MATLAB对[L, U, P]=lu(A)语法使用上述算法（GPLU）。当A是稀疏的、方阵且不是对称正定时，它对[L, U, P, Q] = lu (A)和x=A\b使用right-looking多波前方法（UMFPACK）。

6.3 Right-looking和多波前LU

高斯消元法是LU分解的一种right-looking变体。CSparse中没有使用这种方法，但这里介绍它有两个原因：（1）它导致了对 分解存在的更简单的构造性证明，（2）它构成了UMFPACK的基础，UMFPACK是MATLAB中用于稀疏LU分解的多波前方法。

在每一步，主元列和主元行的外积被从 的右下子矩阵中减去。该方法的推导（忽略主元选择）从一个与right-looking Cholesky分解的(4.7)非常相似的方程开始，

(6.3)

其中 是一个标量，所有三个矩阵都是方阵并且划分相同。其他 选择也是可能的；这种选择导致单位下三角矩阵 和四个方程：

(6.4)

(6.5)

(6.6)
(6.7)

依次求解每个方程导致递归的lu_rightr，用MATLAB编写如下。此函数旨在作为算法的可工作描述，而不是高效实现。

function [L,U] = lu_rightr (A)
n = size (A,1) ;
if (n == 1)
    L = 1 ;
    U = A ;
else
    u11 = A (1,1) ;                             % (6.4)
    u12 = A (1,2:n) ;                            % (6.5)
    l21 = A (2:n,1) / u11 ;                      % (6.6)
    [L22,U22] = lu_rightr (A (2:n,2:n) - l21*u12) ; % (6.7)
    L = [ 1 zeros(1,n-1) ; l21 L22 ] ;
    U = [ u11 u12 ; zeros(n-1,1) U22 ] ;
end

lu_rightr函数使用尾递归，其中递归调用是最后一步（循环的最后两行不做任何工作；它们只是通过(6.4)到(6.7)定义计算的L和U的内容）。尾递归可以很容易地转换为迭代算法，如lu_right函数所示。这通常是right-looking LU分解算法的编写方式，除了在稠密情况下，A通常会被L和U覆盖。

function [L,U] = lu_right (A)
n = size (A,1) ;
L = eye (n) ;
U = zeros (n) ;
for k = 1:n
    U (k,k:n) = A (k,k:n) ;                      % (6.4) and (6.5)
    L (k+1:n,k) = A (k+1:n,k) / U (k,k) ;        % (6.6)
    A (k+1:n,k+1:n) = A (k+1:n,k+1:n) - L (k+1:n,k) * U (k,k+1:n) ; % (6.7)
end

上面的推导是对 分解存在的归纳证明，基本情况为(6.4)，归纳假设来自(6.7)，

(6.8)

仅当每个对角线条目Ukk非零时，分解 才存在。

Partial pivoting导致更稳定的变体，，其中 是置换矩阵。通过partial pivoting，交换A的行，使得每一步的 最大化。这种交换可以针对 的第一列确定，递归将构造 的剩余置换。设 是交换 的两行使得

和 的置换矩阵。如果(6.3)及其在(6.4)到(6.7)中的等价形式直接用于 ，则不能使用归纳假设(6.8)。如果正在证明的陈述是 ，则归纳假设必须应用于具有相同形式的较小维度的矩阵；(6.8)没有置换矩阵。必须改为使用归纳假设

(6.9)

其中P2是一个置换矩阵。为了利用这一点，可以通过将(6.4)到(6.7)应用于 并将(6.6)的两边乘以，将表达式(6.9)合并到一个2x2块矩阵表达式中，得到：

(6.10)

(6.11)

(6.12)

(6.13)

这四个方程可以写成2x2矩阵表达式

(6.14)

方程(6.14)是期望的形式 ，其中

这个归纳推导由下面的lu_rightpr函数演示。它不是一个尾递归过程，因为在递归调用完成后必须将应用于 ，并且也必须构造 。这些置换可以推迟并在分解完成时应用；这就是cs_lu函数所做的。对于稠密矩阵分解，访问 的行要简单得多，并且可以立即应用置换，就像lu_left所做的那样。任一方法都导致相同的 分解。在用非递归实现替换lu_rightpr中的递归并允许用其LU分解覆盖A之后，获得了常规的高斯消元外积形式，如下面的lu_rightp函数所示。

function [L,U,P] = lu_rightpr (A)
n = size (A,1) ;
if (n == 1)
    P = 1 ;
    L = 1 ;
    U = A ;
else
    [x,i] = max (abs (A (1:n,1))) ;              % partial pivoting
    P1 = eye (n) ;
    P1 ([1 i],:) = P1 ([i 1], :) ;
    A = P1*A ;
    u11 = A (1,1) ;                               % (6.10)
    u12 = A (1,2:n) ;                              % (6.11)
    l21 = A (2:n,1) / u11 ;                        % (6.12)
    [L22,U22,P2] = lu_rightpr (A (2:n,2:n) - l21*u12) ; % (6.9) or (6.13)
    o = zeros(1,n-1) ;
    L = [ 1 o ; P2*l21 L22 ] ;                     % (6.14)
    U = [ u11 u12 ; o' U22 ] ;
    P = [ 1 o ; o' P2] * P1 ;
end

function [L,U,P] = lu_rightp (A)
n = size (A,1) ;
P = eye (n) ;
for k = 1:n
    [x,i] = max (abs (A (k:n,k))) ;               % partial pivoting
    i = i + k - 1 ;
    P ([k i],:) = P ([i k], :) ;
    A ([k i],:) = A ([i k], :) ;
    A (k+1:n,k) = A (k+1:n,k) / A (k,k) ;         % (6.10), (6.11)
    A (k+1:n,k+1:n) = A (k+1:n,k+1:n) - A (k+1:n,k) * A (k,k+1:n) ; % (6.12)
end
L = tril (A,-1) + eye (n) ;
U = triu (A) ;

Right-looking稀疏LU分解比left-looking算法复杂得多。它构成了稀疏LU分解的多波前方法的基础。首先考虑 的非零模式对称的情况。考虑一个非对称矩阵，其对称非零模式与图4.2和图6.1中所示的矩阵相同，其中 和 因子显示为一个矩阵。假设没有发生数值主元选择。消去树中的每个节点对应一个前向矩阵，它持有一个秩-1外积。节点k的前向矩阵是一个 的稠密矩阵。如果父节点 及其单个子节点 具有相同的非零模式（），则它们可以合并（合并）成一个代表它们两者的更大的前向矩阵。

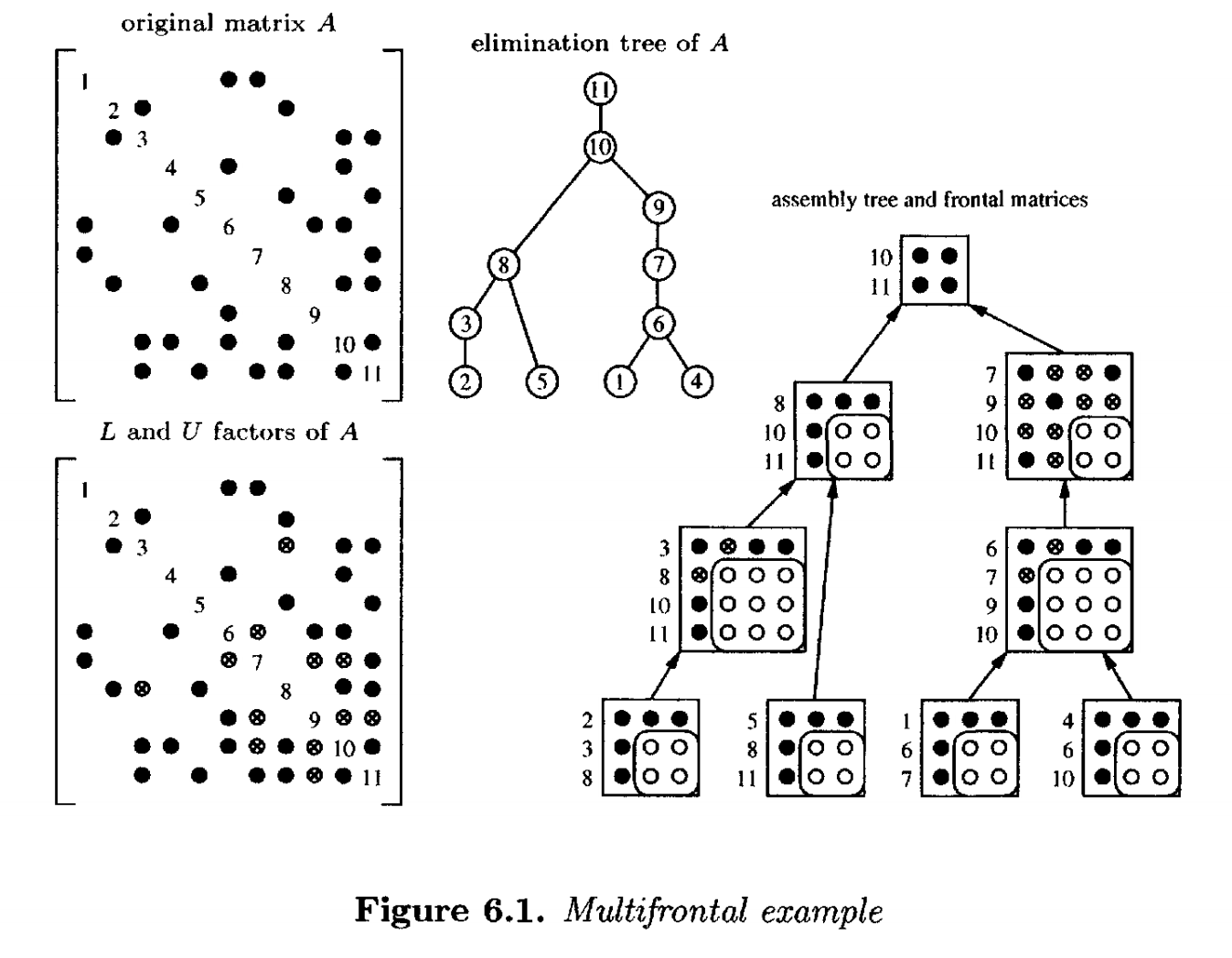
前向矩阵通过组装树相互关联，组装树是消去树的粗略版本（一些节点通过合并合并在一起）。为了分解一个前向矩阵，添加A的原始条目，以及其子节点的贡献块的求和（称为组装）。在前向矩阵内执行一步或多步稠密LU分解，留下其贡献块（其主元行和列的Schur补）。使用稠密矩阵内核（BLAS）可以获得高性能。贡献块被放置在堆栈上，并在组装到其父节点时被删除。

图6.1显示了一个例子。黑圈代表A的原始条目。带圈的x代表填充条目。白圈代表每个前向矩阵贡献块中的条目。前向矩阵之间的箭头代表了数据流和组装树的父子关系。

符号分析阶段确定消去树和合并后的组装树。在数值分解期间，可能需要数值主元选择。在这种情况下，可能可以在前向矩阵的完全组装的行和列内进行主元选择。例如，考虑图6.1中包含对角线元素 和 的前向矩阵。如果 在数值上不可接受，则可以选择 和 作为接下来的两个主元条目。如果这不可行，前向矩阵7的贡献块将比预期的大。这个更大的前向矩阵被组装到其父节点中，导致父前向矩阵比预期的大。在父节点内，最初分配给父节点的所有主元和来自子节点（或任何后代）的所有失败主元构成主元候选集。如果所有这些在数值上都是可接受的，则父贡献块的大小与符号分析预期的大小相同。

如果A的非零模式是非对称的，前向矩阵变成矩形。它们通过列消去树（的消去树）或有向无环图相关联。图6.2显示了一个例子。这与图5.1中用于QR分解示例的矩阵相同。使用列消去树，可以容纳任意的partial pivoting，而无需对树进行任何更改。每个前向矩阵的大小受 的QR分解的Householder更新的大小的限制（第 个前向矩阵的大小最多为 ），无论任何partial pivoting如何。在图6.2的LU因子中， 的原始条目显示为黑圈。当没有发生partial pivoting时的填充条目显示为带圈的 。白圈表示可能由于partial pivoting而变成填充的条目。在这个小例子中，它们都碰巧出现在 中，但一般来说它们可以出现在 和 中。可以像对称模式情况一样进行合并；在图6.2中，节点5和6，以及节点7和8已经合并在一起。每个前向矩阵大小的上界足够大以容纳所有候选主元行，但通常不需要分配这个空间。

在图6.2中，组装树已被展开以说明每个前向矩阵。该树表示前向矩阵之间的关系，但不表示数据流。贡献块的组装不仅可以发生在父子之间，还可以发生在祖先和后代之间。例如，前向矩阵2对 的贡献可以包含到其父节点3中，但这需要向前向矩阵3添加一个额外的列。这个前向矩阵大小的上界是2x4，但如果没有发生partial pivoting，则只需要分配一个2x2的前向矩阵。不是扩大前向矩阵3以包含 条目，而是将该条目组装到祖先前向矩阵4中。因此，前向矩阵之间的数据流由有向无环图表示。

Right-looking方法相对于left-looking稀疏LU分解的一个优点是它可以选择一个稀疏的主元行。Left-looking方法不跟踪 子矩阵的非零模式，因此无法确定其主元行中的非零元数量。Right-looking方法的缺点是实现起来要困难得多。

当A是稀疏的并且要么是非对称的，要么是对称的但不是正定时，MATLAB在 x=A\b 中使用非对称模式多波前方法（UMFPACK）。它也用于[L,U,P,Q]=lu(A)。对于当A稀疏时的[L,U,P]=lu(A)语法，MATLAB使用GPLU，一种类似于cs_lu的left-looking稀疏LU分解。

6.4 进一步阅读

Rose和Tarjan [174]以及Rose，Tarjan和Lueker [175]描述了没有主元选择的 的填充图。Duff和Reid [61]的MA28是一种早期的right-looking稀疏LU分解方法。在[97]中，George和Ng展示了LU分解的非零模式受 的Cholesky分解的限制。符号LU分解的行合并模型是后续论文[98]的主题，该论文给出了更紧的界。cs_lu中使用的left-looking算法（GPLU）归功于Gilbert和Peierls [109]。Duff，Erisman和Reid的著作[53]深入详细地介绍了稀疏LU分解。Duff和Reid [62, 63]提出了用于对称模式非对称矩阵和对称不定矩阵的多波前方法。这些方法早于Davis [27, 28]，Davis和Duff [31, 32]的非对称模式多波前方法以及GPLU。Liu [152]总结了多波前方法，包括LU分解。Gilbert和Liu [103]引入了用于LU分解的消去DAG。Hadfield [122]讨论了消去DAG在非对称模式多波前方法中的使用。Eisenstat和Liu [74, 75]展示了如何通过对称剪枝减少left-looking LU分解中深度优先搜索的工作量，并为稀疏LU分解提供了消去树的理论。Gilbert和Ng [106]概述了确定LU和QR分解非零模式的方法。许多软件包可用于计算稀疏LU分解。它们在第8.6节中进行了总结。

一些稀疏LU分解软件包提供了组合的行和列预缩放和置换选项，例如Duff和Koster [57, 58]描述的方法。这增加了对角线条目的幅度，并增加了在完全没有partial pivoting的情况下计算准确分解的可能性。Li和Demmel [147]展示了静态主元选择在并行稀疏LU算法中特别有用[4, 5, 7, 118, 119, 147, 179, 180]。

练习

6.1. 使用cs_lu, cs_ltsolve和cs_utsolve求解 而不形成 。参见问题6.15的示例应用。

6.2. 减少cs_lu中工作空间xi的大小。注意在调用cs_sprealloc后，L和U都至少包含0个未使用空间。这个空间可以在修改后的cs_spsolve中用于pstack。还要注意L是单位对角线，这简化了cs_spsolve。

6.3. 在cs_lu中实现列主元选择。如果在列中没有找到主元，或者最大的主元候选低于给定容差，则将其置换到矩阵的末尾并尝试下一列。不要修改S->q。

6.4. 编写一个原型为void cs_relu (cs *A, csn *N, css *S)的函数，该函数计算A的LU分解。它应该假设L和U的非零模式已经在之前的cs_lu调用中计算过。A的非零模式应与之前调用cs_lu时相同。使用相同的主元置换。

6.5. 修改cs_lu，使其能够分解数值和结构上的秩亏损矩阵。

6.6. 修改cs_lu，使其能够分解矩形矩阵。

6.7. 推导一个在分解的第k步计算L的第k列和U的第k行的LU分解算法（Crout方法）。编写一个MATLAB原型，然后编写一个C函数，为稀疏矩阵A实现此分解。可选地包含partial pivoting。

6.8. 推导一个在分解的第k步计算L的第k行和U的第k列的LU分解算法。为什么向此算法添加partial pivoting很困难？

6.9. cs_lu的MATLAB接口通过双重转置对L和U进行排序。修改它，使其只需要对L进行一次转置，对U进行一次转置。提示：参见问题6.1。

6.10. 创建cs_slu，除了一个额外选项外，与cs_sqr相同：符号Cholesky分析，用于order=1的情况。将其用作S->lnz和S->unz的猜测。

6.11. 如果cs_sprealloc在cs_lu中失败，该函数只会停止并报告内存不足。然而，请求的内存空间远远超过可能需要的数量。实现一种方案，首先尝试2|L|+n（对于|L|，如当前cs_lu中）。如果失败，慢慢减少请求，直到请求成功或直到请求最小需求（|L|+n-k）失败。U的最小需求是|U|+k+1。此功能无法通过MATLAB mexFunction测试，因为如果mxRealloc失败，它将终止mexFunction。

6.12. 编写一个版本的lu_rightpr，它使用置换向量p而不是置换矩阵。

6.13. 不完全LU分解计算具有更少非零元的L和U的近似值。它作为迭代方法的预 conditioner 很有用。一种计算方法是丢弃计算过程中L和U中的小条目。另一种是使用固定的稀疏模式，例如A的非零模式。基于cs_lu编写一个不完全LU分解。最简单的方法是，当x中的条目被复制到L和U并且lnz和unz递增时，如果条目很小（U的x[i]或L的x[i]/pivot），则不存储它，也不递增相应的unz或lnz计数器。为了丢弃不出现在A中的条目，将A的第k列的模式散布到整数工作向量w中。当将条目存储到U或L中时，仅当w[i]等于amark时才存储该值。如果遇到数值或结构上的零主元，则将其替换为任意值（比如1），并选择一个任意的非主元行（最好是对角线）作为主元行。另请参见MATLAB的luinc函数。Saad [178] 提供了对用于迭代方法的不完全Cholesky和LU分解的详细研究。

6.14. 对称剪枝是一种可以减少计算稀疏三角求解Reach(B)时间的技术。如果 且 ，则计算Reach(B)时不需要L列j中行索引k > i的任何条目。修改cs_lu以利用对称剪枝。如果A具有对称模式并且没有发生partial pivoting，则结果是A的消去树。

6.15. 使用下面的Hager方法 [123] 在 C 中实现一个1-范数条件数估计器。另请参见Higham的实现 [134] 及其推广 [136]。这个问题是在分解 之后需要求解 的一个例子（问题6.1）。另请参见MATLAB中的condest和normest。

function c = cond1est (A) % estimate of 1-norm condition number of A
[m n] = size (A) ;
if (m ~= n | ~isreal (A))
    error ('A must be square and real') ;
end
if isempty(A)
    c = 0 ;
    return ;
end
[L,U,P,Q] = lu (A) ;
if (~isempty (find (abs (diag (U)) == 0)))
    c = Inf ;
else
    c = norm (A,1) * norm1est (L,U,P,Q) ;
end

function est = norm1est (L,U,P,Q) % 1-norm estimate of inv(A)
n = size (L,1) ;
for k = 1:5
    if (k == 1)
        est = 0 ;
        x = ones (n,1) / n ;
        jold = -1 ;
    else
        j = min (find (abs (x) == norm (x,inf))) ;
        if (j == jold) break, end ;
        x = zeros (n,1) ;
        x (j) = 1 ;
        jold = j ;
    end
    x = Q * (U \ (L \ (P*x))) ;                         % x = A\s or inv(A)*s
    est_old = est ;
    est = norm (x,1) ;
    if (k > 1 & est <= est_old) break, end
    s = ones (n,1) ;
    s (find (x < 0)) = -1 ;                             % selection vector s
    x = P' * (L' \ (U' \ (Q'*s))) ;                     % x = A'\s or inv(A')*s
end