牛客网刷算法的启发

文章目录

一、结论
二、示例
- [示例1 noob35](#示例1 noob35)
- [示例2 判断素数-noob31](#示例2 判断素数-noob31)
- [示例3 noob37 数位之和](#示例3 noob37 数位之和)

一、结论

一题多解，启发思路(变化思路，思维要灵活)
注重细节，简化计算
小题目蕴含大思想

详细解释下：

1、刷题过程除了自己先思考如何解题之外，解完之后看看讨论和题解，了解下别人的做法，开阔下思路。一道题可能有多种解法，优先选择靠近题目考察意图的解法；
2、比如目前刷到noob35，发现高斯公式这么写：(1+n)*(n/2) 好理解；但是编程的时候这么写：(1+n)*n/2 这样计算简单，可以避免奇偶数问题，简化计算。还有部分人员在计算素数的时候用到了n&1==1 判断奇数，这都是挺好的做法，可以借鉴。细节里体现了每个解题人的思想。
3、上一篇博客：卡拉兹函数。以及下面示例要介绍的素数的判断等，都体现了小题目包含大思想。认真对待每个小题目，尽可能挖掘有意思的思想，减少刷题的枯燥感，提升兴趣。

二、示例

示例1 noob35

比如：牛客网的算法学习篇-noob35这道题。

这道题本意应该是考察双重循环嵌套，我解题的时候并没有想到这么做,看了其他人的题解之后知道原来也可以这么做。我的做法如下：

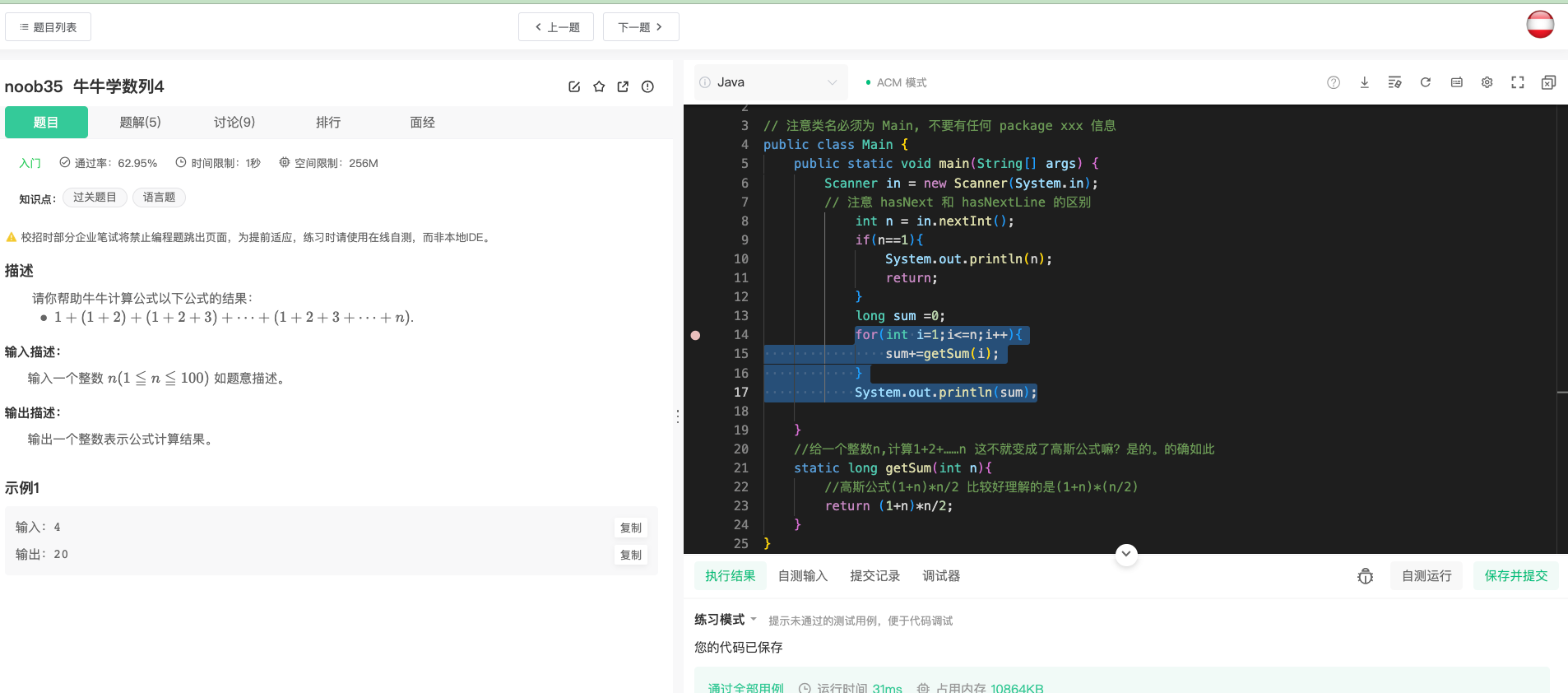
java 复制代码

   /**
     * 牛客网-noob35-牛牛学数列4
     * <p>
     * 计算以下公式结果
     * 1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)+...+(1+2+3+4+5+...+n)
     *
     * @param n
     * @return
     */
    static long nook35V1(int n) {
        //这是我的做法
        long sum = 0;
        for (int i = 1; i <= n; i++) {
            sum += getSum(i);
        }
        System.out.println(sum);
        return sum;
    }

    //给一个整数n,计算1+2+......n 这不就变成了高斯公式嘛？是的。的确如此
    static long getSum(int n) {
        //高斯公式(1+n)*n/2 比较好理解的是(1+n)*(n/2)
        return (long) (1 + n) * n / 2;
    }

以下是看了别人的题解后的做法：

java 复制代码

 static long nook35V2(int n){
        long sum = 0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                sum +=j;
            }
        }
        System.out.println(sum);
        return sum;
    }

示例2 判断素数-noob31

废话不多说，大家看判断一个数是否是素数的两种解法即可。

java 复制代码

/**
     * 判断是否是素数
     * 牛客网-noob31 素数判断
     * <p>
     * 素数：大于1且仅能被1和自身整除的正整数。
     * <p>
     * 算法复杂度 O(n-2)
     *
     * @param n
     * @return
     */
    static boolean isPrime(long n) {
        if (n == 1) {
            return false;
        }
        int i;
        for (i = 2; i < n; i++) {
            //找到一个因数就结束
            if (n % i == 0) {
                System.out.println("遍历次数：" + (i - 1));
                return false;
            }
        }
        System.out.println("遍历次数：" + (i - 1));
        return true;

        //总结：这个写法缺点是当数很大的时候，要遍历很多次，所以核心是优化遍历次数
        /**
         * 这种遍历缺点：
         * 1、当数很大的时候，要遍历很多次，所以核心是优化遍历次数,算法复杂度为：O(n-2);
         * 2、如果一个数就是素数，也需要全部遍历完才能判断出来。而"埃氏筛法"，提出只需筛到√n 即可找出所有素数
         */
    }

java 复制代码

 /**
     * 优化判断素数算法
     *
     * @param n
     * @return
     */
    static boolean isPrimeV2(long n) {
        if (n == 1) {
            return false;
        }
        //2是正整数里唯一的偶数素数，这也意味着其他能被2整数的数（偶数）自然都不是素数。
        if (n == 2) {
            return true;
        }
        //优化点1：排除所有的偶数，因为偶数必然能被2整数。
        // 这块如果有人刻意追求效率，也可以这么写：n &1 == 1 表明是奇数
        if (n % 2 == 0) {
            return false;
        }
        //优化点2： 遍历只用遍历到√num ，控制遍历上限。【核心】埃拉托斯特尼提出的："埃氏筛法"，提出只需筛到√n 即可找出所有素数
        //优化点3：控制步长，只用判断奇数是否是n的因素，再次减少数量。
        int i;
        for (i = 3; i <= Math.sqrt(n); i += 2) {
            if (n % i == 0) {
                return false;
            }
        }
        System.out.println("循环次数：" + (i - 3));
        return true;
    }

示例3 noob37 数位之和

这道题我开始的思路是：如何判断一个数有多少位呢？也想过通过%来取个位，但是百位、千位怎么取？问题是不知道这个数有多大，计算位数好像很麻烦......所以就放弃了取模的做法（这是一种最简单的做法）

其实这个时候应该多思考一下，那就是：一定要知道位数嘛？非要知道位数不可嘛？

大家看下我的做法：

思路：转字符串，通过split()方法拆分成数组，再遍历转换求和。

也能实现但是不太贴合题意。

java 复制代码

//我的做法

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
            int a = in.nextInt();
            if(a<0){
                a = Math.abs(a);
            }
            String str =String.valueOf(a);
            //变成String在拆成单个字母计算，没想到其他方法【后面看了其他解答方法，还是不断%个位简单】 不用知道这个数有多少位，通过这种方法拆分非常简洁。
            String [] strArray =str.split("");
            long sum = 0;
            for(String each :strArray){
               Long eachLong = Long.valueOf(each);
               sum+= eachLong;
            }
            System.out.println(sum);        
    }
}

网友的做法是这样的：

java 复制代码

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
            int a = in.nextInt();
            if(a<0){
                a = Math.abs(a);
            }
            long sum = 0;
            while(a!=0){
                int geWei =a%10;
                sum+=geWei;
                a=a/10;
            }
            System.out.println(sum);        
    }
}

看看人家网友的思路是多么的简洁！