动态规划-Dynamic Programing-DP

文章目录

一、背景
二、三种解法
三、对比下算法复杂度
四、扩展(应用场景)

一、背景

牛客网noob类的题里目前涉及动态规划思想的有noob36 牛牛学数列5- 斐波那契数列

、noob39 牛牛学数列6---f(n)=f(n−1)+2f(n−2)+f(n−3)，这个代表：的三阶线性递推模型。

这2个题目都可以通过多种做法实现，最优解就是动态规划dp解法。

这里用noob39来做示例。

题目如下：

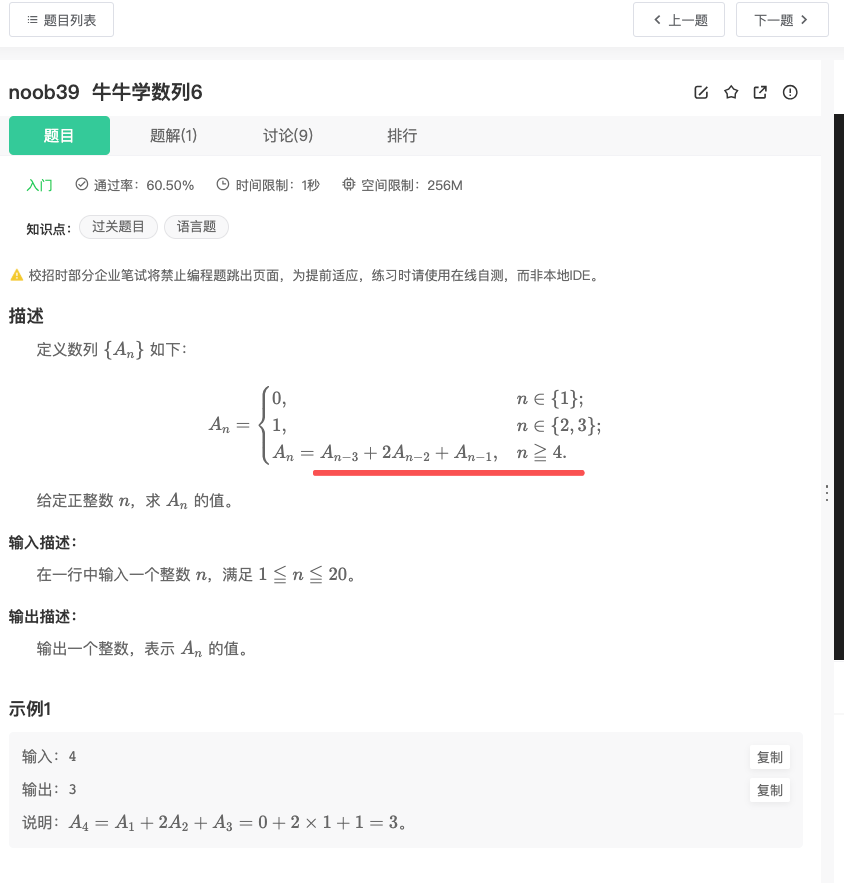
这里提供三种解法：

法1：暴力递归，算法时间复杂度O(3^n)

法2：递归+dp(自上而下) 时间复杂度O(n)

法3：迭代dp:自下而上时间复杂度O(n)

二、三种解法

代码：
gitee提交记录

直接git clone整个nkw项目即可。

java 复制代码

    /**
     * 法1：暴力递归
     * @param n
     * @return
     */
    static int getAnThreeRecursion(int n) {
        if (n == 1) {
            return 0;
        }
        if (n == 2 || n == 3) {
            return 1;
        }
        return getAnThreeRecursion(n - 3) + 2 * getAnThreeRecursion(n - 2) + getAnThreeRecursion(n - 1);
        /**
         * 总结：
         * 递归的问题在于每次要计算到底，存在大量重复计算
         * 比如:A15 =A12 +2*A13+A14
         * 那么：A17 = A13+ 2*A15 + A16
         * A13在计算A15的时候其实已经计算过了，但是在计算A17的时候还是会"递归到底(0 1 1)",当n很大这样浪费大量资源，且时间复杂度为 O(3^n),空间复杂度为：O(n)
         * 时间复杂度：衡量算法执行的总操作数（这里是递归调用的总次数）；
         * 空间复杂度的核心是递归调用栈的深度
         */
    }


    /**
     * 法2：递归+dp(自上而下)
     * @param n
     * @param dp
     * @return
     */
    static int getAnThreeRecursionV2Up2DownDp(int n, Integer[] dp) {
        if (n == 1) {
            return 0;
        }
        if (n == 2 || n == 3) {
            return 1;
        }
        //状态记忆（备忘录）
        if (dp[n - 1] != null) {
            System.out.println("进入了状态记忆备忘录, n的值是:" + n + " 备忘录的值是:" + dp[n - 1]);
            return dp[n - 1];
        }
        int An = getAnThreeRecursionV2Up2DownDp(n - 3, dp) + 2 * getAnThreeRecursionV2Up2DownDp(n - 2, dp) + getAnThreeRecursionV2Up2DownDp(n - 1, dp);
        dp[n - 1] = An;
        return An;
    }

    /**
     * 法3：迭代版dp-自下而上。
     * 【最优解法】
     * 迭代版本DP，无递归，效率略高于备忘录版本的递归
     *
     * @param n
     * @param dp
     * @return
     */
    static int getAnThreeNoRecursionDown2UpDp(int n) {
        if (n == 1) {
            return 0;
        }
        if (n == 2 || n == 3) {
            return 1;
        }
        int[] dp = new int[n];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for (int i = 4; i <= n; i++) {
            //这里要注意 数组下标和计算实际的前三个数的关系，不要搞混淆了。 当然为了更好的和公式对应，我们数组就不要从0开始，从1开始就可以很好的对应起来。
            dp[i - 1] = dp[i - 4] + 2 * dp[i - 3] + dp[i - 2];
        }
        System.out.println("无递归版本迭代DP结果是：" + JSON.toJSONString(dp));
        return dp[n - 1];
    }

看下测试结果：

java 复制代码

  //        noob39(17); //三阶线性递推模型结果是：578949
        //输入：n=17  调用递归状态记忆-getAnThreeRecursionV2Up2DownDp   结果：三阶线性递推模型结果是：58425  状态记忆(备忘录):[0,1,1,3,6,13,28,60,129,277,595,1278,2745,5896,12664,
        // 27201,58425]
        /**
         * 把进入记忆备忘录的日志打印出来看下，在再本子上推算下看和预期是否相符？
         * 进入了状态记忆备忘录, n的值是:4 备忘录的值是:3
         * 进入了状态记忆备忘录, n的值是:5 备忘录的值是:6
         * 进入了状态记忆备忘录, n的值是:4 备忘录的值是:3
         * 进入了状态记忆备忘录, n的值是:5 备忘录的值是:6
         * 进入了状态记忆备忘录, n的值是:6 备忘录的值是:13
         * 进入了状态记忆备忘录, n的值是:6 备忘录的值是:13
         * 进入了状态记忆备忘录, n的值是:7 备忘录的值是:28
         * 进入了状态记忆备忘录, n的值是:8 备忘录的值是:60
         * 进入了状态记忆备忘录, n的值是:7 备忘录的值是:28
         * 进入了状态记忆备忘录, n的值是:8 备忘录的值是:60
         * 进入了状态记忆备忘录, n的值是:9 备忘录的值是:129
         * 进入了状态记忆备忘录, n的值是:9 备忘录的值是:129
         */

        int result = getAnThreeNoRecursionDown2UpDp(17);
        System.out.println("无递归版本迭代DP结果是：" + result);
        /**
         * 计算结果：
         * 无递归版本迭代DP结果是：[0,1,1,3,6,13,28,60,129,277,595,1278,2745,5896,12664,27201,58425]
         * 无递归版本迭代DP结果是：58425
         */

其中对于法2：getAnThreeRecursionV2Up2DownDp()的状态记忆输出日志做了详细研究，核对过程如图：

三、对比下算法复杂度

四、扩展(应用场景)

这个数列：f(n)=f(n−1)+2f(n−2)+f(n−3)，这个代表：的三阶线性递推模型。

名号没有斐波那契数列响亮，不过应用还是蛮广泛的，比如：

组合计数：路径 / 步数规划数字信号处理
三阶递归滤波（工程领域）
生物种群增长建模（生态 / 农业领域）