1、插值的基本定义
设函数 y = f ( x ) y=f(x) y=f(x)在区间 [ a , b ] [a,b] [a,b]上有定义,且已知它在 n + 1 n+1 n+1个互异点 a ≤ x 0 < x 1 < . . . < x n ≤ b a\leq x_0<x_1<...<x_n\leq b a≤x0<x1<...<xn≤b上的函数值 y 0 , y 1 , . . . , y n y_0,y_1,...,y_n y0,y1,...,yn,若存在一个简单函数 p ( x ) p(x) p(x),使得
p ( x i ) = y i , i = 0 , 1 , 2 , . . , n p(x_i)=y_i,i=0,1,2,..,n p(xi)=yi,i=0,1,2,..,n
成立,则称 p ( x ) p(x) p(x)为 f ( x ) f(x) f(x)插值函数。显然,除上述已知 n + 1 n+1 n+1个互异点外,在其他位置上,插值函数 p ( x ) p(x) p(x)和原函数 f ( x ) f(x) f(x)之间并没有明确关系,所以插值总是有误差的。不过,若对原函数和插值函数增加一定的约束,则可能使两者保持一致。下面讨论代数插值情况。
设 p ( x ) p(x) p(x)是次数不超过 n n n的代数多项式,即
p ( x ) = a n x n + a n − 1 x n − 1 + . . . + a 1 x + a 0 (1) p(x)=a_n x^n+a_{n-1}x^{n-1}+...+a_1 x+a_0 \tag{1} p(x)=anxn+an−1xn−1+...+a1x+a0(1)
该函数满足 p ( x i ) = y i p(x_i)=y_i p(xi)=yi,则称 p ( x ) p(x) p(x)为原函数 f ( x ) f(x) f(x)的 n n n次代数插值多项式。该种插值称为代数插值,代数插值的几何意义,其实就是找一条过上述 n + 1 n+1 n+1个互异点的 n n n次代数曲线来近似表示曲线 f ( x ) f(x) f(x)。
可以证明,上述 n n n次插值函数有且只有一个。显然,将 p ( x i ) = y i p(x_i)=y_i p(xi)=yi的条件代入(1)式,得到下面的 n + 1 n+1 n+1阶线性方程组
{ a 0 + a 1 x 0 + a 2 x 0 2 + . . . + a n x 0 n = y 0 a 0 + a 1 x 1 + a 2 x 1 2 + . . . + a n x 1 n = y 1 ⋮ a 0 + a 1 x n + a 2 x n 2 + . . . + a n x n n = y n → [ 1 x 0 . . . x 0 n 1 x 1 . . . x 1 n ⋮ ⋮ . . . ⋮ 1 x n . . . x n n ] [ a 0 a 1 ⋮ a n ] = [ y 0 y 1 ⋮ y n ] \left\{\begin{matrix} a_0+a_1 x_0+a_2 x_0^2+...+a_nx_0^n=y_0 \\ a_0+a_1 x_1+a_2 x_1^2+...+a_nx_1^n=y_1 \\ \vdots \\ a_0+a_1 x_n+a_2 x_n^2+...+a_nx_n^n=y_n \\ \end{matrix}\right. \rightarrow \left[ \begin{matrix} 1 & x_0 & ... & x_0^n \\ 1 & x_1 & ... & x_1^n \\ \vdots & \vdots & ... & \vdots \\ 1 & x_n & ... & x_n^n \\ \end{matrix}\right] \left[ \begin{matrix} a_0 \\ a_1 \\ \vdots \\ a^n \\ \end{matrix}\right] = \left[ \begin{matrix} y_0 \\ y_1 \\ \vdots \\ y^n \\ \end{matrix}\right] ⎩ ⎨ ⎧a0+a1x0+a2x02+...+anx0n=y0a0+a1x1+a2x12+...+anx1n=y1⋮a0+a1xn+a2xn2+...+anxnn=yn→ 11⋮1x0x1⋮xn............x0nx1n⋮xnn a0a1⋮an = y0y1⋮yn
显然,该线性方程组的行列式为
∣ 1 x 0 . . . x 0 n 1 x 1 . . . x 1 n ⋮ ⋮ . . . ⋮ 1 x n . . . x n n ∣ = ∏ i = 1 n ∏ j = 0 i − 1 ( x i − x j ) \begin{vmatrix} 1 & x_0 & ... & x_0^n \\ 1 & x_1 & ... & x_1^n \\ \vdots & \vdots & ... & \vdots \\ 1 & x_n & ... & x_n^n \\ \end{vmatrix} = \prod_{i=1}^n \prod_{j=0}^{i-1}(x_i-x_j) 11⋮1x0x1⋮xn............x0nx1n⋮xnn =i=1∏nj=0∏i−1(xi−xj)
显然,由于 x i x_i xi互不相同,所以上式不为0,所以方程系数 a 0 , . . . , a n a_0,...,a_n a0,...,an可被唯一确,即该插值多项式有且只有一个。
插值问题的关键是求解插值多项式,显然利用上述线性方程组,可直接求得多项式系数的最小二乘解。但计算过程涉及矩阵求逆,计算量较大,后面将探究新的计算方法。
2、拉格朗日插值法
2.1、线性插值情况
我们从一次多项式开始逐步推导。此时有 p ( x i ) = y i , ( i = 0 , 1 ) p(x_i)=y_i,(i=0,1) p(xi)=yi,(i=0,1),显然,可过这两个点作一条直线,目的是用直线 p ( x ) p(x) p(x)来近似表示原函数 f ( x ) f(x) f(x),这种插值称为线性插值。该直线的两点式方程可表示为
p ( x ) = y 0 x − x 1 x 0 − x 1 + y 1 x − x 0 x 1 − x 0 = l 0 ( x ) y 0 + l 1 ( x ) y 1 = ∑ k = 0 1 l k ( x ) y k p(x)=y_0 \frac{x-x_1}{x_0-x_1}+y_1 \frac{x-x_0}{x_1-x_0}=l_0(x)y_0+l_1(x)y_1=\sum_{k=0}^1 l_k(x)y_k p(x)=y0x0−x1x−x1+y1x1−x0x−x0=l0(x)y0+l1(x)y1=k=0∑1lk(x)yk
其中, l 0 ( x ) = x − x 1 x 0 − x 1 l_0(x)=\frac{x-x_1}{x_0-x_1} l0(x)=x0−x1x−x1称为点 x 0 x_0 x0的一次插值基函数, l 1 ( x ) = x − x 0 x 1 − x 0 l_1(x)=\frac{x-x_0}{x_1-x_0} l1(x)=x1−x0x−x0称为点 x 1 x_1 x1的一次插值基函数, 显然 p ( x ) p(x) p(x)是 l 0 ( x ) l_0(x) l0(x)和 l 1 ( x ) l_1(x) l1(x)的线性组合。另外,上述插值基函数满足
l j ( x i ) = δ i j = { 1 , i = j 0 , i ≠ j (2) l_j(x_i)=\delta_{ij}=\left\{\begin{matrix} 1,i=j \\ 0,i\neq j \end{matrix}\right. \tag{2} lj(xi)=δij={1,i=j0,i=j(2)
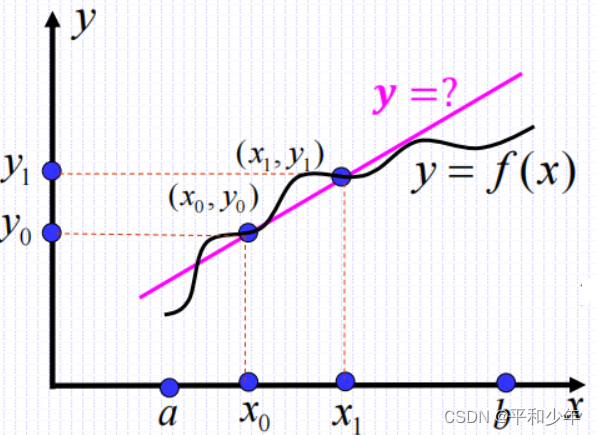
图1. 线性插值示意图
2.2、二次插值情况
此时已知 f ( x ) f(x) f(x)上面三个互异点 ( x i , y i ) , i = 0 , 1 , 2 (x_i,y_i),i=0,1,2 (xi,yi),i=0,1,2,要求构造一个不超过2次的代数多项式 p ( x ) = a x 2 + b x + c p(x)=ax^2+bx+c p(x)=ax2+bx+c,满足 p ( x i ) = y i , ( i = 0 , 1 , 2 ) p(x_i)=y_i,(i=0,1,2) p(xi)=yi,(i=0,1,2)。为便于求解,我们可将 p ( x ) p(x) p(x)重新整理为 p ( x ) = A ( x − x 1 ) ( x − x 2 ) + B ( x − x 0 ) ( x − x 2 ) + C ( x − x 0 ) ( x − x 1 ) p(x)=A(x-x_1)(x-x_2)+B(x-x_0)(x-x_2)+C(x-x_0)(x-x_1) p(x)=A(x−x1)(x−x2)+B(x−x0)(x−x2)+C(x−x0)(x−x1),将三个已知点坐标代入,可求得
A = y 0 ( x 0 − x 1 ) ( x 0 − x 2 ) B = y 1 ( x 1 − x 0 ) ( x 1 − x 2 ) C = y 2 ( x 2 − x 0 ) ( x 2 − x 1 ) A=\frac{y_0}{(x_0-x_1)(x_0-x_2)}\\ B=\frac{y_1}{(x_1-x_0)(x_1-x_2)}\\ C=\frac{y_2}{(x_2-x_0)(x_2-x_1)} A=(x0−x1)(x0−x2)y0B=(x1−x0)(x1−x2)y1C=(x2−x0)(x2−x1)y2
此时可得到插值函数为
p ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) y 0 + ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) y 1 + ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) y 2 = l 0 ( x ) y 0 + l 1 ( x ) y 1 + l 2 ( x ) y 2 = ∑ j = 0 2 l j ( x ) y j p(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2\\ =l_0(x)y_0+l_1(x)y_1+l_2(x)y_2=\sum_{j=0}^2 l_j(x)y_j p(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)y0+(x1−x0)(x1−x2)(x−x0)(x−x2)y1+(x2−x0)(x2−x1)(x−x0)(x−x1)y2=l0(x)y0+l1(x)y1+l2(x)y2=j=0∑2lj(x)yj
其中, l j ( x ) = ∏ i = 0 , i ≠ j 2 x − x i x j − x i l_j(x)=\prod_{i=0,i\neq j}^2 \frac{x-x_i}{x_j-x_i} lj(x)=∏i=0,i=j2xj−xix−xi,显然 l j ( x ) l_j(x) lj(x)同样具有(2)式所示的性质。该插值称为二次插值或抛物线插值。
2.3、n次插值情况
此时,仿照二次插值的构造方法,令
p ( x ) = l 0 ( x ) y 0 + . . . + l n ( x ) y n = ∑ j = 0 n l j ( x ) y j p(x)=l_0(x)y_0+...+l_n(x)y_n=\sum_{j=0}^n l_j(x)y_j p(x)=l0(x)y0+...+ln(x)yn=j=0∑nlj(x)yj
其中, l j ( x ) l_j(x) lj(x)是 n n n次多项式,称为插值基函数,它满足条件
l j ( x i ) = δ i j = { 1 , i = j 0 , i ≠ j , ( i , j = 0 , 1 , . . . , n ) (2) l_j(x_i)=\delta_{ij}=\left\{\begin{matrix} 1,i=j \\ 0,i\neq j \end{matrix}\right. ,(i,j=0,1,...,n) \tag{2} lj(xi)=δij={1,i=j0,i=j,(i,j=0,1,...,n)(2)
显然,此时问题归结为构造满足条件的 n n n次多项式 l j ( x ) l_j(x) lj(x)。事实上,由 l j ( x ) = 0 , i ≠ j l_j(x)=0,i\neq j lj(x)=0,i=j,知道 x 0 , x 1 , . . . , x j − 1 , x j + 1 , . . . , x n x_0,x_1,...,x_{j-1},x_{j+1},...,x_n x0,x1,...,xj−1,xj+1,...,xn都是 l j ( x ) l_j(x) lj(x)的零点,所以可设 l j ( x ) = A ( x − x 0 ) ( x − x 1 ) . . . . ( x − x j − 1 ) ( x − x j + 1 ) . . . ( x − x n ) l_j(x)=A(x-x_0)(x-x_1)....(x-x_{j-1})(x-x_{j+1})...(x-x_n) lj(x)=A(x−x0)(x−x1)....(x−xj−1)(x−xj+1)...(x−xn)。其中, A A A为待定系数,由条件 l j ( x j ) = 1 l_j(x_j)=1 lj(xj)=1,可确定 A = 1 ( x j − x 0 ) ( x j − x 1 ) . . . ( x j − x j − 1 ) ( x j − x j + 1 ) . . . ( x j − x n ) A=\frac{1}{(x_j-x_0)(x_j-x_1)...(x_j-x_{j-1})(x_j-x_{j+1})...(x_j-x_n)} A=(xj−x0)(xj−x1)...(xj−xj−1)(xj−xj+1)...(xj−xn)1,所以
l j ( x ) = ( x − x 0 ) . . . ( x − x j − 1 ) ( x − x j + 1 ) . . . ( x − x n ) ( x j − x 0 ) . . . ( x j − x j − 1 ) ( x j − x j + 1 ) . . . ( x j − x n ) = ∏ i = 0 , i ≠ j n x − x i x j − x i l_j(x)=\frac{(x-x_0)...(x-x_{j-1})(x-x_{j+1})...(x-x_n)}{(x_j-x_0)...(x_j-x_{j-1})(x_j-x_{j+1})...(x_j-x_n)}=\prod_{i=0,i\neq j}^n \frac{x-x_i}{x_j-x_i} lj(x)=(xj−x0)...(xj−xj−1)(xj−xj+1)...(xj−xn)(x−x0)...(x−xj−1)(x−xj+1)...(x−xn)=i=0,i=j∏nxj−xix−xi
由此可得
p ( x ) = ∑ j = 0 n l j ( x ) y j = ∑ j = 0 n y j ( ∏ i = 0 , i ≠ j n x − x i x j − x i ) (3) p(x)=\sum_{j=0}^n l_j(x)y_j=\sum_{j=0}^n y_j(\prod_{i=0,i\neq j}^n \frac{x-x_i}{x_j-x_i})\tag{3} p(x)=j=0∑nlj(x)yj=j=0∑nyj(i=0,i=j∏nxj−xix−xi)(3)
我们称形如(3)式的插值公式为拉格朗日插值。
3、代码实现
分别仿真拉格朗日插值法用于线性插值、抛物线插值和三次插值的情况,仿真代码见附录,仿真结果如下图所示,图中蓝色点表示已知点,红色点表示插值点。
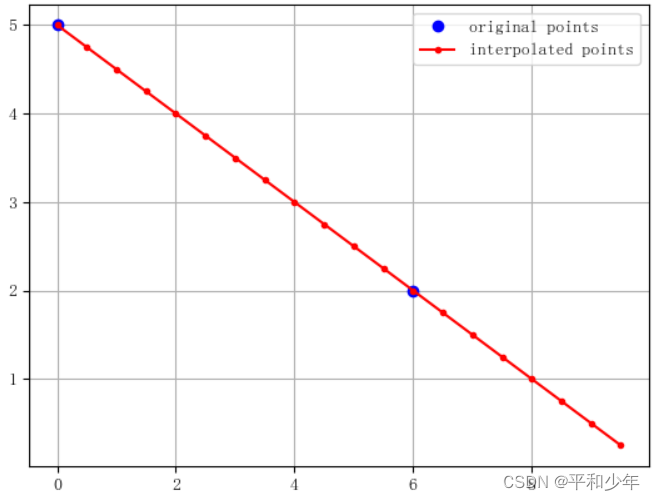
图2. 线性插值的结果
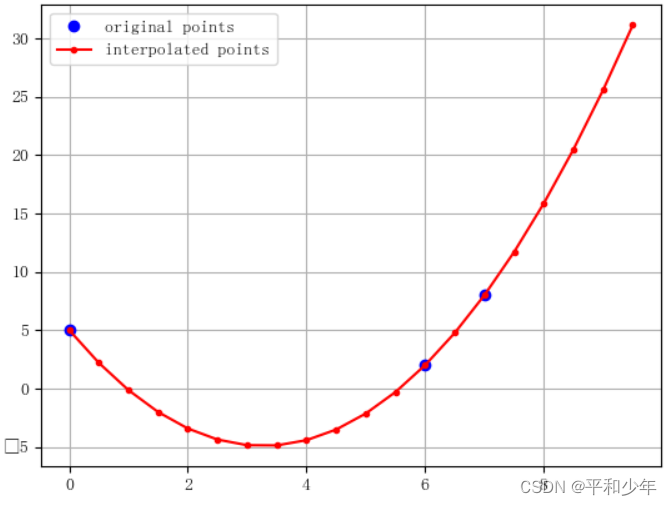
图3. 抛物线插值的结果
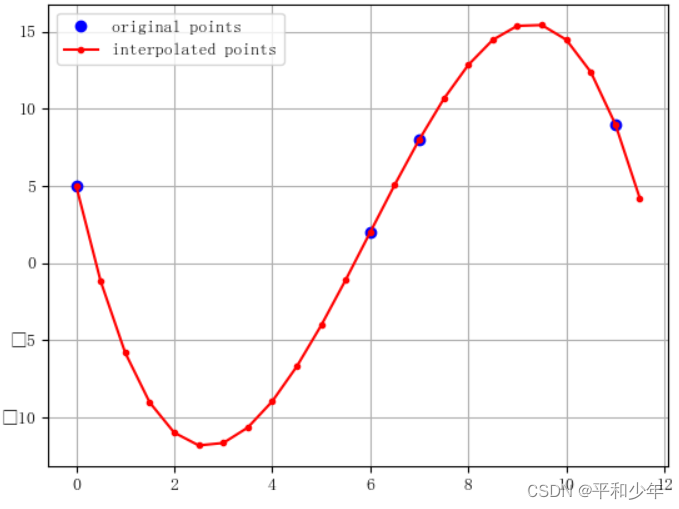
图4. 三次插值的结果
【实现代码】
python
import numpy as np
import matplotlib.pyplot as plt
def lagrange_interpolate(x, xi, yi):
"""
本函数用于实现拉格朗日函数
:param x: 待计算的x坐标
:param xi: 已知的x坐标
:param yi: 已知的y坐标
:return y: 对应x得到的y
"""
if len(xi) != len(yi):
raise ValueError('x dimension is not equal to y dimension!')
# #######################计算拉格朗日基函数##################
lj = np.ones((len(x), len(yi)))
for j in range(0, len(yi), 1):
for i in range(0, len(xi), 1):
if i != j:
lj[:, j] *= ((x - xi[i]) / (xi[j] - xi[i]))
# ####################计算拉格朗日插值结果#####################
y = np.zeros(len(x))
for j in range(0, len(yi), 1):
y += yi[j] * lj[:, j]
return y
if __name__ == '__main__':
xi = np.array([0, 6, 7, 11])
yi = np.array([5, 2, 8, 9])
x = np.arange(0, 12, 0.5)
y = lagrange_interpolate(x, xi, yi)
plt.figure()
plt.plot(xi, yi, 'bo')
plt.plot(x, y, 'r.-')
plt.legend(['original points', 'interpolated points'])
plt.grid()
plt.show()