目录
[1.1 人工神经网络结构](#1.1 人工神经网络结构)
[1.2 神经元/感知器](#1.2 神经元/感知器)
[1.3 激活函数](#1.3 激活函数)
[1.3.1 sign函数](#1.3.1 sign函数)
[1.3.2 sigmoid函数(Logistic函数)](#1.3.2 sigmoid函数(Logistic函数))
[1.3.3 tanh双曲正切函数](#1.3.3 tanh双曲正切函数)
[1.3.4 ReLU函数](#1.3.4 ReLU函数)
[1.4 分类](#1.4 分类)
[2.1 概述](#2.1 概述)
[2.2 处理过程](#2.2 处理过程)
[2.3 例题](#2.3 例题)
[2.4 Matlab实现](#2.4 Matlab实现)
[2.4.1 一个简单程序](#2.4.1 一个简单程序)
[2.4.2 newff------BP神经网络参数设置函数](#2.4.2 newff——BP神经网络参数设置函数)
[2.4.3 train------BP神经网络训练函数](#2.4.3 train——BP神经网络训练函数)
一、人工神经网络
1.1 人工神经网络结构
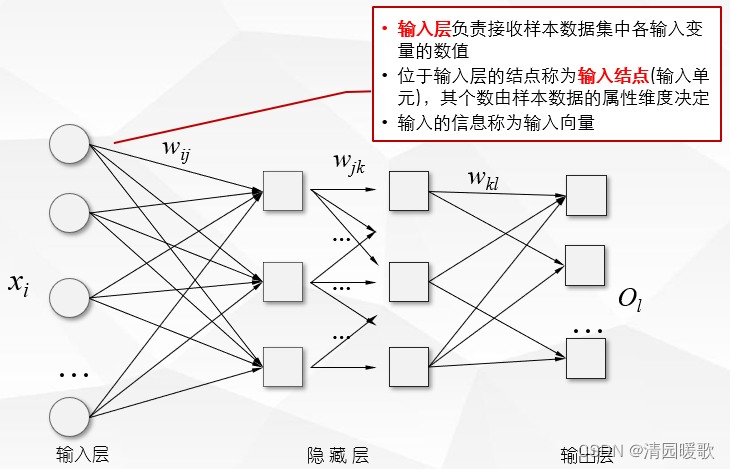
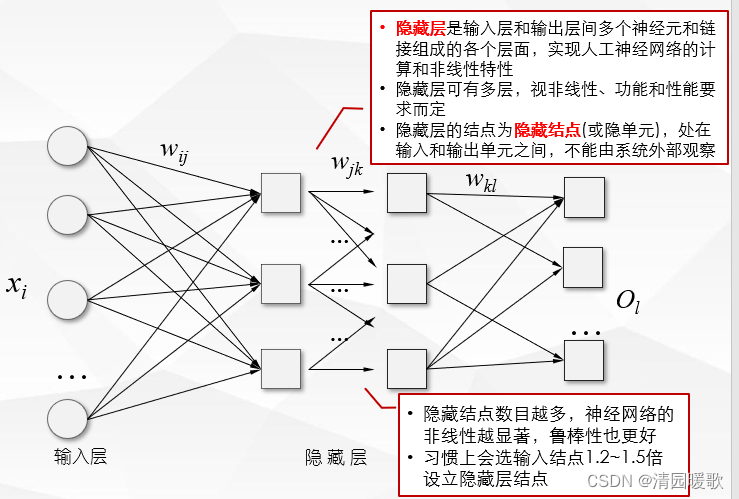
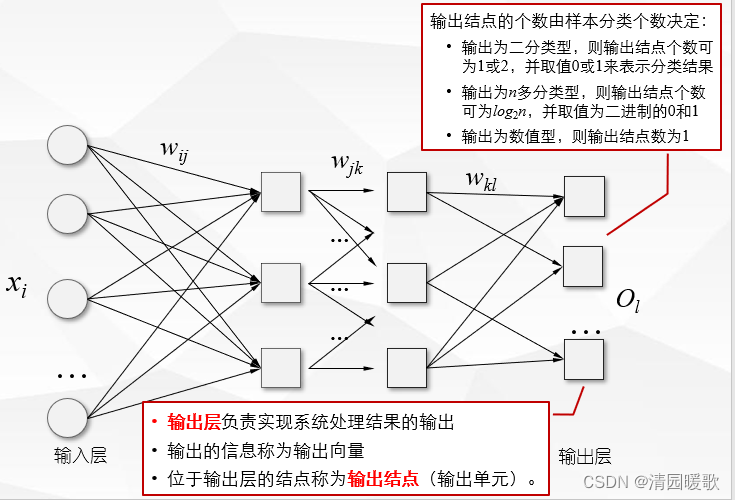
1.2 神经元/感知器
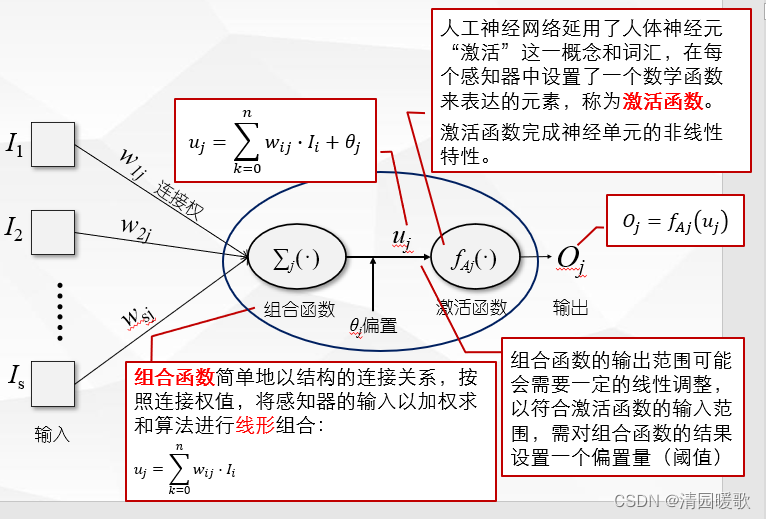
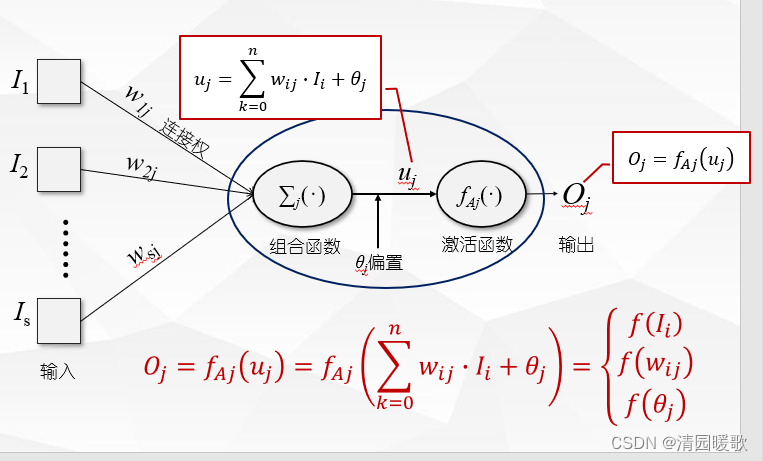
1.3 激活函数
1.3.1 sign函数
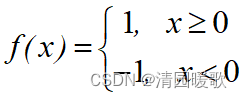
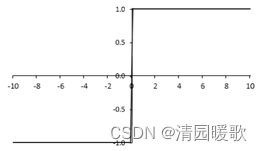
1.3.2 sigmoid函数(Logistic函数)
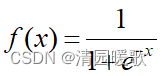
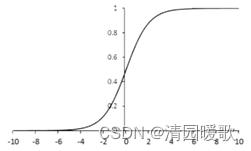
1.输出映射在 ( 0 , 1 ) 之间,输出 范围 有限
2.单调连续,易于求导
3.优化 效果 稳定
4.适合用于输出层感知器的激活函数 。
1.因为 sigmoid 函数具有的饱和 性,容易 产生梯度 消失,导致 训练 失效
2.输出 并不是以 0 为 中心
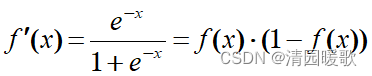
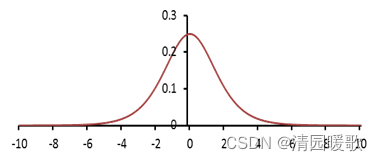
可以看出,sigmoid函数的导数只有在x=0附近的时候有比较好的激活性,在正负饱和区的梯度都接近于0,造成梯度弥散,无法完成深层网络的训练。
1.3.3 tanh双曲正切函数

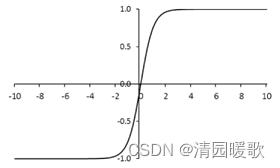
1.取值 范围为 [- 1 , 1]
2.在 特征相差明显时的应用效果 较好,在循环 训练过程中会不断扩大特征 效果
3.是 0 均值 的
4.应用中比 sigmoid 函数有更强的 应用性
5.同样 具有饱和 性,也 会造成梯度 消失
1.3.4 ReLU函数
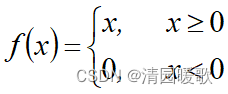
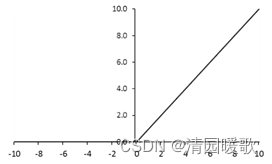
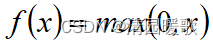
1.用于 某些算法(如随机梯度下降) 时,收敛速度较快
2.当 x <0 时, ReLU 硬 饱和;当 x > 0 时,则 不存在饱和 问题
3.在 x > 0 时保持梯度不 衰减,从而 缓解梯度消失 问题。但随着训练推进,部分 输入会落入硬饱和 区,导致 对应权重无法 更新,导致神经元死亡
4.输出 均值也大于 0
5.偏移 现象和神经元死亡会共同影响网络的收敛性。
1.4 分类
(1)拓扑结构划分
两层、三层、多层神经网络
(2)结点间的连接方式划分
层间连接、层内连接
(3)结点间的连接方向划分
前馈式神经网络BP(Back Propagation)、反馈式神经网络(Feedback)
二、BP人工神经网络
2.1 概述
BP人工神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程 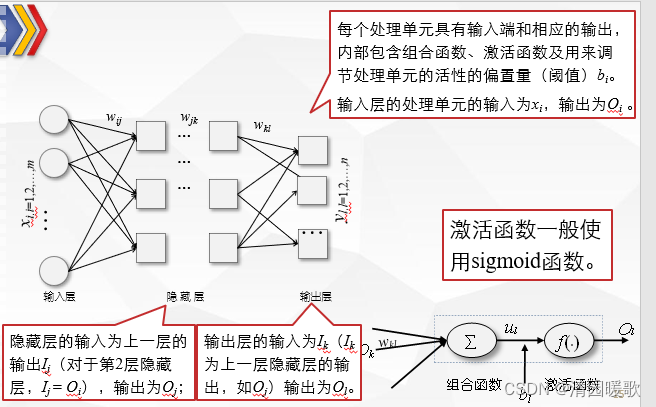
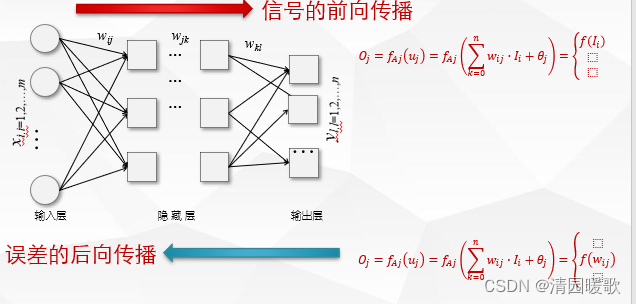
2.2 处理过程
(1)初始化网络权值和处理单元的阈值
最简单的办法就是随机初始化,分别为w**ij,w**jk,...,w**kl和b**ij,b**jk,...,b**kl赋随机值。
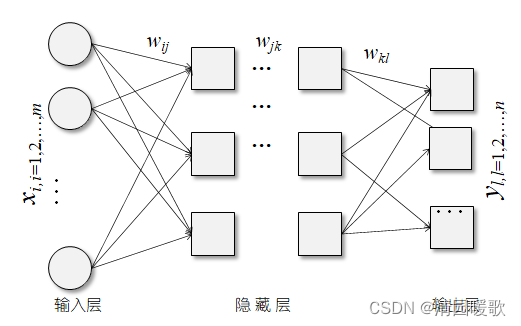
(2)信号的前向传播,计算各处理单元的输出
按照网络连接以及组合函数和激活函数关系公式,逐层计算隐藏层处理单元和输出层处理单元的输入和输出。

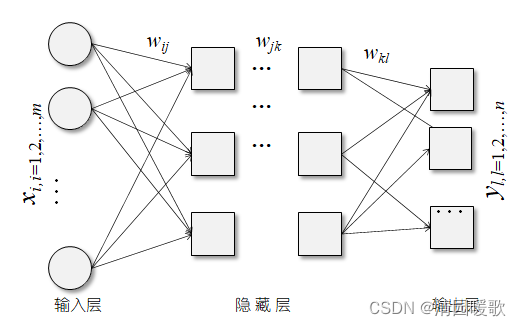
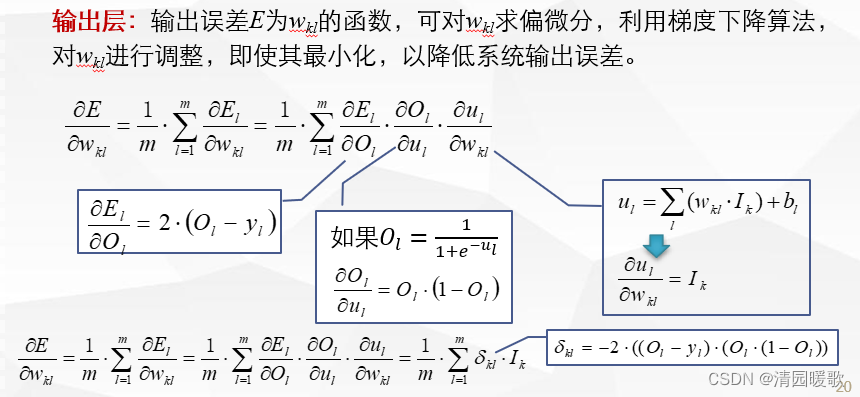
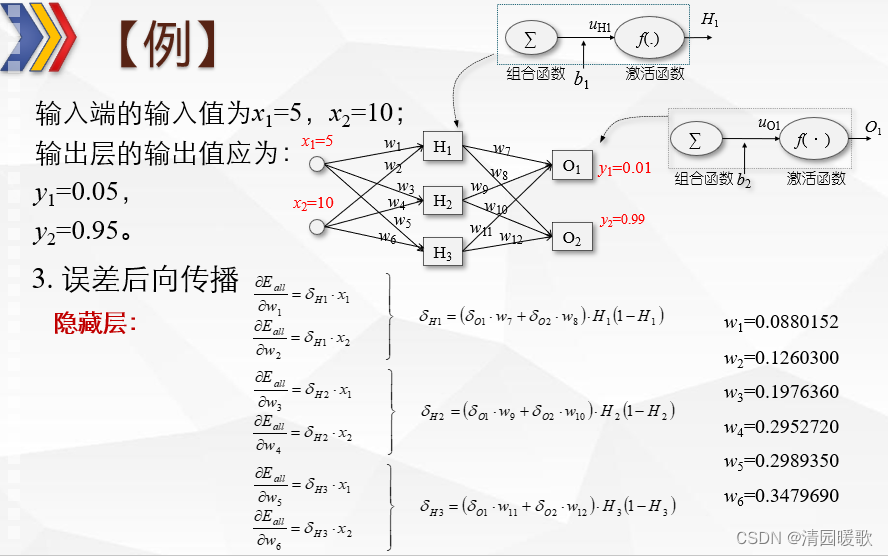
(3)误差后向传播
对于训练数据x**i,输出应为y**l,与人工神经网络实际输出O**l存在差异。
定义系统的总输出误差为系统输出层各处理单元输出误差的平均值
(即各输出O**l与训练数据y**l的差异),
是输出与其期望值的均方差:
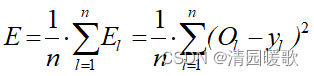
需要根据差异的情况对系统内各连接的权值进行调整,使二者相等或逼近 y**l。

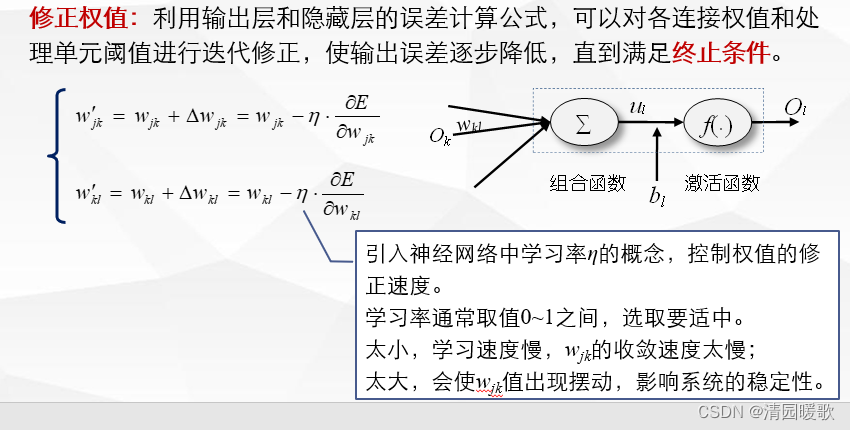
(4)模型评估
(5)模型应用
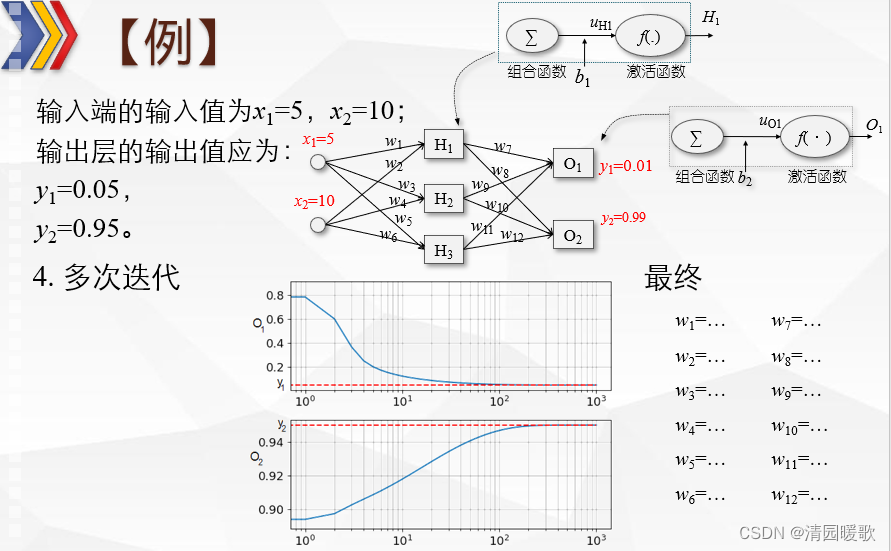
2.3 例题
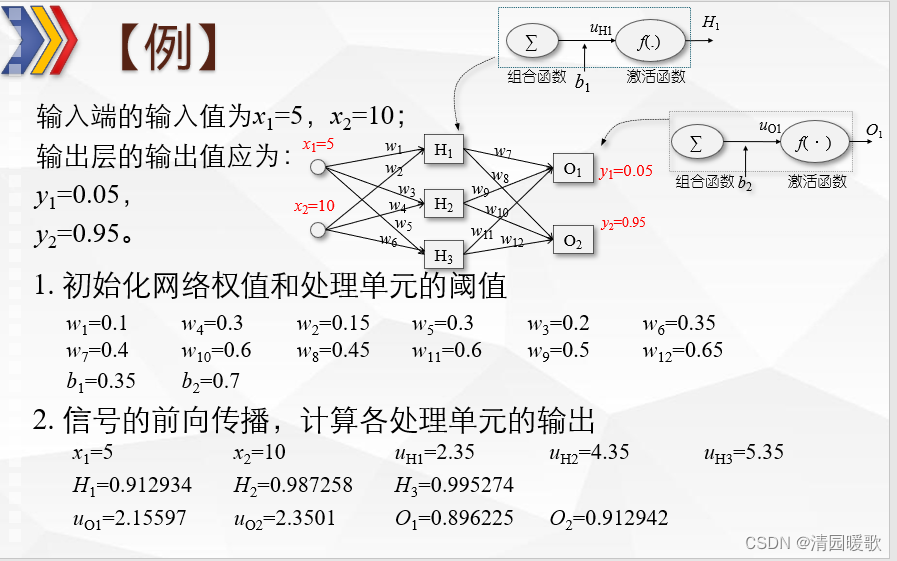
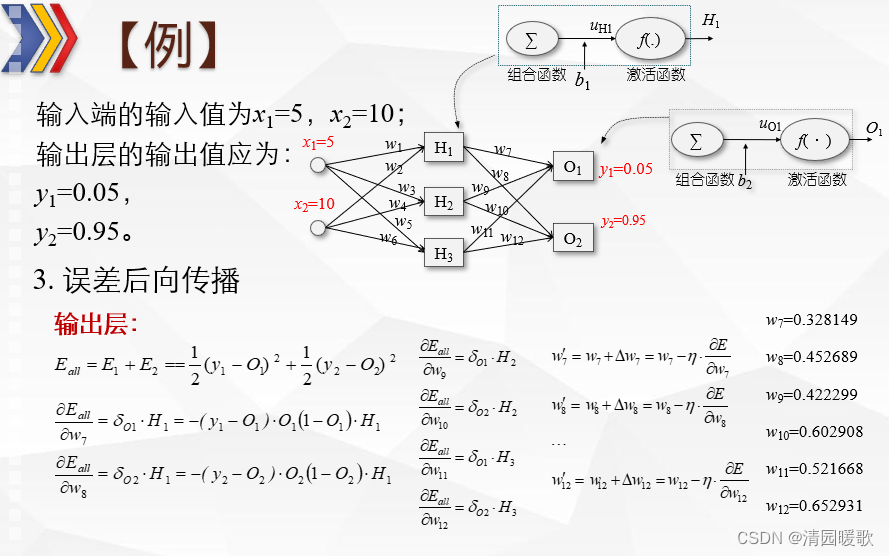
2.4 Matlab实现
2.4.1 一个简单程序
P=[0 1 2 3 4 5 6 7 8 9 10]; %输入
T=[0 1 2 3 4 3 2 1 2 3 4]; %期望输出
ff=newff(P,T,20); %建立一个BP网络,包含20个节点的隐含层
ff.trainParam.epochs=50; %最大训练次数
ff=train(ff,P,T); %训练
Y1=sim(ff,P); %仿真
plot(P,T,'o-');2.4.2 newff------BP神经网络参数设置函数
功能:构建一个BP神经网络
(1) net=newff(P, T, S)
P: R*Q1矩阵,表示创建的神经网络中,输入层有R个神经元。每行对应一
个神经元输入数据的典型值,实际应用中常取其最大最小值。
T: SN*Q2矩阵,表示创建的网络有SN个输出层节点,每行是输出值的典型
值。
S: 标量或向量,用于指定隐藏层神经元个数,若隐藏层多于一层,则写成
行向量的形式。
(2)net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)
TFi: 第i层节点的传递函数,包括线性传递函数purelin, 正切S型传递函数
tansig,对数S型传递函数logsig,默认为"tansig";
BTF: 训练函数,用于网络权值和阈值的调整,默认为基于莱文贝格-马夸
特共轭梯度法的训练函数trainlm,其他参数见下表所示;
一般在使用过程中设置这2个参数,后面5个参数采用系统默认参数。
BP****神经网络训练函数
|-------------------|----------------------|
| 训练函数的意义 | MATLAB****中相应的函数 |
| 梯度下降法 | traingd |
| 动量反传的梯度下降法 | traingdm |
| 动态自适应学习率的梯度下降法 | traingda |
| 带动量动态自适应学习率的梯度下降法 | traingdx |
| 弹性梯度下降法 | trainrp |
| 量化共轭梯度法 | traincg |
| 莱文贝格-马夸特共轭梯度法 | trainlm |
| 弗莱彻-里夫斯共轭梯度法 | traingf |
| 波拉克-里比埃共轭梯度法 | traingp |
| 鲍威尔-比尔共轭梯度法 | traingb |
2.4.3 train------BP神经网络训练函数
功能:用训练函数训练BP神经网络
[net, tr]=train(NET, P, T)
NET: 待训练网络;
P: 输入数据矩阵;
T: 期望输出数据矩阵;
net: 训练好的网络;
tr: 训练过程记录。
BP****神经网络训练函数
|------------------------------|-----------------------|
| 训练参数名称及默认值 | 属性 |
| net.trainParam.epochs=100 | 最大训练次数 |
| net.trainParam.goal=0 | 训练目标 |
| net.trainParam.show=25 | 两次显示之间的训练次数(无显示时取NAN) |
| net.trainParam.time=inf | 最大训练时间(秒) |
| net.trainParam.max_fail=5 | 确认失败的最大次数 |
| net.trainParam.min_grad=1e-6 | 最小性能梯度 |
| net.trainParam.lr=0.2 | 学习速率 |