文章目录
内部点
通俗理解:
给定一个集合 S S S,对于它的内部点 x x x而言,我们以 x x x为圆心、以 R R R为半径画个球,总是存在一个 R R R能够使得我们画的这个球里的所有点,都仍然属于 S S S。
数学表达
如果 S S S是一个集合,点 x x x是 S S S的内部点,当且仅当存在一个 ϵ > 0 \epsilon > 0 ϵ>0,使得 x x x的 ϵ \epsilon ϵ-邻域 B ( x , ϵ ) B(x, \epsilon) B(x,ϵ)完全包含在 S S S中。
边界点
通俗理解:
一个点称为集合的边界点,如果它在集合内部不再存在一个开集(一个不包含边界的子集),而任何足够小的邻域(即这个点周围的任意小的区域)都包含集合内的点和集合外的点。
凸集的边界点有什么特点?
从边界点来看,凸集的边界点一定也可以找到超平面(supporting hyperplane)把它撑(分离开)到某一边去。非凸的在某些点找不到一个平面可以把它撑起来(分离)。

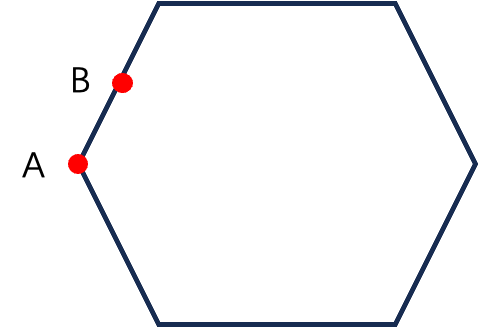
但是边界点不完全相同,又分为极值点和普通的边界点。如下图所示,A点是极值点,B点是普通的边界点。
观察可以发现,B点位于它旁边两个点的连线上,但A点不是。 更数学的表述方式是,极值点不能表示为集合中其他点的凸组合。(关于凸组合的理解可以参考我的文章优化基础(二):线性组合、仿射组合、锥组合、凸组合、线性集合、仿射集合、锥集合、凸集合的理解).
外部点
通俗理解:
x x x是集合 S S S的外部点,则 x x x和 S S S之间一定可以插入一个超平面,可以分开 x x x和 S S S。有趣