文章目录
- 前言
- 正文
-
- 为什么需要透视矫正?
-
- 1、视图坐标空间--->NDC坐标空间(透视投影)
- 2、NDC坐标空间--->屏幕坐标空间
-
- [(1)XYZ坐标范围从 [ − 1 , 1 ] [-1,1] [−1,1],变换到 [ 0 , 1 ] [0,1] [0,1]](#(1)XYZ坐标范围从 [ − 1 , 1 ] [-1,1] [−1,1],变换到 [ 0 , 1 ] [0,1] [0,1])
- [(2)XY分别从 [ 0 , 1 ] [0,1] [0,1] 变换到 [ 0 , s c r e e n _ w i d t h ] [0,screen\_width] [0,screen_width] 和 [ 0 , s c r e e n _ h e i g h t − 1 ] [0, screen\_height -1] [0,screen_height−1]](#(2)XY分别从 [ 0 , 1 ] [0,1] [0,1] 变换到 [ 0 , s c r e e n _ w i d t h ] [0,screen_width] [0,screen_width] 和 [ 0 , s c r e e n _ h e i g h t − 1 ] [0, screen_height -1] [0,screen_height−1])
- 总结:
- 综上:
- 什么是透视矫正?
- 透视矫正如何实现?
- 结尾:喜欢的小伙伴可以点点关注+赞哦
前言
前面章节讲解了面片剔除的内容,这一章节咱们补充一个比较关键的内容:透视矫正。主要包括:为什么?是什么?怎么做?,从这些角度考虑切入!
正文
为什么需要透视矫正?
通过前面章节三角形光栅化 和重心坐标插值 的学习,可以很容易计算出屏幕空间中三角形内部所有点的属性值: f ( P ) = α f ( A ) + β f ( B ) + γ f ( C ) f(P) = \alpha f(A) + \beta f(B) +\gamma f(C) f(P)=αf(A)+βf(B)+γf(C)。
但是我们思考一个问题:屏幕空间坐标的重心坐标插值可以代替空间中三角形的情况么?
这个问题从以下两个坐标变换阶段分析:
- 阶段一:视图坐标空间--->NDC坐标空间(只分析透视投影)
- 阶段二:NDC坐标空间--->屏幕坐标空间
1、视图坐标空间--->NDC坐标空间(透视投影)
(1)直线:
我们先来看一个逆Y轴视角看的示意图:
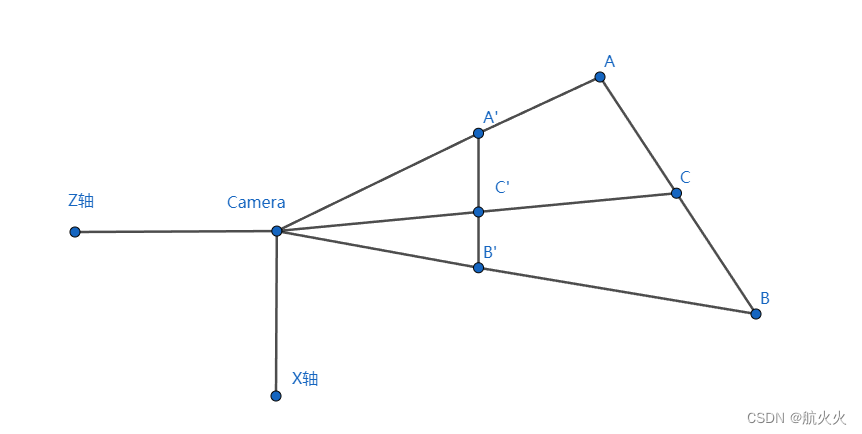
假设一条直线 A B AB AB,投影到近平面上形成 A ′ B ′ A'B' A′B′, A B AB AB 有一个中点 C C C 投影到近平面上为 C ′ C' C′ ,那么我们很显然发现了 C ′ C' C′ 不是 A ′ B ′ A'B' A′B′ 的中点。
从而可知,由于这是逆y轴看,也就说明从视图坐标空间--->NDC坐标空间的X轴坐标出现失真!类似可得,Y轴坐标也出现了失真,Z轴暂且抛开不谈。
紧接着,咱们设 A ′ C ′ / A ′ B ′ = d ′ , A C / A B = d A'C'/A'B' = d',AC/AB=d A′C′/A′B′=d′,AC/AB=d,可得以下等式:
f ( C ) = d ∗ f ( B ) + ( 1 − d ) ∗ f ( A ) f ( C ′ ) = d ′ ∗ f ( B ′ ) + ( 1 − d ′ ) ∗ f ( A ′ ) f(C) = d*f(B) + (1-d)*f(A)\\ f(C') = d'*f(B') + (1-d')*f(A') f(C)=d∗f(B)+(1−d)∗f(A)f(C′)=d′∗f(B′)+(1−d′)∗f(A′)
容易知道: f ( A ) = f ( A ′ ) , f ( B ) = f ( B ′ ) f(A) = f(A'), f(B) = f(B') f(A)=f(A′),f(B)=f(B′),同时根据上图可知 d ! = d ′ d != d' d!=d′ ,所以可以得到 f ( C ) ! = f ( C ′ ) f(C) != f(C') f(C)!=f(C′)
也就是说线段 A B AB AB 中间的任何点的插值计算都会出现偏差。
(2)三角形:
根据上述的直线结论,咱们将其推广到三角形的中心坐标插值计算!
已知视图坐标空间 S A B C S_{ABC} SABC,对应的NDC坐标空间的 S A ′ B ′ C ′ S_{A'B'C'} SA′B′C′, S A B C S_{ABC} SABC内任意一点 P P P 对应NDC坐标空间为 P ′ P' P′,容易得到如下等式:
f ( P ) = α f ( A ) + β f ( B ) + γ f ( C ) f ( P ′ ) = α ′ f ( A ′ ) + β ′ f ( B ′ ) + γ ′ f ( C ′ ) f(P) = \alpha f(A) + \beta f(B) + \gamma f(C)\\ f(P') = \alpha' f(A') + \beta' f(B') + \gamma' f(C')\\ f(P)=αf(A)+βf(B)+γf(C)f(P′)=α′f(A′)+β′f(B′)+γ′f(C′)
容易知道: f ( A ) = f ( A ′ ) , f ( B ) = f ( B ′ ) , f ( C ) = f ( C ′ ) f(A) = f(A'), f(B) = f(B'),f(C) = f(C') f(A)=f(A′),f(B)=f(B′),f(C)=f(C′) ,很容易得出 α 和 α ′ , β 和 β ′ , γ 和 γ ′ \alpha和\alpha',\beta和\beta',\gamma和\gamma' α和α′,β和β′,γ和γ′ 不全相等,所以可以得到 f ( P ) ! = f ( P ′ ) f(P) != f(P') f(P)!=f(P′) 。
总结:
因此,我们得知视图坐标空间->NDC坐标空间,会发生失真,从而影响后续插值算法的计算,从而导致问题!
2、NDC坐标空间--->屏幕坐标空间
我们回顾以下,这个阶段总共做了两件事情:
- 一:XYZ坐标范围从 [ − 1 , 1 ] [-1,1] [−1,1],变换到 [ 0 , 1 ] [0,1] [0,1]
- 二:XY分别从 [ 0 , 1 ] [0,1] [0,1] 变换到 [ 0 , s c r e e n _ w i d t h ] [0,screen\_width] [0,screen_width] 和 [ 0 , s c r e e n _ h e i g h t − 1 ] [0, screen\_height -1] [0,screen_height−1]
(1)XYZ坐标范围从 [ − 1 , 1 ] [-1,1] [−1,1],变换到 [ 0 , 1 ] [0,1] [0,1]
我们很容易想到,这个事情是涉及到均匀缩放和平移,不会影响重心坐标插值等计算!如下图:

(2)XY分别从 [ 0 , 1 ] [0,1] [0,1] 变换到 [ 0 , s c r e e n _ w i d t h ] [0,screen\_width] [0,screen_width] 和 [ 0 , s c r e e n _ h e i g h t − 1 ] [0, screen\_height -1] [0,screen_height−1]
为了直观,这个事情要从两个过程考虑:
第一个过程: 1*1平行投影到一张纸上
第二个过程: 纵横统一缩放 s c r e e n _ w i d t h / s c r e e n _ h e i g h t screen\_width/screen\_height screen_width/screen_height 倍
如下图所示:

这里我们知道第二个过程不会影响重心坐标插值等计算。但是过程一不好说,所以咱们来进行分析过程一!
我们先观察直线的平行投影,如下图所示:
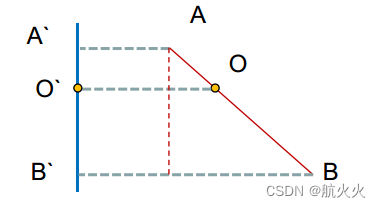
由相似三角形,很容易得到等式 A O : B O = A ′ O ′ : B ′ O ′ AO:BO = A'O':B'O' AO:BO=A′O′:B′O′ ,因此可以知道O点在平行投影前后插值比例不变!
然后咱们看一下空间中三角形平行投影的情况,如下图所示:
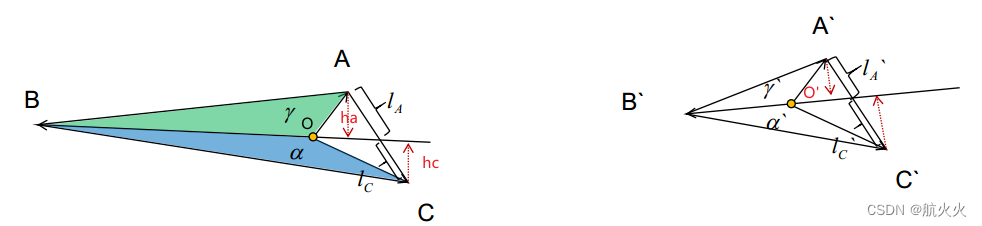
先观察左边三角形ABC,结合之前重心坐标计算公式,可知:
α γ = S B C O S B A O = h c h a \frac{\alpha}{\gamma} = \frac{S_{BCO}}{S_{BAO}} = \frac{h_c}{h_a} γα=SBAOSBCO=hahc
根据相似三角形可以得到:
h c h a = l c l a \frac{h_c}{h_a} = \frac{l_c}{l_a} hahc=lalc
所以可以得到:
α γ = l c l a \frac{\alpha}{\gamma} = \frac{l_c}{l_a} γα=lalc
同理根据右边三角形,咱么可以得到:
α ′ γ ′ = l c ′ l a ′ \frac{\alpha'}{\gamma'} = \frac{l_c'}{l_a'} γ′α′=la′lc′
又因为直线AC在平行投影前后,线段比例保持不变的结论: l a : l c = l a ′ : l c ′ l_a:l_c = l_a':l_c' la:lc=la′:lc′
所以咱们可以知道:
α γ = α ′ γ ′ \frac{\alpha}{\gamma} = \frac{\alpha'}{\gamma'} γα=γ′α′
同理,咱们可得:
α β = α ′ β ′ β γ = β ′ γ ′ \frac{\alpha}{\beta} = \frac{\alpha'}{\beta'}\\ \frac{\beta}{\gamma} = \frac{\beta'}{\gamma'} βα=β′α′γβ=γ′β′
所以最终得到: α : β : γ = α ′ : β ′ : γ ′ \alpha:\beta:\gamma = \alpha':\beta':\gamma' α:β:γ=α′:β′:γ′,又因为 α + β + γ = 1 且 α ′ + β ′ + γ ′ = 1 \alpha+\beta+\gamma=1且\alpha'+\beta'+\gamma'=1 α+β+γ=1且α′+β′+γ′=1,最终可以得到:
α = α ′ β = β ′ γ = γ ′ \alpha = \alpha'\\ \beta = \beta'\\ \gamma = \gamma'\\ α=α′β=β′γ=γ′
于是我们可知平行投影的操作不会影响插值的计算!
总结:
从NDC坐标变换到屏幕空间变换的过程中,不会发生插值计算失真的现象!不需要矫正!
综上:
我们只需要修正视图空间下的重心坐标到NDC空间下的重心坐标关系即可!
什么是透视矫正?
在NDC坐标空间下,已知 △ A ′ B ′ C ′ \triangle{A'B'C'} △A′B′C′ ,且已知三角形内某点 O ′ O' O′的重心坐标为 ( α ′ , β ′ , γ ′ ) (\alpha',\beta',\gamma') (α′,β′,γ′)
在视图坐标空间下,已知 △ A B C \triangle{ABC} △ABC ,且已知三角形内某点 O O O的重心坐标为 ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ)
通过上述分析可知,屏幕空间下计算的重心坐标结果和在NDC下一致。
所以问题可描述为: 通过屏幕空间下的重心坐标 ( α ′ , β ′ , γ ′ ) (\alpha',\beta',\gamma') (α′,β′,γ′)求真正视图坐标空间下的重心插值坐标 ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ)
透视矫正如何实现?
公式推导
已知:视图坐标空间下 △ A B C \triangle{ABC} △ABC;NDC坐标空间下 △ A ′ B ′ C ′ \triangle A'B'C' △A′B′C′,中间经过投影矩阵P和透视除法两个步骤,流程如下:
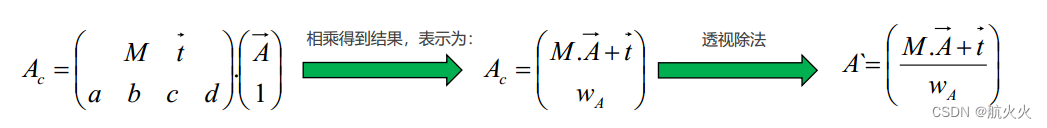
因此,同理可得:
A ′ = ( M A ⃗ + t ⃗ w A ) B ′ = ( M B ⃗ + t ⃗ w B ) C ′ = ( M C ⃗ + t ⃗ w C ) A'= \begin{pmatrix} \frac{M\vec{A} + \vec t}{w_A} \end{pmatrix}\\ B'= \begin{pmatrix} \frac{M\vec{B} + \vec t}{w_B} \end{pmatrix}\\ C'= \begin{pmatrix} \frac{M\vec{C} + \vec t}{w_C} \end{pmatrix}\\ A′=(wAMA +t )B′=(wBMB +t )C′=(wCMC +t )
注意: A ′ 、 B ′ 、 C ′ 为三维向量 A'、B'、C'为三维向量 A′、B′、C′为三维向量
假设在NDC下有一个点 O ′ O' O′,按照重心坐标公式:
O ′ = α ′ A ′ ⃗ + β ′ B ′ ⃗ + γ ′ C ′ ⃗ O' = \alpha'\vec{A'}+\beta'\vec{B'}+\gamma'\vec{C'} O′=α′A′ +β′B′ +γ′C′
将 A ′ , B ′ , C ′ A',B',C' A′,B′,C′分别代入,得到如下:
O ′ = α ′ ( M A ⃗ + t ⃗ w A ) + β ′ ( M B ⃗ + t ⃗ w B ) + γ ′ ( M C ⃗ + t ⃗ w C ) O' = \alpha'\begin{pmatrix} \frac{M\vec{A} + \vec t}{w_A} \end{pmatrix}+\beta'\begin{pmatrix} \frac{M\vec{B} + \vec t}{w_B} \end{pmatrix}+\gamma'\begin{pmatrix} \frac{M\vec{C} + \vec t}{w_C} \end{pmatrix} O′=α′(wAMA +t )+β′(wBMB +t )+γ′(wCMC +t )
假设在视图坐标空间下有一个点 O O O,按照重心坐标公式:
O = α A ⃗ + β B ⃗ + γ C ⃗ O = \alpha\vec{A}+\beta\vec{B}+\gamma\vec{C} O=αA +βB +γC
因为 O ′ O' O′也是由 O O O经过投影变换和透视除法而来,所以类似可得:
O ′ = ( M O ⃗ + t ⃗ w O ) O'= \begin{pmatrix} \frac{M\vec{O} + \vec t}{w_{O}} \end{pmatrix}\\ O′=(wOMO +t )
将 O ⃗ \vec O O 带入可得:
O ′ = ( M ( α A ⃗ + β B ⃗ + γ C ⃗ ) + t ⃗ w O ) O'= \begin{pmatrix} \frac{M(\alpha\vec{A}+\beta\vec{B}+\gamma\vec{C}) + \vec t}{w_{O}} \end{pmatrix}\\ O′=(wOM(αA +βB +γC )+t )
于是咱们结合上述的 O ′ O' O′ 的两个等式表达,可得:
O ′ = α ′ ( M A ⃗ + t ⃗ w A ) + β ′ ( M B ⃗ + t ⃗ w B ) + γ ′ ( M C ⃗ + t ⃗ w C ) = ( M ( α A ⃗ + β B ⃗ + γ C ⃗ ) + t ⃗ w O ) \begin{align} O' &= \alpha'\begin{pmatrix} \frac{M\vec{A} + \vec t}{w_A} \end{pmatrix}+\beta'\begin{pmatrix} \frac{M\vec{B} + \vec t}{w_B} \end{pmatrix}+\gamma'\begin{pmatrix} \frac{M\vec{C} + \vec t}{w_C} \end{pmatrix}\\ &=\begin{pmatrix} \frac{M(\alpha\vec{A}+\beta\vec{B}+\gamma\vec{C}) + \vec t}{w_{O}} \end{pmatrix} \end{align} O′=α′(wAMA +t )+β′(wBMB +t )+γ′(wCMC +t )=(wOM(αA +βB +γC )+t )
由上述可得,适用于任何ABC取值,所以系数必须匹配相等,可得:
α ′ w A = α w O β ′ w B = β w O γ ′ w C = γ w O \frac{\alpha'}{w_A} = \frac{\alpha}{w_O}\\ \frac{\beta'}{w_B} = \frac{\beta}{w_O}\\ \frac{\gamma'}{w_C} = \frac{\gamma}{w_O}\\ wAα′=wOαwBβ′=wOβwCγ′=wOγ
从而,咱们就得到了:
α = α ′ w A w O β = β ′ w B w O γ = γ ′ w C w O \alpha = \frac{\alpha'}{w_A}w_O\\ \beta = \frac{\beta'}{w_B}w_O\\ \gamma = \frac{\gamma'}{w_C}w_O\\ α=wAα′wOβ=wBβ′wOγ=wCγ′wO
这样就得到了重心坐标分别在视图坐标空间和NDC坐标空间的关系 。此时就剩一个未知数 w O w_O wO 。
又因为 α + β + γ = 1 \alpha + \beta + \gamma = 1 α+β+γ=1,咱们将上述的关系式带入,可得:
α ′ w A w O + β ′ w B w O + γ ′ w C w O = 1 \frac{\alpha'}{w_A}w_O+\frac{\beta'}{w_B}w_O+\frac{\gamma'}{w_C}w_O = 1\\ wAα′wO+wBβ′wO+wCγ′wO=1
所以就得到:
1 w O = α ′ w A + β ′ w B + γ ′ w C \frac{1}{w_O} = \frac{\alpha'}{w_A} + \frac{\beta'}{w_B} + \frac{\gamma'}{w_C} wO1=wAα′+wBβ′+wCγ′
咱们大功告成!
于是得到矫正后的重心坐标插值公式:
f ( O ) = α f ( A ) + β f ( B ) + γ f ( C ) = α ′ w A w O f ( A ′ ) + β ′ w B w O f ( B ′ ) + γ ′ w C w O f ( C ′ ) = w O ( α ′ w A f ( A ′ ) + β ′ w B f ( B ′ ) + γ ′ w C ( C ′ ) ) \begin{align} f(O) &= \alpha f(A) + \beta f(B) + \gamma f(C)\\ &= \frac{\alpha'}{w_A}w_O f(A') + \frac{\beta'}{w_B}w_O f(B') + \frac{\gamma'}{w_C}w_Of(C')\\ &= w_O(\frac{\alpha'}{w_A} f(A') + \frac{\beta'}{w_B} f(B') + \frac{\gamma'}{w_C}(C')) \end{align} f(O)=αf(A)+βf(B)+γf(C)=wAα′wOf(A′)+wBβ′wOf(B′)+wCγ′wOf(C′)=wO(wAα′f(A′)+wBβ′f(B′)+wCγ′(C′))
深度Depth插值探讨
什么是Depth
对于某个顶点的Z值,经过视图变换、投影变换、透视触发,然后变换成NDC坐标,再经过屏幕空间变换,变成 [ 0 , 1 ] [0,1] [0,1] 范围内的值,就是Depth!
问题描述
Depth作为一个属性,能够直接用屏幕空间的重心坐标进行插值计算而来呢?
推导
我们先来考察以下,经过透视投影矩阵变换前后,z坐标和w坐标的情况:
p c = [ 1 a s p e c t ∗ tan ( f o v y ∗ 0.5 ) 0 0 0 0 1 tan ( f o v y ∗ 0.5 ) 0 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] ( x e y e z e 1 ) p_c = \begin{bmatrix} \frac{1}{aspect*\tan(fovy*0.5)}&0&0&0\\ 0&\frac{1}{\tan(fovy*0.5)}&0&0\\ 0&0&-\frac{f+n}{f-n}&\frac{-2fn}{f-n}\\ 0&0&-1&0\\ \end{bmatrix} \begin{pmatrix} x_e\\y_e\\z_e\\1 \end{pmatrix} pc= aspect∗tan(fovy∗0.5)10000tan(fovy∗0.5)10000−f−nf+n−100f−n−2fn0 xeyeze1
z和w变化如下:
z c = − f + n f − n z e + − 2 f n f − n w c = − z e z_c = -\frac{f+n}{f-n}z_e + \frac{-2fn}{f-n}\\ w_c = -z_e zc=−f−nf+nze+f−n−2fnwc=−ze
然后观察以下 z c z_c zc经过透视除法,得到ndc坐标如下:
z n d c = f + n f − n + 2 f n f − n 1 z e z_{ndc} = \frac{f+n}{f-n} + \frac{2fn}{f-n}\frac{1}{z_e} zndc=f−nf+n+f−n2fnze1
为了简化,设 z n d c = A + B 1 z e z_{ndc} = A + B\frac{1}{z_e} zndc=A+Bze1
这里的证明我们用反证法,我们需要证明的结论是可以直接用屏幕空间下的重心坐标进行插值Z。
所以,我们假设不能用屏幕空间下的重心坐标进行插值Z,因此得到下列不等式:
z n d c O ≠ α ′ z n d c A + β ′ z n d c B + γ ′ z n d c C z_{ndcO} \neq \alpha' z_ndcA + \beta' z_ndcB + \gamma' z_ndcC zndcO=α′zndcA+β′zndcB+γ′zndcC
将 z n d c = A + B 1 z e z_{ndc} = A + B\frac{1}{z_e} zndc=A+Bze1公式带入,得到了关于视图坐标系下z的不等式:
A + B 1 z e O ≠ α ′ ( A + B 1 z e A ) + β ′ ( A + B 1 z e B ) + γ ′ ( A + B 1 z e C ) A + B\frac{1}{z_eO} \neq \alpha'(A + B\frac{1}{z_eA}) + \beta'(A + B\frac{1}{z_eB}) + \gamma'(A + B\frac{1}{z_eC}) A+BzeO1=α′(A+BzeA1)+β′(A+BzeB1)+γ′(A+BzeC1)
然后两边进行拆分括号,得到:
A + B 1 z e O ≠ A ( α ′ + β ′ + γ ′ ) + B α ′ z e A + B β ′ z e B + B γ ′ z e C A + B\frac{1}{z_eO} \neq A(\alpha'+\beta'+\gamma') + B\frac{\alpha'}{z_eA} + B\frac{\beta'}{z_eB} + B\frac{\gamma'}{z_eC} A+BzeO1=A(α′+β′+γ′)+BzeAα′+BzeBβ′+BzeCγ′
这时候因为 α ′ + β ′ + γ ′ = 1 \alpha'+\beta'+\gamma' = 1 α′+β′+γ′=1,所以可以得到:
B 1 z e O ≠ B α ′ z e A + B β ′ z e B + B γ ′ z e C B\frac{1}{z_eO} \neq B\frac{\alpha'}{z_eA} + B\frac{\beta'}{z_eB} + B\frac{\gamma'}{z_eC} BzeO1=BzeAα′+BzeBβ′+BzeCγ′
因为B不可能为0,所以两边同时除B:
1 z e O ≠ α ′ z e A + β ′ z e B + γ ′ z e C \frac{1}{z_eO} \neq \frac{\alpha'}{z_eA} + \frac{\beta'}{z_eB} + \frac{\gamma'}{z_eC} zeO1=zeAα′+zeBβ′+zeCγ′
这时候我们想想透视投影矩阵应用前后,第4维分量w的变量情况,可以得知: z e = − w c z_e = -w_c ze=−wc,带入得到
1 w O ≠ α ′ w A + β ′ w B + γ ′ w C \frac{1}{w_O} \neq \frac{\alpha'}{w_A} + \frac{\beta'}{w_B} + \frac{\gamma'}{w_C} wO1=wAα′+wBβ′+wCγ′
我们发现,这个结论是我们已经证明相等的,所以假设不成立,所以结论成立!
总结
可以利用屏幕空间的重心插值坐标,直接对Depth属性进行插值。
结尾:喜欢的小伙伴可以点点关注+赞哦
希望对各位小伙伴能够有所帮助哦,永远在学习的道路上伴你而行, 我是航火火,火一般的男人!