目录
[一. 查找算法:](#一. 查找算法:)
[二. 其他算法:](#二. 其他算法:)
一. 查找算法:
1.顺序查找:
序查找,也叫线性查找,是一种最简单的查找算法。
基本原理 :
从数组的第一个元素开始,逐个与要查找的关键字进行比较,直到找到匹配的元素或者遍历完整个数组。
优点:
- 算法简单,易于理解和实现。
缺点:
- 效率相对较低,特别是在数据量较大时。
具体步骤:
- 依次遍历数组中的每个元素。
- 将每个元素与要查找的目标值进行比较。
- 如果找到匹配的元素,返回该元素的位置或其他相关信息;如果遍历完整个数组都没有找到,则表示查找失败。
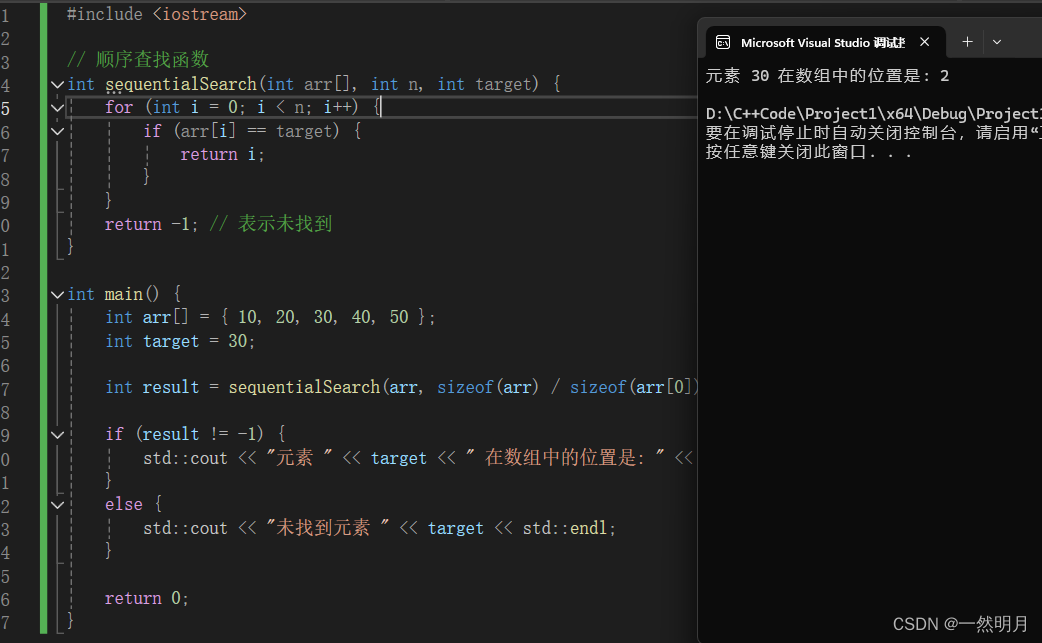
以下是一个用 C++ 实现顺序查找的代码示例:
cpp
#include <iostream>
// 顺序查找函数
int sequentialSearch(int arr[], int n, int target) {
for (int i = 0; i < n; i++) {
if (arr[i] == target) {
return i;
}
}
return -1; // 表示未找到
}
int main() {
int arr[] = { 10, 20, 30, 40, 50 };
int target = 30;
int result = sequentialSearch(arr, sizeof(arr) / sizeof(arr[0]), target);
if (result != -1) {
std::cout << "元素 " << target << " 在数组中的位置是: " << result << std::endl;
}
else {
std::cout << "未找到元素 " << target << std::endl;
}
return 0;
}
2.二分查找:
二分查找是一种在有序数组中查找某一特定元素的搜索算法。
原理 :
不断将数组中间的元素与目标元素进行比较,如果相等则找到;如果目标元素小于中间元素,则在数组的前半部分继续查找;如果目标元素大于中间元素,则在数组的后半部分继续查找,如此反复,直到找到或者确定不存在。
优点 :
查找效率高,时间复杂度为 。
缺点 :
要求数组必须是有序的,并且不适用于频繁插入和删除操作的场景。
具体步骤:
- 定义左边界
left为 0,右边界right为数组长度减 1。 - 进入循环,当
left <= right时:- 计算中间索引
mid = (left + right) / 2。 - 如果中间元素等于目标元素,返回中间索引。
- 如果目标元素小于中间元素,将右边界更新为
mid - 1。 - 如果目标元素大于中间元素,将左边界更新为
mid + 1。
- 计算中间索引
- 循环结束后仍未找到则返回特定表示未找到的值。
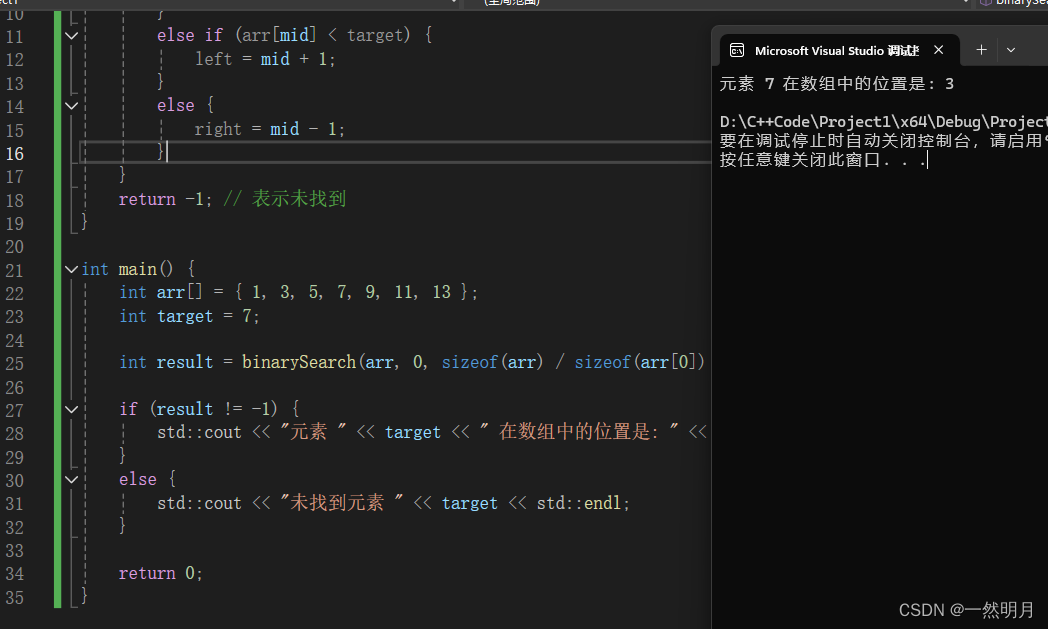
以下是一个用 C++ 实现二分查找的代码示例:
cpp
#include <iostream>
// 二分查找函数
int binarySearch(int arr[], int left, int right, int target) {
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
}
else if (arr[mid] < target) {
left = mid + 1;
}
else {
right = mid - 1;
}
}
return -1; // 表示未找到
}
int main() {
int arr[] = { 1, 3, 5, 7, 9, 11, 13 };
int target = 7;
int result = binarySearch(arr, 0, sizeof(arr) / sizeof(arr[0]) - 1, target);
if (result != -1) {
std::cout << "元素 " << target << " 在数组中的位置是: " << result << std::endl;
}
else {
std::cout << "未找到元素 " << target << std::endl;
}
return 0;
}
二. 其他算法:
1.遍历算法:
遍历算法是用于逐个访问数据结构(如数组、链表、树等)中每个元素的方法。
以下是一些常见的遍历算法:
数组的遍历:
- 顺序遍历:从数组的第一个元素开始,依次访问每个元素直到最后一个。
链表的遍历:
- 通常从链表的头节点开始,通过节点间的指针依次访问下一个节点。
二叉树的遍历:
- 前序遍历:先访问根节点,再递归地对左子树进行前序遍历,最后对右子树进行前序遍历。
- 中序遍历:先递归地对左子树进行中序遍历,再访问根节点,最后对右子树进行中序遍历。
- 后序遍历:先递归地对左子树和右子树进行后序遍历,最后访问根节点。
图的遍历:
- 深度优先遍历:沿着一条路径尽可能深地探索,直到无法继续前进,然后回溯并尝试其他路径。
- 广度优先遍历:先访问距离起始点最近的节点,再依次访问距离稍远的节点。
遍历算法的意义在于能够全面、系统地处理数据结构中的所有元素,以便进行各种操作,如查找、统计、修改等。
例如,在数组中查找特定元素、计算链表中节点的总和、在二叉树中进行特定节点的操作等都依赖于遍历算法。
不同的数据结构和应用场景可能需要选择不同的遍历方式,以达到最佳的效率和效果。
2.求和、求平均值等聚合算法。
a.求和算法:
就是将一组数据中的所有元素依次相加得到总和。
- 简单地遍历数据集合,将每个元素累加到一个累加变量中。
- 适用于各种数据结构,如数组、链表等。
b.求平均值算法:
通常是先利用求和算法得到总和,然后除以元素的数量。
- 先求出总和,再除以元素个数得到平均值。
具体步骤(以数组为例):
- 定义一个变量用于存储总和,初始化为 0。
- 遍历数组的每个元素。
- 将元素累加到总和变量中。
- 计算平均值时,将总和除以数组的长度。
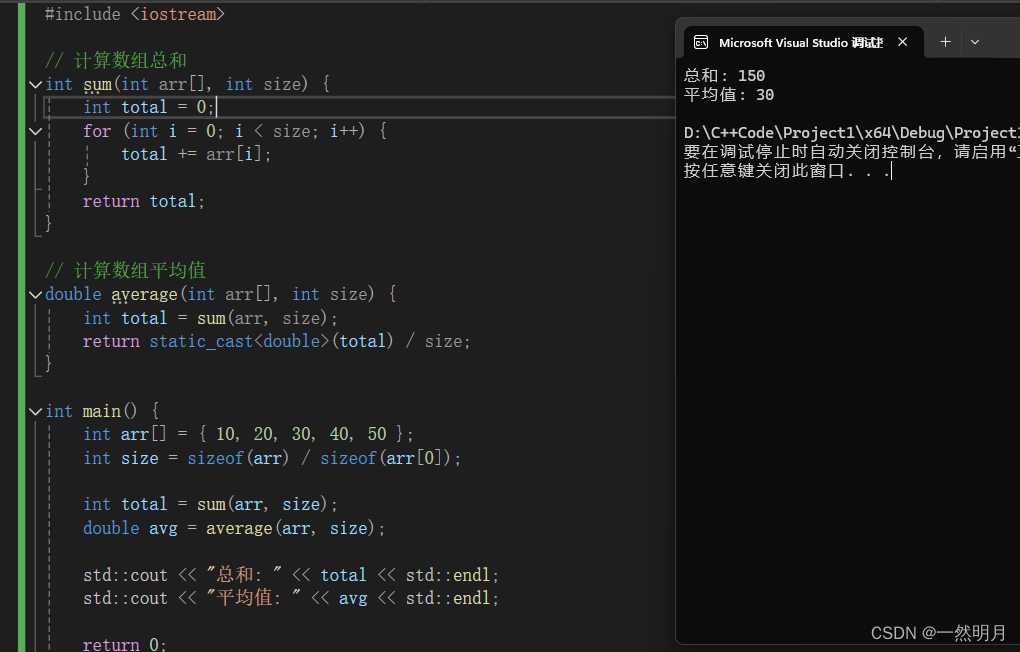
以下是用 C++ 实现求数组元素总和和平均值的代码示例:
cpp
#include <iostream>
// 计算数组总和
int sum(int arr[], int size) {
int total = 0;
for (int i = 0; i < size; i++) {
total += arr[i];
}
return total;
}
// 计算数组平均值
double average(int arr[], int size) {
int total = sum(arr, size);
return static_cast<double>(total) / size;
}
int main() {
int arr[] = { 10, 20, 30, 40, 50 };
int size = sizeof(arr) / sizeof(arr[0]);
int total = sum(arr, size);
double avg = average(arr, size);
std::cout << "总和: " << total << std::endl;
std::cout << "平均值: " << avg << std::endl;
return 0;
}