文章目录
- [一. n维向量概念](#一. n维向量概念)
-
- [1. 向量](#1. 向量)
-
- [1.1. 定义](#1.1. 定义)
- [1.2. 向量的运算规律](#1.2. 向量的运算规律)
- [1.3. 向量的线性表示](#1.3. 向量的线性表示)
- [2. 向量组](#2. 向量组)
-
- [2.1. 向量组矩阵](#2.1. 向量组矩阵)
- [2.2. 向量组的线性组合](#2.2. 向量组的线性组合)
- [2.3. 向量组的线性相关](#2.3. 向量组的线性相关)
- [2.4. 向量组的线性表出](#2.4. 向量组的线性表出)
- [2.5. 极大线性无关组与秩](#2.5. 极大线性无关组与秩)
- [二. 定理](#二. 定理)
-
- [1. 向量的线性表出与非齐次](#1. 向量的线性表出与非齐次)
- [2. 向量组的相关性](#2. 向量组的相关性)
- [3. 整体与部分向量组的相关性](#3. 整体与部分向量组的相关性)
- [4. 向量组的秩与相关性](#4. 向量组的秩与相关性)
- [三. 向量组相关的几何意义](#三. 向量组相关的几何意义)
一. n维向量概念
1. 向量
1.1. 定义
实向量的概念:分量(坐标)、行向量、列向量

1.2. 向量的运算规律
规定行向量与列向量都按矩阵的运算规则来运算
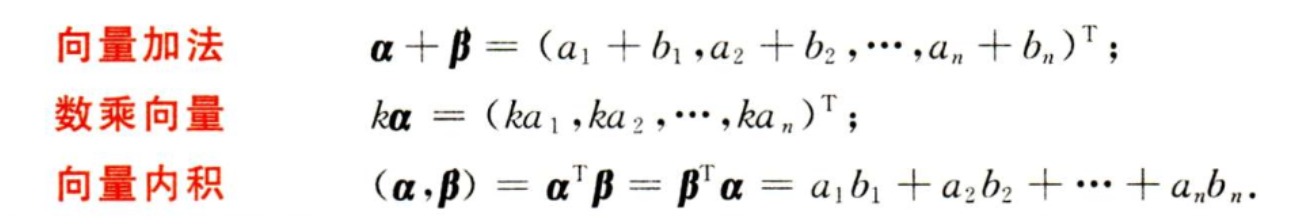
1.3. 向量的线性表示

2. 向量组
2.1. 向量组矩阵
一个含有有限个向量的向量组总可以构成一个矩阵。

2.2. 向量组的线性组合
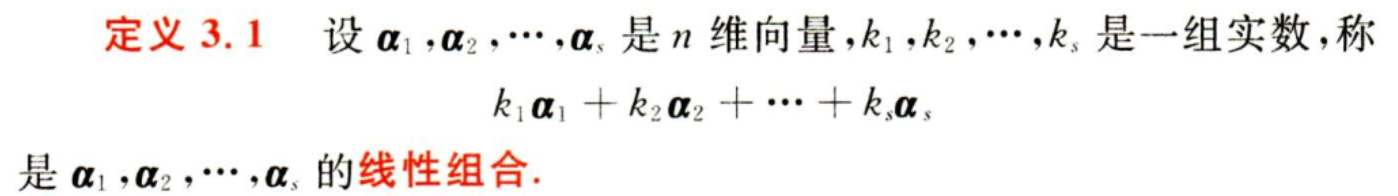
2.3. 向量组的线性相关

2.4. 向量组的线性表出
向量组的线性表出与向量组之间的等价

2.5. 极大线性无关组与秩

极大线性无关组的秩

二. 定理
1. 向量的线性表出与非齐次

2. 向量组的相关性
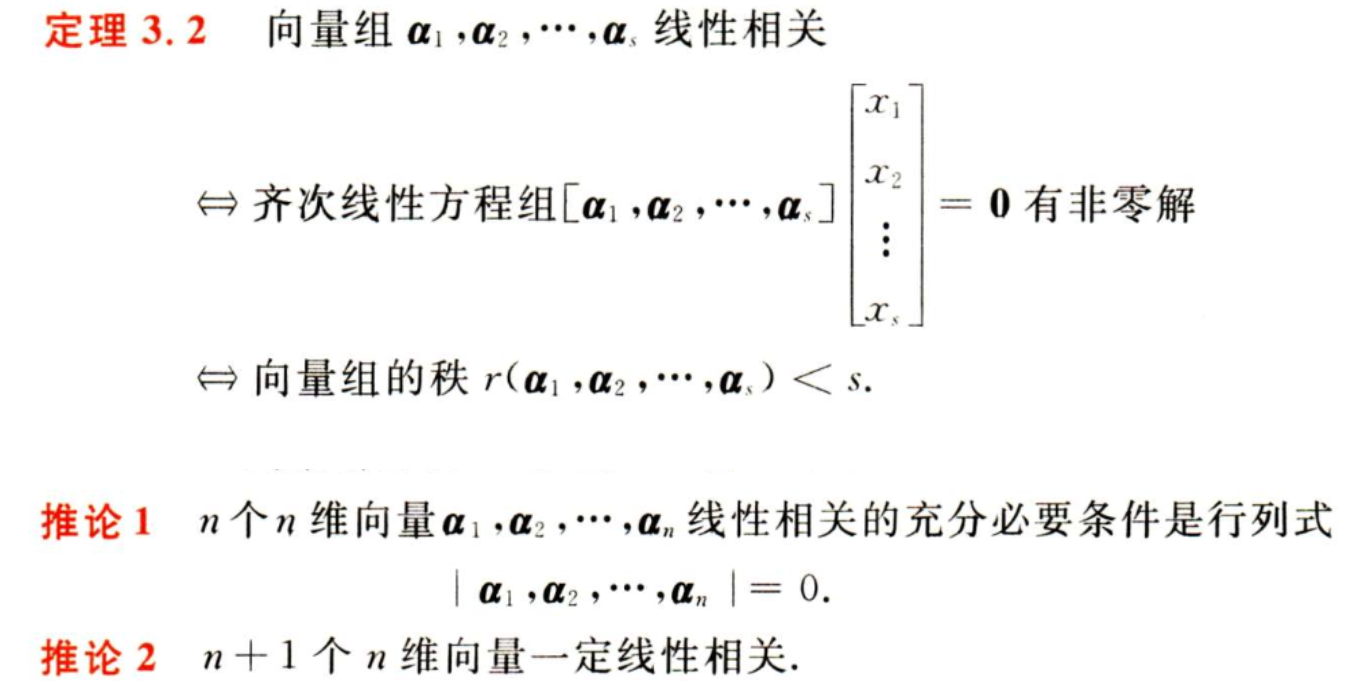
3. 整体与部分向量组的相关性


4. 向量组的秩与相关性
秩越大能够表示的就越多
定理7:
- 如果多数向量能由少数向量表示,则多数向量一定线性相关。
- 且多数向量的秩小于等于少数向量的秩

三. 向量组相关的几何意义

