GAMES101 lec2-数学基础1（线性代数）

一些依赖的内容

• 基本数学：
  • 线性代数，微积分，统计学
• 基本物理：
  • 光学，力学
• 其他
  • 信号处理
  • 数值分析

线性代数

一个旋转的例子

vector 向量

• AB⃗=B−A\vec{AB} = B - AAB =B−A
• 两个核心属性：方向+长度

模长 / 单位向量

• ∣∣a⃗∣∣||\vec{a}||∣∣a ∣∣
• 单位向量 a^=a⃗/∣∣a⃗∣∣\hat a = \vec a / ||\vec a||a^=a /∣∣a ∣∣

向量求和

• 平行四边形法则/三角形法则

坐标系下的向量代数表示

• 默认的向量是列向量

向量的点乘

• 定义： a⃗∗b⃗=∣∣a⃗∣∣ ∣∣b⃗∣∣cos⁡θ\vec a * \vec b = ||\vec a|| \, ||\vec b|| \cos \thetaa ∗b =∣∣a ∣∣∣∣b ∣∣cosθ
• 点乘与方向 ：点乘 与 cos⁡θ\cos \thetacosθ 之间互相计算的方法
• 计算方法 ：a⃗∗b⃗=xaxb+yayb\vec a * \vec b = x_a x_b + y_a y_ba ∗b =xaxb+yayb
• 用于计算一个向量投影到另一个向量： ∣∣b⃗⊥∣∣=∣∣b⃗∣∣∗cos⁡θ||\vec b_{\perp}|| = ||\vec b|| * \cos \theta∣∣b ⊥∣∣=∣∣b ∣∣∗cosθ
• 向量点乘告诉前与后的信息：（相同方向/相反方向）
  >0, <0, 是不是垂直，是不是接近

向量的叉乘

• ∣∣a⃗×b⃗∣∣=∣∣a⃗∣∣ ∣∣b⃗∣∣ sin⁡θ||\vec a \times \vec b|| = ||\vec a|| \, ||\vec b|| \, \sin \theta∣∣a ×b ∣∣=∣∣a ∣∣∣∣b ∣∣sinθ

• 右手螺旋法则（求出方向）

• 不满足交换律：（加上负号） a×b=−b×aa \times b = - b \times aa×b=−b×a

• 三维坐标系，叉乘的应用

• 叉乘性质

  • 自身 a⃗×a⃗=0⃗\vec a \times \vec a = \vec 0a ×a =0
  • 反交换律
  • 结合律 + 分配律

• 代数计算方法（表示成矩阵形式 重要）

  • 

• 应用：判定向量的左右/内外 -> 判断点是否在三角形内部

  • 

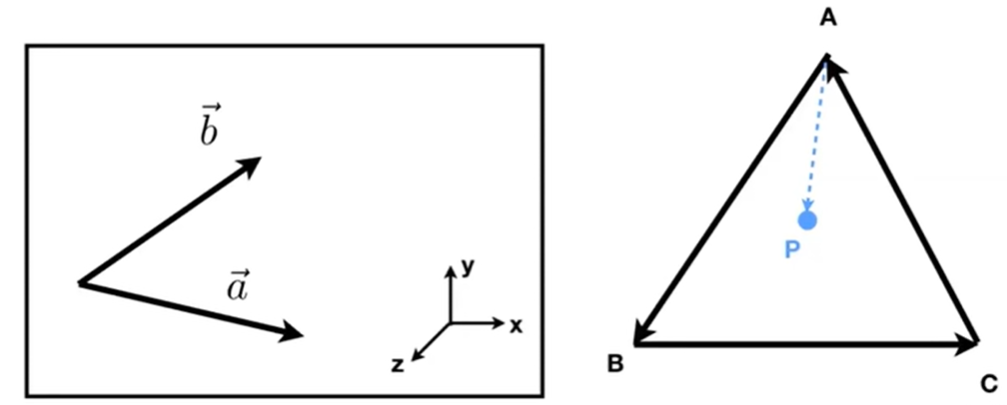
  • sign(AB⃗×AP⃗)==sign(BC⃗×BP⃗)==sign(CA⃗×CP⃗)sign(\vec{AB} \times \vec{AP}) == sign(\vec{BC} \times \vec{BP}) == sign(\vec{CA} \times \vec{CP})sign(AB ×AP )==sign(BC ×BP )==sign(CA ×CP )，如果这个等式成立，那么就表示点在三角形内部

  • AB - BC - CA，是一种轮换对称性，可以理解为 ABCABC 的循环选取

坐标系

• u v w 三维直角坐标系
  • 方便分解，方便计算

Matrix 矩阵

• 在图形学里，常常用矩阵来做基本变换

矩阵的乘积 (m∗n)∗(n∗p)(m*n) * (n*p)(m∗n)∗(n∗p)

• 矩阵乘积不存在交换律

• 结合律 (AB)C=A(BC)(AB)C=A(BC)(AB)C=A(BC)

• 矩阵(x∗m)(x*m)(x∗m) 左乘 向量(m∗1)(m*1)(m∗1)

• 乘积的转置(AB)T=BTAT(A B)^T = B^TA^T(AB)T=BTAT

• 单位矩阵

• 逆矩阵

• 点乘叉乘 - 矩阵乘法

  •